Формулы комбинаторики. Как запомнить и осилить. | by Котя Веллес
Периодически я возвращаюсь к теме математики, так как это очень полезная дисциплина, лежащая в основе человеческого мышления.
Мне понятно, что большинству читать это скучно и противно, но писать всё время про рынок невозможно. Поэтому, полезная тренировка для мозгов.
Вектор развития любой науки идёт от простого к сложному и на этом пути неизбежны потери.
Причём потери в самом главном, в понимании смысла базовых идей.
За деревьями исчезает лес и многим начинает представляться, что чем сложнее, заумнее и «научнее» изложен вопрос, тем это ближе к истине.
На самом деле всё обстоит ровно наоборот. Гениальность в простых понятиях, а все значимые достижения человеческой цивилизации рождаются из комбинации элементарных представлений.
И труднее всего осилить базовые принципы, которыми мучают детей, и которые, в большинстве случаев, сами не понимают.
В связи с этим, двинемся в обратном направлении, используя главную человеческую способность абстрактно мыслить, упрощать, обобщать и идеализировать, сводя сложные понятия к простым, а многомерные пространства к обычной плоскости.
r, в теории вероятностей, определяет число возможных исходов при количестве выборок из общего объёма, меньших самого объёма.
Например:
Выбираем трёх человек из пяти, постоянно возвращая выбранного обратно.
Число возможных вариантов = 5³.
Если бы мы выбирали пять раз из пяти, с возвращением, то была бы предыдущая формула =5⁵.
Как ни странно, но в российских учебниках, напрочь отсутствует рассмотрение двух вышеизложенных формул, как неотъемлемой части комбинаторики.
А без них, последовательная логика при описании предмета, исчезает.
Для россиян комбинаторика начинается с формулы:
n! — представляющей количество перестановок и, одновременно, максимальное число вариантов при выборе без возвращения.
И без первых двух формул, её смысл воспринимается плохо и неполно. Он усечён представлениями о перестановках.
Осмысление и доказательство этой формулы в русскоязычных вариантах требует непростых умственных усилий, в то время как англоязычный вариант Уильяма Феллера, легко выводится из n ^n, и встраивается в общую логику.
r
Р(n по r) — англоязычный вариант, от слова «permutation». Интересно, что в российских и англоязычных вариантах n и r меняются местами. В российском, r –первая или сверху, n –вторая или снизу. В англоязычном наоборот.
Теперь самое главное. А как это нарисовать?
Рис.6
Очевидно, что это площадь трапеции.
Раз предыдущий вариант, n!, был площадью треугольника, то теперь мы его усекаем.
И сразу же, становится понятна запись:
n!/( n- r)!
n! -треугольник.
( n — r)! -его усечение, когда отваливается площадь «n — r» , и остаётся трапеция. Нагляднее некуда.
И последняя, самая трудная для понимания формула, которая представляет собой биноминальные коэффициенты.
С(r по n), С(n по r), (n) r / r!, n!/ r!( n- r)!, (n(n- 1) (n- 2)(n- 3)……… (n- r+1)) / r!
С(r по n), С(n по r) — англоязычные и русскоязычные варианты сходятся на букве С, от слова «combination», но r и n, по-прежнему перевёрнуты местами.
Сама формула получается из предыдущей, делением её на r!.
С(r по n) = A(r по n) / r!
А что это такое и как нарисовать -r! ?
Раз существует треугольник — n!, означающий перестановки из числа n.
То может существовать и треугольник — r!, означающий перестановки из числа r.
И нарисовать его по аналогии, элементарно.
Рис.7.
Закрашено красным.
Т.о., геометрически — символически, наша формула, это площадь заштрихованной трапеции, поделенная на площадь красного треугольника.
Заодно, сразу же, становится понятной запись:
С(r по n) = С(n- r по n)
n!/ r!( n- r)! = n!/ ( n- r)! r!
Действительно,
Рис.8.
Отношения площадей трапеций к треугольникам, что сверху (заштриховано зелёным и жёлтым), что снизу (заштриховано синим и красным), равны.
5*4*3 / 3! = 5*4 / 2!
Как изобразить r! -стало понятно.
Осталось описать его суть.
Для этого рисуем табличку 9.
Рис.9.
Начинаем с самого общего варианта
Есть пять букв. Выбираем из них два раза с возвращением.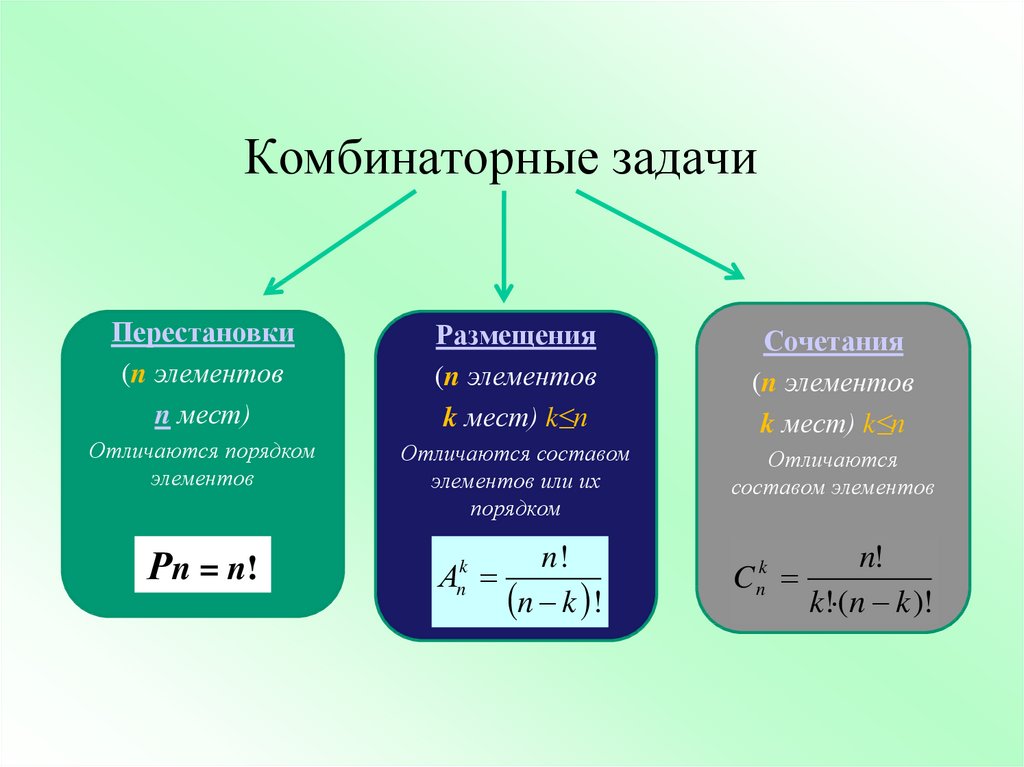
n — не равно площади прямоугольника, а в одном месте,(которое наблюдательный читатель заметит) я не понижаю уровень операции.
Но это никак не помешало нам получить наглядное представление о предмете.
И в этом соль математики!
Все открытия, (на которые я не претендую), происходили примерно таким образом.
Есть задача, не решаемая в привычных аксиомах и единицах.
Все проходят мимо, но находится какой-то чудак, который создаёт новое, искусственное, абстрактное пространство, в котором задача решается, и появляется новый раздел математики или понятие.
Самый простой пример — отрицательные числа.
Совсем недавно, человеческий мир не понимал что это такое. Число баранов не бывает минус один, и выражение: y = 4–5 не имело смысла.
Сегодня, особенно на бирже, отрицательным счётом никого не удивишь.
Основные правила и формулы комбинаторики
Вы можете изучить и скачать доклад-презентацию на
тему Основные правила и формулы комбинаторики.
Презентация на заданную тему содержит 15 слайдов. Для просмотра воспользуйтесь
проигрывателем,
если материал оказался полезным для Вас — поделитесь им с друзьями с
помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Образование» Основные правила и формулы комбинаторики
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Основные правила и формулы комбинаторики Шармин Валентин – кандидат физико-математических наук, доцент, почетный работник высшего профессионального образования РФ
Описание слайда:
Определение комбинаторики
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций (соединений), подчиненных тем или иным условиям, можно составить из принадлежащих данному конечному множеству элементов.
При решении задач комбинаторики используют правила суммы и произведения.
Слайд 3
Описание слайда:
Правило суммы и произведения Правило суммы. Если некоторый объект A можно выбрать способами n, а объект B можно выбрать способами m (не такими, как A), то объект «либо A , либо B» можно выбрать n+m способами. Правило произведения. Если некоторый объект A можно выбрать n способами, а после каждого такого выбора объект B можно выбрать способами m (независимо от выбора объекта A), то пару объектов «A и B» в указанном порядке можно выбрать n*m способами.
Слайд 4
Описание слайда:
Пример
В магазине бытовой техники имеется 8 видов электрических чайников и 10 видов микроволновых печей. Сколькими способами можно: а) совершить покупку, состоящую из одного электроприбора;
б) купить чайник и микроволновую печь?
а) Электрический чайник можно выбрать 8 способами, а микроволновую печь – 10 способами.
Число способов купить один электроприбор (то есть выбрать либо чайник, либо микроволновую печь), по правилу суммы, равно 8+10=18.
б) Купить чайник и микроволновую печь (то есть выбрать пару объектов) можно, по правилу произведения, способами 8*10=80.
Описание слайда:
Перестановки Перестановками из различных элементов называются упорядоченные наборы, содержащие данные элементов. Таким образом, одна перестановка отличается от другой только порядком расположения элементов. Число перестановок из элементов обозначается символом и находится по формуле: где
Слайд 6
Описание слайда:
Пример
Сколькими способами можно расставить 7 различных книг на полке?
Каждый способ расстановки книг отличается от другого способа лишь порядком расположения книг.
Следовательно, число способов равно .
Слайд 7
Описание слайда:
Размещения без повторений Размещениями из различных элементов по элементов называются упорядоченные наборы, содержащие элементов из данных . Одно размещение отличается от другого либо составом элементов, либо порядком их расположения. Число размещений из элементов по обозначается символом и находится по формуле:
Слайд 8
Описание слайда:
Пример Сколькими способами могут быть распределены золотая, серебряная и бронзовая медали между 16 командами, участвующими в соревнованиях? Очевидно, что все возможные тройки призеров отличаются одна от другой либо составом команд, либо порядком их расположения на первом, втором и третьем местах. Значит, число способов равно
Слайд 9
Сочетания
Сочетаниями из различных элементов по элементов называются неупорядоченные наборы, содержащие элементов из данных.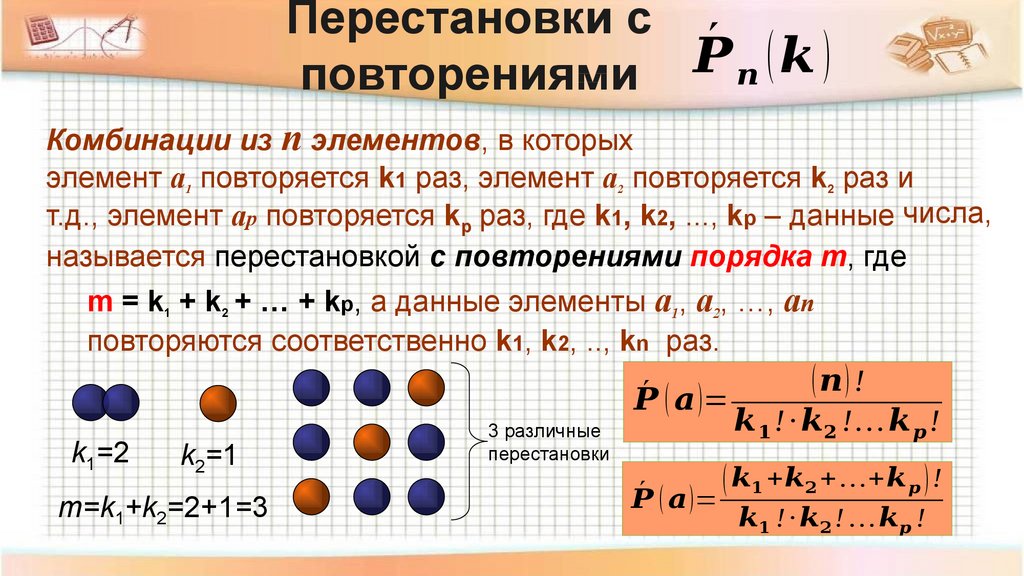
Сочетания отличаются друг от друга только составом элементов.
Число сочетаний из элементов по обозначается символом и находится по формуле:
Слайд 10
Описание слайда:
Задачи Имеется 3 вида конвертов без марок и 9 видов марок одинаковой стоимости. Сколькими способами можно выбрать конверт с маркой для посылки письма? На вершину горы ведут 5 тропинок. Сколькими способами турист может подняться в гору и потом спуститься с нее, если подъем и спуск: а) могут проходить по любым тропинкам; б) должны проходить по разным тропинкам? Сколькими способами из 25 членов научного общества учащихся можно выбрать его председателя, заместителя председателя, редактора газеты и секретаря? В отделе НИИ работают 22 человека. Сколькими способами можно выбрать 3 человек для участия в конференции?
Слайд 11
Описание слайда:
Задачи Сколькими способами можно разместить на скамейке 9 человек? Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что: а) ни одна цифра не повторяется; б) число оканчивается цифрой 3 и все цифры различны?
Слайд 12
Описание слайда:
Задачи
7.
Сколько различных «слов» можно образовать при перестановке букв слова МАТЕМАТИКА?
8. Из 10 различных книг выбирают 4 для посылки. Сколькими способами это можно сделать?
9. Сколько различных «слов» (не обязательно имеющих смысл) можно образовать, переставляя буквы слова: а) ЗАМОК; б) ЗАМОК, если буква К должна стоять на первом месте?
Слайд 13
Описание слайда:
Задачи 10. Студентам надо сдать 4 экзамена за 12 дней. Сколькими способами можно составить расписание экзаменов, если в один день не должно быть двух экзаменов? 11. Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды должны войти 3 нападающих, 2 защитника и 1 вратарь? 12. Имеется 11 наименований товаров. Сколькими способами их можно развезти по трем магазинам следующим образом: 5 наименования – в первый магазин, 4 – во второй, 2 – в третий? Сколькими способами на шахматной доске можно указать: а) две клетки; б) две клетки одного цвета; в) две клетки разного цвета?
Слайд 14
Описание слайда:
Задачи
Из трех инженеров и девяти экономистов должна быть выбрана комиссия в составе семи человек.
Сколькими способами может быть составлена комиссия, если в нее должен войти: а) ровно один инженер; б) хотя бы один инженер?
Сколько четных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не должны повторяться?
Сколькими способами можно поставить в ряд 6 автомобилей так, чтобы два определенных автомобиля оказались рядом?
Сколько автомобильных номеров формата Б ЦЦЦ ББ можно составить, если можно использовать все цифры и те буквы русского алфавита, которые имеют написание, подобное латинским буквам?
Слайд 15
Описание слайда:
ОТВЕТЫ 1. 27. 2. а) 25; б) 20. 3. 303600. 4. 1540. 5. 362880. 6. а) 60; б) 125; в) 12; г) 25. 7. 560. 8. 3003. 9. 151200. 10. 210. 11. 512. 12. а) 120; б) 420; в) 24. 13. 11880. 14. 2520. 15. 6930. 16. а) 2016; б) 992; в) 1024. 17. а) 252; б) 756. 18. 48. 19. 240. 20. 1726272.
Tags Основные правила и формулы комбинаторики
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
19w5220: Асимптотическая алгебраическая комбинаторика | Banff International Research Station
Организаторы
org/Person»> Игорь Пак (Калифорнийский университет в Лос-Анджелесе)Алехандро Моралес (Массачусетский университет в Амхерсте)
Грета Панова (Университет Южной Калифорнии)
Дэн Ромик (Калифорнийский университет
2 9005) Описание
Международная исследовательская станция в Банфе проведет семинар «Асимптотическая алгебраическая комбинаторика» в Банфе с 10 марта 2019 г.до 15 марта 2019 г.
Алгебраическая комбинаторика — это область математики, в которой используются методы абстрактной алгебры, особенно теории групп и теории представлений, в различных комбинаторных контекстах и, наоборот, применяются комбинаторные методы к задачам алгебры и теории представлений. Многие из его проблем возникают из-за необходимости количественного и явного понимания алгебраических явлений.
Его количественные аспекты были сосредоточены на явных перечислительных формулах и комбинаторных интерпретациях размерностей, кратностей, структурных констант. Двумя важными моментами в этой области являются формула произведения длины крючка для подсчета стандартных картин и правило Литтлвуда-Ричардсона. Однако чаще всего такие формулы и правила являются скорее чудом, чем свойством. Неизвестна явная формула произведения для подсчета косых таблиц, редуцированных слов, мономов, полиномов Шуберта и даже дискретных интерпретаций коэффициентов Кронекера, инвариантов Громова-Виттена, полиномов Шуберта. Тем не менее, дискретные объекты алгебраического происхождения, такие как функции Шура, стандартные таблицы и плоские разбиения, также связаны с интегрируемыми моделями конфигураций частиц или димеров в рамках статистической механики. Эти объекты также занимают центральное место в асимптотической теории представлений. В этих областях и, в более общем плане, в теории вероятностей проблемы связаны с пониманием предела большого масштаба или асимптотического поведения, а не с наличием явных точных формул и описаний.
Следовательно, нам необходимо найти асимптотические формулы для основных объектов алгебраической комбинаторики и изучить появляющуюся область асимптотической алгебраической комбинаторики. Основная цель этого семинара состоит в том, чтобы собрать вместе людей из всех соответствующих областей, которые, естественно, очень не пересекаются — алгебраической комбинаторики, аналитической комбинаторики, теории вероятностей, теории представлений, чтобы поделиться результатами и методами и установить асимптотическое исследование объектов и величин в Алгебраическая комбинаторика.
Международная исследовательская станция математических инноваций и открытий в Банфе (BIRS) — это совместное предприятие Канады, США и Мексики, которое обеспечивает среду для творческого взаимодействия, а также обмена идеями, знаниями и методами в области математических наук с соответствующими дисциплины и с промышленностью. Исследовательская станция расположена в Банф-центре в Альберте и поддерживается Канадским советом по естественным наукам и инженерным исследованиям (NSERC), Национальным научным фондом США (NSF), Университетом передового образования и технологий Альберты и Национальным советом науки и технологий Мексики.
КОНАСИТ).
Комбинаторика: определение, шаг за шагом Статьи
Комбинаторика — это раздел математики, изучающий отношения, характеризующие множества, подмножества, списки и мультимножества.
Иногда комбинаторику называют разделом математики, занимающимся счетом; и это верно, но не в том смысле, в каком вас учили считать в детском саду. Хотя комбинаторика имеет дело с нумерацией и определением количества элементов в наборах, она предназначена для поиска способов сделать это без фактического, потенциально утомительного подсчета.
Статьи
Нажмите на название статьи:
- Как решать задачи на комбинации и перестановки
- 5 Выберите 3: определение комбинаций
- Теория графов
- Включение – принцип исключения
- Теорема о мультиномах
- Мультинабор, множественность и множественный выбор
- Дерево вероятностей: примеры, как рисовать простыми шагами
- Вероятностная модель
- Числа Стирлинга второго рода
Перечисления, комбинации, перестановки
Вероятно, вы познакомились с комбинаторикой, когда узнали о комбинациях, перестановках и, возможно, перечислении.
Перечисление — это способ подсчета, который включает организацию подсчитываемых предметов в полный и систематизированный список.
Комбинации включают, вообще говоря, выбор подмножества из большего множества. Примером комбинации может быть выбор трех учеников из класса из 26 человек или сбор трех ягод черники с куста с 600 ягодами. В комбинациях порядок не имеет значения.
Перестановки мало чем отличаются от комбинаций, но здесь набор, который вы выбираете, представляет собой упорядоченный набор или список без повторений. (В комбинаторике мы определяем список как упорядоченную последовательность объектов). Например, если вы выбираете не трех студентов, а президента студенческого совета, вице-президента и секретаря, вы выбираете упорядоченный список и работаете с перестановками.
Комбинаторика также имеет дело со списками , разрешающие повторение; слова , составленные из букв английского языка, являются хорошим примером этого.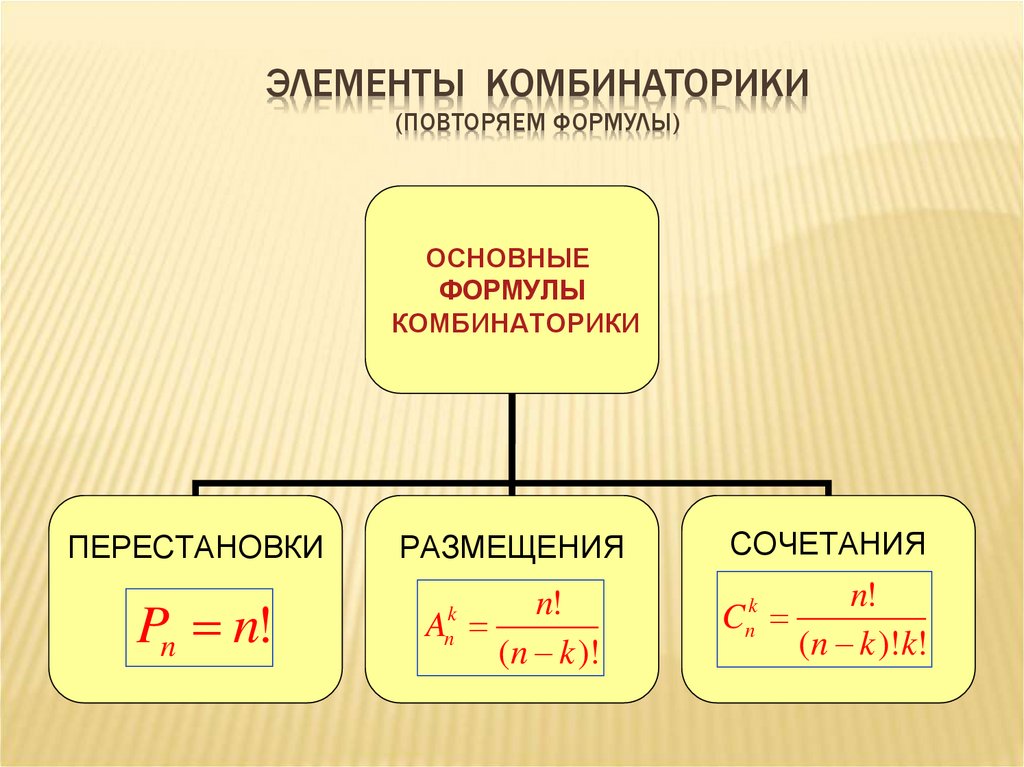
Также есть мультимножества , которые являются неупорядоченными множествами , в которых разрешено повторение.
Примеры комбинаторных задач
Необходимо выбрать комитет из пяти студентов из 30 студентов. Сколько существует возможных вариантов?
Эта классическая комбинаторная задача является примером комбинаций, в которых используется формула комбинаций:
Подставим 30 студентов всего (n), выберем пять (r) в формулу, получим:
30! / (5! (30 – 5)!) = 30! / (5! * 25!) = 142506.
Если бы каждая позиция в комитете была различима, мы бы смотрели на количество перестановок, а не на количество комбинаций. Это выражается как n!/(n-k)!, или 30!/25!, что равняется 17100720.
Комбинаторика и статистика
Комбинаторика и статистика являются связанными областями, и в статистических исследованиях используется множество комбинаторных методов. В частности, такие области, как непараметрическая статистика, статистическая теория распределения, проблемы времени ожидания/теория очередей и изучение моделей урн, в значительной степени основаны на комбинаторных задачах.
Поскольку комбинаторика дает нам ответы на вопрос о количестве возможных результатов, которые мы получаем при выборе подмножеств из больших наборов, комбинаторика также важна при разработке исследовательских проектов или исследований в области социальных наук. Он формирует основу для многих вероятностных задач.
Важные обозначения в комбинаторике
n k подсчитывает количество списков с k элементами, взятыми из n-элементного подмножества. Элементы могут повторяться, и порядок имеет значение. это n k совпадает с n k , с которым вы привыкли работать в алгебре: списки с k элементами и без повторений, взятые из набора из n элементов (подумайте о перестановках).
подсчитывает количество k-элементных подмножеств множества, состоящего из n элементов. Повторения не допускаются, и порядок не имеет значения (подумайте о комбинациях).
подсчитывает количество k-элементных мультимножеств, которые можно взять из n-элементного набора.