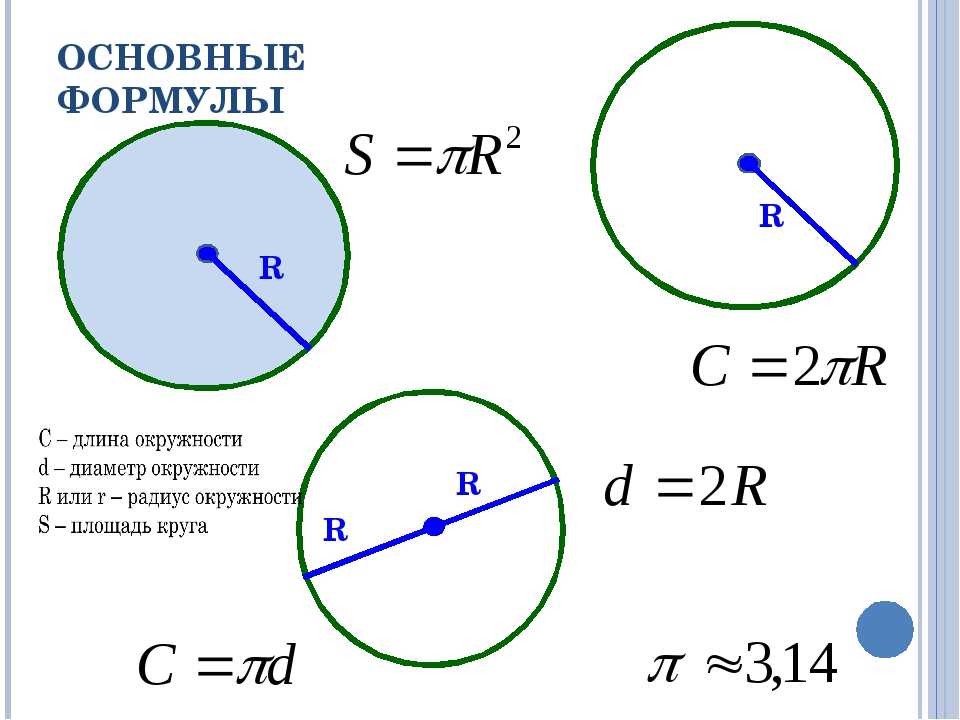
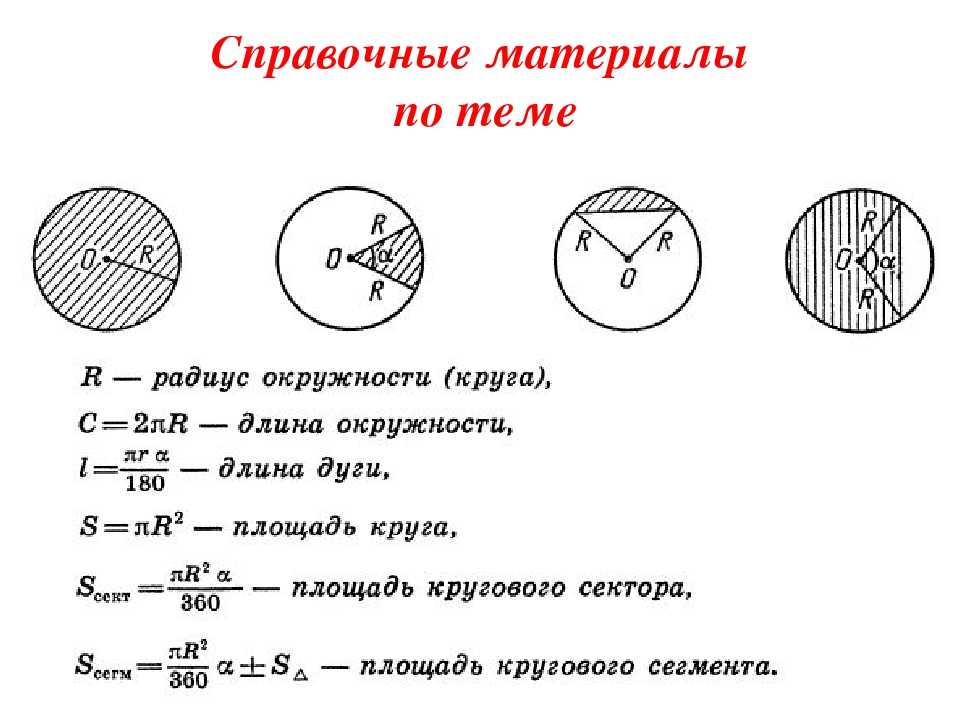
Формулы для длины окружности и площади круга и пример их использования
Окружность и круг — две совершенные плоские фигуры, свойства которых изучают в обязательном порядке в любом школьном курсе геометрии. В этой статье мы рассмотрим, как находить длину окружности и площадь круга, используя простые математические формулы.
В чем разница между окружностью и кругом?
Прежде чем переходить к рассмотрению формул длины окружности и площади круга, следует привести определения этих фигур.
В геометрии под окружностью понимают совокупность точек на плоскости, которые находятся от фиксированной точки на одинаковом расстоянии R. В свою очередь, круг — это набор точек плоскости, которые от заданной точки расположены на расстояниях, равных или меньших, чем некоторое число R. Иными словами, окружность представляет собой одну единственную кривую линию, а круг занимает некоторую площадь. Окружность — это «обод» круга.
Именно поэтому, вопрос, как находить площадь окружности, считается некорректно поставленным.
Окружность (единственная линия) не имеет площади, однако имеет длину. Для круга же разговор о площади имеет смысл, кроме того, также можно говорить и о длине окружности, которая его ограничивает.
Основные свойства рассматриваемых фигур
Окружность и круг обладают рядом общих характеристик, которые кратко перечислим ниже:
- Они имеют радиус R (длина отрезка, соединяющего центр фигуры с ее краем).
- Если провести через них такой отрезок, который пройдет через центр и соединит два края фигуры, то он будет равен 2 * R и называется диаметром (D).
- Любая ось, проходящая через диаметр, делит фигуру на две равные части.
- Поворот на произвольный угол круга или окружности вокруг оси, проходящей через его/ее центр и перпендикулярной плоскости фигуры, является операцией симметрии.
Формулы для длины окружности и площади круга
Познакомившись с понятием и основными свойствами рассматриваемых плоских фигур, можно перейти к количественному определению их размеров.
Длина окружности и площадь круга вычисляются по следующим двум формулам:
1. L = 2 * π * R.
2. S = π * R²
Из этих формул следует, что величина R — радиус — полностью характеризует свойства обеих фигур. Величина L измеряется в метрах (~R), а S — в метрах квадратных (~R²).
В формулах символ π представляет некоторую константу, которая является иррациональным числом (ее нельзя вычислить точно). С точностью до 4 знаков после запятой число π равно 3,1416. Отметим, что при выполнении расчетов эта константа может быть заменена дробью 201/64. Если вычислить значение этой дроби, то получится число 3,1406, которое всего на 0,03 % отличается от истинной константы.
Заметим, что формула для длины окружности справедлива также для определения аналогичной характеристики круга.
Указанные формулы могут быть переписаны через диаметр, учитывая, что D = 2 * R, получаем:
1) L = π * D;
2) S = π * D²/4.
Использование рассмотренных формул для решения задачи
Формулы для площади круга и длины окружности используем для решения задач. Например, у Маши имеется кусок ткани прямоугольной формы, размеры которой равны 5 x 4 метра. Необходимо определить, какого максимального размера круг она сможет вырезать из этой ткани.
Смысл этой задачи состоит в определении размера круга, вписанного в четырехугольник. Эта ситуация изображена на рисунке ниже.
Из рисунка можно заметить, что диаметр вписанного круга D будет равен длине наименьшей стороны четырехугольника, в данном случае D = 4 метра. Зная диаметр, можно непосредственно применить формулы, которые записаны для длины и площади этой фигуры в предыдущем пункте статьи. Имеем:
1. L = π * D = 3,1416 * 4 = 12,5664 м.
2. S = π * D²/4 = 3,1416 * 4²/4 = 12,5664 м².
Мы получили любопытный результат: площадь круга равна точно такой же величине, что и длина его окружности, но единицы измерения являются разными для них.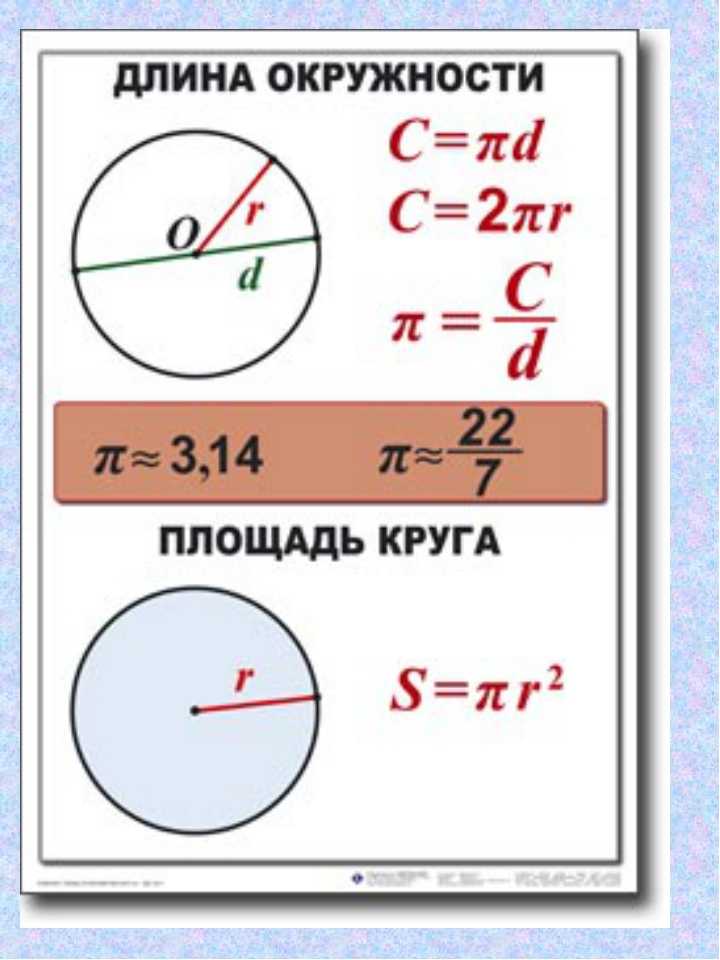
Этот результат является простым совпадением, поскольку D=4 — это единственное число, для которого абсолютные значения L и S равны.
Длина окружности и площадь круга презентация, доклад
ТЕМА
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
Для изучения темы: «Длина окружности и площадь круга» нам потребуется ответить на ряд вопросов
3. Что такое диаметр и радиус окружности?
4. Как связаны между собой диаметр и радиус окружности?
5. Что такое прямая и обратная пропорциональные зависимости?
1. Что называется окружностью?
2. Что называется кругом?
ДЛИНА ОКРУЖНОСТИ
Возьмём круглый стакан, поставим на лист бумаги и обведём его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приближённо равна длине нарисованной окружности (рис.
39).
ДЛИНА ОКРУЖНОСТИ
Длина окружности прямо пропорциональна длине её диаметра!
То есть, отношение длины окружности к длине её диаметра является одним и тем же числом для всех окружностей. Это число обозначают греческой буквой π (читается: «пи»).
Обозначим длину окружности буквой C, а длину диаметра буквой d, получим отношение:
C : d = π
Выразим отсюда C и получим:
С = π · d
Так как диаметр окружности вдвое больше её радиуса
(d = 2r), то длина окружности с радиусом r равна:
C = 2πr
ПРИМЕР
Чему равна длина окружности, если её радиус равен 2,45 м? Значение числа π возьмите равным .
22
7
Нам известны две формулы нахождения длины окружности, но так как нам известен радиус окружности r = 2,45 м, то воспользуемся второй формулой:
C = 2πr
Подставим известные нам значения в формулу и найдём длину окружности:
C = 2 · · 2,45
7
22
ПЛОЩАДЬ КРУГА
A
B
C
D
E
F
K
M
O
r
На рисунке изображены круг и два квадрата ABCD и EFKM.
Радиус круга равен r, поэтому длина стороны квадрата ABCD равна 2r, а его площадь 4r2.
Площадь треугольника EOF вдвое меньше площади квадрата AEOF, поэтому площадь EFKM вдвое меньше площади квадрата ABCD и равна 2r2. Площадь круга S большое площади квадрата EFKM, но меньше площади квадрата ABCD:
2r2
Примерно площадь круга равна 3r2. Можно доказать, что S = π · r2.
ПРИМЕР
Чему равна площадь круга, если её радиус равен 0,7 м? Значение числа π возьмите равным .
22
7
Воспользуемся формулой нахождения площади круга, учитывая что радиус круга: r = 0,7 м.
S = πr2
Подставим известные нам значения в формулу и найдём площадь круга:
S = · (0,7)2 = · 0,49 = 1,54 м2
Ответ: площадь круга равна 1,54 м2
22
7
22
7
ЧИТАЕМ ПРАВИЛЬНО
Формулы длины окружности и площади круга читаются так:
C = πd – «цэ» равно «пи дэ»;
C = 2πr – «цэ» равно двум «пи эр»;
S = πr2 – «эс» равно «пи эр» квадрат.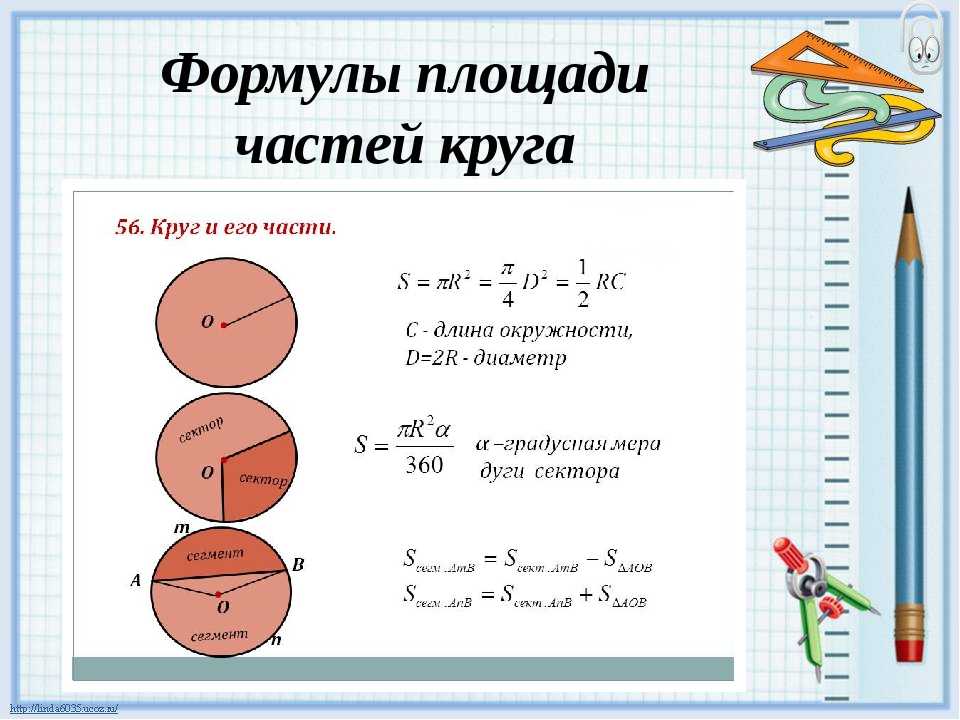
Выражение π ≈ 3,14 читают:
«Пи приближённо равно трём целым четырнадцати сотым».
Страница 141, № 864(1)
Решите задачу, составив пропорцию:
1) В 2,5 кг баранины содержится 0,4 кг белков.
Сколько килограммов белков содержится в 3,2 кг баранины?
Решение задачи под цифрой (1):
Составим таблицу из 2 столбцов: вес баранины и содержания белка:
С увеличением веса баранины, содержание белка увеличивается, значит стрелки направлены вверх, значит мы имеем прямую пропорциональную зависимость.
Составим пропорцию:
3,2
2,5
0,4
x
=
Страница 141, № 864(1)
Продолжение решение задачи под цифрой (1):
Воспользуемся основным свойством пропорций (в верной пропорции произведение крайних членов равно произведению средних) и получим:
2,5 · x = 3,2 · 0,4
(выражаем x: чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель)
x = 3,2 · 0,4 : 2,5
x = 0,512
Ответ: в 3,2 кг баранины содержится 0,512 кг белка.
ВОПРОСЫ ДЛЯ РАЗМЫШЛЕНИЙ
1. Где в реальной жизни может пригодится знание о нахождении длины окружности?
2. Где в реальной жизни может пригодится знание о нахождении площади круга?
3. В каких профессиях могут пригодится полученные знания?
ДОМАШНЕЕ ЗАДАНИЕ
Страница 137 – 139. § 24
№ 848
№ 851
(№ 848 и № 851 решаются по формулам на слайде №5)
№ 864(2)
( № 864(2) решать по примеру № 864(1) )
№ 870
Скачать презентацию
2\)
Использование этих простых формул требует от нас определения нескольких терминов, чтобы мы могли решать задачи с кругами. Во-первых, нам нужно определить радиус, который равен \(r\) в наших двух формулах. Радиус — это расстояние от центра круга до любой точки вне круга. Если бы мы рисовали круг с помощью веревки, привязанной к карандашу, радиусом была бы длина веревки.
Далее следует диаметр, которого нет ни в одной из наших формул. Но это очень важная часть круга, особенно для реальных проблем. 9{2}}{4}\)
На практике эта формула площади используется не так часто, как формула радиуса, но она работает. Когда мы решаем задачу, где диаметр известен, мы обычно просто делим диаметр на 2, чтобы найти радиус, а затем используем формулы радиуса.
Большой \(C\) в формулах — это окружность . Это расстояние по окружности. Это похоже на периметр многоугольника и измеряется в единицах длины, таких как метры и футы. Если бы мы строили круглый забор вокруг двора, вам нужно было бы знать длину окружности, чтобы знать, сколько метров забора нужно купить.
Большой \(A\) в формулах — это площадь круга. Это мера того, сколько квадратных единиц, таких как квадратные сантиметры или квадратные дюймы, поместятся внутри круга. Если бы мы хотели нарисовать большой сплошной круг как часть росписи, нам нужно было бы знать площадь круга, чтобы рассчитать, сколько краски нам нужно купить, чтобы заполнить весь круг.
Наконец, нам нужно определить число пи. Пи — это число. Иногда мы используем 3,14 в качестве приближения числа пи, так как это приблизит нас к реальному ответу. Реальность такова, что пи — иррациональное число, а значит, его нельзя записать в виде дроби. Это также означает, что это десятичная дробь, которая продолжается вечно, но не повторяется. Так что всякий раз, когда мы используем 3,14 или даже эту клавишу пи на калькуляторе, мы используем приближение числа пи, и наш ответ также будет приближением. Точные ответы сохранят число пи как часть ответа, но для реальных задач мы используем приблизительный ответ, поскольку он более полезен при покупке таких вещей, как забор или краска. Никто не продает эти вещи в количествах пи!
Итак, давайте используем наши знания этих терминов для решения некоторых реальных проблем. В ратуше есть гигантские часы, которые требуют ремонта. Циферблат часов необходимо снять и покрасить, а также требуется новая резиновая окантовка по всему периметру, чтобы вода не попадала внутрь.
Высота часов 4,5 метра. Сколько квадратных метров нужно покрасить, и сколько метров кромки нужно купить?
Давайте еще раз посмотрим на наши две формулы.
\(С=2πr\)
92\)
Окрашивающая часть задачи — это наша область. Кромка – это окружность. Мы знаем высоту циферблата наших часов, то есть диаметр. Давайте посчитаем их по одному, начиная с площади.
Первое, что нам нужно сделать, это найти радиус из диаметра, что мы и делаем, разделив на 2. 4.5\text{ м}}{2}\)
\(r=2,25 м\)
Теперь, когда мы знаем радиус, мы можем подставить его в нашу формулу площади. 92\)
Итак, чуть меньше 16 квадратных метров. Нам нужно найти баллончик с краской, которым можно покрыть столько квадратных метров.
А как насчет нашей резиновой окантовки? Найдем длину окружности:
\(C=2πr\)
5π\text{m}\)
\(C=2π(2.25\text{m})\)
\(C=4.
И снова у нас есть точный ответ в виде числа пи. С помощью нашего калькулятора получаем примерный ответ:
\(C\приблизительно{14.14}\text{ m}\)
Нам нужно купить рулон резиновой окантовки длиной более 14,14 метра, чтобы обслуживать наши часы.
Обратите внимание, что окружность является мерой расстояния. Здесь измеряется в метрах. Это может быть очень полезно для определения расстояний при использовании колесных транспортных средств. Например, если мы хотим измерить, какое расстояние мы проезжаем на велосипеде, мы можем использовать окружность шин, чтобы помочь нам.
Давайте попробуем решить задачу:
Как далеко мы проедем на нашем велосипеде BMX, когда объедем квартал? Мы проделываем старый трюк с игральной картой со спицами, чтобы карта издавала звук каждый раз, когда она ударяется о вилку велосипеда. Затем мы подсчитываем, сколько раз звук возникал, когда мы проезжали вокруг квартала.
Окружность шины измерить непросто, но нам это и не нужно. Мы можем измерить высоту шины, которая также является диаметром, а затем использовать формулу для расчета длины окружности.
В нашем велосипеде используются 20-дюймовые колеса, но когда мы измеряем высоту шины, она составляет 24 дюйма или 2 фута. Это диаметр. На этот раз воспользуемся версией формулы для диаметра вместо версии радиуса:
\(C=πd\)
\(C=π(2\text{ft})\)
\(C=2π\text{ ft}\)
Это расстояние, которое проезжает велосипед каждый раз, когда шина делает один оборот. Чтобы найти наше расстояние, нам просто нужно умножить его на количество полных оборотов шины, которое равно 212:
\(\text{ Расстояние}=2π\text{ футов}\times{212}\text{ вращения}\)
\(\text{ Расстояние}=424π\text{ футов}\)
\(\text{ Расстояние}\приблизительно{1,332}\text{ футов}\)
Обзор
Прежде чем мы уйдем, я хочу, чтобы вы сами попробовали один.
У нас есть квадратный двор размером 30 х 30 метров. Мы хотим посадить траву по кругу в центре двора диаметром 20 метров. Сколько квадратных метров травы нам нужно будет засыпать дерном? 92\)
Нам нужно купить много дерна!
Вот площадь и длина окружности. Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Как найти площадь круга?
A
Найдите площадь круга, возведя его радиус в квадрат и умножив на число пи (π).
A = πr 2
Пр. Чему равна площадь круга радиусом 4 см?
А = πr 2 = π(4) 2 = 16π см 2 ≈ 50,27 см 2
Q
Как найти длину окружности?
A
Найдите длину окружности, умножив ее диаметр на число пи (π) или удвоив его радиус и умножив его на число пи.
C = πd или C = 2πr
Пр. Чему равна длина окружности радиусом 2 см?
C = 2πr = 2π(2) = 4π см ≈ 12,56 см
Q
Как найти диаметр круга?
A
Определите диаметр круга, измерив расстояние между двумя самыми дальними точками на круге.
Диаметр всегда проходит через центр окружности.
Q
Как найти радиус окружности?
A
Найдите радиус окружности, соединив центр окружности с любой точкой на окружности или взяв половину диаметра.
Q
Что такое пи?
92\), где r — радиус окружности. Нам не дан радиус круга, но мы можем использовать заданную длину окружности, чтобы найти его. Длина окружности равна:\(C=2r\)
Поскольку длина окружности равна 50,24 дюйма, мы имеем:
\(50,24=2(3,14)r\)
Решая для r, получаем:
\(50,24=23,14r\)
\(50,24=6,28r\)
\(\frac{50,24}{6,28}=\frac{6,28r}{6,28}\)
\(r= 8\)
Подставляя значение радиуса в формулу площади круга, имеем: 92\). Какова окружность круга? Используйте 3.14 для π.
\(75.36\text{ футов}\)
\(37.68\text{ футов}\)
\(226.08\text{ футов}\)
\(150.72\text{ футов}\)
Показать Ответ
Ответ:
Длина окружности равна \(C=2πr\), где \(r\) — радиус окружности.
2\) 92}\)
\(r=12\)
*Извлечение квадратного корня из 144 дает \(\pm12\), но поскольку значения длины не могут быть отрицательными, мы рассматриваем только положительные 12.*
Подстановка значение радиуса в формулу длины окружности, имеем:
\(C=2(3.14)12=75.36\)
Итак, длина окружности равна 75,36 футов.
Скрыть ответ
Вопрос № 4:
Предположим, длина окружности центрального круга футбольного поля составляет 56,52 ярда. Если центральный круг нужно покрасить быстросохнущей акриловой краской, сколько потребуется краски в квадратных футах? Используйте 3.14 для π. 92\), где \(r\) — радиус окружности. Нам не известен радиус центрального круга, но мы можем использовать заданную длину окружности, чтобы найти его.
Длина окружности равна:
\(C=2πr\)
Поскольку длина окружности нашего центрального круга равна 56,52 фута, мы имеем:
\(56,52=2(3,14)r\)
Решение для \(r\) получаем:
\(56,52=2(3,14)r\)
\(56,52=6,28r\)
\(\frac{56,52}{6,28}=\frac{6,28r} {6.
28}\)
\(r=9\) 92\). Какое ограждение нужно для защиты сада? Используйте 3.14 для π.
\(113.4\text{ футов}\)
\(94.2\text{ футов}\)
\(188.4\text{ футов}\)
\(204.5\text{ футов}\)
Показать Ответ
Ответ:
Поскольку нам нужно найти количество ограждений, необходимых для защиты круглого сада, нам нужно найти окружность сада. Длина окружности равна \(C=2πr\), где \(r\) — радиус окружности.
Нам не известен радиус круглого сада, но мы можем использовать заданную площадь круга, чтобы найти его. Площадь круга: 92}\)
\(r=15\)
*Извлечение квадратного корня из 225 дает \(\pm15\), но поскольку значения длины не могут быть отрицательными, мы рассматриваем только положительные 15.*
Подстановка значение радиуса в формулу для длины окружности, имеем:
\(C=2(3.14)(15)=94.2\)
Итак, длина окружности равна 94,2 фута.
Скрыть Ответ
Вернуться к видео по геометрии
243015
Как вычислить площадь и длину окружности
Обновлено 25 апреля 2017 г.
Автор: Jon Zamboni
Учащиеся, начинающие изучать геометрию, могут столкнуться с наборами задач, связанных с вычислением площади и длины окружности. Вы можете решить эти задачи, если знаете радиус круга и можете выполнить простое умножение. Если вы узнаете значение константы π и основные уравнения для свойств круга, вы сможете быстро найти площадь или длину окружности любого круга.
Определение радиуса
Для вычисления длины окружности или площади круга необходимо знать радиус круга. Радиус круга — это расстояние от центра круга до любой точки на краю круга. Радиус одинаков для всех точек на краю круга. Одна из ваших задач может дать вам диаметр вместо радиуса и попросить вас найти площадь или окружность.
Диаметр круга равен расстоянию через центр круга и равен радиусу, умноженному на 2. Таким образом, вы можете преобразовать диаметр в радиус, разделив диаметр на 2. Например, круг диаметром 8 имеет радиус 4,
Определение числа Пи
Когда вы выполняете вычисления, связанные с кругом, вы часто используете число π или число Пи. Пи определяется как длина окружности круга — расстояние вокруг этого круга — деленная на его диаметр. Однако вам не нужно запоминать эту формулу при работе с π, так как это константа. Значение π всегда одно и то же, 3,14.
Вы должны знать, что 3,14 является приблизительным. Полное значение числа пи может растянуться на бесконечное количество цифр справа от запятой (3,14159265… и так далее). Однако 3,14 — достаточно хорошее приближение для большинства расчетов. Если вы не уверены, сколько цифр числа π следует использовать, посоветуйтесь со своим учителем.
Вычисление длины окружности
Как отмечалось выше, длина окружности — это длина линии по краю окружности.