Формулы нахождения площадей: Как найти площадь фигуры, формула

Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. Формулы площади плоских фигур: Формулы площади треугольника Формулы площади квадрата Формула площади прямоугольника Формулы площади параллелограмма Формулы площади ромба Формула площади трапеции Формула площади выпуклого четырехугольника Формулы площади круга Формулы площади эллипса Онлайн калькуляторы для вычисления площадей плоских фигур Формулы площади треугольника Формула площади треугольника по стороне и высоте Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты S =  1 a · h 2 Формула площади треугольника по трем сторонам Формула Герона S = √p(p — a)(p — b)(p — c) Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. S =  1 a · b · sin γ 2 Формула площади треугольника по трем сторонам и радиусу описанной окружности S =  a · b · с 4R Формула площади треугольника по трем сторонам и радиусу вписанной окружности Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. S = p · r где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности, p =  a + b + c   — полупериметр треугольника. 2 Вы можете воспользоваться онлайн калькулятором для расчета площади треугольника. Формулы площади квадрата Формула площади квадрата по длине стороны Площадь квадрата равна квадрату длины его стороны. S = a2 Формула площади квадрата по длине диагонали Площадь квадрата равна половине квадрата длины его диагонали. S =  1 d2 2 где S — Площадь квадрата, a — длина стороны квадрата, d — длина диагонали квадрата. Вы можете воспользоваться онлайн калькулятором для расчета площади квадрата. Формула площади прямоугольника Площадь прямоугольника равна произведению длин двух его смежных сторон S = a · b где S — Площадь прямоугольника, a, b — длины сторон прямоугольника. Вы можете воспользоваться онлайн калькулятором для расчета площади прямоугольника. Формулы площади параллелограмма Формула площади параллелограмма по длине стороны и высоте Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты. S = a · h Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними. S = a · b · sin α Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. S =  1 d1d2 sin γ 2 где S — Площадь параллелограмма, a, b — длины сторон параллелограмма, h — длина высоты параллелограмма, d1, d2 — длины диагоналей параллелограмма, α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма. Вы можете воспользоваться онлайн калькулятором для расчета площади параллелограмма. Формулы площади ромба Формула площади ромба по длине стороны и высоте Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. S = a · h Формула площади ромба по длине стороны и углу Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. S = a2 · sin α Формула площади ромба по длинам его диагоналей Площадь ромба равна половине произведению длин его диагоналей. S =  1 d1 · d2 2 где S — Площадь ромба, a — длина стороны ромба, h — длина высоты ромба, α — угол между сторонами ромба, d1, d2 — длины диагоналей. Вы можете воспользоваться онлайн калькулятором для расчета площади ромба. Формулы площади трапеции Формула Герона для трапеции S =  a + b √(p — a)(p — b)(p — a — c)(p — a — d) |a — b| Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту S =  1 (a + b) · h 2 где S — Площадь трапеции, a, b — длины основ трапеции, c, d — длины боковых сторон трапеции, p =  a + b + c + d   — полупериметр трапеции. 2 Вы можете воспользоваться онлайн калькулятором для расчета площади трапеции. Формулы площади выпуклого четырехугольника Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними: S =  1 d1 d2 sin α 2 где S — площадь четырехугольника, d1, d2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника. Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности S = p · r Формула площади четырехугольника по длине сторон и значению противоположных углов S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ где S — площадь четырехугольника, a, b, c, d — длины сторон четырехугольника, p =  a + b + c + d   — полупериметр четырехугольника, 2 θ =  α + β  — полусумма двух противоположных углов четырехугольника. 2 Формула площади четырехугольника, вокруг которого можно описать окружность S = √(p — a)(p — b)(p — c)(p — d) Вы можете воспользоваться онлайн калькулятором для расчета площади четырехугольника. Формулы площади круга Формула площади круга через радиус Площадь круга равна произведению квадрата радиуса на число пи. S = π r2 Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи. S =  1 π d2 4 где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга. Вы можете воспользоваться онлайн калькулятором для расчета площади круга. Формулы площади эллипса Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи. S = π · a · b где S — Площадь эллипса, a — длина большей полуоси эллипса, b — длина меньшей полуоси эллипса. Вы можете воспользоваться онлайн калькулятором для расчета площади эллипса. Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур Все таблицы и формулы Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Формулы площади и программы для расчета площадей

Содержание:

• Формулы площади треугольника
• Формулы площади квадрата:
• Формула площади прямоугольника:
• Формула площади параллелограмма:
• Формула площади трапеции:
• Формулы площади ромба:
• Формула площади круга:
• Формула площади эллипса:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.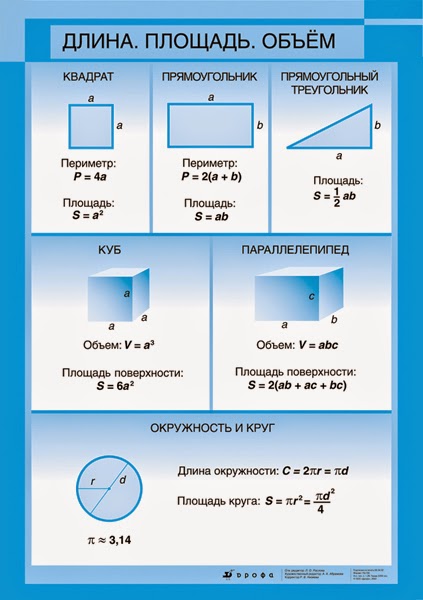

Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

1-ая формула

S — площадь треугольника

a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b

2-ая формула

S — площадь треугольника

a — длина стороны треугольника

h — длина высоты, опущенной на сторону a

3-ья формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

p — полупериметр треугольника

4-ая формула

S — площадь треугольника

r — радиус вписанной окружности

p — полупериметр треугольника

5-ая формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

R — радиус описанной окружности

См. также: Программа для расчета площади треугольника.

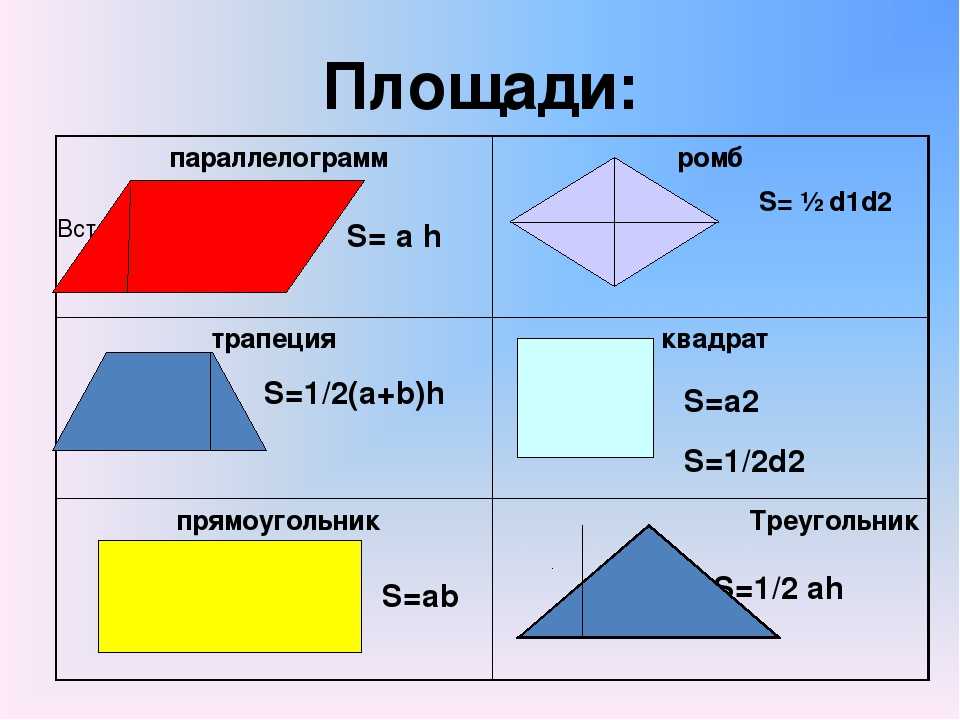
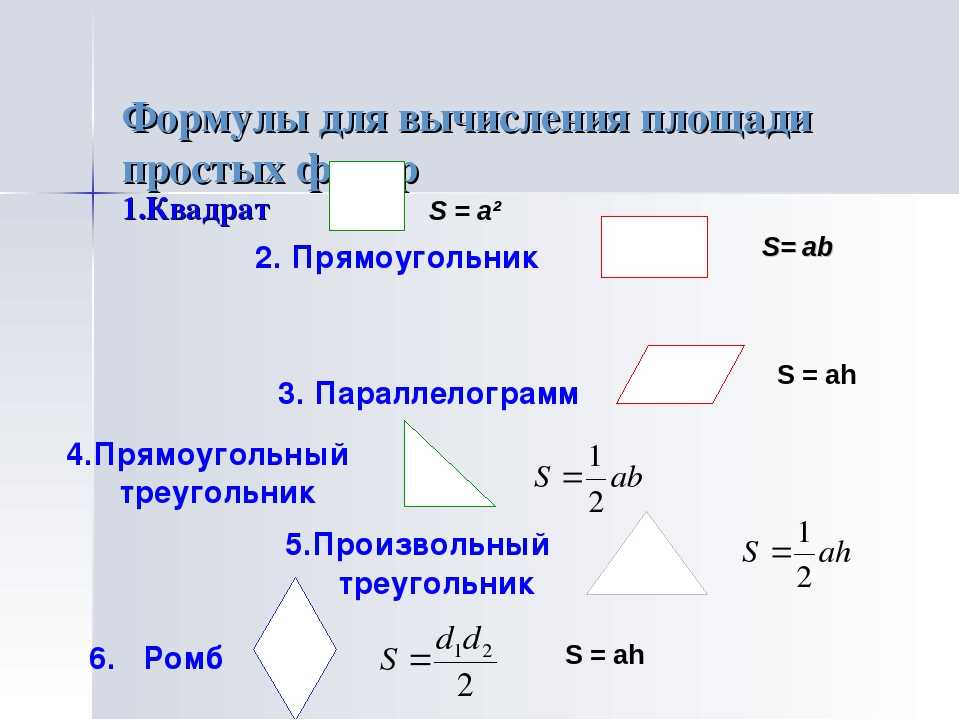
Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S — площадь прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См. также: Программа для расчета площади прямоугольника.

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S — площадь параллелограмма

a — длина основания

h — длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

См. также: Программа для расчета площади трапеции.

Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d₁ — длина 1-ой диагонали

d₂ — длина 2-ой диагонали

См. также: Программа для расчета площади ромба.

Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3.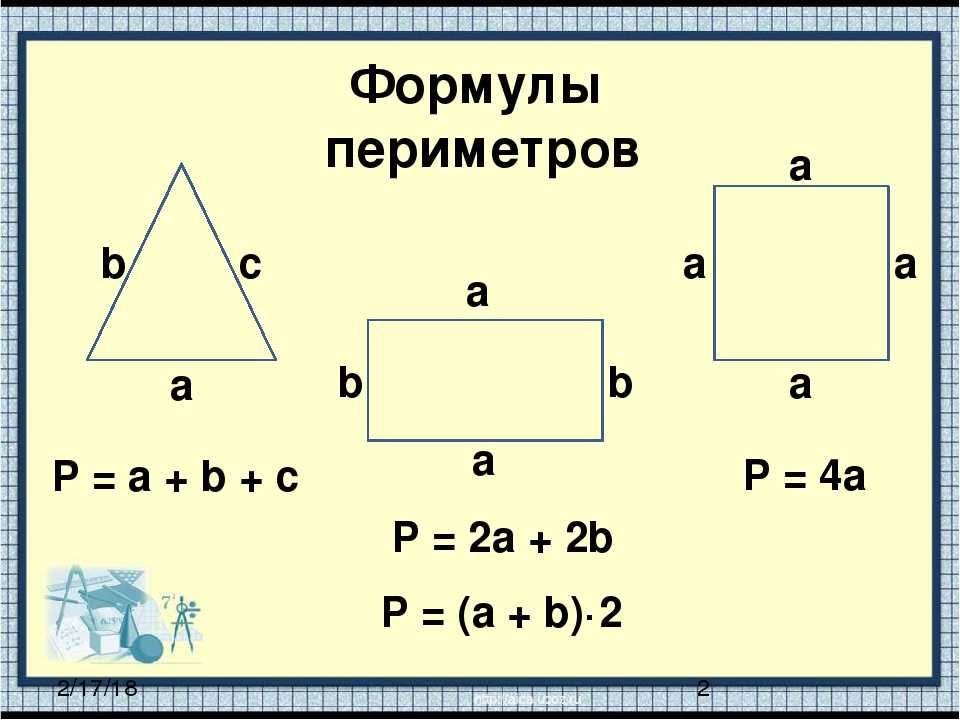 1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S — площадь круга

π — число пи (3.1415)

r — радиус круга

См. также: Программа для расчета площади круга.

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

S — площадь эллипса

π — число пи (3.1415)

a — длина большой полуоси

b — длина малой полуоси

См. также: Программа для расчета площади эллипса.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Формулы площади

Формулы площади

Дом | Учитель | Родители | Глоссарий | О нас

Отправить эту страницу другу по электронной почте

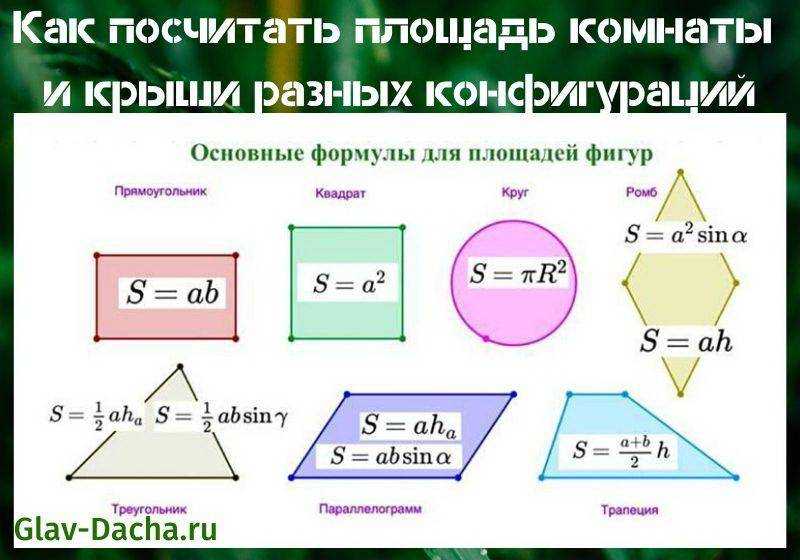
Ресурсы · · · · · ·   Поиск		Формулы площади (Математика | Геометрия | Формулы площади) ( пи = = 3. 141592…) Район Формулы Примечание: «ab» означает «a» умножить на «б». «а 2 » означает «а в квадрате», что то же самое, что «а» умножить на «а». Будьте осторожны!! Считаются единицы. Используйте тот же единицы для всех измерений. Примеры квадрат = a 2 прямоугольник = ab параллелограмм = bh трапеция = ч/2 (б 1 + б 2 ) круг = пи r 2 эллипс = пи r 1 r 2 треугольник = половина длины основания, умноженной на высоту треугольник равносторонний треугольник = треугольник задан SAS (две стороны и противолежащий угол) = (1/2) a b sin C треугольник, заданный a,b,c = [s(s-a)(s-b)(s-c)] когда s = (a+b+c)/2 (формула Герона) правильный многоугольник = (1/2) n sin(360°/n) S 2 когда n = количество сторон и S = ​​длина от центра до угла Единиц Площадь измеряется в квадратных единицах. Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол. Площадь квадрата = сторона умноженная на сторону. Так как каждая сторона квадрата равна то же самое, это может быть просто длина одной стороны в квадрате. Если у квадрата одна сторона равна 4 дюймам, площадь будет равна 4 дюймам, умноженным на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также могут быть записаны в 2 .) Обязательно используйте одни и те же единицы измерения для всех измерений. Нельзя умножать футы на дюймы, это не дает квадрат измерение. Площадь прямоугольника равна длине стороны раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, то что это площадь? НЕПРАВИЛЬНО …. 4 раза по 6 = 24 ПРАВИЛЬНО …. 4 дюйма равно 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута. (или 2 кв. фута, или 2 фута 2 ).
		Связаться с нами | Реклама и спонсорство | Товарищество | Ссылка на нас © 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика.

 

Какова площадь 2D-фигур? Определение, формулы, примеры, факты

Какова площадь 2D-фигур?

Площадь двумерной фигуры — это величина, выражающая область, заключенную в границы двумерной фигуры.

2D означает двумерный. 2D-фигуры — это фигуры с двумя измерениями, такими как ширина и высота. Эти формы не имеют толщины или высоты.

Примерами двумерных фигур являются квадрат, прямоугольник, треугольник, круг и т. д.

Как найти площадь двумерных фигур? Давайте разбираться.

Связанные игры

Площадь двумерных фигур с помощью формул

Мы также можем найти площадь двумерных фигур с помощью формул. Различные формы имеют разные формулы для расчета площади. Давайте разберемся, как найти площадь 2D-фигуры с помощью формулы. В этом разделе вы можете изучить формулы для площади 2D-фигур. 9{\circ}$.

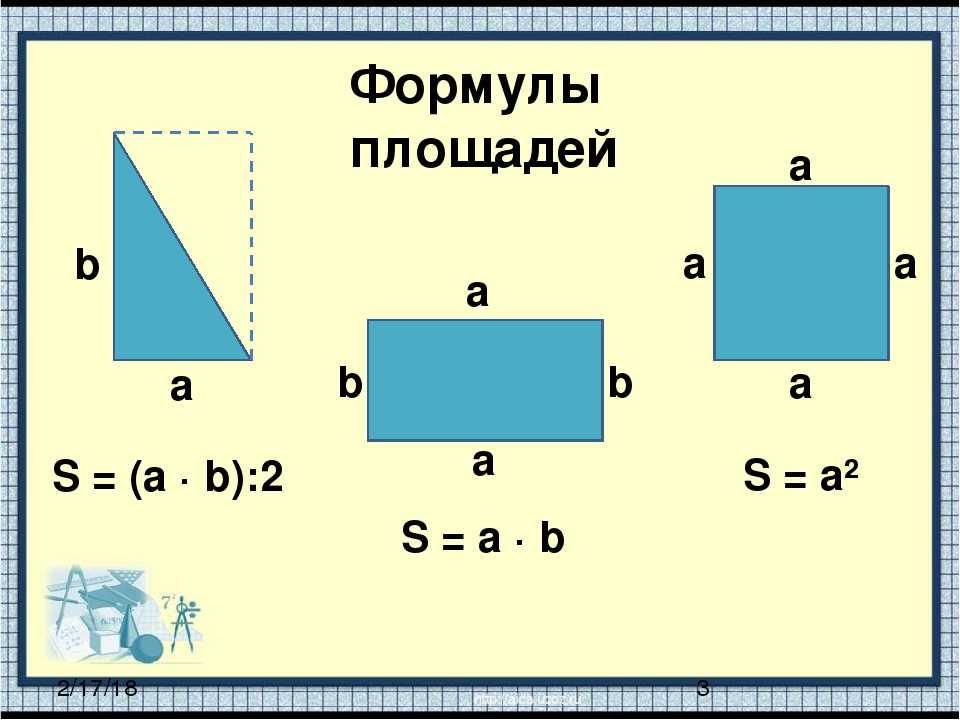
Площадь прямоугольника равна произведению двух его смежных сторон.

Площадь прямоугольника $=$ Длина $\times$ Ширина

Площадь прямоугольника $= \text{l} \times \text{w}$

Мы можем видеть, что при измерении площади прямоугольника, мы учитываем как длину, так и ширину прямоугольника.

Например, у нас есть прямоугольник длиной 8 см и шириной 3 см. Попробуем найти его площадь.

Длина прямоугольника, $\text{l} = 8\; \text{см}$ 9{2}$

Площадь треугольника

Треугольник представляет собой двумерную фигуру с тремя сторонами (ребрами) и тремя вершинами. Треугольник с вершинами A, B и C обозначается как $\Delta$  ABC.

Для заданного треугольника, где высота треугольника равна h, а основание равно b, площадь треугольника можно рассчитать по формуле:

Площадь треугольника $= \frac{1}{2} \times$ основание $\times$ высота

Площадь треугольника $= \frac{1}{2} \times \text{b} \times \text{h}$

Обратите внимание, что основание и высота треугольника перпендикулярны друг другу.

Существуют различные типы треугольников, такие как равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, но формула площади всех видов треугольников одинакова.

На следующем рисунке показаны основание и высота равностороннего треугольника, разностороннего треугольника и прямоугольного равнобедренного треугольника. Обратите внимание, что в прямоугольном равнобедренном треугольнике основание равно высоте.

Возьмем в качестве примера данный треугольник ABC.

В треугольнике ABC основание равно 6 единицам, а высота равна 4 единицам.

Площадь треугольника $= \frac{1}{2} \times$ основание $\times$ высота

Площадь треугольника ABC $=  \frac{1}{2} \times \text{b} \times \ text{h}$

                                  $= \frac{1}{2}  \times 6 \times 4$

                                   $ = 12 $ кв. единиц

Связанные рабочие листы

Площадь двумерных фигур путем подсчета квадратов

Посмотрите на фигуры, приведенные ниже. Мы не сможем использовать базовые формулы для определения площади таких неправильных двумерных фигур. Чтобы вычислить площадь двухмерных фигур, к которым мы не можем применить никакую формулу, у нас есть другой метод, который заключается в подсчете квадратов на сетке.

Теперь, когда мы знаем, что площадь — это область внутри границы 2D-формы, мы можем выразить площадь в терминах единичных квадратов . Квадрат, длина стороны которого равна 1 единице, имеет площадь 1 квадратную единицу.

Чтобы найти площадь двухмерной фигуры с помощью этого метода, мы подсчитываем количество квадратов, покрывающих поверхность фигуры.

При подсчете квадратов мы следуем этим правилам :

• Если фигура покрыта менее чем половиной квадрата, считается, что это ноль.
• Если фигура покрыта более чем половиной квадрата, считается за 1 единицу.
• Если фигура покрыта ровно половиной квадрата, считайте ее как $\frac{1}{2}$ за единицу.
• Если фигура покрыта полным квадратом, считается за 1 единицу.

Найдем площадь данного пятиугольника.

Площадь пятиугольника равна общей площади всех покрытых квадратов $= 6 + 0 + 0 + 6 = 12$ квадратных единиц

Площадь неправильных фигур можно легко найти с помощью этого метода.

Интересные факты!

• Среди всех фигур с одинаковым периметром наибольшую площадь имеет круг.
• Прямоугольник, у которого все стороны равны, называется квадратом.
• Все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
• Обратите внимание, что термин «площадь поверхности» используется для обозначения общей площади всех внешних граней объемной трехмерной фигуры. Площадь — это область, ограниченная границами 2D-формы. Таким образом, площадь поверхности 2D-фигуры есть не что иное, как площадь 2D-фигуры.

Заключение

В следующий раз, когда вы захотите развернуть травяной газон, чтобы покрыть свой передний двор, вы можете найти площадь двора, чтобы определить размер рулонного газона, необходимый для того, чтобы сделать ваш передний двор красивым. 9{2}$

Ширина $= 5\; \text{m}$

Площадь прямоугольника $= \text{l} \times \text{w}$

$35 = \text{l} \times 5$

$355 = \text{l}$

$\text{l} = 7\; \text{m}$

Длина прямоугольника 7 м.

3. Пол прямоугольного зала застелить ковром шириной 200 см. Если длина и ширина зала 20 м и 18 м соответственно, найдите стоимость ковра из расчета 2 доллара за метр.

Решение: 9{2}$

Ширина ковра $= 200\; \текст{см} = 200 \дел 100 = 2\; \text{m}$

Площадь ковра $=$ Площадь зала

Следовательно, длина ковра $= \frac{Площадь зала}{Ширина ковра} = \frac{360}{2} = 180\; \text{m}$

Стоимость ковра $= \$2$ за метр

Следовательно, стоимость ковра $= \$ (180 \times 2) = \$ 360$

4. Найдите площадь данной фигуры.

Решение:

Данную фигуру можно разделить на квадрат и треугольники, как показано на рисунке. 9{2}$

Часто задаваемые вопросы по площади 2D-фигур

Что такое многоугольники?

Двумерные фигуры, состоящие из прямых линий и образующие простую замкнутую фигуру, называются многоугольниками.

Например, квадрат, прямоугольник и треугольник являются примерами многоугольников.

Что такое правильные и неправильные многоугольники?

Правильные многоугольники — это многоугольники с равными сторонами и углами.