Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. Навигация по странице: Формулы объема куба Формулы объема призмы Формулы объема параллелепипеда Формулы объема прямоугольного параллелепипеда Формулы объема пирамиды Формулы объема правильного тетраэдра Формулы объема цилиндра Формулы объема конуса Формулы объема шара Онлайн калькуляторы для вычисления объемов Объем кубаОбъем куба равен кубу длины его грани. Формула объема куба: V = a3 где V — объем куба, Смотрите также онлайн калькулятор для расчета объема куба Объем призмыОбъем призмы равен произведению площади основания призмы, на высоту. Формула объема призмы: V = So h где V — объем призмы, Онлайн калькулятор для расчета объема призмы Формулы площади геометрических фигур для определения площади основания призмы Объем параллелепипедаОбъем параллелепипеда равен произведению площади основания на высоту. Формула объема параллелепипеда: V = So · h где V — объем параллелепипеда, Смотрите также онлайн калькулятор для расчета объема параллелепипеда Объем прямоугольного параллелепипедаОбъем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. Формула объема прямоугольного параллелепипеда: V = a · b · h где V — объем прямоугольного параллелепипеда, b — ширина, h — высота.  Смотрите также онлайн калькулятор для расчета объема прямоугольного параллелепипеда Объем пирамидыОбъем пирамиды равен трети от произведения площади ее основания на высоту. Формула объема пирамиды:
где V — объем пирамиды, Онлайн калькулятор для расчета объема пирамиды Формулы площади геометрических фигур для определения площади основания пирамиды Объем правильного тетраэдраФормула объема правильного тетраэдра:
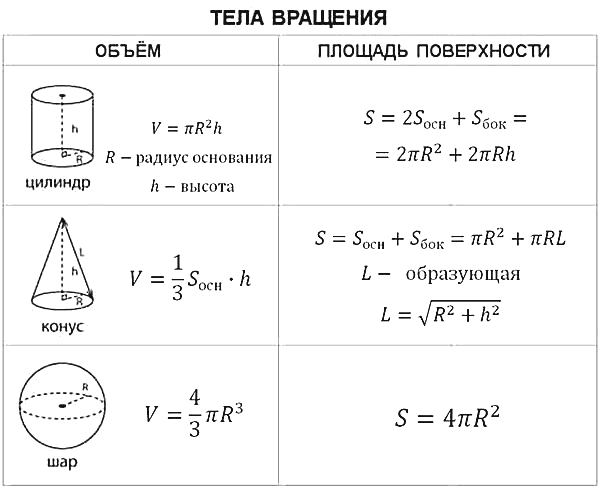
где V — объем правильного тетраэдра, Смотрите также онлайн калькулятор для расчета объема правильного тетраэдра Объем цилиндраОбъем цилиндра равен произведению площади его основания на высоту. Формулы объема цилиндра:
где V — объем цилиндра, Смотрите также онлайн калькулятор для расчета объема цилиндра Объем конусаОбъем конуса равен трети от произведению площади его основания на высоту. Формулы объема конуса:
где V — объем конуса, Смотрите также онлайн калькулятор для расчета объема конуса Объем шараОбъем шара равен четырем третьим от его радиуса в кубе помноженного на число пи. Формула объема шара:
где V — объем шара, Смотрите также онлайн калькулятор для расчета объема шара Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур Все таблицы и формулы Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! |
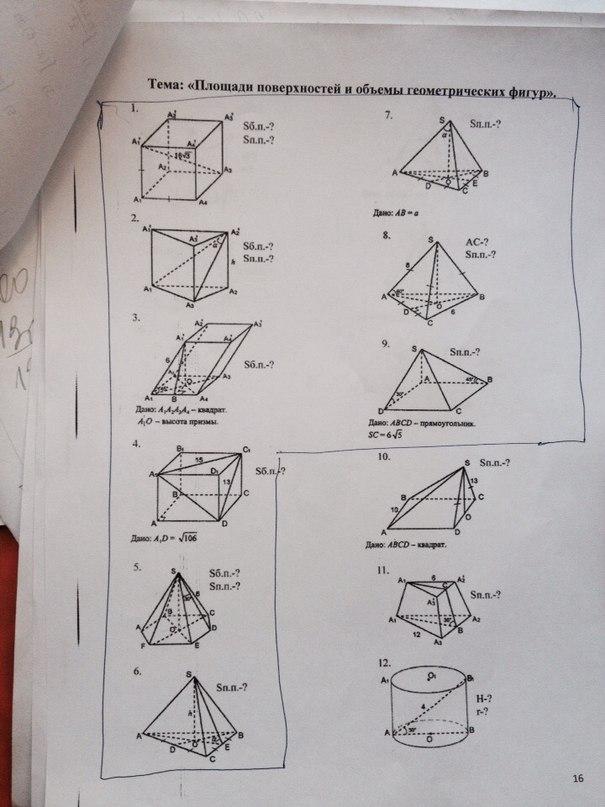
Объемы и площади объемных фигур.
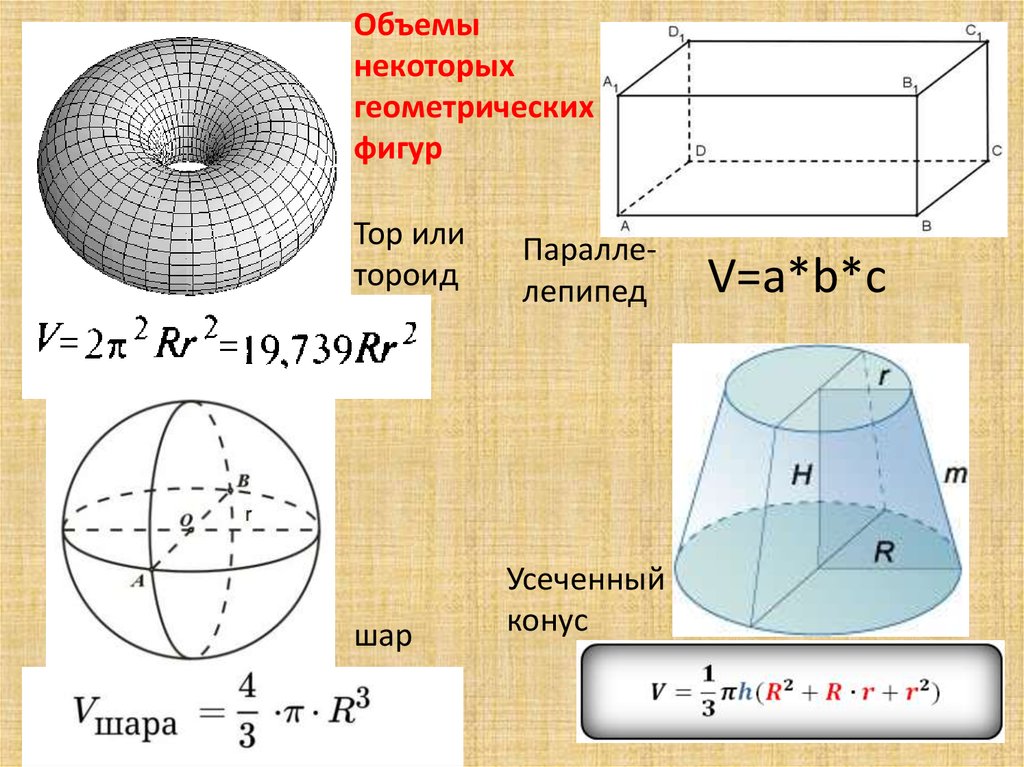Формулы для нахождения объема параллелепипедаЛюбое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов.
Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно.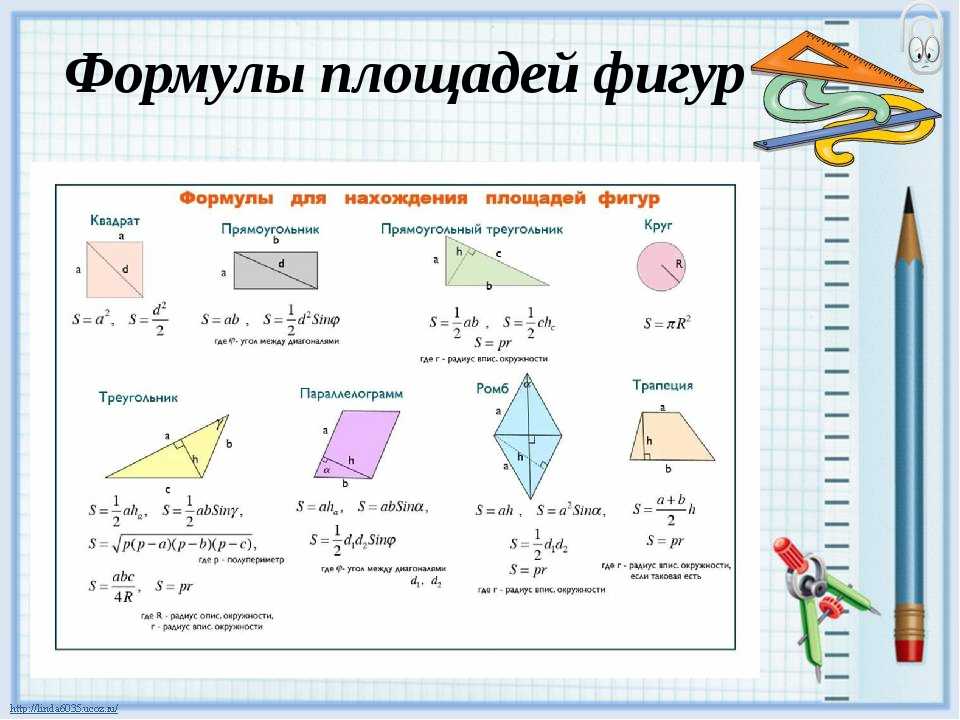
Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике.
Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13.
Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
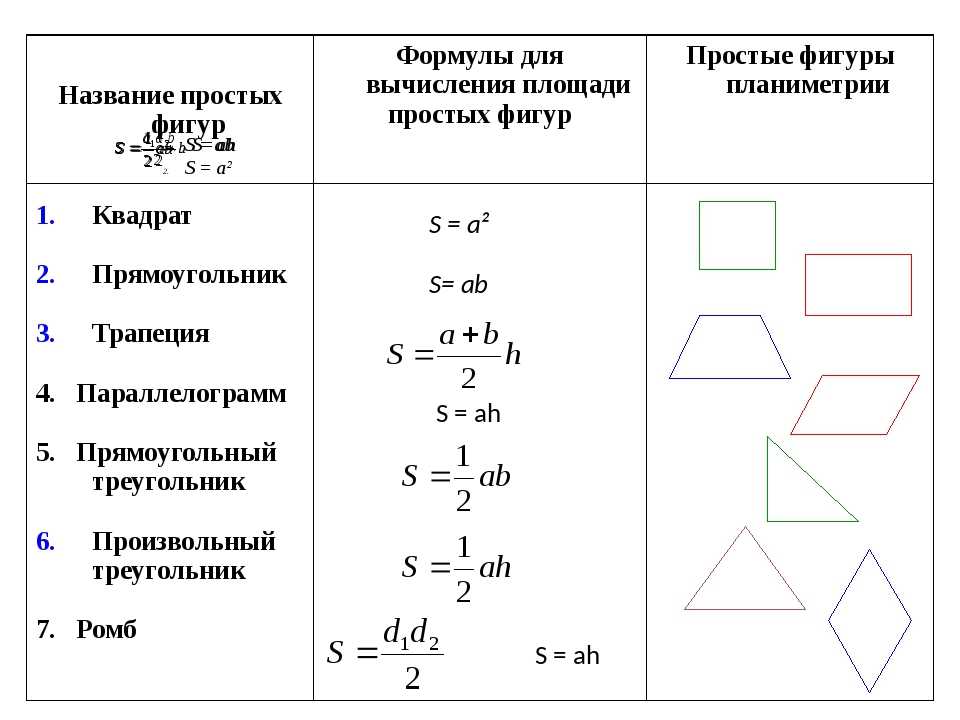
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.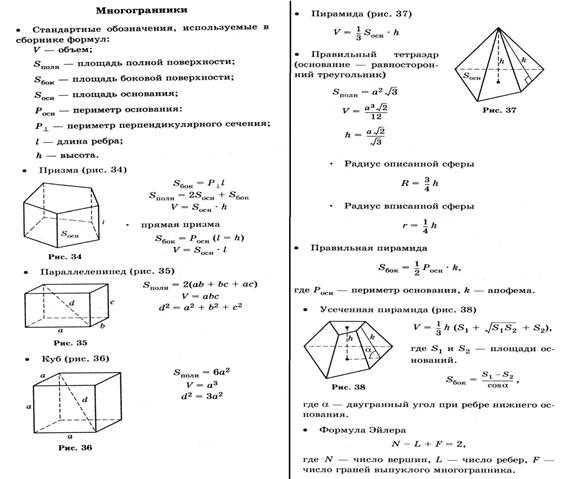
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности.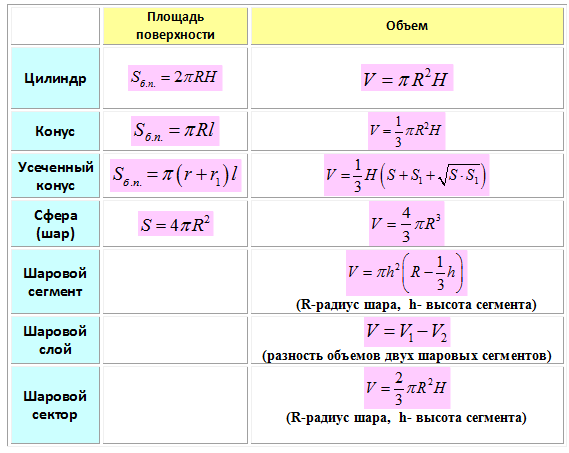
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Формулы объема — вывод, примеры
Формула объема – это математическое выражение, используемое для нахождения общего пространства (вакуума), занимаемого любым трехмерным объектом. Давайте подробно разберемся с формулами объема различных трехмерных форм.
Что такое формула объема?
Формула, используемая для расчета общей кубической емкости, которую может вместить объект, является формулой его объема. Единица объема трехмерной формы выражается в единицах 3 или кубических единицах.
Посмотрите на приведенную ниже диаграмму формул объема, на которой показаны формулы объема соответствующих трехмерных фигур.
Давайте подробно узнаем об общих формулах объема различных форм.
Формулы объема трехмерных фигур
Теперь мы знаем, что формула объема используется для расчета объема трехмерного объекта. В этом разделе мы узнаем о формулах объема с соответствующими размерами различных трехмерных фигур.
Формула объема куба
Формула объема куба зависит от трех сторон куба, где все три стороны равны по размеру. Объем куба – это количество, занимаемое кубом. Общая формула объема куба имеет вид:
- Объем куба = a × a × a = a 3 кубических единиц, , где «a» — длина стороны куба.
- Объем формулы куба с использованием диагонали может быть задан как V = (√3×d 3 )/9, где d – длина диагонали куба.
Формула объема прямоугольного параллелепипеда
Чтобы рассчитать объем пространства, заключенного в прямоугольный параллелепипед, мы используем формулу объема прямоугольного параллелепипеда.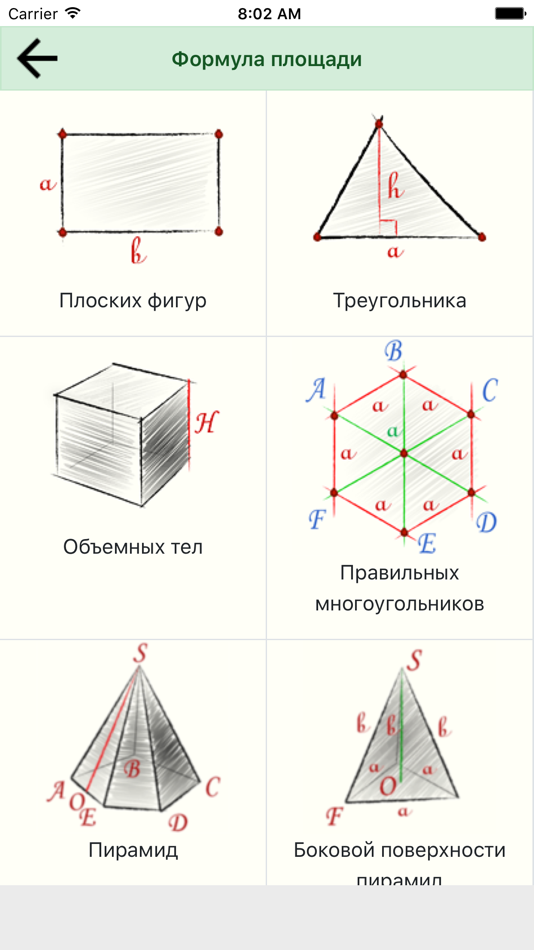
Общая формула объема прямоугольного параллелепипеда математически выражается как:
- Объем прямоугольного параллелепипеда = площадь основания × высота в кубических единицах
- Площадь основания прямоугольного параллелепипеда = l × b квадратных единиц
- Следовательно, объем прямоугольного параллелепипеда, V = l × b × h = lbh единицы 3 , где «l», «b» и «h» представляют длину, ширину и высоту параллелепипеда.
Формула объема конуса
Чтобы вычислить объем пространства, занимаемого конусом трехмерной формы, имеющим круглое основание с радиусом ‘r’ и высотой ‘h’, мы используем формулу объема конуса. Общая формула объема конуса выражается как:
Объем конуса, В = (1/3)πr 2 ч кубических единиц.
Здесь
- ‘r’ — радиус основания (окружности) конуса
- ‘h’ — высота конуса
- π — константа со значением 22/7 (или) 3,142.
Формула объема цилиндра
Формула объема цилиндра используется для определения количества пространства (вместимости), занимаемого внутри него.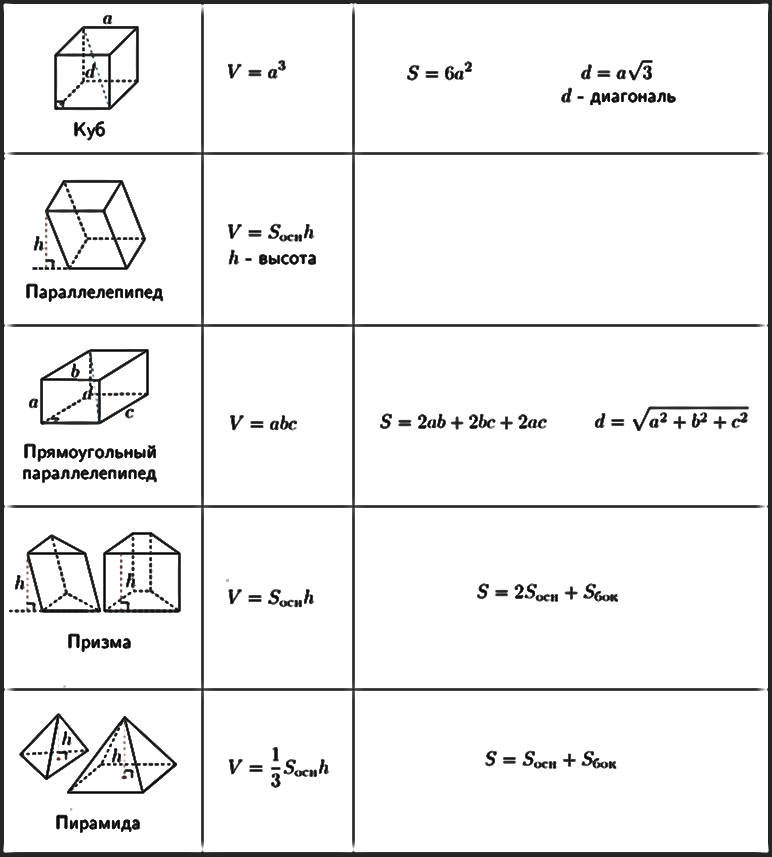
Мы знаем, что основанием правильного кругового цилиндра является окружность, а площадь окружности радиуса «r» равна πr 2 . Таким образом, формула объема цилиндра:
Объем цилиндра = πr 2 ч кубических единиц
Здесь
- ‘r’ – радиус основания (окружности) цилиндра
- ‘h’ — высота цилиндра
- π — это константа, значение которой равно 22/7 (или) 3,142.
Таким образом, объем цилиндра прямо пропорционален его высоте и квадрату радиуса. то есть объем цилиндра становится четырехкратным, если радиус цилиндра удваивается.
Объемная формула сферы
Мяч является прекрасным примером, который напоминает форму сферы. Это трехмерный твердый объект с круглой структурой. Количество воздуха, находящегося в шаре, называется объемом шара или шара. Формула объема сферы задается следующим образом:
Объем сферы = (2/3)πr 2 ч
Если диаметр сферы = 2r
Следовательно, объем сферы равен (2/3)πr 2 h = (2/3)πr 2 (2r) = (4/3)πr 3 кубических единиц
Объем шара равен (4/3)πr 3 кубических единиц
Здесь
- ‘ r’ – радиус сферы
- ‘h’ — высота сферы
- π — это константа, значение которой равно 3,142 или 22/7.
Формула объема полушария
Полушарие является половиной сферы, мы можем легко вывести формулу объема полушария, используя формулу объема сферы. Теперь, учитывая, что радиус сферы равен r единиц, а объем сферы равен (4/3)πr 3 .
Таким образом, объем полушария может быть задан как: V = ½ (4/3)πr 3
Объем полушария = (2/3)πr 3 кубических единиц
Здесь,
- ‘r’ — радиус полушария
- π — это константа, значение которой равно 3,142 или 22/7.
Формула объема призмы
Формула объема призмы определяется как произведение площади основания и высоты призмы. Это математически выражается как:
Объем призмы V = B × h единиц 3 .
Здесь
- «B» — базовая площадь в квадратных единицах
- «h» — высота призмы в единицах.
Существует семь типов призм в зависимости от формы основания призмы.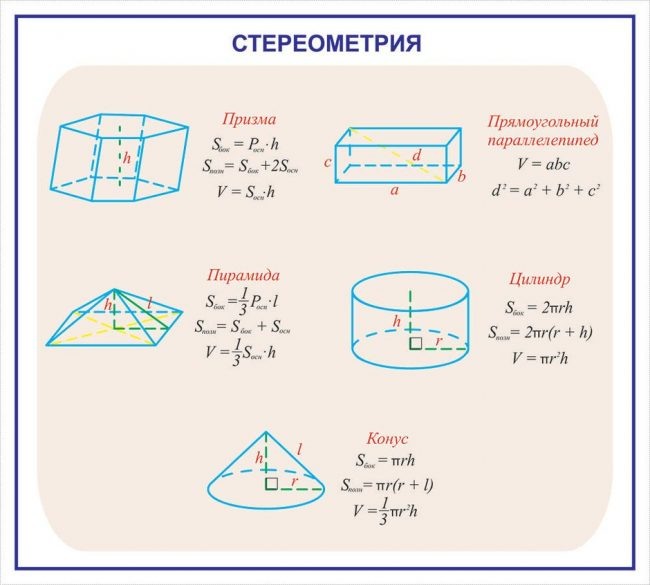
Формула объема призм зависит от различных оснований призм. Ознакомьтесь с объемом призмы, чтобы понять концепцию формул объема различных призм.
Формула объема пирамиды
Объем пирамиды составляет одну треть объема призмы (т. е. их основания и высоты равны). Таким образом,
Объем пирамиды (V) = (1/3) (Bh) единиц 3 , где
- B = площадь основания пирамиды в квадратных единицах
- h = Высота пирамиды (высота) в единицах
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Заказать бесплатный пробный урок
Примеры формулы объема
Пример 1: Цилиндрический резервуар имеет радиус 3 единицы и высоту 8 единиц. Используя формулу объема, найдите объем цилиндра, найдите его площадь поверхности.
Решение:
Дано: r = 3 единицы, h = 8 единиц
При подстановке значений в формулу объема цилиндра имеем
Объем цилиндра = πr 2 ч
V = π(3) 2 (8)
V = π × 9 × 8 90 101
V = 72 π 90 101
Подставляя значение π = 3,14
V = 72 × 3,14 = 226,08 единиц 3
Объем цилиндра равен 226,08 единиц 3
Пример 2: Учитывая, что радиус конуса равен 4 единицы, а высота конуса – 9 единиц. Используя формулу объема, определите объем конуса.
Решение:
Дано: радиус = 4 единицы и высота = 9ед.
Формула объема конуса = (1/3)πr 2 ч.
=1/3 × 3,14 × 4 2 × 9
=1/3 × 452,16 90 101
=150,72 единиц 3
∴Объем конуса будет 150,72 единиц 3
Пример 3: длина – 9 дюймов, ширина – 7 дюймов, а высота 5 дюймов.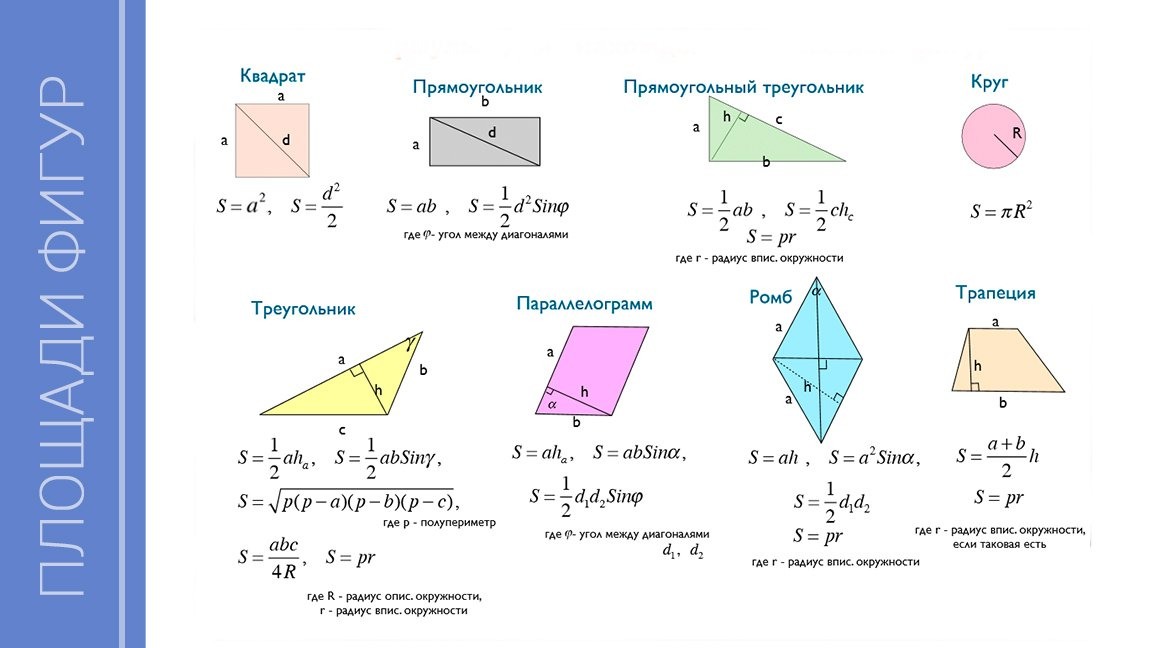
Решение: Дана длина прямоугольного параллелепипеда = 9дюймов, ширина прямоугольного параллелепипеда = 7 дюймов, а высота прямоугольного параллелепипеда = 5 дюймов.
Формула объема прямоугольного параллелепипеда = l × b × h 90 101
Подставив значения l, b и h в формулу объема, получим
V = 9 × 7 × 5
= 315
= 315 дюймов 3
∴Объем прямоугольного параллелепипеда будет 315 дюймов 2
Часто задаваемые вопросы по формулам объема
Что такое формула объема для прямоугольного параллелепипеда?
Формула объема прямоугольного параллелепипеда: l × b × h кубических единиц. Здесь «l», «b» и «h» обозначают длину, ширину и высоту прямоугольного параллелепипеда.
Какая связь между формулой объема сферы и полушария?
Формула объема полушария составляет половину формулы объема сферы. Это дается как:
Объем полусферы = ½ (формула объема сферы) = ½ (4/3)πr 3 = (2/3)πr 3 кубических единиц , где «r» – радиус полушария/сферы.
Какова формула объема конуса?
Формула объема конуса математически выражается как V = (1/3)πr 2 ч куб.ед. Здесь «r» — радиус основания конуса, а «h» — высота конуса.
Какая связь между формулами объема призмы и пирамиды?
Формула объема пирамиды составляет 1/3 формулы объема призмы. Это дается как:
Объем пирамиды = 1/3 (формула объема призмы) = 1/3 (Bh) кубических единиц, где ‘B’ – площадь основания пирамиды/призмы, выраженная в единицах 2 и ‘h’ высота пирамиды/призмы, выраженная в единицах.
Формулы объема
Здесь мы предлагаем вам формулы объема для некоторых распространенных трехмерных фигур, а также для эллипсоида и полого цилиндра, которые не так распространены.
Куб:
Объем = a 3 = a × a × a
Цилиндр:
Объем = π × r 2 × h
π = 3,14
h высота
r радиус
Сплошной прямоугольный или параллелепипед:
Объем = l × w × h
l — длина
w — ширина
h — высота
Сфера:
Объем = (4 × π × r 3 )/3
π = 3,14
r — радиус
Конус:
Объем = (π × r 2 × h)/3
pi = 3,14
r — радиус
h — высота
Пирамида:
Объем = (B × h)/3
B — площадь основания
h — высота
Менее распространенные формулы объема
Эллипсоид:
Объем = (4 × π × a × b × c)/3
Использование π = 3,14
Полый цилиндр:
Объем = π × R 2 × h — π × r 2 × h
Объем = π × h ( R 2 — r 2 )
Используйте π = 3,14.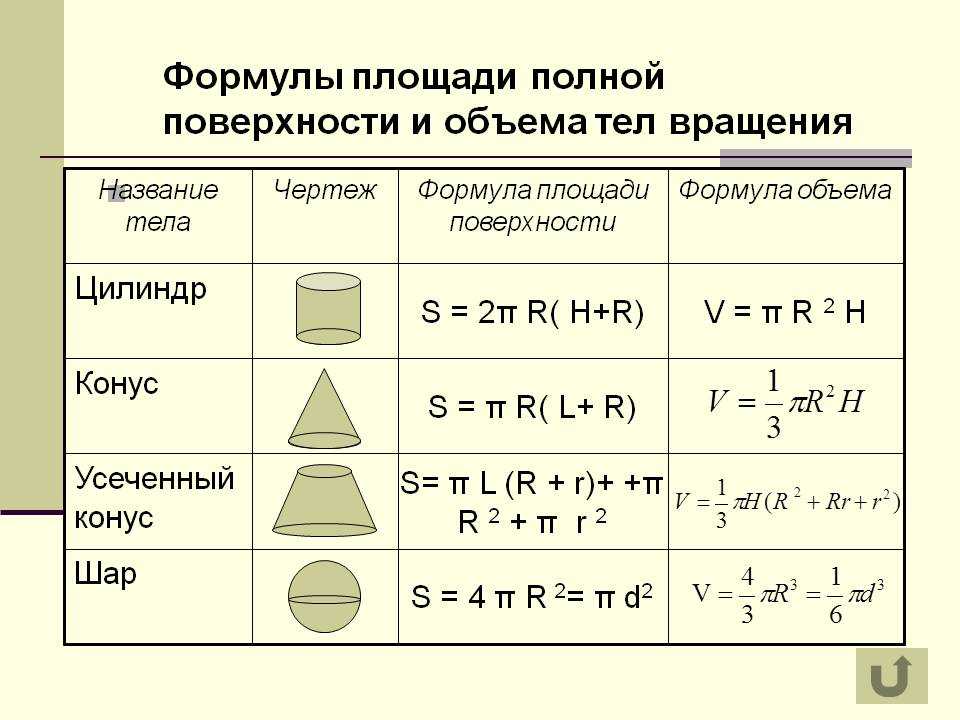
Как использовать формулы объема для расчета объема
Объем куба
Длина стороны = a = 2 см
Объем = (2 см) = 2 см × 2 см × 2 см = 8 см 3 = 8 кубических сантиметров
Объем цилиндра
Высота 8 дюймов, радиус 2 дюйма.
Объем = π × r 2 × h = 3,14 × (2 дюйма) 2 × 8 дюймов = 3,14 × 4 × 8 дюймов 3
Объем = 3,14 × 32 дюйма 3 = 100,48 дюйма 2 = 100,48 кубических дюймов
Объем прямоугольного или прямоугольного тела
Длина 6 см, ширина 3 см, высота 5 см.
Объем = л × ш × в = 6 × 3 × 5 = 90 см 3 = 90 куб. × п × r 3 )/3 = [4 × 3,14 × (20) 3 ]/3 = 3,14 × (20) 3 × 4
Объем = 3,14 × 8000 × 4 = 3,14 × 32000 = 100480
Объем конуса
Радиус равен 3, а высота равна 4.
Объем = (π × г 2 × h)/3 = [3,14 × (3) 2 × 4]/3 = 3,14 × 9 × 4
Объем = 3,14 × 36 = 113,04
Объем пирамиды
9 0002 Пирамида имеет высота 6 футов.
Найдите объем, если основанием пирамиды является квадрат длиной 2 фута.Объем = (B × h)/3
B = площадь основания = 2 фута × 2 фута = 4 фута 2
Объем = (4 × 6)/3 фута 3 = 24/3 фута 3 = 8 футов 3 = 8 кубических футов
Объем эллипсоида
Радиусы эллипсоида равны 1 см, 2 см и 3 см.
Объем = (4 × π × a × b × c)/3 = (4 × 3,14 × 1 × 2 × 3)/3
Объем = (3,14 × 4 × 6)/3 = (3,14 × 24)/ 3 = 81,64/3 = 25,12 см 3 = 25,12 кубических сантиметра
Объем полого цилиндра
Внешний радиус равен 8, внутренний радиус равен 6, а высота равна 10.
Объем = π × h ( R 2 — r 2 ) = π × 10 ( 8 2 — 6 2 ) = π × 10 ( 64 – 36)
Объем = π × 10 (28) = π × 280 = 879,2
Общая формула для нахождения объема призм, таких как треугольные призмы мс или прямоугольные призмы
Объем призмы равен произведению площади основания и высоты призмы.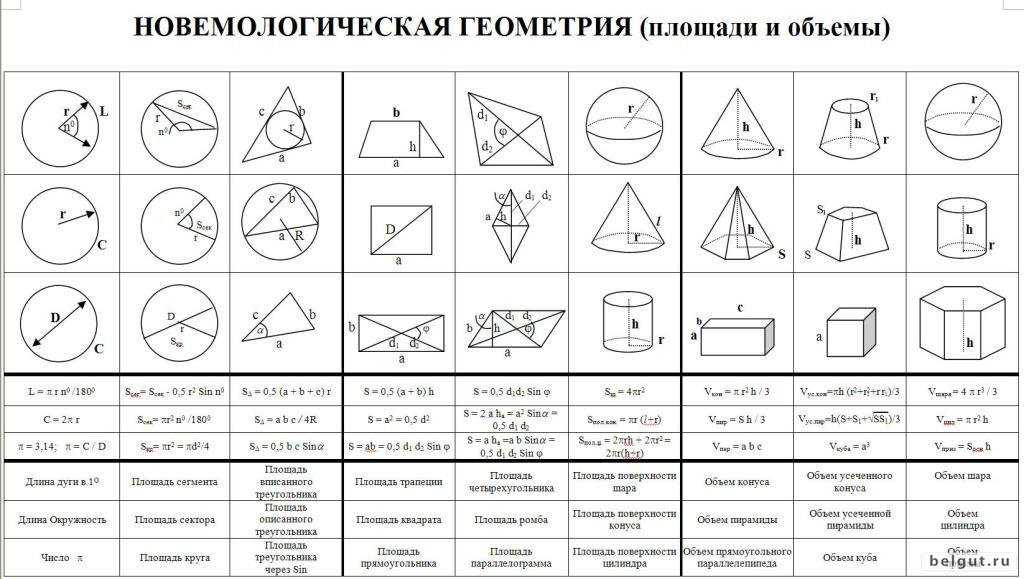
V = Bh
Пара примеров, показывающих, как найти объем призмы
Треугольная призма
1. Найдите объем треугольной призмы, показанной на рисунке выше, используя приведенную ниже формулу.
V = Bh
Размеры треугольного основания 12 м и 20 м.
Высота треугольной призмы h = 10 м.
B = площадь треугольного основания = (20 умножить на 12)/2 = 240/2 = 120 м 2
V = 120 умножить на 10 = 1200
Объем треугольной призмы 1200 куб.
Трапециевидная призма
2. Найдите объем трапециевидной призмы, показанной на рисунке выше, используя приведенную ниже формулу.
V = Bh
Основанием трапециевидной призмы является трапеция со следующими размерами.
b 1 = 12 футов, b 2 = 8 футов и высота = 7 футов.
Высота трапециевидной призмы равна перпендикулярному расстоянию или 20 футов
B = площадь основания = [(b 1 + b 2 )h]/2
B = [(12 + 8)7]/2
B = [(20)7]/ 2
B = 140/2
B = 70 кв.