Формулы окружность: Длина окружности и площадь круга — урок. Геометрия, 9 класс.

Содержание

Калькулятор Формулы Окружности — Mathcracker.Com

Инструкции: Используйте этот калькулятор формулы окружности, чтобы вычислить значение окружности для круга с заданным радиусом r, указанным в поле ниже.

Подробнее об окружности круга

Этот калькулятор позволит вам вычислить окружность круга для заданного радиуса. Для этого необходимо ввести правильное выражение для радиуса. Это может быть любое допустимое числовое выражение, например ‘2’ или ‘1/3’. Единственное ограничение — оно должно быть положительным.

Как только вы укажете правильный радиус, будет использована формула окружности с указанием всех шагов.

окружность это мера длины, полученная, если мы получим круг и сможем его «выпрямить», почти как если бы круг состоял из тонкой вермишели, и мы могли бы разрезать его, и фактически измерить длину вермишели.

Как вычислить окружность круга?

Идея о том, что окружность круга — это длина, геометрически ясна, но ее не так просто воплотить в реальное измерение. Математикам потребовались столетия, чтобы вывести формулу окружности круга:

\[\displaystyle C = 2 \pi r \]

Действительно, просто, но очень концептуально. Математики искали что-то простое, но они искали что-то более «квадратное». Эта загадочная константа $\pi$ стала необходимым концептуальным шагом для фундаментального разграничения квадратов и кругов.

Как вычислить окружность круга с радиусом

Шаг 1: Определите радиус предоставленной окружности. Если он отрицательный, то вы не можете продолжить
Шаг 2: Уравнение $ C = 2 \pi r $, и вставьте в него известное значение r
Шаг 3: Если фактическая окружность зависит от $\pi$, вы можете оставить ее в терминах $\pi$, или использовать калькулятор, чтобы оценить его числовое значение

Шаг 4: Если r задан в единицах длины, используйте те же единицы длины для окончательного результата окружности

Процесс нахождения окружности круга и вычисления окружности тривиальны — достаточно воспользоваться формулой, подставив в нее значение r.

Вопрос: что такое окружность?

Хотя расчеты тривиальны, вы, возможно, все еще думаете, что такое окружность и что она собой представляет. И это логично, ведь математикам из древних греков потребовалось немало размышлений, чтобы придумать ответ на этот вопрос.

Окружность — это длина окружности или, по крайней мере, так она определяется. Теперь, хотя идея существования четко определенной длины окружности легко принимается, достижение согласия относительно того, как определяется «длина», является концептуальной проблемой.

Калькулятор перевода диаметра в окружность

Шаг 1: Если вместо радиуса вам предоставлен диаметр d, определите его и возможную единицу длины. Она должна быть положительной, иначе вы не сможете продолжить
Шаг 2: Поскольку мы знаем, что d = 2r, мы просто вычислим радиус r, разделив диаметр на 2
Шаг 3: Затем используем обычное уравнение $ C = 2 \pi r $ и подставляем значение, которое мы рассчитали для r

Другой способ увидеть это — непосредственно вычислить окружность от диаметра используя формулу $C = \pi d$.

Зачем мне формула окружности, если я могу использовать калькулятор

Справедливое замечание. Хотя в данном конкретном случае очень важно понять, откуда взялась формула окружности. Это очень простая формула, но в ней заложен глубокий смысл. Вы можете использовать Калькулятор окружности конечно, особенно если он показывает шаги, как в этом случае.

Существует множество применений окружности, и, что более важно, она порождает множество других понятий.

Пример: вычисление окружности

Используйте формулу окружности, чтобы найти окружность круга радиусом $r =\frac{3}{4}$.

Отвечать: Нам нужно найти окружность $C$ круга, а из предоставленной информации мы знаем, что радиус круга равен $r = \frac{3}{4}$.

Теперь формула для окружности имеет вид $C = 2\pi r$, и поэтому все, что нам нужно сделать, это подставить в эту формулу известное значение известного радиуса $r = \frac{3}{4}$. Получается следующее:

\[ \begin{array}{ccl} C & = & \displaystyle 2 \pi r \\\\ \\\\ & = & \displaystyle 2 \pi \cdot \frac{3}{4} \\\\ \\\\ & = & \displaystyle \frac{3}{2}\pi{} \end{array} \]

На этом расчеты завершены. Мы выяснили, что окружность круга равна $\displaystyle C = \frac{3}{2}\pi{}$.

Пример: другой расчет окружности

Теперь предположим, что диаметр круга равен d = 2.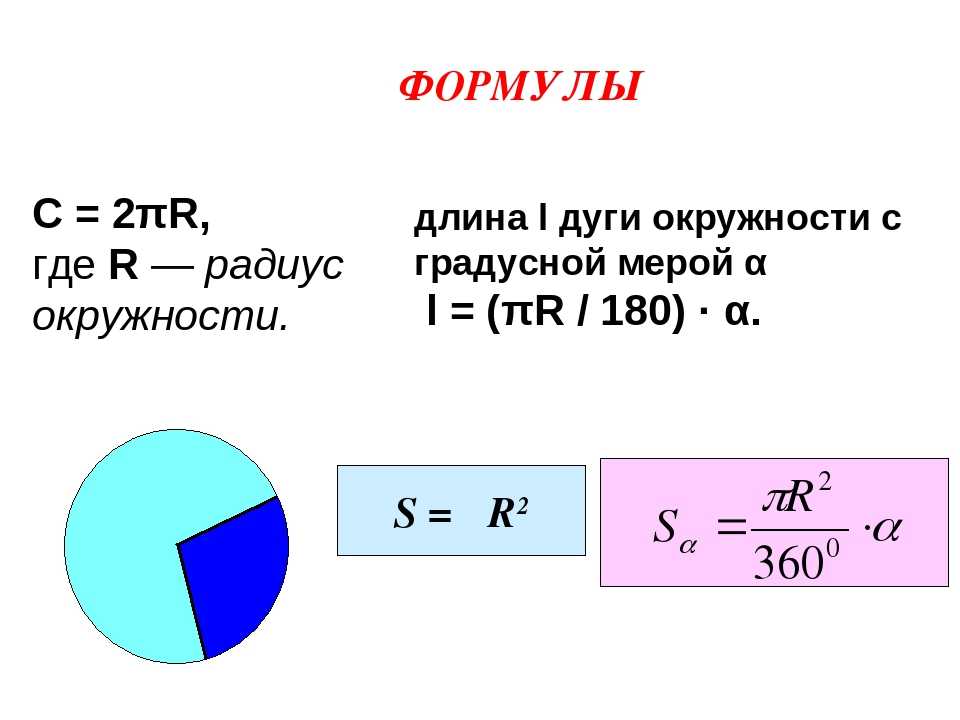 Вычислите его окружность.

Отвечать: Нам нужно найти окружность $C$ круга, а диаметр известен и равен d = 2. Поскольку диаметр должен быть равен удвоенному радиусу, делаем вывод, что радиус окружности равен $r = 1$.

Следовательно, используя формулу для окружности:

\[ C = \displaystyle 2 \pi r = 2 \pi \cdot 1 = 2\pi \]

тогда окружность равна $\displaystyle C = 2\pi{}$.

Пример: другой пример

Можно ли найти окружность круга для радиуса r = -3?

Отвечать: Нет. Чтобы найти действительную окружность, радиус должен быть положительным.

Другие полезные сопутствующие калькуляторы

Существует множество других вещей, которые вы хотели бы сделать с окружностями. Например, вы можете захотеть вычислить площадь круга , или найти уравнение окружности . Обратите внимание, что для вычисления периметра требуется только радиус, а не все уравнение окружности.

В некоторых случаях у вас будет уравнение окружности в общем виде что может потребовать некоторых манипуляций с формула окружности найти радиус и вычислить его окружность.

Способ эмпирических формул. Окружность головы

У новорожденного ребенка окружность головы в среднем 35 см.

В возрасте 6 месяцев окружность головы составляет 43 см.

В первые 6 месяцев жизни окружность головы увеличивается на 1,5 см, посте 6 месяцев – на 0,5 см. формулы следующие.

До 6 месяцев: 43 – 1,5 · (6 – n)

После 6 месяцев: 43 + 0,5 · (n – 6)

где n – возраст ребенка в мес.

К 1 году окружность головы около 47 см. (допустимые пределы ± 2 см).

После года окружность головы увеличивается более медленно, достигая к 5 годам 50см, а за все последующие годы до 15-16 лет увеличивается еще на 5-6 см.

До 5 лет окружность головы увеличивается в среднем на 1 см за год, после 5 лет – на 0,6 см. Формулы следующие:

От 1 до 5 лет 50 – 1 · (5 – n)

После 5 лет 50 + 0,6 · (n – 5)

где n – возраст ребенка в годах.

У девочек окружность головы несколько меньше, чем у мальчиков.

Способ эмпирических формул. Окружность грудной клетки

Окружность грудной клетки у новорожденного 33-35 см и колеблется в зависимости от веса при рождении. Окружность грудной клетки увеличивается более интенсивно, чем окружность головы. И эти два показателя сравниваются в возрасте 4 мес.

В возрасте 6 месяцев окружность грудной клетки составляет 45 см.

До 6 месяцев окружность грудной клетки увеличивается за каждый месяц на 2 см, после 6 месяцев до 1 года – на 0,5 см. Формулы для расчета долженствующего показателя окружности грудной клетки следующие:

До 6 месяцев: 45 – 2 · (6 – n)

От 6 мес. до 1 года: 45 + 0,5 · (n – 6)

где n – возраст ребенка в мес.

В возрасте 10 лет окружность грудной клетки составляет 63 см. От 1 года до 10 лет прибавка окружности грудной клетки составляет 1,5 см, после 10 лет – 3 см. Формулы для расчетов следующие:

От 1 года до 10 лет: 63 – 1,5 · (10 – n)

После 10 лет: 63 + 3 · (n — 10)

где n – возраст ребенка в годах.

Алгоритм расчета при использовании эмпирических формул

При использовании эмпирических формул используется следующий алгоритм расчета:

По формуле рассчитывается долженствующий показатель;
Вычисляется абсолютная разница между фактическим показателем и долженствующим;
Вычисляется процентная значимость разницы, т. е. составляется пропорция:

долженствующий показатель – 100 %

разница – X

Если отклонение от долженствующего показателя не превышает 7 %, такой показатель (вес, рост) называется средний.

Отклонение показателя от 8 до 20 % от долженствующей величины расценивается как выше среднего или ниже среднего.

Отклонение более, чем на 20 % расценивается как высокий или низкий показатель (рост, вес).

Оценка показателей физического развития по центильным таблицам

Второй способ оценки показателей физического развития – по центильным таблицам.

Учитывая наблюдающееся варьирование различных показателей физического развития ребенка, нужно знать так называемое нормальное или гаусс-лаплассовское распределение. График нормального распределения Гаусса – Лапласса выглядит в виде параболы, где по горизонтальной оси отмечается величина признака, по вертикальной оси – частота встречаемости признака.

Для составления центильных таблиц необходимо большое количество измерений по каждому параметру в каждой возрастной группе – 500 или 1000. Но, если, допустим, взять 100 мальчиков в возрасте 10 лет и поставить их в порядке возрастания, т.е. первый мальчик самый маленький, а последний – самый большой, то получиться, что мальчик, который будет стоять третий по порядку, имеет рост 126,4 см (это третий центиль). Десятый в ряду мальчик имеет рост 129,2 см (это десятый центиль). И так далее.

Центили указывают процент детей, которые имеют показатель физического развития (рост, вес, окружность головы, груди) ниже указанного в таблице. Например, 10 % мальчиков 10-летнего возраста имеют рост меньше 129,2 см. и, соответственно 90 % – больше.

Показатели физического развития, находящиеся в интервале:

между 25-м и 75-м центилями, называются средние;
между 75-м и 90-м центилями – выше среднего;
между 90-м и 97-м центилями – высокие;
более 97-го центиля – очень высокие, как правило это патология.

Показатели, находящиеся в интервале:

от 25-го до 10-го центиля – ниже среднего;
от 10-го до 3-го центиля – низкие;
ниже 3-го центиля – очень низкие, как правило это патология.

Например, мальчик 10-летнего возраста имеет рост 128 см. Этот показатель находится в интервале между 10-м и 25-м центилями, он называется ниже среднего. Заключение: рост мальчика ниже среднего.

2, где r равно радиусу, а координаты (x,y) равны центру окружности. Переменные h и k представляют горизонтальные или вертикальные сдвиги на круговой диаграмме.

круг центр радиус формула расстояния уравнение для окружности

Итак, как вы знаете, окружность — это бесконечное множество точек, равноудаленных от центра, хорошо? Что мы собираемся сделать сейчас, так это взглянуть на нахождение уравнения для окружности.
Мы видим круг радиусом 4 с центром в начале координат, хорошо? Итак, что мы знаем, так это то, что у нас есть начало координат, поэтому у нас есть точка 0, 0, и у нас есть куча точек, которые составляют 4 единицы, и мы перемещаемся оттуда, хорошо? Таким образом, мы не знаем, какова наша конкретная точка, мы просто знаем, что это будут x, y, и мы знаем, что расстояние от начала координат равно 4. Что мы можем сделать, так это использовать формулу расстояния, потому что мы смотрим на расстояние между точкой и началом координат, так что, надеюсь, вы помните формулу расстояния, так как расстояние равно квадратному корню из х минус х один в квадрате плюс у минус у одна величина в квадрате, хорошо? Таким образом, все, что нам нужно сделать в этом случае, — это расстояние от начала координат до нашей точки — это просто радиус, в данном случае 4, и мы имеем дело с точкой, которая, как мы знаем, равна 0, 0, поэтому мы можем просто подставить 0, 0 для х один и у один, и в итоге мы получим 4 равно х в квадрате плюс у в квадрате и гигантский квадратный корень из этого хорошо х минус 0 это просто х в квадрате это х в квадрате, у-0 у, у в квадрате у в квадрате хорошо? Итак, что я хочу сделать сейчас, так это избавиться от этого квадратного корня, все, что мне нужно сделать, это возвести в квадрат обе стороны, и в итоге мы получим 16, равное х в квадрате плюс у в квадрате. Итак, это конкретное уравнение для этого конкретного круга.
Сейчас я хочу посмотреть на общее уравнение, хорошо? Итак, для общего уравнения допустим, что у нас есть радиус r, и мы центрируемся вокруг точки hk, хорошо? Я все равно собираюсь перейти к нашей формуле расстояния, и поэтому наше расстояние в этом случае будет расстоянием от центра до другой стороны, которое равно r, поэтому вы получите r равный квадрату корень из разницы x наш первый x это просто переменная минус h количество в квадрате плюс y минус k, y в квадрате мы берем квадратный корень из всего, что тогда точно так же, как мы делали раньше, мы хотим возвести в квадрат обе стороны, чтобы избавиться от этого квадратного корня и в итоге мы получаем, что r в квадрате равно количеству x минус h в квадрате плюс y минус k в квадрате количества. И это общее уравнение для окружности, хорошо? Таким образом, мы знаем, глядя на него, мы узнаем центр, и мы также узнаем радиус.

Уравнения окружностей

Для этого урока вам необходимо понять технику: Завершение площади

В то время как важная техника завершение квадрата находится на кончиках ваших пальцев, самое время обсудить уравнения окружностей.

Предположим, что у окружности есть центр $\,(h,k)\,$ и радиусом $\,r\,$ (где $\,r \ge 0\,$). Пусть $\,(x,y)\,$ — типичная точка на этом круге. См. диаграмму ниже.

Расстояние от $\,(x,y)\,$ до $\,(h,k)\,$ должен равняться $\,г\,$: 92$$

Чтобы исключить надоедливый квадратный корень, квадрат с обеих сторон. Таким образом, мы имеем:

УРАВНЕНИЯ КРУГОВ (стандартная форма)

Уравнение окружности с центром $\,(h,k)\,$ и радиус $\,r\,$ (где $\,r\ge 0\,$): $$ \cssId{s17}{(xh)^2 + (yk)^2 = r^2} $$ Эта форма уравнения часто называется 92 \end{выравнивание} $$

Таким образом, $\,h = 3\,$ $\,к = -5\,$ и $\,r = \sqrt{15}\,. $ Графики уравнений в виде круга с центром $\,(h,k) = (3,-5)\,$ и радиус $\,r = \sqrt{15}\,.$

Студенты иногда любят думать из этого так:

$x$-значение центра круг — это значение $\,x\,$, которое делает $\,x-h\,$ равны нулю.
В нашем примере, что делает $\,x-3\,$ равен нулю? Ответ: $\,3\,$
$y$-значение центра круга это значение $\,y\,$, которое делает $\,y-k\,$ равен нулю.
В нашем примере что делает $\,y+5\,$ равным нулю? Ответ: $\,-5\,$
Радиус круга равен квадрату корень правой части уравнения.
В нашем примере, что такое квадратный корень $\,15\,$? Ответ: $\,\sqrt{15}\,$ 92 = 15
Вуаля!
Как распознать уравнение окружности
К сожалению, круги не всегда даются вам в этой красивой стандартной форме. Иногда они даны вам всем умножается. В этой ситуации вы все равно должны быть в состоянии признать, что вы имеете дело с кругом, и вы должны быть в состоянии поместить его в стандартную форму. 92} $$
Если бы уравнение изначально было дано вам в таком виде, вы все еще должны быть в состоянии распознать его как круг! (Для развлечения введите это последнее уравнение в Вольфрам Альфа убедить себя, что мы все еще имеем дело с одним и тем же кругом.) 92\,$ члены находятся на той же стороне уравнения , тогда у них будет одинаковый коэффициент.
Эти наблюдения приводят к следующему способу распознавания кругов:
УЗНАНИЕ КРУГОВ (когда они не в стандартной форме) 92\,$ члены, и они должны иметь тот же коэффициент, когда они на одном сторону уравнения.
Вам разрешено (но не обязательно) иметь $\,x\,$ $\,y\,$ и постоянные члены. У вас может не быть других типов терминов. 92 = -1\,.$ В этом случае нет действительных чисел $\,x\,$ и $\,y\,$, которые делают уравнение верным.
Следующий пример иллюстрирует процесс распознавания уравнения окружности и придать ему стандартную форму чтобы его можно было легко изобразить на графике. 92\,$ типы термов, и у них одинаковый коэффициент когда они находятся на одной стороне уравнения. Другими членами этого уравнения являются $\,x\,$ и постоянные термины, которые являются допустимыми типами терминов для круга. Следовательно, это уравнение окружности.
Оформите его в стандартной форме следующим образом: 92$
Переименуйте, чтобы упростить идентификацию.
Таким образом, это круг с центром $\,(\frac{5}{6},0)\,$ и радиус $\,\frac{11}{6}\,.$ Проверьте этот результат с помощью Вольфрам Альфа! (Возможно, вам придется щелкнуть вкладку «Свойства», чтобы получить некоторые из желаемая информация.)
Зная центр и радиус круга, всегда есть четыре точки, которые легко построить. Начните с центра, и двигаться вверх/вниз влево/вправо на величину радиуса.
Еще один способ обрести уверенность в себе работа заключается в том, чтобы проверить хотя бы один из этих четырех простых точек в исходном уравнении.
No related posts.