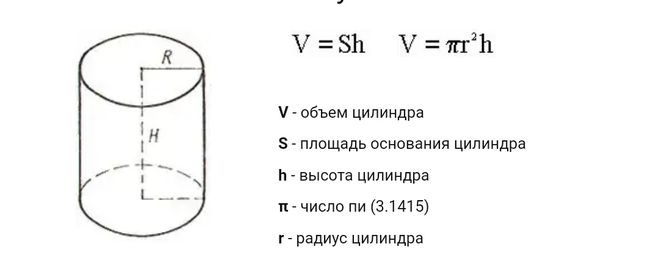
площадь боковой поверхности. Формула площади боковой поверхности цилиндра
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
- Образующей называют условно высоту цилиндра.
 При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело. - Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого – это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
- Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
- Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.

Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания – R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая – L.
- Высота – H.
- Площадь основания – Sосн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра – h1,h2 (минимальная и максимальная).
- Площадь боковой поверхности – Sбок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры – V.
- Площадь полной поверхности – S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность.
 Как известно, она получается благодаря движению образующей по заданной кривой.
Как известно, она получается благодаря движению образующей по заданной кривой. - Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина – параллельные хорды стереометрической фигуры.
- Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем – для прямого.
Примеры с разобранным решением
Задача 1.
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается <ACD = 30°
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра.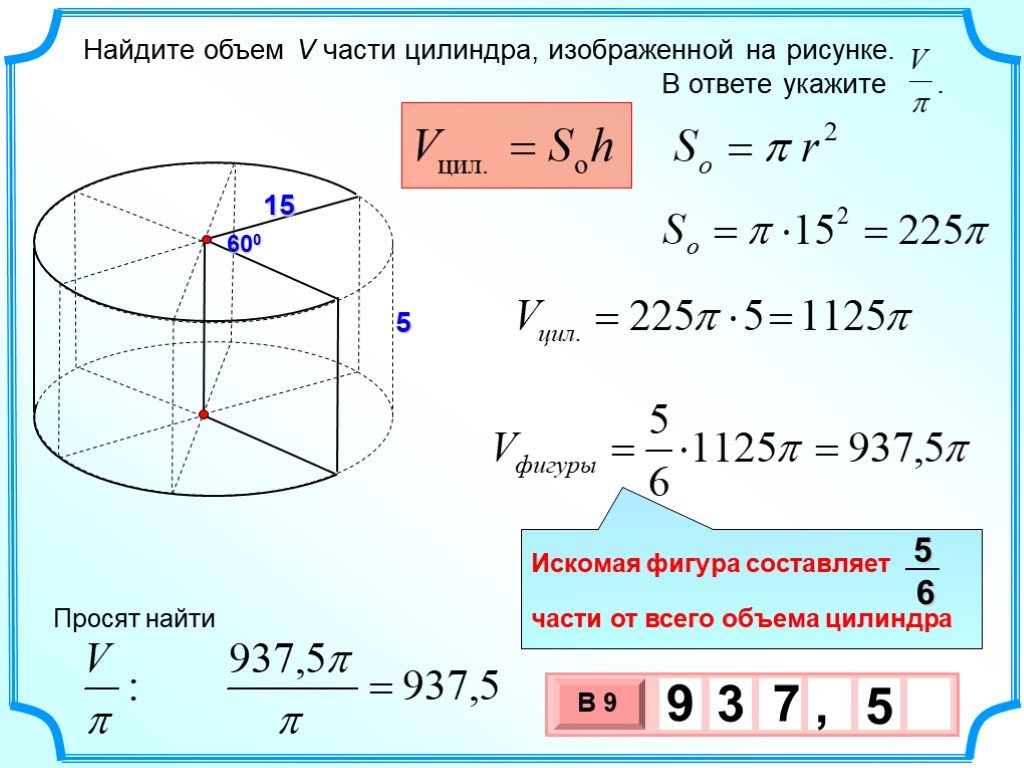 Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Задача 2.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: Smin будет достигнута при h = 1/32 см, R = 64 см.
Задача 3.
Дана стереометрическая фигура – цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.
Решение.
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² – ВМ²
МК² = 17² – 15²
МК² = 64
МК = 8
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг – проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD – диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC – прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD – трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Пример 1.
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Пример 2.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
Площадь стен цилиндра. Как найти площадь цилиндра
Цилиндр – это фигура, состоящая из цилиндрической поверхности и двух окружностей, расположенных параллельно. Расчет площади цилиндра – это задача геометрического раздела математики, которая решается достаточно просто.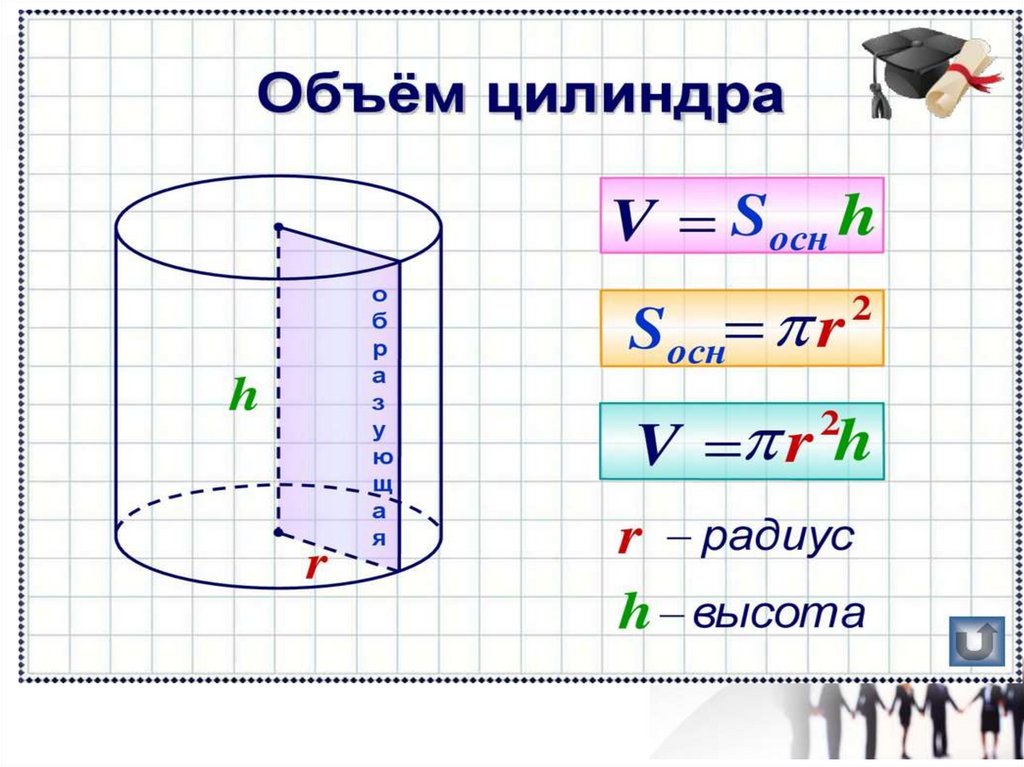 Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Существует несколько методов ее решения, которые в результате всегда сводятся к одной формуле.
Как найти площадь цилиндра – правила вычисления
- Чтобы узнать площадь цилиндра, необходимо две площади основания сложить с площадью боковой поверхности: S= Sбок.+ 2Sосн. В более развернутом варианте данная формула выглядит так: S= 2 π rh+ 2 π r2= 2 π r(h+ r).
- Площадь боковой поверхности данного геометрического тела можно высчитать, если известны его высота и радиус окружности, лежащей в основании. В данном случае можно выразить радиус из длины окружности, если она дана. Высота может быть найдена, если в условии задано значение образующей. В этом случае образующая будет равна высоте. Формула боковой поверхности данного тела выглядит так: S= 2 π rh.
- Площадь основания считается по формуле нахождения площади круга: S osn= π r 2 . В некоторых задачах может не даваться радиус, но задаваться длина окружности. С данной формулы радиус выражается достаточно легко.
 С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра. - При выполнении всех этих расчетов число π обычно не переводится в 3,14159… Его нужно просто дописывать рядом с числовым значением, которое было получено в результате проведения вычислений.
- Далее необходимо лишь умножить найденную площадь основания на 2 и прибавить к полученному числу вычисленную площадь боковой поверхности фигуры.
- Если в задаче указывается, что в цилиндре есть осевое сечение и это – прямоугольник, то решение будет немного другим. В таком случае ширина прямоугольника будет являться диаметром окружности, лежащей в основании тела. Длина фигуры будет равна образующей или высоте цилиндра. Необходимо высчитать нужные значения и подставить в уже известную формулу. В данном случае ширину прямоугольника нужно разделить на два, чтобы найти площадь основания. Для нахождения боковой поверхности длина умножается на два радиуса и на число π.
- Можно высчитать площадь данного геометрического тела через его объем.
 Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
Для этого нужно из формулы V=π r 2 h вывести недостающую величину. - В вычислении площади цилиндра нет ничего сложного. Нужно только знать формулы и уметь выводить из них величины, необходимые для проведения расчетов.
При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.
Понятие цилиндра
Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.
- Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
- Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.

- Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
- Под осью подразумевают прямую, проходящую через оба основания фигуры.
- Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.
Существуют разновидности данной объемной фигуры:
- Под круговым подразумевают цилиндр, направляющая которого — это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
- Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
- Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
- Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.

Условные обозначения
Традиционно основные «компоненты» цилиндра принято называть следующим образом:
- Радиус основания — R (он же заменяет аналогичную величину стереометрической фигуры).
- Образующая — L.
- Высота — H.
- Площадь основания — S осн (иначе говоря, необходимо найти указанный параметр круга).
- Высоты скошенного цилиндра — h 1 ,h 2 (минимальная и максимальная).
- Площадь боковой поверхности — S бок (если ее развернуть, то получится своего рода прямоугольник).
- Объем стереометрической фигуры — V.
- Площадь полной поверхности — S.
«Компоненты» стереометрической фигуры
Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.
Основными составляющими фигуры являются:
- Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.

- Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
- Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина — параллельные хорды стереометрической фигуры.
- Под осевым сечением подразумевают расположение плоскости через центр тела.
- И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.
Основные формулы для работы с цилиндром
Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.
Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем — для прямого.
Примеры с разобранным решением
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается
Решение. Поскольку известны величины диагонали и угла, то в таком случае:
- CD = AC*cos 30°.
Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.
Аналогично, можно найти и значение AD:
- AD = AC*sin 30°
Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.
Она равна сумме предыдущих двух площадей.
Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?
Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.
Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.
Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.
Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.
Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.
Дана стереометрическая фигура — цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см.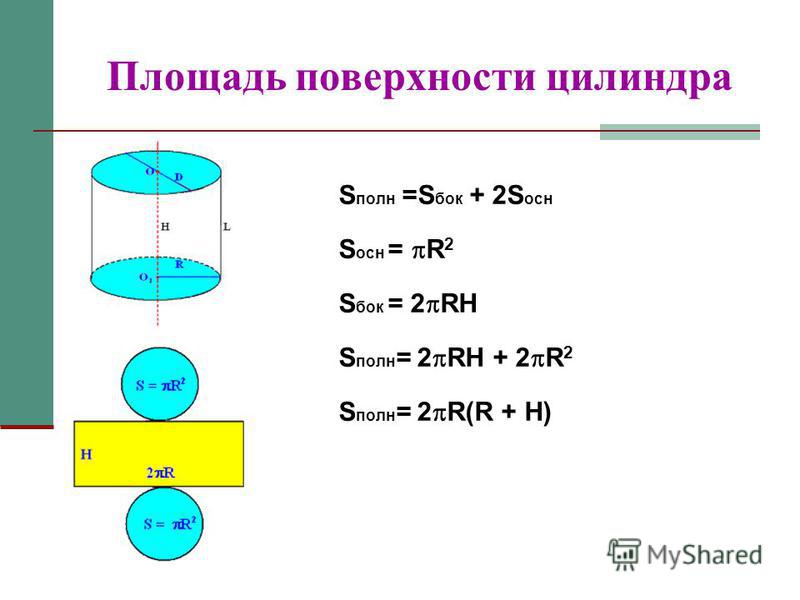
Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.
ВК² = ВМ² + МК²
МК² = ВК² — ВМ²
МК² = 17² — 15²
Отсюда можно сделать вывод, что МК = ВС = 8 см.
Следующий шаг — проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.
AD — диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.
BC — прямая, расположенная на плоскости имеющегося прямоугольника.
ABCD — трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.
Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.
Для этого необходимо найти величины AD и ОС.
Ответ: сечение располагается 3 см от оси.
Задачи на закрепление материала
Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания — Q, площадь осевого сечения — М. Необходимо найти S. Иными словами, полную площадь цилиндра.
Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.
Представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью.
Цилиндр состоит из боковой поверхности и двух оснований. Формула площади поверхности цилиндра включает в себя отдельный расчет площади оснований и боковой поверхности. Так как основания в цилиндре равны, то полная его площадь будет рассчитываться по формуле:
Пример расчета площади цилиндра мы рассмотрим после того, как узнаем все необходимые формулы. Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Для начала нам понадобится формула площади основания цилиндра. Так как основанием цилиндра является круг, то нам потребуется применить :
Мы помним, что в этих расчетах используется постоянное число Π = 3,1415926, которое рассчитано как соотношение длины окружности к ее диаметру. Это число является математической константой. Пример расчета площади основания цилиндра мы также рассмотрим чуть позже.
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
А теперь рассмотрим задачу, в которой нам потребуется рассчитать полную площадь цилиндра. В заданной фигуре высота h
= 4 см, r
= 2 см. Найдем полную площадь цилиндра.
Для начала рассчитаем площадь оснований:
Теперь рассмотрим пример расчета площади боковой поверхности цилиндра. В развернутом виде она представляет прямоугольник. Его площадь рассчитывается по приведенной выше формуле. Подставим в нее все данные:
Полная площадь круга представляет собой сумму двойной площади основания и боковой:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета :
Цилиндр (происходит из греческого языка, от слов «каток», «валик») — это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.
Цилиндрическая поверхность — это поверхность, которая получена прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия — направляющей.
Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:
1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется
2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.
У него угол между образующей линией и основанием не является прямым.
3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.
Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.
Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:
Sp = 2п Rh + 2п R2 = 2п R (h+R).
Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.
Данная цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.
Развертка — это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.
Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:
Если взять круговой, прямой цилиндр, то для него:
P = 2п R, а Sb = 2п Rh.
Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.
К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.
Чтобы вычислить цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая — диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.
Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды.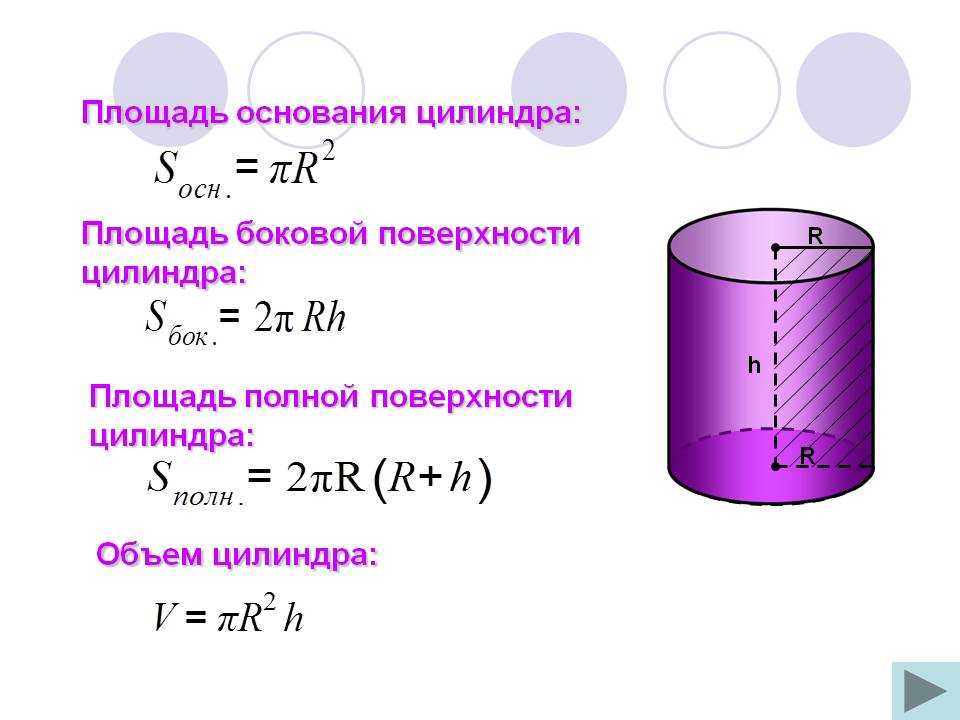 Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника — это искомая которой ищется по звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:
Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника — это искомая которой ищется по звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:
С2 = А2 + В2.
Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.
Площадь окружности равна:
S окр. = 2п R2.
Чтобы найти R, нужно ее длину C разделить на 2п:
R = C \ 2п, где п — число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.
Формула радиуса цилиндра:
где V — объем цилиндра, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb — площадь боковой поверхности, h — высота
Цилиндр — геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S — площадь полной поверхности, h — высота
Площадь поверхности цилиндра — формулы, вывод, решенные примеры и часто задаваемые вопросы
Цилиндр представляет собой трехмерную твердую форму, имеющую два параллельных круглых основания, соединенных криволинейной поверхностью на фиксированном расстоянии. Его также можно рассматривать как набор круглых дисков, уложенных друг на друга.
Его также можно рассматривать как набор круглых дисков, уложенных друг на друга.
Отрезок, соединяющий центры круговых оснований, называется осью цилиндра. Расстояние между осью и внешней изогнутой поверхностью называется радиусом (r) цилиндра, а перпендикулярное расстояние между двумя параллельными круговыми основаниями называется высотой (h) цилиндра.
Примеры цилиндров: свечи, резервуар для воды, трубы, колодец и т. д.
Эксперты в Веданту составили эту статью, чтобы помочь учащимся легко усвоить концепции. Прочтите полную статью, чтобы узнать о следующих концепциях:
Площадь поверхности цилиндра
В геометрии площадь любой формы — это область, покрытая ею на плоскости. Цилиндр состоит из двух типов поверхностей: одна представляет собой криволинейную поверхность, а другая представляет собой круглое основание. Площадь обоих круговых оснований одинакова.
Площадь поверхности цилиндра можно разделить на два типа:
Площадь криволинейной поверхности (CSA)
Общая площадь поверхности (TSA)
Площадь криволинейной поверхности (CSA) цилиндра 90 Площадь криволинейной поверхности цилиндра определяется как площадь его криволинейной поверхности или площадь, полученная после исключения площади двух его круглых оснований.
 Ее также называют площадью боковой поверхности (LSA).
Ее также называют площадью боковой поверхности (LSA).CSA цилиндра с радиусом основания «r» и высотой «h» определяется по формуле:
Площадь криволинейной поверхности (CSA) цилиндра = 2πrh кв. единиц.
Общая площадь поверхности (TSA) цилиндра
Общая площадь поверхности цилиндра определяется как сумма площадей его криволинейной поверхности и двух круглых оснований.
TSA цилиндра с радиусом основания ‘r’ и высотой ‘h’ определяется по формуле:
Общая площадь поверхности (TSA) цилиндра = площадь криволинейной поверхности + площадь двух его круглых оснований
или,
TSA цилиндра = CSA цилиндра + площадь двух его круглых оснований
= 2πrh + 2πr2 кв. с цветными бумагами. Покрытие должно быть сделано с минимальным количеством бумаги. Итак, для покрытия цилиндра сначала возьмите прямоугольный лист бумаги, длина которого (l) как раз достаточна, чтобы обернуть цилиндр, а ширина равна высоте (h) цилиндра, как показано на рисунке ниже.
(Изображения скоро будут обновлены)
Следует отметить, что длина (l) прямоугольного листа равна длине окружности круглого основания, которая равна 2πr.
Площадь прямоугольного листа дает площадь криволинейной поверхности цилиндра.
Таким образом, площадь изогнутой поверхности цилиндра = площадь прямоугольной листа бумаги
= длина × ширина
= окружность круглого основания × h
= 2πr × h
Следовательно, площадь криволинейной поверхности цилиндра = 2πrh кв.
Теперь, если верх и низ цилиндра нужно также оклеить цветной бумагой, то для этого нам понадобятся две круглые области радиусом r и площадью πr2 каждая.
Таким образом, общая площадь поверхности цилиндра = площадь криволинейной поверхности + площадь двух круглых областей
= CSA цилиндра + πr2 + πr2
= 2πrh + 2πr2
Следовательно, общая площадь поверхности цилиндра = 2πr (h + r) кв. цилиндра.
цилиндра.
Решенные Примеры:
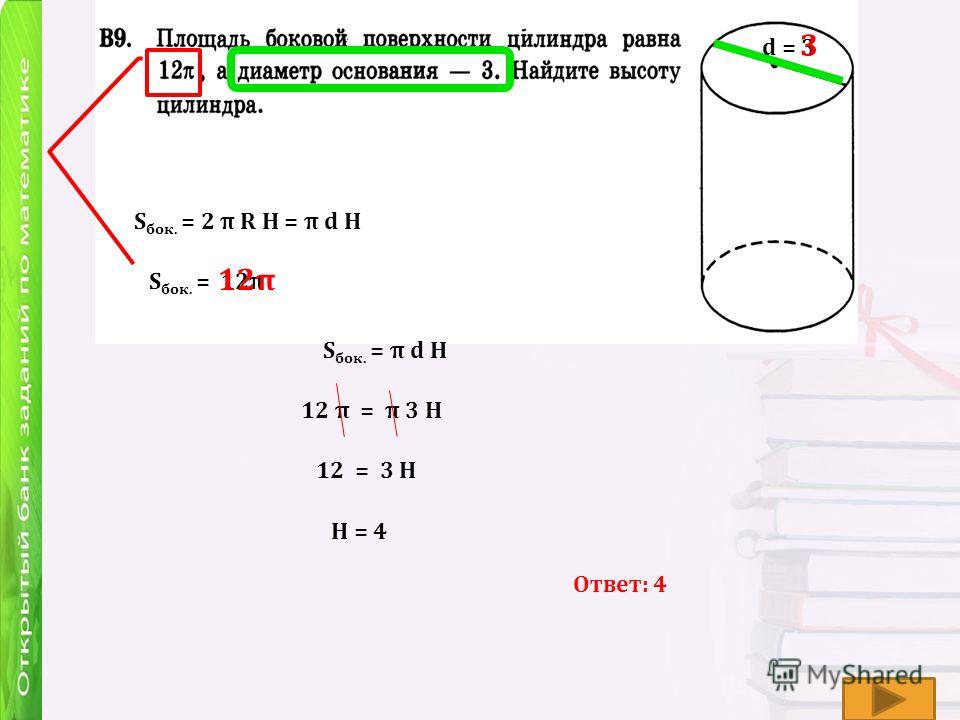
Q.1. Цилиндрический столб диаметром 50 см и высотой 7 м. Найдите стоимость покраски криволинейной поверхности столба из расчета 12 ₹ за кв.м.
Решение: Дано, высота (h) цилиндрического столба = 7 м
А, радиус (r) круглого основания = 50/2 см = 25 см = 0,25 м
Итак, площадь криволинейной поверхности цилиндрического столба = 2πrh Sq. Units
= 2 × (22/7) × 0,25 × 7
= 2 × (22/7) × (25/100) × 7
= 11 кв. MTS
Учитывая, что стоимость покраски 1 кв.м площади составляет ₹12.
∴ стоимость покраски 11 кв.м площади = 11 × 12 = 132 ₹
Таким образом, стоимость покраски криволинейной поверхности столба из расчета 12 ₹ за кв.м. составляет 132 фунта стерлингов.
Q.2. Площадь криволинейной поверхности прямоугольного кругового цилиндра с радиусом основания 7 см равна 110 см2. Найдите высоту цилиндра.
Найдите высоту цилиндра.
Решение: Дано, радиус основания (r) цилиндра = 7 см.
А, площадь изогнутой поверхности цилиндра = 110 см2
Пусть высота цилиндра равна h.
Тогда 2πrh = 110 см2
⇒ 2 × (22/7) × 7 × h = 110 см2
⇒ h = 2,5 см.
Следовательно, высота правого кругового цилиндра равна 2,5 см.
Q.3. Сколько квадратных метров листового металла потребуется для изготовления закрытого цилиндрического резервуара высотой 1,8 м и диаметром основания 140 см?
Решение: Дано, высота закрытого цилиндрического резервуара = 1,8 м
Радиус (r) круглого основания = 140 см/2 = 70 см = 0,7 м
Итак, площадь металлического листа, необходимая для изготовления замкнутого цилиндрического резервуара = общая площадь поверхности цилиндра = 2πr (h + r)
(22/7) × 0,7 × 2,5
= 2 × (22/7) × (7/10) × (25/10)
= 11 кв.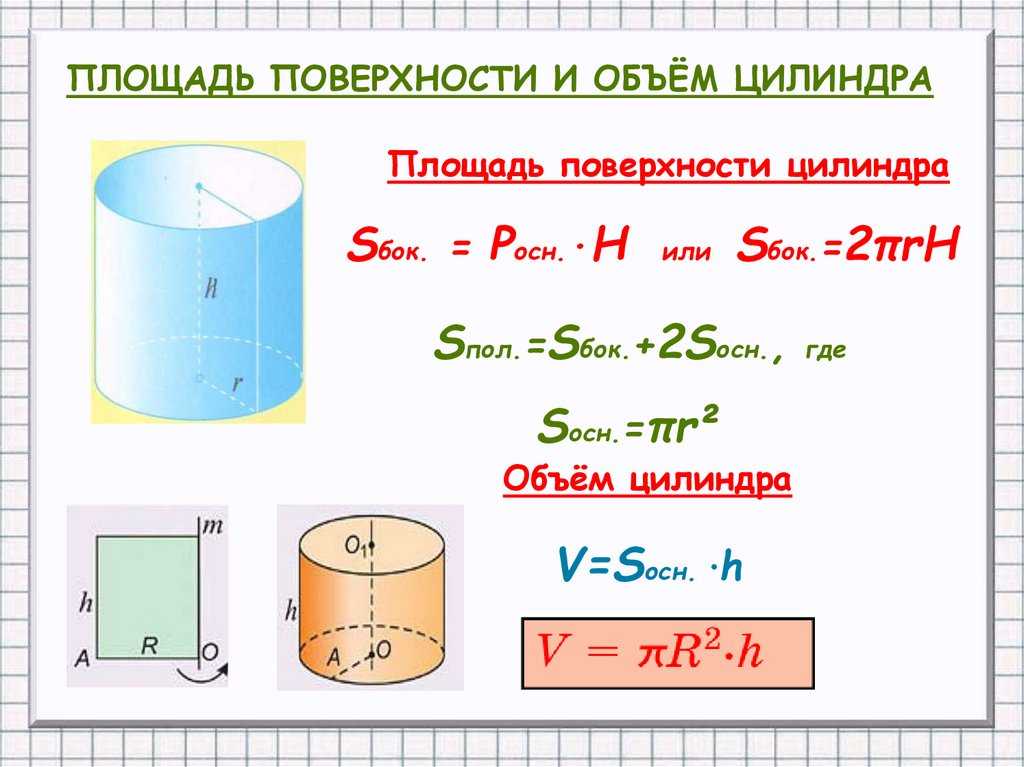 сделать закрытый цилиндрический резервуар площадью 11 кв.м.
сделать закрытый цилиндрический резервуар площадью 11 кв.м.
Формулы цилиндров — xGeometry
- Дом
- ›
- Формулы
- ›
- Цилиндр
| 92$$
| Данные | Формула |
|---|---|
| Объем | В = π г × ч |
| Радиус | г = √( В / (π × ч)) |
| Высота | ч = В / (π × r 2 ) |
| Объем | В = A база × h |
| Базовая зона | А база = В/ч |
| Высота | ч = В/А база |
| Боковая поверхность | S широта = 2 π r × h |
| Радиус | г = В / (2 π ч) |
| Высота | ч = В / (2 π г) |
| Базовая зона | A база = π r 2 |
| Радиус | г = √(A основание /π) |
| Общая площадь | S до = 2 × A основание + S шир. |

 При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
 Как известно, она получается благодаря движению образующей по заданной кривой.
Как известно, она получается благодаря движению образующей по заданной кривой.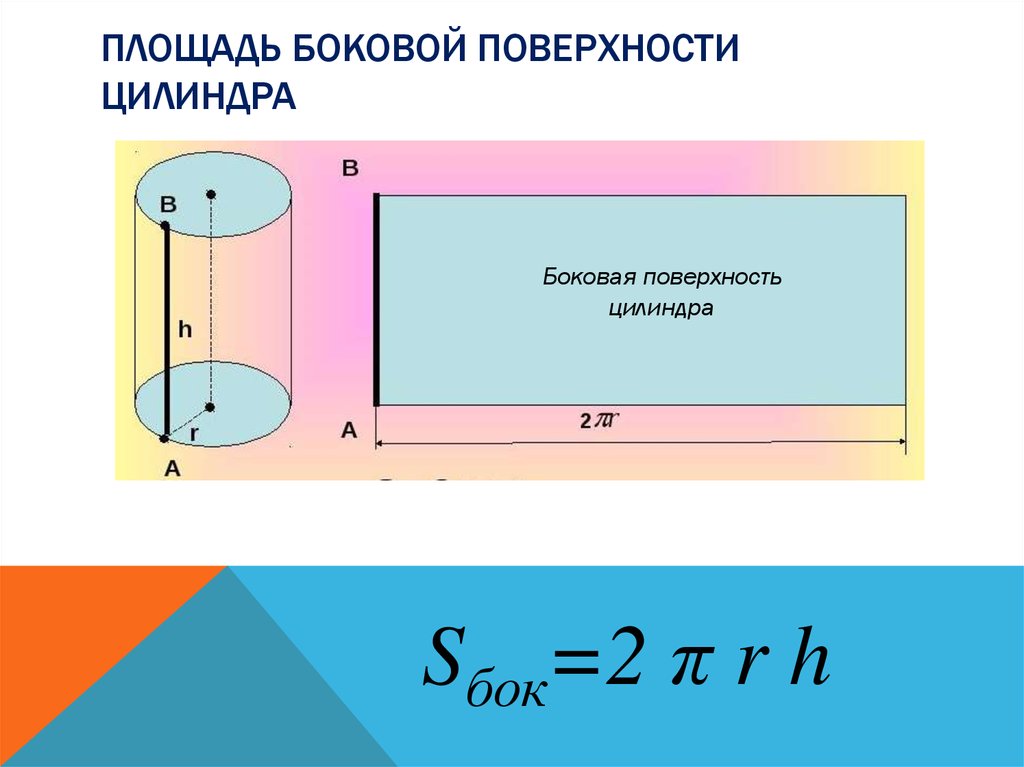 С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.
С=2π r, r= С/2π. Нужно также помнить о том, что радиус – это половина диаметра.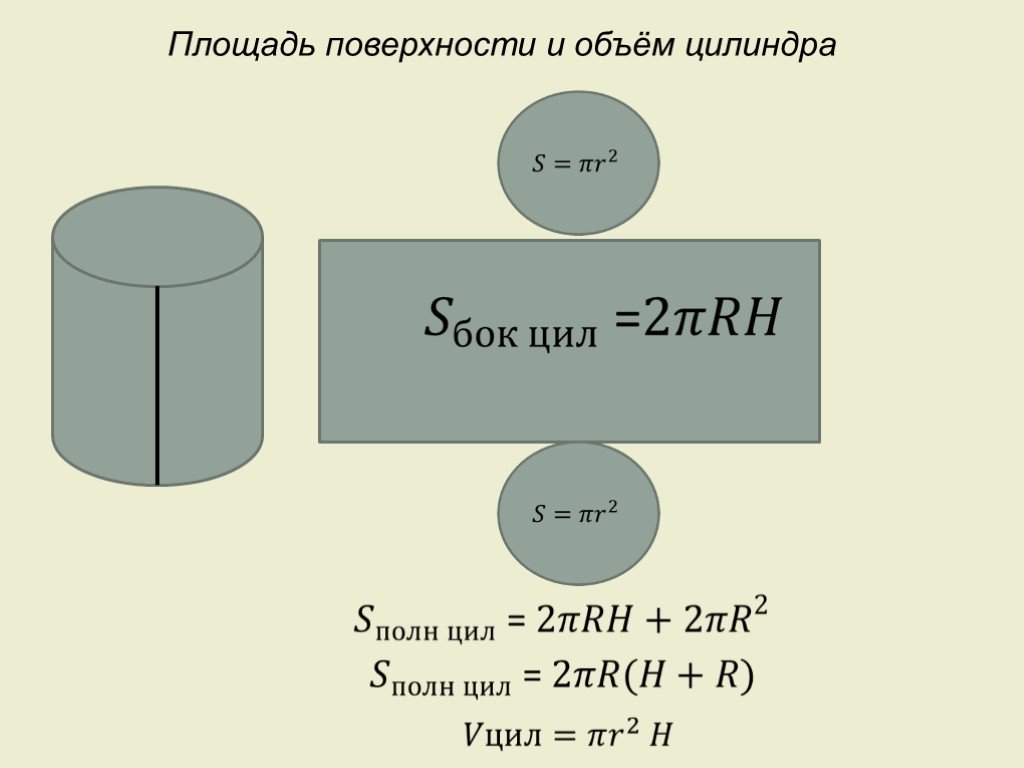 Для этого нужно из формулы V=π r 2 h вывести недостающую величину.
Для этого нужно из формулы V=π r 2 h вывести недостающую величину.