Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции:
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Решение высшей математики онлайн
‹— Назад
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.
Определение 7.1 Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .
Пример 7.1 Рассмотрим функцию . График имеет вертикальную асимптоту , поскольку при выполняется условие , а также при выполняется условие .
Рис.7.1.Вертикальная асимптота функции
Пример 7.2 Рассмотрим функцию . Её график имеет вертикальную асимптоту , так как при . То, что при функция не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать, при .)
Рис.7.2.Вертикальная асимптота функции
Пример 7.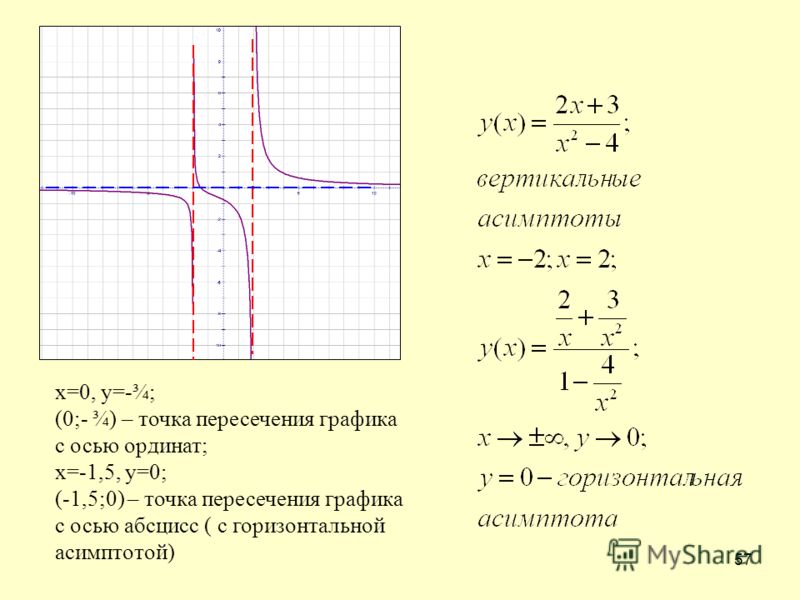 3 Рассмотрим функцию . Прямая является вертикальной асимптотой графика , так как при . Заметим, что слева от точки функция вообще не определена.
3 Рассмотрим функцию . Прямая является вертикальной асимптотой графика , так как при . Заметим, что слева от точки функция вообще не определена.
Рис.7.3.Вертикальная асимптота функции
Пример 7.4 График функции не имеет при вертикальной асимптоты, так как — ограниченная (числом 1) и, следовательно, локально ограниченная при и не стремящаяся к бесконечности функция. Хотя аргумент синуса — функция — имеет вертикальную асимптоту .
Рис.7.4.График функции не имеет вертикальной асимптоты
Пример 7.5 Прямая не является вертикальной асимптотой графика функции , поскольку здесь нельзя утверждать, что при или функция стремится к бесконечности. При некоторых малых значениях значения могут быть как угодно велики, однако при других малых функция обращается в 0: так, при ( ) значения функции равны и стремятся к бесконечности при , а при всех вида ( ) значения функции равны 0. В то же время как те, так и другие точки при увеличении попадают всё ближе и ближе к точке 0. Значит, функция не является бесконечно большой при , и прямая — не асимптота.
При некоторых малых значениях значения могут быть как угодно велики, однако при других малых функция обращается в 0: так, при ( ) значения функции равны и стремятся к бесконечности при , а при всех вида ( ) значения функции равны 0. В то же время как те, так и другие точки при увеличении попадают всё ближе и ближе к точке 0. Значит, функция не является бесконечно большой при , и прямая — не асимптота.
Рис.7.5.График функции не имеет вертикальной асимптоты
Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.
Определение 7.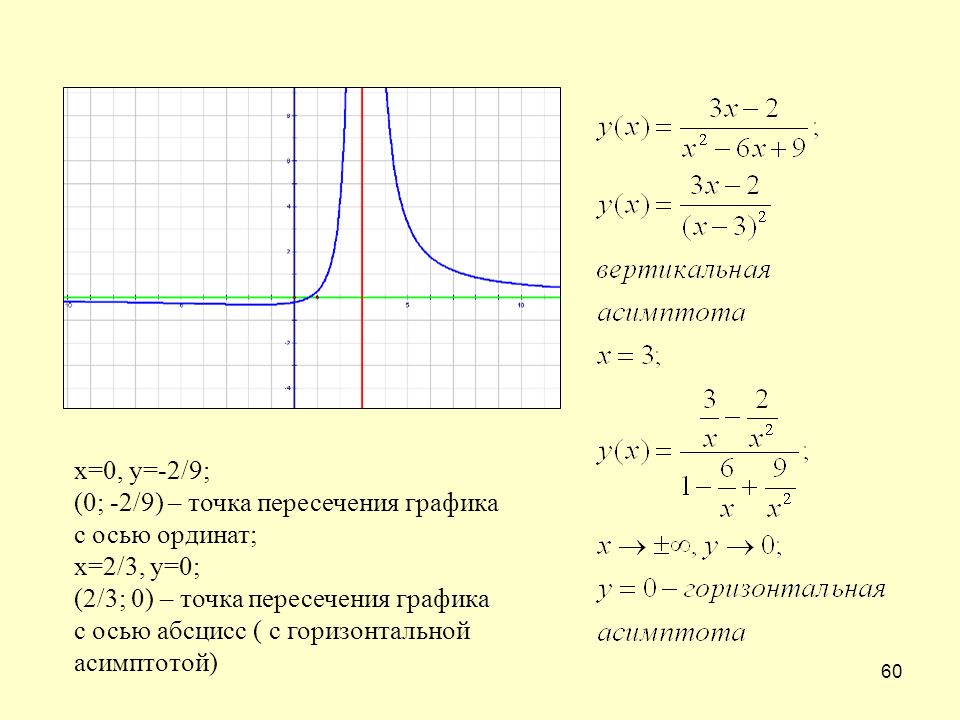 2 Наклонной асимптотой графика функции при называется прямая , если выполнены два условия:
2 Наклонной асимптотой графика функции при называется прямая , если выполнены два условия:
1) некоторый луч целиком содержится в ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при :
| (7.1) |
Наклонной асимптотой графика функции при называется прямая , если
1) некоторый луч целиком содержится в ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при :
Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при
В случае, если наклонная асимптота расположена горизонтально, то есть при , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота — частный случай наклонной асимптоты; прямая является горизонтальной асимптотой графика при или , если
Таким образом, горизонтальная асимптота — частный случай наклонной асимптоты; прямая является горизонтальной асимптотой графика при или , если
или
соответственно.
Пример 7.6 Рассмотрим функцию . График этой функции имеет наклонную асимптоту при . Действительно,
при
Однако эта функция не определена ни на каком луче вида , так что её график не может иметь асимптоты при .
Рис.7.7.Наклонная асимптота функции
Пример 7. 7 График функции имеет горизонтальную асимптоту как при , так и при , поскольку, очевидно, при . Можно сказать также, что асимптота при у этого графика совпадает с асимптотой при .
7 График функции имеет горизонтальную асимптоту как при , так и при , поскольку, очевидно, при . Можно сказать также, что асимптота при у этого графика совпадает с асимптотой при .
Рис.7.8.Горизонтальная асимптота функции
Аналогично определению наклонной асимптоты можно дать также более общее определение:
Определение 7.3 Линия называется асимптотической линией графика функции при (или при ), если обе эти функции определены на некотором луче (или луче ) и разность ординат графиков стремится к 0 при (или при , соответственно).
Если функция — линейная, то есть график — наклонная прямая, то асимптотическая линия — это наклонная асимптота.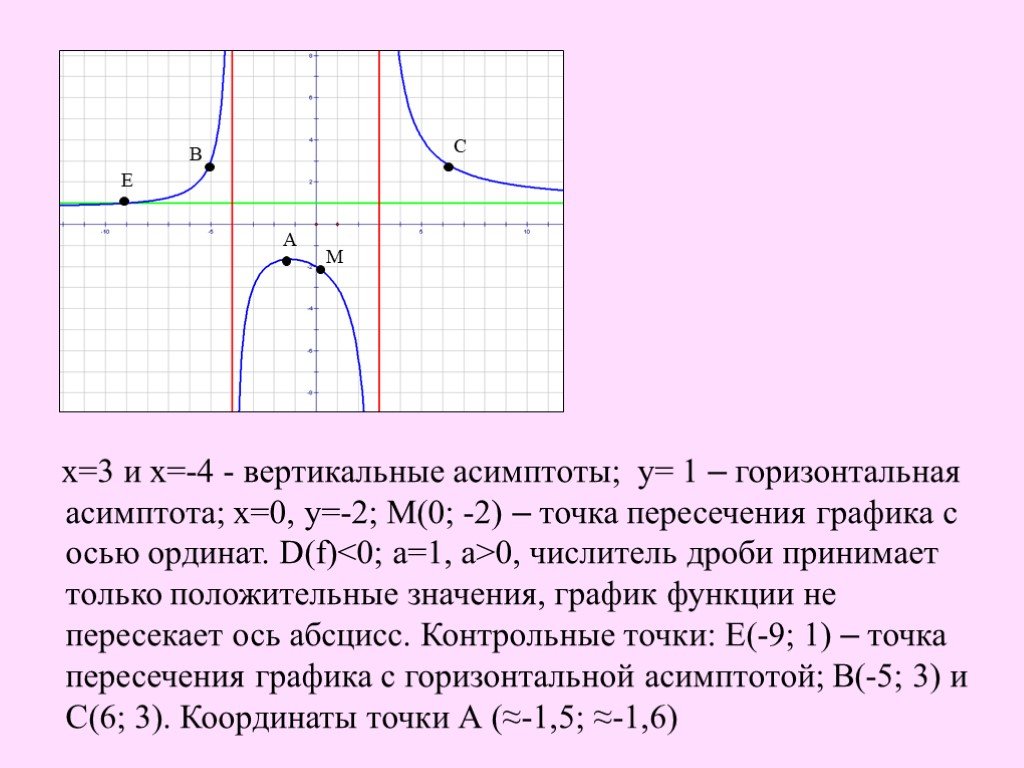 Однако и другие линии бывает естественно рассматривать в качестве асимптотических.
Однако и другие линии бывает естественно рассматривать в качестве асимптотических.
Пример 7.8 Рассмотрим функцию . При график этой функции имеет асимптотическую линию , поскольку разность между и , равная, очевидно, , стремится к 0 при .
Рис.7.9.Асимптотическая линия графика функции
Замечание 7.1 Функции и входят в определение асимптотической линии симметрично: если график — асимптотическая линия для графика , то и — асимптотическая линия для . На практике, однако, естественно считать асимптотической линией тот из двух графиков, который задаётся более простой формулой и вид которого известен.
Пример 7.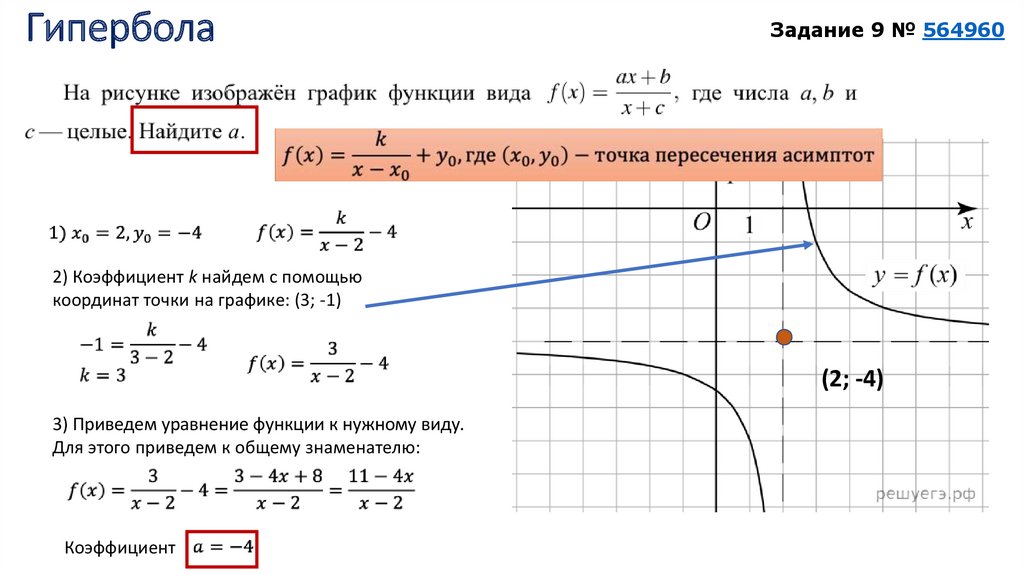 9 Рассмотрим функцию . Так как при , то естественно рассматривать график как асимптотическую линию при для графика исследуемой функции .
9 Рассмотрим функцию . Так как при , то естественно рассматривать график как асимптотическую линию при для графика исследуемой функции .
Рис.7.10.Асимптотическая линия для графика функции при
Вернёмся к наклонным асимптотам — прямым линиям с уравнением . Для их нахождения в тех случаях, когда значения и не очевидны, можно применять следующую теорему.
Теорема 7.1 Прямая служит наклонной асимптотой для графика при (или при ) в том и только том случае, когда
| (7.2) |
и
(7. 3) 3) |
(соответственно, если
и
Таким образом, для нахождения наклонной (или горизонтальной, если получится ) асимптоты достаточно найти два указанных предела и, затем, . Прямая будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.
Доказательство теоремы. Докажем теорему в случае ; доказательство при проводится совершенно аналогично.
Перепишем условие (7.1), задающее асимптоту, в виде
Так как первый множитель , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть
Но и , так что
откуда следует равенство (7. 2). Теперь число уже известно.
2). Теперь число уже известно.
Подставляя это число в формулу (7.1), находим, что
откуда следует равенство (7.3).
Пример 7.10 Найдём наклонные асимптоты графика .
Попробуем отыскивать сразу оба предела, и при , и при .
Итак, и при , и при имеем и , так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение , то есть, фактически, асимптота только одна.
Рис.7.11.График и его наклонная асимптота
Замечание 7.2 Из определения асимптоты не следует, что если асимптоты при и при для одного и того же графика существуют, то они непременно совпадают.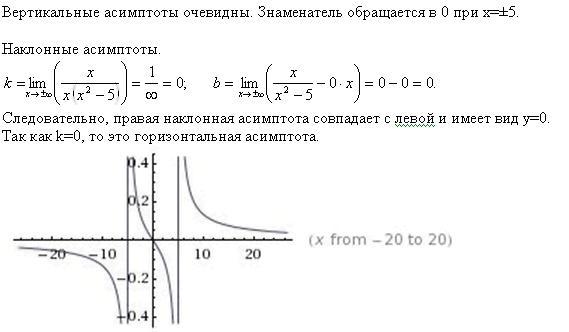 Это могут быть и различные прямые, как показывает следующий простой пример.
Это могут быть и различные прямые, как показывает следующий простой пример.
Пример 7.11 Рассмотрим график . При график приближается к горизонтальной асимптоте , а при — к другой горизонтальной асимптоте .
Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты
Различными могут оказаться и не обязательно горизонтальные асимптоты:
Пример 7.12 Рассмотрим функцию . Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.
Сначала найдём асимптоту при . Согласно доказанной теореме, имеем:
Таким образом, при наклонной асимптотой служит прямая .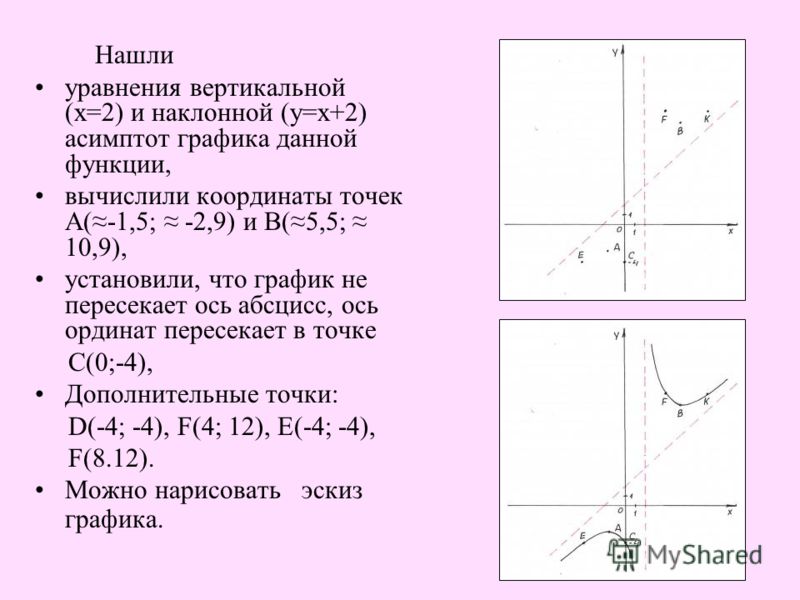
Теперь найдём асимптоту при . Имеем:
Поскольку , мы можем считать, что в допредельном выражении . В полученной дроби поделим числитель и знаменатель на положительное число . Тогда под корнем нужно будет поделить на , и получится:
Вычисление проведите сами в качестве упражнения. При этом получается , так что наклонная асимптота при имеет уравнение .
Рис.7.13.График и его две наклонных асимптоты
Замечание 7.3 Если график имеет асимптоту (например, при ) и существует предел производной:
то . Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты17.
Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты17.
Однако асимптота может существовать и в случае, когда производная не имеет никакого предела при . Дело в том, что значения могут совершать мелкие, но частые колебания относительно ординаты асимптоты, так что значения производной могут при этом испытывать незатухающие колебания. Проиллюстрируем эту возможность следующим примером.
Пример 7.13 Рассмотрим функцию . Очевидно, что прямая — это асимптота графика при , так как первое слагаемое имеет предел, равный 0, при . Однако вычисление производной даёт
а эта функция при росте совершает колебания, причём при больших второе слагаемое становится пренебрежимо малым, и значения колеблются примерно между и 3. Следовательно, производная не имеет предела при .
Следовательно, производная не имеет предела при .
Если же рассмотреть функцию , то её производная оказывается даже неограниченной на любом луче вида , хотя прямая по-прежнему служит асимптотой графика (проведите вычисления, доказывающие это, самостоятельно в качестве упражнения).
Не так уж редко встречается случай, когда, найдя наклонные и вертикальные асимптоты графика и исследовав поведение функции слева и справа от вертикальных асимптот, мы уже достаточно хорошо можем представить себе поведение функции.
Пример 7.14 Рассмотрим функцию . Мы можем заметить, что — чётная функция, поскольку она зависит только от и, следовательно, не меняет знак при смене знака . Заметим также, что .
Знаменатель обращается в 0 при , то есть при и при . Тем самым, прямые и — это вертикальные асимптоты. Подробнее разберём порведение функции при приближении к . Если , то и, следовательно, . Числитель при всех , так что дробь положительна. Значит, при . При (и ) имеем , поэтому и , так что при . Вследствие чётности функции получаем также, что при и при .
Если , то и, следовательно, . Числитель при всех , так что дробь положительна. Значит, при . При (и ) имеем , поэтому и , так что при . Вследствие чётности функции получаем также, что при и при .
Найдём теперь наклонные асимптоты. Вычисляя параметры и по формулам (7.2) и (7.3), получаем:
Таким образом, асимптоты при и при совпадают и имеют уравнение .
Суммируя сказанное, мы можем представить себе, что график функции ведёт себя примерно так:
Рис.7.14.График функции
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Асимптоты — горизонтальные, вертикальные, наклонные (наклонные)
Асимптоты — это воображаемые линии, к которым очень близок общий график функции или часть графика.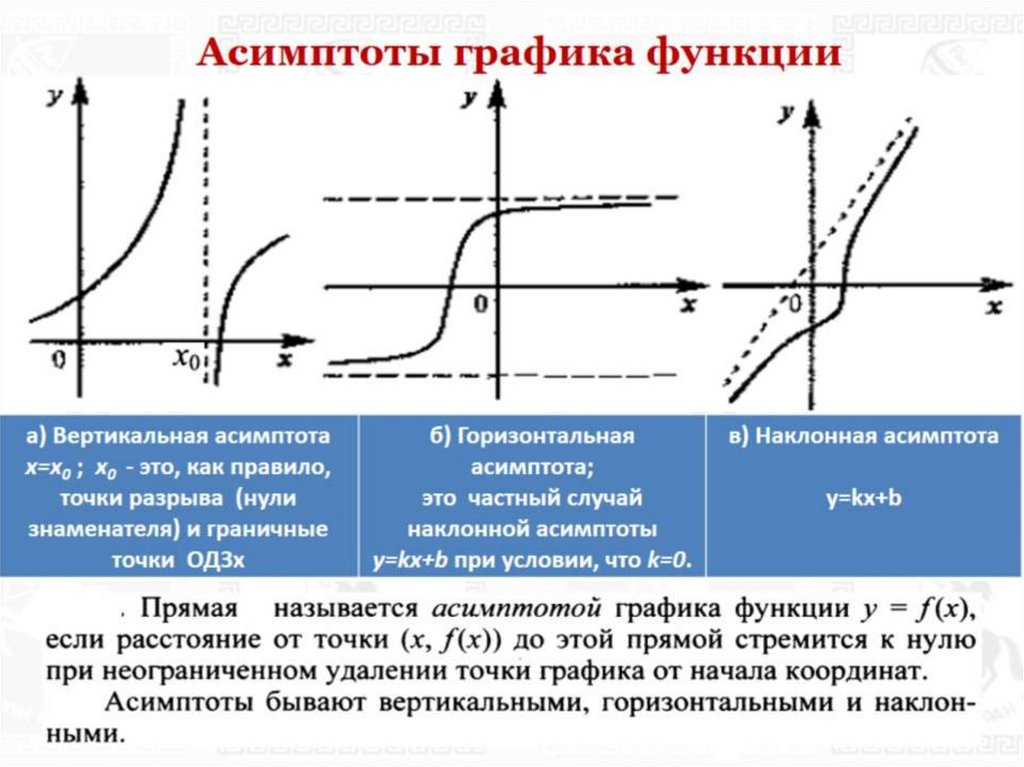 Асимптоты очень полезны при построении графика функции, поскольку они помогают подумать о том, каких линий кривая не должна касаться.
Асимптоты очень полезны при построении графика функции, поскольку они помогают подумать о том, каких линий кривая не должна касаться.
Давайте узнаем об асимптотах и их типах, а также о процессе их нахождения на дополнительных примерах.
| 1. | Что такое асимптота? |
| 2. | Типы асимптот |
| 3. | Как найти асимптоты? |
| 4. | Как найти вертикальные и горизонтальные асимптоты? |
| 5. | Разница между горизонтальной и вертикальной асимптотами |
| 6. | Наклонная асимптота (Наклонная асимптота) |
| 7. | Как найти наклонную асимптоту? |
| 8. | Часто задаваемые вопросы по асимптотам |
Что такое асимптота?
Асимптота — это линия, к которой приближается кривая, но никогда не касается кривой.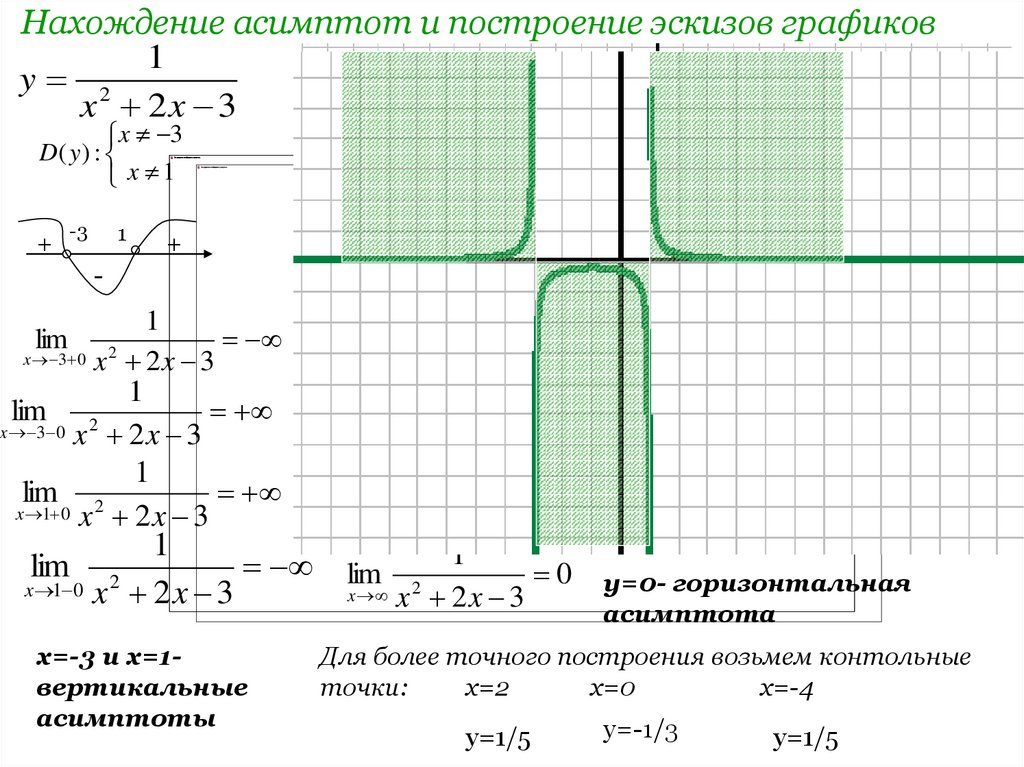 т. е. асимптота — это прямая, к которой сходится график функции. Обычно нам не нужно рисовать асимптоты при построении графиков функций. Но нанесение их пунктирными линиями (воображаемыми линиями) заставляет нас позаботиться о том, чтобы кривая не касалась асимптоты. Следовательно, асимптоты — это просто воображаемые линии. Расстояние между асимптотой функции y = f(x) и ее графиком приблизительно равно 0, когда либо значение x, либо y стремится к ∞ или -∞.
т. е. асимптота — это прямая, к которой сходится график функции. Обычно нам не нужно рисовать асимптоты при построении графиков функций. Но нанесение их пунктирными линиями (воображаемыми линиями) заставляет нас позаботиться о том, чтобы кривая не касалась асимптоты. Следовательно, асимптоты — это просто воображаемые линии. Расстояние между асимптотой функции y = f(x) и ее графиком приблизительно равно 0, когда либо значение x, либо y стремится к ∞ или -∞.
Типы асимптот
Существует 3 типа асимптот.
- Горизонтальная асимптота (ГА) — это горизонтальная линия, поэтому ее уравнение имеет форму y = k.
- Вертикальная асимптота (VA) — это вертикальная линия, поэтому ее уравнение имеет форму x = k.
- Косая асимптота (Наклонная асимптота) — это наклонная линия и, следовательно, ее уравнение имеет вид y = mx + b.
Вот рисунок, иллюстрирующий все типы асимптот.
Как найти асимптоты?
Поскольку асимптота представляет собой горизонтальную, вертикальную или наклонную линию, ее уравнение имеет вид x = a, y = a или y = ax + b.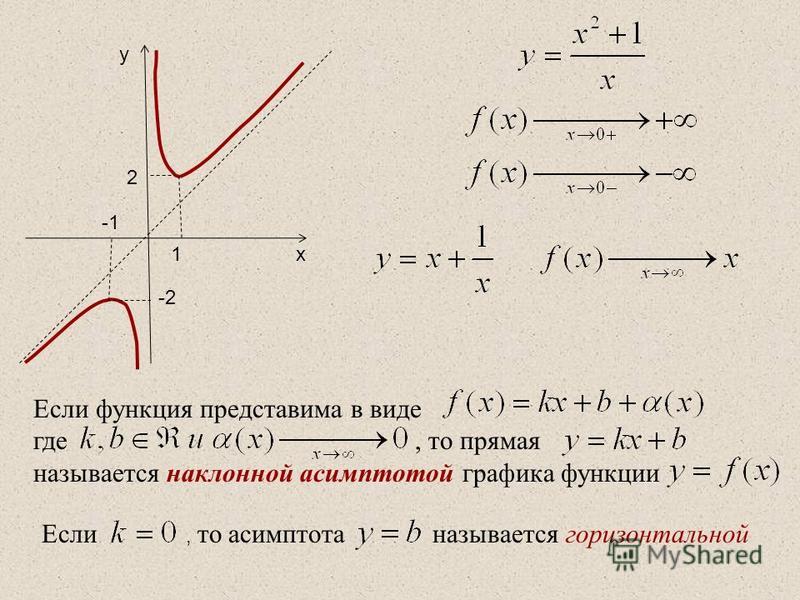
- Горизонтальная асимптота имеет вид y = k, где x→∞ или x→ -∞. т. е. это значение одного/обоих пределов lim ₓ→∞ f(x) и lim ₓ→ -∞ f(x). Чтобы узнать, как найти горизонтальную асимптоту, нажмите здесь.
- Вертикальная асимптота имеет вид x = k, где y→∞ или y→ -∞. Чтобы узнать, как легко находить вертикальные асимптоты, нажмите здесь.
- Наклонная асимптота имеет вид y = mx + b, где m ≠ 0. Другое название наклонной асимптоты — наклонная асимптота. Обычно он существует для рациональных функций, и mx + b — это частное, полученное путем деления числителя рациональной функции на ее знаменатель.
Давайте подробнее изучим процесс нахождения каждой из этих асимптот в следующих разделах.
Как найти вертикальную и горизонтальную асимптоты?
Обычно мы изучаем асимптоты рациональной функции. Конечно, мы можем найти вертикальную и горизонтальную асимптоты рациональной функции, используя приведенные выше правила.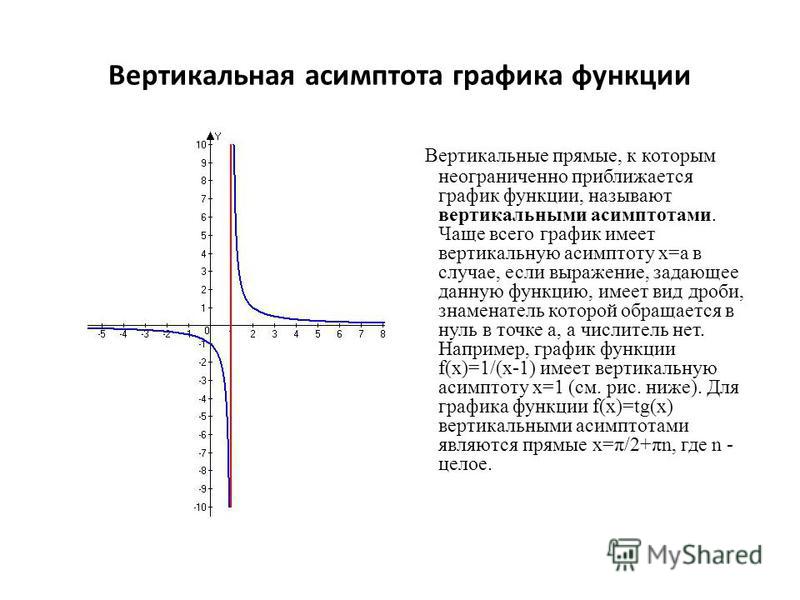
Нахождение горизонтальных асимптот рациональной функции
Метод нахождения изменений горизонтальной асимптоты по степеням многочленов в числителе и знаменателе функции.
- Если оба многочлена имеют одинаковую степень, разделить коэффициенты при старших членах. Это ваша асимптота!
- Если степень числителя меньше знаменателя, то асимптота расположена на y = 0 (это ось x).
- Если степень числителя больше знаменателя, то горизонтальной асимптоты нет!
Пример: В функции f(x) = (3x 2 + 6x) / (x 2 + x) степень числителя = степени знаменателя (= 2). Таким образом, ее горизонтальная асимптота равна
y = (старший коэффициент числителя) / (старший коэффициент знаменателя) = 3/1 = 3.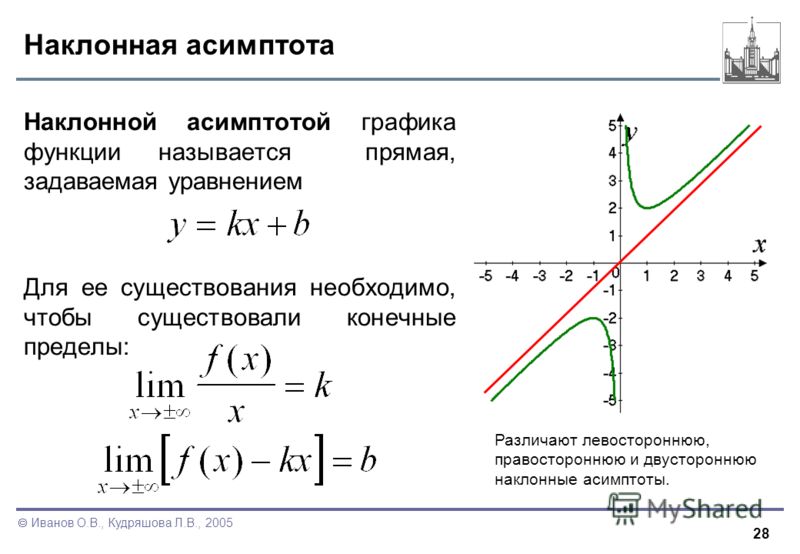
Следовательно, ее HA равна y = 3.
Нахождение вертикальных асимптот рациональной функции
Чтобы найти вертикальную асимптоту рациональной функции, мы сначала упрощаем ее до наименьших членов, приравниваем ее знаменатель к нулю, а затем находим значения x.
Пример: Упростим функцию f(x) = (3x 2 + 6x) / (x 2 + x).
f(x) = 3x (x + 2) / x (x + 1) = 3(x+2) / (x+1).
Когда мы устанавливаем знаменатель = 0, x + 1 = 0. Отсюда x = -1.
Значит, его ВА равен x = -1.
Обратите внимание, что, поскольку x отменяется при упрощении, x = 0 является дырой на графике. Это означает, что ни одна точка на графиках не соответствует x = 0.
Мы можем видеть как HA, так и VA этой функции на графике ниже. Кроме того, обратите внимание на отверстие в точке x = 0,9.0003
Разница между горизонтальной и вертикальной асимптотами
Вот несколько различий между горизонтальной и вертикальной асимптотами:
| Горизонтальная асимптота | Вертикальная асимптота |
|---|---|
Он имеет форму y = k. | Он имеет форму x = k. |
| Получается, если взять предел как x→∞ или x→ -∞. | Получается, если принять предел как y→∞ или y→ -∞. |
| Иногда может пересекать кривую. | Он никогда не пересечет кривую. |
Наклонная асимптота (Наклонная асимптота)
Как следует из названия, наклонная асимптота не параллельна ни оси x, ни оси y, и, следовательно, ее наклон не равен 0 и не равен нулю. Она также известна как наклонная асимптота. Его уравнение имеет вид y = mx + b, где m — ненулевое действительное число. Рациональная функция имеет наклонную асимптоту только тогда, когда ее числитель ровно на 1 больше знаменателя, и, следовательно, функция с наклонной асимптотой никогда не может иметь горизонтальную асимптоту.
Как найти наклонную асимптоту?
Наклонная асимптота рациональной функции получается делением ее числителя на знаменатель с использованием длинного деления. Частное от деления (независимо от остатка), которому предшествует «у =», дает уравнение наклонной асимптоты. Вот пример.
Частное от деления (независимо от остатка), которому предшествует «у =», дает уравнение наклонной асимптоты. Вот пример.
Пример: Найдите наклонную асимптоту y = (3x 3 — 1) / (x 2 + 2x).
Разделим 3х 3 — 1 на х 2 + 2x с использованием длинного деления.
Следовательно, y = 3x — 6 является наклонной/наклонной асимптотой данной функции.
Важные замечания по асимптотам:
- Если функция имеет горизонтальную асимптоту, то она не может иметь наклонную асимптоту и наоборот.
- Полиномиальные функции, функции синуса и косинуса не имеют горизонтальных или вертикальных асимптот.
- Тригонометрические функции csc, sec, tan и cot имеют вертикальные асимптоты, но не имеют горизонтальных асимптот.
- Экспоненциальные функции имеют горизонтальные асимптоты, но не имеют вертикальных асимптот.
- Наклонная асимптота получается делением многочленов в длину.

☛ Похожие темы:
- Калькулятор асимптот
- Калькулятор графических функций
- Графический калькулятор
Часто задаваемые вопросы по асимптотам
Что означают асимптоты?
Асимптоты — это воображаемые линии на графике функции, к которым часть кривой очень близка, но асимптота никогда не касается графика. Функция может иметь 3 типа асимптот:
- Горизонтальная асимптота (HA)
- Вертикальная асимптота (ВА)
- Наклонная асимптота (Наклонная асимптота)
Как найти горизонтальную и вертикальную асимптоты показательной функции?
Показательная функция имеет вид y = a х + б. Вот правила нахождения горизонтальной и вертикальной асимптот экспоненциальной функции.
- Поскольку экспоненциальная функция определена везде, она не имеет вертикальных асимптот.
- При x→∞ или x→ -∞, y → b.
 Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b.
Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b.
Мы также можем нарисовать экспоненциальный график, чтобы определить асимптоты.
Что такое асимптота простыми словами?
Асимптота – это горизонтальная/вертикальная/наклонная линия, к которой кривая очень близка, но не касается асимптоты.
Каковы правила нахождения асимптот?
Вот правила нахождения асимптот функции y = f(x).
- Для нахождения горизонтальных асимптот применим предел x→∞ или x→ -∞.
- Чтобы найти вертикальные асимптоты, примените предел y→∞ или y→ -∞.
- Чтобы найти наклонную асимптоту (если есть), разделите числитель на знаменатель.
Как найти горизонтальную и вертикальную асимптоты логарифмической функции?
Логарифмическая функция имеет форму y = log (ax + b).
- Его вертикальная асимптота получается путем решения уравнения ax + b = 0 (что дает x = -b/a).
- При x→∞ или x→ -∞ y не стремится ни к какому конечному значению.
 Следовательно, она не имеет горизонтальной асимптоты.
Следовательно, она не имеет горизонтальной асимптоты.
Как найти наклонную асимптоту?
Рациональная функция имеет наклонную асимптоту только тогда, когда ее числитель имеет степень всего на одну больше, чем степень знаменателя. Он получается путем деления числителя на его знаменатель с использованием длинного деления многочленов.
Как асимптоты помогают в графическом построении рациональных функций?
Асимптоты очень полезны при графическом отображении функций, поскольку они определяют, должна ли кривая разбиваться по горизонтали и по вертикали. При построении графика кривая никогда не должна касаться асимптот.
Каждая ли рациональная функция имеет наклонную асимптоту?
Нет, не каждая рациональная функция имеет наклонную асимптоту. Рациональная функция имеет наклонную асимптоту только тогда, когда степень ее числителя больше степени знаменателя.
Математическая сцена — Функции 2 — Урок 3
Математическая сцена — Функции 2 — Урок 3 — Рациональные функции и асимптоты| 2009 Расмус Эф ог Джанн Сак | Функции 2 |
Урок 3
Рациональный
функции и асимптоты
Функция вида
где t(x) и n(x) — многочлены, называется рациональной функцией.
Графики рациональных функций можно узнаваемы по тому факту, что они часто распадаются на две или более частей. Эти части выходят за пределы системы координат по воображаемой прямой линии, называемой асимптота.
Давайте посмотрим на функцию
Этот график следует горизонтальной линии (красная на
диаграмме) по мере его перемещения из системы влево или вправо. Это
горизонтальная асимптота с уравнением y = 1. При приближении x к значениям 1 и
1 график построен по вертикальным линиям (синие). Эти вертикальные асимптоты
происходят, когда знаменатель функции n(x) равен нулю (не
числитель).
Чтобы найти уравнения вертикальных асимптот, мы должны решить уравнение:
x 2 1 = 0
х 2 = 1
х = 1 или х = 1
Рядом с значения х = 1 и x = 1 график идет почти вертикально вверх или вниз, а функция стремится либо к +∞, либо к ∞.
Получаем
горизонтальная асимптота, потому что
числитель и знаменатель, t(x) = x 2 и n(x) = x 2 1 почти равны, поскольку x становится все больше и больше.
Если, например, x = 100, то x 2 = 10000 и x 2 1 = 9999, так что, разделив одно на другое, мы получим почти 1.
Чем больше значение x, тем ближе мы к 1.
Вертикальные асимптоты можно найти, решив уравнение n(x) = 0, где n(x) — знаменатель функции (примечание: это применимо только в том случае, если числитель t (x) не равен нулю для одного и того же x ценить). Горизонтальные асимптоты можно найти, найдя предел |
Пример 1
Найдите асимптоты для функция .
Чтобы найти вертикаль асимптотой решаем уравнение
х 1 = 0
х = 1
График имеет вертикальную асимптота с уравнением х = 1,
Чтобы найти горизонталь асимптота, которую мы вычисляем .
Числитель всегда занимает
значение 1, поэтому чем больше x становится, тем меньше становится дробь. Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.
Например
если x = 1000, то f(x) = 001. По мере увеличения x f(x) становится все ближе и ближе
до нуля.
Это говорит нам о том, что у = 0 (которая является осью x) является горизонтальной асимптотой.
Наконец нарисуйте график в ваш калькулятор, чтобы подтвердить то, что вы нашли.
|
| Пример выше
предлагает следующее простое правило: Рациональная функция, у которой степень знаменателя выше чем степень числителя имеет ось x как горизонтальную асимптота. |
Пример 2
Найдите асимптоты для .
Сразу видно, что вертикальных асимптот нет, так как знаменатель никогда не может быть равен нулю.
x 2 + 1 = 0
x 2 = 1 не имеет вещественных раствор
Теперь посмотрим, что происходит, когда x становится бесконечно большим:
Метод, который мы использовали ранее для решения этого типа
Проблема состоит в том, чтобы разделить на наибольшую степень x.
| Разделить все на x 2 и затем отменить | |
| дроби, где х стоит в знаменателе а не числитель стремится к 0 . |
График имеет горизонтальную асимптота г = 2 .
Теперь нарисуем график с помощью калькулятора
Сначала выберите ГРАФИК в меню.
Затем введите формулу будьте осторожны, чтобы включить скобки, как показано
Вот что такое калькулятор показывает нам. График фактически пересекает свою асимптоту в одной точке. (Это никогда не может происходит с вертикальной асимптотой).
Пример 3
Теперь пример, где числитель на одну ступень выше знаменателя.
. Числитель является полиномом второй степени, а знаменатель – полиномом второй степени. первая степень.
первая степень.
Сначала вертикаль асимптоты:
х 1 = 0
x = 1
Одна вертикальная асимптота с уравнением x = 1 .
Мы используем длинное деление и разделить числитель на знаменатель
Теперь мы можем переписать ф(х):
Мы знаем, что это означает, что f(x) ≈ x + 1 по мере увеличения x.
говорит нам, что прямая линия у = х + 1 есть наклонная асимптота
График показан ниже.
Если мы хотим спекулировать на дальнейшие возможности, мы можем видеть, что если степень числителя равна 2 степени больше, чем у знаменателя, то график выходит за пределы система координат по параболической кривой и так далее.
Пример 4
Найдите асимптоты функция .
В этом примере деление
уже сделано, так что мы можем видеть, что есть наклонная асимптота с
уравнение y
= х .
Чтобы найти вертикаль асимптоты решаем уравнение п(х) = 0,
x 2 1 = 0
x 2 = 1
х = 1 или х = 1
Вертикальные асимптоты х = 1 и х = 1.
Вот график
1) Вертикальные асимптоты
может произойти, когда знаменатель n(x) 2) Если степень
знаменатель n(x) больше, чем у 3) Если степень
знаменатель n(x) такой же, как у 4) Если степень
знаменатель n(x) на единицу меньше, чем у |

 3
3 14159..
14159..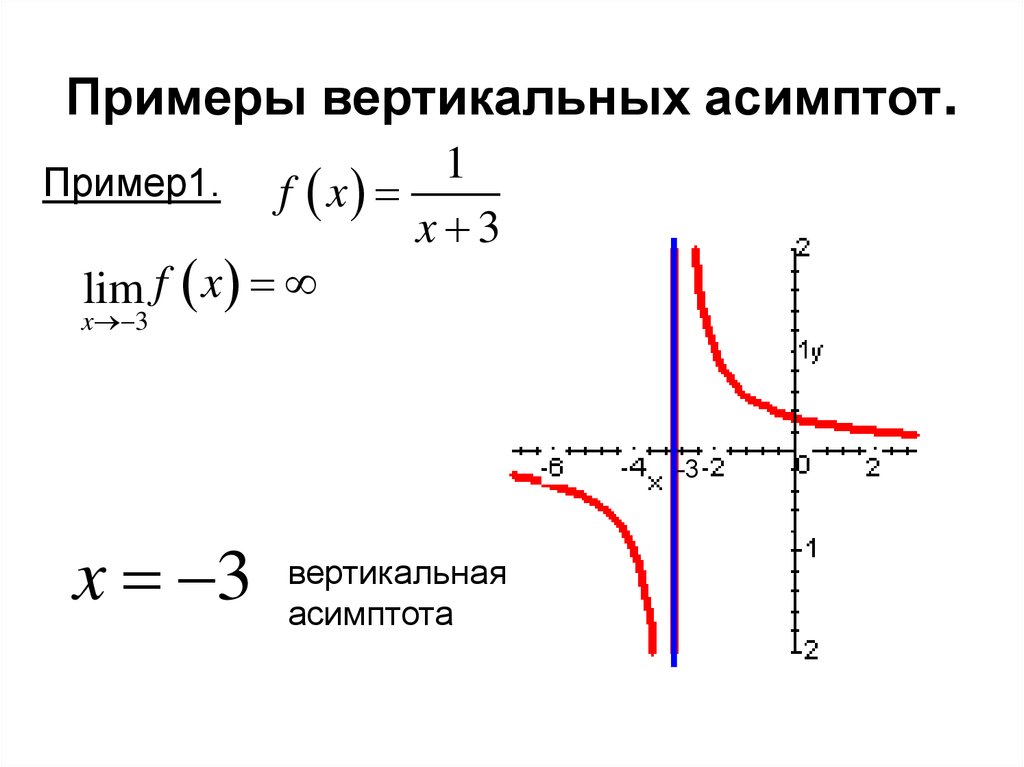
 Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b.
Следовательно, горизонтальная асимптота y = a 90 105 x 90 106 + b равна y = b. Следовательно, она не имеет горизонтальной асимптоты.
Следовательно, она не имеет горизонтальной асимптоты.