Расчет балок онлайн. Примеры расчета
Срочная онлайн-помощь
- Главная
- Теоретическая часть
- Как пользоваться сайтом — помощник по онлайн-расчетам на сайте
- Расчет балок, построение эпюр, вычисление прогибов, подбор сечений
- Расчет балок онлайн. Примеры расчета
Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.
Балка на двух опорах. Построение эпюр
Для этого типа балок сервис позволяет определить и подробно расписывает:
- реакции опор
- эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- по уравнениям метода начальных параметров вычисляются прогибы и углы поворота.
 Записываются и сами уравнения метода начальных параметров по участкам.
Записываются и сами уравнения метода начальных параметров по участкам.
Посмотреть пример »
Консольная балка. Построение эпюр.
Для этого типа балок сервис позволяет определить и подробно расписывает:
- построение эпюр поперечных сил и изгибающих моментов
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- вычисляются прогибы и углы поворота.
Посмотреть пример »
Статически неопределимая балка. Подбор сечения.
Для такого типа балок Вы можете получить
- только результаты расчета — (эпюры Q и M).
Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается, но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.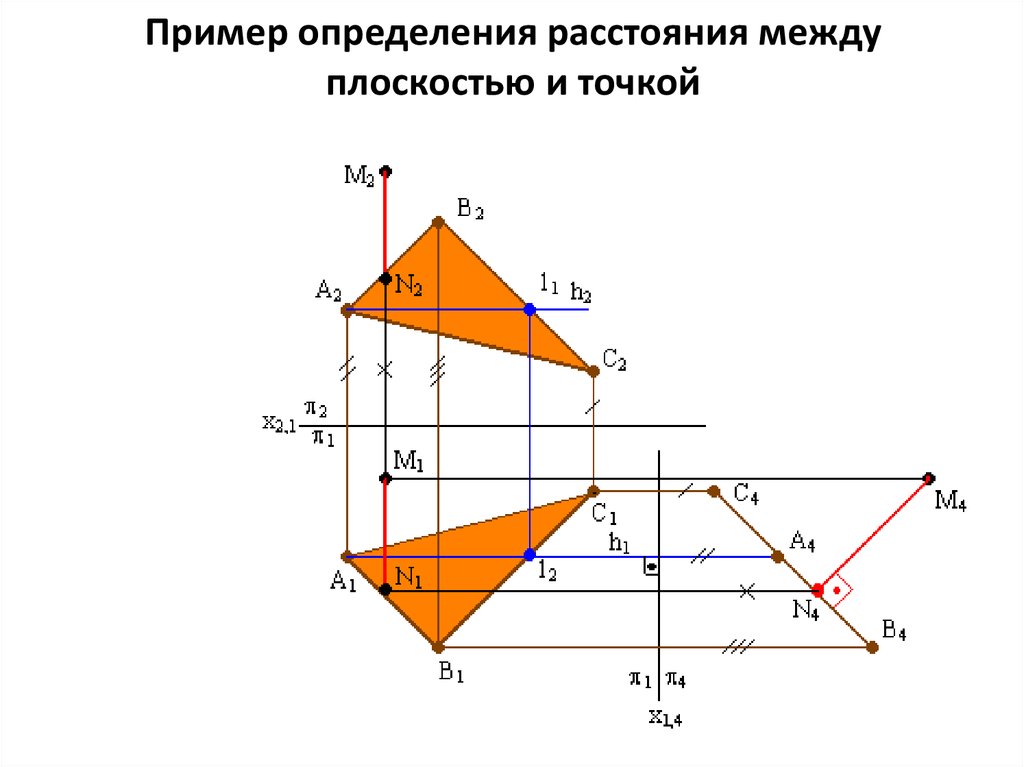
Посмотреть пример »
Балка с промежуточными шарнирами
Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.
Посмотреть пример »
Партнерская программа
Мы согласны отдать Вам 30% своего дохода за рекламу нашего сайта на Вашей площадке ПодробнееПомощь: сопромат, строймеханика, прикладная механика Telegram bluewhite22WhatsAppInstagram
Онлайн калькулятор: Построение эпюр внутренних усилий
Данный онлайн калькулятор предназначен для построения эпюр внутренних усилий. Эпюра внутренних усилий — график, показывающий характер изменения внутренних усилий по длине стержня. Построение эпюр необходимо для определения положения наиболее нагруженного (опасного) сечения стержня. Калькулятор наглядно изображает эпюру изгибающего момента M и поперечной силы Q. Теорию и формулы расчета можно найти ниже под калькулятором.
Калькулятор наглядно изображает эпюру изгибающего момента M и поперечной силы Q. Теорию и формулы расчета можно найти ниже под калькулятором.
Эпюры поперечных сил и моментов в простой балке
Расстояние между опорами, м
Нагрузка
| Расстояние от опоры A | Нагрузка | Значение | Направление | Направление момента | Протяженность | Изменение | ||
|---|---|---|---|---|---|---|---|---|
51020501001000
Нагрузка
Расстояние от опоры A
Отрицательное, если нагрузка приложена к точке, лежащей левее опоры.
Значение
Направление↓ вниз↑ вверх
Направление момента↻ По часовой стрелке↺ Против часовой стрелки
Протяженность
Изменение\ Убывание/ Возрастание
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;L;50.5;up;anticlockwise;50.5;increase
Загрузить данные из csv файла
Детали
Точность вычисления
Знаков после запятой: 2
Эпюры внутренних сил и моментов в балке
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Внутренние силы
Для иллюстрации внутренних сил, действующих в балке под нагрузкой, рассмотрим следующий рисунок.
Мысленно рассечем балку на два сегмента в точке B, где мы будем определять внутренние силы, действующие в балке.
Внутренние силы, действующие в сечении балки можно показать как внешние, на диаграмме свободного тела рассеченной балки. Компонента NB, действующая вдоль балки, называется нормальной силой. В калькуляторе мы не рассматриваем нормальную силу, так как можно ввести только поперечные нагрузки.
Компонента внутренних сил QB, действующая параллельно сечению называется поперечной силой. На рисунке отражена только y-составляющая поперечных сил, в действительности возможна еще и z-составляющая. Калькулятор не допускает поворота нагрузки вокруг оси x, поэтому в наших вычислениях эта составляющая отсутствует.
Моменты MB называются изгибающими моментами. Изгибающий момент равен сумме моментов всех внешних сил, приложенных к рассматриваемой части балки, относительно центра тяжести проведенного сечения.
Компоненты сил препятствуют относительному смещению двух сегментов, моменты препятствуют относительному вращению.1
Построение эпюр методом интегрирования.
Мы будем искать формулы для вычисления значений поперечной силы Q(x) и изгибающего момента M(x) отдельно для разных участков балки.
Границами участков являются характерные точки: концевые сечения балки, точки опор, точки приложения сосредоточенных сил и моментов, точки начала и конца действия распределенных нагрузок.
Для каждого участка, вычисляется интеграл от функции распределенной нагрузки q(x) для определения поперечной силы Q(x), следующим шагом вычисляется интеграл от Q(x) для определения функции изгибающего момента M(x) в соответствии с формулами:
2
Распределенная нагрузка q(x) в нашем калькуляторе может быть линейной, равномерно убывающей или возрастающей. В первом случае q(x) — константа , во втором — линейная функция: kx+b, в случае отсутствия распределенных нагрузок на участке q(x)=0, поперечная сила будет равна константе.
В первом случае q(x) — константа , во втором — линейная функция: kx+b, в случае отсутствия распределенных нагрузок на участке q(x)=0, поперечная сила будет равна константе.
Таким образом для отыскания функций Q(x) и M(x) потребуется вычисление неопределенного интеграла от многочлена и вычисление константы интегрирования. Константу интегрирования можно найти, зная какую либо точку, через которую проходит искомая функция. См.: Интеграл многочлена.
В качестве такой точки будем брать значения Q(x) и M(x) по левой границе участка.
Q(xl) будет равно значению функции поперечной силы Q(x) для предыдущего участка в точке l, смещенное на величину сосредоточенной силы (или опорной реакции) в этой точке. Если сила действует вверх, то смещение положительно, если вниз — отрицательно.
M(xl) будет равно значению функции изгибающего момента M(x) для предыдущего участка в точке l, смещенное на величину сосредоточенного момента, приложенного к этой точке. Если сосредоточенный момент направлен по часовой стрелке, то смещение положительно, в противном случае — отрицательно.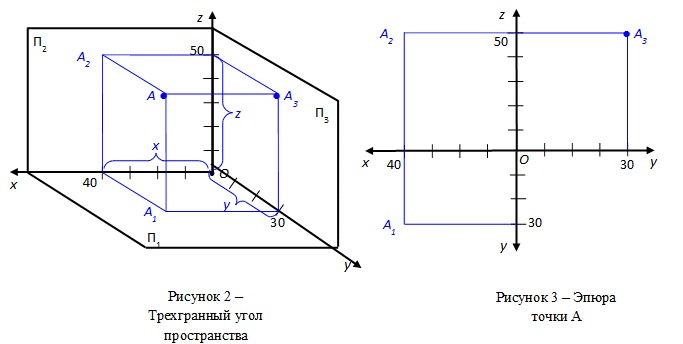
Значение Q(x) на левом краю балки будет соответствовать сумме сосредоточенных сил и опорной реакции в этой точке, или будет равно нулю при отсутствии таковых. Значение M(x) по краям балки равно сумме значений сосредоточенных моментов приложенных к концам балки. Если сосредоточенных моментов в этих точках нет, то M(x) будет равен нулю.
Знаки для М(x) и Q(x) можно связать с характером деформации балки при действии внешних сил. Если изгибающий момент в сечении положителен, то балка в этом сечении гнется выпуклостью вниз, если же он отрицателен, то балка гнется выпуклостью вверх.
Пример
Рассмотрим получение функций Q(x) и M(x) на примере:
Открыть этот пример
- Первым делом вычисляются реакции опор. Посмотреть как они находятся можно в этом калькуляторе.
Получаем реакции опор: - Балка делится на участки по ключевым точкам с координатами: 0, 2, 4, 5, 6.
Участок А — характерные точки 0,2
Участок B — характерные точки 2,4
Участок C — характерные точки 4,5
Участок D — характерные точки 5,6 - Для каждого участка находим формулу распределенной нагрузки, интегрируем ее дважды получая формулу для поперечных сил Q(x) и изгибающих моментов M(x).
 Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.
Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.Распределенная нагрузка на участке равна: q(x) = 5. Найдем функцию поперечной силы на участке, путем интегрирования функции распределенной нагрузки:
5x2 — 11.56x = 0 + 2.5 · 02 — 11.56 · 0 получаем значение C = 0
Выразим константу C = Q(x)+5x, и подставим в формулу x=0 и значение поперечной силы в этой точке. Поперечная сила на концах балки равна нулю, но в точке 0 она изменена реакцией опоры VA=11.56кН, которая направленна вверх. Соответственно поперечная сила в точке 0 будет равна Q(0) = 0 + 11.56 = 11.56.
Поэтому C = 11.56 — 5 ⋅ 0 = 11.56
Формула для поперечной силы на участке А:
Интегрируя функцию поперечной силы, получаем функцию изгибающего момента:
Аналогичным образом, значение момента на концах балок = 0, сосредоточенных моментов в начальной точке нет, поэтому M(0) = 0.
Подставляя x=0 и M(0) = 0 в выражение для C = M(x) + 2.
Формула для изгибающего момента на участке А:
Чтобы найти распределенную нагрузку q(x) воспользуемся уравнением прямой линии по двум точкам.
По точкам (2;0) и (4;8) получаем уравнение для распределенной нагрузки: q(x) = 4x-8.
Найдем функцию поперечной силы на участке, интегрируя полученную функцию распределенной нагрузки.
По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(2)=-5∙2+11.56 = 1.56. Аналогично, как и на предыдущем участке вычисляем интеграл и константу интегрирования по точке (2;1.56).
Получим формулу для поперечной силы на участке B:
см. расчет
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(2) = -2.5 ∙ 22 + 11.56 ∙ 2 + 0= 13.12 .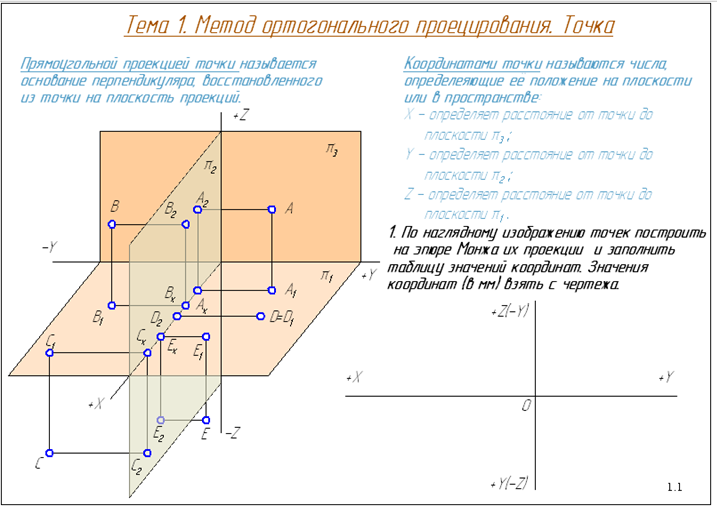
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке B:
см. расчет
По формуле Q(x) для предыдущего участка вычисляем значение Q на левой границе участка: Q(4) = -2 ∙ 42 + 8 ∙ 4 – 6.44 = -6.44.
Сосредоточенная сила скачком изменяет Qx в данной точке, она направлена вниз и потому отрицательна: Q(4) = -6.44 — 4 = -10.44
На третьем участке нет распределенной нагрузки, поперечная сила равна константе по последней точке.
Получим формулу для поперечной силы на участке С:
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(4) = -0.67 ∙ 43 + 4 ∙ 42 – 6.44 ∙ 4 + 15.33 = 10.91
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке С:
см. расчет
расчет
К данному участку также не приложена распределенная нагрузка, поперечная сила равна константе.
Формула для поперечной силы на участке D:
По формуле из предыдущего участка вычислим значение момента на левой границе участка: M(5) = -10.44 ∙ 5 + 52.67 = 0.47
Сосредоточенный момент скачком изменяет Mx в данной точке, он направлен по ходу часовой стрелки и поэтому положителен: M(5) = 0.47 + 10 = 10.47
Интегрируя формулу Q(x) и вычисляя константу интегрирования по граничной точке получим формулу для изгибающего момента на участке D:
см. расчет
Чтобы проверить правильность формул найдем значения поперечной силы и изгибающего момента в крайней точке балки.
Сосредоточенная сила в данной точке по величине равна опорной реакции с противоположным знаком. Изгибающий момент на концах балки равен нулю.
R.
 C.Hibbeler Engineering mechanics. Statics 12th edition, стр. 330 ↩
C.Hibbeler Engineering mechanics. Statics 12th edition, стр. 330 ↩Н. М. Беляев. Сопротивление материалов, М.: Издательство «Наука», 1965г, изд. 14, 231 стр. ↩
балка внутренний момент Инженерные поперечные силы теоретическая механика эпюра
Исчисление III — Цилиндрические координаты
Онлайн-заметки Пола
Главная
/
Исчисление III
/
Трехмерное пространство
/ Цилиндрические координаты
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 12.12: Цилиндрические координаты
Как и в двумерном пространстве, стандартная система координат \(\left( {x,y,z} \right)\) называется декартовой системой координат. В последних двух разделах этой главы мы рассмотрим некоторые альтернативные системы координат для трехмерного пространства.
Начнем с цилиндрической системы координат. Это довольно просто, поскольку это не что иное, как расширение полярных координат в трех измерениях. Это не только расширение полярных координат, но мы расширяем его в третье измерение так же, как мы расширяем декартовы координаты в третье измерение. Все, что мы делаем, это добавляем \(z\) в качестве третьей координаты. \(r\) и \(\theta\) такие же, как с полярными координатами. 93}\).
\(r\) и \(\theta\) такие же, как с полярными координатами. 93}\).
Преобразования для \(x\) и \(y\) — это те же преобразования, которые мы использовали, когда рассматривали полярные координаты. Итак, если у нас есть точка в цилиндрических координатах, декартовы координаты можно найти с помощью следующих преобразований.
\[\begin{align*}x & = r\cos \theta \\ y & = r\sin \theta \\ z & = z\end{align*}\]
Третье уравнение — это просто подтверждение того, что \(z\)-координата точки в декартовых и полярных координатах одинакова. 92} = 100\)
Показать все решения Скрыть все решения
a \(r = 5\) Показать решение
В двух измерениях мы знаем, что это круг радиуса 5. Поскольку мы теперь в трех измерениях и в уравнении нет \(z\), это означает, что он может свободно изменяться. Итак, для любого заданного \(z\) у нас будет окружность радиуса 5 с центром на оси \(z\).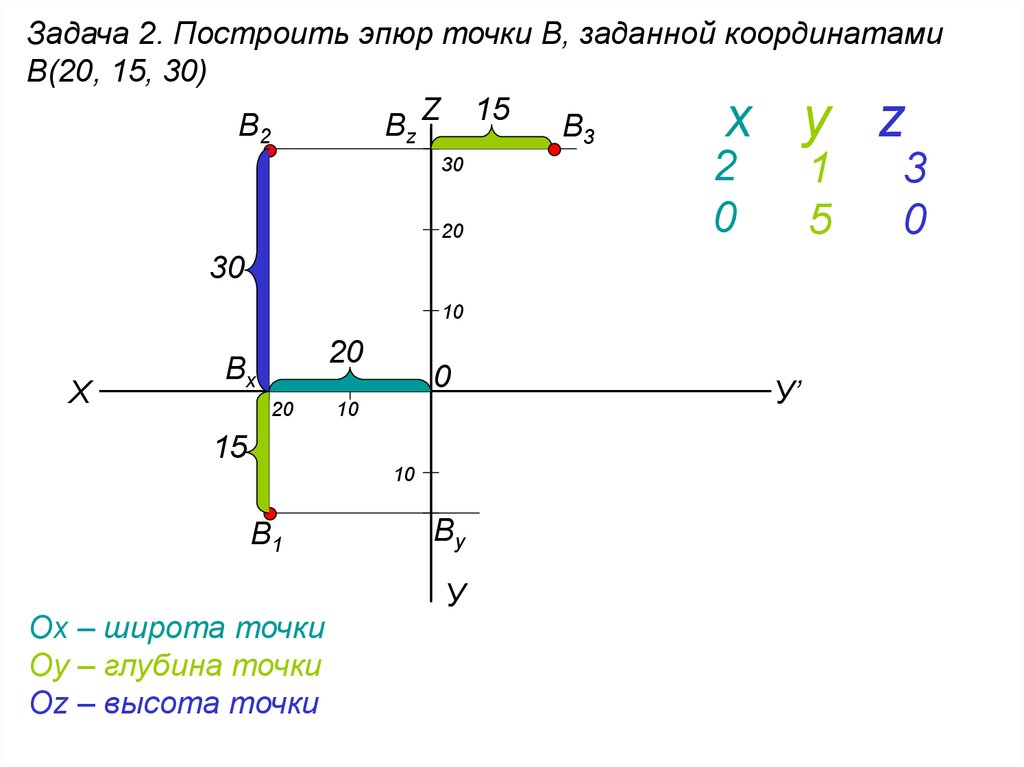
Другими словами, у нас будет цилиндр радиуса 5 с центром на оси \(z\). 92}\конец{выравнивание*}\]
Из раздела о поверхностях квадрата мы знаем, что это уравнение конуса.
3. Прямоугольные координаты
Хорошим способом представления функции является графическое представление. представление.
Графики дают нам визуальную картину функция.
Наиболее распространенный способ построения графика функции — использование прямоугольной системы координат . Состоит из:
xy(0, 0)IIIIIIIVОткрыть изображение на новой страницех — ось;
и -ось;
Происхождение `(0,0)`; и
Четыре квадранта, обычно обозначаются I, II, III, IV.
Декартова плоскость
Откуда все это взялось?
Рене Декарт
Система координат x-y также называется декартовой системой координат , по имени ее разработчика, Рене Декарта (1596 — 1650). Эта графическая система была невероятно важна для развития науки и техники.
Эта графическая система была невероятно важна для развития науки и техники.
Обычно значения независимой переменной (обычно значения x ) размещаются по горизонтали
ось, а значения зависимой переменной (обычно значения и ) размещаются по вертикали.
ось.
Значение x , называемое абсциссой , является перпендикулярное расстояние P от оси y .
Значение y , называемое ординатой , является перпендикулярное расстояние P от оси x .
Значения x и y вместе, записанные как ( x , y ) называются координатами точка P .
Она называется «прямоугольной» системой координат, потому что используется масштаб x 9.Ось 0011 равномерно распределена, как и шкала вдоль оси y . Существуют и другие системы, в которых масштаб неравномерный (см. логарифмические и полулогарифмические графики), а некоторые даже круглые (см. полярные координаты)
полярные координаты)
Калькулятор преобразования полярных координат в прямоугольные
Если вы хотите преобразовать комплексные числа из полярной формы в прямоугольную, воспользуйтесь онлайн-калькулятором полярных чисел в прямоугольные.
Пример 1
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
Найдите точки `A(2, 1)` и `B(-4, -3)` на прямоугольная система координат.
Ответить
Чтобы правильно ответить на этот вопрос, нам нужно сделать следующее:
- Пометить оси x и y .
- Нанесите шкалу на оси (числа) так, чтобы точки помещались на графике.
- Затем поставьте точки над нужными точками `A` и `B`.
Вот наш результат.
1234-1-2-3-4123-1-2-3-4xy(-4, -3)(2, 1)Открыть изображение на новой страницеПример 2
Три вершины прямоугольника — это `A(-3,-2)`, `B(4,-2)` и
`С(4,1)`.
Где находится четвертая вершина `D`?
Ответить
Вот положения точек `A`, `B` и `C`:
12345-1-2-3-4-5123-1-2-3-4-5xyABCОткрыть изображение на новой страницеПоскольку наоборот стороны прямоугольника равны и параллельно, мы видим, что:
y координата D должна быть `1`
Координата D x должна быть `-3`
Мы заключаем, что координаты D равны `(-3, 1)`.
Вот наш завершенный прямоугольник:
12345-1-2-3-4-5123-1-2-3-4-5xyABCDОткрыть изображение на новой страницеПример 3
Где находятся все точки `(x , y)`, для которых `x < 0` и `y < 0`?
Ответить
Имеем:
- `x < 0` означает, что `x` отрицательно,
- и `y < 0` также означает, что `y` отрицательный,
Так что единственный регион где обе координаты по всем точкам
отрицательные — это » третий квадрант
(III) «.

 Записываются и сами уравнения метода начальных параметров по участкам.
Записываются и сами уравнения метода начальных параметров по участкам.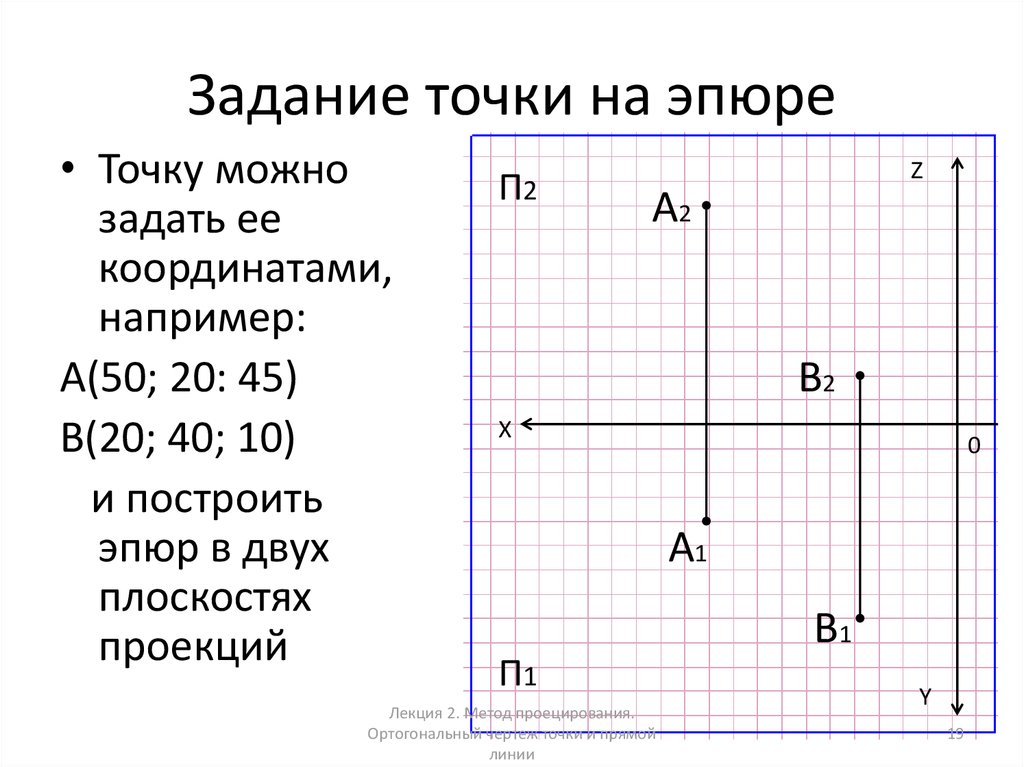 Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.
Константы интегрирования вычисляются по левой границе участка по формулам для предыдущих участков.
 C.Hibbeler Engineering mechanics. Statics 12th edition, стр. 330 ↩
C.Hibbeler Engineering mechanics. Statics 12th edition, стр. 330 ↩