Формулы площади и периметра всех фигур 4 класс: Формулы периметра

Как найти периметр фигур, его обозначение, измерение

Поможем понять и полюбить математику

Начать учиться

Обычно мы справляемся с разными жизненными ситуациями теми способами, к которым мы привыкли. На самом деле, подходящих вариантов может быть больше, как и формул в математике для решения одной задачи. В этой статье рассмотрим, как вычислить периметр фигуры разными способами.

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

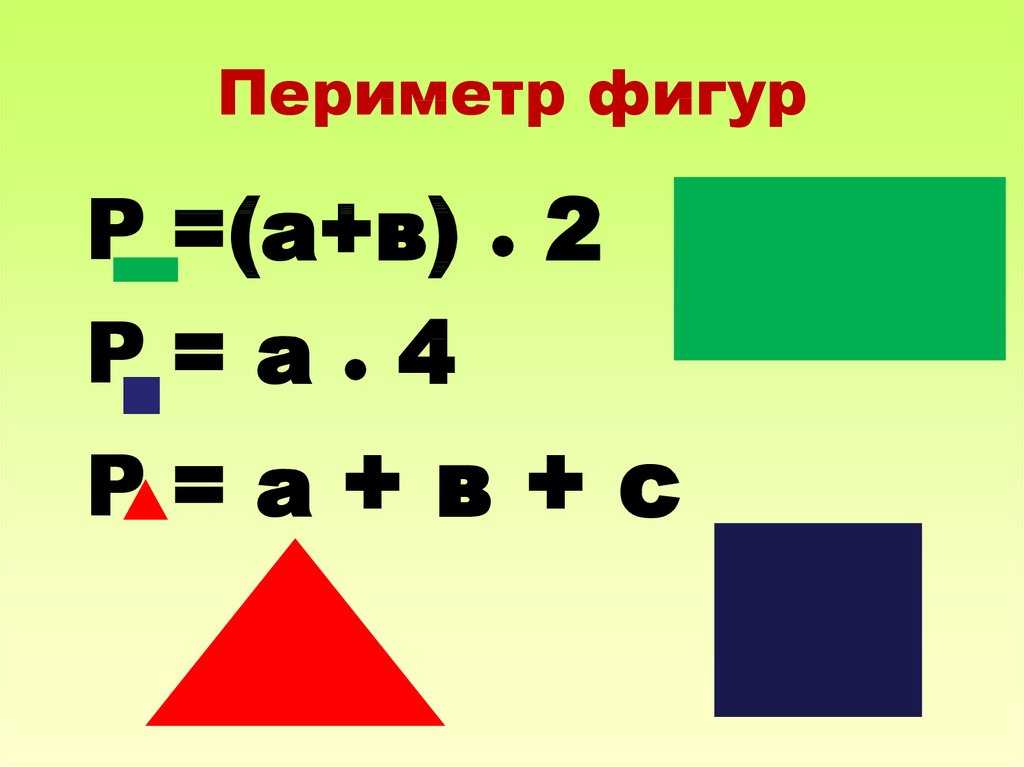
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Площадь прямоугольника равна 80 см

2, длина составляет 10 см. Чему равен периметр фигуры?

Как решаем:

• Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
• Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
• Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;

Ответ: 36 см.

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны? 

Как решаем:

• Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
• Известно, что равнобедренный треугольник имеет две равные стороны;
• Далее делим получившуюся сумму на два: 34 : 2 = 17 см;

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Как решаем:

• Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
• Длина окружности равна π × 2 × 20 = 40π см;

Ответ: 40π см.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

983.2K

Как найти площадь треугольника

К следующей статье

250.1K

Как найти периметр прямоугольника

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Площадь и периметр треугольника: формула и как найти

Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.

Формула периметра треугольника

Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Расчет периметра треугольника

Формула площади треугольника

1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площадь, a – основание, h – высота.

Расчет:

Площадь =

2. Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)

Расчет:

Площадь =

 

3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.

Расчет:

угол =

Площадь =

 

4. Формула Герона или площадь треугольника по его трем сторонам: S = √p · (p — a)(p — b)(p — c),
где a, b и c это стороны треугольника и p – половина периметра треугольника.

Расчет:

p = (a+b+c)/2 =

Площадь =

Что такое периметр треугольника?

Периметром треугольника называется сумма длин всех его сторон.

Как найти/вычислить периметр треугольника?

Для получения периметра треугольника нужно сложить все его стороны: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Чему равен периметр треугольника?

Периметр треугольника равен сумме всех его сторон.

Как найти/посчитать площадь треугольника?

Для того, чтобы вычислить площадь треугольника, можно использовать одну из формул ее вычисления, используя доступные вводные данные.

1. произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
   где S это площдаь, a – основание, h – высота.
2. по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
   где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)
3. по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
   где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.
4. по трем сторонам: S = √p · (p — a)(p — b)(p — c)
   ,
   где a, b и c это стороны треугольника и p – половина периметра треугольника.

Данный сайт использует файлы куки для обеспечения наилучшей функциональности и эфективности работы. Продолжая пользоваться сайтом вы соглашаетесь с политикой использования куки. Согласен Подробнее

Периметр, площадь и объем

Горячая математика

1. периметр из многоугольник (или любая другая замкнутая кривая, например круг) — это расстояние вокруг внешней стороны.

2. область из простая, замкнутая, плоская кривая — это объем пространства внутри.

3. объем из твердый 3 Д форма — это количество пространства, вытесненного ею.

Некоторые формулы для общих 2 -мерные плоские фигуры и 3 -мерные тела приведены ниже. Ответов один, два, или три измерения;

периметр измеряется в линейные единицы , область измеряется в квадратные единицы , и объем измеряется в кубические единицы .

Стол 1 . Формулы периметра
Форма	Формула	Переменные
Квадрат	п «=» 4 с	с это длина стороны квадрата.
Прямоугольник	п «=» 2 л + 2 Вт	л и Вт длины сторон прямоугольника (длина и ширина).
Треугольник	а + б + с	а , б , и с являются длинами сторон.
Прямоугольный треугольник с ножками а и б (видеть Теорема Пифагора )	п «=» а + б + а 2 + б 2	а и б это длины двух катетов треугольника
Круг	п «=» С «=» 2 π р «=» π д	р это радиус и д это диаметр.

Таблица 2. Формулы площади
Форма	Формула	Переменные
Квадрат	А «=» с 2	с это длина стороны квадрата.
Прямоугольник	А «=» л Вт	л и Вт длины сторон прямоугольника (длина и ширина).
Треугольник	А «=» 1 2 б час	б и час это основание и высота
Треугольник	А «=» с ( с − а ) ( с − б ) ( с − с ) где с «=» а + б + с 2	а , б , и с это длины сторон и с это полупериметр
Параллелограмм	А «=» б час	б это длина основания и час это высота.
Трапеция	А «=» б 1 + б 2 2 час	б 1 и б 2 — длины параллельных сторон и час расстояние (высота) между параллелями.
Круг	А «=» π р 2	р это радиус.

Таблица 3. Формулы объема
Форма	Формула	Переменные
Куб	В «=» с 3	с это длина стороны.
Правая прямоугольная призма	В «=» л Вт ЧАС	л это длина, Вт это ширина и ЧАС это высота.
Призма или цилиндр	В «=» А час	А площадь основания, час это высота.
Пирамида или конус	В «=» 1 3 А час	А площадь основания, час это высота.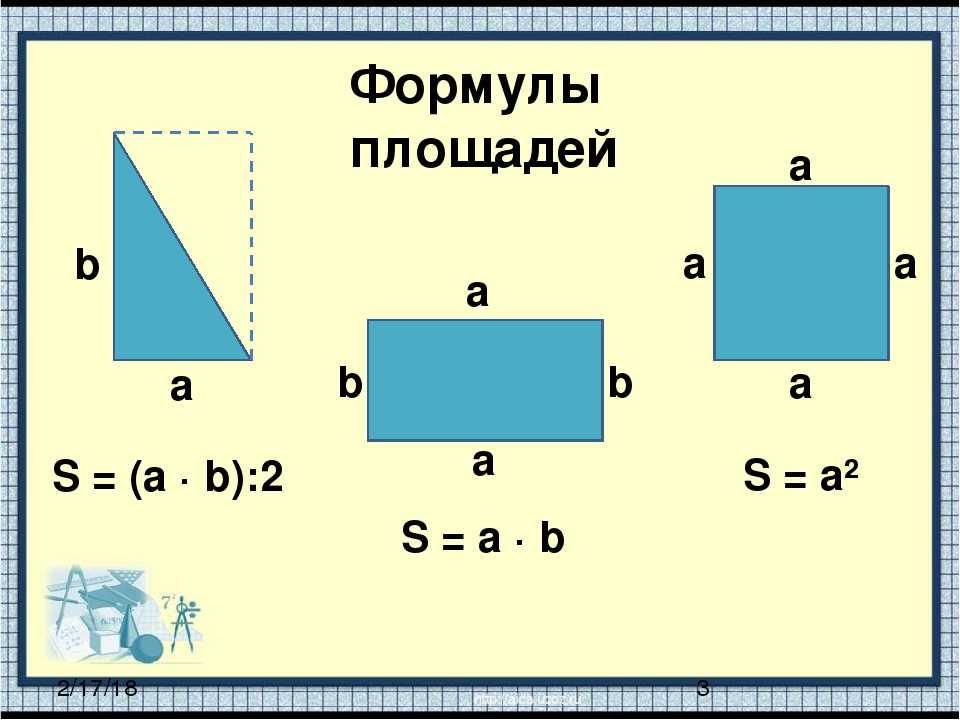
Сфера	В «=» 4 3 π р 3	р это радиус.

Периметр и площадь — формулы для всех фигур

Дата последнего обновления: 07 апреля 2023 г.0005

•

Просмотров сегодня: 4,07k

Для двумерной фигуры периметр относится к границе или пути вокруг фигуры. С другой стороны, площадь двумерной фигуры — это пространство, занимаемое на поверхности фигуры. Существуют различные типы фигур, но наиболее распространенными являются квадрат, прямоугольник, треугольник, круг и т. д. В этом содержании вы сможете узнать периметр и площадь основных фигур.

 

Начнем!

1. Прямоугольник

(Изображение будет загружено в ближайшее время)

 

Прямоугольник — это фигура, у которой противоположные стороны равны, а все углы прямые (90 градусов).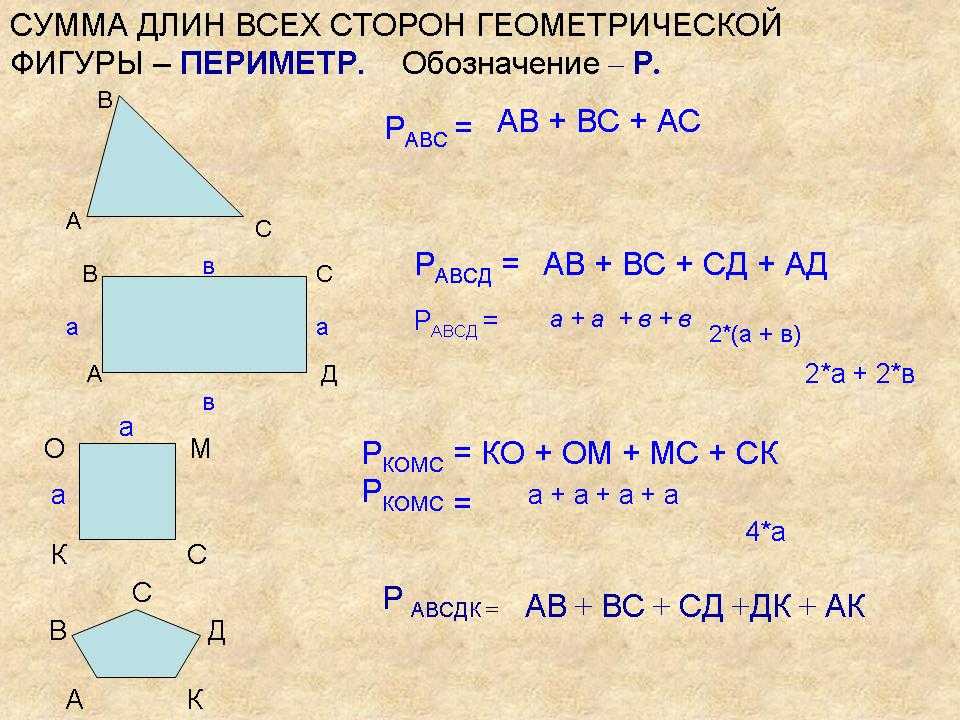

Периметр прямоугольника = \[2 ( a + b )\]

Площадь прямоугольника = \[ a \times b \]

 

2. Квадрат

(Изображение будет загружено в ближайшее время)

 

5

5 Квадрат – это фигура, у которой все четыре стороны равны, а все углы равны 90 градусов.

Периметр квадрата = \[ 4 \times a \] 9{2} \]

 

Примечание. Здесь значение числа пи равно \[\frac{22}{7} \] или 3,14. Вы можете использовать любой из них, если он не указан в вопросе.

 

4. Треугольник

(Изображение будет загружено в ближайшее время)

 

Треугольник – это фигура с тремя углами и тремя прямыми линиями. Треугольники можно разделить на три вида, например:

1. Равносторонний треугольник

Периметр равностороннего треугольника = 3 a 9{2} \]

 

2. Равнобедренный треугольник

Периметр равнобедренного треугольника = 2s + b

Площадь равнобедренного треугольника = \[\frac{1}{2} \times\] b \[\ times\] hb 

 

3. Разносторонний треугольник

Периметр разностороннего треугольника = a + b + c

Площадь разностороннего треугольника = \[\frac{1}{2} \times b \times h \ ]

 

5.

Параллелограмм

(Изображение скоро будет загружено)

 

Эта фигура представляет собой четырехугольник, противоположные стороны которого параллельны.

Периметр параллелограмма = \[2 ( a + b ) \]

Площадь параллелограмма = \[b \times h\]

 

Это параллелограмм, стороны которого равны.

Площадь ромба = \[a \times h \]

Периметр ромба = \[4 \times a \]

7. Трапеция

Эта фигура представляет собой четырехугольник, который имеет как минимум 1 пару параллельных сторон .

Периметр трапеции = \[a_1 + a_2 + b_1 + b_2 \]

Площадь трапеции = \[(\frac{( a1 + a2 )}{2}) \times h \]

 

8. Regular N-Gon

(Изображение будет загружено в ближайшее время)

 

Правильным многоугольником называется многоугольник, у которого число сторон и углов одинаковы.