Формулы производных функций — полная таблица с примерами
Содержание:
- Формулы производных функций
- Производная показательной функции
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
А теперь более подробно история и откуда они взялись.
К основным, знакомым вам элементарным функциям относятся линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Производные первых трёх функций из этого списка вы находить научились (формулу производной степенной функции, правда, ещё предстоит вывести).
Производный расчет является наиболее важной операцией в дифференциальном расчете. |
Чтобы получить формулу производной показательной функции , воспользуемся графическими соображениями.
Рассмотрим графики показательных функций при и проведём к ним в их общей точке
(0; 1) касательные (рис. 66). Угловой коэффициент касательной в зависимости от может быть равен любому положительному числу. На рисунке 66 выделен график, касательная к которому имеет угловой коэффициент 1, т. е. параллельна прямой .
Обозначим буквой основание этой показательной функции .
Из рисунка видно, что . Однако это довольно грубое приближение. Встретившись в 10 классе с числом как основанием натуральных логарифмов , вы использовали более точное приближение .
С числом математики познакомились не как с основанием соответствующей показательной функции, а как с пределом последовательности: .
Возможно вам будут полезны данные страницы:
Формула Байеса |
Как найти производную: примеры решения |
Таблица производных |
Таблица производных полная: для студентов |
Доказательство существования этого предела довольно трудоёмко, но с помощью калькулятора этот предел можно достаточно точно вычислить.
Для этого будем находить значения выражения , увеличивая значения :
Число является иррациональным и не может быть выражено в виде конечной десятичной дроби, однако можно найти его приближение с любой точностью, например .
Равенство единице углового коэффициента касательной к графику функции в точке означает, что в этой точке значение производной равно .
Обозначение «» было выбрано в честь великого математика Леонарда Эйлера (1707—1783) и является первой буквой его фамилии Euler. В последней главе учебника вы увидите знаменитые формулы Эйлера, в которых это число фигурирует.
Используя значение производной в нуле, найдём производную функции в произвольной точке :
Получить формулу производной показательной функции с произвольным основанием поможет формула производной сложной функции.
Поскольку , имеем:
.
Производная показательной функции
Похожим способом, находя сначала угловой коэффициент касательной к графику функции в точке , можно получить формулы производных тригонометрических функций.
В 10 классе говорилось, что графики функций и вблизи начала координат сливаются с прямой (рис.67).
Значит, .
Можно было воспользоваться тригонометрическим кругом. Поскольку ось тангенсов касается тригонометрического круга (рис. 68), то .
Рис. 67 Рис. 68
Найдём теперь производную функции в произвольной точке :
Правила нахождения производных, тригонометрические формулы и формула производной сложной функции помогают получить производные косинуса, тангенса и котангенса.
.
Из основных элементарных функций остались логарифмическая и обратные тригонометрические функции. Выведем формулы их производных.
По определению логарифма при имеем: . Последнее равенство задаёт функцию у неявно, что, однако, не мешает найти производные от обеих его частей: .
Заменяя на и выражая , получим: . Конечно, следует помнить, что , так как .
Для натурального логарифма из этой формулы получим: .
Аналогичным способом выведем формулы обратных тригонометрических функций.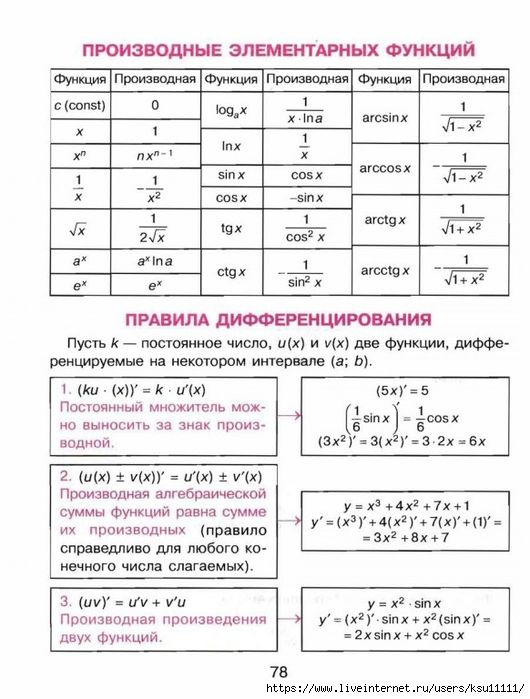
По определению арксинуса при ; имеем: .
Находим производные от обеих частей последнего равенства: . Поскольку при значения косинуса неотрицательны,
.
Следовательно, .
Аналогично получаются следующие формулы.
Нам осталось выполнить данное в пункте 7 обещание и вывести формулу производной степенной функции , где — любое действительное число.
Рассмотрим функцию при . Прологарифмируем равенство и найдём производные от обеих частей:
.
Заменим у его выражением через .
Примечание.
При показатель степени функции может быть только целым числом. Пользуясь свойством чётности степенной функции с чётным показателем, формулой производной сложной функции и свойством нечётности степени с нечётным показателем, имеем при
( — целое):
Если же показатель степени нечётный: ( — целое), то при имеем:
Таким образом, формула производной степени распространяется и на промежуток .
При производная функции существует только при .
Графики взаимно обратных функций симметричны относительно прямой . Этим фактом можно воспользоваться при выводе формулы производной обратной функции.
Сравним угловые коэффициенты симметричных касательных к графикам взаимно обратных функций и в их точках и ; соответственно (рис. 69). В силу упомянутой симметрии и, .
Рис. 69
Это означает, что угловые коэффициенты рассматриваемых касательных взаимно обратны. Поскольку , a , получаем формулу производной обратной функции.
В этой формуле не производная сложной функции, а значение производной функции в точке .
Пусть теперь , a . Зная производную функции , из формулы производной обратной функции при значении получим формулу производной логарифма.
Таблица производных.
Вычисление производной — важнейшая операция в дифференциальном исчислении.
Навигация по странице: Общие формулы дифференцирования функций Таблица производных основных элементарных функций Производные логарифмов Производные тригонометрических функций Производные обратных тригонометрических функций Производные гиперболических функций
Онлайн калькулятор: Решение производных
Общие формулы дифференцирования функций
В этих формулах u и v — произвольные дифференцируемые функции вещественной переменной, а c — вещественная константа.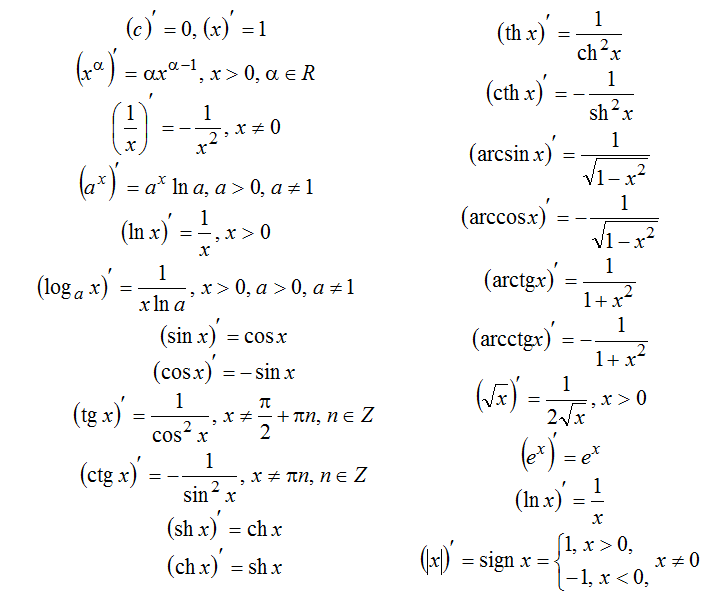
Этих формул достаточно для дифференцирования любой элементарной функции.
(c · u)′ = c · u ′
(u + v)′ = u ′ + v ′
(u · v)′ = u ′ · v + u · v ′
| ( | u | ) | ′ | = | u ′ · v — u · v ′ |
| v | v2 |
Таблица производных основных элементарных функций
Производная от константы
c ′ = 0, где c = constПроизводная степенной функции
(xn )′ = n · xn — 1Производная показательной функции
(a x )′ = ax · ln aПроизводная экспоненты
(ex )′ = exПроизводные логарифмов
| (loga x)′ = | 1 |
| x · ln a |
| (ln x)′ = | 1 |
| x |
Производные тригонометрических функций
(sin x)′ = cos x
(cos x)′ = -sin x
| (tg x)′ = | 1 |
| cos 2 x |
| (ctg x)′ = — | 1 |
| sin 2 x |
Производные обратных тригонометрических функций
| (arcsin x)′ = | 1 |
| √1 — x2 |
| (arccos x)′ = — | 1 |
| √1 — x2 |
| (arctg x)′ = | 1 |
| 1 + x2 |
| (arcctg x)′ = — | 1 |
| 1 + x2 |
Производные гиперболических функций
(sh x)′ = ch x
(ch x)′ = sh x
| (th x)′ = | 1 |
| ch2 x |
| (cth x)′ = — | 1 |
| sh2 x |
Формулы сокращенного умножения Формулы и свойства степеней Формулы и свойства корней Формулы и свойства логарифмов Формулы и свойства арифметической прогрессии Формулы и свойства геометрической прогрессии Тригонометрические формулы Обратные тригонометрические формулы Таблица производных
Все таблицы и формулы
Попробуйте онлайн калькуляторы из темы пределы и производные функцийОнлайн калькулятор.
Решение пределов онлайн.Онлайн калькулятор. Решение производных онлайн.Показать все онлайн калькуляторы
Попробуйте онлайн калькуляторы для вычисления интеграловОнлайн калькулятор. Решение интегралов онлайн.Онлайн калькулятор. Решение определенных интегралов онлайн.Показать все онлайн калькуляторы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
2 u )(du)/dx`Частные случаи
`d/dx sh x = ch x``d/dx «csch»\ x = — coth x «csch»\ x `
`d /dx ch x = sinh x `
`d/dx «sech»\ x = — tanh x «sech»\ x `
`d/dx tanh x = 1 — tanh3 x `
`d/dx coth х = 1 — coth3 х `
Производная тригонометрических функций: шаги
Давайте сделаем перерыв и на минутку подумаем о пляже. Мы видим волны в море, волейбольный мяч, подпрыгивающий вверх и вниз. Если мы сосредоточимся на горизонте, то увидим плавающий буй. Он поднимается и опускается по морским волнам!
Обычный сценарий на пляже, pixabay.
com
Что общего у всех этих вещей? Ответ заключается в том, что их движение периодично. P эриодические функции описывают такие вещи, как морские волны. Периодические функции — это функции, которые повторяют свои выходные данные через равные промежутки времени. Тригонометрические функции являются яркими примерами периодических функций. По этой причине важно знать, как дифференцировать тригонометрические функции.
Значение производной тригонометрических функций
Вам может быть интересно, что значит найти производную тригонометрической функции.
Нахождение производной функции означает, что вы находите другую функцию, которая описывает скорость ее изменения.
То есть производная функции — это другая функция, которая описывает, как изменяется исходная функция. Это делается независимо от того, с какими функциями вы имеете дело, и тригонометрические функции не исключение!
Обычно приводятся формулы для производных всех видов функций.
Здесь вы узнаете, как найти производные тригонометрических функций.
Формулы для производных тригонометрических функций
Существует шесть основных тригонометрических функций:
Функция синуса: \( \sin{x}.\)
Функция косинуса: \( \cos{x }.\)
Функция тангенса: \( \tan{x}.\)
Функция котангенса: \( \cot{x}.\)
Функция секанса: \( \sec{x}.\)
Функция косеканса: \( \csc{x}.\)
Тригонометрические функции являются связующим звеном между тригонометрией и исчислением. Все шесть тригонометрических функций являются периодическими функциями.
Напоминание о графиках этих функций и их периодов см. в разделе Тригонометрические функции.
Давайте теперь посмотрим на каждую из их производных.
Производные основных тригонометрических функций:
$$\frac{\mathrm{d}}{\mathrm{d}x}\sin{x}=\cos{x},$$
$$ \ frac {\ mathrm {d}} {\ mathrm {d} x} \ cos {x} = — \ sin {x}, $ $ 92{x},$$
$$\frac{\mathrm{d}}{\mathrm{d}x}\sec{x}=\left( \sec{x} \right)\left(\tan {x}\right),$$
и
$$\frac{\mathrm{d}}{\mathrm{d}x}\csc{x}=-\left( \csc{x} \right )\left(\cot{x}\right).
$$
Обратите внимание, что все производные тригонометрических функций включают большее количество тригонометрических функций. Эта связь является признаком периодичности тригонометрических функций!
Давайте посмотрим, как найти производную некоторых тригонометрических функций, используя приведенные выше производные вместе с основными правилами дифференцирования.
Производные тригонометрических функций и цепное правило
Давайте посмотрим, как дифференцировать тригонометрические функции с помощью цепного правила.
Найдите производную \( f(x)=\sin{2x}.\)
Ответ:
Чтобы найти эту производную, вам нужно будет использовать цепное правило. Пусть \( u=2x.\) Тогда по степенному правилу
$$u'(x)=2.$$
Итак, теперь, используя цепное правило,
$$\begin{align}f'( x) &= \left( \frac{\mathrm{d}}{\mathrm{d}u}\sin{u} \right) \left(\frac{\mathrm{d}u}{\mathrm{d }x} \right) \\[0.5em] &= \left( \cos{u} \right) (2) \\ &= 2\cos{u}.
\end{выравнивание}$$ 92} \right).$$
Примеры производных тригонометрических функций
Вычисление требует практики! Вы также должны иметь возможность использовать больше правил дифференциации, таких как Правило продукта и Правило частного.
Найдите производную от \( f(x)=x \left(\sin{x}\right).\)
Ответ:
Поскольку у вас есть произведение функций, начните с использования правила произведения, то есть
$$f'(x)=\left( \frac{\mathrm{d}}{\mathrm{d}x} x \right) \sin{x} + x \left(\frac{\mathrm{ d}}{\mathrm{d}x} \sin{x} \right).$$
Вы можете найти производную \( x \) с помощью степенного правила,
$$\frac{\mathrm{d}}{\mathrm{d}x} x= 1,$$
и производная функции синуса есть функция косинуса
$$\frac{\mathrm{d}}{\mathrm{d}x}\sin{x}=\cos{x}. производная от \( f(x) \) равна
$$\begin{align}f'(x) &= \left( \frac{\mathrm{d}}{\mathrm{d}x} x \right ) \sin{x} + x \left(\frac{\mathrm{d}}{\mathrm{d}x} \sin{x} \right) \\[0.
5em] &= (1)\sin{ x}+x\left( \cos{x} \right) \\ &= \sin{x}+x \cos{x}.\end{align}$$ 92.\) Наконец, подставьте обратно \( u=\sin{x},\), получив
$$h'(x)=2 \left( \sin{x} \right) \left( \cos{x } \right) .$$
Помните, практика ведет к совершенству!
Распространенные ошибки
Время от времени все совершают ошибки. Здесь вы увидите некоторые распространенные ошибки при дифференцировании тригонометрических функций.
Одной из распространенных ошибок является ошибка в знаках при дифференцировании функции косинуса, функции котангенса или функции косеканса, то есть
$$\frac{\mathrm{d}}{\mathrm{d}x} \cos{x} \neq \sin{x}. $$
Обязательно поставить минус!
$$\frac{\mathrm{d}}{\mathrm{d}x} \cos{x} = -\sin{x}. $$
Один из простых способов запомнить знаки производных тригонометрических функций — обратить внимание на название функции. Если оно начинается с «co», например, co синус, co тангенс и co секанс, то производная имеет отрицательный знак.
Другая распространенная ошибка возникает при дифференцировании функции секанса или функции косеканса. Помните, что при дифференциации этих функций вы должны записывать правильные входные данные 92} \справа). $$
Будьте осторожны, если вы дифференцируете тригонометрические функции с разными входными данными. Выполнение действий шаг за шагом поможет вам не перепутать входные данные!
Производные обратных тригонометрических функций
Вам также может понадобиться найти производные обратных тригонометрических функций, таких как арксинус, арктангенс и т. д. Ознакомьтесь с нашей статьей о производных обратных тригонометрических функций для глубокого обсуждения!
Производные тригонометрических функций — основные выводы 92{x},$$
$$\frac{\mathrm{d}}{\mathrm{d}x}\sec{x}=\left( \sec{x} \right)\left(\tan {x}\right),$$
и
$$\frac{\mathrm{d}}{\mathrm{d}x}\csc{x}=-\left( \csc{x} \right )\left(\cot{x}\right).$$
- Ошибки в знаках.
