« Разложение разности квадратов на множители»
Главная → Публикации → Алгебра → Конспект занятия → 7 класс → Тема: « Разложение разности квадратов на множители»
Урок изучения нового материала и первичного закрепления по теме « Разложение разности квадратов на множители» построен с использованием технологии системно-деятельностного подхода. Урок рассчитан на 40 минут. Усвоение данного материала является основой для успешного решения заданий ОГЭ в части преобразования выражений, решения задач.
Содержимое публикации
Тема: «Разложениеразностиквадратовнамножители»
Типурока:Изучениеновогоматериала
Целиурока:
вывестиформулусокращенногоумножениядляразложенияразностиквадратов на множители; научиться выполнять разложение разности квадратов на множители; применять формулы разности квадратов для тождественных преобразований выражений
развиватьумениематематическиграмотновыражатьсвоимысли;способностьделатьсамостоятельныевыводынаосновепрактическихдействий;
формировать познавательный интерес к предмету, воспитывать умениеработатьвгруппе.
Оборудование:проектор,раздаточныематериалы.
Ходурока:
1.Мотивация к учебной деятельности.
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с формулами сокращенного умножения.
-Здравствуйте, ребята! Рада вас приветствовать! Над какой темой мы начали работать прошлых уроках? (Формулы сокращенного умножения)
– Что мы научились находить? (Квадрат суммы двух выражений, квадрат разности двух выражений, выполнять разложение на множители с помощью этих формул, произведение разности двух выражений на их сумму).
2. Актуализация знаний и фиксация затруднения в деятельности.
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: правило умножения разности двух выражений на их сумму;
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать затруднение в деятельности, демонстрирующее недостаточность имеющихся знаний: разложение разности квадратов на множители
На доске записаны задания для устной работы.
-Сегодня мы с вами на уроке изучим ещё одну формулу, которая позволит нам выполнять вычисления быстро и легко вычисления.
Представьте в виде многочлена:
(a—b)(a+b)=
-Как называются эти формулы?
-Зачем мы их изучаем?
-А если поменять местами левую и правую части первых двух выражений, что получим? (записать под диктовку ченика на доске)
=
-Нарушится равенство? А как применить эти формулы в данных примерах?
= (100)
(400)
18∙22= (396)
Ученики объясняют свои вычисления и говорят ответы.
= ?
3. Выявление причины затруднения и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
-В чем возникло затруднение? (При вычислении значения квадратов чисел 215 и 214)
-Почему большинство справились с предыдущим примером? (На прошлых урока мы выполняли задания такого вида)
-Что мы использовали при вычислении выражений такого типа? (Правило умножения разности двух выражений на их сумму).
– Как вы думаете, какая цель стоит перед нами сегодня на уроке? (Найти способ быстрого счета для примеров вида а2-в2).
-Что мы можем использовать при нахождении значения числового выражения? (Формулы, законы математики, правила)
-Какая из известных формул может быть использована? (( а-в)(а+в)=а2-в2).
-А в каком виде мы должны ее использовать? (Поменять местами левую и правую части).
-Как мы называем операцию замены многочлена произведением? (Разложением на множители)
— Сформулируйте тему урока. (Разложение разности квадратов на множители)
Какова цель урока? (Научиться выполнять разложение разности квадратов на множители, применять правило умножения разности двух выражений на их сумму для рационального вычисления значений выражений).
–Запишите тему. (На доске открывается тема урока.)
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме.
-Давайте запишем формулу (а-в)(а-в)= а2— в2
-А в каком виде мы ее будем применять? (Меняем местами правую и левую части).
–Итак, имеем а2-в2 = (а-в)(а+в). Это тождество называется формулой разности квадратов.
-Прочитайте данное тождество. (Разность квадратов равна произведению разности двух выражений на их сумму)
-Где мы можем подтвердить правильность наших рассуждений. Обратимся к учебнику стр.177, найдите соответствующее правило и прочитайте его.
Верными оказались наши предположения и рассуждения?
-Как мы можем использовать данную формулу?? (Для быстрого счета, для разложения на множители).
-А сейчас, зная эту формулу, вычислите результат выражения, вызвавшего затруднение.
=(215-214)(215+214)=1*429=429
-Разложите на множители:
49х2-16у6=(7х)2-(4у3)2=(7х-4у3)(7х+4у3)
Сформулируйте алгоритм разложения на множители:
1.Представить двучлен в виде разности квадратов.
2.Выполнить разложение по формуле а2-в2= (а-в)(а+в).
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Поодномучеловекувыходяткдоске(пожеланию),остальныеработаютвтетрадях
1.Установите соответствие:
— = (3-a)(3+a)
9- = (x-y)(x+y)
-400 (4y-9)(4y+9)
0,64-25 (0,8-5x)(0,8+5x)
-81+16 (p-20)(p+20)
2.
Разложитьнамножители:
— | 100−
1.
|
Разложитьнамножители: 1.Разложитьнамножители:
» Алгебра
Разложение на множители с помощью формул квадрата суммы и квадрата разности
Класс 7 Дата _________________ Урок ____ Учитель ________________________
Тема: «Разложение на множители с помощью формул квадрата суммы и квадрата разности»
Тип урока: комбинированный урок.
Цель урока: формирование навыков разложения многочлена на множители с помощью формул квадрата суммы и квадрата разности;
Задачи.
Обучающая: обеспечить усвоение материала всеми учащимися; учить и научить каждого ученика самостоятельно добывать знания; формировать навыки, умения, которые обеспечивают успешное выполнение деятельности.
Развивающая: способствовать развитию математического кругозора, мышления: умения анализировать, выделять главное, сравнивать, обобщать и систематизировать, развивать устную и письменную речи, внимание и память; продолжить работу по развитию умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученных знаний.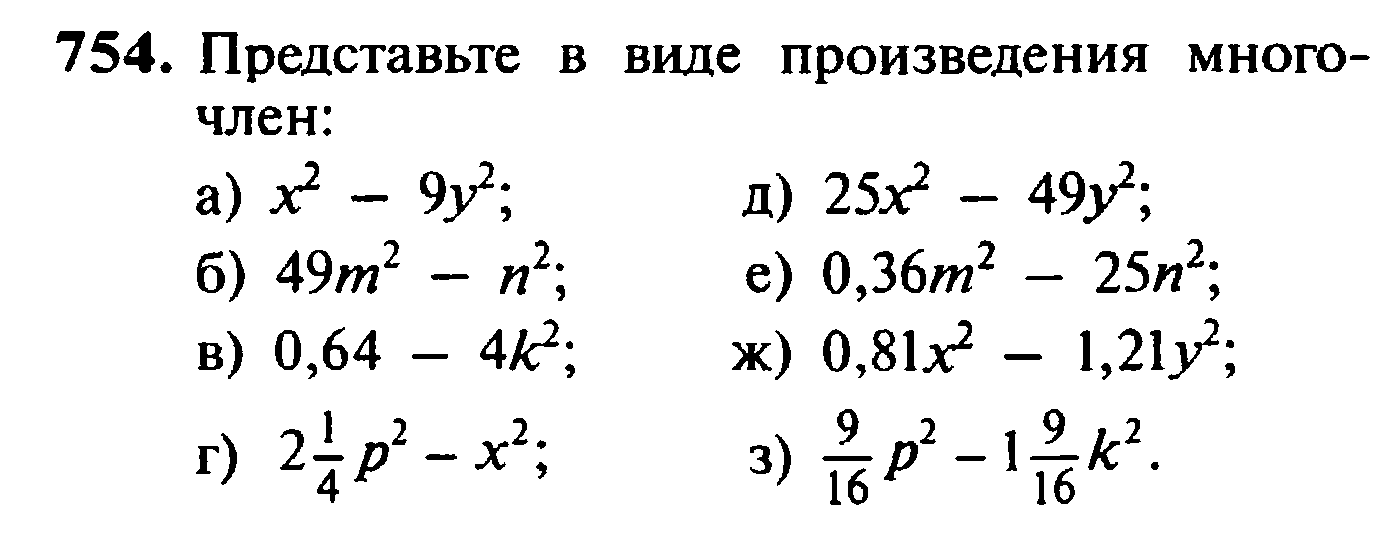
Воспитывающая: содействовать воспитанию интереса к математике, активности, дисциплинированности, честности, ответственности за свой труд и труд одноклассника, воспитание навыков самоконтроля и взаимоконтроля.
Ход урока
Организационный момент
Мы изучили с вами тему “Возведение в квадрат суммы и разности двух выражений”. На прошлом уроке выяснили, как можно применить эти формулы для разложения многочленов на множители. Ваша задача на этом уроке, показать, как вы усвоили изученный материал и как вы умеете применять полученные знания, а также как на сегодняшний день вы сами оцениваете свои знания.
Актуализация опорных знаний
Формулой называется символьная запись, содержащая некоторое утверждение.
а) При записи формул были допущены ошибки . Найдите и исправьте их.
1) (а+в)2 =а2+ав+в2
Ответ : (а+в)2=а2+2ав+в2
2) (а-с)2=а2-2ав+в2
Ответ : (а-в)2=а2-2ав+в2
3) (а+в)3=а3+а2в+ав2-в3
Ответ : (а-в)3=а3-3а2в+3ав2-в3
4) (а-в)3=а3-3ав+3ав-в3
Ответ : (а-в)3=а3-3а2в+3ав2-в3
б) В таблицах представлены выражения.
Выберите правильный ответ.
Ответы:
Задание | 1 | 2 | 3 |
(с+3)2= | с2 — 6с + 9 | с2 + 2с + 9 | с2 + 6с + 9 |
(4-2у)2= | 16 + 16у + у2 | 16 — 16у + у2 | 8 — 8у + у2 |
(9+5х)2= | 25х2+90х+81 | 25х2+81 | 25х2-90х- 81 |
Проверка домашнего задания «Математический диктант»
Запишите:
Квадрат числа а
Удвоенное число b
Сумму х и у
Сумму квадрата х и куба у
Удвоенное произведение а и b
Утроенное произведение c и d
Квадрат суммы а и b
Квадрат разности х и у
Произведение b и квадрата а
Произведение куба а и удвоенного числа b
Баллы 8-10 – «5»
5-7 – «4»
1-4 – «3»
Изучение нового материала
— Попробуйте разложить на множители такое выражение:
(Если ребята не догадались, указываем на то, что в этом выражении есть квадрат одного выражения, квадрат второго, и их удвоенное произведение)
— Верно.
Это .
— При разложении этого многочлена на множители использовали ли мы вынесение общего множителя за скобки? (Нет) А способ группировки? (Нет)
— Значит, мы имеем дело с новым способом разложения многочлена на множители. Этот способ называется разложением многочлена на множители с помощью формул сокращённого умножения.
— Любую формулу можно использовать, читая её как слева направо, так и справа налево. Поскольку , то и .
— Чтобы успешно пользоваться новым приёмом, нужно научиться распознавать в выражении квадраты одночленов и удвоенные произведения одночленов.
Первичное закрепление знаний
Работа с учебником № 833, №834, №837 – на доске и в тетрадях.
Релаксация
«Лентяй»
Сегодня мои дети много занимались, играли и, наверное, устали. Я предлагаю вам немного полениться.
Представьте себе, что вы – лентяи и нежитесь на мягком, мягком ковре. Вокруг тихо и спокойно, вы дышите легко и свободно. Ощущение приятного покоя и отдыха охватывает все ваше тело. Вы спокойно отдыхаете, вы ленитесь. Отдыхают ручки у.., отдыхают ножки у … Приятное тепло охватывает все ваше тело, вам лень шевелиться, вам приятно. Ваши руки, ноги, все тело расслаблено. Чувство приятного покоя наполняет вас изнутри. Вы отдыхаете, вы ленитесь. Приятная лень разливается по всему телу. Вы наслаждаетесь полным покоем и отдыхом, который приносит вам силы и хорошее настроение.
Потянитесь, сбросьте с себя лень и на счет «три» откройте глаза.
Закрепление изученного материала
Дидактическая игра в парах.
-Некоторые из формул сокращенного умножения были известны ещё в древности. Эти формулы часто помогают при вычислениях. Каждая пара учеников должна решить свой пример. Найти в схеме букву, соответствующую ответу и поставить её под номером своей карточки.
Полученное имя принадлежит известному математику, который с помощью формул сокращённого умножения доказал равенство (2а + в)2 = 4(а + в) а + в2
Примеры решают на местах в парах, помогая друг другу.
Карточки
1) (в2 + 2а2)2
3) (а2 – 3в)2
5) (а – 3в)2
2) (2в2 + 3а)2
4) (2а – 3в)2
6) (2в – 3а)2
Е) в4 – 4а2в2 – 4а2
Д) 4в2 – 12ав + 9а2
Л) 4а2 – 12ав + 9в2
К) а4 – 6а2в + 9 в2
И) а2 – 6aв + 9в2
В) 4в2 – 12в2а + 9а2
1 2 3 4 5 6
Е В К Л И Д
Историческая справка.
-Слово о Евклиде предоставляется одному из учащихся, подготовленному заранее.
Евклид – древнегреческий математик.
Автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Его научная деятельность протекала в Александрии в III в. до н.э. Евклид – первый математик Александрийской школы. Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвёл итог предшествующему развитию греческой математики. Также Евклид – автор работ по астрономии, оптике, музыке и другим наукам. (Математика, Большой энциклопедический словарь М., Большая Российская энциклопедия, 1998 г.).
Оценивание
Ребята, вы сегодня были молодцы! Мы справились с поставленной задачей. И мне бы хотелось, чтобы Вы оценили самостоятельно свою работу.
Домашнее задание
п. 33 – читать, № 835, 838, 851 – письменно, 847* – для более сильных учащихся.
Творческое задание: домашнее задание для учителя, предварительно разделив класс на три группы, каждая из которых должна придумать по два примера используя формулы сокращенного умножения.
SMS – рефлексия
Учащимся предлагается на бумажных мобильных телефонах написать SMS – сообщение учителю о том, как прошёл урок, оценить как плодотворно онг работал.
Итог урока. Установка на успех
Итак, ребята, давайте с вами подведём итог нашего урока, ответив на следующие вопросы:
Для чего нужны формулы сокращённого умножения? (чтобы облегчить процесс умножения).
Сформулируйте формулу квадрата суммы двух выражений (квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго выражения)
Сформулируйте формулу квадрата разности двух выражений (квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго выражения)
ФСУ отражают частные случаи умножения многочленов, которые очень часто встречаются.
Вот почему следует навсегда запомнить такой важный инструмент в математике, как ФСУ. Мы с Вами еще в начале пути. Нам еще предстоит познакомиться со многими другими формулами математики.
На этом урок окончен, спасибо вам за урок!.
Решения по математике для 7 класса, глава 15 по математике
- Решения для учебников
- Класс 7
- Математика
- алгебраические формулы разложение квадратов
Решения по математике Решения по математике для 7 класса Глава 15 Алгебраические формулы Расширение квадратов представлены здесь с простыми пошаговыми объяснениями. Эти решения для расширения квадратов алгебраических формул чрезвычайно популярны среди учащихся 7-го класса.
Все вопросы и ответы из Книги решений по математике для класса 7 по математике, глава 15, предоставляются здесь для вас бесплатно. Вам также понравится отсутствие рекламы в Mathematics Solutions Solutions от Meritnation. Все решения по математике Решения для класса 7 по математике подготовлены экспертами и на 100% точны.
Страница № 93:
Вопрос 1:
Развернуть.
(I) (5 A +6 B ) 2 (ii) A2+B32 (III) 2p-3q2 (iv) x-2×2
(v) AX+by2 (VI) 7m-42 (vii) x +122 (viii) a-1a2
Ответ:
Известно, что ( A + B ) 2 = A 2 + 2 AB 1 AB 21 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 1 AB 2 2 AB 1. + б 2 и ( а — б ) 2 = a 2 − 2 ab + b 2 .
i 5a+6b2=5a2+2×5a6b+6b2=25a2+60ab+36b2
ii a2+b32=a22+2×a2×b3+b32=a24+ab3+b29
iii 2p-3q2=2p2-2× 2p×3q+3q2=4p2-12pq+9q2
iv x-2×2=x2-2×x×2x+2×2=x2-4+4×2
v ax+by2=ax2+2×ax×by+by2=a2x2+ 2axby+b2y2
vi 7m-42=7m2-2×7m×4+42=49m2-56m+16
vii x+122=x2+2×x×12+122=x2+x+14
viii a-1a2 =a2-2×a×1a+1a2=a2-2+1a2
Номер страницы 93:
Вопрос 2:
Какой из приведенных ниже вариантов является квадратом бинома 8 — 1x ?
(i) 64 — 1×2 (ii) 64 +1×2 (iii) 64 — 16x + 1×2 (iv) 64 +16x + 1×2
Ответ:
Данным биномом является 8-1x.
8-1×2=82-2×8×1x+1×2 ∵ a-b2=a2-2ab+b2=64-16x+1×2
Следовательно, правильный ответ — вариант (iii).
Страница № 93:
Вопрос 3:
Какой из приведенных ниже биномов равен m 2 n 2 + 14 mnpq + 49 p 2 q 2 расширение?
(I) ( M + N ) ( стр.
(iv) ( mn + 7 pq )
Ответ:
Проверим каждый из заданных вариантов.
(i) ( m + n )( p + q )
= M ( P + Q ) + N ( P + Q )
= MP + MQ + NP + nq 2 2 2 2 2 2 . вариант.
(II) ( млн. — PQ ) 2
= ( MN ) 2 — 2 × ( мл ) × PQ ) + ( MN ) × ) ( MN ) × ) ( MN ) × ) + ( млн. М ) × ). [∵ ( a − b ) 2 = a 2 − 2 ab + b 2 ]
= m 2 n 2 − 2 mnpq + p 2 q 2
So, it не правильный вариант.
(III) (7 MN + PQ ) 2
= (7 MN ) 2 + 2 × (7 мл ) × ( PQ 1)+ ()+ ()+ (1).
2 [∵ ( a + b ) 2 = a 2 + 2 ab + b 2 ]
= 49 m 2 n 2 + 14 mnpq + p 2 q 2
Так что это не правильный вариант.
(IV) ( млн. + 7 PQ ) 2
= ( MN ) 2 + 2 × ( MN ) × (7 PQ ) ( MN ) × (7 PQ )+ (7 ). 2 [∵ ( a + b ) 2 = a 2 + 2 ab + b 2 ]
= m 2 n 2 + 14 mnpq + 49 p 2 q 2
Итак, правильный вариант.
Следовательно, правильный ответ — вариант (iv).
Страница № 93:
Вопрос 4:
Используйте формулу расширения, чтобы найти значения.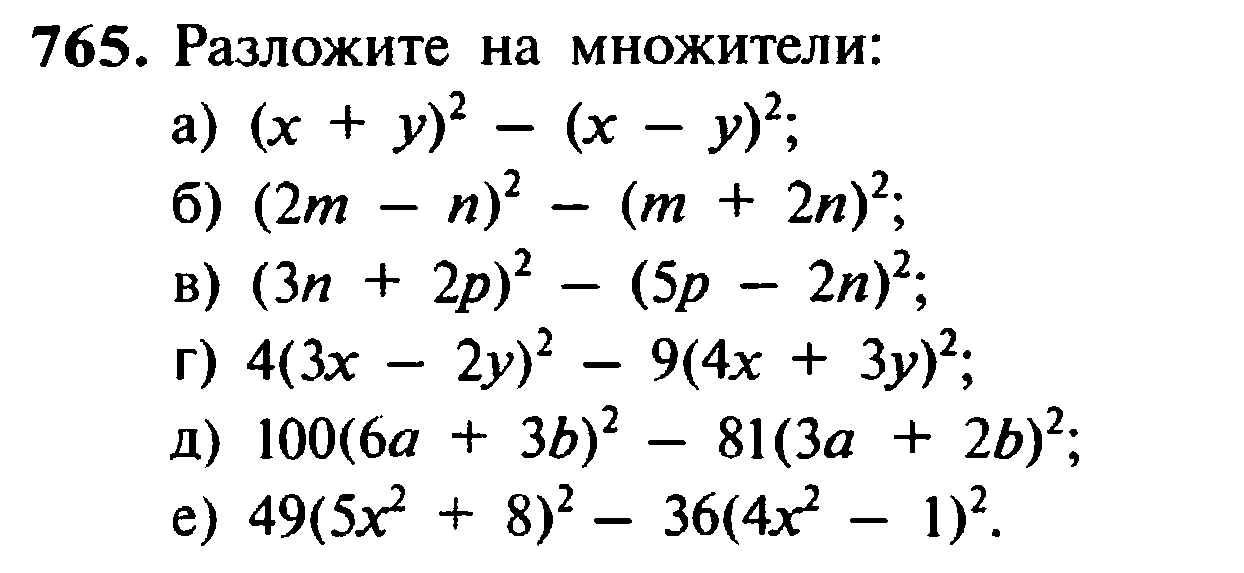
(и) (997) 2 (ii) (102) 2 (iii) (97) 2 (iv) (1005) 2
Ответ:
Известно, что, ( b + a ) 2 = a 2 + 2 ab + b 2 and ( a − b ) 2 = a 2 − 2 ab + б 2
(i) (997) 2
= (1000 − 3) 2
= (1000) 2 — 2 × 1000 × 3 + (3) 2
= 1000000 — 6000 +
= 994009
(II) (102) 2
= (100 + 2) 555) 2
= (100 + 2) 55555555. 2
= (100) 2 + 2 × 100 × 2 + (2) 2
= 10000 + 400 + 4
= 10404
(iii) (1 007 – 907–
- 6 2 ) 2
= (100) 2 — 2 × 100 × 3 + (3) 2
= 10000 — 600 +
= 9409
(IV) (1005) 2
= (100012 (IV) (1005) 2
= (1000).
+ 5) 2
= (1000) 2 + 2 × 1000 × 5 + (5) 2
= 1000000 + 10000 + 25
= 1010025
. умножить следующее.
(i) ( x + y ) ( x — y ) (ii) (3 x -5) (3 x + 5) + 2 a 9002 6) ( a -6) (iv) x5 + 6 x5 — 6
Ответ:
Известно, что ( a + б ) ( а — б ) = а 2 — б 2 .
i x+yx-y=x2-y2=x2-y2
ii 3x-53x+5=3×2-52=9×2-25
iii a+6a-6=a2-62=a2-36
iv x5+6×5 -6=x52-62=x225-36
Страница № 93:
Вопрос 2:
Используйте формулу, чтобы найти значения.
(i) 502 × 498 (ii) 97 × 103 (iii) 54 × 46 (iv) 98 × 102
Ответ:
0021 б ) ( а — б ) = а 2 — б 2 .
(i) 502 × 498
= (500 + 2) × (500 − 2)
= (500) 2 − (2) 2
= 250000 − 4
7 = 24 × 103
= (100 − 3) × (100 + 3)
= (100) 2 − (3) 2
= 10000 − 9
= 9991
= 7 (iii) 66 0 4 + 4) × (50 − 4)
= (50) 2 − (4) 2
= 2500 − 16
= 2484
(iv) 98 × 102
= (100 – 2) × (100 + 2)
= (100) 2 − (2) 2 70 9 0 9006 = 9996
Страница № 94:
Вопрос 1:
Факторизируйте следующие выражения и запишите их в форме произведения.
(I) 201 A 3 B 2 , (II) 91 XYT 2 , (III) 24 A 925 2 69 2 9 269 29 1 9 29 1 9 29 1 9 29 29 1 19219 21 1 .0025 2 , (iv) tr 2 s 3
Answer:
(i) 201 a 3 b 2
= 3 × 67 × a × a × a × b × b
(ii) 91 xy t 2
= 7 × 13 × x × y × t × t
(iii) 24 а 2 б 2
= 2 × 2 × 2 × 3 × a × a × b × b
(iv) tr 2 s 3
= t × r × r × s × s × s
Страница № 94:
Вопрос 1:
Факторизируйте следующие выражения.
(i) p 2 — q 2 (ii) 4 x 2 — 25 Y 2 (III) Y 2 — 4 (IV) P 2 — 125
(V) x 2 2 -11666666666666666612 (V) x 2 2 -116666666666666 гг. 2 — 1×2 (vii) a 2 b — ab (viii) 4 x 2 y — 6 x 2
(ix) 12y2 — 8z2 (x) 2×2 — 8y2
Ответ:
i p2-q2=p2-q2=p+qp-q ∵ a+ba-b=a2-b2
(ii) 4×2-25y2=2×2-5y2=2x+5y2x-5y ∵ a2-b2=a+ba-b
iii y2-4=y2-22=y+2y-2 ∵ a2-b2=a+ba -b
iv p2-125=p2-152=p+15p-15 ∵ a2-b2=a+ba-b
v 9×2-116y2=3×2-14y2=3x+14y3x-14y ∵ a2-b2=a+ba -b
vi x2-1×2=x2-1×2=x+1xx-1x ∵ a2-b2=a+ba-b
vii a2b-ab=aba-1
viii 4x2y-6×2=2x22y-3
ix 12y2-8z2 =12y2-16z2=12y2-4z2=12y+4zy-4z ∵ a2-b2=a+ba-b
x 2×2-8y2=2×2-4y2=2×2-2y2=2x+2yx-2y
Развернуть и разложить на множители Квадратичный Выражения
Расширение квадратных выражений:
Квадратные выражения — это алгебраические выражения, в которых переменная имеет показатель степени 2 .
Например: x 2 + 3x + 4
Для расширения квадратных уравнений используйте метод FOIL (First, Outside, Inside, Last) .
Первый Снаружи Внутри Последний
Пример 1
Расширить ( x + 3 ) ( x + 2 ) без и с использованием FOIL.
Ответ (без использования ФОЛЬГИ):
( х + 3 ) ( х + 2 )
= х ( х + 2 ) + 3 ( х + 2 )
= х 2 + 2х + 3х + 6
= x 2 + 5x + 6
Ответ (с использованием ФОЛЬГИ):
( х + 3 ) ( х + 2 )
= х 2 + 2х + 3х + 6
= x 2 + 5x + 6
Пример второй
( x + 4 ) ( x – 2 )
= х 2 – 2х + 4х – 8
= x 2 + 2x – 8
Пример третий
( 2x + 5 ) ( 3x – 8 )
= 6x 2 – 16x + 15x – 40
= 2x 2 – x – 40
Вопросы – Расширить с помощью ФОЛЬГИ
Q1.
( х + 6 ) ( х + 5 )
Q2. ( х – 5 ) ( х – 4 )
Q3. ( 2x + 5 ) ( 6x – 2 )
Ответы
А1. х 2 + 11х + 30
А2. х 2 – 9х + 20
А3. 12x 2 + 26x – 10
Perfect Squares
( x + a ) 2 = x 2 + 2AX + A 2
(x — A) 2 = x 2 — 2AX + A 2
Пример четыре
(x + 5)
.
= (х + 5) (х + 5)
= x 2 + 10x + 25
Пример пятый
( x – 3 ) 2
= ( x – 3 ) ( x – 3 )
= x 2 – 6x + 9
Вопросы – разверните эти идеальные квадраты
Q1. ( х + 7 ) 2
Q2. ( 2x + 5 ) 2
Ответы
А1. х 2 + 14х + 49
А2. 4x 2 + 20x + 25
Разность квадратов
( x + a ) ( x – a ) = x 2 – a 2
+ Пример Шесть ( 9 x ) – 5 )
= х 2 – 5х + 5х – 25
= x 2 – 25
Пример семь
( x – 3 ) ( x + 3 )
= х 2 – 3х + 3х – 9
= x 2 – 9
Вопросы — разверните эти разности квадратов
Q1.