Формулы умножения в тригонометрии: Формулы произведения тригонометрических функций: sin, cos, tg, ctg

6.3 Основные математические формулы. Формулы сокращённого умножения:

1. 2.

3.

4.5.

Формулы тригонометрии:

1. 2.

3. 4. .

5.

6.

7. 8.

9.

10.

11.

12.

13. 14.

Формулы приведения.

Функция

Значения тригонометрических функций некоторых углов.

	0
	0				1		0		0
	1				0			0	1
	0		1				0		0
			1		0			0

Таблица производных и дифференциалов основных

Элементарных функций.

№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

6.

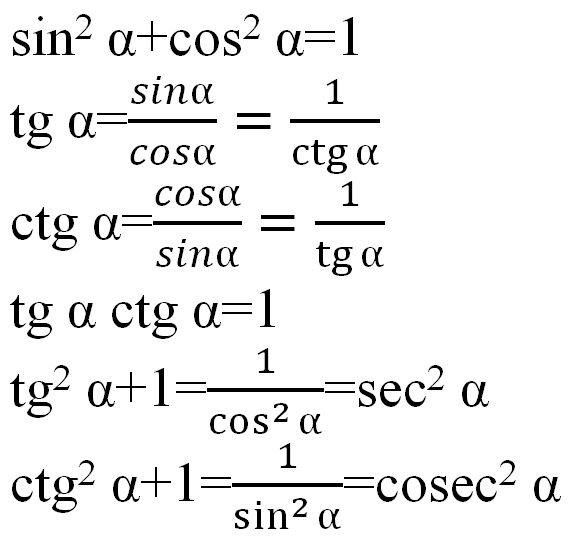4 Образец оформления обложки с контрольной работой. Федеральное агентство по образованию Государственное образовательное учреждение

высшего профессионального образования

«Камская государственная инженерно-экономическая академия»

кафедра Высшей математики

Контрольная работа

по дисциплине «Математика»

Вариант № ____

(номера выполняемых заданий: _________________________)

Выполнил: студент группы №_______

Ф.И.О. студента_________

зач. книжка — № _________

Проверил: преподаватель кафедры ВМ

Ф. И.О. преподавателя_____

Формулы сокращенного умножения. Схема Горнера. Основные приемы преобразования графиков. Тригонометрия (основные формулы, формулы сложения и двойного угла, формулы понижения степени и универсальная подстановка)

Формулы сокращенного умножения. Схема Горнера. Основные приемы преобразования графиков. Тригонометрия (основные формулы, формулы сложения и двойного угла, формулы понижения степени и универсальная подстановка)

Математика \ Высшая математика

Страницы работы

1 страница (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Формулы сокращенного умножения: 1.  2.  3.  Схема Горнера: Разделим многочлен f(x)=x3+5x2-3 на (x-5) а=5; b2=a3=1; b1=b2*5+a2; b0=b1*5+a1, a1=0, не забыть, что не существующие члены принимаются за 0. a3 a2 a1 a0 1 5 0 -3 5 1 10 50 247 b2 b1 b0 R Точка минимума (максимума) квадратичной функции:	Тригонометрия: Основные формулы:	Уравнения тригонометрические.
		Значения тригонометрических функций: 0 30 p/6 45 p/4 60 p/3 90 p/2 180 p 270 3p/2 360 2p sin 0 1/2 Ö2/2 Ö3/2 1 0 -1 0 cos 1 Ö3/2 Ö2/2 1/2 0 -1 0 1 tg 0 Ö3/3 1 Ö3 — 0 — 0 ctg — Ö3 1 Ö3/3 0 — 0 —
		Логарифмы: Основ. лог. тождеств.
	Формулы сложения: Формулы двойного и тройного угла
Основные приемы преобразование графиков: f(x+a) Перенос графика f(x) влево на a f(x)+b Перенос графика f(x) вверх на a —f(x) Симметрия относительно оси OX f(-x) Симметрия относительно оси OY ½f(x)½ Часть графика в верхней полуплоскости и на оси OX без изменения, а вместо части графика в нижней полуплоскости строим симметричную ей относительно оси OX f(½x½) Часть графика в правой полуплоскости и на оси OY без изменения, а вместо части графика в левой полуплоскости строим симметричную ей относительно оси OY f(kx) (k>0) При k>1 сжатие к точке (0;0) вдоль оси OX в k раз; при 0<k<1 растяжение от точки (0;0) вдоль оси OX в 1/k раз kf(x) (k>0) При k>1растяжение от точке (0;0) вдоль оси OY в k раз; при 0<k<1 сжатие к точки (0;0) вдоль оси OY в 1/k раз
		Производная. 1. Дифференцирование: Уравнение касательной (не вертикальной к графику функции y=f(x) в точке графика с абсциссой x0: Производная сложной функции:
	Формулы понижения степени Универсальная подстановка , не забыть  про ОДЗ тангенса.
	Суммы в произведение Произведение в сумму Формула дополнительного угла
		Прогрессии Арифметическая Геометрическая Формула общего члена Характеристическое свойство (исп. часто) Формула суммы n первых членов Другие формулы Формула суммы бесконечно убывающий геометрической прогрессии (0<|q|<1):

Похожие материалы

Информация о работе

Скачать файл

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

7.4: Формулы суммы-произведения и произведения-суммы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1370

• OpenStax
• OpenStax

Цели обучения

• Экспресс-продукты в сумме.
• Выразите суммы как продукты.

Группа марширует по полю, создавая потрясающий звук, который поддерживает толпу. Этот звук распространяется как волна, которую можно интерпретировать с помощью тригонометрических функций.

Рисунок \(\PageIndex{1}\): Марширующий оркестр Калифорнийского университета в Лос-Анджелесе (кредит: Эрик Чан, Flickr).

Например, рисунок \(\PageIndex{2}\) представляет звуковую волну для музыкальной ноты A. В этом разделе мы исследуем тригонометрические тождества, лежащие в основе таких повседневных явлений, как звуковые волны. 9

Выражение произведений в виде сумм произведение косинуса и синуса в виде суммы. Мы можем использовать формулы произведения на сумму

, , которые выражают произведения тригонометрических функций в виде сумм. Давайте сначала исследуем тождество косинуса, а затем тождество синуса.

Выражение произведений в виде сумм для косинуса

Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса . Если мы сложим два уравнения, мы получим:

\[\begin{align*} \cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta)\\[4pt ] \underline{+ \cos \alpha \cos \beta-\sin \alpha \sin \beta}&= \underline{ \cos(\alpha+\beta) }\\[4pt] 2 \cos \alpha \cos \ beta&= \cos(\alpha-\beta)+\cos(\alpha+\beta)\end{align*}\]

Затем мы делим на 2, чтобы выделить произведение косинусов:

\[ \cos \alpha \cos \beta= \dfrac{1}{2}[\cos(\alpha-\beta)+\cos( \alpha+\beta)] \label{eq1}\]

Как: Произведение косинусов выразить в виде суммы

1. Напишите формулу произведения косинусов.
2. Подставить данные углы в формулу.
3. Упростить.

Пример \(\PageIndex{1}\): запись произведения в виде суммы с использованием формулы произведения на сумму для косинуса

Запишите следующее произведение косинусов в виде суммы: \(2\cos\left(\dfrac{7x}{2}\right) \cos\left(\dfrac{3x}{2}\right)\).

Решение

Начнем с записи формулы произведения косинусов (Уравнение \ref{eq1}):

\[ \cos \alpha \cos \beta = \dfrac{1}{2}[ \ cos(\alpha-\beta)+\cos(\alpha+\beta) ] \nonumber \]

Затем мы можем подставить заданные углы в формулу и упростить.

\[\begin{align*} 2 \cos\left(\dfrac{7x}{2}\right)\cos\left(\dfrac{3x}{2}\right)&= 2\left(\ dfrac{1}{2}\right)[ \cos\left(\dfrac{7x}{2}-\dfrac{3x}{2}\right)+\cos\left(\dfrac{7x}{2} +\dfrac{3x}{2}\right) ]\\[4pt] &= \cos\left(\dfrac{4x}{2}\right)+\cos\left(\dfrac{10x}{2} \right) \\[4pt] &= \cos 2x+\cos 5x \end{align*}\]

Упражнение \(\PageIndex{1}\)

Используйте формулу произведения на сумму (уравнение \ref{eq1}), чтобы записать произведение в виде суммы или разности: \(\cos(2\theta)\ потому что (4 \ тета) \).

Ответить

\(\dfrac{1}{2}(\cos 6\theta+\cos 2\theta)\)

Выражение произведения синуса и косинуса в виде суммы

Далее мы выведем формулу произведения на сумму синуса и косинуса из формул суммы и разности для синуса . Если мы добавим тождества суммы и разности, мы получим:

\[\begin{align*} \cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta)\\ [4pt] \underline{+ \cos \alpha \cos \beta-\sin \alpha \sin \beta}&= \cos(\alpha+\beta)\\[4pt] 2 \cos \alpha \cos \beta&= \cos(\alpha-\beta)+\cos(\alpha+\beta)\\[4pt] \text{Затем делим на 2, чтобы выделить произведение косинусов:}\\[4pt] \cos \alpha \ cos \beta&= \dfrac{1}{2}\left[\cos(\alpha-\beta)+\cos(\alpha+\beta)\right] \end{align*}\]

Пример \(\PageIndex{2}\): Запись произведения в виде суммы, содержащей только синус или косинус

Выразите следующее произведение в виде суммы, содержащей только синус или косинус и не содержащей произведений: \(\sin(4\theta )\cos(2\тета)\).

Решение

Напишите формулу произведения синуса и косинуса. Затем подставьте данные значения в формулу и упростите.

\[\begin{align*} \sin \alpha \cos \beta&= \dfrac{1}{2}[ \sin(\alpha+\beta)+\sin(\alpha-\beta) ]\\[ 4pt] \sin(4\theta)\cos(2\theta)&= \dfrac{1}{2}[\sin(4\theta+2\theta)+\sin(4\theta-2\theta) ]\\[4pt] &= \dfrac{1}{2}[\sin(6\theta)+\sin(2\theta)] \end{align*}\]

Упражнение \(\PageIndex{2}\)

Используйте формулу произведения на сумму, чтобы записать произведение в виде суммы: \(\sin(x+y)\cos(x−y)\).

Ответить

\(\dfrac{1}{2}(\sin 2x+\sin 2y)\)

Выражение произведения синусов через косинус

Выражение произведения синусов через косинус также получается из тождеств суммы и разности для косинуса. В этом случае мы сначала вычтем две формулы косинуса:

\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \underline{-\cos(\ alpha+\beta)}&= -(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\\[4pt] \cos(\alpha-\beta)-\cos(\alpha+\beta) &= 2 \sin \alpha \sin \beta\\[4pt] \text{Затем делим на 2, чтобы выделить произведение синусов:}\\[4pt] \sin \alpha \sin \beta&= \dfrac{ 1}{2}[ \cos(\alpha-\beta)-\cos(\alpha+\beta) ] \end{align*}\]

Аналогичным образом мы могли бы выразить произведение косинусов через синус или вывести другое формулы произведения на сумму.

ФОРМУЛЫ ПРОИЗВЕДЕНИЯ НА СУММУ

Формулы произведения на сумму следующие:

\[\cos \alpha \cos \beta=\dfrac{1}{2}[\cos(\ alpha-\beta)+\cos(\alpha+\beta)]\]

\[\sin \alpha \cos \beta=\dfrac{1}{2}[\sin(\alpha+\beta)+\sin (\alpha-\beta)]\]

\[\sin \alpha \sin \beta=\dfrac{1}{2}[\cos(\alpha-\beta)-\cos(\alpha+\beta) ]\]

\[\cos \alpha \sin \beta=\dfrac{1}{2}[\sin(\alpha+\beta)−\sin(\alpha−\beta)]\]

Пример \ (\PageIndex{3}\): Выразите произведение в виде суммы или разности

Запишите \(\cos(3\theta) \cos(5\theta)\) в виде суммы или разности.

Решение

У нас есть произведение косинусов, поэтому начнем с написания соответствующей формулы. Затем подставляем данные углы и упрощаем.

\[\begin{align*} \cos \alpha \cos \beta&= \dfrac{1}{2}[\cos(\alpha-\beta)+\cos(\alpha+\beta)]\\[ 4pt] \cos(3\theta)\cos(5\theta)&= \dfrac{1}{2}[\cos(3\theta-5\theta)+\cos(3\theta+5\theta) ]\\[4pt] &= \dfrac{1}{2}[\cos(2\theta)+\cos(8\theta)]\qquad \text{Использовать четно-нечетное тождество} \end{align*} \]

Упражнение \(\PageIndex{3}\)

Используйте формулу произведения на сумму для вычисления \(\cos \dfrac{11\pi}{12} \cos \dfrac{\pi}{12}\ ).

Ответить

\(\dfrac{−2−\sqrt{3}}{4}\)

Выражение сумм в виде произведений

Некоторые задачи требуют обратного процесса, который мы только что использовали. Формулы суммы к произведению позволяют нам выразить суммы синуса или косинуса в виде произведений. Эти формулы могут быть получены из тождеств произведения на сумму. Например, с помощью нескольких замен мы можем получить тождество суммы и произведения для синус . Пусть \(\dfrac{u+v}{2}=\alpha\) и \(\dfrac{u−v}{2}=\beta\).

Затем

\[\begin{align*} \alpha+\beta&= \dfrac{u+v}{2}+\dfrac{u-v}{2}\\[4pt] &= \dfrac{2u} {2}\\[4pt] &= u \end{align*}\]

\[\begin{align*} \alpha-\beta&= \dfrac{u+v}{2}-\dfrac{u-v }{2}\\[4pt] &= \dfrac{2v}{2}\\[4pt] &= v \end{align*}\]

Таким образом, замена \(\alpha\) и \(\ бета\) в формуле произведения на сумму с подстановочными выражениями имеем

\[\begin{align*} \sin \alpha \cos \beta&= \dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)]\\[4pt ] \sin \left ( \frac{u+v}{2} \right ) \cos \left ( \frac{u-v}{2} \right )&= \frac{1}{2}[\sin u + \sin v]\qquad \text{Замените} (\alpha+\beta) \text{ и } (\alpha\beta)\\[4pt] 2\sin\left(\dfrac{u+v}{2} \right) \cos\left(\dfrac{u-v}{2}\right)&= \sin u+\sin v \end{align*}\]

Другие тождества суммы-произведения выводятся аналогично.

ФОРМУЛЫ СУММЫ-ПРОИЗВЕДЕНИЕ

Формулы суммы-произведения следующие:

\[\sin \alpha+\sin \beta=2\sin\left(\dfrac{\alpha+\beta}{2}\right)\cos \left(\dfrac{\alpha-\beta}{2}\right)\]

\[\sin\alpha-\sin\beta=2\sin\left(\dfrac{\alpha-\beta}{ 2}\right)\cos\left(\dfrac{\alpha+\beta}{2}\right)\]

\[\cos \alpha-\cos \beta=-2\sin\left(\dfrac{ \alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)\]

\[\cos \alpha+\cos \beta=2\sin\ влево(\dfrac{\alpha+\beta}{2}\right)\sin\left(\dfrac{\alpha-\beta}{2}\right)\]

Пример \(\PageIndex{4}\): Запись разности синусов в виде произведения

Запишите следующее выражение разности синусов в виде произведения: \(\sin(4\theta)−\sin(2\theta) \).

Решение

Начнем с написания формулы разности синусов.

\[\begin{align*} \sin \alpha-\sin \beta&= 2\sin\left(\dfrac{\alpha-\beta}{2}\right)\cos\left(\dfrac{\ alpha+\beta}{2}\right)\\[4pt] \text {Подставьте значения в формулу и упростите. }\\[4pt] \sin(4\theta)-\sin(2\theta)& = 2\sin\left(\dfrac{4\theta-2\theta}{2}\right) \cos\left(\dfrac{4\theta+2\theta}{2}\right)\\[4pt ] &= 2\sin\left(\dfrac{2\theta}{2}\right) \cos\left(\dfrac{6\theta}{2}\right)\\[4pt] &= 2 \sin \тета \cos(3\тета) \end{выравнивание*}\]

Упражнение \(\PageIndex{4}\)

Используйте формулу приведения суммы к произведению, чтобы записать сумму в виде произведения: \(\sin(3\theta)+\sin(\theta)\).

Ответить

\(2\sin(2\тета)\cos(\тета)\)

Пример \(\PageIndex{5}\): вычисление с использованием формулы приведения суммы к произведению

Вычисление \(\cos(15°)−\cos(75°)\). Проверьте ответ с помощью графического калькулятора.

Решение

Начнем с написания формулы разности косинусов. 9{\ circ}) \\ [4pt]
& = -2 \ влево (\ dfrac {\ sqrt {2}} {2} \ вправо) \ влево (- \ dfrac {1} {2} \ вправо) \\ [4pt]
&= \dfrac{\sqrt{2}}{2}
\end{align*}\]

Пример \(\PageIndex{6}\): Подтверждение личности

Подтверждение личности:

\[\dfrac{\cos(4t)−\cos(2t)}{\sin(4t)+\sin(2t)}=−\tan t\]

Решение

Начнем с левую часть, более сложную часть уравнения, и переписать выражение, пока оно не совпадет с правой частью.

\[\begin{align*} \dfrac{\cos(4t)-\cos(2t)}{\sin(4t)+\sin(2t)}&= \dfrac{-2 \sin\left( \dfrac{4t+2t}{2}\right) \sin\left(\dfrac{4t-2t}{2}\right)}{2 \sin\left(\dfrac{4t+2t}{2}\ справа) \cos\left(\dfrac{4t-2t}{2}\right)}\\[4pt] &= \dfrac{-2 \sin(3t)\sin t}{2 \sin(3t)\ cos t}\\[4pt] &= -\dfrac{\sin t}{\cos t}\\[4pt] &= -\tan t \end{align*}\]

Анализ

Отзыв что проверка тригонометрических тождеств имеет свой собственный набор правил. Процедуры решения уравнения не совпадают с процедурами проверки личности. Когда мы подтверждаем тождество, мы выбираем одну сторону для работы и делаем замены до тех пор, пока эта сторона не превратится в другую сторону. 92 \ тета \ конец {выравнивание *} \]

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий с идентификаторами продуктов и сумм.

• Сумма идентификаторов продуктов
• Sum to Product и Product to Sum Identities

Ключевые уравнения

Формулы произведения на сумму

\[\cos \alpha \cos \beta=\dfrac{1}{2}[\cos(\alpha-\beta)+\cos(\ альфа+\бета)] \номер\]

\[\sin \alpha \cos \beta=\dfrac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)] \nonumber \]

\[\sin \alpha \sin \beta=\dfrac{1}{2}[\cos(\alpha-\beta)−\cos(\alpha+\beta)] \nonumber \]

\[\cos \alpha \sin \ beta=\dfrac{1}{2}[\sin(\alpha+\beta)−\sin(\alpha−\beta)] \nonumber \]

Формулы суммы к произведению

\[\sin \alpha+\sin \beta=2\sin(\dfrac{\alpha+\beta}{2})\cos(\dfrac{\alpha-\beta}{2}) \nonumber \]

\[\sin \ альфа-\sin\beta=2\sin(\dfrac{\alpha-\beta}{2})\cos(\dfrac{\alpha+\beta}{2}) \nonumber \]

\[\cos \alpha-\cos \beta=-2\sin(\dfrac{\alpha+\beta}{2})\sin(\dfrac{\alpha-\beta}{2}) \nonumber \ ]

\[\cos \alpha+\cos \beta=2\sin(\dfrac{\alpha+\beta}{2})\sin(\dfrac{\alpha-\beta}{2}) \nonumber \]

Ключевые понятия

• Из тождеств суммы и разности мы можем вывести формулы произведения на сумму и формулы произведения суммы на синус и косинус.
• Мы можем использовать формулы произведения на сумму, чтобы переписать произведения синусов, произведения косинусов и произведения синусов и косинусов в виде сумм или разностей синусов и косинусов. См. пример \(\PageIndex{1}\), пример \(\PageIndex{2}\) и пример \(\PageIndex{3}\).
• Мы также можем получить тождества суммы-произведения из тождеств произведения-суммы, используя подстановку.
• Мы можем использовать формулы суммы к произведению, чтобы переписать сумму или разность синусов, косинусов или произведений синуса и косинуса как произведения синусов и косинусов. См. пример \(\PageIndex{4}\).
• Тригонометрические выражения часто проще вычислить с помощью формул. См. пример \(\PageIndex{5}\).
• Тождества можно проверить с помощью других формул или преобразования выражений в синусы и косинусы. Для проверки тождества мы выбираем более сложную сторону знака равенства и переписываем ее до тех пор, пока она не преобразуется в другую сторону. См. Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\).

---

Эта страница под заголовком 7.4: Формулы суммы к продукту и продукту к сумме распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. Произведение на формулы суммирования
   2. источник@https://openstax. org/details/books/precalculus
   3. Суммирование формул произведения

Reddit — Погрузитесь во что угодно

Похоже, вы используете новый Reddit в старом браузере. Сайт может работать некорректно, если вы не обновите свой браузер! Если вы не обновляете свой браузер, мы предлагаем вам посетить старый Reddit.

Нажмите J, чтобы перейти к ленте. Нажмите на знак вопроса, чтобы узнать остальные сочетания клавиш

Поиск по всему Reddit

Нашел Интернет!

Ленты

Популярные

Темы

ValheimGenshin ImpactMinecraftPokimaneHalo InfiniteCall of Duty: WarzonePath of ExileHollow Knight: SilksongEscape from TarkovWatch Dogs: Legion

NFLNBAMegan AndersonAtlanta HawksLos Angeles LakersBoston CelticsArsenal F.C.Philadelphia 76ersPremier LeagueUFC

GameStopModernaPfizerJohnson & JohnsonAstraZenecaWalgreensBest BuyNovavaxSpaceXTesla

CardanoDogecoinAlgorandBitcoinLitecoinBasic Attention TokenBitcoin Cash

The Real Housewives of AtlantaThe BachelorSister Wives90 Day FianceWife SwapThe Amazing Race AustraliaMarried at First SightThe Real Housewives of DallasMy 600-lb LifeLast Неделя сегодня вечером с Джоном Оливером

Kim KardashianDoja CatIggy AzaleaAnya Taylor-JoyJamie Lee CurtisNatalie PortmanHenry CavillMillie Bobby BrownTom HiddlestonKeanu Reeves

Animals and PetsAnimeArtCars and Motor VehiclesCrafts and DIYCulture, Race, and EthnicityEthics and PhilosophyFashionFood and DrinkHistoryHobbiesLawLearning and EducationMilitaryMoviesMusicPlacePodcasts and StreamersPoliticsProgrammingReading, Writing, and LiteratureReligion and SpiritualityScienceTabletop GamesTechnologyTravel

Создайте учетную запись, чтобы подписаться на ваши любимые сообщества и начать участвовать в обсуждениях.

r/

тригонометрия

PostsWiki

r/тригонометрия

r/тригонометрия

r/Тригонометрия — это место для обсуждения и обсуждения тригонометрии. Домашние задания разрешены ради обучения, но, пожалуйста, не просите других сделать всю вашу работу за вас. Весь контент должен быть на английском языке. Будьте вежливы, уважительны и следуйте Reddiquette. Помните, что правила Reddit также остаются в силе.

Создан 8 января 2009 г.

---

---

ImpressumReport Netzdg Content

Отчет о справочнике. Политика по содержимому коде

. аналогичные технологии, чтобы предоставить вам лучший опыт. Принимая все файлы cookie, вы соглашаетесь с тем, что мы используем файлы cookie для предоставления и обслуживания наших услуг и сайта, улучшения качества Reddit, персонализации контента и рекламы Reddit, а также измерения эффективности рекламы. Отклоняя необязательные файлы cookie, Reddit может по-прежнему использовать определенные файлы cookie для обеспечения надлежащей работы нашей платформы.