Функция у х модуль – Графики функций с модулем

Содержание

Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»

Разделы: Математика

“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”

Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.

Ход урока

I. Вводное слово учителя

Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х

2 математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.

Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.

Модуль и квадратичная функция

Построение графиков функций:

Y = АХ² + ВX + C,
Y = АХ² + ВX + C ,
Y = АХ²+ ВХ + С

II. Устная работа

1) Дать определение модуля числа Х

2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).

3) Найти на рисунке график функции Y = –Х²+ 4Х – 3.

4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?

5) Вспомнить, как построить график функции Y = Х

По определению модуля

График функции Y = Х симметричен относительно оси У.

III. Построение графиков функций:

Y = АХ² + ВX + C,

Y = АХ²+ ВХ + С

Работа проводится в группах, т.к. графики в К–1 в) и К–3 в) одинаковы, их необходимо сравнить и сделать вывод (всего 3 группы). Каждой группе выдается карточка, в ней 3 задания. Учащиеся должны построить графики квадратичной функции, содержащей модуль, используя определение модуля и сделать вывод: как построить график данной функции, используя график квадратичной функции и симметрию относительно осей координат.

Работа в группах.

Задание: построить график функции, используя:

а) определение модуля;
б) график функции Y = АХ²+ ВХ + С;
в) симметрию относительно осей координат.

а) Y = Х² – 4 Х + 3
б) Y = Х² – 4 Х + 3
в) Y = Х² – 4 Х + 3

а) Y = Х² + 2 Х – 3
б) Y = Х² + 2 Х – 3
в) Y = Х² + 2 Х – 3

а) Y = –Х² + 4 Х – 3
б) Y = –Х² + 4 Х – 3
в) Y = –Х² + 4 Х – 3

IV. Учащиеся делают вывод о расположении графиков указанных функций

Вопрос: а) Как построить график функции Y = f (X)?

(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х< 0.
2 способ. Построить график функции Y = f (X) и отобразить правую часть графика симметрично относительно оси Y).

б) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).

в) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)

г) Почему графики функций Y = –Х² + 4X – 3 и Y = Х² – 4X + 3 одинаковы?

(Так как А = А , –А = А)

V.

У рассмотренных функций под знаком модуля была независимая переменная. Теперь рассмотрим функции, где под знаком модуля стоит либо сама функция, либо и функция, и независимая переменная одновременно, т.е. зависимости вида

Y = АХ² + ВX+ C и Y = АХ² + ВX + C

Приведем конкретные примеры.

а) Y = Х² – 4X+ 3

По определению

Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х

2 – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.

б) Y = Х² – 4X+ 3

Сначала строим график функции Y = Х² – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х² – 4X+ 3 , т.е. график функции Y = Х² – 4X+ 3 отображаем относительно оси Х.

VI. Творческое задание

Дана функция Y = Х² + 2X– 3

Выполнить всевозможные преобразования данной квадратичной функции с модулем.

10.03.2005

Поделиться страницей:

urok.1sept.ru

8 класс. Алгебра. Модуль действительного числа. — Функция y = IxI.

Комментарии преподавателя

Вспомним определение: модулем неотрицательного действительного числа

называют само это число: |х| = х;

модулем отрицательного действительного числа называют противоположное число: |х| = – х.

Записывают так:

Тогда вместо у = |х| можно записать:

Построим график этой функции.

Сначала построим прямую у = х на луче [0;+∞), а затем прямую у = –х на открытом луче (–∞; 0). Т.о., получаем график функции у = х.

Довольно часто в ходе решения задач с квадратными корнями возникают ситуации, приводящие к понятию модуля.

Источник конспекта: http://znaika.ru/catalog/8-klass/algebra/Grafik-u=%7Ckh%7C.-Tozhdestvo√%28a²%29-=%7Ca%7C.

Источник видео: http://www.youtube.com/watch?v=4YdBGNourEg

Файлы

Нет дополнительных материалов для этого занятия.

www.kursoteka.ru

Графики функций содержащих модуль Методическое пособие Модуль для

Графики функций, содержащих модуль. Методическое пособие «Модуль» для 10 Б класса

Графики функций и

Два способа построения графиков 1)На основании определения модуля. 2) С помощью геометрических преобразований графиков.

Построение графика функции 1 способ. если х ≥ 0 если х

Построение графика 2 способ. Используем свойство чётности этой функции. Строим график функции для всех х ≥ 0 и отразим полученную часть симметрично оси ординат.

Пример 1 способ у 00 0 -2 х

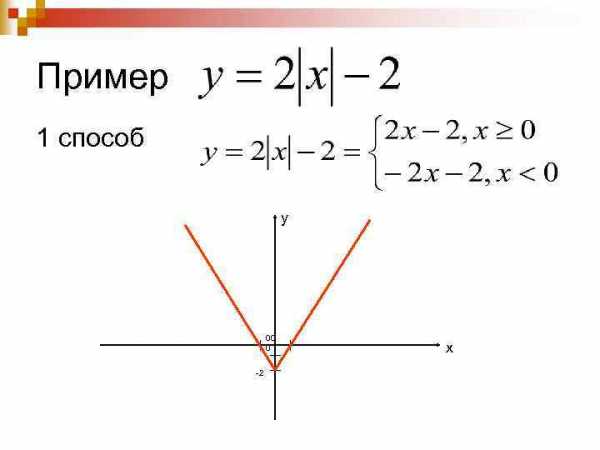
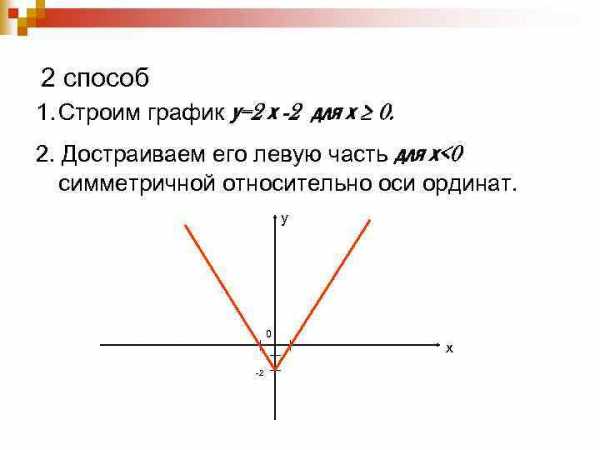2 способ 1. Строим график у=2 х -2 для х ≥ 0. 2. Достраиваем его левую часть для х

Пример 1 способ

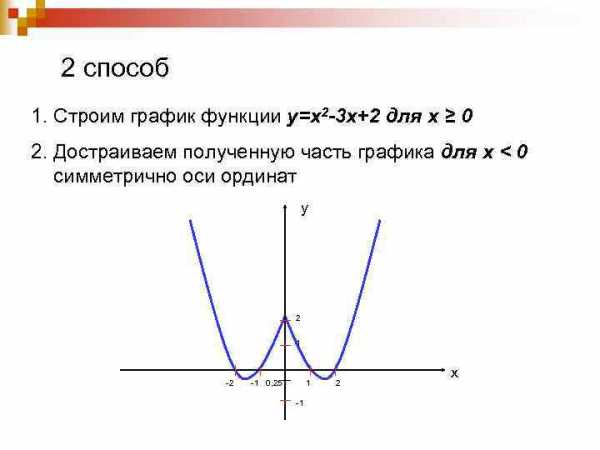2 способ 1. Строим график функции у=х2 -3 х+2 для х ≥ 0 2. Достраиваем полученную часть графика для х

Построение графика функции 1 способ. График состоит из двух графиков, расположенных в верхней полуплоскости

2 способ. 1. Строим график функции у = f (x). 2. Часть графика у = f (x), лежащую над осью абсцисс сохраняем. 3. Часть графила, лежащую под осью абсцисс отображаем симметрично относительно оси абсцисс.

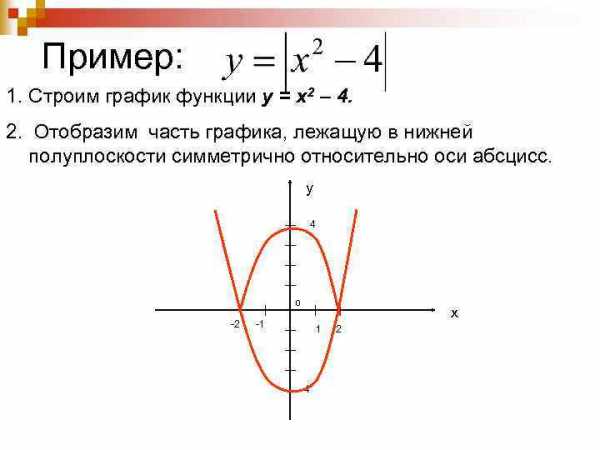Пример: 1. Строим график функции у = х2 – 4. 2. Отобразим часть графика, лежащую в нижней полуплоскости симметрично относительно оси абсцисс. у 4 0 -2 х -1 1 -4 2

График функции

Алгоритм построения 1. Строим график функции для х ≥ 0 2. Отображаем полученную часть графика симметрично относительно оси ординат. 3. Отображаем симметрично относительно оси абсцисс часть графика расположенную в нижней полуплоскости

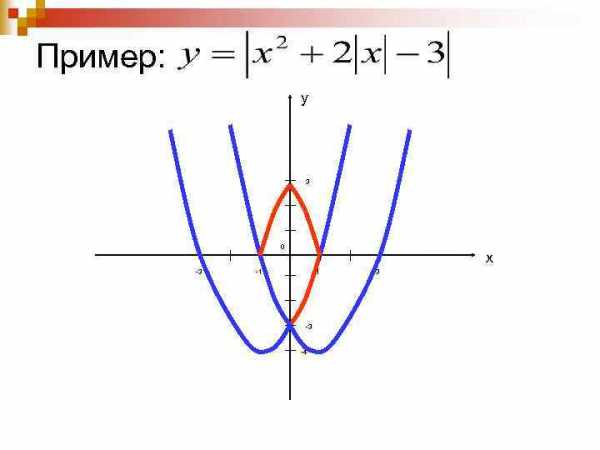Пример: у 3 0 -3 х -1 1 -3 -4 3

Графики кусочно-линейных функций

График функции Графиком непрерывной кусочно-линейной функцией является ломаная линия с двумя бесконечными крайними звеньями. 1 -ый способ: на основании определения модуля. Пример: числовую ось на 3 промежутка. 1. x ≤ 1 y=1 -x+3 -x=4 -2 x 2. 1≤x ≤ 3 y=x-1+3 -x=2 3. x>3 y=x-1+x-3=2 x-4 Точки x=1 и x=3 разбивают

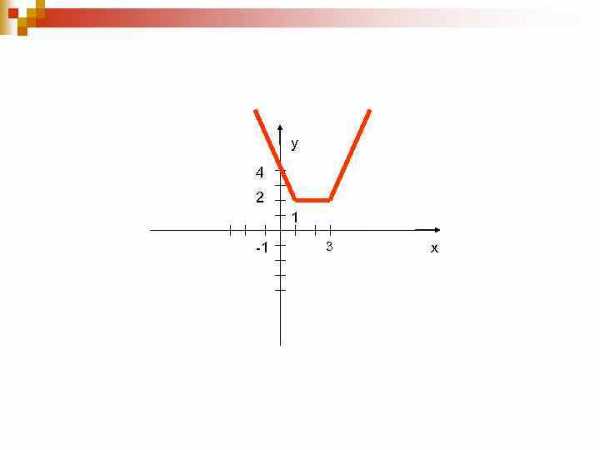y 4 2 1 -1 3 x

2 способ. Метод вершин Алгоритм: 1. находим нули подмодульных выражений. 2. Составим таблицу, в которой кроме этих нулей записывается по одному целому значению х слева и справа от них. 3. Наносим эти точки на координатной плоскости и соединяем последовательно, точки перелома и есть вершины ломаной.

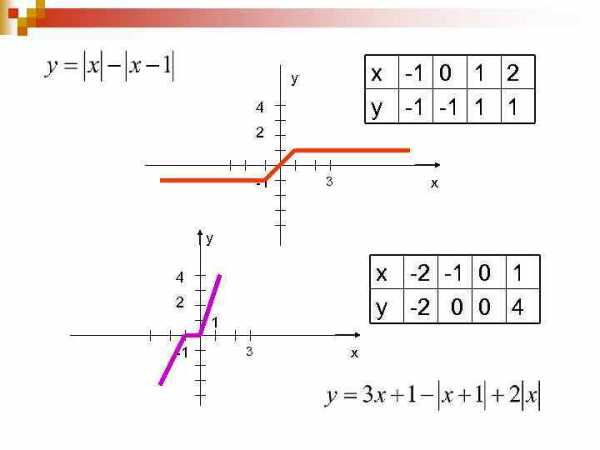х -1 0 1 2 у -1 -1 1 1 y 4 2 -1 3 x у х -2 -1 0 1 у -2 0 0 4 4 2 1 -1 3 x

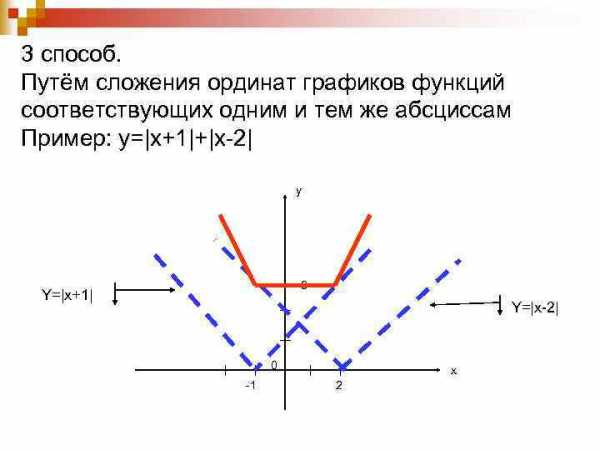3 способ. Путём сложения ординат графиков функций соответствующих одним и тем же абсциссам Пример: y=|x+1|+|x-2| у 3 Y=|x+1| Y=|x-2| 0 -1 х 2

График зависимостей

График зависимости |y|=f(x) Y= ± f(x), где f(x) ≥ 0 Алгоритм построения графиков зависимости. 1. Строим график функции у = f(х) для тех х из области определения, при которых f(х) ≥ 0. 2. Отобразим полученную часть графика симметрично оси абсцисс. График данной зависимости состоит из графиков двух функций: у=f(x) и у=-f(x), где f(x) ≥ 0

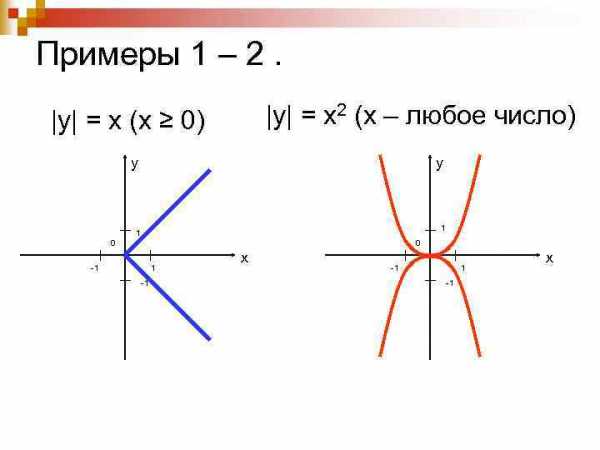Примеры 1 – 2. |y| = x 2 (х – любое число) |y| = x (х ≥ 0) у у 1 1 0 0 -1 1 -1 х

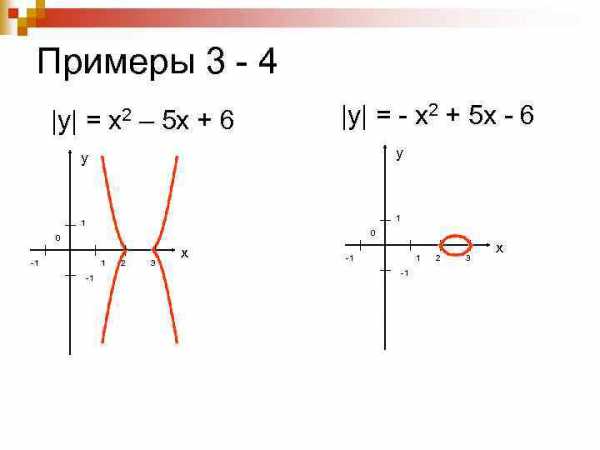Примеры 3 — 4 |y| = x 2 – 5 х + 6 |y| = — x 2 + 5 х — 6 у у 1 1 0 0 -1 1 -1 2 3 х

present5.com

Презентация к уроку по алгебре (9 класс) на тему: построение графиков функций с модулем 9 класс

Слайд 2

График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х

Слайд 3

y =

Слайд 4

у = | х ² — х -6 | Проверь 1.Построим график функции у =х ² — х -6 2 . Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.

Слайд 6

Для построения графика функции у = |f(х) | достаточно : 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)

Слайд 7

График функции у = f |(х)|

Слайд 8

Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х) для х>0; 2. Для х

Слайд 10

Построить график функции у=0,25 х ² — | х | -3. 1) Поскольку | х | = х при х≥0, требуемый график совпадает с параболой у=0,25 х² — х — 3. Если х

Слайд 11

Построить график функции у = | 2|х | — 3| 1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х | >1,5 т.е. х 1,5 а) у = 2х — 3 , для х > 0 б) д ля х 0 б) д ля х

Слайд 12

1. у = | 2|х | — 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.

Слайд 13

у = | х ² – 5|х| | 1. Построим у = х ² – 5 |х|, для х ² – 5 |х| > 0 т.е. х > 5 и х 0 б) д ля х 0 б) д ля х

Слайд 14

2. у = | х ² – 5|х| | а ) Построим график функции у = х ² – 5 х для х>0. б) Построим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.

Слайд 15

о х 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 у 9 8 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 Найдите все положительные значения к , при которых прямая у=кх пересекает в одной точке ломанную, заданную условиями: Х >3 Х

Слайд 16

-1 -2 -3 -4 -5 -6 1 2 3 4 5 6 7 1. у = I х I 2. у = I х +1 I Ответ: (- 1 ; 4 ) , (-4;-1), (4;1). Построить о -7 -6 -5 -4 -3 -2 -1 9 8 7 6 5 4 3 2 1 у х 2. у = I х +1 I – 4 Решить систему уравнений

nsportal.ru

Функция y= ІхІ — презентация по Алгебре

53335531463039513235404944384142294843374734365045565452

Скопируйте код и вставьте его на свой сайт.

Функция y= ІхІ

Описание презентации по отдельным слайдам:

1 слайд

Функция Подготовил Кожемяко Никита, 9 класс 2008г.

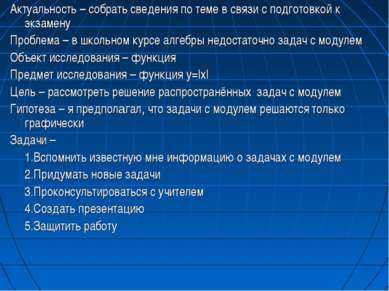2 слайд

Актуальность – собрать сведения по теме в связи с подготовкой к экзамену Проблема – в школьном курсе алгебры недостаточно задач с модулем Объект исследования – функция Предмет исследования – функция у=|x| Цель – рассмотреть решение распространённых задач с модулем Гипотеза – я предполагал, что задачи с модулем решаются только графически Задачи – 1.Вспомнить известную мне информацию о задачах с модулем 2.Придумать новые задачи 3.Проконсультироваться с учителем 4.Создать презентацию 5.Защитить работу

3 слайд

Определение модуля В математике через |x| обозначается абсолютная величина, или модуль числа х. Абсолютная величина числа х равна этому числу, если х>0, равна противоположному числу –х, если x

4 слайд

1.D(f)=(-∞;+∞) 2.E(f)=[0;+∞) 3.Ограничена снизу 4.Возрастает на[0;+∞) убывает на(-∞;0] 5.Чётная функция 6. 7.Непрерывна х у Свойства функции График функции

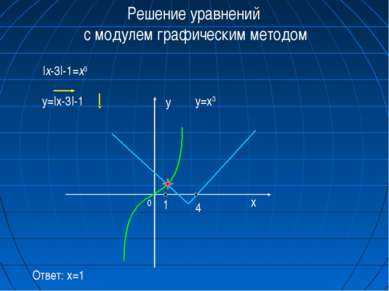5 слайд

Решение уравнений с модулем графическим методом |x-3|-1=x3 y=|x-3|-1 y=x3 0 x 1 4 Ответ: x=1 у

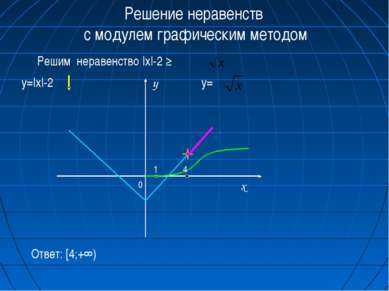
6 слайд

Решение неравенств с модулем графическим методом Решим неравенство |x|-2 ≥ y=|x|-2 y= 0 x y 1 4 Ответ: [4;+∞)

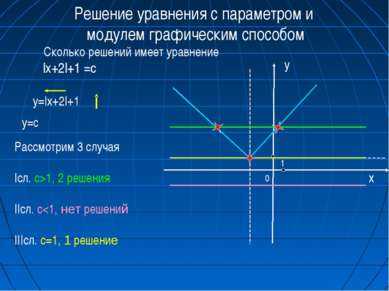
7 слайд

0 x 1 Решение уравнения с параметром и модулем графическим способом Рассмотрим 3 случая Iсл. c>1, 2 решения IIсл. c

8 слайд

Аналитический метод решения уравнения с модулем Решим уравнение|x-3|=5 I способ Рассмотрим два случая 1 случай x-3≥0 x-3=5 x=5+3 x=8, 8-3≥0 (и) 2 случай x-3

9 слайд

Алгоритм решения уравнений с модулем Найти нули модулей. Отметить нули на координатной прямой. Решить уравнение на каждом из промежутков с помощью системы. Написать ответ.

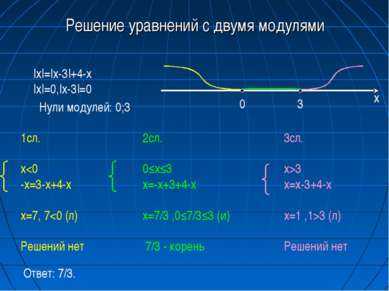
10 слайд

Решение уравнений с двумя модулями |x|=|x-3|+4-x |x|=0,|x-3|=0 Нули модулей: 0;3 0 3 х 1сл. x3 (л) Решений нет Ответ: 7/3.

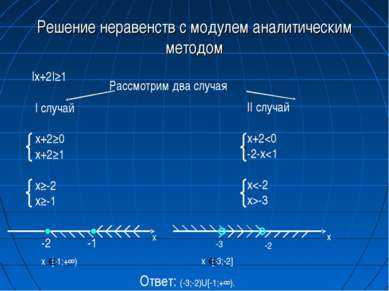
11 слайд

Решение неравенств с модулем аналитическим методом |x+2|≥1 Рассмотрим два случая I случай x+2≥0 x+2≥1 x≥-2 x≥-1 II случай x+2

12 слайд

Решение неравенств с модулем различными методами Третий способ. Имеем: |x-2.5|>2. Геометрически выражение |x-2.5| означает расстояние р(x-2.5) на координатной прямой между точками х и 2.5. Значит, нам нужно Найти все такие точки х, которые удалены от точки 2.5 более, чем на 2- это точки из промежутков (-∞;0.5) и (4.5;+∞) Итак, получили следующее решения неравенства: х4.5. Четвёртый способ. Поскольку обе части заданного неравенства неотрицательны, то возведение их в квадрат есть равносильное преобразование неравенства. Получим |2x-5|2>42 Воспользовавшись тем что |x|2=x2, получим (2x-5-4)(2x-5+4)>0 Применив метод интервалов получим тот же ответ.

13 слайд

Алгоритм решения неравенств с модулем Найти нули модулей. Отметить нули на координатной прямой. Решить неравенство на каждом из промежутков с помощью системы. Написать ответ.

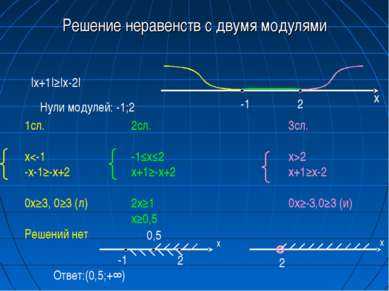
14 слайд

Решение неравенств с двумя модулями |x+1|≥|x-2| Нули модулей: -1;2 -1 2 х 1сл. x2 х+1≥х-2 0x≥-3,0≥3 (и) Ответ:(0,5;+∞) -1 2 х 0,5 2 х

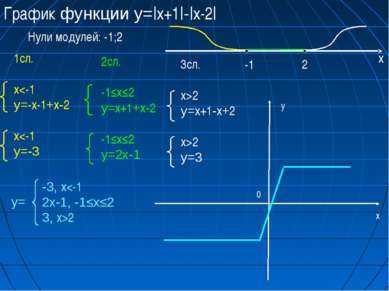
15 слайд

График функции у=|x+1|-|x-2| Нули модулей: -1;2 1сл. x2 у=3 -3, x2 х у 0 у=

16 слайд

Выводы В ходе работы над проектом моя гипотеза не подтвердилась. Я не только вспомнил графический способ, но и научился решать уравнения и неравенства аналитическим методом и строить графики с несколькими модулями. В дальнейшем можно рассмотреть аналитический метод решения неравенств и уравнений с модулем и параметром.

17 слайд

Список литературы Алгебра:Для 8 кл.:учеб. пособие для учащихся шк. и классов с углуб.изуч математики/ Н.Я.Виленкин, Г.С.Сурвило и др., под ред. Н.Я.Виленкина – М.: Просвещение. Мордкович А.Г. И др. Алгебра.9кл.: В двух частях. Ч.2: Задачник для общеообразоват. учреждений/М.:Мнемозина, 2004 г. Мордкович А.Г. И др. Алгебра.9кл.: В двух частях. Ч.2: Учебник для общеообразоват. учреждений/М.:Мнемозина, 2004 г. Мордкович А.Г. И др.Алгебра и начала анализа 10-11кл.: В двух частях. Ч.1: Задачник для общеообразоват. учреждений/М.:Мнемозина, 2004 г. Математика: Учеб. Для 6 кл. сред. шк./Н.Я. Виленкин и др. М.: Просвещение, 1993.

Чтобы скачать материал, введите свой email, укажите, кто Вы, и нажмите кнопку

Нажимая кнопку, Вы соглашаетесь получать от нас email-рассылку

Если скачивание материала не началось, нажмите еще раз «Скачать материал».

843386189098993410105112961225512350

331013319433332333533347733583336003361333615336823369034417

У вас есть презентация, загружайте:

Для того чтобы загрузить презентацию на сайт, необходимо зарегистрироваться.

uslide.ru