Функции формула: Формула функции — задание. Алгебра, 8 класс.

Содержание

Курс дифференциального и интегрального исчисления. Том 1

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 1.

Курс дифференциального и интегрального исчисления. Том I Фихтенгольц в 3 томах, Том 1. В книгах представленны все разделы современной высшей матиматеки, правила, задания и примеры их решения, теория и практика.

ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
2. Упорядочение области рациональных чисел.
3. Сложение и вычитание рациональных чисел.
4. Умножение и деление рациональных чисел.
5. Аксиома Архимеда.
§ 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
7.

Упорядочение области вещественных чисел.
8. Вспомогательные предложения.
9. Представление вещественного числа бесконечной десятичной дробью.
10. Непрерывность области вещественных чисел.
11. Границы числовых множеств.
§ 3. Арифметические действия над вещественными числами
13. Свойства сложения.
14. Определение произведения вещественных чисел.
15. Свойства умножения.
16. Заключение.
17. Абсолютные величины.
§ 4. Дальнейшие свойства и приложения вещественных чисел
19. Степень с любым вещественным показателем.
20. Логарифмы.
21. Измерение отрезков.
ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Варианта и ее предел
23. Предел варианты.
24. Бесконечно малые величины.
25. Примеры.
26. Некоторые теоремы о варианте, имеющей предел.
27. Бесконечно большие величины.
§ 2. Теоремы о пределах, облегчающие нахождение пределов
29. Леммы о бесконечно малых.
30. Арифметические операция над переменными.
31. Неопределенные выражения.

32. Примеры на нахождение пределов.
33. Теорема Штольца и ее применения.
§ 3. Монотонная варианта
35. Примеры.
36. Число е.
37. Приближенное вычисление числа е.
38. Лемма о вложенных промежутках.
§ 4. Принцип сходимости. Частичные пределы
40. Частичные последовательности и частичные пределы.
41. Лемма Больцано — Вейерштрасса
42. Наибольший и наименьший пределы.
ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Понятие функции
44. Функциональная зависимость между переменными. Примеры.
45. Определение понятия функции.
46. Аналитический способ задания функции.
47. График функции.
48. Важнейшие классы функций.
49. Понятие обратной функции.
50. Обратные тригонометрические функции.
51. Суперпозиция функций. Заключительные замечания.
§ 2. Предел функции
53. Сведение к случаю варианты.
54. Примеры.
55. Распространение теории пределов.
56. Примеры.
57. Предел монотонной функции.
58. Общий признак Больцано—Коши.

59. Наибольший и наименьший пределы функции.
§ 3. Классификация бесконечно малых и бесконечно больших величин
61. Шкала бесконечно малых.
62. Эквивалентные бесконечно малые.
63. Выделение главной части.
64. Задачи.
65. Классификация бесконечно больших.
§ 4. Непрерывность (и разрывы) функций
67. Арифметические операции над непрерывными функциями.
68. Примеры непрерывных функций.
69. Односторонняя непрерывность. Классификация разрывов.
70. Примеры разрывных функций.
71. Непрерывность и разрывы монотонной функции.
72. Непрерывность элементарных функций.
73. Суперпозиция непрерывных функций.
74. Решение одного функционального уравнения.
75. Функциональная характеристика показательной, логарифмической и степенной функций.

76. Функциональная характеристика тригонометрического и гиперболического косинусов.
77. Использование непрерывности функций для вычисления пределов.
78. Степенно-показательные выражения.
79.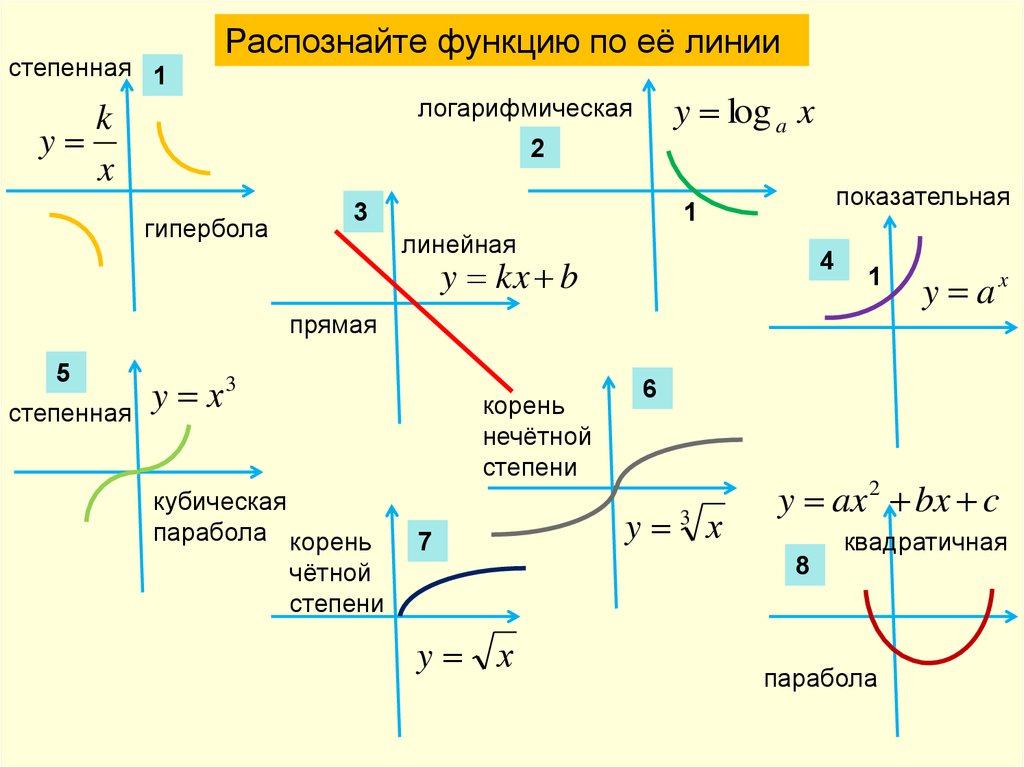

Примеры.
§ 5. Свойства непрерывных функций
81. Применение к решению уравнений.
82. Теорема о промежуточном значении.
83. Существование обратной функции.
84. Теорема об ограниченности функции.
85. Наибольшее и наименьшее значения функции.
86. Понятие равномерной непрерывности.
87. Теорема Кантора.
88. Лемма Бореля.
89. Новые доказательства основных теорем.
ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 1. Производная и ее вычисление
91. Задача о проведении касательной к кривой.
92. Определение производной.
93. Примеры вычисления производных.
94. Производная обратной функции.
95. Сводка формул для производных.
96. Формула для превращения функции.
97. Простейшие правила вычисления производных.
98. Производная сложной функции.
100. Односторонние производные.
101. Бесконечные производные.
102. Дальнейшие примеры особых случаев.
§ 2. Дифференциал
104. Связь между диффереицируемостью и существованием производной.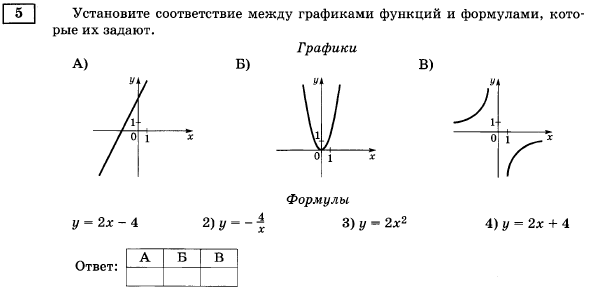

105. Основные формулы и правила дифференцирования.
106. Инвариантность формы дифференциала.
107. Дифференциалы как источник приближенных формул.
108. Применение дифференциалов при оценке погрешностей.
§ 3. Основные теоремы дифференциального исчисления
110. Теорема Дарбу
111. Теорема Ролля.
112. Формула Лагранжа.
113. Предел производной.
114. Формула Коши.
§ 4. Производные и дифференциалы высших порядков
116. Общие формулы для производных любого порядка.
117. Формула Лейбница.

118. Примеры.
119. Дифференциалы высших порядков.
120. Нарушение инвариантности формы для дифференциалов высших порядков.
121. Параметрическое дифференцирование.
122. Конечные разности.
§ 5. Формула Тейлора
124. Разложение произвольной функции; дополнительный член в форме Пеано.
125. Примеры.
126. Другие формы дополнительного члена.
127. Приближенные формулы.
§ 6. Интерполирование
129. Дополнительный члеп формулы Лагранжа.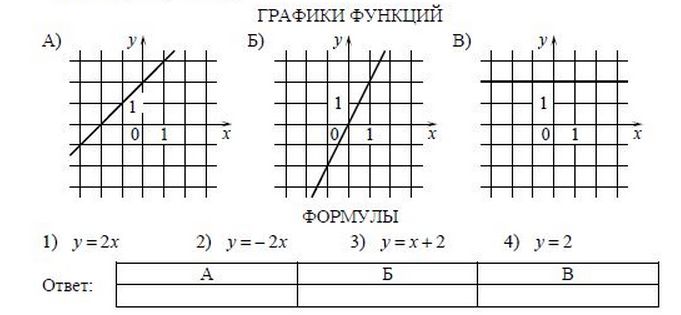

130. Интерполирование с кратными узлами. Формула Эрмита.
ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
§ 1. Изучение хода изменения функции
132. Условие монотонности функции.
133. Доказательство неравенств.
134. Максимумы и минимумы; необходимые условия.
136. Достаточные условия. Первое правило.
136. Примеры.
137. Второе правило.
138. Использование высших производных.
139. Разыскание наибольших и наименьших значений.

140. Задачи.
§ 2. Выпуклые (и вогнутые) функции
142. Простейшие предложения о выпуклых функциях.
143. Условия выпуклости функции.
144. Неравенство Иенсена и его приложения.
145. Точки перегиба.
§ 3. Построение графиков функций
147. Схема построения графика. Примеры.
148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
149. Примеры.
§ 4. Раскрытие неопределенностей
151. Неопределенность вида oo/oo
152. Другие виды неопределенностей.
§ 5. Приближенное решение уравнений
154.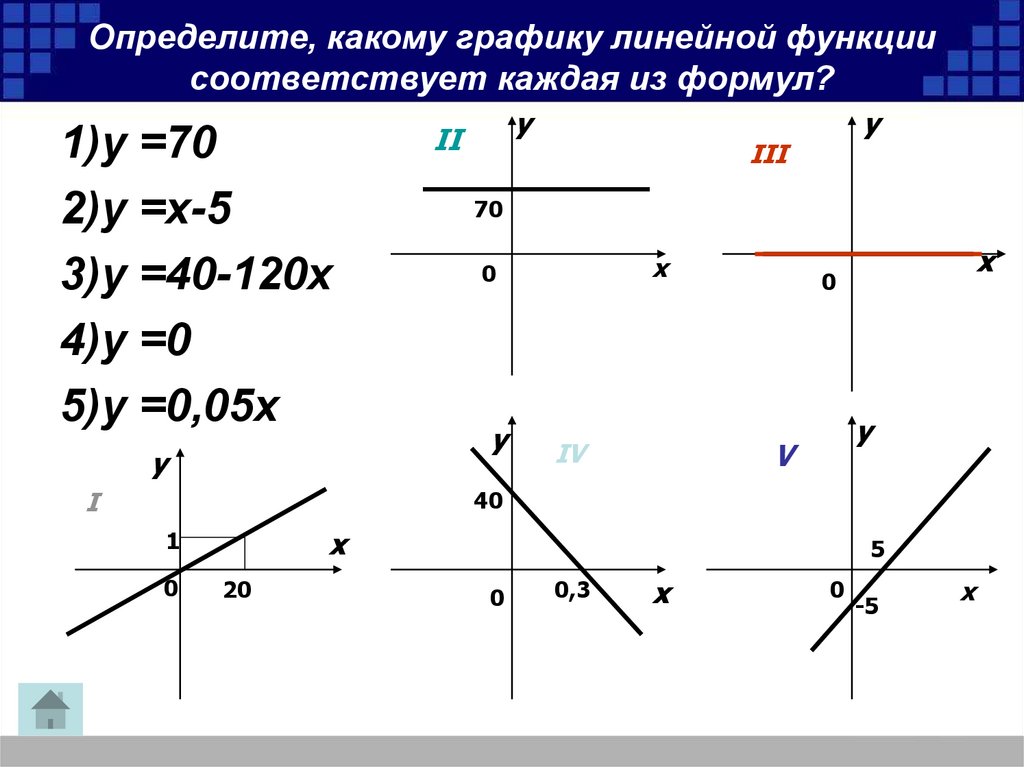

Правило пропорциональных частей (метод хорд).
155. Правило Ньютона (метод касательных).
156. Примеры в упражнения.
157. Комбинированный метод.
158. Примеры и упражнения.
ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
159. Функциональная зависимость между переменными. Примеры.

160. Функции двух переменных и области их определения.
161. Арифметическое n-мерное пространство.
162. Примеры областей в n-мерном пространстве.
163. Общее определение открытой и замкнутой области.
164. Функции n переменных.
165. Предел функции нескольких переменных.
166. Сведение к случаю варианты.
167. Примеры.
168. Повторные пределы.
§ 2. Непрерывные функции
170. Операции над непрерывными функциями.
171. Функции, непрерывные в области. Теоремы Больцано—Коши.
172. Лемма Больцано—Вейерштрасса.
173. Теоремы Вейерштрасса.
174. Равномерная непрерывность.
175. Лемма Бореля.
176. Новые доказательства основных теорем.
§ 3. Производные и дифференциалы функций нескольких переменных
178.

Полное приращение функции.
179. Полный дифференциал.
180. Геометрическая интерпретация для случая функции двух переменных.
181. Производные от сложных функций.
182. Примеры.
183. Формула конечных приращений.
184. Производная по заданному направлению.
185. Инвариантность формы (первого) дифференциала.
186. Применение полного дифференциала в приближенных вычислениях.
187. Однородные функции.
188. Формула Эйлера.
§ 4. Производные и дифференциалы высших порядков
190. Теорема о смешанных производных.
191. Обобщение.
192. Производные высших порядков от сложной функции.
193. Дифференциалы высших порядков.
194. Дифференциалы сложных функций.
195. Формула Тейлора.
§ 5. Экстремумы, наибольшие и наименьшие значения
197. Достаточные условия (случай функции двух переменных).
198. Достаточные условия (общий случай).
199. Условия отсутствия экстремума.
200. Наибольшее и наименьшее значения функции. Примеры.
201.

Задачи.
ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
§ 1. Формальные свойства функциональных определителей
203. Умножение якобианов.
204. Умножение функциональных матриц (матриц Якоби).
§ 2. Неявные функции
206. Существование неявной функции.
207. Дифференцируемость неявной функции.
208. Неявные функции от нескольких переменных.
209. Вычисление производных неявных функций.
210. Примеры.
§ 3. Некоторые приложения теории неявных функций
212. Метод неопределенных множителей Лагранжа.
213. Достаточные для относительного экстремума условия.
214. Примеры и задачи.
215. Понятие независимости функций.
216. Ранг матрицы Якоби.
§ 4. Замена переменных
218. Примеры.
219. Функции нескольких переменных. Замена независимых переменных.
220. Метод вычисления дифференциалов.
221. Общий случай замены переменных.
222. Примеры.
ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
§ 1. Аналитическое представление кривых и поверхностей
224.

Примеры.
225. Кривые механического происхождения.
226. Кривые на плоскости (в полярных координатах). Примеры.
227. Поверхности и кривые в пространстве.
228. Параметрическое представление.
229. Примеры.
§ 2. Касательная и касательная плоскость
231. Примеры.
232. Касательная в полярных координатах.
233. Примеры.
234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
235. Примеры.
236. Особые точки плоских кривых.
237. Случай параметрического задания кривой.
§ 3. Касание кривых между собой
239. Примеры.
240. Характеристические точки.
241. Порядок касания двух кривых.
242. Случай неявного задания одной из кривых.
243. Соприкасающаяся кривая.
244. Другой подход к соприкасающимся кривым.
§ 4. Длина плоской кривой
246. Направление на кривой.
247. Длина кривой. Аддитивность длины дуги.
248. Достаточные условия спрямляемости. Дифференциал дуги.
249. Дуга в роли параметра.

Положительное направление касательной.
§ 5. Кривизна плоской кривой
251. Круг кривизны и радиус кривизны.
252. Примеры.
253. Координаты центра кривизны.
254. Определение эволюты и эвольвенты; разыскание эволюты.
255. Свойства эволют и эвольвент.
256. Разыскание эвольвент.
ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ

Функция IF | Справочные статьи Smartsheet

Оценивает логическое выражение и возвращает то или иное значение в зависимости от того, истинно это выражение или ложно.

Пример использования

=IF([Дата выполнения]1 > [Дата выполнения]2; «Дата 1 больше»; «Дата 2 больше»)

Синтаксис

IF(

logical_expression
value_if_true
[
value_if_false
]

)

logical_expression
—
выражение, которое будет оцениваться. Должно быть истинно или ложно.
value_if_true
—
значение или формула, которое будет возвращено, если логическое выражение истинно.
value_if_false
—(необязательно)
значение или формула, которое будет возвращено, если логическое выражение ложно. Если эта часть отсутствует, будет возвращено пустое значение.

Примечания об использовании

Функции IF можно вкладывать одну в другую, чтобы оценивать несколько логических выражений сразу.
Smartsheet считывает операторы IF в формуле слева направо и отображает одно из значений в зависимости от того, какое выражение первым было оценено как истинное. Если функции IF вложены одна в другую, необязательный результат return_if_false будет возвращён только в том случае, если все логические выражения будут признаны ложными.

Примеры

В примере ниже используется информация из этой таблицы.

Номер строки	Артикул	Статус	Дата заказа	В наличии?
1	C001	Зелёный	15.12.2019	истина
2	C002	Красный	12. 12.2019	ложь
3	C003	Жёлтый	15.12.2019	истина
4	C004	Зелёный	20.12.2019	истина

Вот несколько примеров использования функции IF() применительно к таблице выше.

Формула	Описание	Результат
=IF([Статус]1 = «Красный», «В зоне риска», «Вовремя»)	ЕСЛИ в строке 1 столбца «Статус» содержится значение «Красный», возвращается значение «В зоне риска», а если нет, возвращается значение «Вовремя».	Вовремя
=IF([Дата заказа]2 < TODAY(), «Красный», IF([Дата заказа]2 > TODAY(), «Жёлтый», IF([Дата заказа]2 = TODAY(), «Зелёный»)))	ЕСЛИ значение строки 2 в столбце «Дата заказа» меньше СЕГОДНЯ, возвращается значение «Красный». ЕСЛИ значение строки 2 в столбце «Дата заказа» больше СЕГОДНЯ, возвращается значение «Жёлтый». ЕСЛИ значение строки 2 в столбце «Дата заказа» равняется СЕГОДНЯ, возвращается значение «Зелёный».	Красный
=IF([Дата заказа]3 < TODAY(), «Красный», IF(AND[Дата заказа]3 >= TODAY(), ([Дата заказа]3 < TODAY(+7))? «Жёлтый», «Зелёный»))	ЕСЛИ значение строки 3 в столбце «Дата заказа» меньше СЕГОДНЯ, возвращается значение «Красный». ЕСЛИ значение строки 2 в столбце «Дата заказа» больше или равняется СЕГОДНЯ, И находится в диапазоне менее следующих 7 дней, возвращается значение «Жёлтый». Если ни то, ни другое условие не применимы, возвращается значение «Зелёный».	Жёлтый
=IF(COUNTIF([Артикул]:[Артикул], [Артикул]@row) > 1, 1, 0)	Поиск дубликатов ЕСЛИ в столбце «Артикул» имеется более одного вхождения артикула из текущей строки, в этой строке будет поставлен флажок. Если дубликаты отсутствуют, флажок проставляться не будет.	Нет отмеченных строк

Остались вопросы?

Используйте шаблон Руководство по работе с формулами, чтобы просмотреть дополнительные ресурсы и изучить более 100 формул. Руководство содержит глоссарий, описывающий каждую функцию, обращение с которой вы сможете отработать на практике, и примеры как часто используемых, так и более сложных функций.

Изучить примеры того, как эту функцию применяют другие пользователи Smartsheet, или задать интересующий вас вопрос можно в Сообществе Smartsheet.

Обратиться к Сообществу

Формула и функция — Статистика Как

Функции > Формула и функция

Содержание:

Что такое формула?
Что такое функция?
Формула и функция в Excel

Формула — это математическое предложение по крайней мере с одной переменной. Например, 2 + 4 — это не формула (переменной нет), а 2x + 4 — это формула, потому что есть переменная. Формулы используются в математике для описания отношений. Переменные могут быть любой буквой от a до z, но вы должны следовать примерно общие правила написания формул :

Сокращение переменных до одной буквы . Например, если у вас есть переменная для веса, сократите ее до w , а не we или wt. Это потому, что когда у вас есть две переменные в формуле, это означает их умножение, поэтому «wt» означает «w * t».
Используйте строчные буквы a, b, c, … z.
Опустите знак умножения (если только вы не умножаете два числа, например 2*4). Пишите 2х, а не 2*х.
Поместите сначала число , если вы умножаете переменную на число. Пишите 2x, а не x2.

В общей математике и начальной алгебре вы работаете с формулами . Но в исчислении вы работаете с функциями . Разница между формулами и функциями заключается в том, как они устроены: функций — это особый тип формулы с ровно одним выходом (y) для каждого входа (x).

Например, если вы подставите «2» в формулу y = x ² , есть только один выход: 4. Это функция.
Если вы подставите 2 в формулу x = y ² , для каждого входа (значения x) есть две возможности: 8 и -8.

Давайте посмотрим на это графически:
При x = 2 синяя функция y = x ² имеет один выход (синяя звездочка), а формула y = x ² имеет два выхода (оранжевые звездочки).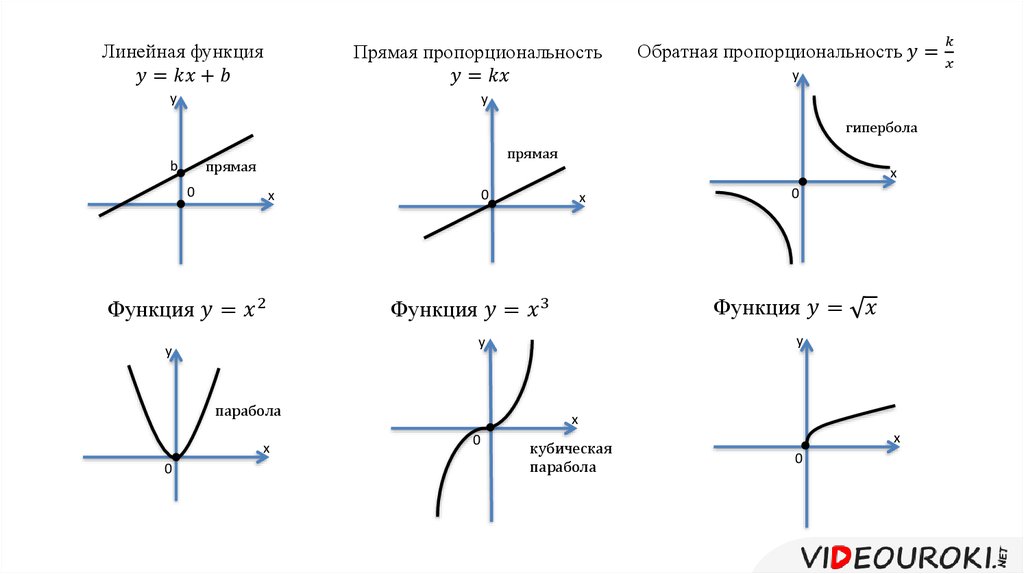

Все функции являются формулами, но не все формулы являются функциями.

«Функция» в Excel — это предопределенная формула. Все встроенные функции Excel также являются функциями в традиционном смысле (т. е. вы получите один вывод для каждого ввода).

В качестве примера предположим, что вы хотите добавить строку чисел от 1 до 4. Все формулы в Excel начинаются со знака равенства «=». Таким образом, вы можете ввести формулу «=1+2+3+4». Вы также можете вызвать встроенную функцию СУММ, чтобы сделать то же самое: =СУММ(1,2,3,4).

При выполнении таких небольших вычислений нет большой разницы между формулой и функцией в Excel. Большая разница проявляется, когда вы имеете дело с большими объемами данных в ячейках (для чего и был разработан Excel). Если бы у вас было 1000 чисел в столбце А, может потребоваться некоторое время, чтобы написать формулу со всеми числами от 1 до 1000:
=1+2+3+4+5+6…1000
Но вы можете ввести функцию, которая суммирует все числа между ячейками A1 и ячейками A2 за секунды:
СУММ(A1:A1000).

Ссылки

График создан с помощью Desmos.com.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Формула против функции» От StatisticsHowTo.com : элементарная статистика для всех нас! https://www.statisticshowto.com/formula-vs-function/

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Функции формул

Следующая статья также применима к приложениям SAP Build. Щелкните здесь, чтобы вернуться на справочный портал.

Введение

Функции формул, или просто формулы, — это выражения, которые позволяют создавать алгоритмы в приложении. Они следуют той же концепции, что и формулы «электронной таблицы» Excel, и заимствуют у них контекстно-зависимые функции.

С помощью формул вы можете выполнять любые преобразования с соответствующими данными, такими как информация об устройстве и системе, местоположение GPS, значения датчиков, свойства данных и состояние приложения. Например: рассчитать расстояние между двумя координатами, преобразовать поле даты в локальный формат, предсказать будущие значения на основе исторических данных, рассчитать процентные ставки по ипотеке, подтвердить общую стоимость при проверке корзины и многое другое.

Формулы — это один из типов привязки компонентов, что означает, что вы можете использовать формулы практически в любом месте приложения. Чтобы привязать значение компонента «Текст» к формуле, нажмите значок привязки на вкладке «Свойства» и выберите « Formula » в качестве желаемого типа привязки.

Использование формульных функций

значение предварительного просмотра на холсте просмотра. Нажмите на первое поле под «Формулой», чтобы открыть редактор формул. Пример результатов» вы можете увидеть вывод формулы. Каждое выражение дополнительно проверяется, устраняя возможные ошибки и заранее предупреждая вас, если формула неверна. На скриншоте ниже вы можете видеть переменную приложения со значением 123 складывается с целым числом 1 , в результате получается 124 .

Операторы формул

Арифметические операторы + , - , * и /
Логические операторы || , && и !
Сравнения == , === , != , !== , < , <= , >

147 
 Остатки  %  
 Условные  <условие> ?  :  
 Экранирующий символ:  \  
 Чтобы избежать обратной косой черты в JavaScript, используйте две обратные косые черты:  \\ 
 Типы формул 
 Существует два типа формул: статические (переменные) и динамический (Функции). Статические используются для взаимодействия со статическими данными  , начиная от предварительно установленных переменных приложения и заканчивая системными переменными, полученными с устройства. Функции, с другой стороны, позволяют выполнять сложные действия и  динамическая  генерация выходных данных на основе предоставленных входных данных.
  Ниже вы найдете введение для каждого подтипа формулы вместе с примерами использования. 
 Переменные 
 Переменные приложения 
  Назначение 
 Чтение/изменение переменных приложения.
  Использование  (Замените  {имя}  на соответствующее имя.)
  appVars.{имя} 
  Пример 
 IF(IS_EQUAL(appVars.appVariableOne, true), «Переменная 1 истинна», «Переменная 1 ложна»)
 
  Объяснение  : 
  Функция IF  создает оператор IF, который проверяет, равна ли переменная приложения "appVariableOne" значению "true" с помощью функции  IS_EQUAL . В случае, если оно «истинно», формула выводит первую строку. Если "false", то выводится второе.
 Переменные данных 
  Назначение 
 Чтение/изменение переменных данных.
  Использование 
  данные.{имя} 
  Пример 
 IS_EMAIL(data.usersList[0].email)
 
  Объяснение  : 
 Переменная данных  usersList  имеет поле с именем  электронная почта  . Используя функцию  IS_EMAIL , мы можем проверить, действительно ли электронное письмо   запись этой переменной данных является действительным адресом электронной почты. Выход «true» указывает на то, что запись действительно является электронной почтой.
 Параметры страницы 
  Назначение 
 Чтение/изменение параметров страницы.
  Использование 
  параметры {имя} 
  Пример 
 ПРОПИСНЫМИ БУКВАМИ (params.pageParameterOne)
 
  Объяснение  : 
 С помощью  CAPITALIZE , мы можем писать каждое слово в параметре страницы  pageParameterOne  с заглавной буквы.
 Переменные страницы 
  Назначение 
 Чтение/изменение переменных страницы.
  Использование 
  pageVars.{имя} 
  Пример 
 ДЛИНА(pageVars.pageVariableOne)
 
  Объяснение  : 
  Функция LENGTH  возвращает количество символов в переменной страницы  pageVariableOne  .
 Свойства выбранного компонента 
  Назначение 
 Взаимодействие (чтение/изменение) со свойствами компонента.
  Использование 
  сам.{собственность} 
  Пример 
 IF(IS_EQUAL(self.visible, true), "Компонент виден", "Компонент не виден")
 
  Объяснение  : 
 Используя функции  IF  и  IS_EQUAL , мы проверяем видимость компонента. Если формула определяет, что компонент  является видимым , она возвращает «Компонент виден». В противном случае будет вывод «Компонент не виден».
 Переменные датчика 
  Назначение 
 Взаимодействие с данными, собранными датчиками устройства, т. е. акселерометром.
  Использование 
  SensorVars. {имя} 
  Пример 
 ROUND(sensorVars.accelerometer.latestValue.x + sensorVars.accelerometer.latestValue.y)
 
  Объяснение  : 
  sensorVars.accelerometer.latestValue.    x   предоставляет значение ускорения по оси  X , а  sensorVars.accelerometer.latestValue.    у   дает ось  Y . Используя математическое выражение  +  (плюс), мы находим их сумму. Функция  ОКРУГЛ  округляет результат до первого десятичного знака.
 Системные переменные 
  Назначение 
 Взаимодействовать с системными данными устройства, т.е. активным браузером или моделью телефона.
  Использование 
  системные переменные. {имя} 
  Пример 
 "Вы используете " + systemVars.browser.browserCodeName + " браузер."
 
  Объяснение  : 
 Используя знак плюс (  +  ), мы можем использовать имя браузера устройства в предложении. Он будет отображаться по-разному в зависимости от пользователя.
 Переменные темы 
  Цель 
 Взаимодействие с переменными темы приложения.
  Использование 
  тема.${имя} 
  Пример 
 ЦВЕТ(тема.$smartColorPalette_app.negative)
 
  Объяснение  : 
  theme.$smartColorPalette_app.negative  получает текущий «негативный» цвет, предварительно установленный в шестнадцатеричном формате. Функция  COLOR  преобразует его в цвет RGB.
 Функции 
 Побитовые 
 Функция побитовой формулы работает с числом на уровне его отдельных битов.
   BIT_NOT(10)    = -11  
 Выполняет логическое отрицание каждого бита, формируя дополнение заданного числа.
   BIT_AND(14, 9)    = 8  
 Двоичная операция, которая принимает два числовых представления и выполняет логическую операцию  И  для каждой пары соответствующих битов.
   БИТ_ИЛИ(14, 9)    = 15  
 Выполняет логическую операцию  включительно  ИЛИ над каждой парой соответствующих битов.
   BIT_XOR(14, 9)    = 7  
 Выполняет логическую операцию  исключающее ИЛИ  для каждой пары соответствующих битов.
   BIT_SHIFT_{направление}(число, сдвиг)   
 При сдвиге влево двоичные нули сдвигаются вправо; при арифметическом сдвиге вправо знаковый бит сдвигается влево,
 Color 
 Набор функций для работы с цветами. Обратитесь к справочным страницам для более подробной информации.
 Примеры
  RGB(0, 128, 250) 
 Вы можете использовать функцию  RGB  для создания 16777216 возможных цветов, используя цветовую систему  R  ed,  G  reen и  B  lue. 
  НАСЫЩЕННОСТЬ("rgb(0, 128, 250)", 50) 
 Насыщает (повышает интенсивность и четкость) цвет на заданный процент. В качестве входных данных принимает цвет в формате RGB или HEX. 
 Дата 
 Позволяет работать с датами и временем. Обратитесь к справочным страницам для более подробной информации.
 Примеры
  СЕЙЧАС() 
 Возвращает текущую дату и время в формате  ГГГГ-ММ-ДД ЧЧ:ММ:СС . 
  FORMAT_DATETIME_LOCAL(СЕЙЧАС(), "ДД-ММ-ГГ ЧЧ:ММ") 
 Форматирует дату и время в удобном для человека формате. Дает возможность опустить ненужные поля и изменить порядок в желаемом порядке. 
 Инжиниринг 
 Сбор инженерных функций. В настоящее время содержит только варианты функции Бесселя. Обратитесь к справочным страницам для более подробной информации.
 Функция Бесселя
 Набор математических функций, систематически полученных немецким астрономом Фридрихом Вильгельмом Бесселем в ходе исследования решений одного из уравнений движения планет Кеплера. Уравнение Бесселя: 
 Финансовый 
 Выполнение различных финансовых манипуляций. Обратитесь к справочным страницам для более подробной информации.
 Пример
  FUTURE_VALUE(0,5, 12, 1000) 
 Вычисляет будущую стоимость аннуитетных инвестиций, где  0,5  — процентная ставка,  12  — количество платежей, а  1000  — сумма взноса за период.
 Список 
 Выполнение операций со списками. Обратитесь к справочным страницам для более подробной информации.
 Пример
  СЧЕТ(data.usersList) 
 Возвращает  количество элементов  в заданном списке. В этом случае переменная данных — это список. 
 Математика 
 Библиотека математических выражений и методов. Обратитесь к справочным страницам для более подробной информации.
 Примеры
  ФАКТОРИАЛ(6) 
 Вычисляет факториал предоставленного числа.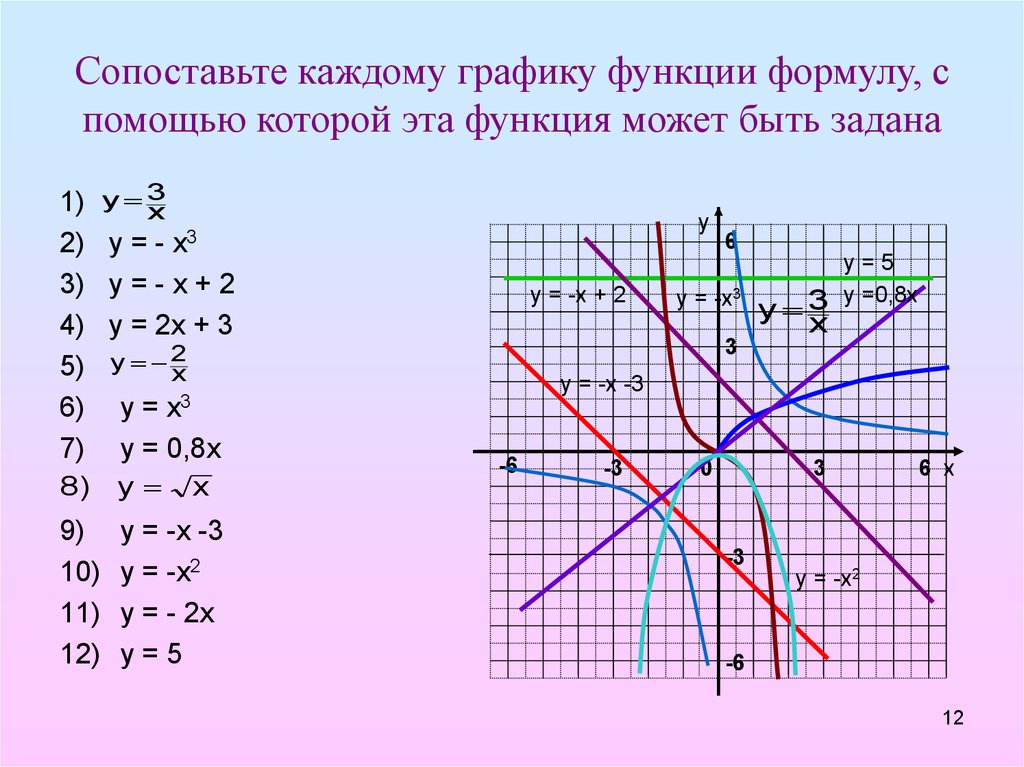 
  RANDOM_INTEGER_BETWEEN(1100) 
 Рандомизирует число между предоставленными целыми числами, 
 Object 
 Представляет доступные методы JavaScript  Object . Обратитесь к справочным страницам для более подробной информации.
 Примеры
  ПРОСМОТР(appVars.object, "имя") 
 Считывает значение свойства "  name  " объекта  appVars.object  . 
  SET_KEY(appVars.object, "имя", "Джон") 
 Устанавливает для параметра "имя" значение "Джон". Переопределяет предыдущее значение. 
 Статистические 
 Список операций, используемых в статистической математике. Обратитесь к справочным страницам для более подробной информации.
 Примеры
  ПЕРЕСТАНОВКА(5, 3) 
 Возвращает количество перестановок ( ) для заданных входных данных.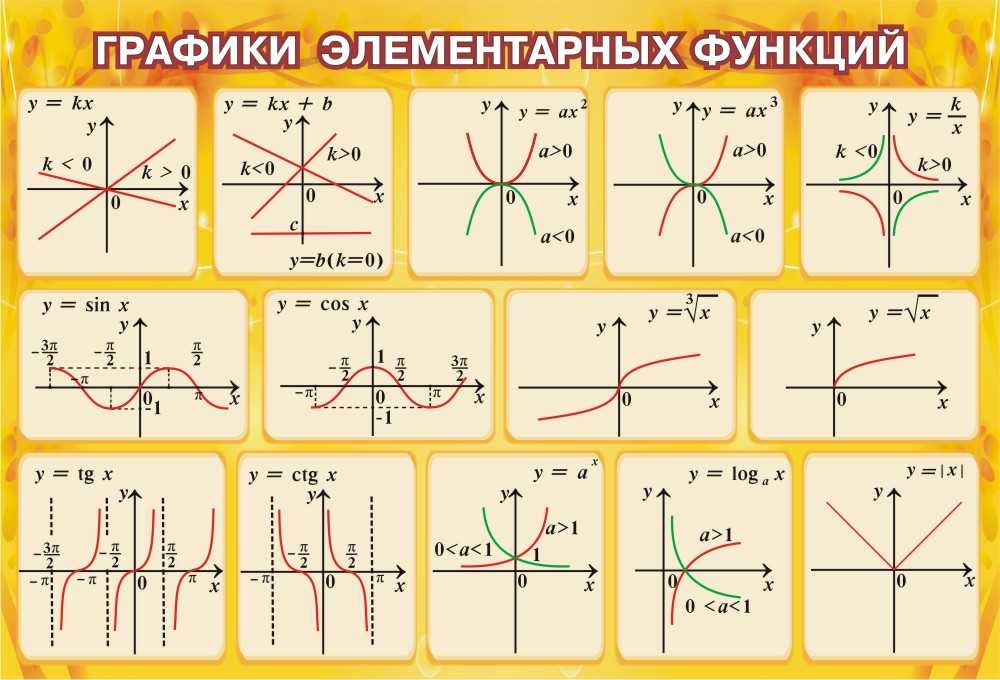 
  КОМБИНА (5, 3) 
 Возвращает количество комбинаций ( ) для заданных входных данных 
 Текст 
 Текстовые операции. Обратитесь к справочным страницам для более подробной информации.
 Примеры
  APPEND_URL_PARAMETERS("https://appgyver.com/", { href: "#" }) 
 Добавляет указанный параметр URL-адреса ( href: "#" ) к тексту URL-адреса ( https://appgyver.com/ ) 
  REPLACE_ONE_REGEX("Документация AppGyver 20:00 @ 01.01.2022", "[a-zA-Z]+", "SAP AppGyver") 
 Использует регулярное выражение для замены текстовой/числовой строки. Используйте генератор регулярных выражений, если вы не знакомы с языком шаблонов. 
 Утилита 
 Выбор различных служебных функций программирования, например, операторы IF или кодировщики Base64.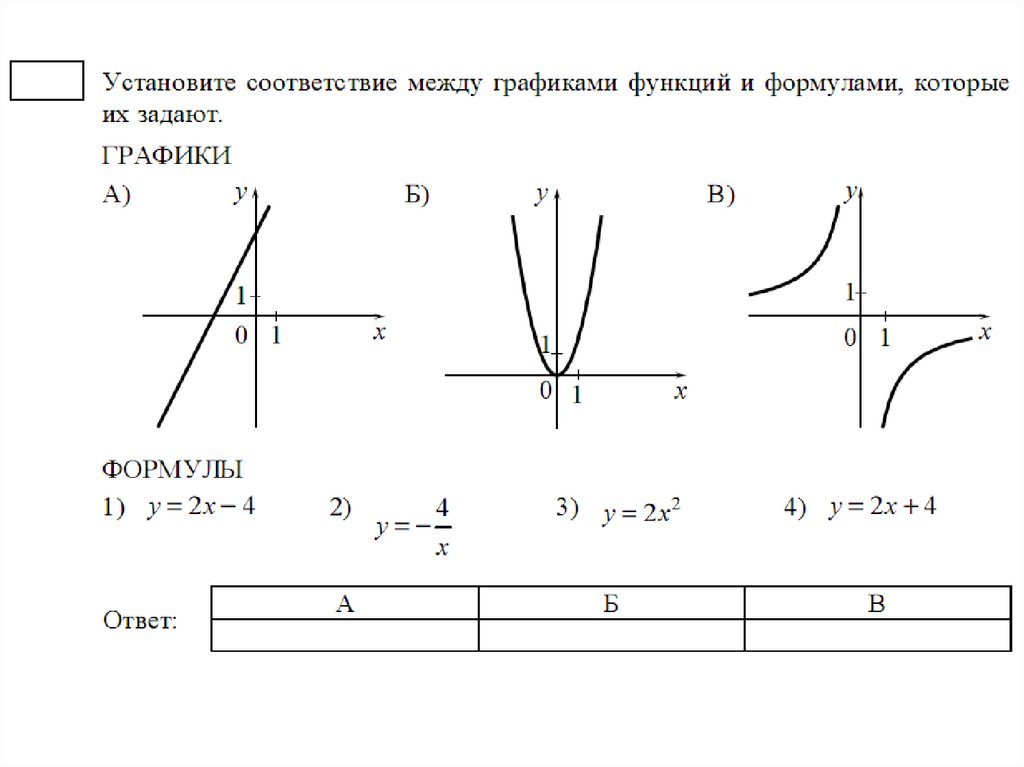 Обратитесь к справочным страницам для более подробной информации.
 Примеры
  ENCODE_BASE64 ("Привет, мир!") 
 Кодирует предоставленную текстовую строку в Base64. 
  FILENAME_IS_IMAGE("cat.svg") 
 Проверяет, имеет ли данный текст расширение файла, принадлежащее изображению. 
 Криптография 
 Криптография использует математические методы для преобразования данных и предотвращения их чтения или подделки посторонними лицами. Это позволяет обмениваться защищенными сообщениями даже в присутствии злоумышленников ¹ .
 Примеры
  RIPEMD160("Мой секретный пароль") 
 Вычисляет хэш RIPEMD160 предоставленного текста. Возвращаемое значение представляет собой 160-битный хэш, закодированный как текст с 40 шестнадцатеричными цифрами.
No related posts.