Косинус | это… Что такое Косинус?
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Содержание
|
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически.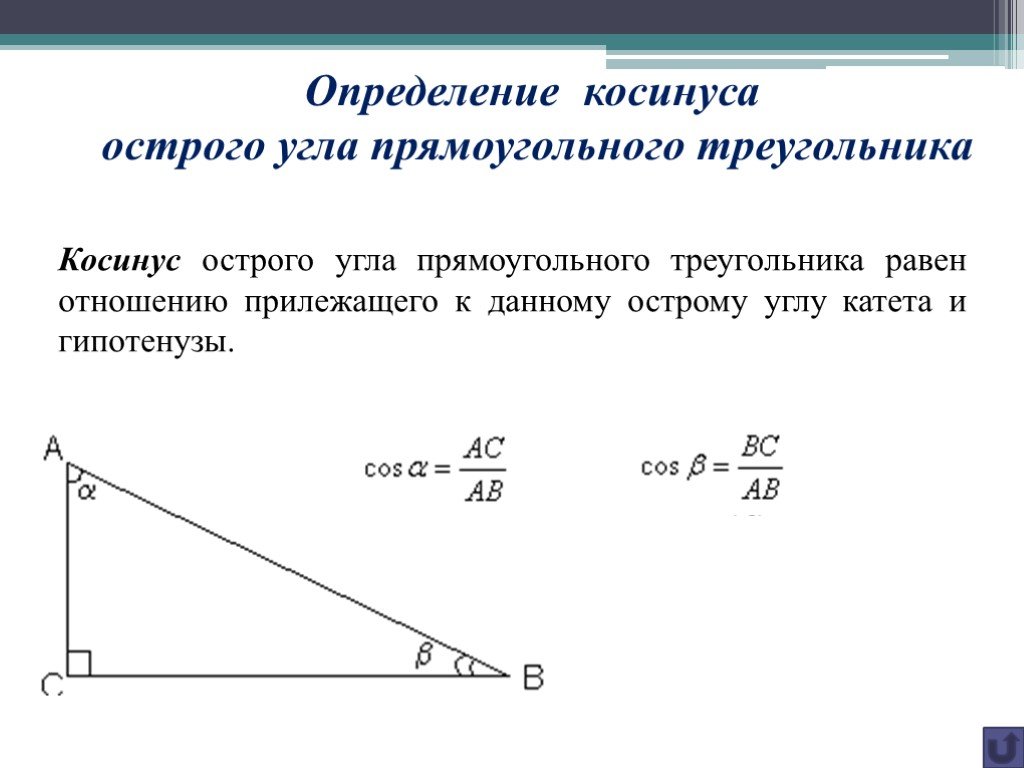
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате
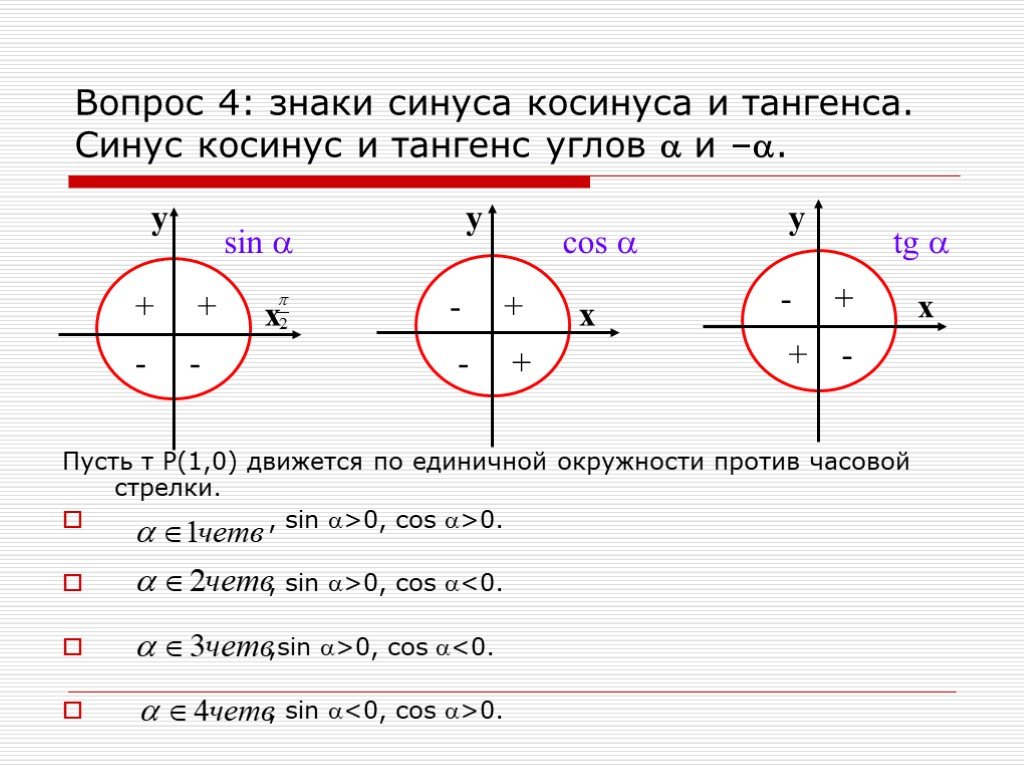 На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
На рисунке 3 показаны величины тригонометрических функций для единичной окружности.Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
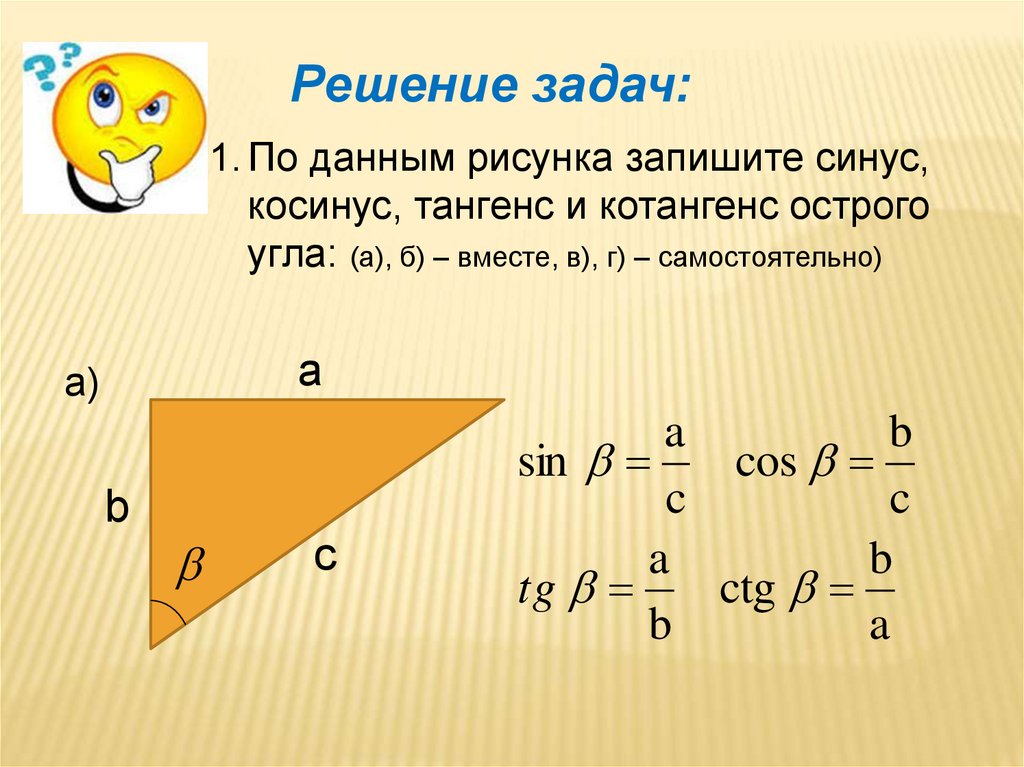
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу.
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
- где Bn — числа Бернулли.
- где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
Значения косинуса и синуса на окружности.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные.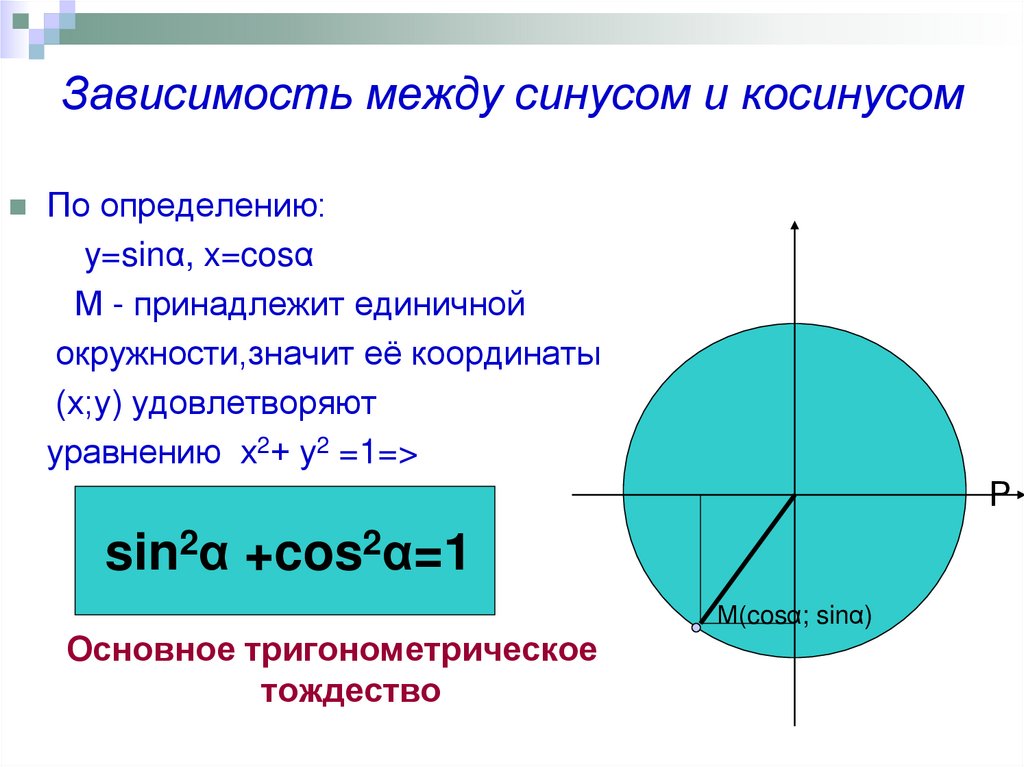 Остальные четыре функции — нечётные, то есть:
Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.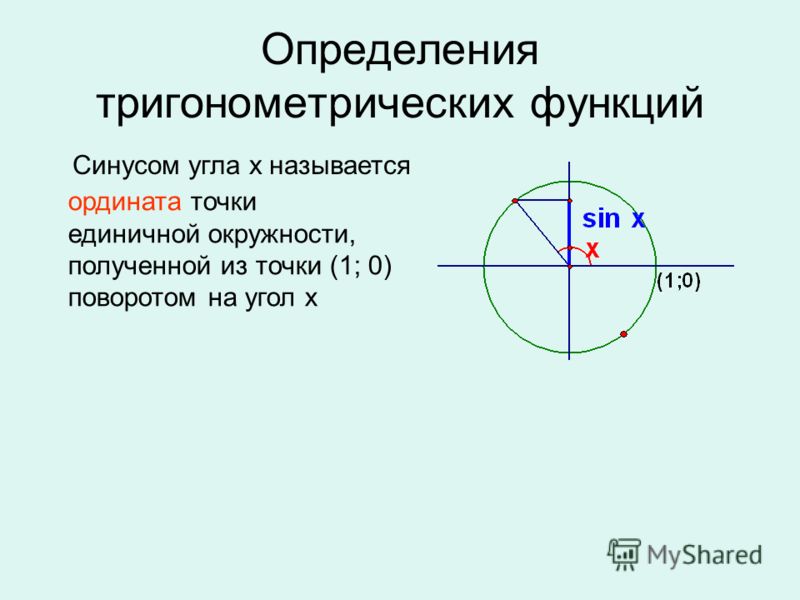
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха».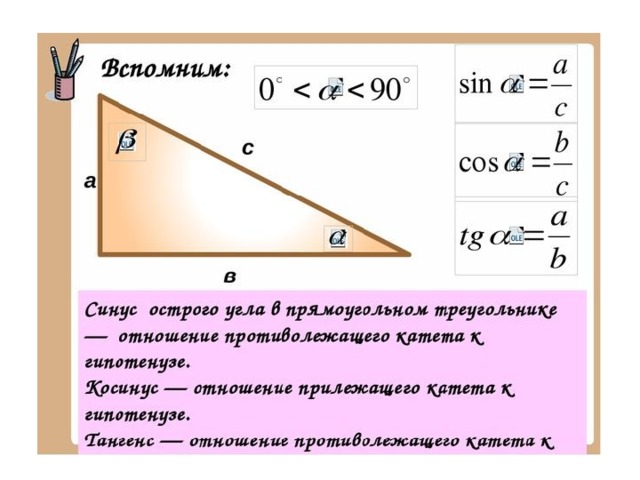 При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.

Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Синусоидальная функция — исчислениеЭта статья о конкретной функции от подмножества действительных чисел до действительных чисел. В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию. Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. д.), мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как . Содержание
ОпределениеОпределение единичной окружностиСинусоидальная функция , обозначенная , определяется следующим образом. Рассмотрим единичный круг с центром в начале координат, описанный как следующее подмножество координат: Для действительного числа мы определяем следующим образом:
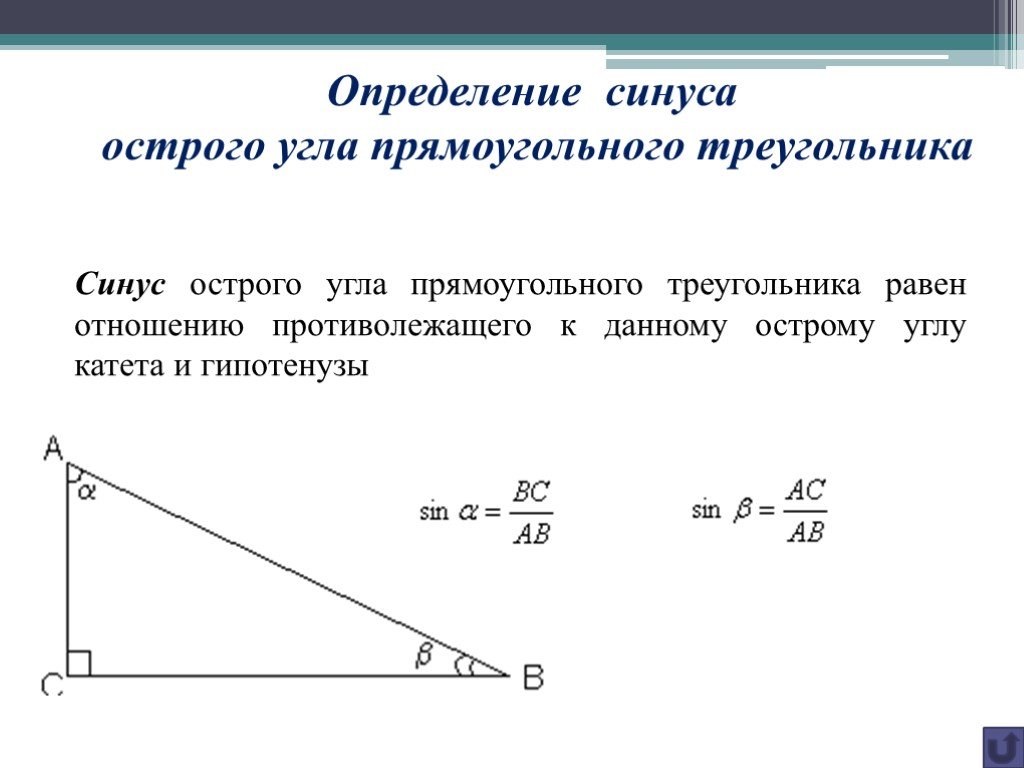
Определение соотношения треугольников (работает для острых углов)Для острого угла , т. е. для открытого интервала , можно определить следующим образом:
Основные данные
Личности
Связанные функцииКомпозиция с другими функциямиНиже приведены некоторые составные функции формы для подходящей функции:
Произведение с другими функциями
ДифференцированиеПервая производнаяВыводим формулу из предела: Вот полное доказательство: В силу того, что предел линейный, указанный выше предел можно переписать как: Теперь нам нужно вычислить два предела по отдельности. Первое ограничение: Таким образом, мы выразили предел как произведение пределов, где один из множителей стремится к нулю, а другой — к единице, поэтому предел равен нулю. Второй предел равен 1, как видно непосредственно. Таким образом, мы получаем, что ответ: Это упрощает до Вторая производнаяПроизводная равна , поэтому мы получаем: Старшие производныеПоследовательность производных периодична с периодом 4:
В частности, мы получаем, что для любого неотрицательного целого числа: Аналогично, у нас также есть: Другими словами, дифференцирование времени функции эквивалентно смещению графика влево. ИнтегрированиеПервая первообразнаяИмеем: Определенные интегралыСреднее значение за период равно 0. Таким образом: Поскольку нечетно, среднее значение на любом интервале, симметричном относительно начала координат, равно нулю: Кроме того, интеграл от on и on равен 1 каждый, что дает среднее значение на этих интервалах: Интегрирование преобразованных версий функцииИмеем для , используя интегрирование линейного преобразования функции: Далее, среднее значение за период равно 0. Высшие первообразныеОбщее выражение для второй первообразной: В общем случае первообразная равна или , в зависимости от значения по модулю 4. Общее выражение представляет собой частную первообразную плюс произвольный многочлен степени не выше . Интегрирование произведения с многочленами Используя интегрирование по частям, мы знаем, что знание первых первообразных достаточно для определения повторным применением интегрирования по частям. Например, функция , т. е. произведение функции тождества и функции синуса, может быть интегрирована с помощью знаний о том, как дважды интегрировать функцию синуса: Дифференциальные уравненияФункция синуса и ее преобразования возникают как решение многих дифференциальных уравнений, включая полиномиальные дифференциальные уравнения. Некоторые из них перечислены ниже.
Степенной ряд и ряд ТейлораВычисление ряда ТейлораКак отмечалось выше, имеем: В частности, это означает, что: Таким образом, последовательность производных в нуле (начиная с ) равна . Таким образом, ряд Тейлора: Ряд Тейлора равен степенному рядуСинусоида является глобально аналитической функцией: ряд Тейлора для синусоидальной функции действительно везде сходится к этой функции. Это можно доказать несколькими способами. Один из методов состоит в том, чтобы использовать то, что равномерно ограниченные производные влекут за собой аналитику. В качестве альтернативы мы могли бы отметить, что удовлетворяет некоторому дифференциальному уравнению , заставляя его быть заданным степенным рядом. Таким образом, мы имеем, что: Предельные вычисленияНулевой порядокУ нас есть следующий предел: Таким образом, порядок нуля в точке 0 равен 1, а остаток равен 1. Пределы высшего порядкаУ нас есть предел: Предел можно рассчитать одним из двух способов:
|

 1.1 Определение тригонометрических функций для острых углов
1.1 Определение тригонометрических функций для острых углов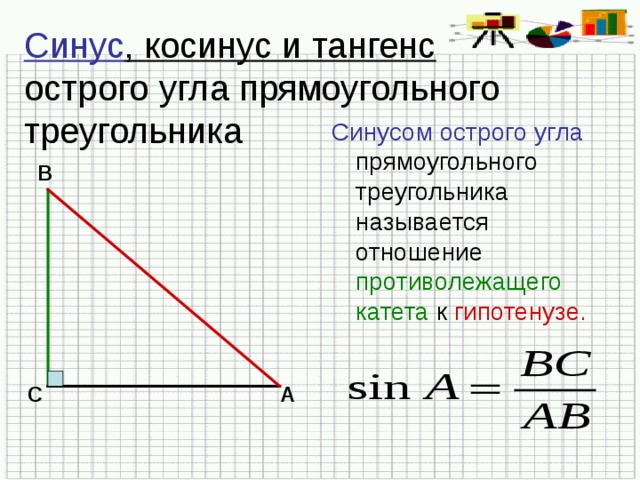
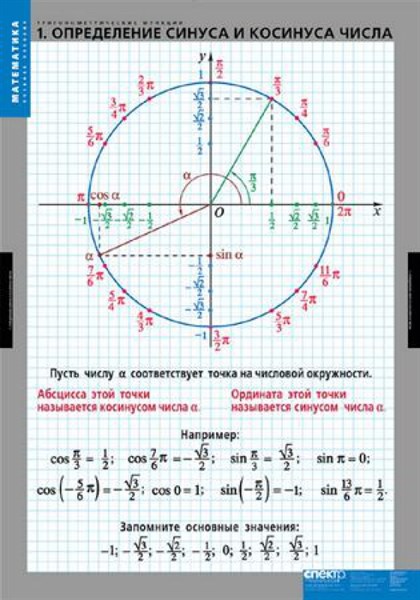 Косинус равен к длине стороны, примыкающей к q, деленной на длину гипотенузы треугольника. Таким способом мы можем найти косинус любого q в диапазоне 0 £ д £ 90°.
Косинус равен к длине стороны, примыкающей к q, деленной на длину гипотенузы треугольника. Таким способом мы можем найти косинус любого q в диапазоне 0 £ д £ 90°.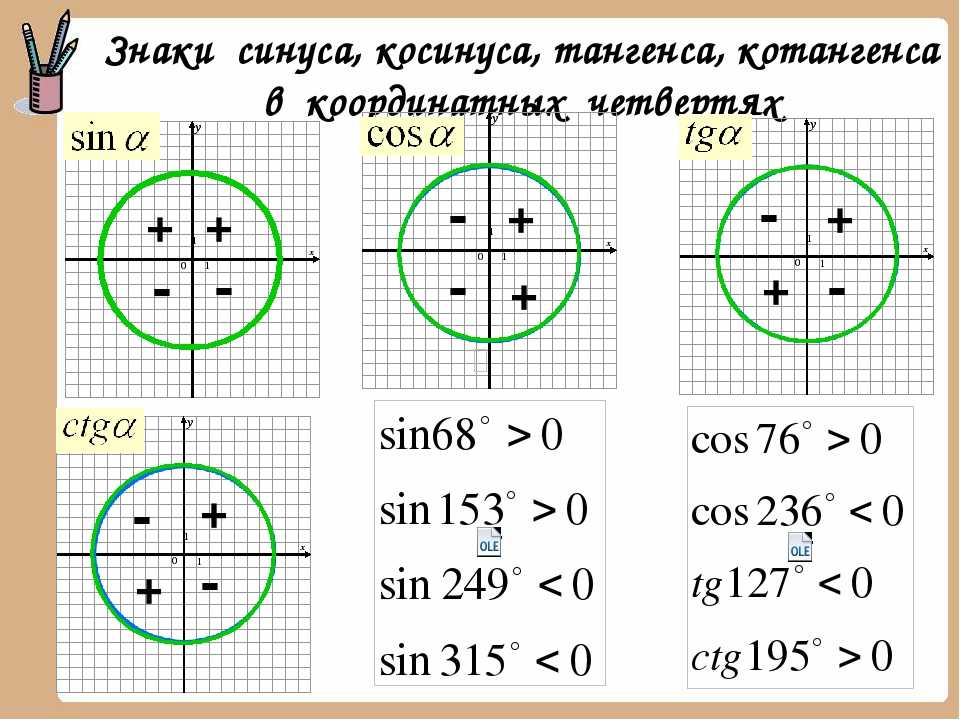

 4 Высшие производные
4 Высшие производные

 Обратите внимание сначала, что оба предела не зависят от .
Обратите внимание сначала, что оба предела не зависят от .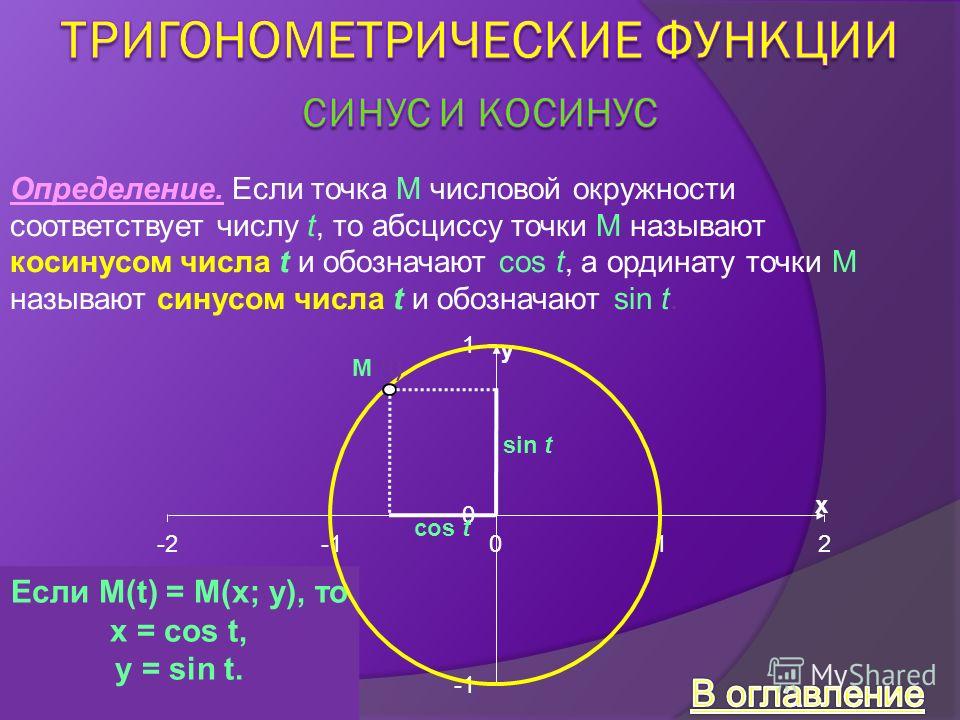
 Поскольку синусоидальную функцию можно антидифференцировать любое количество раз, это позволяет нам антидифференцировать любую полиномиальную функцию синуса.
Поскольку синусоидальную функцию можно антидифференцировать любое количество раз, это позволяет нам антидифференцировать любую полиномиальную функцию синуса.
