| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
§ 3.
 УРАВНЕНИЯ
УРАВНЕНИЯ|
Причина |
При каких преобразованиях это может происходить |
Пример неправильного (или неполного) решения |
|
|
1. Появление посторонних корней |
|||
|
в) применение к обеим частям уравнения функции, которая не является возрастающей или убывающей. |
Возведение обеих частей уравнения в четную степень или применение к обеим частям уравнения тригонометрических функций (см. с. 272) |
х — 1 = 2х + 1. Возведем обе части уравнения в квадрат: (х — 1)2 = (2х + 1)2. Получим 3х2 + 6х = 0, х1 = 0, х2 = —2 |
|
|
2. Потеря корней |
|||
|
Явное или неявное сужение ОДЗ заданного уравнения, в частности выполнение преобразований, в ходе которых происходит неявное деление на нуль |
1. |
х2= х. Поделив обе части уравнения на х, получим х = 1 |
|
|
2. Сложение, вычитание, умножение или деление обеих частей уравнения на выражение, ОДЗ которого уже, чем ОДЗ заданного уравнения |
х2 = 1. Если к обеим частям уравнения прибавить , то получим уравнение x2 + x = 1 + x, у которого только один корень х = 1 |
|
|
|
Где ошибка |
Как получить правильное (или полное) решение |
Пример правильного (или полного) решения |
|
|
при решении уравнения |
|||
|
х1 = 0 не является корнем заданного уравнения |
Выполнить проверку подстановкой корней в заданное уравнение |
В данном уравнении не было необходимости возводить в квадрат. х — 1 = 2х + 1. ►х — 2х = 1 + 1, х = —2. Ответ: —2. < Если применить возведение в квадрат, то проверка показывает, что х2 = —2 — корень, a х1 = 0 — посторонний корень |
|
|
при решении уравнения |
|||
|
Потеряли корень х = 0, поскольку после деления на х фактически получили уравнение 2 ОДЗ которого: х( Ф)= 0, то есть сузили ОДЗ заданного уравнения. |
Те значения, на которые сузилась ОДЗ, необходимо рассмотреть отдельно |
► 1. При х = 0 получаем 02 = 0 — верное равенство, таким образом, х = 0 — корень. 2. При х Ф 0 получаем 2 х = 1 Ответ. 0; 1. (Конечно, удобнее решать так: x2 — x = 0, х (х — 1) = 0, х = 0 или х = 1.) |
|
|
Потеряли корень х = —1, поскольку ОДЗ данного уравнения: х — любое число, а x существует только при х 1 0. |
В данном уравнении не было необходимости прибавлять к обеим частям -\/x. ► х2 = 1, х = ±1. Ответ: ±1. (Если бы пришлось прибавить к обеим частям yfx, то при x < 0 данное уравнение необходимо рассмотреть отдельно, и тогда получим еще и корень х = —1.) |
|
|
|
Объяснение и обоснование 1. Конечная ОДЗ. Напомним, что в случае, когда дано уравнение f (x) = g (x), общая область определения для функций f (x) и g (x) называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции f (x), так и области определения функции g (x). Таким образом, каждый корень |
|
уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях за счет анализа ОДЗ получить решение уравнения. Например, если дано уравнение л/x — 2 + V4 — 2x = 3x — 6, то его ОДЗ можно [x — 210 Jx 12, задать с помощью системы Решая эту систему, получаем — {4 — 2x 10. {x < 2, то есть х = 2. Таким образом, ОДЗ данного уравнения состоит только из одного значения х = 2. Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то достаточно подставить это значение переменной в уравнение. В результате получаем верное числовое равенство (0 = 0). Следовательно, х = 2 — корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме х = 2. Рассмотренный пример позволяет выделить о р и е н т и р для решения аналогичных уравнений: |
|
Если f (x) > а, то равенство f (x) = g (x) не может выполняться, потому что g (x) < а, то есть при f (x) > а данное уравнение корней не имеет. |
|
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 8. Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения f1 (x) + f2 (x) + … + fn (x) = 0, в котором все функции- слагаемые неотрицательны (f1 (x) 1 0; f2 (x) 1 0; …; fn (x) 1 0). • Если предположить, что f1 (x) > 0, то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма f2 (x) + . Например, чтобы решить уравнение x4 + | x — 1 | = 2x2 — 1, достаточно перенести все члены в одну сторону, записать уравнение в виде (x2 — 1)2 + | x — 1 | = 0 и учесть, что функции (x2 — 1)2 и | x — 1 | неотрицательные. Таким образом, данное уравнение равносильно системе |
|
Из второго уравнения получаем х = 1, что удовлетворяет и всей системе. 3. Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения. Полезно помнить специальные теоремы о корнях уравнения. Теор ем а 1. Если в уравнении f (я) = а функция f (я) возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке. Графически утверждение теоремы проиллюстрировано на рисунке 39. Прямая у = а пересекает график возрастающей на промежутке [а; в] функции у = f (x) только в одной точке. Это и означает, что уравнение f (x) = а не может иметь больше одного корня на промежутке [а; в]. Докажем это утверждение аналитически. |
|
9 Если на промежутке [а; в] уравнение имеет корень x 0, то f (x0) = а. Теор ема 2. Если в уравнении f (x) = g (x) функция f (x) возрастает на некотором промежутке, а функция g (x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке. Графически утверждение теоремы проиллюстрировано на рисунке 40. |
|
в Если на промежутке [а; в] уравнение имеет корень x Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет. Например, чтобы решить уравнение x3 + x = 10, достаточно заметить, что функция f (x) = x3 + x является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что x = 2 — корень* этого уравнения (23 + 2 = 10; 10 = 10). Таким образом, данное уравнение f (x) = 10 имеет единственный корень x = 2. Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно. |
|
Решим с помощью теоремы 2 уравнение x + x = —. |
|
► Сначала следует учесть его ОДЗ: x Ф 0 и вспомнить, что функция у = 2 на |
|
всей области определения не является ни убывающей, ни возрастающей (с. 28), но она убывает на каждом из промежутков (—то; 0) и (0; +“). Поэтому рассмотрим каждый из этих промежутков отдельно. |
|
1) При x > 0 данное уравнение имеет корень x = 1 (1 +1 = -,2 = 2). Функция f (x) = x3 + x возрастает при x > 0 (как было показано выше, она 2 возрастает на множестве R), а функция g (x) = — убывает на промежутке x x > 0. Таким образом, данное уравнение f (x) = g (x) при x > 0 имеет единственный корень x = 1. |
|
Комментарий Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти. Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ (х Ф 0) x4 > 0, то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. |
|
Задача 2 Решите систему уравнений |
|
Рассмотрим функцию |
|
Решение Jx 10, f (t) = Vt +13. На своей области определения (t 1 0) эта функция является возрастающей (как сумма двух возрастающих функций). Jx = у, системе — [x2 + 3у2 = 36. Подставляя x = у во второе уравнение системы, имеем 4у2 = 36, у2 = 9, у = ±3. Учитывая, что на ОДЗ у 1 0, получаем у = 3. Тогда x = у = 3. Ответ: (3; 3). <1 |
|
\4x- -x2 + 3у2 = 36. Комментарий Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство f (x) = f (у) для возрастающей функции возможно тогда и только тогда, когда х = у, поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. Вопросы для контроля 1. Объясните на примерах, как можно использовать свойства функций при решении уравнений. 2*. Обоснуйте правильность ориентиров по решению уравнений с использованием свойств функций, приведенных в таблице 8 (с. 60). |
9.3 – Радикальные функции | Hunter College – MATh201
Цели обучения
- (9.3.1) – Оценка радикальных функций
- (9.3.2) – Нахождение области определения радикальной функции
В этом разделе мы расширим нашу предыдущую работу с функциями, включив радикалы. Если функция определяется радикальным выражением, мы называем ее радикальной функцией .
Функция квадратного корня: [latex]f(x) = \sqrt{x}[/latex].
Функция кубического корня [latex]f(x) = \sqrt[3]{x}[/latex]. 92+4}[/латекс].
Чтобы вычислить радикальную функцию, мы находим значение [latex]f(x)[/latex] для заданного значения [latex]x[/latex] точно так же, как мы делали это в нашей предыдущей работе с функциями.
ПРИМЕР
Для функции [латекс]f(x) = \sqrt{2x-1}[/латекс] найдите [латекс]f(5)[/латекс]
Показать решение
ПРИМЕР
Для функции [латекс]f(x) = \sqrt{-4x+5}[/латекс] найдите [латекс]f(-5)[/латекс]
Показать решение
Попробуйте
В следующем примере мы оцениваем функцию кубического корня.
ПРИМЕР
Для функции [латекс]f(x) = \sqrt[3]{x-29}[/латекс] найдите [латекс]f(2)[/латекс]
Показать решение
Для функции квадратного корня [latex]f\left(x\right)=\sqrt[]{x}[/latex] мы не можем извлечь квадратный корень из отрицательного действительного числа, поэтому домен должен быть 0 или выше. Диапазон также исключает отрицательные числа, поскольку квадратный корень из положительного числа [latex]x[/latex] определяется как положительный, хотя квадрат отрицательного числа [latex]-\sqrt{x}[/latex] также дает нам [латекс]x[/латекс]. Ниже приведен график функции извлечения квадратного корня:
Ниже приведен график функции извлечения квадратного корня:
Для функции кубического корня [latex]f\left(x\right)=\sqrt[3]{x}[/latex] домен и диапазон включают все действительные числа. Обратите внимание, что нет проблем с извлечением кубического корня или любого корня из нечетного целого числа из отрицательного числа, и результирующий результат будет отрицательным (это нечетная функция). Вот график функции кубического корня:
Мы используем это, чтобы найти области определения других радикальных функций.
Как: Дана функция, записанная в виде уравнения, включая четный корень, найти область определения.
- Идентификация входных значений.
- Поскольку имеется четный корень, исключите все действительные числа, которые приводят к отрицательному числу в подкоренном члене. Установите подкоренное число больше или равное нулю и найдите [латекс]х[/латекс].
- Решение(я) являются областью определения функции. Если возможно, запишите ответ в интервальной форме.

Пример: нахождение области определения функции с четным корнем
Найдите область определения функции [latex]f\left(x\right)=\sqrt{7-x}[/latex].
Решение
ПРИМЕР
Найдите область определения функции [latex]f\left(x\right)=\sqrt{5+2x}[/latex].
Решение
Попробуйте
Пример: поиск домена и диапазона
Найдите домен и диапазон [latex]f\left(x\right)=2\sqrt{x+4}[/latex].
Решение
Как найти область определения функции квадратного корня
Обновлено 5 декабря 2020 г.
Автор Джек Джерард
В математике область определения функции говорит вам, для каких значений числа x функция действительна. Это означает, что любое значение внутри этого домена будет работать в функции, а любое значение, выходящее за пределы домена, — нет. Некоторые функции (например, линейные функции) имеют домены, включающие все возможные значения x . Другие (например, уравнения, в которых x стоит в знаменателе) исключают определенные значения x , чтобы избежать деления на ноль. Функции квадратного корня имеют более ограниченные области применения, чем некоторые другие функции, поскольку значение внутри квадратного корня (известное как подкоренное число) должно быть положительным числом, чтобы результат был «действительным».
Некоторые функции (например, линейные функции) имеют домены, включающие все возможные значения x . Другие (например, уравнения, в которых x стоит в знаменателе) исключают определенные значения x , чтобы избежать деления на ноль. Функции квадратного корня имеют более ограниченные области применения, чем некоторые другие функции, поскольку значение внутри квадратного корня (известное как подкоренное число) должно быть положительным числом, чтобы результат был «действительным».
TL;DR (слишком длинное; не читал)
Область определения функции извлечения квадратного корня — это все значения x , в результате которых подкоренное число равно или больше нуля.
Функции извлечения квадратного корня
Функция извлечения квадратного корня — это функция, содержащая радикал, который чаще называют квадратным корнем. Если вы не уверены, как это выглядит,
f(x) = \sqrt{x}
считается базовой функцией квадратного корня. В данном случае x не может быть отрицательным числом; все радикалы должны быть равны или больше нуля, чтобы результат был реальным. Если вы можете включить «мнимые» числа (с i , определенным как квадратный корень из −1), тогда все становится сложнее, но в большинстве случаев вам нужно рассматривать только действительные числа.
В данном случае x не может быть отрицательным числом; все радикалы должны быть равны или больше нуля, чтобы результат был реальным. Если вы можете включить «мнимые» числа (с i , определенным как квадратный корень из −1), тогда все становится сложнее, но в большинстве случаев вам нужно рассматривать только действительные числа.
Это не означает, что все функции квадратного корня так же просты, как квадратный корень из одного числа. Более сложные функции квадратного корня могут иметь вычисления внутри радикала, вычисления, которые изменяют результат радикала, или даже радикал как часть более крупной функции (например, в числителе или знаменателе уравнения). Примеры этих более сложных функций выглядят так:
f(x) = 2\sqrt{x + 3} \text{ или } g(x) = \sqrt{x — 4}
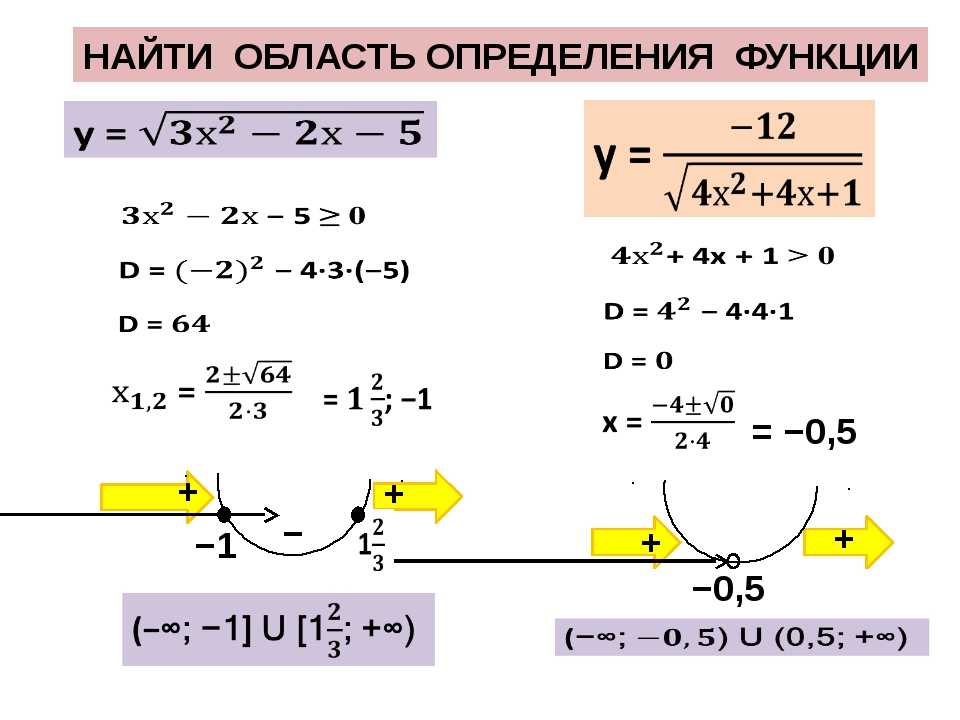
Область определения функций квадратного корня
Для вычисления области определения квадрата корневой функции, решите неравенство x ≥ 0, заменив x подкоренным числом. Используя один из приведенных выше примеров, вы можете найти домен
Используя один из приведенных выше примеров, вы можете найти домен
f(x) = 2\sqrt{x + 3}
, установив подкоренную черту ( x + 3) равной x в неравенстве. Это дает вам неравенство
x + 3 ≥ 0
, которое можно решить, вычитая 3 с обеих сторон. Это дает вам решение x ≥ −3, что означает, что все значения вашего домена x больше или равны −3. Вы также можете написать это как [ −3, ∞), где скобка слева показывает, что −3 является определенным пределом, а скобка справа показывает, что ∞ таковым не является. Поскольку подкоренное число не может быть отрицательным, вам нужно вычислять только положительные или нулевые значения.
Диапазон функций извлечения квадратного корня
Понятие, относящееся к области определения функции, — это ее диапазон. В то время как домен функции — это все значения x , допустимые в пределах функции, ее диапазон — все значения y , в которых функция действительна.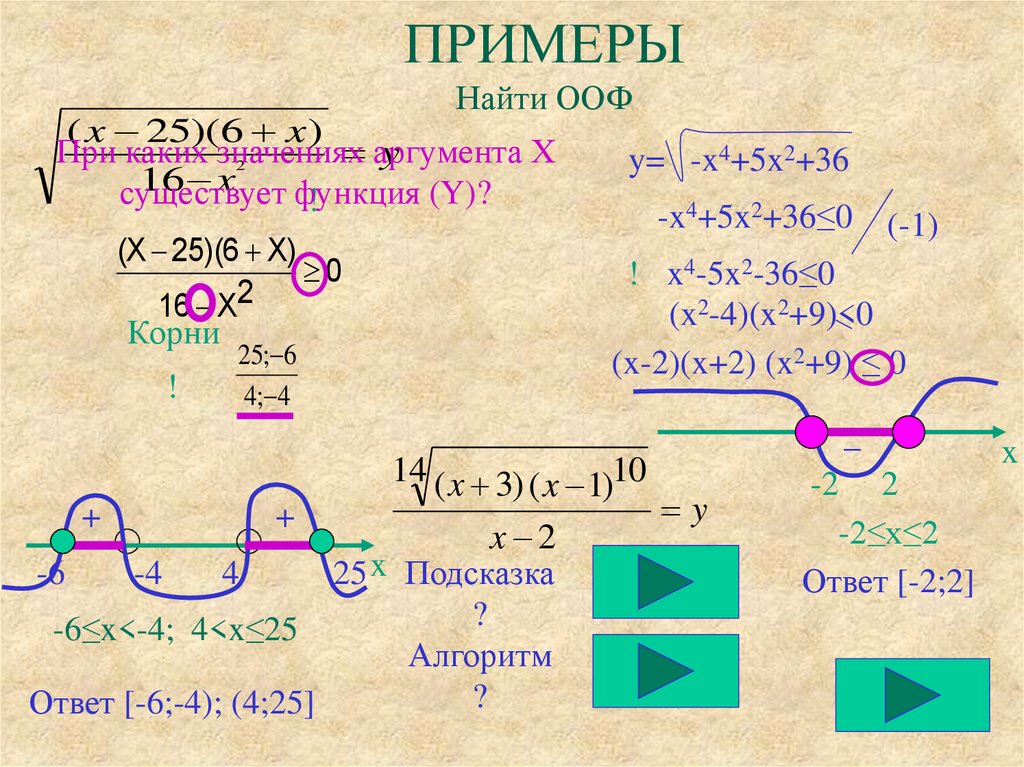

 Деление обеих частей уравнения на выражение с переменной
Деление обеих частей уравнения на выражение с переменной


 Остается только случай f (x) = a, но, учитывая необходимость выполнения равенства f (x) = g (x), имеем, что тогда и g (x) = а. Таким образом, мы обосновали, что выполнение равенства f (x) = g (x) (при условии f (x) 1 а и g (x) < а) гарантирует одновременное выполнение равенств f (x) = а и g (x) = а (и наоборот, если одновременно выполняются равенства f (x) = а и g (x) = а, то выполняется и равенство f (x) = g (x)). Как было показано в п. 3.1, это и
Остается только случай f (x) = a, но, учитывая необходимость выполнения равенства f (x) = g (x), имеем, что тогда и g (x) = а. Таким образом, мы обосновали, что выполнение равенства f (x) = g (x) (при условии f (x) 1 а и g (x) < а) гарантирует одновременное выполнение равенств f (x) = а и g (x) = а (и наоборот, если одновременно выполняются равенства f (x) = а и g (x) = а, то выполняется и равенство f (x) = g (x)). Как было показано в п. 3.1, это и .. + fn (x) будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при f1 (x) > 0 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство f 1 (x) + f2 (x) + … + fn (x) = 0 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
.. + fn (x) будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при f1 (x) > 0 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство f 1 (x) + f2 (x) + … + fn (x) = 0 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
 Других корней быть не может, поскольку для возрастающей функции f (x) при x > x0 получаем неравенство f (x) > f (x0) = а, а при x < x0 — неравенство f (x) < f (x0) = а. Таким образом, при x Ф x0 f (x) Ф а. Аналогично и для убывающей функции при x Ф x0 получаем f (x) Ф а.
Других корней быть не может, поскольку для возрастающей функции f (x) при x > x0 получаем неравенство f (x) > f (x0) = а, а при x < x0 — неравенство f (x) < f (x0) = а. Таким образом, при x Ф x0 f (x) Ф а. Аналогично и для убывающей функции при x Ф x0 получаем f (x) Ф а. Аналогично и при x < x0 f (x) Ф g (x).
Аналогично и при x < x0 f (x) Ф g (x).

 Тогда первое уравнение заданной системы, которое имеет вид f (x) = f (у), равносильно уравнению x = у. Таким образом, на ОДЗ заданная система равносильна
Тогда первое уравнение заданной системы, которое имеет вид f (x) = f (у), равносильно уравнению x = у. Таким образом, на ОДЗ заданная система равносильна а = в.
а = в.