Математика — 9
3-4 | Функция y = x3 и ее график |
Функция y = x3 определена при всех значениях x . Функция
принимает отрицательное значение при отрицательном
значении x (куб отрицательного числа — отрицательное
число), положительное значение при положительном
значении x (куб положительного числа положительное
число). При x=0, y= 0. То есть, областью определения и
множеством значений функции y = x3 являются все действительные
числа.
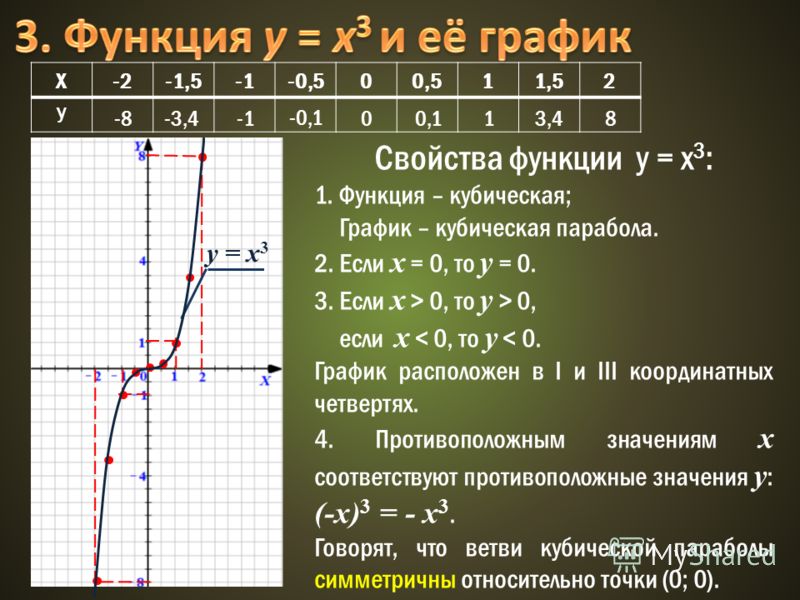
Графиком функции y = x3 называется кубическая парабола.
График функции проходит через начало координат и расположен в I и III четвертях.
Если значение x заменить его противоположным значением –х , тогда
функция будет принимать противоположное значение:
 к. y = x3, то (-x)3 = -x3 = — y. Значит, каждой точке (x; y) графика функции соответствует
точка (–x; –y), симметричная относительно начала координат на
данном графике. Таким образом, график функции y= x3 симметричен относительно
начала координат.
к. y = x3, то (-x)3 = -x3 = — y. Значит, каждой точке (x; y) графика функции соответствует
точка (–x; –y), симметричная относительно начала координат на
данном графике. Таким образом, график функции y= x3 симметричен относительно
начала координат.Обучающие задания
- a) Какие из точек A(-2; 8), B(2; 8), C(- 1
2 ; — 1
8 ), D(-3; -27) расположены на графике функции, являющейся кубической параболой?
b) Сколько точек находится на кубической параболе с ординатами 8; -1?
c)При каком значении m кубическая парабола проходит через точку N( m; -8)? - a) При каком значении аргумента значение функции y = x3 равно 6?
b) Постройте график функции y = x3. Найдите приблизительное значение абсциссы точки, ордината которой равна 6.
c) Сравните полученные результаты предыдущих пунктов. - Постройте в одной координатной плоскости графики функций y = x3 и y = 2 — x, отметьте их точки пересечения.

- На рисунке изображены графики функций y = x3,
y = (x + 3)3, y = (x – 2)3 – 1
Определите, какой график соответствует какой функции. - Точка N(–1; 1) находится на графике функции y = x3 + n. Какие из точек A(1; 3), B(0; 0), C(–2; –8), D(–2; –6) тоже находятся на графике этой функции?
- Найдите объем куба, длина ребра которого 4 см.
b) На сколько изменится объем куба, если длину ребра увеличить на 1 см?
BestMaths
- Home
- Year 11 (Yr 12 NZ, KS 4)
- Year 11 Topics
- Cubic Graphs
- Year 11 Topics
- Year 11 (Yr 12 NZ, KS 4)
A cubic function is a многочлен степени три .
напр. y = x 3 + 3x 2 — 2x + 5
Кубические графы можно построить, найдя точки пересечения x и y.
Поскольку кубические графы не имеют осей симметрии, точки поворота должны быть найдены с помощью исчисления.
Кубики эскизов
Метод 1: Факторизация.
Если уравнение имеет форму y = (x − a)(x − b)(x − c), следует использовать следующий метод:
Шаг 1: Найдите точки пересечения по оси x, положив y = 0. Шаг 2: Найдите точку пересечения с осью y, положив x = 0. Шаг 3: Нанесите указанные выше точки, чтобы нарисовать кубическую кривую.
напр.
Нарисуйте график y = (x — 2) (x + 3) (x — 1)
Шаг 1:
Найдите точки пересечения по оси x, положив y = 0,
0 = (x − 2)(x + 3)(x − 1)x = 2 или -3 или 1
Шаг 2:
Найдите точки пересечения по оси y, положив x = 0
y = (0 − 2)(0 + 3)(0 − 1)
y = -2 x 3 x -1
y = 6
Шаг 3:
и нарисуйте кривую.
Примечание. Функции с повторяющимся множителем имеют график, который только касается оси x. например у = (х — 2) 2 (х + 1)
Метод 2: Преобразование
График основной кубической у = х 3 показан на диаграмме.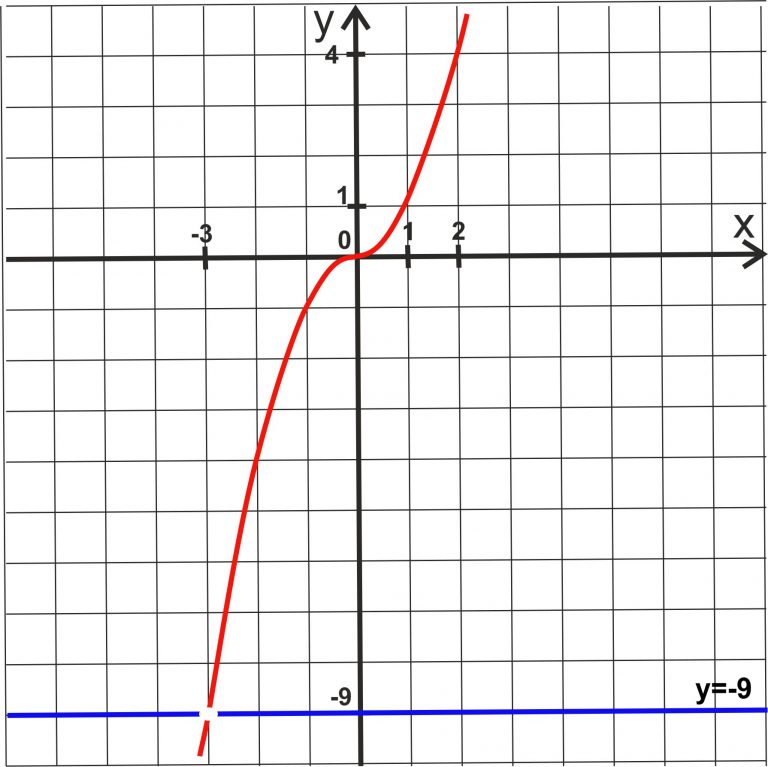

 Нарисуйте график y = (x — 2) (x + 3) (x — 1)
Нарисуйте график y = (x — 2) (x + 3) (x — 1)