Таблица пи значений: Таблица значений тригонометрических функций

Содержание

Функция ПИ

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции ПИ в Microsoft Excel.

Описание

Возвращает число 3,14159265358979 — математическую константу «пи» с точностью до 15 цифр.

Синтаксис

ПИ()

У функции ПИ нет аргументов.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Радиус
3
Формула	Описание	Результат
=ПИ()	Возвращает число «пи». 2)	Площадь круга с радиусом, указанным в ячейке A3.	28,27433388

Таблицы тригонометрических функций

Таблица основных тригонометрических функций для углов 0, 30, 45, 60, 90, … градусов

Из тригонометрических определений функций $\sin$, $\cos$, $\tan$ и $\cot$ можно узнать их значения для углов $0$ и $90$ градусов:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ не определяется;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ не определяется.

В школьном курсе геометрии при изучении прямоугольных треугольников находят тригонометрические функции углов $0°$, $30°$, $45°$, $60°$ и $90°$.

Найденные значения тригонометрических функций для указанных углов в градусах и радианах соответственно ($0$, $\frac{\pi}{6}$, $\frac{\pi}{4}$, $\frac{\pi}{3}$, $\frac{\pi}{2}$) для удобства запоминания и использования заносят в таблицу, которую называют тригонометрической таблицей, таблицей основных значений тригонометрических функций и т. п.

При использовании формул приведения, тригонометрическая таблица может быть расширена до угла $360°$ и соответственно $2\pi$ радиан:

Применяя свойства периодичности тригонометрических функций, каждый угол, который будет отличаться от уже известного на $360°$, можно рассчитать и записать в таблицу. Например, тригонометрическая функция для угла $0°$ будет иметь такое же значение и для угла $0°+360°$, и для угла $0°+2 \cdot 360°$, и для угла $0°+3 \cdot 360°$ и т.д.

С помощью тригонометрической таблицы можно определить значения всех углов единичной окружности.

В школьном курсе геометрии предполагается запоминание основных значений тригонометрических функций, собранных в тригонометрической таблице, для удобства решения тригонометрических задач.

Использование таблицы

В таблице достаточно найти необходимую тригонометрическую функцию и значение угла или радиан, для которых эту функцию нужно вычислить. На пересечении строки с функцией и столбца со значением получим искомое значение тригонометрической функции заданного аргумента.

На рисунке можно увидеть, как найти значение $\cos⁡60°$, которое равно $\frac{1}{2}$.

Аналогично используется расширенная тригонометрическая таблица. Преимуществом ее использования является, как уже упоминалось, вычисление тригонометрической функции практически любого угла. Например, легко можно найти значение $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300°$:

Таблицы Брадиса основных тригонометрических функций

Возможность расчета тригонометрической функции абсолютно любого значения угла для целого значения градусов и целого значения минут дает использование таблиц Брадиса. Например, найти значение $\cos⁡34°7’$. Таблицы разделены на 2 части: таблицу значений $\sin$ и $\cos$ и таблицу значений $\tan$ и $\cot$.

Таблицы Брадиса дают возможность получить приближенное значение тригонометрических функций с точностью до 4-х знаков после десятичной запятой.

Использование таблиц Брадиса

Используя таблицы Брадиса для синусов, найдем $\sin⁡17°42’$.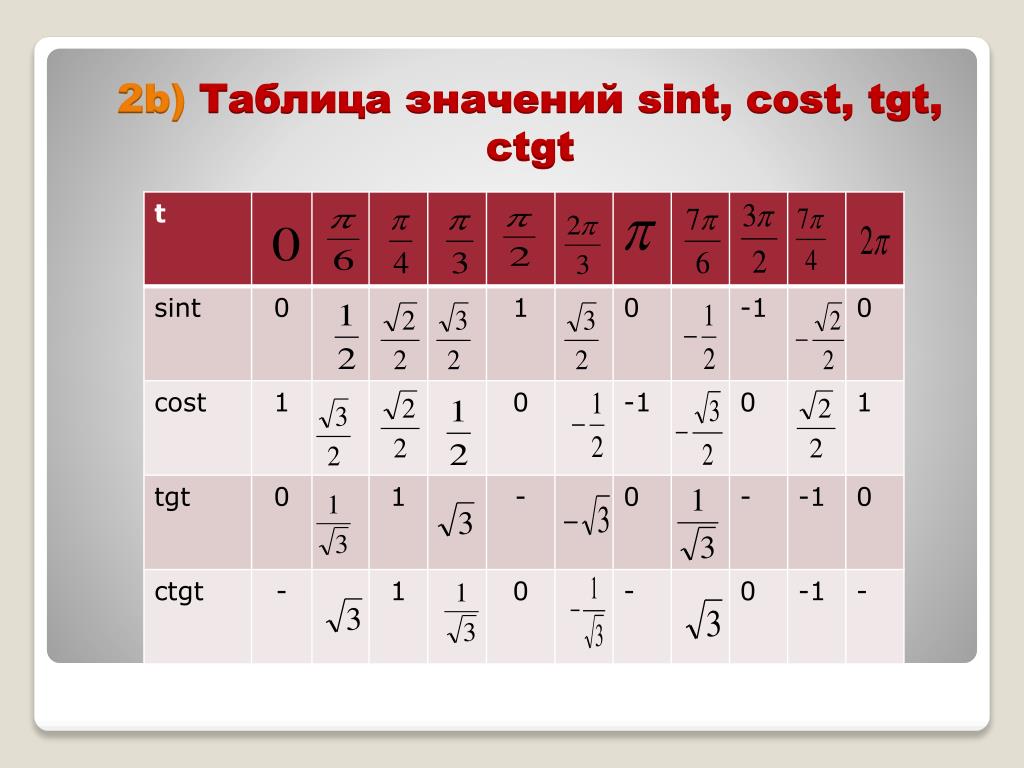 Для этого в столбце слева таблицы синусов и косинусов находим значение градусов – $17°$, а в верхней строке находим значение минут – $42’$. На их пересечении получаем искомое значение:

$\sin17°42’=0,304$.

Для нахождения значения $\sin17°44’$ нужно воспользоваться поправкой в правой части таблицы. В данном случае к значению $42’$, которое есть в таблице, нужно добавить поправку для $2’$, которая равна $0,0006$. Получим:

$\sin17°44’=0,304+0,0006=0,3046$.

Для нахождения значения $\sin17°47’$ также пользуемся поправкой в правой части таблицы, только в этом случае за основу берем значение $\sin17°48’$ и отнимаем поправку для $1’$:

$\sin17°47’=0,3057-0,0003=0,3054$.

При расчете косинусов выполняем аналогичные действия, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, $\cos20°=0,9397$.

Для значений тангенса до $90°$ и котангенса малого угла поправок нет. Например, найдем $\tan 78°37’$, который по таблице равен $4,967$.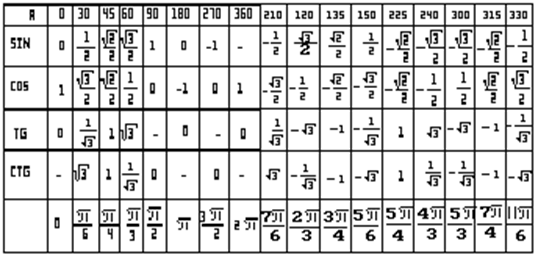

Найдем $\cot 2°13’=25,83$.

Таблицы значений pi(x) и pi2(x)

Введение

Некоторые из моих вычислительных проектов требуют вычисления функции для каждого простого числа. внутри заданного интервала. Для защиты от случайных вычислительных ошибок (обычно подсистема памяти), вычисления внутри каждого интервала должны выполняться не менее двух раз и должны отбрасывать, если результаты не совпадают. Гораздо менее надежным и менее дорогим вариантом является проверить, согласуется ли количество простых чисел внутри анализируемого интервала с независимым счет, полученный другими способами. Это количество простых чисел можно легко вычислить, если таблица значений функции счета простых чисел

pi(x) , который подсчитывает количество простых чисел не больше чем x , содержит записи для двух конечных точек интервала.

Когда p и p+2 являются простыми числами, говорят, что они образуют пару простых чисел-близнецов.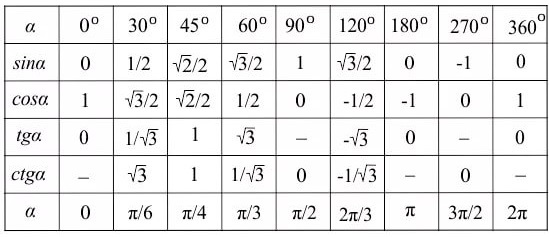 В в отличие от pi(x) , единственный известный способ подсчитать количество пар простых чисел-близнецов с p<=x , обозначаемый как pi2(x) , должен сгенерировать их все.

Потому что в свободном доступе обширные таблицы значений pi(x) и pi2(x) являются довольно редко (кроме моих собственных столов, Таблицы Томаса Р. Найсли являются единственным обширным известных мне), чтобы иметь возможность проверить свои вычисления, я составил таблицы, описанные ниже. Для pi(x) эти таблицы были сделаны частично с моей неэффективной реализацией Вариант Лагариаса-Миллера-Одлызко метода Мейселя-Лемера, описанный в [1] и частично с моей эффективной реализацией метода Делеглиза-Рива вариант того же метода, описанного в [2] и в [3]. Для 922) [1k, сжато с помощью gzip]
» Последнее обновление сделано 7 декабря 2008 г.

Предупреждение: Некоторые значения pi(x) были перепроверены путем запуска того же программу дважды, обычно на одной и той же машине, используя одни и те же внутренние параметры.

Таким образом, у них есть были перепроверены на случайные машинные ошибки, но не на алгоритмические или непротиворечивые машинные ошибки (например, печально известная аппаратная ошибка Pentium fdiv). Тем не менее, я на 99,99% уверены, что все результаты, представленные в этих таблицах, верны. Все перекрестные проверки (разные машины и/или разные внутренние параметры) выполненные до сих пор производили точно такие же полученные результаты.

Сравнение

pi(x) и li(x)

Теорема о простых числах утверждает, что pi(x) не сильно отличается от так называемого логарифмический интеграл li(x) , определенный

                     х дт
li(x) = P.V. ИНТЕГРАЛ    ------ .
                     0 лог(т)

Известно, что li(x)-pi(x) бесконечно часто меняет знак. Однако известно также что отрицательные значения li(x)-pi(x) встречаются крайне редко [4]. Пусть

         ли(х) - пи(х)
H(x) = 2 ------------- .
  ли (кв. (х))

Мы позволили себе заменить pi(sqrt(x)) его приближением li(sqrt(x)) в определение H(x) ; это было сделано только для упрощения его вычисления. Было показано в [5], чем H(x) можно довольно хорошо аппроксимировать с помощью

 грех (т журнал (х))
H(x,L) = 1 + 2 СУММ ------------- ,
 0 < т < L т
 913  нулей известны
лежат на критической линии, как показано в 2004 году Ксавьером Гурдоном. На следующем рисунке представлены
функция  H(x) , вычисленная с использованием данных в наших таблицах  pi(x)  (синяя кривая), а также
его аппроксимация с использованием только первых десяти и первых ста нулей
дзета-функция в верхней части критической линии (желтая кривая и белая кривая,
соответственно). Из рисунка видно, что аппроксимация достаточно хорошо отражает
"низкочастотное" поведение 912    
   
 указанные в этих таблицах до 1 марта 2008 года, были слишком малы (на единицу).
 Таблицы значений 
 pi(x) mod 2  Используя идеи [6], можно вычислить  pi(x) по модулю 2  быстро с помощью очень простой программы. Используя идеи раздела 2.1 этой статьи, возможно,
в сочетании со способом быстрого вычисления нескольких значений суммы Мёбиуса
функция [7], сделает программу еще быстрее. Представленные результаты
ниже были созданы нашей первоначальной простой реализацией, которая имеет вычислительную сложность
из 930  . Предполагая, что значения  t log(x)  равномерно распределены
по модулю  2pi  , где  t  по-прежнему мнимая часть нуля, можно
моделировать члены, не используемые в формуле, как случайную величину Гаусса с нулевым средним и
приблизительное стандартное отклонение, которое легко вычислить. К сожалению, это стандартное отклонение
медленно уменьшается с количеством используемых нулей, до такой степени, что в сто раз больше числа
нулей дает нам менее одной дополнительной цифры точности. Оценки в следующей таблице
следует сравнивать с точными значениями в таблицах, приведенных выше (разумеется, для значений 
  x , для которых известны точные значения).
 Оценка некоторых значений  pi(x)  [66 КБ, сжато с помощью gzip] 
 » Последнее обновление сделано 11 декабря 2012 г.
 Каталожные номера 
 [1]   Дж. К. Лагариас ,  В. С. Миллер  и  Андрей Одлызко  ,  Вычисление pi(x): метод Мейселя-Лемера  ,
Математика вычислений, том. 44, нет. 170, стр. 537-560, апрель 1985 г.
 [2]   М. Делегиз  и  Дж. Риват ,  Вычисление pi(x): метод Мейселя, Лемера, Лагариаса, Миллера, Одлызко   ,
Математика вычислений, том. 65, нет. 213, стр. 235-245, январь 1996 г.
 [3]   Томас Оливейра и Силва ,  Вычисление pi(x): комбинаторный метод  ,
Revista do DETUA, vol. 4, нет. 6, стр. 759–768, март 2006 г.
 [4]   Картер Бэйс  и  Ричард Х. Хадсон  ,  Новая граница для наименьшего x с pi(x)>li(x)  ,
Математика вычислений, том. 69, нет. 231, стр. 1285-1296, 2000.
 [5]   Картер Бэйс  и  Ричард Х. Хадсон  ,  Нули L-функций Дирихле и нерегулярности в распределении простых чисел  ,
Математика вычислений, том. 69, нет. 230, стр. 861-866, 2000.
 [6]   Теренс Тао  ,  Эрнест Крут III  и  Харальд Хельфготт  ,  Детерминированные методы нахождения простых чисел 
  ,
Mathematics of Computation, опубликовано в электронном виде 23 августа 2011 г.
 [7]   Марк Делегиз  и  Жоэль Рива  ,  Вычисление суммирования функции Мёбиуса  ,
Экспериментальная математика, Vol. 5, № 4, стр. 291-295, 1996.
 Дополнительные ссылки 
 Основные страницы.
 Распределенные вычисления  pi(x)  для больших значений  x  .
 Страница подтверждения моей гипотезы Гольдбаха.
 Моя главная страница пробелов.
 Страница с наименее примитивными корнями.
 Моя простая, но быстрая реализация сегментированного решета Эратосфена.
 Кратность числа Пи: определение и пример 
 Одним из лучших способов закрепить что-либо в памяти является повторение. Вот почему в школе детей заставляют снова и снова складывать, вычитать, умножать и делить. Они являются основой математики, и их нужно помнить вечно. Несмотря на то, что большинство людей не являются поклонниками математики, они все же могут выполнять сложения и умножения.
 В этой статье вы узнаете о  кратных пи  , нечетных и четных кратных пи, а затем приведете несколько примеров.
 Определение кратности числа Пи 
 Давайте, прежде всего, разберемся, что подразумевается под кратностью числа.
  кратное   число  — это произведение, полученное при умножении этого числа на целое число. Можно сказать, что это таблица умножения этого числа.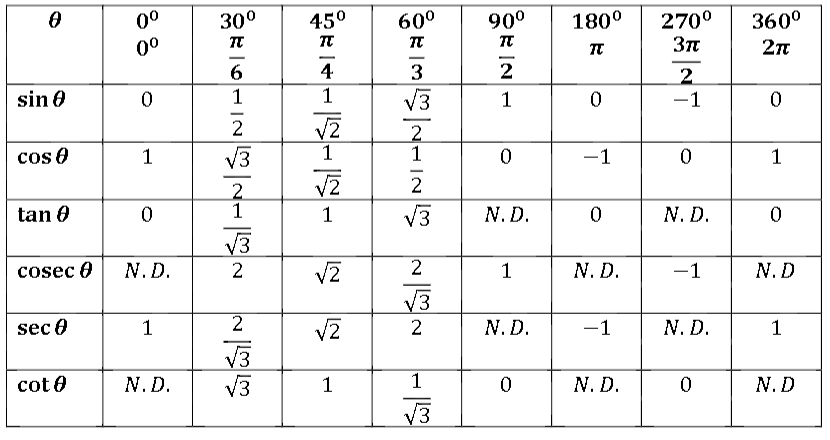
 Давайте рассмотрим пример кратных чисел.
 Некоторые числа, кратные \( 2 \), равны \( 2 \), \( 4 \), \( 6 \), \( 8 \) и так далее. Они получаются путем умножения \( 2 \) на положительные целые числа.
 Теперь посмотрим, что такое число пи.
  Пи  — математическая константа. Это отношение длины окружности к ее диаметру.
 Отношение длины окружности к ее диаметру
 Число Пи. Аппроксимированное  числовое значение  для пи равно \( 3,14159265359\). Число больше, чем это, но часто приближается к \( 3.142 \) . Следовательно, нахождение кратных числу пи выполняется так же, как нахождение кратных любого числа.
 Символ числа пи — \( \pi \).
 \( \pi \) было приближено к более чем 31,4 триллионам знаков после запятой.
 Из приведенного выше определения кратности числа и пи мы теперь знаем, что означают кратности числа пи.
  Кратные числа пи  — это произведение, полученное при умножении числа пи на целое число.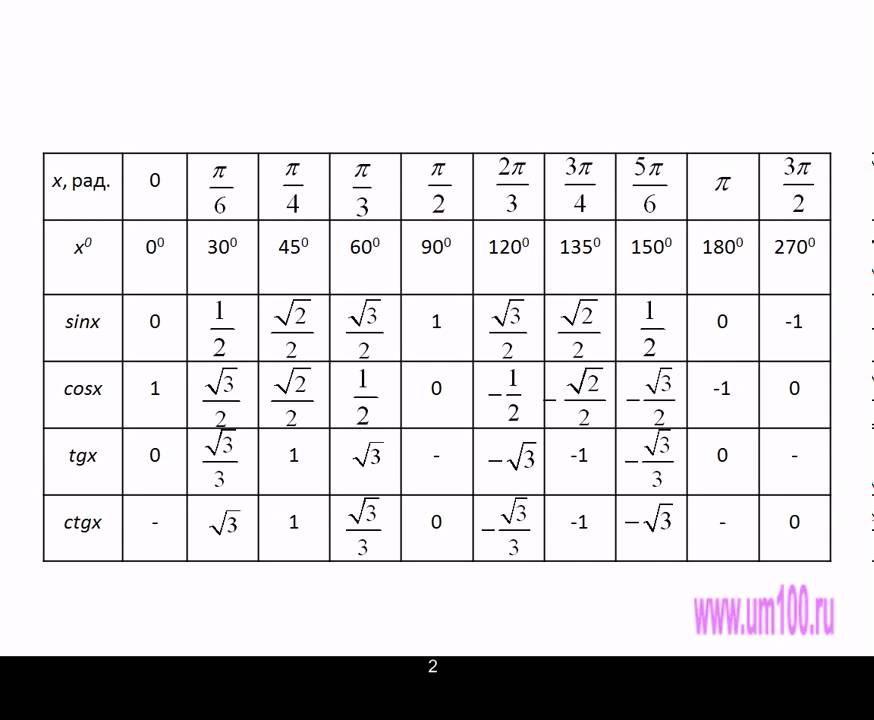
 Нечетные числа числа Пи 
 Давайте посмотрим, что произойдет, если \( \pi \) умножить на нечетное число.
  нечетных кратных  числа \( \pi \) — это все множители числа pi, полученные путем умножения \( \pi \) на нечетные числа.
 Нечетные числа — это числа, которые не делятся на 2. Примеры: \( 1 \), \( 3 \), \( 5 \), \( 7 \), \( 9 \) .....
 Из приведенного выше определения видно, что для нахождения нечетных кратных \( \pi \) вам придется умножить на нечетное число. При этом может не быть необходимости умножать числовое значение \(\pi \). Вы можете просто использовать символ и обращаться с ним как с алгеброй. См. пример ниже.
 Некоторые нечетные числа, кратные \(\pi \):
 \[ \begin{align} \pi \cdot 1 &= \pi, \\ \pi \cdot 3 &= 3\pi , \\ \pi \cdot 5 &= 5\pi , \\ \dots \end{align} \]
 и этот список можно продолжить!
 Вы видите, что нечетные кратные получаются путем умножения \(\pi \) на нечетные числа.
 Четное число Пи 
 Как насчет умножения \( \pi \) на четное число?
  четных кратных  числа \( \pi \) — это все числа, кратные \( \pi \), полученные путем умножения \( \pi \) на четные числа.
 Четные числа — это числа, которые делятся на два. Их можно разделить на две равные пары или части. Примеры: \( 2 \), \( 4 \), \( 6 \), \( 8 \), \( 10 \) ......
 Из вышеприведенных определений мы видим, что для нахождения даже кратные \( \pi \), вам придется умножать на четное число. При этом может не понадобиться использовать числовую аппроксимацию \(\pi \). Вы можете просто использовать символ и обращаться с ним как с алгеброй. Взгляните на пример ниже.
 Некоторые четные кратные \(\pi \) равны
 \[ \begin{align} \pi \cdot 2 &= 2\pi , \\ \pi \cdot 4 &= 4\pi , \\ \pi \ cdot 6 &= 6\pi ,\\ \dots \end{align}\]
 Вы можете видеть, что четные числа получаются путем умножения \(\pi \) на четные числа.
 Число Пи, кратное десятичным числам 
 Иногда при умножении на \( \pi \) требуется приблизительное значение, а не точное. Здесь вы собираетесь использовать числовое значение \(\pi \), чтобы найти его кратные. Приблизительное значение \( \pi \) само по себе является десятичным числом, поэтому нахождение его кратных таким образом приведет к десятичному числу.
 Вы также можете найти нечетные или четные кратные \( \pi \) в десятичном виде. Все, что вам нужно сделать, это определить кратные, которые являются нечетными или четными. В приведенном ниже примере показано, как получить число, кратное \(\pi \).
 Некоторые десятичные кратные приближения \(\pi \) равны
 \[ \begin{array}{lll} \pi \cdot 1 & \ приблизительно 3,142 \cdot 1 &= 3,142 , \\ \pi \cdot 2 & \приблизительно 3,142 \cdot 2 &= 6,284, \\ \pi \cdot 3 & \приблизительно 3,142 \cdot 3 & = 9,426 .\end{массив} \]
 Кратные числа Пи/4 
 Пи/4, часто пишется как \( \frac{\pi}{4}\), является дробью, и можно найти кратные дроби. Все, что вам нужно сделать, это умножить на целые числа.
 Давайте посмотрим на первые пять кратных \(\frac{\pi}{4} \).
 Первые пять кратных \( \frac{\pi}{4} \):
 \[ \begin{align} \frac{\pi}{4} \cdot 1 &= \frac{\pi {4} , \\ \frac{\pi}{4} \cdot 2 &= \frac{\pi}{2} , \\ \frac{\pi}{4} \cdot 3 &= \frac{ 3\pi}{4} , \\ \frac{\pi}{4} \cdot 5 &= \frac{5\pi}{4}. \end{выравнивание} \]
 Вы также можете найти кратные \(\frac{\pi}{2} \), \(\frac{pi}{3} \), \(\frac{\pi}{6} \) и любые другую дробь через \( \pi \) точно так же, как в приведенном выше примере.
 Примеры, кратные числу пи 
 Давайте рассмотрим несколько примеров кратных \( \pi \).
 Каковы первые пять кратных \( \pi \)?
 
  Раствор. 
 Чтобы получить первые пять кратных \( \pi \), мы умножим \( \pi \) на целые числа \( 1 \), \( 2 \), \( 3 \), \( 4 \) и \( 5 \).
 \[ \begin{align} \pi \cdot 1 & = \pi \\\pi \cdot 2 & = 2\pi \\\pi \cdot 3 & = 3\pi \\\pi \cdot 4 & = 4\pi \\\pi \cdot 5 & = 5\pi \\ \end{align} \]
 Следовательно, первые пять кратных равны \(\pi \), \(2\pi \), \ (3\пи \), \(4\пи \) и \(5\пи \). Обратите внимание, что первые пять кратных \( \pi \) включают как четные, так и нечетные кратные.
 Возьмем другой пример.
 Каковы первые три нечетных кратных \( \pi \)?
  Раствор. 
 Чтобы получить первые три нечетных кратных \( \pi \), вы умножаете \( \pi \) на \( 1 \), \( 3 \) и \( 5 \), которые являются нечетными числами.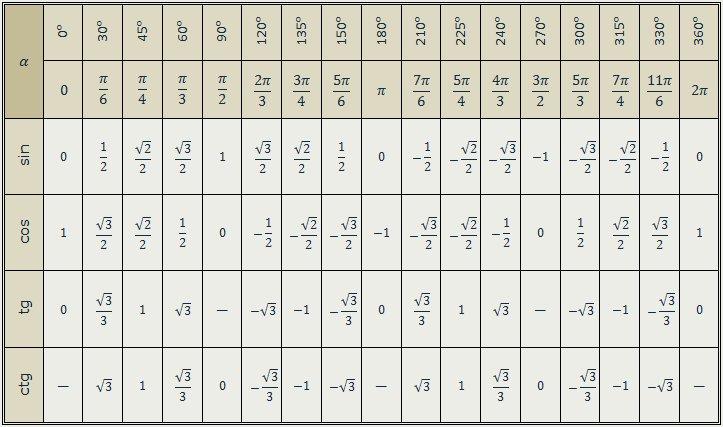
 \[ \begin{align} \pi \cdot 1 & = \pi \\ \pi \cdot 3 & = 3\pi \\ \pi \cdot 5 & = 5\pi \\ \end{align} \ ]
 Таким образом, первые три нечетных числа равны \(\pi \), \(3\pi \) и \(5\pi \).
 Давайте посмотрим на другой пример.
 Перечислите некоторые числа, кратные \( \pi \) в десятичных дробях.
  Раствор. 
 Чтобы получить некоторые кратные \( \pi \) в десятичных дробях, вам нужно будет умножить числовое значение \( \pi \), которое примерно равно \( 3,142 \).
 \[ \begin{align} \pi \cdot 1 & \приблизительно 3,142 \\ \pi \cdot 2 & \приблизительно 6,284 \\ \pi \cdot 3 & \приблизительно 9,426 \\ \pi \cdot 4 & \приблизительно 12,568 \\ \pi \cdot 5 & \ приблизительно 15,71 \\ \pi \cdot 6 & \ приблизительно 18,852 \\ \end{align} \]
 Следовательно, некоторые кратные \( \pi \) в десятичных дробях : \( 3,142 \), \( 6,284 \), \( 9.426 \), \( 15,71 \) и \( 18,852 \) \(\dots \) 
 Давайте возьмем пример на четных кратных \(\pi \).
 Выведите первые четыре четных кратных \( \frac{pi}{4} \).
  Раствор. 
 Чтобы найти четные числа, кратные \( \frac{pi}{4} \), нам придется умножить на \( 2 \), \( 4 \), \( 6 \) и \( 8 \ ), которые являются четными числами.
 \[ \begin{align} \frac{\pi}{4} \cdot 2 & = \frac{\pi}{2} \\ \frac{\pi}{4} \cdot 4 & = \pi \\ \frac{\pi}{4} \cdot 6 & = \frac{3\pi}{2} \\ \frac{\pi}{4} \cdot 8 &= 2\pi \\ \end{ выровнять} \]
 Таким образом, первые \( 4 \) четные кратные: \( \frac{\pi}{2} \), \( \pi \), \( \frac{3\pi}{2} \) и \( 2\пи \).
 Давайте посмотрим еще один пример.
 Перечислите некоторые числа, кратные \( \frac{\pi}{2} \).
  Раствор. 
 Некоторые кратные \( \frac{\pi}{2} \):
 \[ \begin{align} \frac{\pi}{2} \cdot 1 &= \frac{\ pi}{2} \\ \frac{\pi}{2} \cdot 2 &= \pi \\ \frac{\pi}{2} \cdot 3 &= \frac{3\pi}{2} \ \ \frac{\pi}{2} \cdot 4 &= 2\pi \\ \frac{\pi}{2} \cdot 5 &= \frac{5\pi}{2} \\ \frac{\ pi}{2} \cdot 6 &= 3\pi \\ \frac{\pi}{2} \cdot 7 &= \frac{7\pi}{2} \\ \end{align} \]
 Таким образом, некоторые кратные \( \frac{\pi}{2} \): \( \frac{\pi}{2} \), \( \pi \), \( \frac{ 3\pi}{2} \), \( 2\pi \), \( \frac{5\pi}{2} \), \( 3\pi \), \( \frac{7\pi} {2}\) .
No related posts.