Функция косинус ее свойства и график: Свойства функции y = cosx и её график — урок. Алгебра, 11 класс.

Содержание

График функции y sin 1. Синус (sin x) и косинус (cos x) – свойства, графики, формулы

На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.

Тема: Тригонометрические функции

Урок: Функция y=sinx, её основные свойства и график

При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.

Определим закон соответствия для .

Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).

Каждому значению аргумента ставится в соответствие единственное значение функции.

Из определения синуса вытекают очевидные свойства.

На рисунке видно, что т.к. это ордината точки единичной окружности.

Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.

Например, угол на единичной окружности соответствует точке на графике (рис. 2)

Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).

Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.

Рассмотрим свойства функции :

1) Область определения:

2) Область значений:

3) Функция нечетная:

4) Наименьший положительный период:

5) Координаты точек пересечения графика с осью абсцисс:

6) Координаты точки пересечения графика с осью ординат:

7) Промежутки, на которых функция принимает положительные значения:

8) Промежутки, на которых функция принимает отрицательные значения:

9) Промежутки возрастания:

10) Промежутки убывания:

11) Точки минимума:

12) Минимум функции:

13) Точки максимума:

14) Максимум функции:

Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.

А. Г. Мордковича. -М.: Мнемозина, 2007.

№№ 16.4, 16.5, 16.8.

Дополнительные веб-ресурсы

3. Образовательный портал для подготовки к экзаменам ().

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.

Леонардо да Винчи

Используемые технологии: проблемного обучения, критического мышления, коммуникативного общения.

Цели:

Развитие познавательного интереса к обучению.
Изучение свойств функции у = sin x.
Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.

Задачи:

1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.

2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.

Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.

Воспитывать у учащихся познавательную активность, чувство ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; культуру общения.

Ход урока

1 этап. Актуализация опорных знаний, мотивация изучения нового материала

«Вход в урок».

На доске написаны 3 утверждения:

Тригонометрическое уравнение sin t = a всегда имеет решения.
График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
График тригонометрической функции можно построить, используя одну главную полуволну.

Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».

Учитель ставит цели и задачи урока.

2. Актуализация знаний (фронтально на модели тригонометрического круга ).

Мы уже познакомились с функцией s = sin t.

1) Какие значения может принимать переменная t. Какова область определения этой функции?

2) В каком промежутке заключены значения выражения sin t.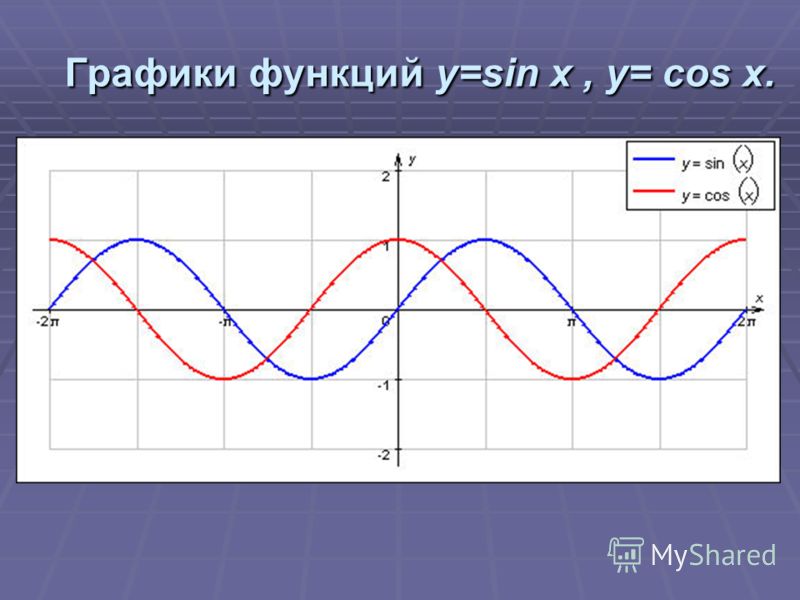 Найти наибольшее и наименьшее значения функции s = sin t.

3) Решите уравнение sin t = 0.

4) Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция s = sin t возрастает на отрезке и убывает на отрезке ).

5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.

х	0
у	0			1			0

2 этап.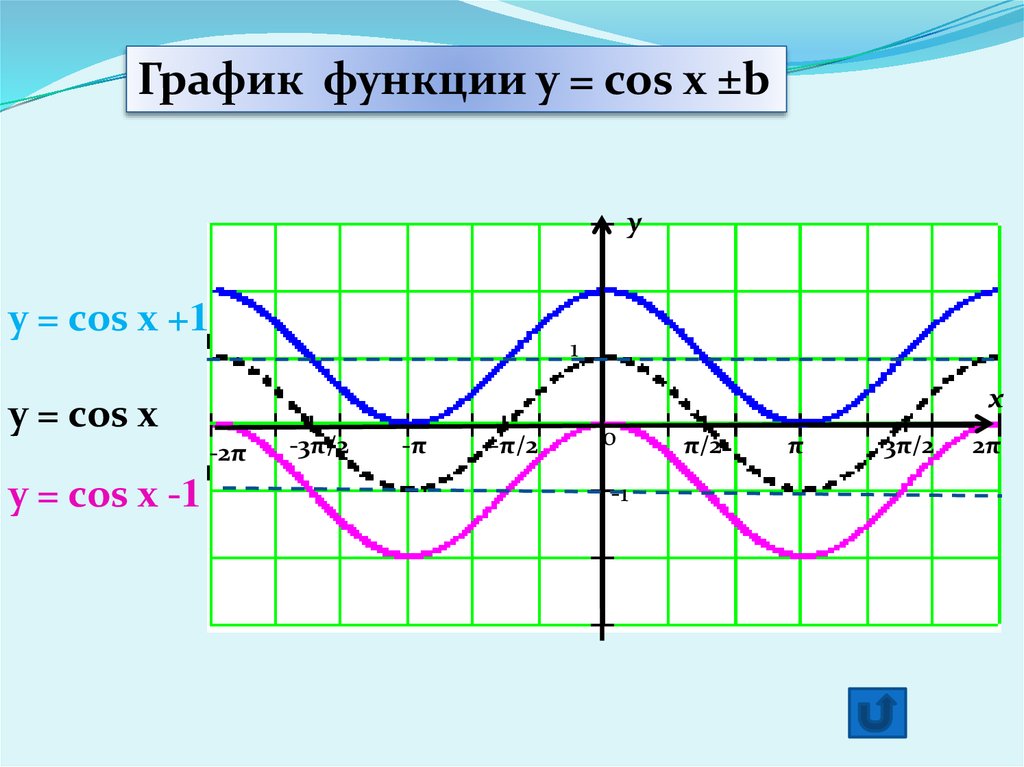 Восприятие, осмысление, первичное закрепление, непроизвольное запоминание

4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях

6. № 10.18 (б,в)

5 этап. Итоговый контроль, коррекция, оценка и самооценка

7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».

8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)

Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Геометрическое определение синуса и косинуса

|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.

Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус — нечетная. Функция косинус — четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	— ∞	— ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

{ -∞

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Презентация «Функция y=cosx, ее свойства и график». Презентация «Функция y=sinx, ее свойства и график» Презентация построение графика косинуса

Графики и свойства тригонометрических функций синуса и косинуса График функции y = sinx График функции y = sinx Свойства функции y = sinx Свойства функции y = sinx График функции y = cosx График функции y = cosx Свойства функции y = cosx Свойства функции y = cosx Сравнение свойств функций y = sinx и y = cosx Сравнение свойств функций y = sinx и y = cosx

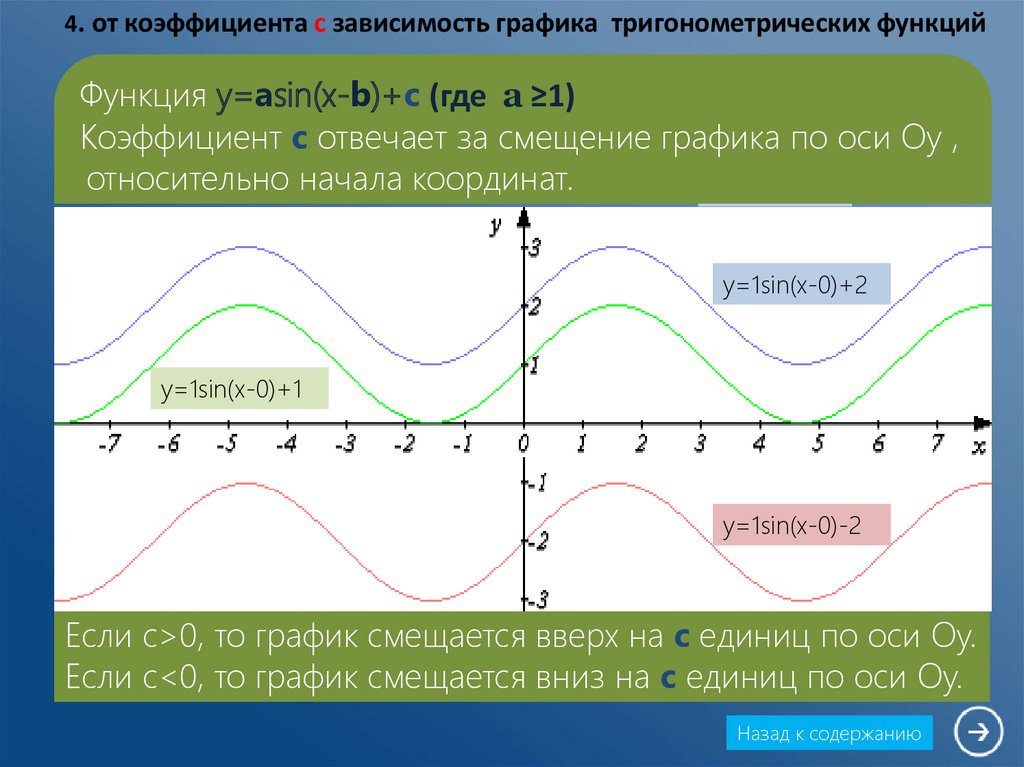
Свойства функции y = sinx 6.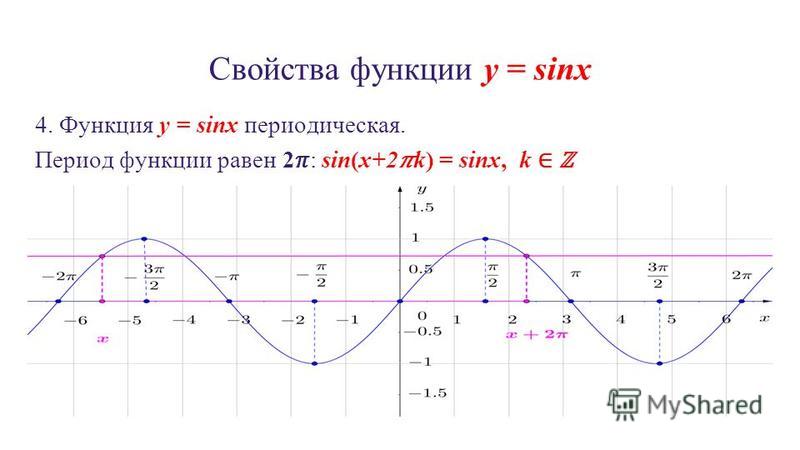 Промежутки знакопостоянства функции y = sinx: sinx > 0 при x (2k; +2k), sinx 0 при x (2k; +2k), sinx 0 при x (2k; +2k), sinx 0 при x (2k; +2k), sinx 0 при x (2k; +2k), sinx title=»Свойства функции y = sinx 6. Промежутки знакопостоянства функции y = sinx: sinx > 0 при x (2k; +2k), sinx

Свойства функции y = cosx 6. Промежутки знакопостоянства функции y = cosx: cosx > 0 при x (-/2+k;/2+k), k cosx 0 при x (-/2+k;/2+k), k cosx 0 при x (-/2+k;/2+k), k cosx 0 при x (-/2+k;/2+k), k cosx 0 при x (-/2+k;/2+k), k cosx title=»Свойства функции y = cosx 6. Промежутки знакопостоянства функции y = cosx: cosx > 0 при x (-/2+k;/2+k), k cosx

Сравнение свойств функций y = sinx и y = cosx Функцияy = sinxy = cosx Область определения D(sinx) = D(cosx) = Множество значенийE(sinx) = [-1,1]E(cosx) = [-1,1] Четность и нечетность нечетная четная Нули функции x = k, k x = /2+k, k Промежутки знакопостоянства y(x)>0 x (2k; +2k)x (- /2+k; /2+k) k y(x) 0 x (2k; +2k)x (- /2+k; /2+k) k y(x)

Раздел в математике тригонометрия включает в себя изучение таких понятий, как синус, косинус, тангенс и котангенс.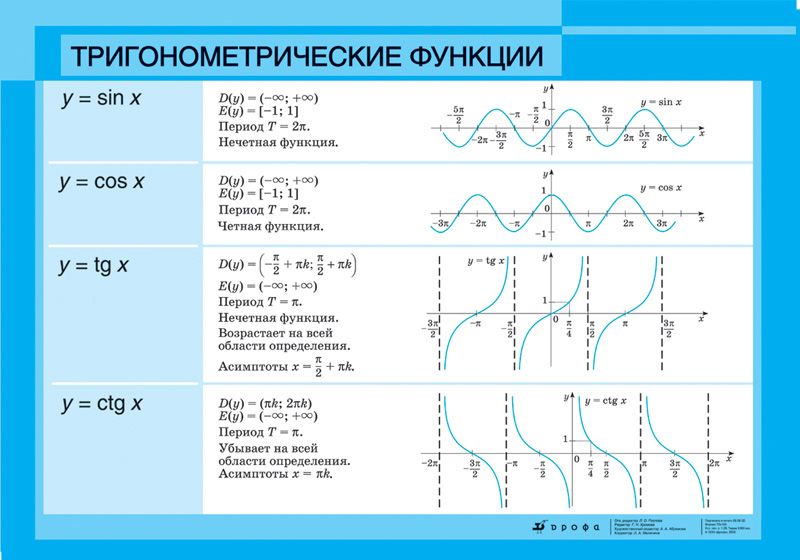 В отдельности школьникам необходимо будет рассмотреть каждую функцию, изучить характер поведения на графике, рассмотреть периодичность, область определения, область значений и другие параметры.

Итак, функция синуса. На первом слайде выводится общий вид функции. В качестве аргумента используется переменная t.

Первым делом, как и при каждой функции, рассматривается область определения, которая указывает на то, какие значения может принимать аргумент. В случае синуса — это вся числовая ось. Увидеть это можно впоследствии на графике функции.

Второе свойство, которое рассматривается на примере синуса — это четность. Синусоид является нечетной. Это объясняется тем, что функция от -х будет равняться функции со знаком минус. Для того чтобы вспомнить данный материал, можно вернуться в предыдущие презентации и просмотреть.

Демонстрируется данное свойство на единичной окружности, которая появляется в левой стороне слайда. Таким образом, свойство доказывается и геометрически.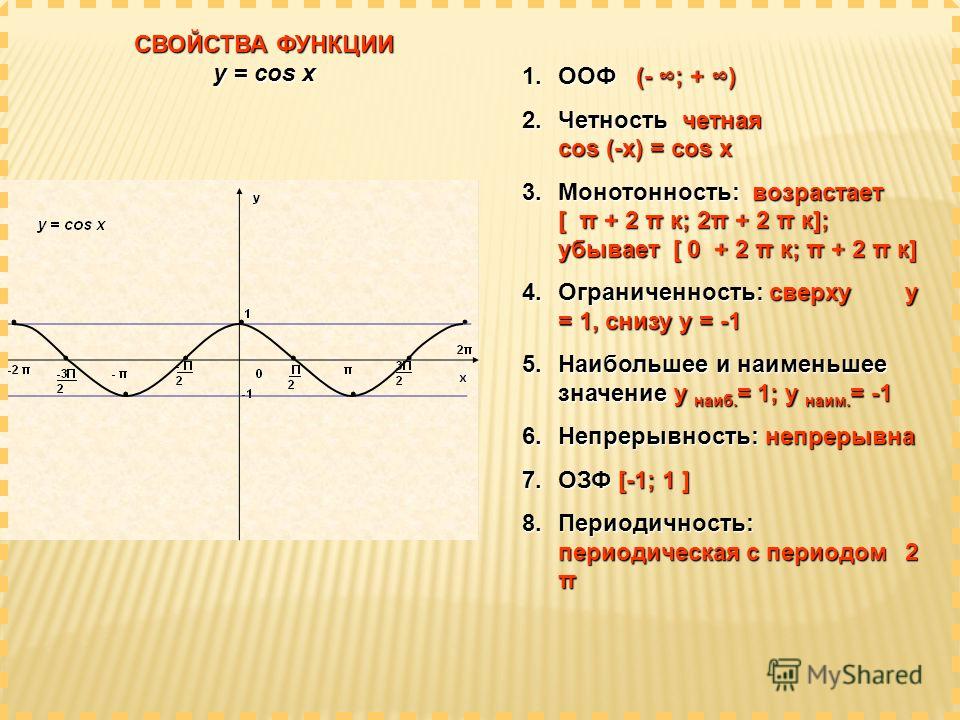

Третье свойство, которое необходимо также рассмотреть — это свойство монотонности. На некоторых отрезках функция возрастает, на некоторых — убывает. Это дает нам возможность назвать синусоиду монотонной функцией. Так как интервалов возрастания и убывания бесконечное число, отмечается это периодичностью.

Четвертое свойство — ограниченность. Синусоида является ограниченной и сверху, и снизу. Минимальное значение, при этом, — 1, максимальное +1. Таким образом, функция синуса ограниченная и сверху, и снизу.

Дается определение синусоиды, которые необходимо заполнить. Далее рассматриваются различные деформации синусоиды при разных значениях.

После того, как даны определение, продолжается рассматривание свойств функции синуса. Она является непрерывной. Это наглядно видно на графике функции. Никаких точек разрыва не существует.

Последний слайд показывает, как графическим образом можно решить уравнение, в котором содержится функция синуса. Такой способ упростит решение и сделает его более наглядным.

«Функция y=cos x» — Нули функции, положительные и отрицательные значения. Найдем несколько точек для построения графика. Y = cos (x – a). Преобразование графика функции y = cos x. Функция y = cos x. Y = cos x + A (свойства). Свойства. Симметричное отражение относительно оси абсцисс. График функции. Четность, нечетность.

«Свойства обратных тригонометрических функций» — Укажите область значений функции. Решить уравнения. Найдите значение выражения. Решение уравнений. Работа в группах. Элективный курс по математике. Аркфункции. Решим систему уравнений. Исследовательская работа. Укажите область определения функции. Повторение. Тройка удовлетворяет исходному уравнению.

«Функции тангенса и котангенса» — Свойства функции у=tgx. Решения. Корни уравнения. График. Построение графика. Свойства функций. Значение. Дробь. Основные свойства функции. Функция y = tgx. Основные свойства. у=ctgx. График функции у=ctgx. Числа.

«Преобразование тригонометрических графиков» — Функция синус. Преобразование графиков тригонометрических функций. Характеристика графика гармонического колебания. График функции y=f(x)+m. Функция косинус. График функции y=f(|x|). График функции y=|f(x)|. Характеристика преобразований графиков функций. Y=f(x). Функция тангенс. Участки полученного графика.

«Аркфункции» — Функционально-графический метод решения уравнений. Arctgx. Функция. Тригонометрические функции. Свойства аркфункций. У = arcctgх. Arcctg t = a. Arccosx. Графический метод решения уравнений. Область значений. Равенство. Определения. Выражение. Определение. Arctg t. Arccos t. Множество действительных чисел.

«Алгебра «Тригонометрические функции»» — Тригонометрические функции углового аргумента. Таблица значений тригонометрических функций некоторых углов. Справочник по алгебре и началам анализа. Решение тригонометрических неравенств. Решение тригонометрических уравнений. Преобразование сумм тригонометрических функций в произведения. Тригонометрия.

«Аркфункции» — Arctg t.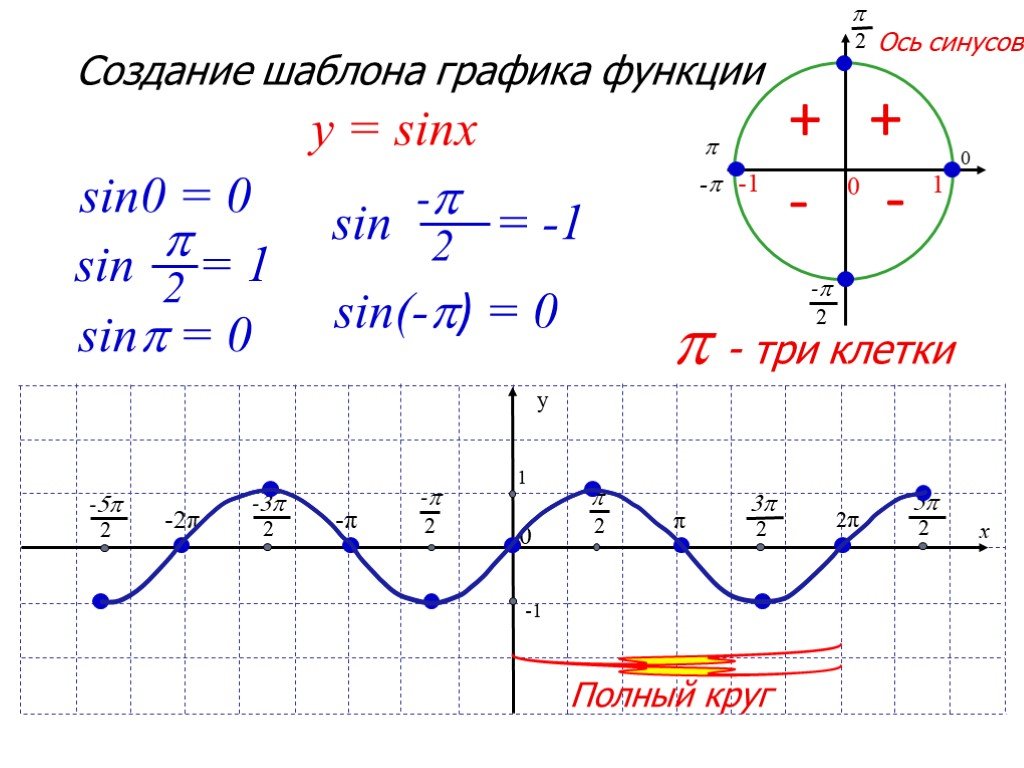 Определения. Область определения функции. Arcctg t = a. Функция. У = arcctgх. Arccosx. Множество действительных чисел. Функционально-графический метод решения уравнений. Найдите значения выражений. Равенство. Тригонометрические функции. Область определения. Свойства аркфункций. Определение.

«Алгебра «Тригонометрические функции»» — Решение однородных тригонометрических уравнений. Решение тригонометрических неравенств. Тригонометрия. Тангенс и котангенс. Решение простейших тригонометрических уравнений. Арксинус. Содержание. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Решение уравнений и неравенств.

«Функции тангенса и котангенса» — Свойства функций. Построение графика. Функция y = tgx. Числа. Значение. Корни уравнения. График функции у=ctgx. Дробь. Решения. График. Свойства функции у=tgx. Основные свойства функции. у=ctgx. Основные свойства.

«Преобразование тригонометрических графиков» — Y=f(x). График функции y=f(|x|). Параллельный перенос. График функции y=|f(|x|)|. Растяжение. Преобразование графиков тригонометрических функций. График функции y=f(x). Функция косинус. Функция синус. Характеристика преобразований графиков функций. График функции y=|f(x)|. Функция котангенс. Функция тангенс.

«Свойства обратных тригонометрических функций» — Решить уравнения. Исходное уравнение. Найдите значение выражения. Решение. Исследовательская работа. Работа в группах. Тройка удовлетворяет исходному уравнению. Решим систему уравнений. Решение уравнений. Укажите область значений функции. Вычислить. Аркфункции. Обратные тригонометрические функции. Элективный курс по математике.

«Функция y=cos x» — Y = | cos x |. Область определения. Y = — cos x (свойства). График функции. Y = cos (x – a) (свойства). Y = cos | x |. Множество значений. Как найти область определения. Y = cos x + A. Распространим полученный график на всей числовой прямой. Периодичность. Y = k · cos x (свойства). Найдем несколько точек для построения графика.

Всего в теме 18 презентаций

Одним из важных терминов в тригонометрии является косинус. В этой презентации будет рассматриваться функция косинуса, построен ее график. Подробно будут приводиться все свойства, которыми она обладает.

На первом слайде, прежде чем начать рассмотрение непосредственно функции, напоминается одна из формул приведения. Ранее она была подробно продемонстрирована вместе с доказательством.

Данная формула говорит о том, что функцию косину можно заменить синусом при определенных внесениях изменения в аргументе. Таким образом, уже изучив синусоиды, школьники смогу построить данную функцию. В результате они получат график функции косинуса.

График функции можно увидеть на втором слайде. Можно обратить внимание, что синусоида лишь сместилась на Пи/2. Таким образом, в отличие от синусоиды, график функции косинуса не проходит через точку (0;0).

Первым делом стоило бы рассмотреть область определения функции. Это важный момент и с этого начинается анализ любой функции в математике.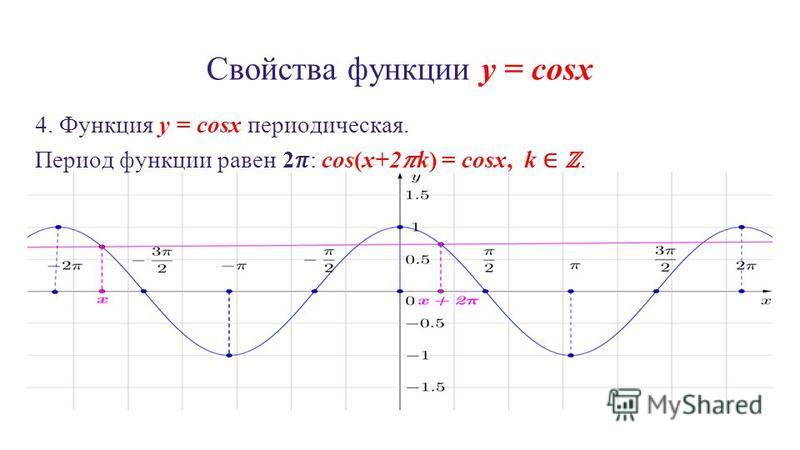 Областью определения данной функции является вся числовая ось. Это отчетливо видно на графике функции.

В отличие от синуса, функция косинуса является четной. То есть, если изменить знак аргумента, знак функции не изменится. Четность же обуславливается свойством синуса.

На определенных интервалах функция возрастает, на определенных — убывает. Это говорит о том, что функция косинуса является монотонной. Данные интервалы показаны на следующем слайде. На графике наглядно можно увидеть возрастание и убывание функции.

Пятое свойство — это ограниченность. Функция косинуса имеет ограниченность и сверху, и снизу. Минимальным значением является -1, а максимальным -+1.

Так как нет точек разрыва и острых пиков — функция косинуса, как и функция синуса, является непрерывной.

На последнем слайде демонстрируется обобщенно все свойства, которые были рассмотрены в презентации. Это ряд основных характеристик, которыми обладает функция косинуса. Запомнив их, можно с легкостью справиться с рядом уравнений, которые содержат косинус. Проще всего будет освоить данные свойства в случае полнейшего понимания сути.

СВОЙСТВА ФУНКЦИЙ СИНУС И КОСИНУС — 386 слов

Удовлетворительные эссе

386 слов
3 страницы

Открыть документ

386 слов

Грамматика

Плагиат

Письмо

Оценка

СВОЙСТВА ФУНКЦИЙ СИНУС И КОСИНУС

СВОЙСТВА ФУНКЦИЙ СИНУС И КОСИНУС:

1. Функции синуса и косинуса являются периодическими с периодом 2π.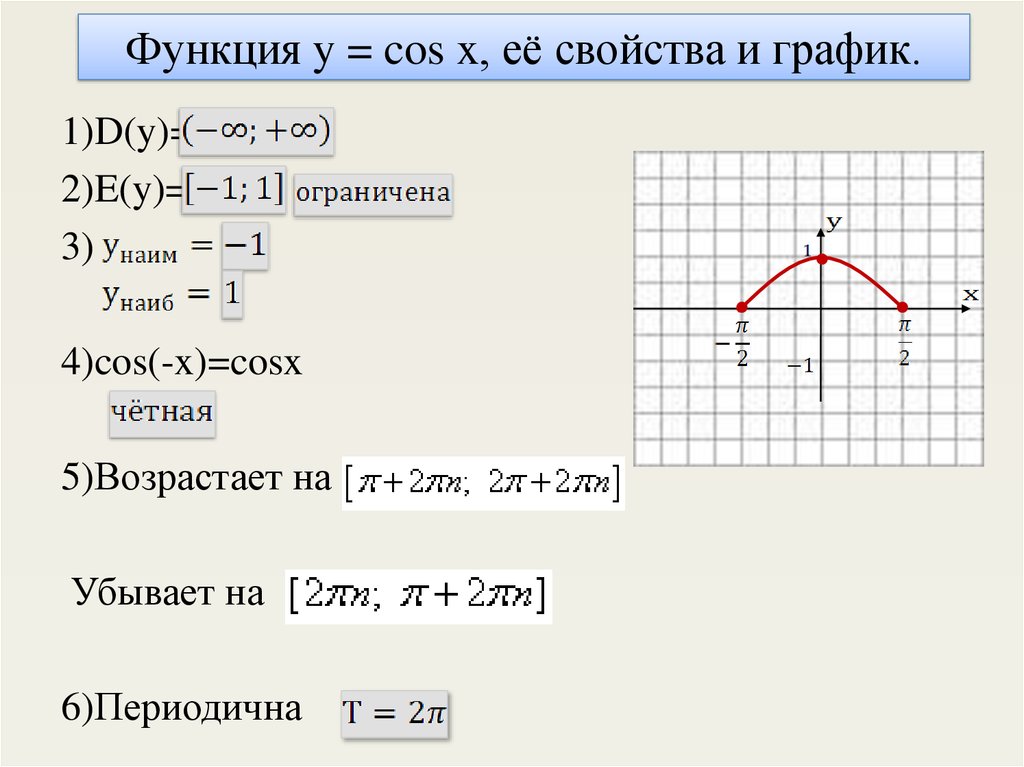
2. Функция синуса является нечетной функцией, поскольку ее график симметричен относительно начала координат, а функция косинуса является четной функцией, поскольку ее график симметричен относительно оси y.
3. Синусоидальные функции:
a. Возрастание в интервалах [0, π/2] и [3π/2, 2π]; и
б. Убывающий в интервале [π/2, 3π/2], за период 2 π.
4. Функция косинуса:
a. Возрастание в интервале [π, 2π]; и
б. Убывающий в интервале [0, π] за период 2π.
5. Функции синуса и косинуса являются непрерывными функциями.
6. Областью определения функций синуса и косинуса является множество всех действительных чисел от -1 до 1
7. Амплитуда функций синуса и косинуса равна 1, так как половина суммы нижней границы равна 1, то есть ½[|1|]+[|-1|]=2/2 или 1.
8. Максимальное и минимальное значения функций синуса и косинуса равны 1 и -1 соответственно, которые попеременно встречаются посередине между точки, где функция равна нулю.

Синусная функция косинусная функция

Квадрат

AS изменяется
значений SIN S

от 1 до 0
от 0 до (-1)

III
От круга до 3-х участков/2
от 0 до (-1)
(-1) до 0

IV
от 3-х участков/2 до 2-х участков
(-1) до 0
от 0 до 1

Заметив квадрант, в котором находится конечная точка P(S), вы можете определить алгебраический знак функций синуса и косинуса в различных квадрантах, как показано в таблице ниже.

Quadrant

SIN S
COS S
I

+
+
II

+
—
III

—
—
IV

—
+

. 0 КВАДРАТ II – 2 КВАДРАТ II – π

Продолжить чтение

Вы также можете найти эти документы полезными

Удовлетворительные эссе
Проверка перед расчетом 3
- 240 слов
- 4 страницы
Проверка перед расчетом 3
Для задач 14 – 16 определите экстремумы для каждой функции. Классифицируйте каждое как относительное (локальное) или абсолютное (глобальное) максимальное или минимальное значение.…
- 240 слов
- 4 страницы
Удовлетворительные эссе
Подробнее
Удовлетворительные эссе
Акт 1 Сцена 1 Домашнее задание
- 606 слов
- 3 страницы
Акт 1 Сцена 1 Домашнее задание
4) Опять же, если бы мы начали, когда секундная стрелка была на 3, была бы амплитуда по-прежнему равна…
- 606 слов
- 3 страницы
Удовлетворительные эссе
Подробнее
Хорошие эссе
Подразделение 2 Лаборатория горных материалов 2 3 Идентификация магматических пород
- 761 слов
- 4 страницы
Подразделение 2 Лаборатория горных материалов 2 3 Идентификация магматических пород
Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2[pic], а тангенс и котангенс имеют период[pic].…
- 761 слов
- 4 страницы
Хорошие эссе
Подробнее
Хорошие эссе
выпускной экзамен по алгебре
- 555 слов
- 6 страниц
выпускной экзамен по алгебре
б. При каких значениях for встречаются максимальное(ые) значение(я), минимальное(ые) значение(я) и нули?…
- 555 слов
- 6 страниц
Хорошие эссе
Подробнее
Удовлетворительные эссе
МАТЕМАТИКА 209 Неделя 1 Индивидуальная
- 627 слов
- 4 страницы
МАТЕМАТИКА 209 Неделя 1 Индивидуальная
2. Найдите область определения функции и запишите ответ в интервальной записи. Объясните словами или покажите расчеты.…
- 627 слов
- 4 страницы
Удовлетворительные эссе
Подробнее
Удовлетворительные эссе
БЛОК ОДИН ВИКТОРИНА ПО МАТЕМАТИКЕ 110
- 1699 слов
- 12 страниц
БЛОК ОДИН ВИКТОРИНА ПО МАТЕМАТИКЕ 110
Обратная связь: Правильно! Если точка находится на отрицательной оси x, первая координата отрицательна, а вторая координата равна нулю.…
- 1699 слов
- 12 страниц
Удовлетворительные эссе
Подробнее
Удовлетворительные эссе
Композиция и инверсия
- 486 слов
- 2 страницы
Композиция и инверсия
Далее мы должны сравнить две пары функций друг с другом. Сначала потренируемся.…
- 486 слов
- 2 страницы
Удовлетворительные эссе
Подробнее
Удовлетворительные эссе
6.02 Алгебра 2
- 253 слова
- 2 страницы
6.02 Алгебра 2
Нарисуйте график функции f(x) = –x4 – 4 вручную и опишите конечное поведение. (1 балл)…
- 253 слова
- 2 страницы
Удовлетворительные эссе
Подробнее
Хорошие эссе
Учебное пособие Pt1420 Unit 6
- 864 Слова
- 4 страницы
Учебное пособие Pt1420 Unit 6
3. |Показывается график и дается c-значение. Для этой задачи используйте график, чтобы найти .|…
- 864 Слова
- 4 страницы
Хорошие эссе
Подробнее
Удовлетворительные эссе
Учебное задание: общая функция
- 572 слова
- 3 страницы
Учебное задание: общая функция
Используйте общий график f(x) с областью определения [–6, –3] и [–2, 6], чтобы ответить на приведенные ниже вопросы.…
- 572 слова
- 3 страницы
Удовлетворительные эссе
Подробнее
Хорошие эссе
MAT 126 Тест, неделя 3
- 678 слов
- 4 страницы
MAT 126 Тест, неделя 3
Найдите домен и диапазон отношения и укажите, является ли отношение функцией. {(7, 2), (8, 2), (9, 2), (10, 2)}…
- 678 слов
- 4 страницы
Хорошие эссе
Подробнее
Удовлетворительные эссе
Тригонометрия и 6. а. 23 Б.
- 531 слов
- 3 страницы
Тригонометрия и 6. а. 23 Б.
а. Sin E = 0,387 б. Грех Е = 0,900 с. Кос Е =…
- 531 слов
- 3 страницы
Удовлетворительные эссе
Подробнее
Удовлетворительные эссе
Триггерные вопросы C3
- 1677 слов
- 7 страниц
Триггерные вопросы C3
Следовательно, решите уравнение 4 sin q – 3 cos q = 3, чтобы найти значения q между…
- 1677 слов
- 7 страниц
Удовлетворительные эссе
Подробнее
Хорошие эссе
Обзорная статья по тригонометрии
- 2020 Слов
- 9 страниц
Обзорная статья по тригонометрии
Тригонометрия, 8-е изд.
No related posts.