| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.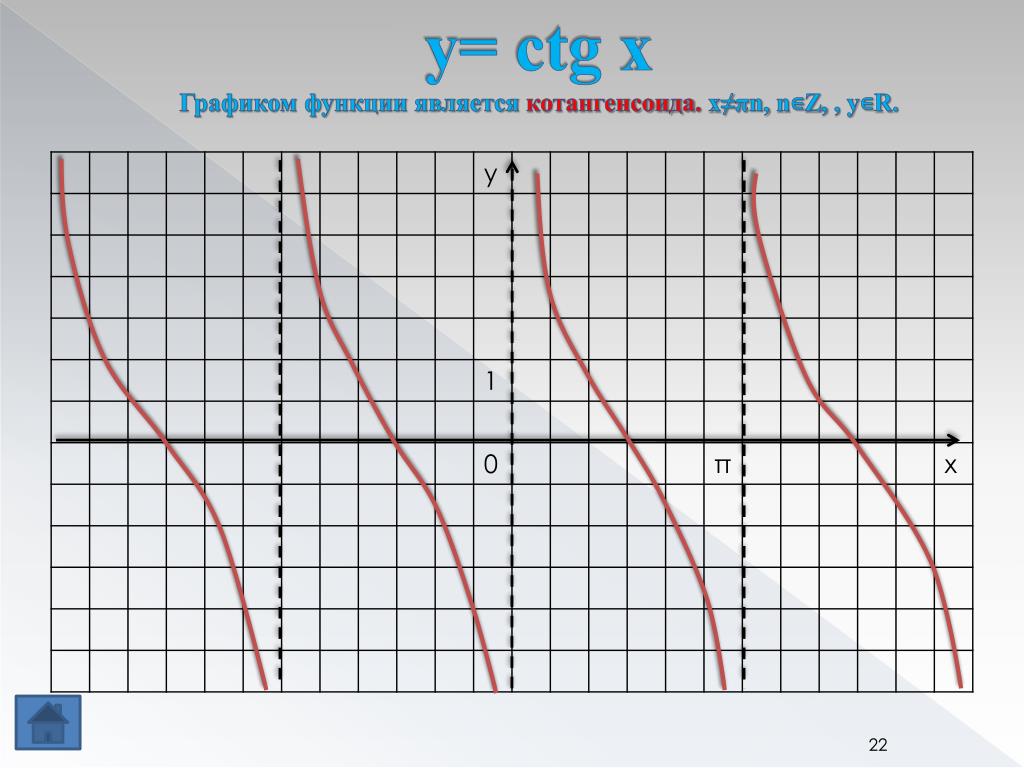 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.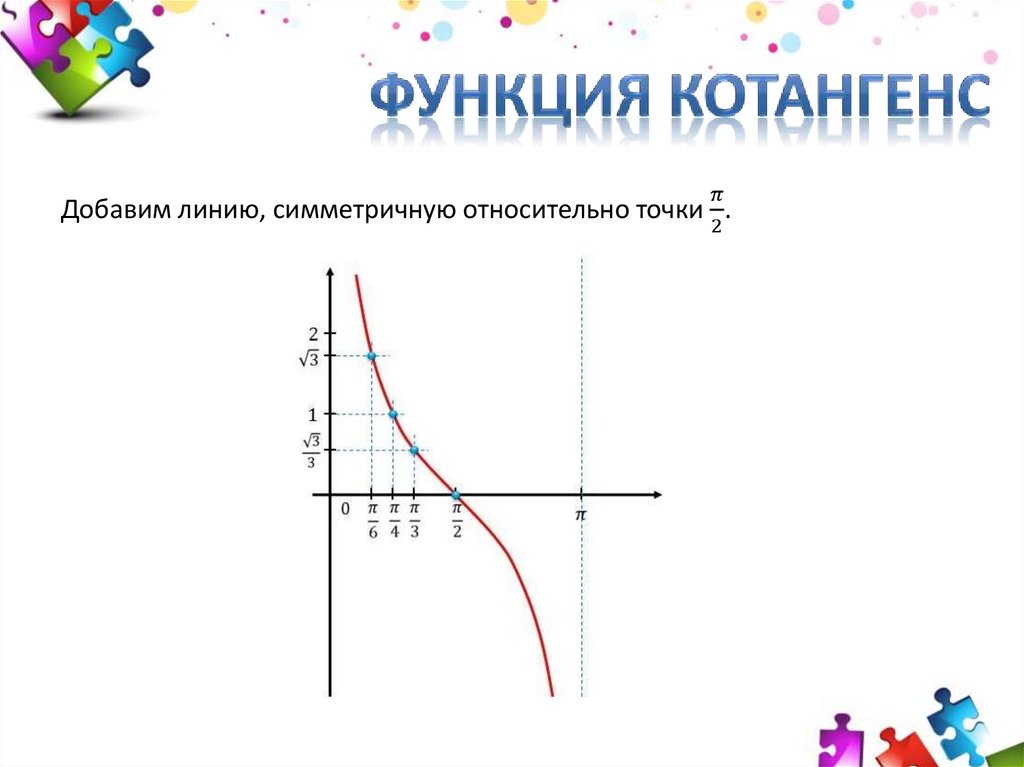 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.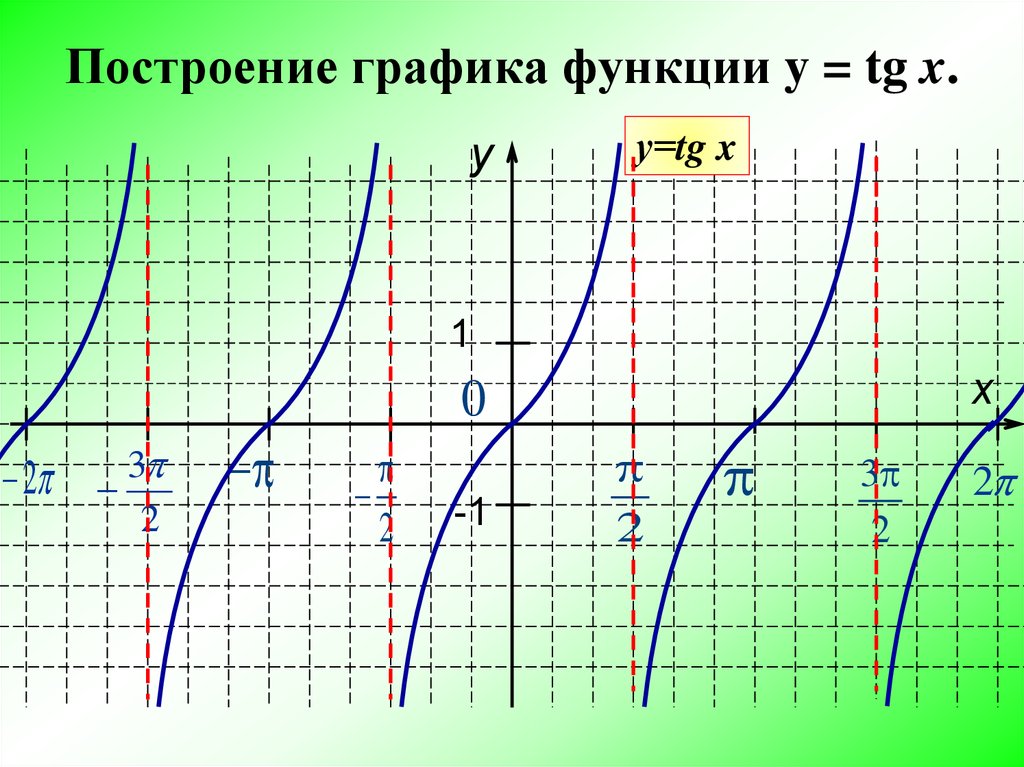 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
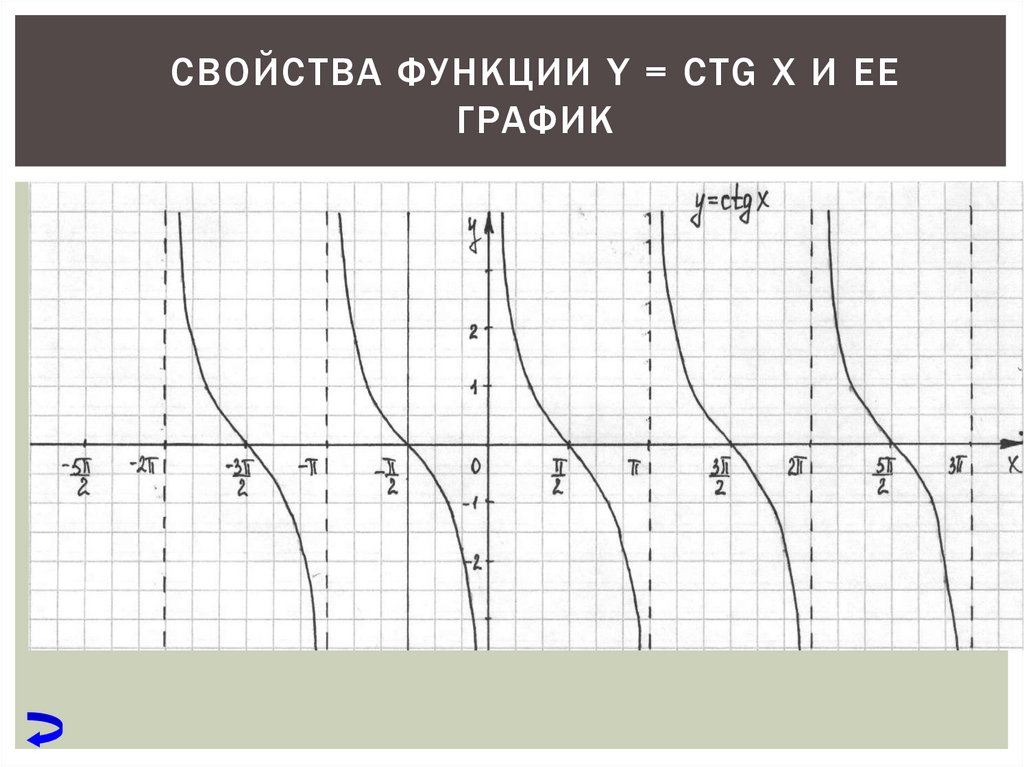
| Урок Повторение. Арккотангенс и решение уравнения ctgx=a 1. Введение. График функции y=ctgx, x∈(0;π) На уроке рассматривается понятие функции арккотангенс, как обратной для функции котангенс на промежутке . По теореме о существовании обратной функции прямая функция должна быть непрерывной и монотонной. Функция не непрерывна и не монотонна на всей своей области определения, а на промежутке она непрерывна, монотонна и пробегает все значения из области значений. Значит, существует обратная функция для нее на этом промежутке, она называется арккотангенс. По графику на промежутке (рис. 1) можно находить значения арккотангенсов некоторых углов. Рис. 1. 2. Понятие арккотангенса числа и его свойства Определение: Арккотангенсом числа называется такой угол из промежутка , котангенс которого равен числу Свойство 1: для любого числа Пример 1. Найти Решение: 1-й способ: по графику на рис. 1: 2-й способ: по свойству Свойство 2: для любого числа Пример 2. (проверка свойства): 3. Некоторые значения арккотангенса на единичной окружности с линией котангенсов Построим единичную окружность и проведем линию котангенсов. Рис. 2. Примеры 3. (рис. 2): 4. Решение уравнения ctgx=a Пример 4. Решить уравнение Решение: отметим на линии котангенсов точку и соответствующие точки на единичной окружности (рис. 3). Рис. 3. Ответ: Решение уравнения в общем виде: Пример 5. Решить уравнение Решение: запишем решение по общей формуле относительно значения : Ответ: 5. Итог урока На уроке был рассмотрен график функции на промежутке поскольку на этом промежутке функция непрерывна и монотонна и пробегает все свои значения от до Также было рассмотрено понятие арккотангенса числа и решено уравнения вида . Каталог: image uploads -> docs -> distant жүктеу/скачать 143 Kb. Достарыңызбен бөлісу: |
Изучите анимации этих функций с их производными здесь:
Дифференциальный интерактивный апплет — тригонометрические функции.
Если u = f ( x ) является функцией x , то используя цепное правило, мы имеем:
`(d(csc u))/(dx)=-csc u\ cot u(du)/(dx)`
`(d(сек u))/(dx)=sec u\ tan u(du)/(dx)`
`(d(cot u))/(dx)=-csc^2u(du)/(dx)` 94 3x желтовато-коричневый 3x`
1.
Найдите производную от y = csc 2 (2 x 2 ).
Ответить
Это пример функции функции функции, и нам нужно применить цепное правило 3 раза.
Пусть u = 2 x 2 и v = csc у.е.
Итак, y = v 2
`(dy)/(dx)=(dy)/(dv)(dv)/(du)(du)/(dx)` 92 2x tan 2x`
3. Найдите производную от 3 cot( x + y ) = cos y 2 .
Ответить
Это неявная функция .
3 раскладушка( x + y ) = cos y 2
Для левой стороны положим u = x + y.
Дифференциация 3 кроватки u дает нам:
92(x+y)`Производные от Sec, Csc и Cot: расчет
Говорить о тригонометрических функциях все равно, что говорить о фильме или сериале.
Вы сразу придумываете имена главных героев шоу! Но как насчет некоторых второстепенных персонажей? Они так же важны, как и другие персонажи истории, просто у них меньше экранного времени.
Сказав это, наверное, когда вы говорите о тригонометрических функциях, на ум приходят функции синуса и косинуса, а может быть, и функция тангенса. Но всего у нас шесть тригонометрических функций! Пришло время уделить немного экранного времени функциям секанса, косеканса и котангенса.
Функция секанса, а также функции косеканса и котангенса вместе известны как обратные функции , поскольку они обратны основным тригонометрическим функциям. Здесь вы узнаете, как найти производную каждого из них.
Производная функции секущей сек
Функция секанса является обратной функцией косинуса.
Функция секанса обозначается как
\[\sec{x}\]
и является обратной величиной функция косинуса , то есть
\[\sec{x}=\frac{1}{\cos{x}}.
2{x}}. \конец{выравнивание}\] 92{x}} \\ &= \left( \frac{1}{\cos{x}} \right) \left(\frac{\sin{x}}{\cos{x}} \right). \end{align}\]
На последнем шаге вы можете снова переписать обратную величину косинуса как секанс, а также использовать тригонометрическое тождество
\[\frac{\sin{x}}{\ cos{x}}=\tan{x},\]
получение
\[ \frac{\mathrm{d}}{\mathrm{d}x}\sec{x} = (\sec{x} )(\tan{x}).\]
Вышеприведенное выражение обычно встречается в таблицах производных, просто написанных без круглых скобок. Это дает вам формулу для производной секущей функции.
Производная функции секущей равна
\[ \frac{\mathrm{d}}{\mathrm{d}x}\sec{x} = \sec{x}\,\tan{x}.\ ]
Производная функции котангенса cot
Пришло время перейти к функции котангенса, которая является обратной функцией тангенса.
Функция котангенса обозначается как
\[\cot{x}\]
и является обратной величиной функции тангенса , , то есть
\[\cot{x}=\frac{1 }{\тан{х}}.
\]
Одной из особенностей функций тангенса и котангенса является то, что они также могут быть записаны как рациональные функции с использованием функций синуса и косинуса, как показано на одном из шагов, необходимых для нахождения производной функции секанса. Для функции тангенса вы можете написать
\[\tan{x}=\frac{\sin{x}}{\cos{x}}.\]
Поскольку функция котангенса является обратной функцией тангенса , вы также можете найти функцию котангенса, записанную как рациональную функцию, используя функции синуса и косинуса, то есть
\[\begin{align} \cot{x} &= \frac{1}{\tan{x}} \\ &= \frac{1}{\frac{\sin{x}}{\cos {Икс}}}. \end{align}\]
Используя свойства дробей, вы можете записать это как
\[\cot{x}=\frac{\cos{x}}{\sin{x}},\]
это означает, что функция котангенса также может быть записана как частное функции косинуса и функции синуса.
Вы можете использовать приведенное выше тождество, чтобы найти производную функции котангенса. Поскольку это частное двух функций, вам нужно будет использовать правило отношения, поэтому 92{x}.
\]
Производная функции косеканса csc
Наконец, вы также найдете обратную функцию синуса.
Функция косеканса обозначается как
\[\csc{x}\]
и является обратной функцией синуса , то есть
\[\csc{x}=\frac{1 }{\sin{x}}.\]
Вы можете найти производную функции косеканса точно так же, как и с функцией секанса. Начните с записи функции косеканса через функцию синуса, 92{x}} \\ &= -\left(\frac{1}{\sin{x}} \right) \left(\frac{\cos{x}}{\sin{x}} \right) .\end{align}\]
Наконец, перепишем обратное выражение и воспользуемся функцией котангенса, так что
\[\frac{\mathrm{d}}{\mathrm{d}x}\csc{x} = — (\csc{x})(\cot{x}).\]
И снова вы, скорее всего, обнаружите, что формула написана без круглых скобок.
Производная функции косеканса равна
\[\frac{\mathrm{d}}{\mathrm{d}x}\csc{x}=-\csc{x}\,\cot{x}. \]
Производная функции арксеканса
Вы видели, что функция секанса является обратной величиной функции косинуса.
{-1}{x},\]
, где вы должны иметь в виду, что \(-1\) , а не показатель степени, он используется для обозначения обратной функции.
Не забывайте, что обратное , а не , то же самое, что и обратное .
Всякий раз, когда вы говорите об обратных функциях, вы должны быть осторожны с их доменом. Для функции арксеканса вы должны учитывать, что выходы функции секанса таковы, что\[ |\sec{x}| \geq 1, \]
, поэтому областью определения функции арксеканса будут все числа, абсолютное значение которых больше или равно \(1\), то есть
\[ (-\infty,-1] \cup [1,\infty).\]
Кроме того, поскольку функция секанса является периодической функцией, можно получить один и тот же результат на двух разных входах. Чтобы убедиться, что арксеканс является функцией, этот диапазон должен быть ограничен, и обычно его выходы находятся между \(0\) и \(\pi\), за исключением \(\frac{\pi {2}\), поэтому
\[ 0 \leq \mathrm{arcsec}{\, x} \leq \pi, \text{where,}\, \mathrm{arcsec}{\, x} \neq \frac{\pi}{2}.
\pi/_2\), за исключением \(0 \). это 92,\]
, поэтому цепное правило говорит вам, что
\[ f'(x)= \frac{\mathrm{d}}{\mathrm{d}u}\sec{u} \frac{\mathrm {d}u}{\mathrm{d}x}.\]
Используя правило степени, вы получаете
\[ \frac{\mathrm{d}u}{\mathrm{d}x} = 4x ,\]
, поэтому
\[f'(x)=\left(\frac{\mathrm{d}}{\mathrm{d}u} \sec{u} \right) (4x), \]
Теперь используйте производную функции секанса, что даст вам
\[ f'(x) = (\sec{u}\,\tan{u}) (4x).\]
Наконец, подставьте обратно \ (u\) и переставить, то есть 92}.\]
Вы также можете использовать правило произведения для нахождения производных обратных тригонометрических функций!
Найдите производную от
\[ g(x) = x\cot{x}.\]
Решение:
Здесь вам нужно будет использовать правило произведения, то есть
\[ g’ (x) = \ left (\ frac {\ mathrm {d}} {\ mathrm {d} x} x \ right) \ cot {x} + x \ left ( \ frac {\ mathrm {d}} {\ mathrm {d}x}\cot{x} \right).
\]
Затем используйте степенное правило и производную функции котангенса, так что 9{\csc{х}}\csc{х}\,\кроватка{х}. \end{align}\]
Производные sec, csc и cot — Основные выводы
- Функции секанса, косеканса и котангенса вместе известны как обратные тригонометрические функции.
- Функция секанса является обратной функцией косинуса, \[\sec{x}=\frac{1}{\cos{x}}.\]
- Функция косеканса является обратной функцией синуса, \ [\csc{x}=\frac{1}{\sin{x}}.\]
- Функция котангенса является обратной величиной функции тангенса, \[\cot{x}=\frac{1}{\ тан{х}}.\] 92{x}.\]
- Обратные тригонометрические функции, также известные как аркус-функции, являются обратными функциями тригонометрических функций. Обратные тригонометрические функции не такие же, как обратные тригонометрические функции.
- Производные обратных тригонометрических функций могут быть получены с помощью неявного дифференцирования и некоторых тригонометрических тождеств.

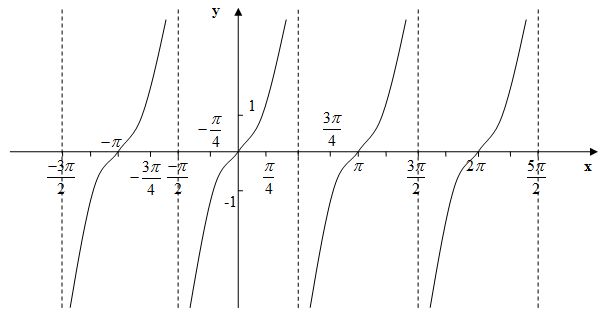
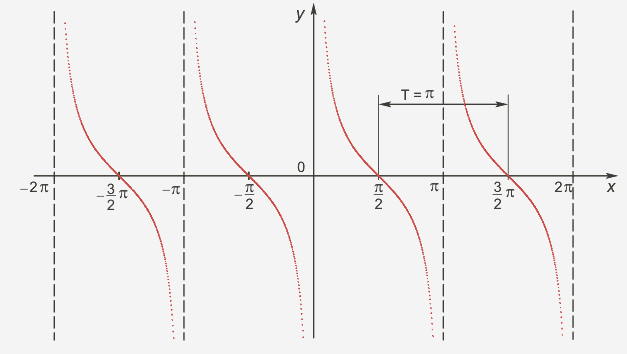 Отметим на окружности точки , найдем соответствующие точки на линии котангенсов (рис. 2).
Отметим на окружности точки , найдем соответствующие точки на линии котангенсов (рис. 2). Строение и разнообразие цветов
Строение и разнообразие цветов Найдите производную от y = csc 2 (2 x 2 ).
Найдите производную от y = csc 2 (2 x 2 ).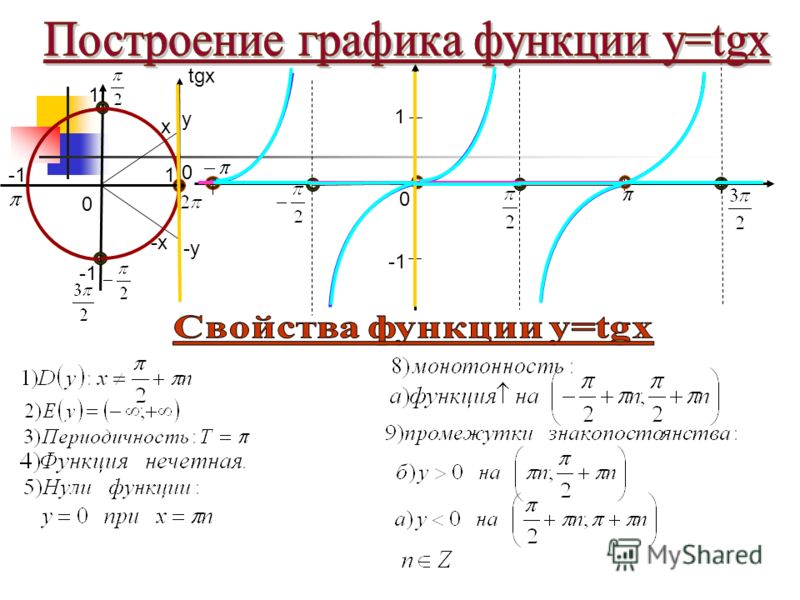 Вы сразу придумываете имена главных героев шоу! Но как насчет некоторых второстепенных персонажей? Они так же важны, как и другие персонажи истории, просто у них меньше экранного времени.
Вы сразу придумываете имена главных героев шоу! Но как насчет некоторых второстепенных персонажей? Они так же важны, как и другие персонажи истории, просто у них меньше экранного времени. 2{x}}. \конец{выравнивание}\] 92{x}} \\ &= \left( \frac{1}{\cos{x}} \right) \left(\frac{\sin{x}}{\cos{x}} \right). \end{align}\]
2{x}}. \конец{выравнивание}\] 92{x}} \\ &= \left( \frac{1}{\cos{x}} \right) \left(\frac{\sin{x}}{\cos{x}} \right). \end{align}\]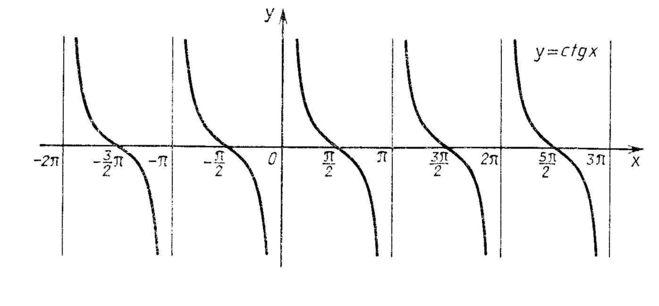 \]
\] \]
\] {-1}{x},\]
{-1}{x},\]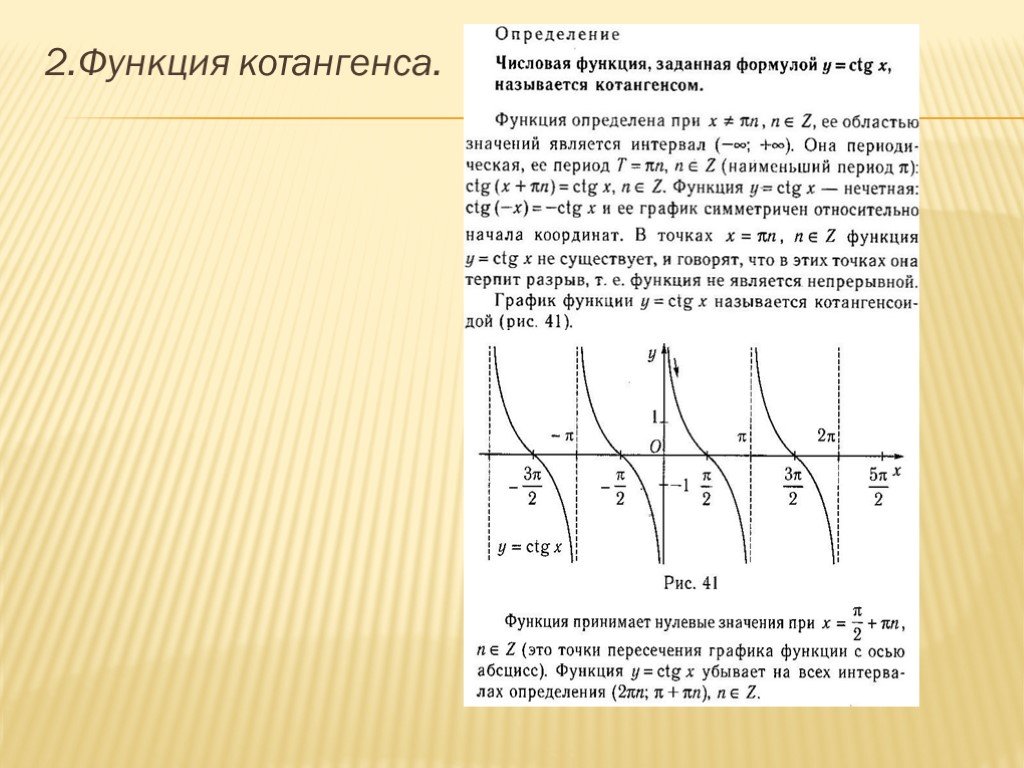 \pi/_2\), за исключением \(0 \). это 92,\]
\pi/_2\), за исключением \(0 \). это 92,\] \]
\]