Функция сферы в трехмерном пространстве: Сфера в трёхмерном пространстве

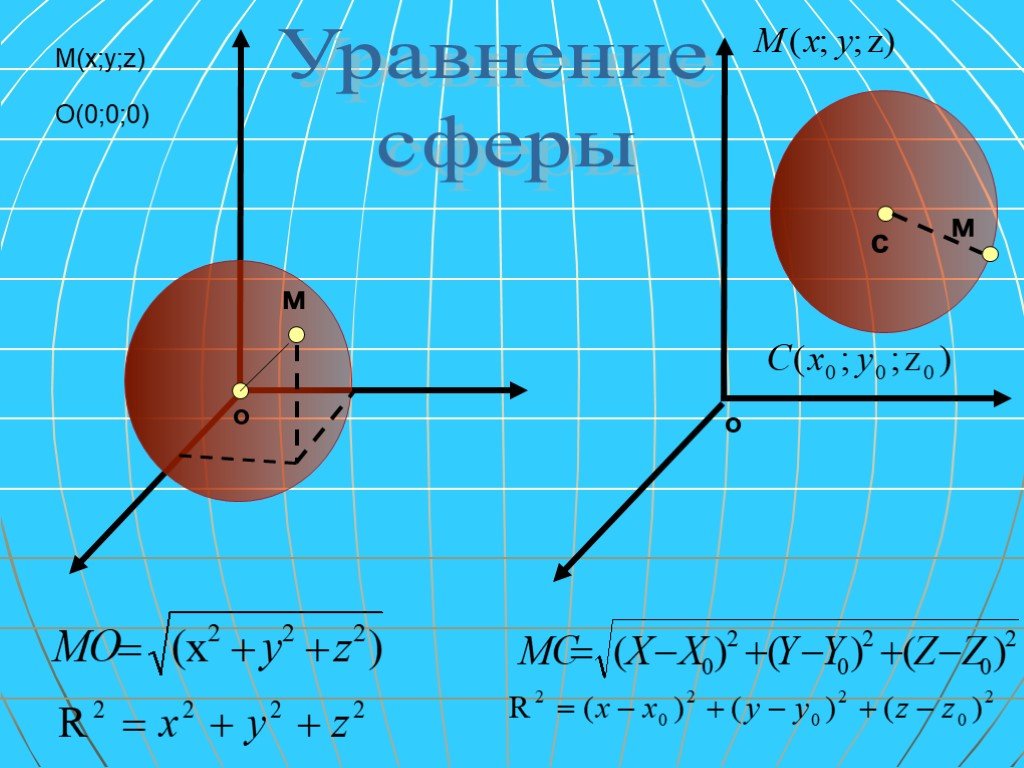
Сфера в трёхмерном пространстве

Уравнение

где   — координаты центра сферы,   — её радиус.

Параметрическое уравнение сферы с центром в точке  :

где   и 

29) Аксиомы стереометрии и их следствия

Аксиома 1.  Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2.  Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.  Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.

30)взаимное расположение двух прямых

Взаимное расположение двух прямых на плоскости.

   Этот вопрос уже обсуждался в предыдущей лекции, когда обауравнения данных прямых записывались в каноническом или параметрическом виде. Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

     и 

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1) если  , то 

прямые   и   совпадают;

2) если  , то прямые    и 

    параллельные;

3) если  , то прямые пересекаются.

   Доказательство. Условие   равносильно коллинеарности нормальных векторов данных прямых:

. Поэтому, если  , то   и прямыепересекаются.

   Если же  , то  ,  ,   иуравнение прямой   принимает вид:

 или  , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности  , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

   Если же прямые не совпадают и не пересекаются, то остается случай  , т.е. прямые параллельны.

Теорема доказана.

   Заметим, что если прямые пересекаются, то для нахождения координатих точки пересечения достаточно решить систему двух уравнений

 сдвумя неизвестными:

                             .                               (4)

Следствие. Пусть   – определитель системы (4). Если  , то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:

                                   ,                                (5)

где  ,  .

Если  , то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.

   Доказательство. По определению определителя второго порядка

                       .

Если  , то   и  , т.е. прямые пересекаются икоординаты точки пересечения можно найти по формулам Крамера (5).

Если же  , то   и  , т.е. либо прямые параллельны и тогда 

система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.

следствие доказано.

31)параллельность прямых и плоскостей

Определение 2.3. 

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Если прямая a параллельна плоскости α, то пишут a || α.

Т еорема 2.4. Признак параллельности прямой и плоскости.

Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.

Доказательство

Т еорема 2.5. Теорема о следе.

Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой 

b, то b || a.

Доказательство

О пределение 2.4. 

Прямую b иногда называют следом плоскости β на плоскости α.

Признак параллельности прямых и плоскостей

Теорема  Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.    Доказательство  Пусть α — плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.

32)параллельное проектирование и его свойства Изображение на плоскости пространственных фигур обычно осуществляется с помощью параллельного проектирования этих фигур на некоторую плоскость. При этом должны выполняться следующие правила изображения, вытекающие из свойств параллельного проектирования:

1. Если прямая не параллельна проектирующей и не совпадает с ней, то проекция этой прямой есть прямая.

2. Проекции параллельных прямых, не параллельных проектирующей, параллельны или совпадают.

3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

33) ортогональное проецирование Направление проецирования перпендикулярно (ортогонально) плоскости проекций S   π₁ (рис. 1.11). Ортогональное проецирование является частным случаем параллельного проецирования.

Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести:

.

Рис. 1.10. Пример инвариантного свойства 9

.

Рис. 1.11. Ортогональная проекция прямого угла

а) простоту графических построений для определения ортогональных проекций точек;

б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.

Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей.

Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования.

10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11)

На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций π₁. По инвариантному свойству 9 этот угол проецируется на плоскость π₁ без искажения, т. е.   А₁В₁D₁=90°.

Возьмем на проецирующем луче DD₁ произвольную точку С, тогда полученный   АВС будет прямым, т. к. АВ   ВВ₁DD₁.

Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций π₁, будет прямой угол А₁В₁D₁.

34)перпендикулярность прямых в пространстве Перпендикуля́рность

 — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности.

математика — Уравнение окружности в пространстве

Вопрос задан 6 лет 2 месяца назад

Изменён 5 лет 3 месяца назад

Просмотрен 7k раз

Есть задача вывести уравнение (найти несколько точек) окружности по точке центра и нормали плоскости окружности. Я убрал точку центра и принял её (0,0,0) для простоты (потом просто прибавлю к результатам координаты моего центра).

В чем проблема. Уравнение сферы x²+y²+z²=R² Уравнение плоскости Ax+By+Cz=0, где N(A,B,C) — вектор нормаль.

Мое уравнение — это система последних двух уравнений.

Далее у меня затык… Мне нужно найти серию точек по окружности по часовой стрелке через шаг α=360°/N.

Я так понял, то данное уравнение мне необходимо не просто решить а еще и привести к сферическим координатам. Но как? Математику знаю нормально но тут явно затупил.

UPD: Есть еще некий вариант решения, зная (X,Y) нужных точек окружности на плоскости, получить (X,Y,Z) путём «вращения» осей взаимозависимости от N(A,B,C) но как это реализовать вопрос..

• математика
• геометрия

0

Вы пошли довольно сложным путем. Все делается проще.

Для начала, надо построить ортонормированную систему координат в плоскости окружности. Для этого надо найти любой вектор, перпендикулярный вектору нормали. Это — самая «некрасивая» часть решения. И в этом месте надо не бояться ставить условные операторы — согласно «теореме о причесывании ежа» из топологии, без них не обойтись.

Самый простой способ повернуть вектор на прямой угол — векторно умножить его на что-нибудь. Но если перемножаемые вектора будут близки по направлению — пострадает точность (а если они коллинеарны — будет ноль).

Поэтому предлагаю рассмотреть три базисных вектора (i, j и k) и умножить на тот, который «самый непохожий». Для этого найдем координату с наименьшим модулем. Пусть, для определенности, |A| < |B| и |C|. Значит, умножаем на вектор i и получаем первый из векторов базиса местной системы координат:

i₁ = n x i = (Ai + Bj + Ck) x i = -Bk + Cj

Теперь снова умножим его на вектор нормали и получим второй вектор базиса:

j₁ = n x i₁ = (Ai + Bj + Ck) x (-Bk + Cj) = (раскройте скобки сами)

Теперь осталось нормировать базисные вектора, чтобы они стали единичными — и можно воспользоваться параметрическим уравнением окружности:

r = r₀ + R cos φ i₁ / |i₁| + R sin φ j₁ / |j₁|

6

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

{3}$ не имеет точного «уравнения» в том смысле, что круг на плоскости или сфера в пространстве имеют уравнение. {n}$ при $n \geq 2$.) 9{2} = 0. $$

$\endgroup$

4

$\begingroup$

Подсказка: Окружность — это пересечение сферы с плоскостью.

$\endgroup$

7

$\begingroup$

Чтобы указать круг в 3D, вам нужно знать его центр, радиус, а также то, как он «наклонен», что означает, в какой плоскости он живет. Таким образом, вам понадобятся два уравнения, одно из которых определяет соответствующую сферу (которое определяет центр и радиус) и один, определяющий соответствующую плоскость (которая определяет наклон). 93$ — нормаль к плоскости окружности с $|n| = r$, где $r$ — радиус окружности.

Это представление восходит к Лагерру: Э. Н. Лагерр, Sur l’emploi des imaginaires dans la g’eom’etrie de l’espace, Nouvelles Annales de Math., Series 2, vol. xi, (1872 г.).

См. также П. Бэрд, Конформные слоения на окружности и комплексные изопараметрические функции на евклидовом трехмерном пространстве. Мат. проц. Кембридж Филос. Soc., 123, (1998) 273–300.

$\endgroup$

$\begingroup$

Ссылаясь на 2-ю точку маркера @Hwang выше, если вы знаете две из 3 координат точки на окружности, вычислить 3-ю тривиально. Решение для второй координаты с точки зрения 1-й — просто утомительная алгебра. Здесь я показываю, как найти $x$ в терминах $y$, с некоторыми заменами переменных, чтобы сделать уравнения простыми (это добавляет умственную сложность, чтобы уменьшить кажущуюся сложность уравнений). Имея два уравнения и 3 неизвестных, легко составить уравнение одного неизвестного через второе (заменив, чтобы удалить третье). Это дает уравнение вида $$A(X’)^{2}+ BX’ + C = 0$$ 9{2}$).

$\endgroup$

сфер — Нахождение 4-й точки в трехмерном пространстве, зная 3 другие точки и 2 расстояния до 4-й точки от них

(Это не ответ на поставленный вопрос как таковой, но объясняет, как эффективно выполнять трилатерацию.)

В 3D вам нужны четыре фиксированные точки (которые не находятся на одной плоскости) и их расстояния до неизвестной точки, чтобы точно определить местоположение неизвестной точки.

Три фиксированные точки (которые не лежат на одной линии) и их расстояния до неизвестной точки обычно дают вам две возможности, симметрично отраженные плоскостью, образованной тремя фиксированными точками.

Допустим, неизвестная точка находится в $\vec{p} = (x, y, z)$, три фиксированные точки находятся в $\vec{v}_1 = (x_1 , y_1 , z_1)$, $\ vec{v}_2 = (x_2 , y_2 , z_2)$ и $\vec{v}_3 = (x_3 , y_3 , z_3)$ на расстояниях $d_1$, $d_2$ и $d_3$ от неизвестной точка соответственно. Решение системы уравнений $$\left\lbrace\begin{выровнено} \left\lVert \vec{p} — \vec{p}_1 \right\rVert &= \lvert d_1 \rvert \\ \left\lVert \vec{p} — \vec{p}_2 \right\rVert &= \lvert d_2 \rvert \\ \left\lVert \vec{p} — \vec{p}_3 \right\rVert &= \lvert d_3 \rvert \\ \end{выровнено}\right . 2} \\ \end{выровнено}\right.$$ В исходной системе координат $$\vec{p} = \vec{v}_1 + u \hat{e}_1 + v \hat{e}_2 + w \hat{e}_3 \quad \iff \quad \left\lbrace\begin{выровнено} x &= x_1 + u X_1 + v X_2 + w X_3 \\ y &= y_1 + u Y_1 + v Y_2 + w Y_3 \\ z &= z_1 + u Z_1 + v Z_2 + w Z_3 \\ \end{выровнено}\right.$$ отметив, что если $w$ не вещественное число, то решения нет; если $w \ приблизительно 0$, то есть одно решение; а в противном случае есть два решения, одно с положительным $w$, а другое с отрицательным $w$.

Если вы знаете расстояния до четырех фиксированных точек, вам действительно нужна только четвертая точка (не компланарная с тремя другими фиксированными точками), чтобы определить, какой это случай. Если расстояния содержат шум, может иметь смысл вычислить результат, используя каждую уникальную тройку ($123$, $124$, $134$ и $234$), и вернуть их среднее значение.

В псевдокоде для трилатерации следует предварительно вычислить значения, зависящие только от фиксированных точек:

 Пусть ex1 = x2 - x1
Пусть ey2 = y2 - y1
Пусть ez2 = z2 - z1
Пусть h = sqrt( ex1*ex1 + ey1*ey1 + ez1*ez1 )
Если ч <= эпсилон:
 Ошибка: первая и вторая точки расположены слишком близко.
No related posts.