10 класс. Алгебра. Тригонометрические функции. Модификация графиков. Функции y=tg x, y=ctg x. — Функция y=tgx, ее свойства и график.
Комментарии преподавателяФункция y=tgt, её свойства и график
Напоминание:
Определение: Функцией называется закон, по которому каждому допустимому значению ставится в соответствие единственное значение y.
Множество всех точек координатной плоскости называется графиком функции
На отрезке задана функция (рис. 1).
По определению, каждому значению ставится в соответствие только одно значение И обратно: значение функции может достигаться при нескольких значениях аргумента:
Дадим определение функции или .
Нам важен закон, по которому каждому значению ставится в соответствие
Зададим произвольное Значение откладывается на числовой окружности по часовой стрелке либо против часовой стрелки, в зависимости от знака Получаем единственную точку M с единственной парой координат (рис.
2).
Координату называют косинусом числа координату синусом числа
Тангенсом числа называется отношение синуса к косинусу
Нам известно, что каждому значению аргумента ставится в соответствие единственное значение функции Покажем это графически.
Проведем касательную к числовой окружности в точке A. Заданному значению соответствует единственная точка M, единственная прямая OM и единственная точка T пересечения прямой OM и касательной (рис. 3).
Наша цель – найти координаты точки T, для этого решим систему уравнений.
Ордината точки равна
Прямую называют линией тангенсов.
Докажем, что область значений тангенса – это все действительные числа,
Доказательство:
Зададим любое действительное значение и докажем, что оно достигается хотя бы при одном значении аргумента.
Отложим на линии тангенсов, получим точку (рис. 4).
Соединим её с точкой O, получим прямую которая пересекает числовую окружность хотя бы в одной точке M, а, значит, существует единственная дуга и хотя бы одно значение которое равно длине дуги.
Любому действительному значению аргумента соответствует единственное значение функции. Но любому значению функции соответствует хотя бы одно значение аргумента.
Таким образом, мы задали любое значение функции и доказали, что оно достигается хотя бы при одном значении аргумента.
Отметим два важных свойства функции
1. Нечетность функции.
Т.е.
2. Докажем, что период функции равен
Таким образом, для любого значения выполняется
Эти свойства функции позволяют нам легко построить её график. Период функции равен значит, мы можем изучить её свойства и построить график на любом участке длиной
Нечетность функции позволяет симметрично отобразить участок графика относительно начала координат.
С учетом этого построим график функции на промежутке (рис. 5).
Мы получили график функции на заданном промежутке. Можно было построить график и по известным табличным значениям. Например:
Из построенного графика функции на промежутке видно, что функция возрастает. Докажем это.
Рассмотрим график на промежутке Точки (рис. 6).
Докажем, что
Доказательство:
На промежутке функция возрастает, значит (рис. 7).
На промежутке функция убывает, значит (рис. 8).
значит, функция возрастает на промежутке
Зная свойства функции, мы можем построить её график на всей области определения.
В точках проходят вертикальные асимптоты (рис. 9).
Рассмотрим основные свойства функции
1) Область определения:
2) Функция периодическая с периодом
3) Функция нечетная.
4) Функция возрастает и непрерывна на любом интервале
5) Функция не ограничена.
6) Функция не имеет ни минимального, ни максимального значения.
7)
Задача. Решить уравнение
Решение:
На промежутке функция монотонно возрастает, значит, на этом промежутке значение достигается при единственном значении аргумента (рис. 10).
С учетом периодичности получаем
Ответ:
Мы рассмотрели функцию её свойства и график. На следующем уроке рассмотрим функцию
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/funktsiya-y-tgx-ee-svoystva-i-grafik
http://www.youtube.com/watch?v=GegtVbMiems
http://5klass.net/datas/algebra/Osnovnye-trigonometricheskie-funktsii/0022-022-Svojstva-funktsii-y-tg-x.jpg
http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.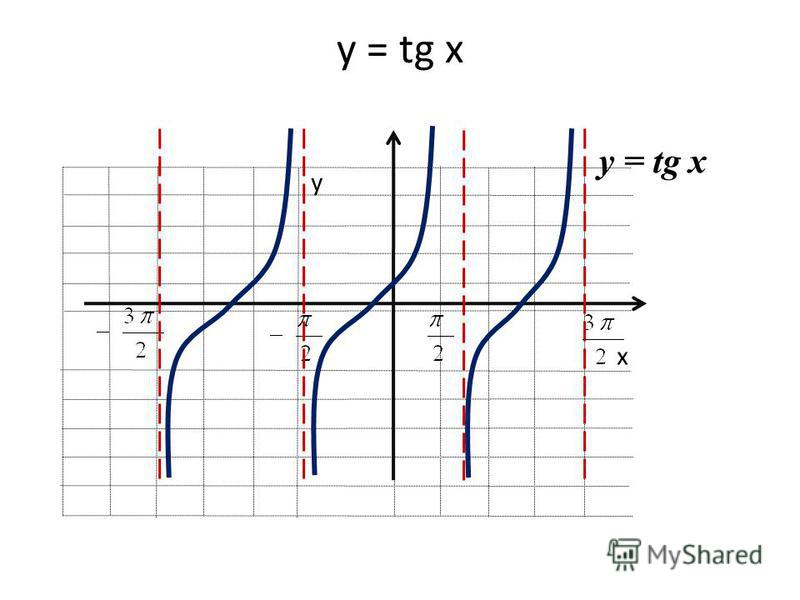
pdf
http://v.5klass.net/zip/2418f24263056cb69cc9115af959108a.zip
конспект урока «Функция тангенс, ее график и свойства.»
Главная / Старшие классы / Алгебра
Скачать
25.07 КБ, 1441893.docx Автор: Елфимова Ирина Ивановна, 20 Фев 2016
Конспект урока «Функция тангенс. ее график и ее свойства». 10 класс. Это конспект открытого урока на муниципальном уровне. Конспект составлен в соответствии с требованиями к уроку в рамках ФГОС.
Автор: Елфимова Ирина Ивановна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | конспект урока «Функция тангенс, ее график и свойства.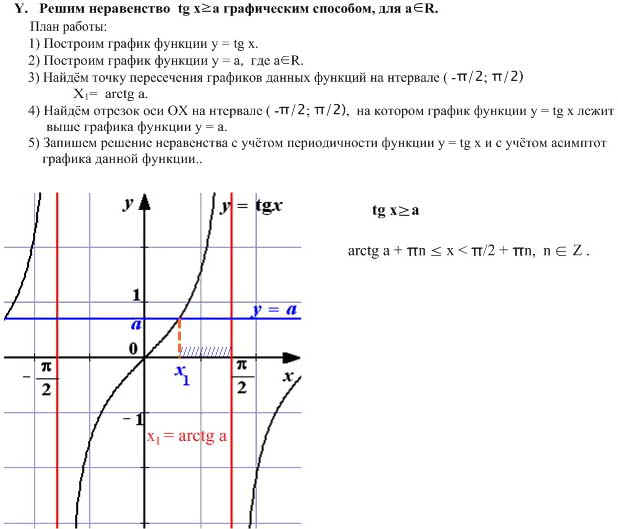 » | 20 Фев 2016 | |
| разное | Конспект урока «Квадратичная функция и ее график» | Занина Альбина Вагисовна | 21 Мар 2015 |
| разное | Конспект урока «Квадратичная функция и ее график» | Занина Альбина Вагисовна | 21 Мар 2015 |
| документ | КОНСПЕКТ УРОКА «ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК» | Волкова Ольга Владимировна | 24 Дек 2015 |
| разное | Презентация урока «Линейная функция и ее график» | Александрова Елена Юрьевна | 14 Янв 2016 |
| разное | Конспект урока алгебры по теме «Линейная функция и ее график» | Ражева Оксана Станиславовна | 1 Апр 2015 |
| документ | План-конспект урока «Линейная функция и ее график» алгебра 7 кл.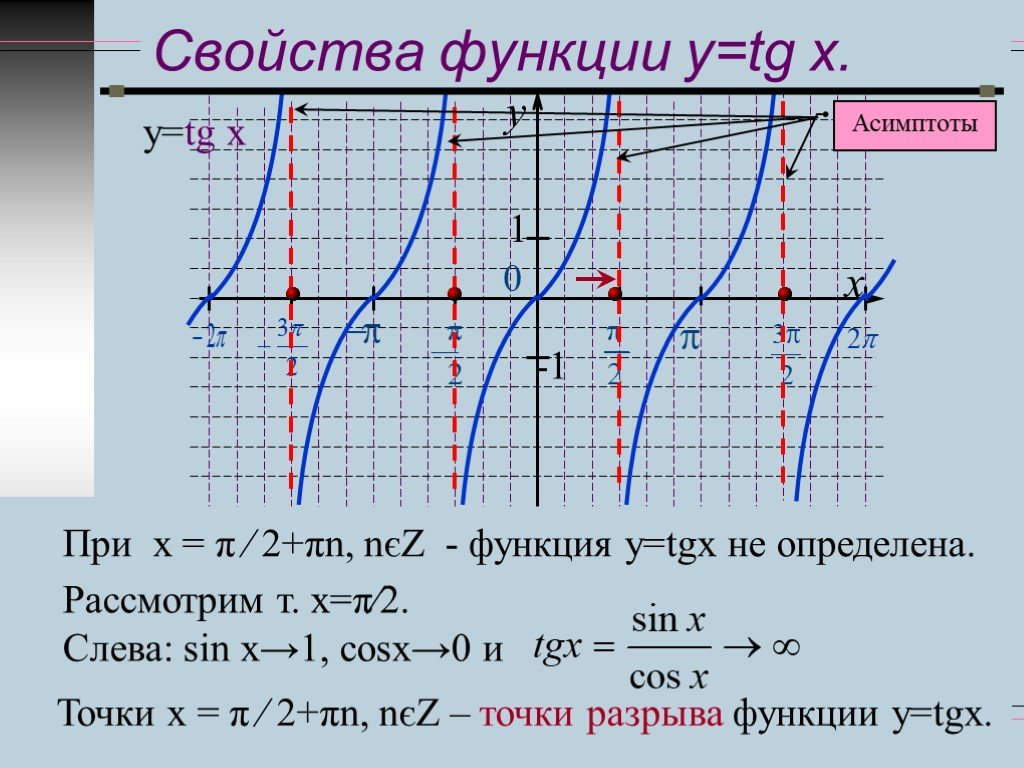 | Волкова Виктория Александровна | 1 Апр 2015 |
| разное | план-конспект открытого урока по теме :» Функция у=х² и ее график» | Шаехова Лейля Ленаровна | 1 Апр 2015 |
| документ | Конспект урока по математике «Линейная функция и ее график» | Светлана | 20 Сен 2015 |
| презентация, документ | Методическая разработка урока в 10 классе по теме «Степенная функция, ее свойства и график» | Иванова Наталья Константиновна | 21 Мар 2015 |
| презентация, документ | Разработка урока по алгебре.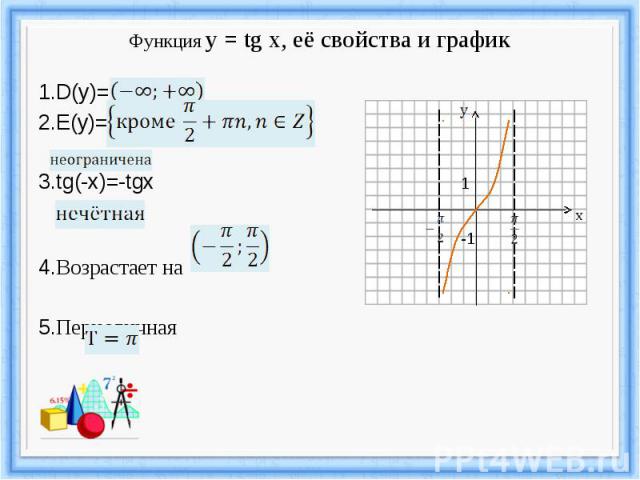 Тема «Функция у=х2, ее график и свойства» 8 класс. Диск Диск Диск | Иноземцева Ирина Юрьевна | 1 Апр 2015 |
| презентация, документ | Разработка урока по теме «Показательная функция, ее свойства и график» | Шорикова Мария Андреевна | 14 Ноя 2015 |
| презентация, документ, таблица | Методическая разработка урока по теме: «Показательная функция, ее свойства и график | Попова Лариса Анатольевна | 1 Апр 2015 |
| разное | План-конспект урока «Число е. Показательная функция с основанием е, её свойства и график» | Грудинина Мария Михайловна | 1 Апр 2015 |
| презентация, документ | Конспект урока «Функция y=kx^2, её свойства и график» в 8 классе | Хахалина Наталья Владимировна | 5 Сен 2015 |
| документ | Конспект урока «Линейная функция и её график» | Юдина Татьяна Николаевна | 1 Апр 2015 |
| разное | Методическая разработка урока по алгебре в 7 классе «Линейная функция, ее свойство и график» | Хробостова Ирина Владимировна | 1 Апр 2015 |
| документ | Методическая разработка урока «Квадратичная функция и ее график» | Пузатых Екатерина Николаевна | 4 Апр 2015 |
| документ | Практическая работа «Линейная функция и ее график» | Новоселова Светлана Григорьевна | 4 Апр 2015 |
| документ | «Линейная функция и ее график» 7 класс | Тумат Байлан Дарыйхуураковна | 9 Авг 2015 |
| презентация | ПРЕЗЕНТАЦИЯ «ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК» | Турчанинова Светлана Александровна | 15 Окт 2015 |
| презентация | Презентация к уроку алгебры по теме «Функция квадратного корня, ее свойства и график» Урок 1. (8 класс) | Токарева Инна Александровна | 21 Мар 2015 |
| презентация | Презентация к уроку «Квадратичная функция. Ее свойства и график» 8 класс | Дьячкова (Алексеева) Татьяна Алексеевна | 1 Апр 2015 |
| презентация | Презентация к уроку алгебры по теме «Функция квадратного корня, ее свойства и график» Урок 2 (8 класс) | Токарева Инна Александровна | 4 Апр 2015 |
| презентация, документ | Открытый урок «Показательная функция, ее свойства и график» | Скляренко Елена Владимировна | 7 Июл 2015 |
| разное | Тема урока «Квадратичная функция, ее график и свойства» 9 класс. (часть 2) | Ефремова Наталья Валерьевна | 12 Окт 2015 |
| разное | Тема урока «Квадратичная функция, ее график и свойства» 9 класс. (часть 1) | Ефремова Наталья Валерьевна | 12 Окт 2015 |
| презентация, документ | Тема урока «Квадратичная функция, ее график и свойства» 9 класс. | Ефремова Наталья Валерьевна | 17 Окт 2015 |
| документ | ТЕМА УРОКА: «Показательная функция, ее свойства и график» | Заира Сергеевна Кудзиева | 14 Фев 2016 |
| документ | План-конспект урока с использованием ЭОР (электронных образовательных ресурсов) по теме «Функция y=ax^2, её график и свойства» (алгебра, 9 класс) | Краузе Татьяна Валентиновна | 1 Апр 2015 |
| разное | Конспект урока по алгебре в 7 классе. Тема урока: «Линейная функция и ее график» | Лилия Александровна Кандруцкая | 21 Мар 2015 |
| разное | Конспект урока по алгебре в 7 классе. Тема урока: «Линейная функция и ее график» | Лилия Александровна Кандруцкая | 21 Мар 2015 |
| документ | Конспект урока: «Синус, косинус и тангенс угла» | Шушпанова Ирина Владимировна | 21 Мар 2015 |
| разное | Конспект урока и презентация к уроку по алгебре в 7 классе по теме «Линейная функция и ее график» | Санина Зоя Ивановна | 23 Янв 2016 |
| презентация | Показательная функция, ее свойства и график( тест) | Лысенко Ирина Борисовна | 21 Мар 2015 |
| презентация | Квадратичная функция, ее свойства и график. | Шурчкова Людмила Васильевна | 21 Мар 2015 |
| документ | Функция y = kx2, ее свойства и график | Шарапова Арюна Санжиевна | 31 Мар 2015 |
| презентация, документ | Квадратичная функция ее график и свойства | Елена Ивановна Кормилина | 1 Апр 2015 |
| презентация, документ | Показательная функция ,ее график и свойства | Кураленя Наталия Олеговна | 5 Июн 2015 |
| презентация | презентация потеме Функция тангенса, ее график и свойства. | Елфимова Ирина Ивановна | 20 Фев 2016 |
Видео с вопросами: Определение графика касательной функции
Стенограмма видео
Что из следующего является графиком 𝑦 равно тангенсу 𝑥?
Давайте начнем с напоминания о некоторых ключевых свойствах функции тангенса. тангенс 𝑥 является периодическим с периодом 180 градусов. Итак, один и тот же паттерн на его графике повторяется на каждом интервале длиной 180 градусов. График тангенса 𝑥 имеет вертикальные асимптоты, и они расположены на 90 градусов плюс любое целое число, кратное 180 градусам. Эти асимптоты возникают, когда cos 𝑥 равен нулю. Чтобы помочь нам определить, какой график представляет функцию тангенса, мы можем явно записать положение некоторых из этих асимптот. Они возникают при отрицательных 90 градусов, 90 градусов, 270 градусов и так далее.
Последнее свойство, которое мы запомним, состоит в том, что корни функции тангенса совпадают с корнями функции синуса.
И это 180𝑛 градусов, где 𝑛 — любое целое число. Итак, корни встречаются при любом целом кратном 180 градусам. Давайте начнем с рассмотрения первого свойства, которое говорит нам, что период касательного графа равен 180 градусам. Глядя на график (A), мы видим, что этот график имеет период 90 градусов, поэтому мы можем исключить этот график. Однако каждый из четырех других графиков имеет правильный период в 180 градусов.
Давайте рассмотрим второе свойство, которое говорит нам, что мы должны видеть вертикальные асимптоты при 90 градусах плюс 180𝑛 градусов. Теперь, поскольку мы уже проверили периодичность в 180 градусов, нам достаточно будет проверить, существует ли вертикальная асимптота в 90 градусов. Все варианты (C), (D) и (E) имеют вертикальную асимптоту, когда 𝑥 равно 90 градусам, а вариант (B) — нет. Мы видим, что когда 𝑥 равно 90 градусам, значение функции на графике (B) равно нулю. Итак, по этой причине мы можем исключить вариант (Б).
Далее нам нужно рассмотреть корни каждого графа.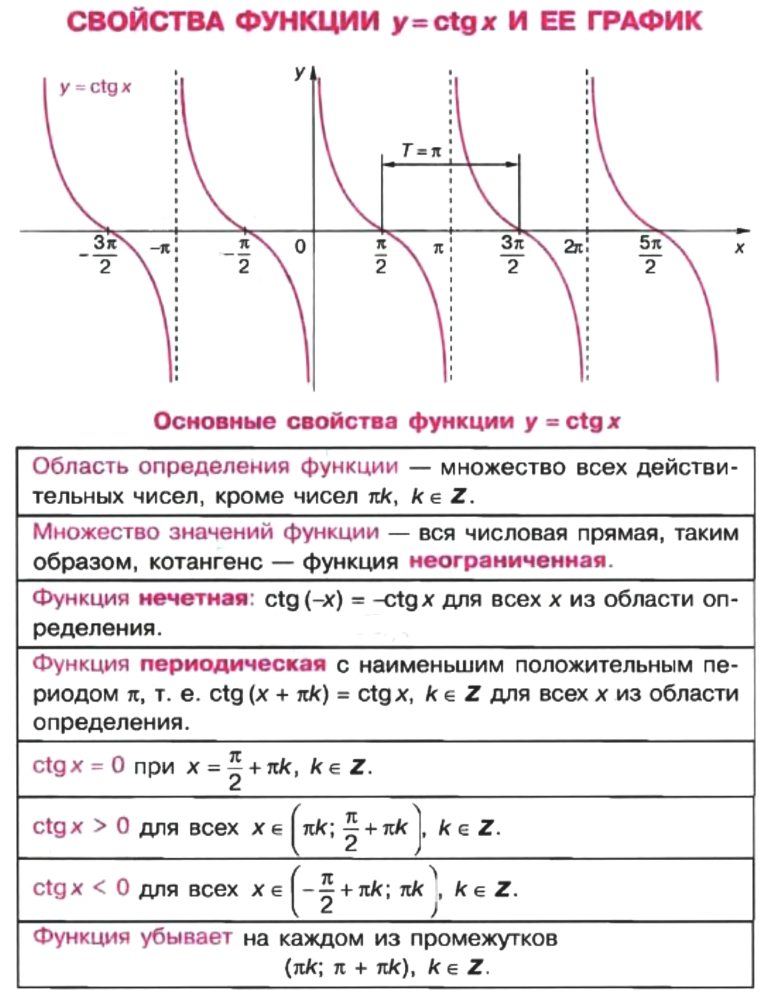
Мы знаем, что корни функции тангенса находятся под углом 180 𝑛 градусов, где 𝑛 — любое целое число. Опять же, поскольку мы уже проверили периодичность, достаточно будет проверить, равен ли нулю корень графа в точке 𝑥. Каждый из вариантов (D) и (E) имеет корень в точке 𝑥, равный нулю. График пересекает ось 𝑥 при этом значении, а вариант (C) — нет. Таким образом, мы можем исключить вариант (C).
У нас остается только два графика, варианты (D) и (E), каждый из которых имеет правильную периодичность, правильные вертикальные асимптоты и правильные корни. Чтобы различить два графика, отметим, что функция на графике (D) отрицательна в интервале между нулем и 90 градусов, а функция на графике (Е) положительна в этом интервале. Углы между 0 и 90 градусами представляют собой острые переплетения или углы в первом квадранте единичной окружности. Поскольку функция тангенса положительна для острых углов, это означает, что график (D) не является графиком функции тангенса.
Мы можем напомнить себе, почему тангенс положителен в первом квадранте, если вспомним, что координаты любой точки единичной окружности равны cos 𝜃, sin 𝜃, где 𝜃 — угол против часовой стрелки между положительной осью 𝑥 и радиусом, соединяющим которые указывают на происхождение.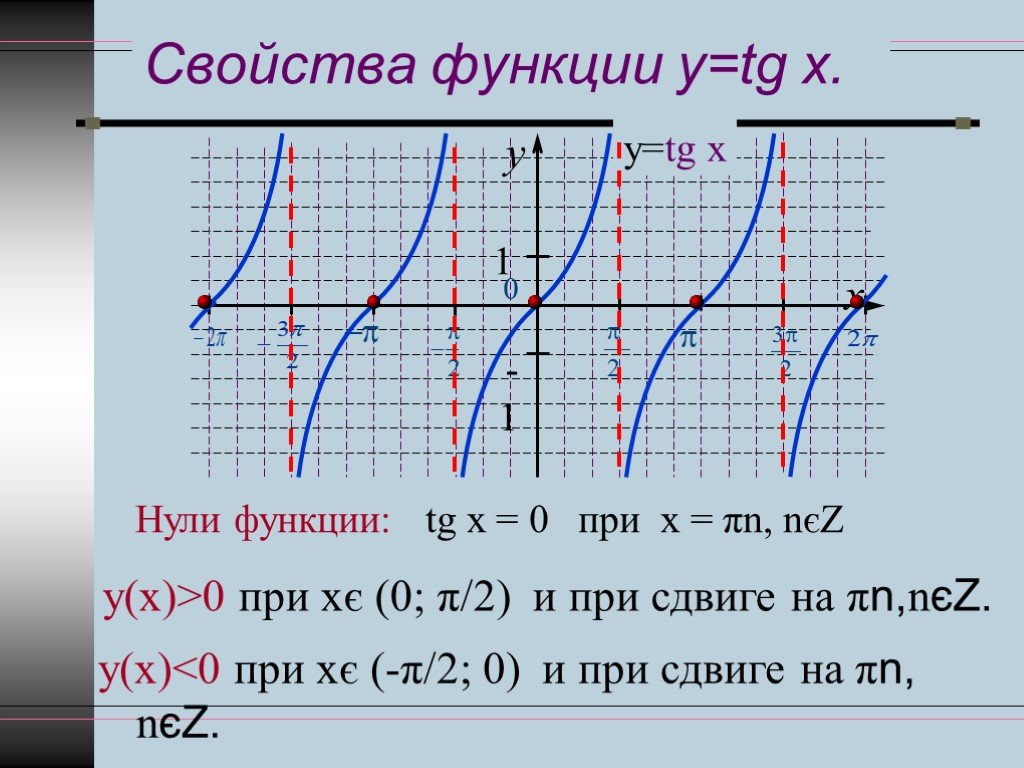
В первом квадранте и 𝑥-, и 𝑦-координаты положительны. Итак, косинус и синус оба положительны. Поскольку тангенс угла 𝜃 равен греху 𝜃 по косинусу 𝜃, отсюда следует, что тангенс также положителен в первом квадранте.
Итак, вспомнив ключевые свойства функции тангенса, мы обнаружили, что график 𝑦 равен tan 𝑥 является графиком (E).
реальный анализ — Что характеризует касательную?
Вы не можете доказать эквивалентность между точным, правильным математическим определением и неточным, интуитивным, неверным попыткой определения.
Представление о том, что касательная — это «линия, которая касается кривой только один раз», мягко говоря, абсурдна. Как уже отмечалось, это означало бы, что каждая строка , кроме , фактическая касательная — это «касательная» к горизонтальной линии $x=0$ в любой заданной точке. Что вертикальная линия, проходящая через начало координат, является касательной к оси $x$ в точке $(0,0)$ и т. д.
По сути, в основе вашего вопроса лежит много серьезных проблем.
Но самые важные из них:
- Неправда, что линия, касающаяся графика только один раз вблизи точки, является касательной.
Просто заметьте, что для любой функции $y=f(x)$ вертикальная линия $x=a$ пересекает график только один раз; однако она почти никогда не является касательной к графику. И многие линии обычно пересекают график только один раз: все линии между $y=x+1$ и $y=-x+1$ пересекают $y=\cos(x)$ только в точке $(0,1)$, но ни одна из них не является касательной к $y=\cos(x)$. 92\sin\left(\frac{1}{x}\right) &\text{if}x\neq 0,\\ 0 &\text{если}x=0 \end{массив}\right.$$ имеет $y=0$ в качестве касательной в точке $(0,0)$, но эта прямая пересекает график бесконечно много раз на любом интервале вида $(-\delta,\delta)$ при $\delta\gt 0 $.
Вы можете возразить, что это надуманная функция. Неважно . На самом деле, есть много функций, бесконечно много, для которых 2 не работает. Нет хорошего понятия «большинство функций», которое вы можете сформулировать, чтобы сделать 2 выше верным для «большинства функций».
Это просто неправильно.
Теперь лучше интуиция заключается в том, что касательная — это прямая линия, которая «очень близко соответствует графику» в точке и «около нее». Можем ли мы сделать это точным?
Да. Предположим, что $y=f(x)$ — граф, а $(a,f(a))$ — точка на графе. Нам нужна линия $y=mx+b$ с двумя свойствами:
$y=mx+b$ проходит через точку $(a,f(a))$. Для этого мы должны иметь $f(a) = ma + b$.
Из всех прямых, проходящих через точку $(a,f(a))$, касательная «наилучшим образом аппроксимирует» график $y=f(x)$. То есть относительная ошибка, полученная при использовании линии вместо функции, достигает $0$, когда $x$ приближается к $a$.
«Относительная ошибка» — это мера того, насколько велика ошибка по отношению к размеру входных данных. Если я скажу вам, что измеряю расстояние и ошибаюсь на целых пятьсот метров, это неплохо, если я пытаюсь вычислить, как далеко находится Луна, но это довольно паршивое приближение, если я пытаясь выяснить, как далеко экран компьютера от моего лица.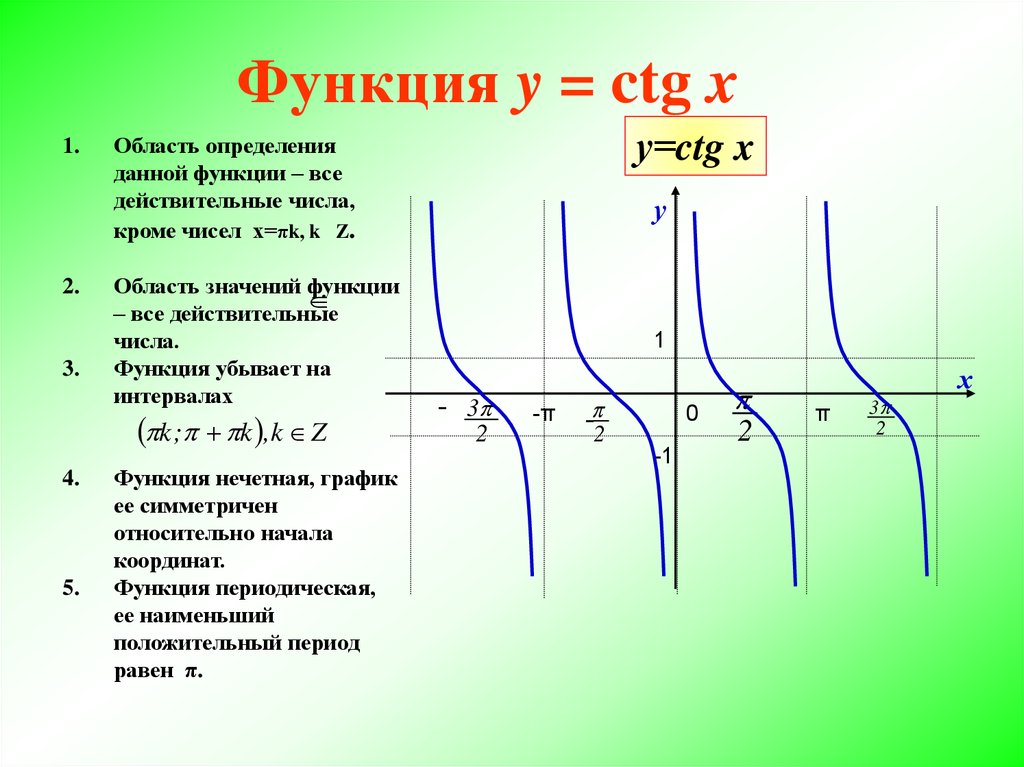
Абсолютная ошибка при использовании прямой $y=mx+b$ вместо функции $y=f(x)$ будет равна расстоянию между значением на прямой и значением на графике функции. То есть $E(x_0) = |(mx_0+b) — f(x_0)|$.
Поскольку мы пытаемся быть «близкими к $a$», относительная ошибка показывает, насколько велика эта абсолютная ошибка относительно того, насколько далеко мы от $a$. Таким образом, относительная ошибка в $x_0$: $$R(x_0) = \frac{E(x_0)}{|x-x_0|} = \left|\frac{(mx_0+b)-f(x_0)}{x-x_0}\right|.$ $
Определение. Прямая $y=mx+b$ касается графика $y=f(x)$ в точке $(a,f(a))$ тогда и только тогда, когда (i) прямая проходит через точка $(a,f(a))$; и (ii) относительная ошибка достигает $0$, когда $x_0$ приближается к $a$; то есть, $\lim\limits_{x\to a}R(x) = 0$.
С помощью этого определения довольно просто показать, что рассматриваемая линия должна иметь наклон, равный $f'(a) = \lim\limits_{x\to a}\frac{f(x)-f(a )}{x-a}$, поэтому должна быть строка $y=f'(a)(x-a) + f(a)$.