Функция значение: Что такое Функция в Алгебре?

Содержание

Что такое Функция в Алгебре?

Поможем понять и полюбить математику

Начать учиться

131.8K

Мы знаем, как соответствовать определенным чертам: быть вежливым, опрятным, инициативным. А как быть соответствиям между числовыми множествами — узнаем в этой статье про математические функции.

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину

у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу

x ставит в соответствие число y, которое в два раза больше, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю.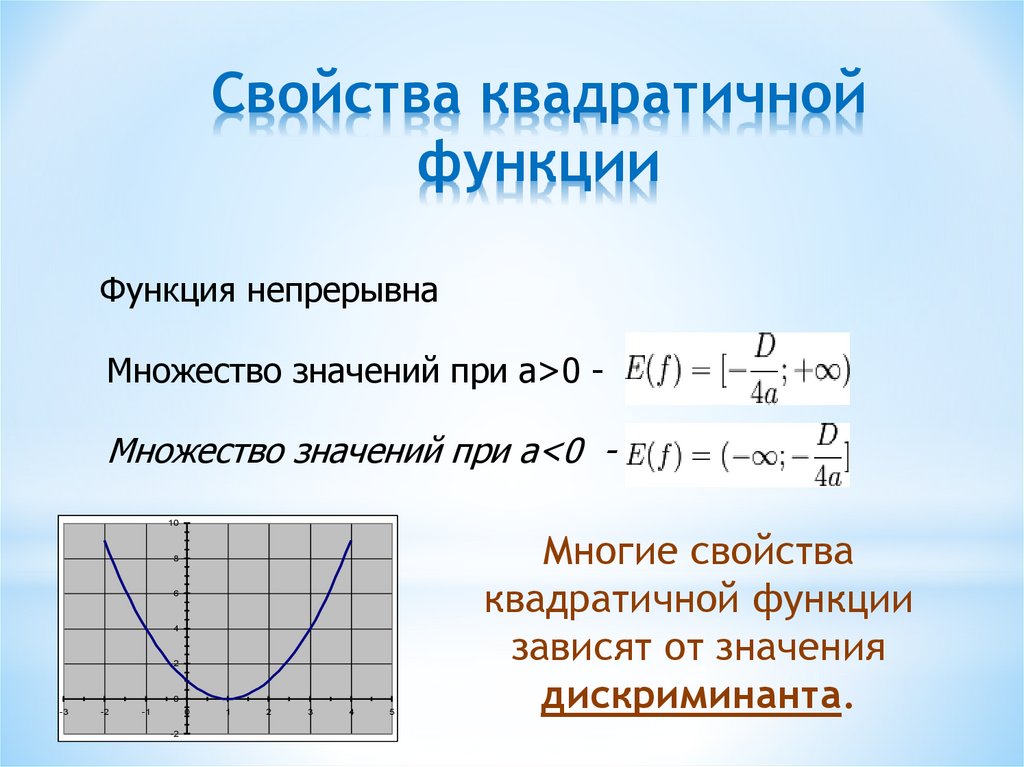

Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

-3

-2

-1

у = 3х +2

-7

-4

-1

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Способы задания функции

Функция — это зависимость «y» от «x», где «x» является переменной или

аргументом функции, а «y» — зависимой переменной или значением функции.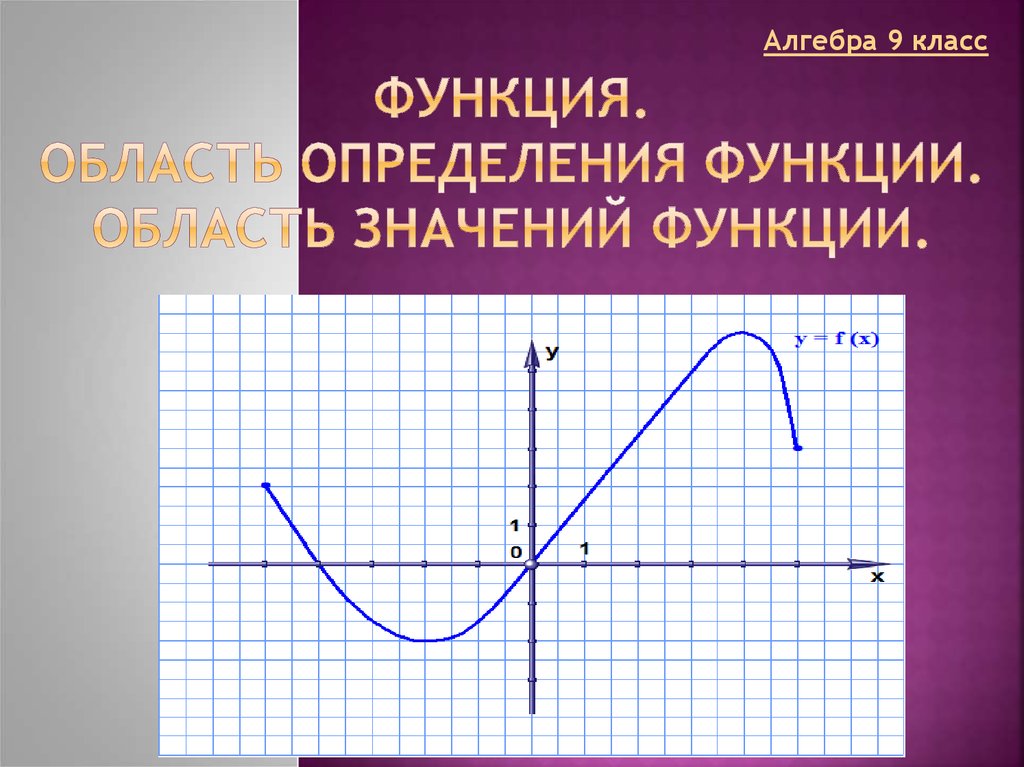

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задать функцию формулой

Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».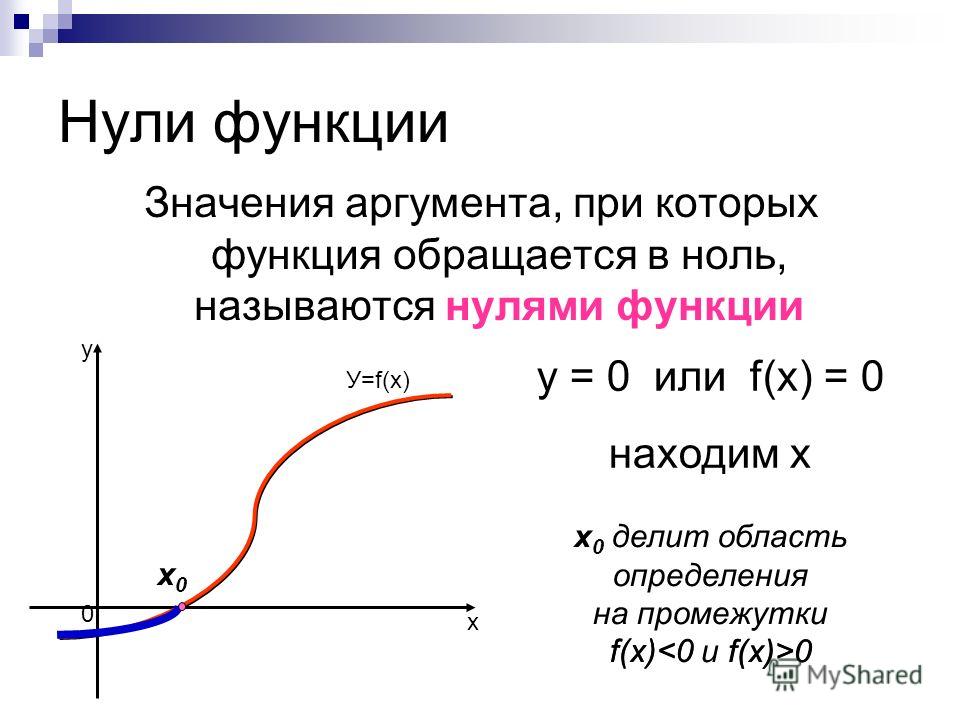

Пример. Дана функция: y(x) = 32x + 5.

Найти: значения функции «y» при x = 0.

Как рассуждаем:

Подставим в формулу вместо «x» число «0». Запишем расчет.

y(0) = 32 * 0 + 5 = 5

Ответ: y = 5.

Задать функцию таблицей

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Пример. Дана функция: y(x) = −x + 4.

Найти: значения «y» при x = -1, x = 0 и x = 1.

Как рассуждаем:

1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.

2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3

Не путаем знаки!

Когда в функцию нужно подставить отрицательное число — включаем внимательность на максимум. Возьмите нужное число в скобки, чтобы точно не потерять знак минус.

3. Запишем полученные результаты в таблицу:

x	y
−1	5
0	4
1	3

Так мы получили табличный способ задания функции y(x) = −x + 4.

Задать функцию графиком

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.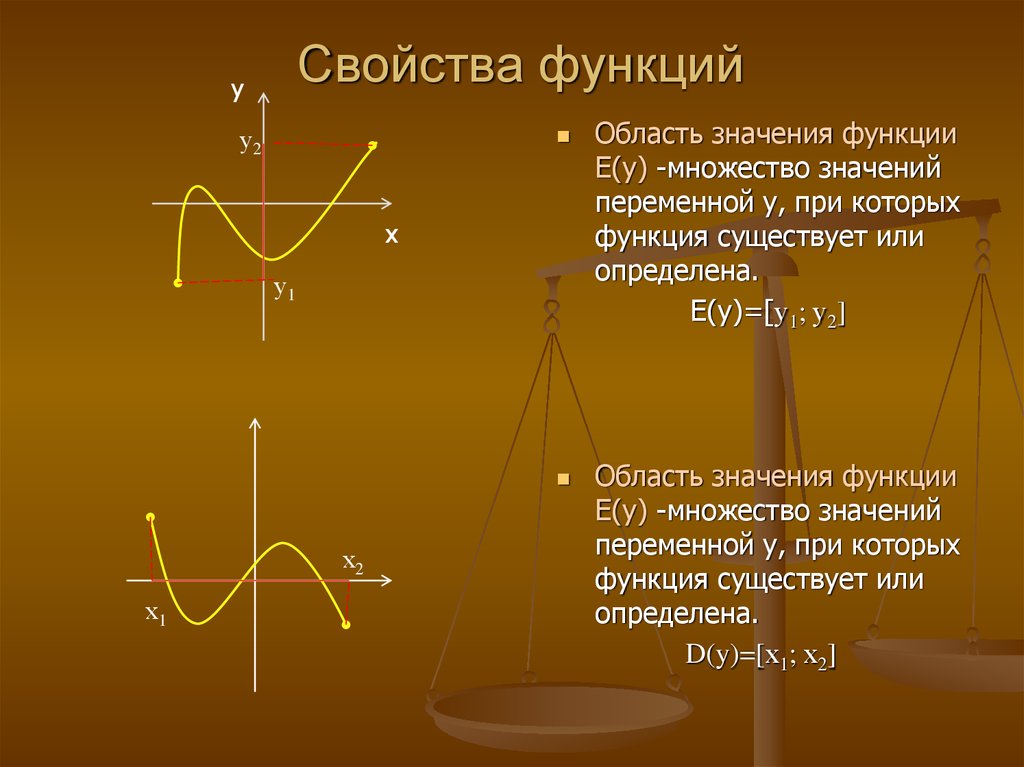

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».

Пример. Дана функция: y(x) = −2x + 1.

Найти: значения «y» для произвольных «x», а именно −1, 0, 1.

Как рассуждаем:

1. Подставим данные значения х в функцию и запишем результаты:

x	Рассчет
−1	y(−1) = −2 * (−1) + 1 = 2 + 1 = 3
0	y(0) = −2 * 0 + 1 = 0 + 1 = 1
1	y(1) = −2 * 1 + 1 = −2 + 1 = −1

2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).

Дадим названия каждой точке и запишем их координаты:

Имя точки	x	y
A	−1	3
B	0	1
C	1	−1

3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.

4. Соединим отмеченные точки прямой.

Проведенная прямая будет графиком функции y(x) = −2x + 1.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Иррациональные числа

К следующей статье

105.1K

Как найти координаты точки?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Функция ЗНАЧЕН — Служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще. ..Меньше

В этой статье описаны синтаксис формулы и использование значения в Microsoft Excel.

Описание

Преобразует строку текста, отображающую число, в число.

Синтаксис

ЗНАЧЕН(текст)

Аргументы функции ЗНАЧЕН описаны ниже.

Примечания

Текст может быть в любом формате, допускаемом в Microsoft Excel для числа, даты или времени. Если текст не соответствует ни одному из этих форматов, функция ЗНАЧЕН возвращает значение ошибки #ЗНАЧ!.
Обычно функцию ЗНАЧЕН не требуется использовать в формулах, поскольку необходимые преобразования значений выполняются в Microsoft Excel автоматически. Эта функция предназначена для обеспечения совместимости с другими программами электронных таблиц.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=ЗНАЧЕН(«1 000 ₽»)	Числовой эквивалент текстовой строки «1 000 ₽»	1000
=ЗНАЧЕН(«16:48:00»)-ЗНАЧЕН(«12:00:00»)	Числовой формат, эквивалентный 4 часам 48 минутам — «16:48:00»-«12:00:00» (0,2 или 4:48)	0,2

Функция Таблица значений Калькулятор — Указанная F(x)

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор функций (таблица значений)

Инструмент для вычисления различных значений функции из ее уравнения f(x) и заданных значений для вычислить их изображения с помощью калькулятора функций и составить таблицу значений.

Результаты

Калькулятор функций (таблица значений) — dCode

Теги: Функции

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор функций

Функция f=
Переменная
Отображение числового (приблизительного) значения, если возможно

Рассчитать f для

Вычислить f для переменной =

Генератор таблиц значений

Вычислить f для нескольких значений переменных

Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)

См. также: Образ функции — Прообраз функции — Калькулятор

Найти уравнение по значениям

⮞ Перейдите к: Функция поиска уравнений

Ответы на вопросы (FAQ)

Что такое таблица значений? (Определение)

Массив значений — это список чисел, к которым применяется функция. Он связывает число со значением, полученным функцией, и дает представление о ее поведении. 92 $ has for table of values

x	f(x)
1	1
2	4
3	9
4	16

Как вычислить значения функции?

Значение (или образ) функции $f(x)$ — это значение функции $f$ для указанного значения $x$.

Пример: $ f(x) = 3x $ тогда при $ x = 2 $ значение $ f(2) = 6 $

Расчет значений можно производить на всей области определения функции. Любое вычисление значения за пределами домена определения приведет к ошибке.

Совокупность значений может быть представлена в виде кривой, которая является графическим представлением функции.

Как вычислить прообраз значения?

В dCode есть инструмент для вычисления прообраза по функции, т.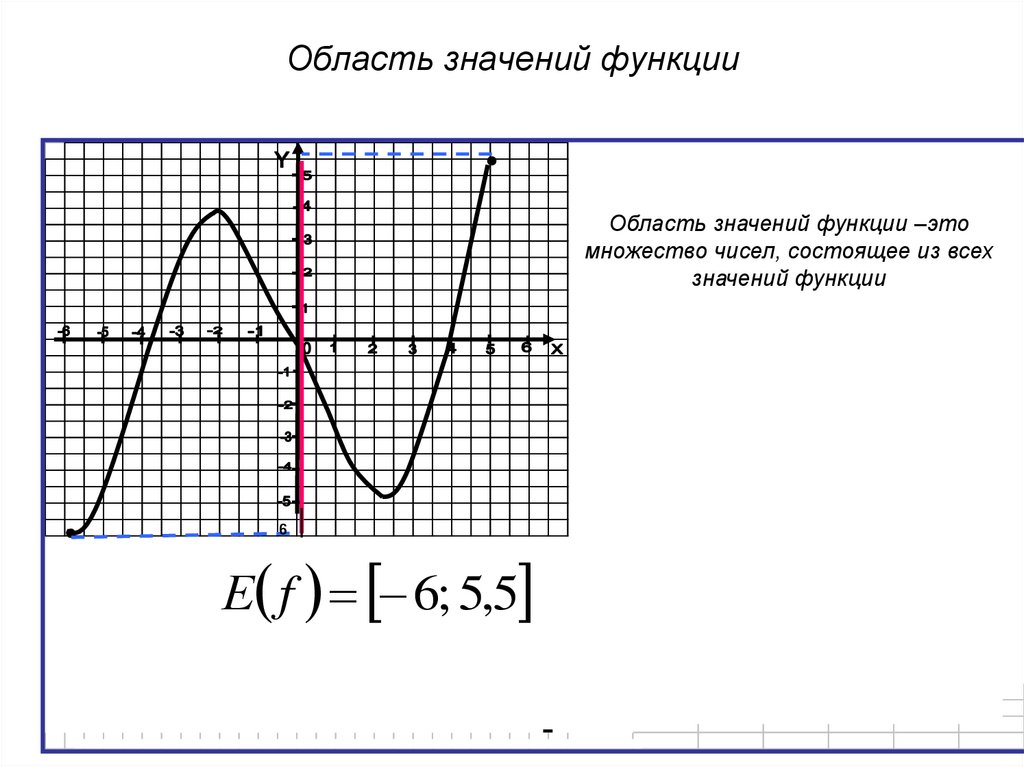 е. значений $ x $, для которых функция имеет заданное значение.

Как применить функцию ко всей таблице значений?

Обычно требуется, чтобы применил функцию к множеству/последовательности/списку значений, например к столбцу Excel. Указание математической функции для применения, и dCode автоматически рассчитает все значения.

Исходный код

dCode сохраняет за собой право собственности на исходный код «Калькулятор функций (таблица значений)». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор функций (Таблица значений)», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор), или функции «Калькулятор функций (Таблица значений)» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab, и т. д.), а все загрузки данных, сценарии или доступ к API для «Калькулятора функций (таблица значений)» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Калькулятор функций (Таблица значений)» или любых его результатов разрешено, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .txt осуществляется нажатием значка export
Ссылка на источник (библиография):
18.04.2023, https://www.dcode.fr/function-value-calculator

Сводка

Калькулятор функций
Поиск уравнения по значениям
Что такое таблица значений? (Определение)
Как вычислить значения функции?
Как вычислить прообраз значения?
Как применить функцию ко всей таблице значений?

Похожие страницы

Прообраз функции
Изображение функции
Функция поиска уравнения
Калькулятор
Polynomial Degree
Error Function
Domain of Derivative of a Function
DCODE’S TOOLS LIST

Support

Paypal
Patreon
More

Forum/Help

Keywords

calculation, функция,изображение,список,таблица,значение,число,операция

Ссылки

▲

Функция ЗНАЧЕНИЕ — служба поддержки Майкрософт

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Больше. ..Меньше

В этой статье описаны синтаксис формулы и использование ЗНАЧЕНИЕ функция в Microsoft Excel.