Косинус всегда положительный. Самостоятельная работа с обратной связью
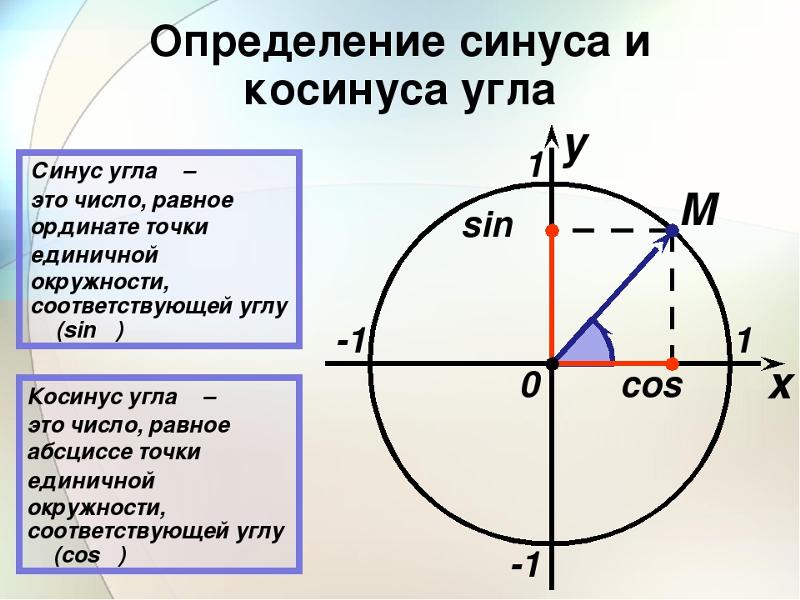
Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а .
Синус — функция числа x . Ее область определения
Область значений синуса — отрезок от -1 до 1 , так как любое число этого отрезка на оси ординат является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек.
Период синуса
Знак синуса:
1. синус равен нулю при , где n — любое целое число;
2. синус положителен при , где n — любое целое число;
3. синус отрицателен при
Где n — любое целое число.
Синус — функция нечетная x и -x , то их ординаты — синусы — окажутся также противоположными. То есть для любого x .
1. Синус возрастает на отрезках , где
2. Cинус убывает на отрезке , где n — любое целое число.
При ;
при .
Косинус
Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинусом угла в а радиан называется косинус числа а .
Косинус — функция числа. Ее область определения — множество всех чисел, так как у любого числа можно найти ординату изображающей его точки.
Область значений косинуса — отрезок от -1 до 1 , так как любое число этого отрезка на оси абсцисс является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек.
Период косинуса равен . Ведь через каждые положение точки, изображающей число, в точности повторяется.
Знак косинуса:
1. косинус равен нулю при , где n — любое целое число;
2.
3. косинус отрицателен при , где n — любое целое число.
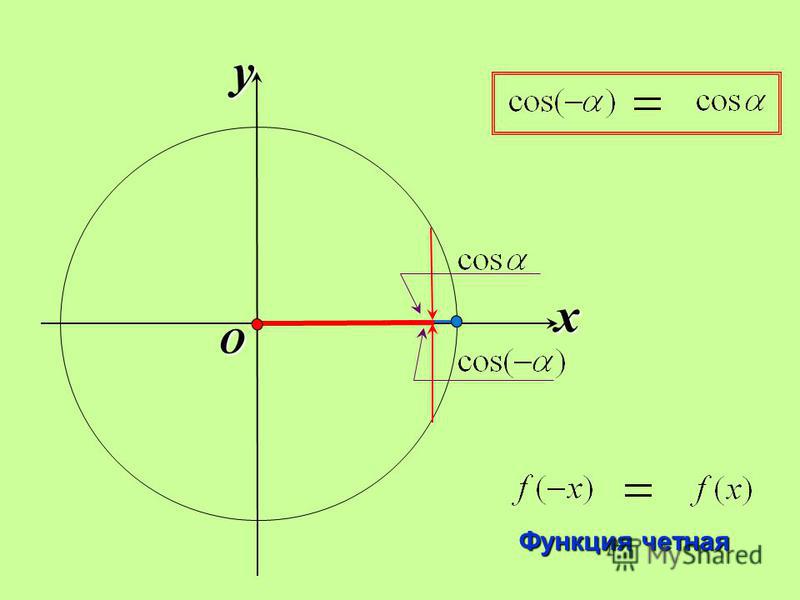
Косинус — функция четная . Во-первых, область определения этой функции есть множество всех чисел, а значит, симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x , то их абсциссы — косинусы — окажутся равными. То есть
для любого x .
1. Косинус возрастает на отрезках , где n — любое целое число.
2. Косинус убывает на отрезках , где n — любое целое число.
при ;
при .
Тангенс
Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: .
Тангенсом угла в а радиан называется тангенс числа а .
Тангенс — функция числа. Ее
 И так как косинус равен нулю при , то , где .
И так как косинус равен нулю при , то , где .Область значений тангенса
Период тангенса x (не равные ), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию тангенсов в некоторой точке t . Вот и получится, что , то есть число является периодом тангенса.
Знак тангенса: тангенс — отношение синуса к косинусу. Значит, он
1. равен нулю, когда синус равен нулю, то есть при , где n — любое целое число.
2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при , где а — любое целое число.
3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при , где а — любое целое число.
Тангенс — функция нечетная . Во-первых, область определения этой функции симметрична относительно начала отсчета.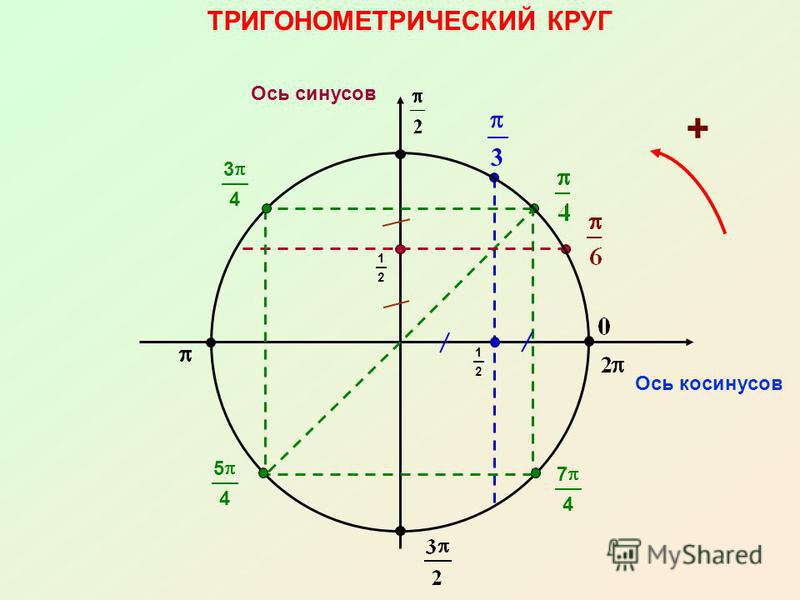 А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .
А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .
Вот и получилось, что .
Значит, тангенс возрастает на каждом участке своей области определения , то есть на всех интервалах вида , где а — любое целое число.
Котангенс
Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: . Котангенсом угла в а радиан называется котангенс числа а . Котангенс — функция числа. Ее область определения — множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при , то , где
Область значений котангенса — множество всех действительных чисел.
Период котангенса равен . Ведь если взять любые два допустимые значения x (не равные ), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию котангенсов в некоторой точке t . Вот и получится, что , то есть, что число является периодом котангенса.
Вот и получится, что , то есть, что число является периодом котангенса.
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Yandex.RTB R-A-339285-1
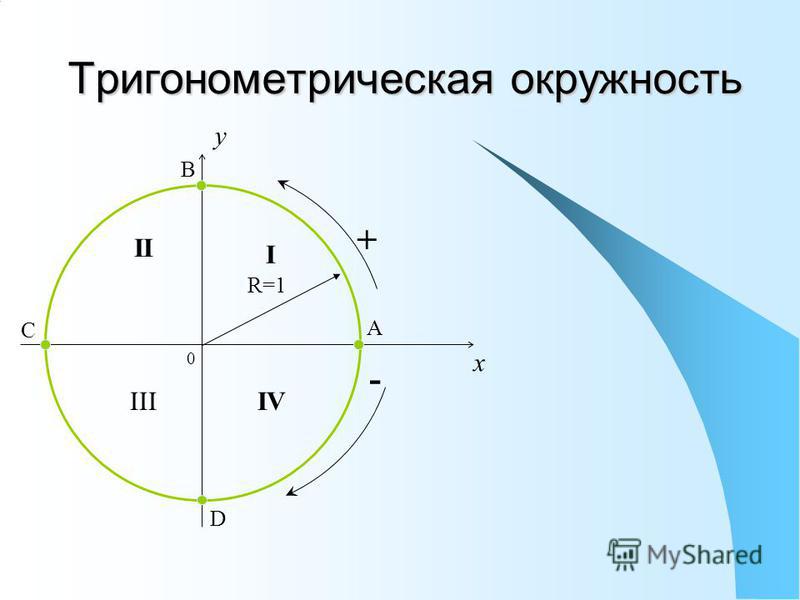
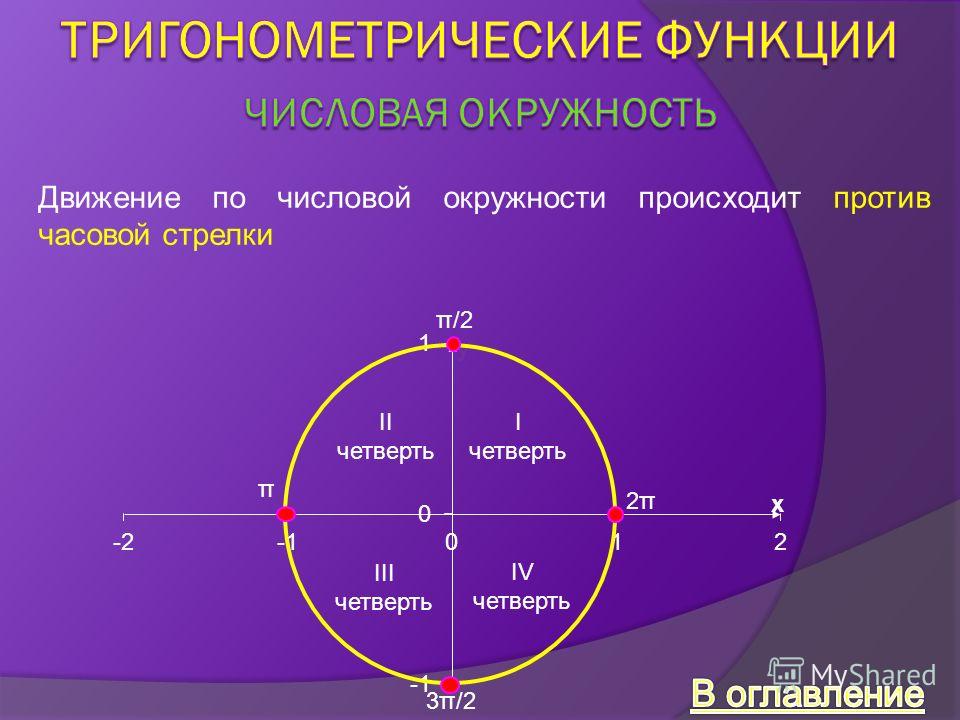
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
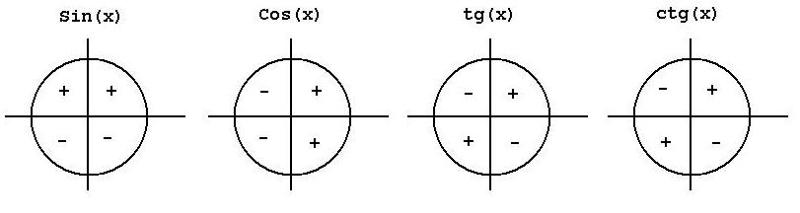
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций.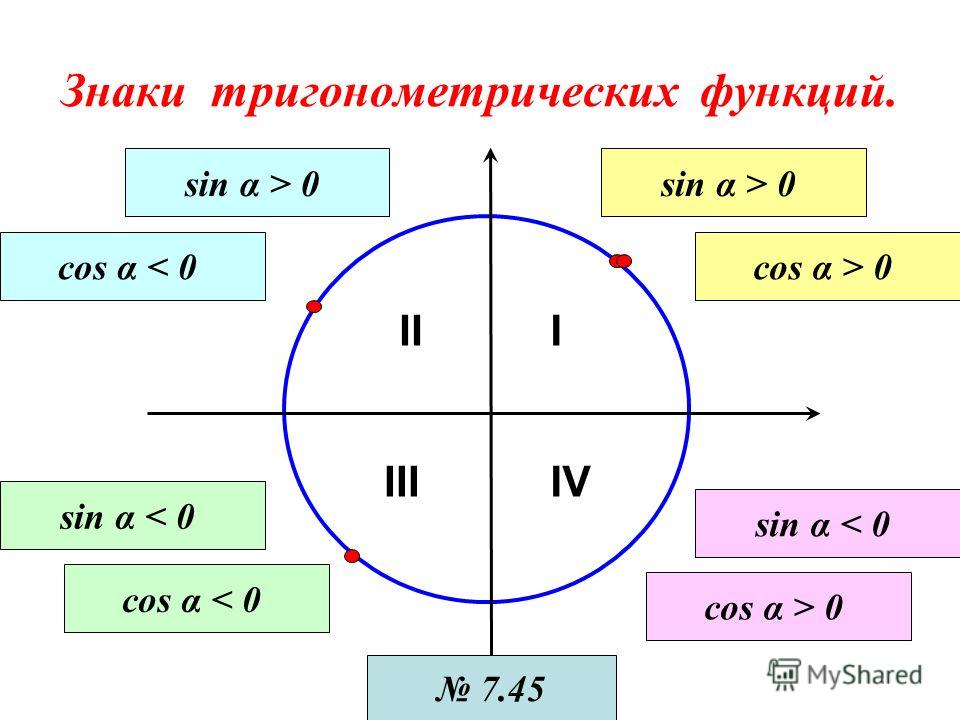 Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)
Вновь обратимся к единичной окружности.
Точка A 1 (x , y) — результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , — y) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая — (x , — y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.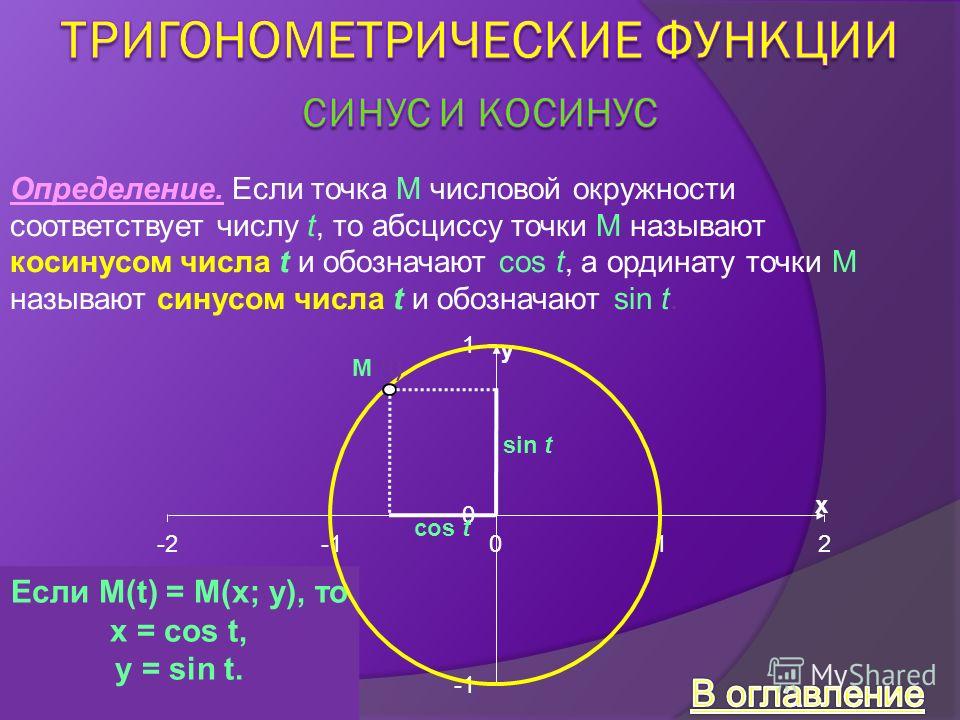
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы.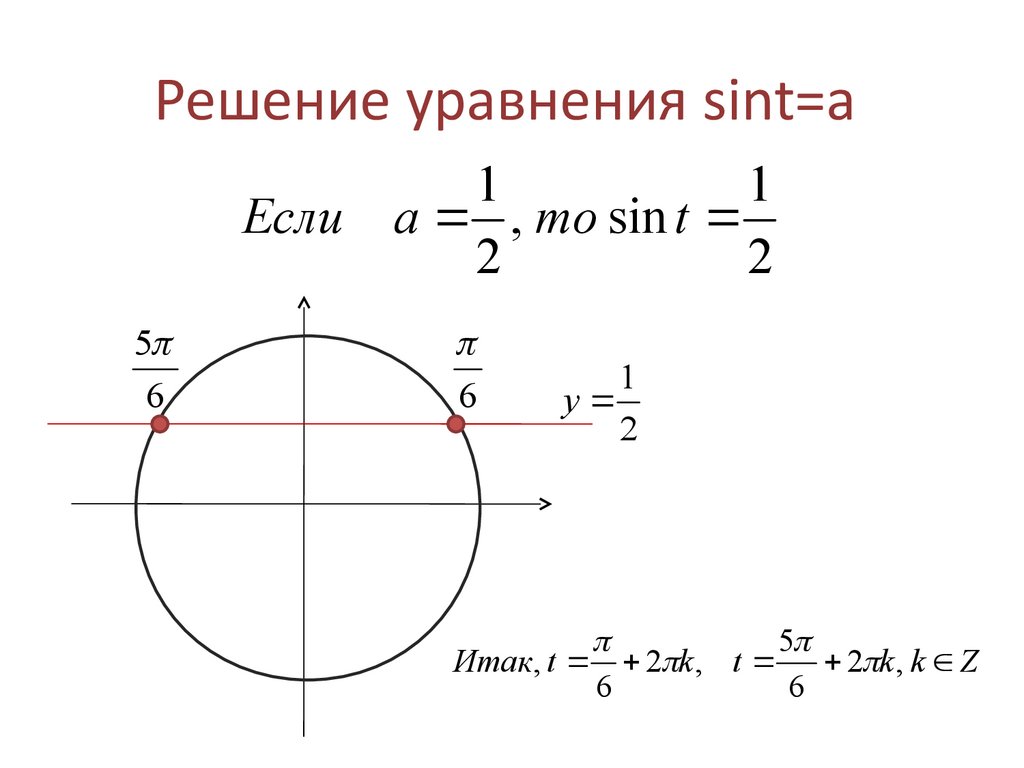 И вы скоро будете знать как!
И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.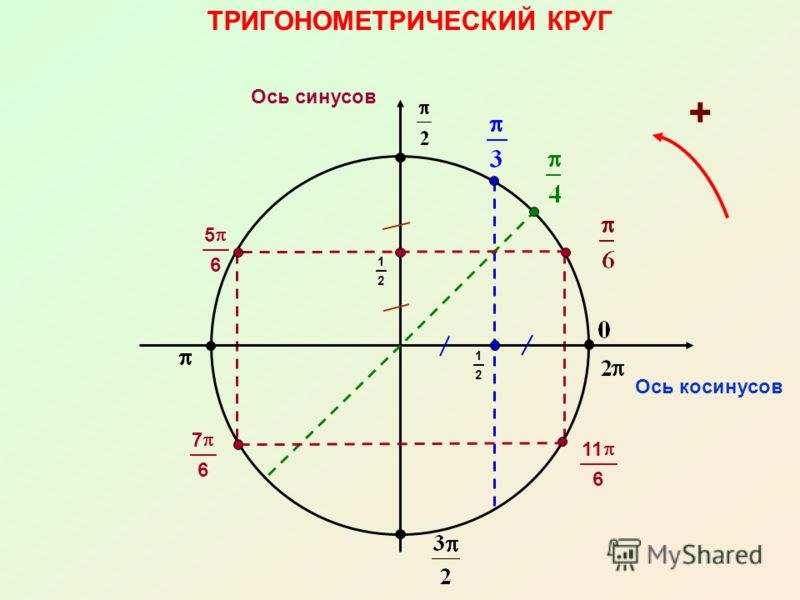
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
| ГОСТы, СНиПы Карта сайта TehTab. Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
| |||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||
Синус, косинус и тангенс в четырех квадрантах
Помните эту картинку? Мы использовали его, чтобы запомнить знаки трех основных тригонометрических соотношений — синуса, косинуса и тангенса в четырех квадрантах.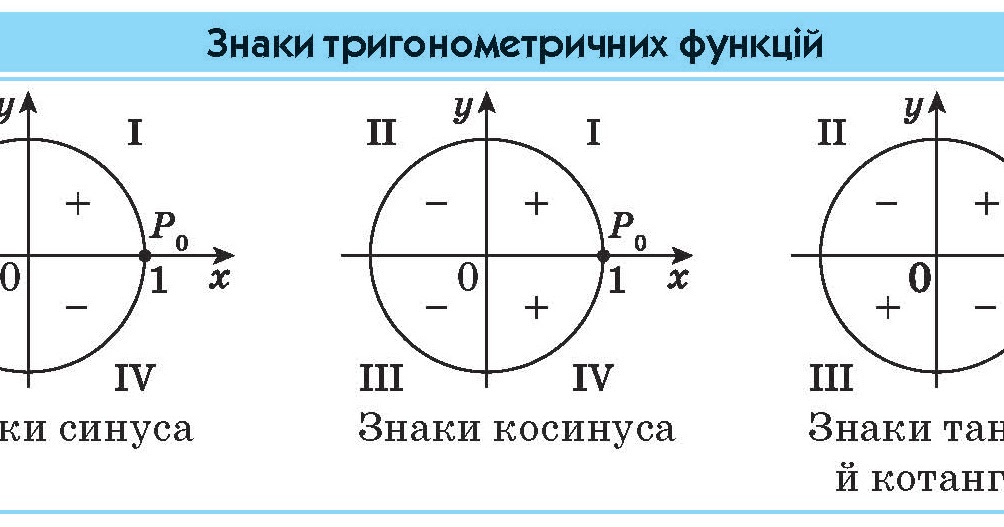 Каждая буква ( ASTC или CAST ) представляет собой тригонометрическую функцию, положительную в каждом квадранте, например C озин положителен в 4-м квадранте и т. д., а A все три положительны в первом квадранте.
Каждая буква ( ASTC или CAST ) представляет собой тригонометрическую функцию, положительную в каждом квадранте, например C озин положителен в 4-м квадранте и т. д., а A все три положительны в первом квадранте.
Студенты иногда использовали мнемонические приемы, чтобы запомнить порядок:
- A LL S CIENCE T WHINEERS C
- A LL S TUDENTS T AKE C Gemistr принимать разные знаки в разных квадрантах?
Стороны прямоугольного треугольника
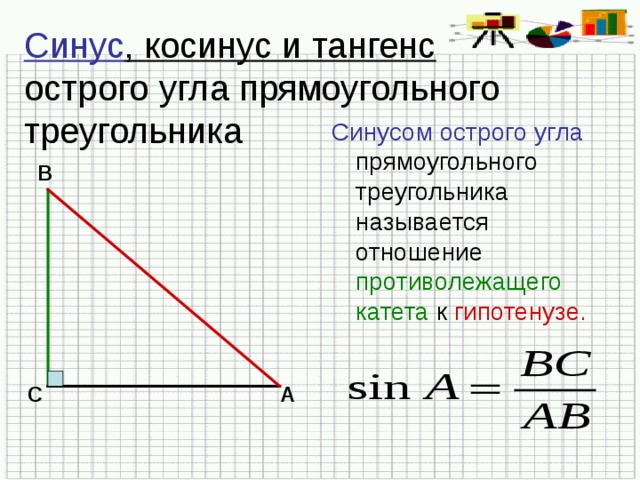
Сначала нам нужно определить эти отношения (или функции тригонометрии), а для этого будет проще, если мы назовем стороны треугольника.
Треугольник (с ненулевой площадью) может иметь не более одного прямого угла (90°). Для таких прямоугольных треугольников трем сторонам присваиваются специальные имена относительно одного из углов, отличных от 90° (назовем его углом a ):
- Гипотенуза – сторона, расположенная напротив прямого угла
- Смежная – сторона, примыкающая к углу a , не являющаяся гипотенузой
- Противоположная – сторона, расположенная напротив угла a
Для одного конкретного угла a , напр.
 a = 30°, три основные тригонометрические функции — синус, косинус и тангенс — являются отношением длин двух из трех сторон:
a = 30°, три основные тригонометрические функции — синус, косинус и тангенс — являются отношением длин двух из трех сторон:- Синус: sin(a) = Противоположная / гипотенуза
- Косинус: cos( a) = Смежный / Гипотенуза
- Касательная: tan(a) = Противоположный / Смежный
Все это хорошо, когда угол a находится между 0° и 90°. Что происходит, когда угол a не острый?
Синус, косинус и тангенс в квадранте 1
Разместим прямоугольный треугольник на стандартных декартовых осях для угла a , который находится между 0° и 90° (мы говорим, что угол a находится в квадранте-1 ). На всех приведенных ниже рисунках длины нормированы на гипотенузу, т. Е. Гипотенуза всегда имеет длину 1,0 и показана как радиус единичной окружности.
Для угла a , который находится в квадранте 1, мы видим, что смежная сторона лежит на «оси х» и находится в направлении положительной х.
 При этом сторона , противоположная , также находится в направлении положительного y. Следовательно, все три стороны – прилежащая, противолежащая и гипотенуза – все положительны. Таким образом, все три отношения ( A ) положительны.
При этом сторона , противоположная , также находится в направлении положительного y. Следовательно, все три стороны – прилежащая, противолежащая и гипотенуза – все положительны. Таким образом, все три отношения ( A ) положительны.Синус, косинус и тангенс в квадранте 2
Когда угол a находится в квадранте 2 (между 90° и 180°), однако, 9Сторона 0003 , смежная со стороной , расположена в отрицательном направлении по оси x, а сторона , противоположная стороне , все еще находится в положительном направлении по оси y. Следовательно, косинус и тангенс отрицательны, и только синус ( S ) положителен.
Синус, косинус и тангенс в квадранте 3
Когда угол a находится в квадранте 3 (между 180° и 270°), обе стороны , примыкающие к , и , противоположные 9004, отрицательные 900.
 Следовательно, синус и косинус отрицательны, а поскольку тангенс ( T ) — деление двух отрицательных чисел, это единственная положительная тригонометрическая функция.
Следовательно, синус и косинус отрицательны, а поскольку тангенс ( T ) — деление двух отрицательных чисел, это единственная положительная тригонометрическая функция.Синус, косинус и тангенс в квадранте 4
Наконец, когда угол a находится в квадранте 4 (между 270° и 360°), смежная сторона направлена назад вдоль положительного направления x, в то время как противоположная сторона по-прежнему находится в положительном направлении оси Y. Следовательно, синус и тангенс отрицательны, и только косинус ( C ) положителен.
Приложение Trigonometry Quadrant
Это простое интерактивное приложение, иллюстрирующее изменение знаков трех основных тригонометрических соотношений — синуса, косинуса, тангенса в четырех квадрантах. Поверните угол мышью или коснитесь, чтобы показать углы в разных квадрантах, и посмотрите, как значения синуса, косинуса и тангенса изменяются со сторонами прямоугольного треугольника.

Этот интерактивный манипулятор также является отличным способом показать три отношения как функции относительно угла a , т. е. прокручивая угол от 0° до 360°, мы видим, что значения трех тригонометрических функций описывают стандартные кривые синуса, косинуса и тангенса.
Как найти положительный косинус
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Тригонометрия » косинус » Как найти положительный косинус
В каких квадрантах значение косинуса положительное?
Возможные ответы:
4 -й только
. Пояснение:
Косинус положительный в квадрантах 1 st и 4 th и отрицательный в квадрантах 2 nd и 3 rd
Сообщить об ошибке
Что из следующего равно ?
Возможные ответы:
Правильный ответ:
Объяснение:
Здесь мы используем коэффициенты SOHCAHTOA и тот факт, что csc x = 1 / sin x.

Косинус x = длина прилежащей стороны / длина гипотенузы
Косеканс x = 1 / sin x = гипотенуза / противолежащая сторона
(прилежащая / гипотенуза) * (гипотенуза / противолежащая) = прилежащая / противолежащая = котангенс x.
Сообщить об ошибке
и находится между и . Какова ценность ?
Возможные ответы:
Правильный ответ:
Объяснение:
Для к , мы это знаем . Итак, возникает вопрос, каково значение , где . Следовательно, он спрашивает, каково значение , которое .
Сообщить об ошибке
С точностью до , чему равен косинус от начала координат до ? Допустим вращение против часовой стрелки.
Возможные ответы:
Правильный ответ:
Объяснение:
Если нужно достичь точки , то мы можем представить себе прямоугольный треугольник со сторонами и , и гипотенузой .


 ru
ru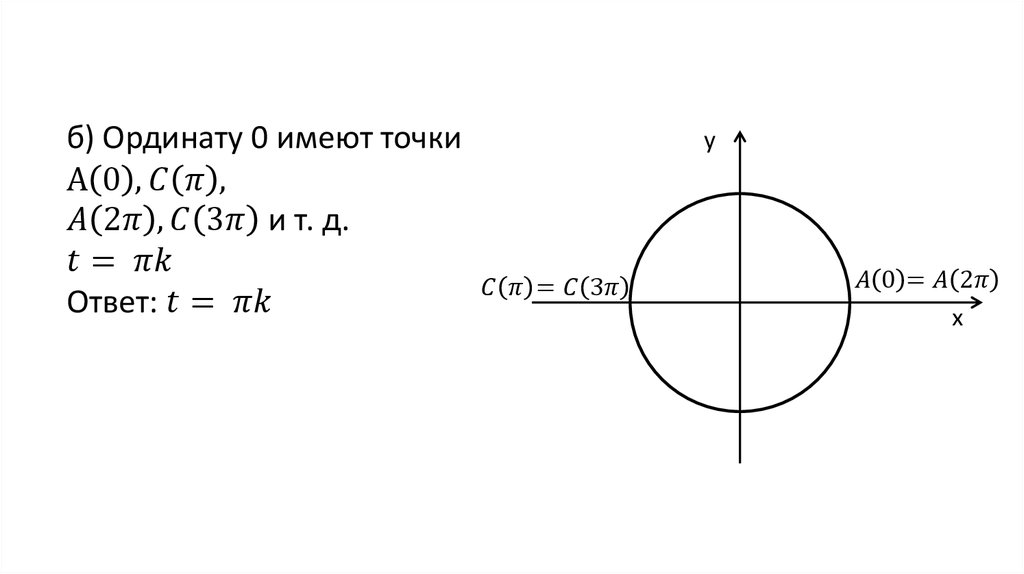
 ru:
ru: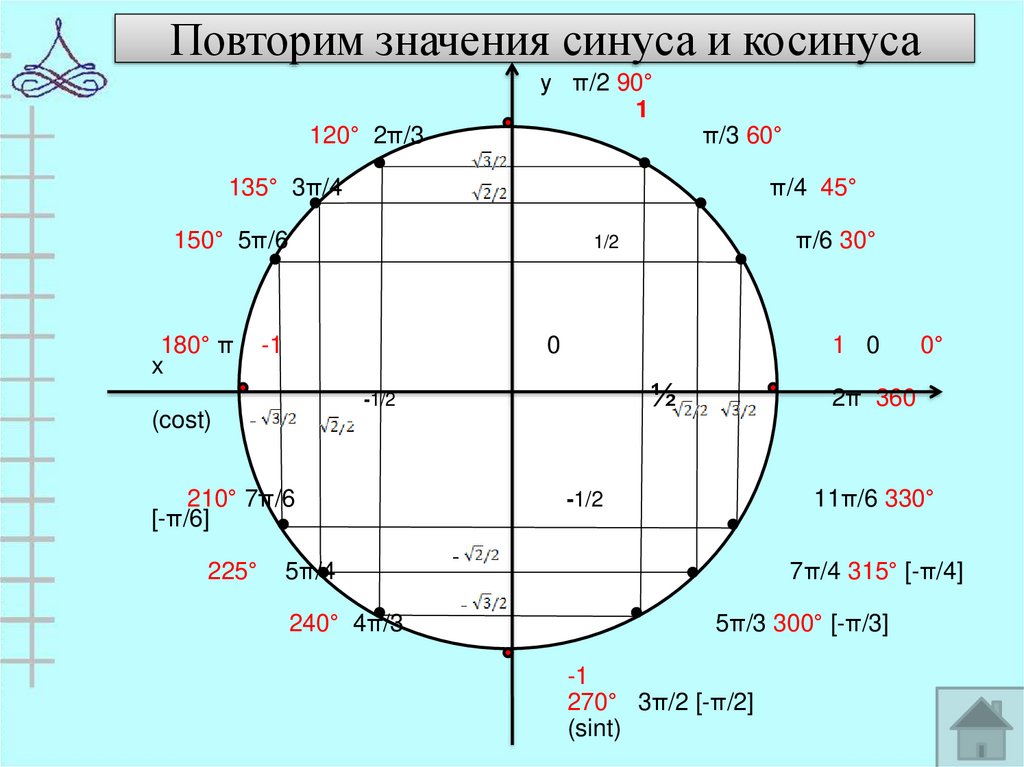 a = 30°, три основные тригонометрические функции — синус, косинус и тангенс — являются отношением длин двух из трех сторон:
a = 30°, три основные тригонометрические функции — синус, косинус и тангенс — являются отношением длин двух из трех сторон: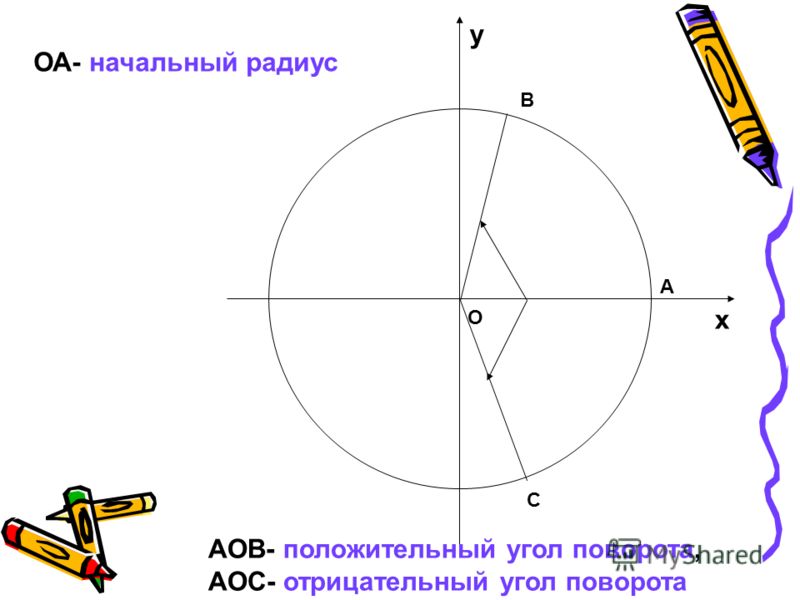 При этом сторона , противоположная , также находится в направлении положительного y. Следовательно, все три стороны – прилежащая, противолежащая и гипотенуза – все положительны. Таким образом, все три отношения ( A ) положительны.
При этом сторона , противоположная , также находится в направлении положительного y. Следовательно, все три стороны – прилежащая, противолежащая и гипотенуза – все положительны. Таким образом, все три отношения ( A ) положительны.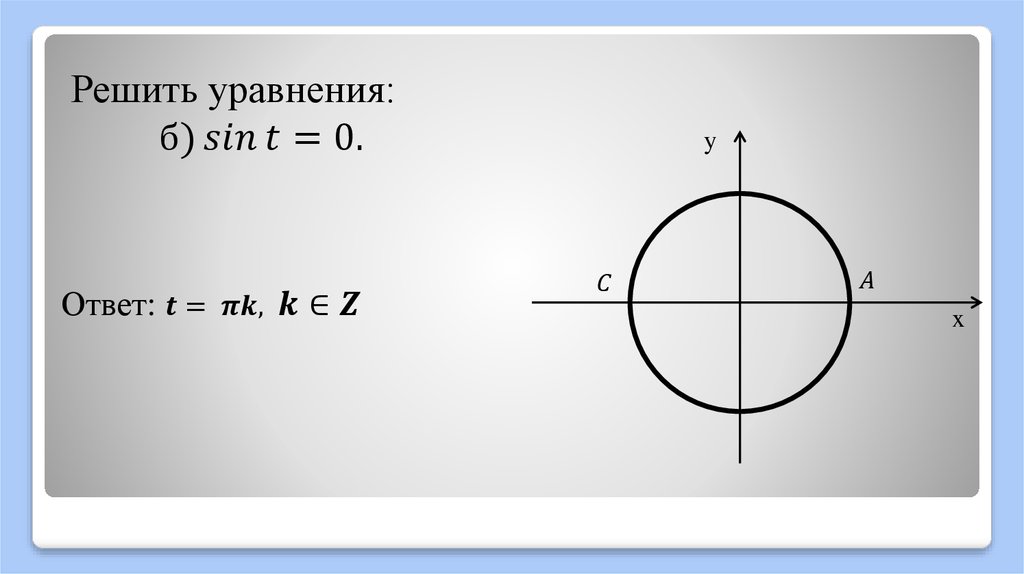 Следовательно, синус и косинус отрицательны, а поскольку тангенс ( T ) — деление двух отрицательных чисел, это единственная положительная тригонометрическая функция.
Следовательно, синус и косинус отрицательны, а поскольку тангенс ( T ) — деление двух отрицательных чисел, это единственная положительная тригонометрическая функция.