Что такое tg в геометрии: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

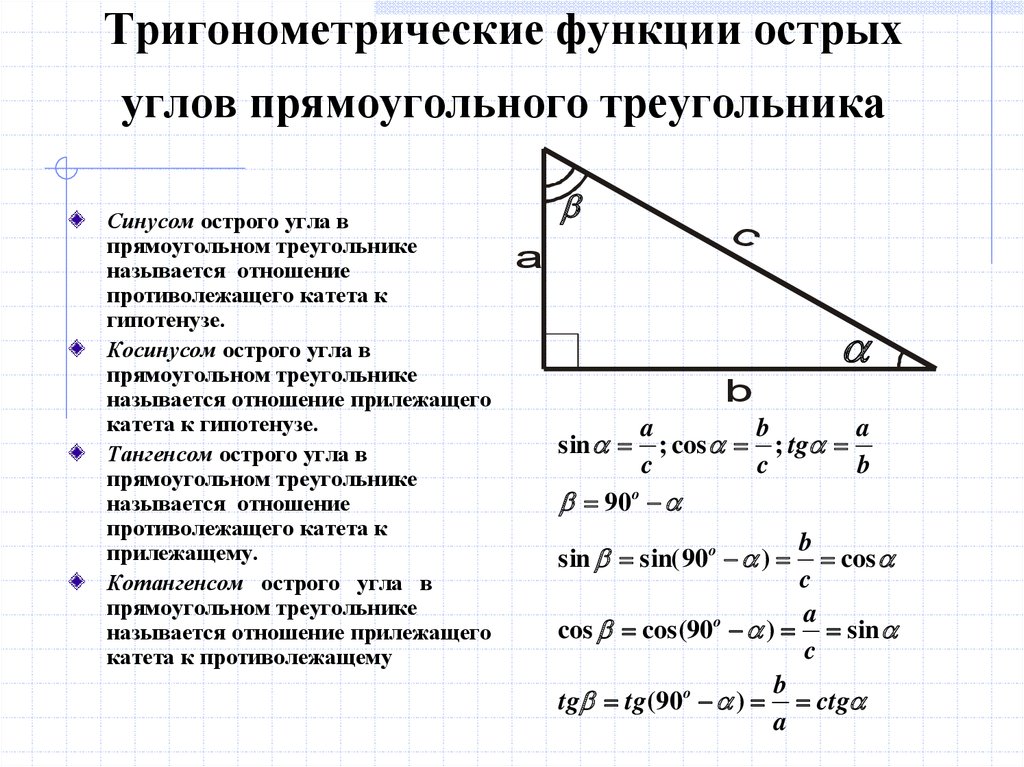
Конспект урока по геометрии 9 класс»Синус ,косинус ,тангенс угла»

II. Изучение нового материала.

1.                 Понятие единичной полуокружности (рис. 290).(слайд  4)

Введем прямоугольную систему координат Оху и построим полуокружность радиуса 1 с центром в начале координат, расположенную в первом и втором квадрантах. Данная полуокружность называется единичной (см. рис. 290 в учебнике). (слайд )

Запись в тетрадях:

Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.

 2. Понятие синуса и косинуса для углов 0° ≤ a ≤ 180°  (слайд 5):

   Из точки О проведем луч h , пересекающий единичную полуокружность в точке М (х;у). обозначит буквой a угол между лучом h и положительной полуосью абсцисс.

        Если луч h совпадает с положительной полуосью абсцисс, то будем считать, что a = 0 °.

Если угол a острый, то из прямоугольного треугольника DOM имеем,

sin a =  , a cos a = .

Но OM = 1, MD  это ордината, OD — абсцисса, поэтому  sin a ордината у точки М, cos a это абсцисса х точки М.

 

Запись на доске и в тетрадях:

Если угол a острый, то из прямоугольного треугольника DOM имеем,

sin a =  , a cos a = .

Но OM = 1, MD = y, OD = x,

поэтому sin a = y, cos a = x.   (1)

Если угол a прямой, тупой или развернутый, это углы AOC, AON и AOB на рисунке 290 учебника, или a = 0 °, то синус и косинус угла a также определим по формулам (1).

Таким образом, для любого угла a из промежутка 0° ≤ a ≤ 180° синусом угла a называется ордината у точки М, косинусом угла a — абсцисса х точки М.

Так как координаты (х; у) точек единичной полуокружности заключены в промежутках 0 ≤ у ≤ 1, — 1 ≤ х ≤ 1, то для любого a из промежутка 0° ≤ a ≤ 180° справедливы неравенства:

0 ≤ sin a ≤ 1, — 1≤ cos a ≤ 1

Запись в тетрадях:

Т.к. 0 ≤ у ≤ 1, — 1 ≤ х ≤ 1, то для любого a из промежутка 0° ≤ a ≤ 180°

0                   ≤ sin a ≤ 1, — 1≤ cos a ≤ 1.

 

3.Нахождение значений синуса и косинуса для углов 0°, 90° и 180

°.(слайд 6)

 А теперь найдем значения синуса и косинуса для углов 0°, 90° и 180°. Для этого рассмотрим лучи OA, OC и OB, соответствующие этим углам (см. рис.290). Так как точки А, С и B имеют координаты А (1; 0), С (0; 1), В (-1; 0), то

Sin 0° = 0, sin 90° = 1, sin 180° = 0, cos 0° = 1, cos 90° = 0, cos 180° = — 1. (2)

 

Запись в тетрадях:

 

Sin 0° = 0, sin 90° = 1, sin 180° = 0, cos 0° = 1, cos 90° = 0, cos 180° = — 1

 

4. Определение тангенса угла  a  (a

 90°) (слайд 7,8):

tg  a  =  при  a   90°; tg 0° = 0; tg 180° = 0.

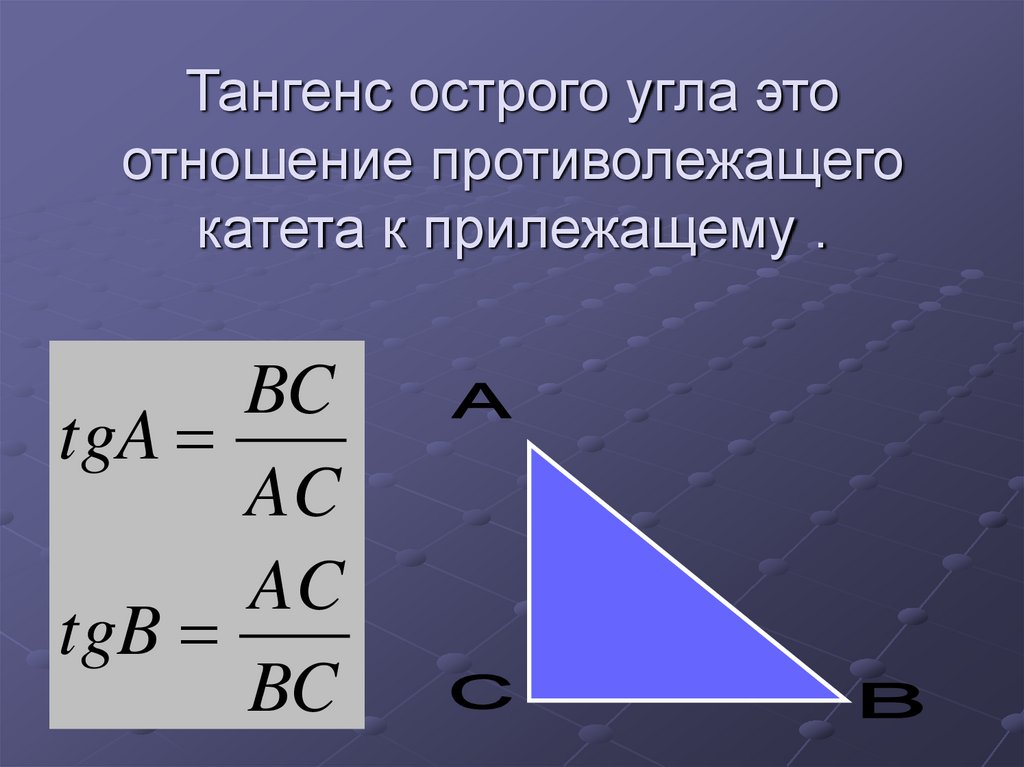
Так как из прямоугольного треугольника DOM тангенс — это отношение противолежащего катета к прилежащему tg = , то тангенс будет равен отношению синуса угла a к косинусу угла a  tg = . Существует еще функция, обратная тангенсу — котангенс, и он равен отношению косинуса угла a к синусу ctg =  .

Запись на доске и в тетрадях:

Т.к. tga = , то   tga = , ctga =  .

 

 

Так как tga =  , то при a = 90° тангенс угла a не определен, так как  cos 90° = 0 знаменатель обращается в нуль. Котангенс угла ctg a=  не определен при a = 0 °, a =  180 ° , так как знаменатель sin 0° = 0, sin 180° = 0 обращается в нуль. Используя формулы (2), находим:

tg 0 ° = 0, tg 180 ° = 0.

ctg 90° = 0.

Запишите это в тетради.  (слайд 7)

Запись в тетрадях:

Т.к. tga =  , то при a = 90°   тангенс угла a не определен.

tg 0 ° = 0, tg 180 ° = 0,

т. к. ctga =   , то при a = 0 °, a =  180 °    котангенс угла a  не определен

ctg 90° = 0.

 

5.Основное тригонометрическое тождество.

(слайд 9)

На рисунке 290 учебника изображены система координат Оху и полуокружность АСВ с центром О. Эта полуокружность является дугой окружности, уравнение которой имеет вид х² + у² = 1. Подставив сюда выражения для х и у из формул sin = x, cos = y, получим равенство

sin² a + cos² a = 1, (4)

Которое выполняется для любого угла a из промежутка 0° ≤ a ≤ 180°. Равенство (4) называется основным тригонометрическим тождеством. В  VIII классе оно было доказано для острых углов. Запишите в тетради информацию со слайда. (слайд 9)

Запись в тетрадях:

 Основное тригонометрическое тождество.

Для любого угла a из промежутка 0° ≤ a ≤ 180° верно

sin² a + cos² a = 1 — основное тригонометрическое тождество.

 

III. Закрепление изученного материала.

Решение задач. № 1012, 1013 (б), № 1014 (а), № 1015 (а, в)

№ 1012. Проверьте, что точки М₁(0; 1), М₂ (  ; ), лежат на единичной полуокружности. Выпишите значения синуса, косинуса и тангенса углов АОМ₁, АОМ₂

 

Дано: М₁(0; 1), М₂ (  ; )

Найти: sin, cos, tg углов: АОМ₁, АОМ₂

Решение:

Чтобы проверить, принадлежат ли точки единичной полуокружности, мы должны координаты точек подставить в уравнение окружности х² + у² = 1.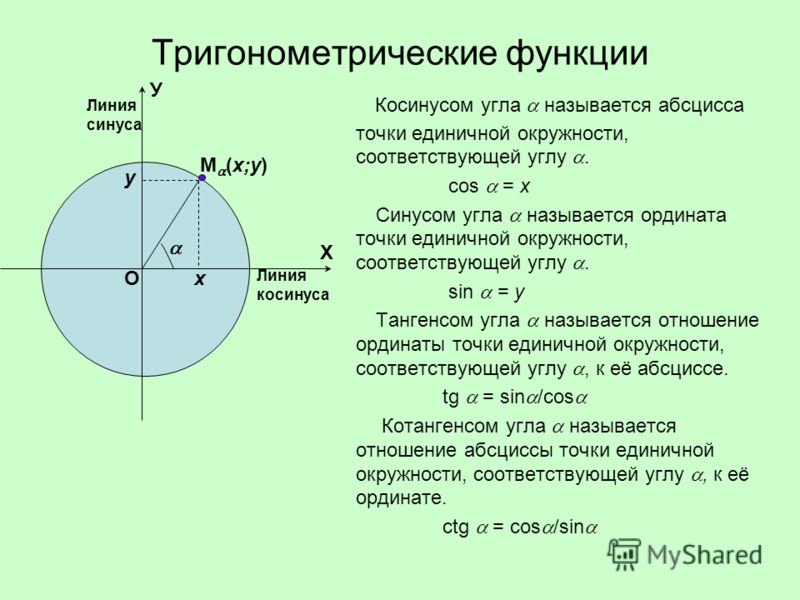

М₁

(0; 1), 0² + 1² = 0 +1 = 1, следовательно М₁  Окр (0; 1).

М₂ (  ; ),  +  = 1,  +  = 1, 1 = 1, следовательно М₂  Окр (0; 1).

 

Найдем значения синуса, косинуса и тангенса углов АОМ₁, АОМ₂. Так как синус — это ордината точки, косинус — это абсцисса точки, а косинус, это отношению синуса к косинусу, находим их значение.

Находим синус, косинус и тангенс угла АОМ_1.

Т.к. sin a = y, cos a = x, tg =

sinÐАОМ₁= 1, cosÐАОМ₁ = 0.

sinÐАОМ₂ = , cosÐАОМ₂ = , tg ÐАОМ₂ = .

 

1013 (б) .

Дано: cosa  =.

Найти: sin a.

Решение

sin² a  + cos²a = 1; sin²a  = 1 – cos²a; sina =.

sina  =.

Ответ: .

 

№ 1014 (а) .

 

№ 1015 (а, в).

Дано: а) cos a = 1;

           в) sin a =   и 0° < a < 90°.

Найти: tg a.

Решение:

a) tg = ,

sin² a + cos² a = 1;

sin² a = 1 — cos² a;

sin² a = 1 —  = 1 —  = 0; sin a = 0.

tg =  =  = 1.

 

в) sin² a + cos² a = 1;

cos² a = 1 — sin² a;

cos² a = 1 —  = 1 —  = ;

т.к. 0° < a < 90° , cos a > 0, cos a = .

tg a  =  = 1.

 

5. Подведение итогов урока. Рефлексия. 

 

Итак, сегодня на уроке мы изучили синус, косинус и тангенс угла. Теперь ответьте на следующие вопросы: (слайд10)

Что называется синусом угла?

Что называется косинусом угла?

Что такое тангенс угла?

Что такое котангенс угла?

Какое основное тригонометрическое тождество вы знаете?

Домашнее задание §1, пп. 93 — 95, №№ 1014, 1015 (б, г).

 

 

 

 

Решение домашней работы.

 

№ 1014.

Дано: а)  sin a = ;

           б) sin a = ;

           в) sin a = .

Найти: cos a.

Решение.

а) Выразим cos a из основного тригонометрического тождества sin² a + cos² a = 1.

cos² a = 1 — sin² a;

cos² a = 1 —  = 1 —  = ;

cos a = ± .

б) Аналогично:

cos² a = 1 —  = 1 —  = ;

cos a = ±.

в) cos² a = 1 — 0  = 1

cos a = ± 1.

 

№ 1015(б, г).

Дано: б) cos a = — ;

           г) sin a =  и 90° < a < 180 °.

Найти: tg a.

Решение.

б) tg = ,

sin² a + cos² a = 1;

sin² a = 1 — cos²

a;

sin² a = 1 —  = 1 —  = ,

sin a = ± .

tg =  =  = .

г) cos² a = 1 — sin² a;

cos² a = 1 —  = 1 —  =

т.к. 90° < a < 180 °, то sin a > 0, sin a =  ,

tg =  =  = .

 

 

решение

г) sin a  =  и 90° < a  < 180°.  Угол    a расположен  во  II четверти, значит,  cos a  < 0. Найдем cos a, используя основное тригонометрическое тождество:

cos² a  = 1 – sin²a

cos a  = ;

найдем tg a.

tg a  = .

Ответ: .

 

 

«Синус, косинус и тангенс в решении задач»

Урок геометрии в 9-м классе по теме: «Синус, косинус и тангенс в решении задач»

• Толмашова Светлана Николаевна

Разделы: Математика

---

Цели урока: 

• Обобщить и систематизировать знания по теме;
• Совершенствовать навыки:
  • использования sin, cos, tg  угла и формул приведения для нахождении неизвестных элементов треугольника;
  • использования основного тригонометрического тождества;
• Рассмотреть решение задач  группы В4 из материалов ЕГЭ на применение знаний, умений и навыков по данной теме.

Тип урока:  урок обобщения и систематизации знаний, умений и навыков учащихся по теме.

ТСО: доска, плакаты, мультимедийный проектор, раздаточный материал.

ХОД УРОКА

1. Организационный момент

2. Повторение

а) Повторить теоретический материал по теме:

• определение sin, cos, tg острого угла прямоугольного треугольника;
• основное тригонометрическое тождество;
• формулы приведения;

(во время повторения  1 ученик выходит к доске и выбирает инструменты урока, 2 ученик по рисункам записывает равенства к заданию)

б) Записать по рисунку равенства для нахождения неизвестных элементов.

(Презентация. Слайд 2)

3. Разминка.  Решение задач по готовым чертежам.

1) В треугольнике АВС угол  С равен 90^о, АВ = 20, АС = 10. Найдите sin А. (Слайд 4)

2) В треугольнике АВС угол  С равен 90^о, cos В = ,  АВ = 13. Найдите АС. (Слайд 5)

3) В треугольнике АВС угол  С равен 90^о, АВ = 5, АС = 4. Найдите tg А. (Слайд 6)

4. Основная часть: разбор заданий из материалов ЕГЭ (задачи В4)

1) В треугольнике АВС угол  С  равен 90^о, sin А = , АС = 4, СН – высота. Найдите ВН. (Слайд 8)

2) В треугольнике АВС угол С равен 90^о, АВ = 5,  АС = 4.  Найдите синус внешнего угла треугольника при вершине А. (Слайд 9)
3) В треугольнике АВС угол С  равен 90^о,  tg А = .  Найдите sin А.   (слайд 10)

5. Проверочная работа по вариантам   (Приложение 1)

Проверочная работа для более подготовленных учащихся (Приложение 2)

6. Домашнее задание (Приложение 3)

Дополнительные задачи (Приложение 4)

5. 08.2012

тригонометрия — лучший способ обозначения некоторых тригонометрических функций («tg» vs «tan», «ctg» vs «cot»)

спросил 10 лет, 2 месяца назад

Изменено 2 года, 6 месяцев назад

Просмотрено 8к раз

$\begingroup$

Как лучше всего обозначать тангенс и другие тригонометрические функции: tg или tan , ctg или cot . Какие обозначения обычно используются и стандартизируются?

• тригонометрия
• обозначения

$\endgroup$

2

$\begingroup$

В текущих учебниках США обычно используются и стандартизированы $\tan$ и $\cot$. Также: $\sin, \cos, \sec, \csc$. В других странах и в 19го века, вы найдете другие.

$\endgroup$

$\begingroup$

Стандарт

ISO 80000-2 Величины и единицы. Часть 2. Математические знаки и символы используется в естественных науках и технике

совершенно ясно: правильные символы $\tan x$ (п.2-13.4) и $\cot x$ (п.2-13.5).

Цитируя стандарт: «$\text{tg } x$, $\text{ctg } x$ не следует использовать».

$\endgroup$

6

$\begingroup$

Некоторые люди знакомы с tg , а некоторые люди знакомы с tan . Итак, для широкого использования просто определите нотацию. Я думаю, это решит вашу проблему.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Карта TG

С картой TG уже введенные геометрические элементы (треугольники, сегменты и остальное) можно перемещать, вращать, отражать и/или масштабировать. Также возможно дублирование структуры.

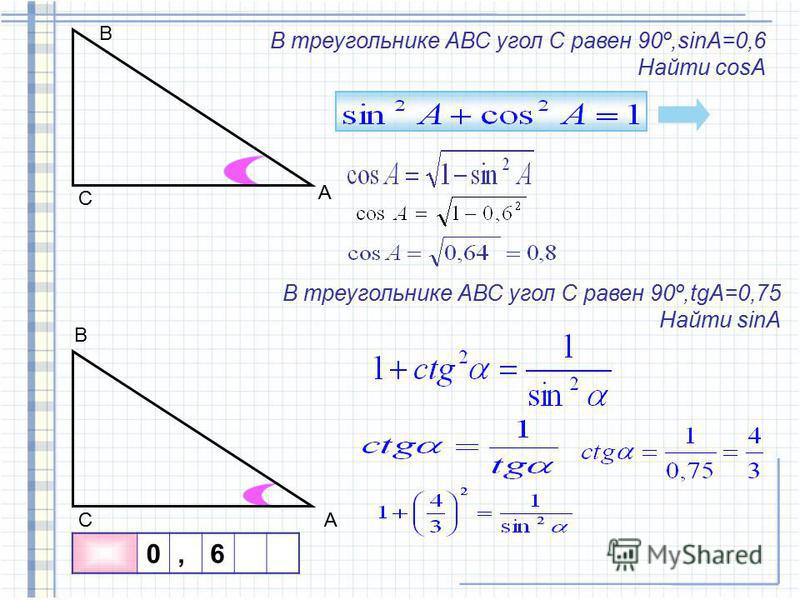
На вкладке «Конструкция» в группе «Изменить» нажмите на значок «Перевести геометрию» (TG).

Рис. 1. Диалоговое окно TG — Преобразование геометрии.

Количество копий

Количество копий, например, если установлено 3 выбранных элемента будут повернуты, переведены, отражены и масштабированы 3 раза, так что будет Всего 4 конструкции. Если установлено значение 0, существующие элементы поворачиваются, перемещаются, зеркально отмасштабированы, а количество элементов остается прежним.

Использовать выбор метки

Если эта опция не отмечена, то карта TG применяется ко всем ранее определенная геометрия. Если эта опция отмечена, выборочная обработка меток включена. возможный.

Копировать структуры, начиная с метки

Вместе с окончанием на этикетке можно использовать карту TG только для выбранной части структуры. Карта ТГ применяется только к тем элементам, метка которых лежит в пределах диапазон, установленный здесь (см. также карты LA и CB, а также общее обсуждение этикетки диапазоны). Если второе поле оставить пустым, будут отображаться только структуры с установленной в поле меткой. считается первое поле.

Примечание. Определенные типы элементов на указанных этикетках можно исключить из выбора ниже в карточке.

Приращение метки для новых структур

Каждой вновь созданной структуре будет присвоена метка, увеличивается на это значение по сравнению с исходной структурой. Исключением является метка 0, которая сохраняется.

Включить

Эта группа может использоваться для указания типов элементов (при условии, что они удовлетворяют критерий метки) поворачиваются/переводятся.

Вращение вокруг оси X

Угол поворота топор вокруг оси X в градусах.

Вращение вокруг оси Y

Угол поворота да вокруг оси Y в градусах.

Вращение вокруг оси Z

Угол поворота аз вокруг оси Z в градусах.

Перемещение по оси X

Перевод △х в направлении X в метрах (масштабируется картой SF).

Перемещение по оси Y

Перевод △г в направлении Y в метрах (масштабируется картой SF).

Перемещение по оси Z

Перевод △z в направлении Z в метрах (масштабировано картой SF).

Зеркало о плоскости в точке X равной

Геометрия зеркально отражается вокруг плоскости в точке X, равной заданной константе. Если нет указано значение, зеркальное отображение вокруг плоскости не выполняется.

Зеркало о плоскости при Y равном

Геометрия зеркально отражается вокруг плоскости в точке Y, равной заданной константе. Если нет указано значение, зеркальное отображение вокруг плоскости не выполняется.

Зеркало о плоскости при Z равном

Геометрия зеркально отражается вокруг плоскости по оси Z, равной постоянной указано. Если значение не указано, зеркальное отображение вокруг плоскости не выполняется.

Масштабный коэффициент

Коэффициент масштабирования γ , с помощью которого необходимо масштабировать структуры. (Если оставить пустым, по умолчанию 1):

• Для сегментов провода масштабируется радиус провода, а также координаты начальная и конечная точки.
• Коэффициент масштабирования γ применяется после того, как переводы/повороты были проводим, например, новые координаты после перевода/поворота будут масштабируется. Это означает, что эффективным переводом является значение, указанное в TG. карты, умноженной на коэффициент масштабирования. (Если это нежелательно, то два разных Можно использовать карты TG — первая применяет только масштабирование, а вторая выполняет только перевод).

Когда карта SY (симметрия) используется до карты TG, карта TG сбрасывает симметрию, если новые структуры делают недействительной симметрию. Случаи, когда симметрия не сбрасывается, это когда, например, самолет г=0 является плоскостью симметрии, а карта TG указывает вращение вокруг ось Z для симметричного выбора элементов. В этом случае симметрия сохраняется.

Трансляция, вращение, зеркальное отображение и масштабирование выполняются как одно преобразование. порядок поворота, перевода, масштабирования, а затем зеркального отображения.

Если делается более одной копии, последующие точки генерируются из предыдущей точки с использованием такое же отношение.

С картой TG одновременное вращение вокруг нескольких осей, а также перемещение в возможно несколько направлений. Точка (х, у, г) , например, угловая точка треугольника преобразуется в новая точка

(1)[xTyTzT]=γM⋅[xyz]+γ[ΔxΔyΔz]

с матрицей вращения

(2)M=[cosαycosαz−cosαysinαzsinαycosαxsinαz+sinαxsinαycosαzcosαxcosαz−sinαxsinαysinαz−sinαxcosαysinαxsinαz−cosαxsinαycosαzsinαxcosαz+cosα0xsinαysinαzcozcos]

Умножение на матрицу вращения М эффективно поворачивает точку сначала на угол аз вокруг оси Z, затем на угол αy вокруг оси Y и, наконец, под углом ах вокруг оси X. Важно отметить что второе вращение вокруг оси Y представляет глобальную Ось Y. Это также эквивалентно вращению ах вокруг оси X, затем вращая αy вокруг нового ты ось и, наконец, вращение аз вокруг нового г» ось.

Углы преобразования, используемые Feko в этом порядке, обычно называемые углами Кардана, в отличие от широко используемых углов Эйлера. Если вращение должно производиться в другом порядке (например, сначала вокруг оси X, затем вокруг оси Y и, наконец, вокруг ось Z), то можно просто использовать несколько последовательных карт TG. Но так как такой же алгоритм вращения используется и на других Feko карты (например, AC или AR), если нельзя использовать несколько карт, здесь должен быть указан короткий сегмент кода PREFEKO, который иллюстрирует, как углы могут быть преобразованы: 92)) #cb2=#cb1*#cc1/#cc2 #ca2=#ca1*#cc2/#cc1 #sa2=#cc2*(#sa1*#cc1-#ca1*#sb1*#sc1)/(#cb1*#cc1) #sb2=#sa1*#sc1+#ca1*#sb1*#cc1 #sc2=#cc2*(#ca1*#sc1-#sa1*#sb1*#cc1)/(#cb1*#cc1) ** Наконец вычислить углы, которые должны быть использованы в Feko в карточке TG ** для порядка вращения сначала вокруг z, затем вокруг y, а затем вокруг x #a2=град(atan2(#sa2,#ca2)) #b2=градус(атан2(#sb2,#cb2)) #c2=градус(атан2(#sc2,#cc2))

Версия файла example_18.