§6. Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии
Определение. Генеральной дисперсией DГ называют среднее арифметическое квадратов отклонения значений признака Х генеральной совокупности от его среднего значения .
Если различны, то , где N – объём выборки.
Если имеют частоты , то .
Определение. Генеральным средним квадратическим отклонением называют .
Определение. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если различны, то .
Если имеют частоты , то .
Замечание. При решении практических задач выборочную дисперсию удобнее находить по следующей формуле:
(3)
Определение. Выборочным средним квадратичным
отклонением
Выборочным средним квадратичным
отклонением
Задача. По данным выборки найти оценку для неизвестной DГ.
Если в качестве оценки для DГ взять DВ, то эта оценка является смещённой, а именно
(без доказательства). (4)
Значит, эта оценка будет приводить к систематическим ошибкам (давая заниженное значение генеральной дисперсии).
Для получения несмещенной оценки исправим выборочную дисперсию, умножив её на .
Определение. Исправленной (эмпирической) дисперсией называется
. (5)
Значит,
, или ,
где – несмещённая оценка генеральной дисперсии
DГ.
Действительно,
Можно доказать, что – состоятельная оценка DГ, а значит также состоятельная оценка DГ (т.к. множитель при ).
Замечание. При больших значениях n обе оценки и различаются мало и введение поправочного коэффициента теряет смысл.
Для оценки среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение . не является несмещённой оценкой Г.
Определение. Точечной называют оценку, которая определяется одним числом.
Рассмотренные оценки являются точечными.
xi | -2 | -1 | 0 | 1 | 2 |
ni | 10 | 20 | 40 | 20 | 10 |
Решение.
xi | -2 | -1 | 0 | 1 | 2 |
ni | 10 | 20 | 40 | 20 | 10 |
| 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Найдем смещённую
оценку генеральной дисперсии –
воспользуемся формулой (3): .
Выборочную среднюю найдем по формуле (2): . Отсюда, .
Несмещённую оценку генеральной дисперсии найдем по формуле (5): .
Задачи _______________________________________________________
Из генеральной совокупности извлечена выборка. Найти несмещённую оценку генеральной средней.
xi 2
5
7
10
ni
16
12
8
14
Из генеральной совокупности извлечена выборка.
 Найти
несмещенную оценку генеральной
средней.
Найти
несмещенную оценку генеральной
средней.xi
1
3
6
26
ni
8
40
10
2
Найти выборочную среднюю по данному распределению выборки:
xi
2560
2600
2620
2650
2700
ni
2
3
10
4
1
Найти выборочную дисперсию по данному распределению выборки:
xi
340
360
375
380
ni
20
50
18
12
Найти выборочную дисперсию по данному распределению выборки:
xi
0,01
0,04
0,08
ni
5
3
2
Найти выборочную дисперсию по данному распределению выборки:
xi
0,1
0,5
0,6
0,8
ni
5
15
20
10
Найти выборочную дисперсию по данному распределению выборки:
xi
18,4
18,9
19,3
19,6
ni
5
10
20
5
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi
102
104
108
ni
2
3
5
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi
0,1
0,5
0,7
0,9
ni
6
12
1
1
Найти исправленную выборочную дисперсию по данному распределению выборки:
xi | 23,5 | 26,1 | 28,2 | 30,4 |
ni | 2 | 3 | 4 | 1 |
§6.
 Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии
Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной дисперсии по исправленной дисперсии Определение. Генеральной дисперсией DГ называют среднее арифметическое квадратов отклонения значений признака Х генеральной совокупности от его среднего значения .
Если различны, то , где N – объём выборки.
Если имеют частоты , то .
Определение. Генеральным средним квадратическим отклонением называют .
Определение. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если различны, то .
Если имеют частоты , то .
Замечание. При решении практических задач выборочную дисперсию удобнее находить по следующей формуле:
(3)
Определение. Выборочным средним квадратичным
отклонением называют .
Выборочным средним квадратичным
отклонением называют .
Задача. По данным выборки найти оценку для неизвестной DГ.
Если в качестве оценки для DГ взять DВ, то эта оценка является смещённой, а именно
(без доказательства). (4)
Значит, эта оценка будет приводить к систематическим ошибкам (давая заниженное значение генеральной дисперсии).
Для получения несмещенной оценки исправим выборочную дисперсию, умножив её на .
Определение. Исправленной (эмпирической) дисперсией называется
. (5)
Значит,
, или ,
где – несмещённая оценка генеральной
дисперсии DГ.
Действительно,
Можно доказать, что – состоятельная оценка DГ, а значит также состоятельная оценка DГ (т.к. множитель при ).
Замечание. При больших значениях n обе оценки и различаются мало и введение поправочного коэффициента теряет смысл.
Для оценки среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение . не является несмещённой оценкой Г.
Определение. Точечной называют оценку, которая определяется одним числом.
Рассмотренные оценки являются точечными.
Пример 9. Выборка задана следующим ДCР. Найти смещённую и исправленную оценку для дисперсии.
xi | -2 | -1 | 0 | 1 | 2 |
ni | 10 | 20 | 40 | 20 | 10 |
Решение. Предварительно найдем для каждой
варианты соответствующую относительную
частоту и результаты внесем в таблицу.
Объём выборки n = 100.
Предварительно найдем для каждой
варианты соответствующую относительную
частоту и результаты внесем в таблицу.
Объём выборки n = 100.
xi | -2 | -1 | 0 | 1 | 2 |
ni | 10 | 20 | 40 | 20 | 10 |
wi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Найдем смещённую
оценку генеральной дисперсии –
воспользуемся формулой (3): .
Выборочную среднюю найдем по формуле (2): . Отсюда, .
Несмещённую оценку генеральной дисперсии найдем по формуле (5): .
ДИСП.Г (функция ДИСП.Г)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Вычисляет дисперсию для генеральной совокупности. Логические значения и текст игнорируются.
Синтаксис
ДИСП.Г(число1;[число2];…)
Аргументы функции ДИСП.Г описаны ниже.
-
Число1 Обязательный. Первый числовой аргумент, соответствующий генеральной совокупности.
- org/ListItem»>
Число2… Необязательный. Числовые аргументы 2—254, соответствующие генеральной совокупности.
Замечания
-
В функции ДИСП.Г предполагается, что аргументы представляют собой всю генеральную совокупность. Если данные являются только выборкой из совокупности, для вычисления дисперсии следует использовать функцию ДИСП.В.
-
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.

-
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст и значения ошибок в массиве или ссылке игнорируются.
-
Аргументы, которые представляют собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы включить логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию ДИСПРА.
-
Функция ДИСП.Г вычисляется с помощью следующего уравнения:
где x — выборочное среднее СРЗНАЧ(число1,число2,…), а n — размер выборки.

Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Прочность |
||
|
1 345 |
||
|
1,301 |
||
|
1,368 |
||
|
1,322 |
||
|
1,310 |
||
|
1,370 |
||
|
1,318 |
||
|
1,350 |
||
|
1,303 |
||
|
1,299 |
||
|
Формула |
Описание |
Результат |
|
=ДИСП. |
Дисперсия предела прочности для всех инструментов в предположении, что всего было произведено 10 инструментов (используется генеральная совокупность). |
678,84 |
|
=ДИСП.В(A2:A11) |
Дисперсия, с использованием функции ДИСП.В, которая оценивает только тестируемую выборку. Результат отличается от результата функции ДИСП.Г. |
754,27 |
Выборочная несмещенная дисперсия — statanaliz.info
Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
«Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
Выборочная несмещенная дисперсия:
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. В знаменателе несмещенной оценки n-1 вместо n.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.
До новых встреч на блоге statanaliz. info.
info.
Поделиться в социальных сетях:
Характеристики выборки и генеральной совокупности
- Основные понятия математической статистики
- Среднее значение выборки
- Дисперсия выборки. Стандартное отклонение
- Погрешности выборки
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использованию статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов N из генеральной совокупности и из выборки n называются соответственно объемом генеральной совокупности N и объемом выборки n.
Статистическое описание и вероятностные модели применяются к физическим, экономическим, социологическим, биологическим процессам, обладающим тем свойством, что хотя результат отдельного измерения физической величины X не может быть предсказан с достаточной точностью, но значение некоторой функции от множества результатов повторных измерений может быть предсказан с существенно лучшей точностью. Такая функция называется статистикой. Часто точность предсказания некоторой статистики возрастает с возрастанием объема выборки.
Наиболее известные статистики – относительная частота, выборочные средние, дисперсия. Когда возрастает объем выборки n, многие выборочные статистики сходятся по вероятности к соответствующим параметрам теоретического распределения величины X. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением вероятности случайной величины. Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Различные значения наблюдаемого признака, встречающегося в совокупности, называются вариантами. Частоты вариантов выражают доли (удельные веса) элементов совокупности с одинаковыми значениями признака. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующим им частотами.
Значения, находящиеся в середине вариационного ряда, принято делить на собственно средние и структурные средние. Собственно среднее — это арифметическое среднее. Структурные средние — мода и медиана. Кроме того, чтобы охарактеризовать структуру вариационного ряда, используют квартили, квинтили, децили и процентили. Теперь обо всём по порядку.
Среднее арифметическое значение генеральной совокупности находят по формуле:
(1)
где
— число единиц генеральной совокупности,
— значение j-го наблюдения.
Если величина выборки X может принимать значения с вероятностями соответственно , то средним значением величины X для выборки (её математическим ожиданием E(x) ,будет
или
или же (2)
для негруппированных выборок и
(3)
для группированных выборок, где
— число единиц выборки,
— число классов,
— значение i-го класса,
— частота i-го класса.
Пример 1. В таблице даны значения средней температуры воздуха в населённом пункте N в 2014 году:
| Месяц | |
| 1 | -2,3 |
| 2 | -4,0 |
| 3 | 2,0 |
| 4 | 9,0 |
| 5 | 10,0 |
| 6 | 19,4 |
| 7 | 19,9 |
| 8 | 17,1 |
| 9 | 14,9 |
| 10 | 7,3 |
| 11 | 2,2 |
| 12 | -0,3 |
Найти среднюю температуру воздуха.
Решение. Найдём среднюю температуру воздуха как среднее значение для негруппированной выборки:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пример 2. В таблице – данные о группировке сельских хозяйств по урожайности зерновых:
Урожайность зерновых в центнерах с га | Число сельских хозяйств – абсолютное | Удельный вес сельских хозяйств – в процентах |
до 5,0 | 4244 | 6,2 |
5,1-10,0 | 10446 | 15,2 |
10,1-15,0 | 18956 | 27,5 |
15,1-20,0 | 20207 | 29,3 |
20,1-25,0 | 8159 | 11,9 |
25,1-30,0 | 4145 | 6,0 |
30,1-35,0 | 1316 | 1,9 |
35,1-40,0 | 792 | 1,2 |
40,1-45,0 | 183 | 0,3 |
45,1-50,0 | 182 | 0,3 |
50,1-55,0 | 161 | 0,2 |
Всего | 68791 | 100,0 |
Найти среднюю урожайность зерновых.
Решение. Так как имеем только группированные данные и неизвестна средняя урожайность каждой группы, как приближенные значения к средней каждой группы примем центры интервалов:
Центры интервалов | ||
2,5 | 4222 | 10610,0 |
7,5 | 10446 | 78345,0 |
12,5 | 18956 | 236950,0 |
17,5 | 20207 | 363622,5 |
22,5 | 8159 | 183577,5 |
27,5 | 4145 | 113987,5 |
32,5 | 1316 | 42770,0 |
37,5 | 792 | 29700,0 |
42,5 | 183 | 7777,5 |
47,5 | 182 | 8645,0 |
52,5 | 161 | 8452,5 |
Всего | 68791 | 1074437,5 |
Найдём требуемую в условии задачи среднюю урожайности зерновых:
Итак, средняя урожайность по выборке составляет 15,6 центнеров с га.
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Модой называют значение, которое в вариационном ряду встречается чаще других. Моду можно найти на гистограмме как самый высокий столбец.
Например, в выборке, значения которой 20, 50, 60, 70, 80, 20, 20, 75, 70, 20, 80, 20, 50, 60, модой является 20.
Медианой называют значение, которое находится в середине вариационного ряда. Первая половина элементов выборки меньше этого значения, а вторая половина — больше.
Если в выборке нечётное число элементов, то за медиану принимают собственно серединное значение. Например, в выборке, значения которой 14, 15, 18, 21, 27, медианой является 18.
Если в выборке чётное число элементов, то медиану находят, выбирая два значения,
которые находятся в середине и вычисляя их среднее арифметическое. Например, есть выборка 11, 14, 15, 18, 21, 27. Медиану находят так: (15+18)/2 = 16,5.
Медиану находят так: (15+18)/2 = 16,5.
По аналогии с медианой, которая делит значения выборки на две части, вводят понятие квартилей, которые делят вариационный ряд на 4 равные части.
Децили делят вариационный ряд уже на 10 одинаковых частей, а квинтили — на 5. Процентили делят вариационный ряд на 100 равных частей.
Дисперсией величины называется среднее значение квадрата отклонения величины от её среднего значения. Дисперсию генеральной совокупности рассчитывают по формуле:
(4)
Дисперсию выборки рассчитывают по формуле:
(5)
для негруппированных выборок и
(6)
для группированных выборок.
Пример 3. В таблице – данные о возрасте жителей административной территории Т в 2013 году. Не будем приводить эту таблицу из-за её громоздкости. Отметим лишь, что в таблице дана численность
каждого из возрастов (по одному году, например, 33 года, 40 лет, 65 лет и т.д.) в группах от 0 лет по 94 года (включительно) и численность всей возрастной группы
в интервале 95-99 лет, а также численность жителей старше 100 лет.
Не будем приводить эту таблицу из-за её громоздкости. Отметим лишь, что в таблице дана численность
каждого из возрастов (по одному году, например, 33 года, 40 лет, 65 лет и т.д.) в группах от 0 лет по 94 года (включительно) и численность всей возрастной группы
в интервале 95-99 лет, а также численность жителей старше 100 лет.
Требуется найти средний возраст жителей административной территории и дисперсию среднего возраста.
Решение. Найдём средний возраст. Так как данные в таблице являются данными генеральной совокупности, находим средний возраст генеральной совокупности:
В таблице – данные о числе жителей каждого возраста, исключение же – жители в возрасте 95-99 лет и старше 100 лет. Поэтому рассчитали центр интервала возрастной группы 95-99 лет: 97 лет и в расчётах использовали его.
Так как число жителей старше 100 лет относительно небольшое, чтобы упростить расчёты, нижнюю границу интервала приняли за значение признака.
Итак, средний возраст жителей административной территории Т – 38,2 года
Найдём теперь его дисперсию:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
Пройти тест по теме Теория вероятностей и математическая статистика
Пример 4. Найти дисперсию урожайности зерновых в сельских хозяйствах, используя данные примера 2.
Решение. Средняя урожайность по выборке составляет 15,6 центнеров с га. Чтобы найти дисперсию, создадим дополнительную таблицу.
Центры интервалов | Число хозяйств | |||
2,5 | 4244 | -13,1 | 172,1 | 730412,3 |
7,5 | 10446 | -8,1 | 65,9 | 688558,6 |
12,5 | 18956 | -3,1 | 9,7 | 184391,3 |
17,5 | 20207 | 1,9 | 3,5 | 71505,7 |
22,5 | 8159 | 6,9 | 47,3 | 386328,5 |
27,5 | 4165 | 11,9 | 141,2 | 585113,6 |
32,5 | 1316 | 16,9 | 285,0 | 375024,0 |
37,5 | 792 | 21,9 | 478,8 | 379196,9 |
42,5 | 183 | 26,9 | 722,6 | 132234,9 |
47,5 | 182 | 31,9 | 1016,4 | 184986,0 |
52,5 | 161 | 36,9 | 1360,2 | 218995,1 |
Всего | 68791 | — | — | 393679,1 |
Теперь у нас есть всё, чтобы найти дисперсию:
Пример 5. Найти дисперсию температуры в населённом пункте N в 2009 году, используя данные примера 1.
Найти дисперсию температуры в населённом пункте N в 2009 году, используя данные примера 1.
Решение. Данная выборка – негруппированная, найдём дисперсию температуры для негруппированной выборки:
Стандартное отклонение равно положительному корню из дисперсии. Стандартное отклонение генеральной совокупности находят по формуле
(7)
Стандартное отклонение выборки находят по формуле
. (9)
для негруппированных выборок и
(10)
для группированных выборок.
Погрешности выборки характеризуют, насколько значительная ошибка допущена при замещении генеральной совокупности выборкой. Сколь бы тщательно ни подбирали выборку, параметр генеральной совокупности и оценка выборки Т всегда будут отличаться. Их разница является погрешность выборки .
Их разница является погрешность выборки .
Среднюю стандартную погрешность выборки находят по формуле
(11)
Средняя стандартная погрешность выборки характеризует рассеяние средних арифметических выборки по отношению к средним генеральной совокупности: чем больше погрешность, тем дальше среднее арифметическое выборки может находиться от среднего генеральной совокупности. В свою очередь, чем меньше погрешность, тем ближе к среднему генеральной совокупности находится среднее выборки. При увеличении числа наблюдений n стандартная погрешность уменьшается.
Стандартную погрешность называют также абсолютной погрешностью средней величины и нередко записывают .
Пример 6. Найти стандартную погрешность средней урожайности сельских хозяйств и интервал оценки, используя результаты примеров 2 и 4.
Решение. В примере 2 найдена средняя урожайность зерновых, равная 15,6 центнеров с га. В примере 4 найдена дисперсия урожайности, равная 57,2. Найдём стандартное отклонение урожайности:
В примере 2 найдена средняя урожайность зерновых, равная 15,6 центнеров с га. В примере 4 найдена дисперсия урожайности, равная 57,2. Найдём стандартное отклонение урожайности:
Найдём теперь стандартную погрешность:
Интервал оценки средней урожайности:
Статистика — не Ваша специализация? Закажите статистическую обработку данных
К началу страницы
Пройти тест по теме Теория вероятностей и математическая статистика
| Назад | Листать | Вперёд>>> |
Всё по теме «Математическая статистика»
Характеристики выборки и генеральной совокупности: среднее значение, дисперсия, погрешности выборки
Доверительный интервал для математического ожидания
Распределение Стьюдента и малые выборки
Проверка статистических гипотез
Корреляционная зависимость. Коэффициент парной корреляции. Основы корреляционного анализа
Коэффициент парной корреляции. Основы корреляционного анализа
Парная линейная регрессия. Задачи регрессионного анализа
Множественная корреляция, её коэффициент. Частная корреляция
Множественная линейная регрессия. Улучшение модели регрессии
Дисперсионный анализ: соединение теории и практики
CFA — Дисперсия и стандартное отклонение | программа CFA
Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений.
Второй подход к расчету отклонений состоит в их возведении в квадрат.
Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:
- Дисперсия определяется как среднее квадратов отклонений от среднего значения.
- Стандартное отклонение — это положительный квадратный корень дисперсии.
Далее обсуждается расчет и использования дисперсии и стандартного отклонения. 2 \over N } \) (Формула 11)
2 \over N } \) (Формула 11)
где
- \(\mu\) [мю] — это среднее генеральной совокупности, а
- \(N\) — размер генеральной совокупности.
Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех \(N\) элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на \(N\).
Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.
Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.
Рассмотрим пример.
Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2. 0%.
0%.
Следовательно, дисперсия прибыли в процентах от выручки составляет:
(1/3)[(0.9 — 2.0)2 + (1.6 — 2.0)2 + (3.5 — 2.0)2]
= (1/3)(-1.12 + -0.42 + 1.52)
= (1/3)(1.21 + 0.16 + 2.25) = (1/3)(3.62) = 1.21
Стандартное отклонение генеральной совокупности.
Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.
Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.
Формула стандартного отклонения генеральной совокупности.
Стандартное отклонение генеральной совокупности (или просто стандартное отклонение, а также среднеквадратическое отклонение, от англ. ‘population standard deviation’), определяемое как положительный квадратный корень из дисперсии генеральной совокупности, составляет:
\( \Large \dst
\sigma = \sqrt{\sum_{i=1}^{N} ( X_i — \mu )^2 \over N} \) (Формула 12)
где
- \(\mu\) [мю] — это среднее генеральной совокупности, а
- \(N\) — размер генеральной совокупности.

Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: \( \sqrt{1.21} \) = 1.10.
Как дисперсия, так и стандартное отклонение являются примерами параметров распределения. В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.
Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.
Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12.
Мы обсудим эти вычисления далее.
Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12, как в следующем примере.
Пример расчета стандартного отклонения для генеральной совокупности.
В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.
Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.
Критериями являются:
- сохранение капитала (эффективность на медвежьем рынке),
- непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,
- доступность (дисквалификация фондов, которые закрыты для новых инвесторов), и
- долгосрочные показатели эффективности после уплаты налогов.

Оборачиваемость или оборот портфеля, показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.
|
Фонд |
Годовой оборот портфеля (%) |
|---|---|
|
Bruce Fund (BRUFX) |
10 |
|
CGM Focus Fund (CGMFX) |
360 |
|
Hotchkis And Wiley Small Cap Value A Fund (HWSAX) |
37 |
|
Aegis Value Fund (AVALX) |
20 |
|
Delafield Fund (DEFIX) |
49 |
|
Homestead Small Company Stock Fund (HSCSX) |
1 |
|
Robeco Boston Partners Small Cap Value II Fund (BPSCX) |
32 |
|
Hotchkis And Wiley Mid Cap Value A Fund (HWMAX) |
72 |
|
T Rowe Price Small Cap Value Fund (PRSVX) |
9 |
|
Guggenheim Mid Cap Value Fund Class A (SEVAX) |
19 |
|
Wells Fargo Advantage Small Cap Value Fund (SSMVX) |
16 |
|
Stratton Small-Cap Value Fund (STSCX) |
11 |
Источник: Forbes (2013). 2 \) = 107,190/12 = 8,932.50.
2 \) = 107,190/12 = 8,932.50.
Для расчета стандартного отклонения находим квадратный корень:
\( \sigma = \sqrt{ 8,932.50 } \) = 94.51%.
Единицей измерения дисперсии является процент в квадрате, поэтому единицей измерения стандартного отклонения также является процент.
Решение для части 3:
Если генеральная совокупность четко определена как фонды Forbes Honor Roll за один конкретный год (2013 г.), и если под оборотом портфеля понимается конкретный одногодичный период, о котором отчитывается Forbes, то применение формул генеральной совокупности для дисперсии и стандартного отклонения уместно.
Результаты 8,932.50 и 94.51 представляют собой, соответственно, перекрестную дисперсию и стандартное отклонение годового оборота портфеля для фондов Forbes Honor Roll за 2013 год.
Фактически, мы не могли должным образом использовать фонды Honor Roll для оценки дисперсии оборота портфеля (например) любой другой по-разному определенной генеральной совокупности, потому что фонды Honor Roll не являются случайной выборкой из какой-либо большей генеральной совокупности взаимных фондов США. 2 \over n-1 } \) (Формула 14)
2 \over n-1 } \) (Формула 14)
где
- \( \overline X \) — среднее значение выборки, а
- \(n\) — количество наблюдений в выборке.
Чтобы рассчитать стандартное отклонение выборки, мы сначала вычисляем дисперсию выборки, используя приведенные выше шаги. Затем мы берем квадратный корень из выборочной дисперсии.
Пример, приведенный ниже, иллюстрирует расчет выборочной дисперсии и стандартного отклонения выборки для двух взаимных фондов, представленных ранее.
Пример расчета выборочной дисперсии и стандартного отклонения выборки.
После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см. Пример расчета размаха и среднего абсолютного отклонения для оценки риска).
Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.
|
Год |
Фонд Selected |
Фонд T. Rowe Price |
|---|---|---|
|
2008 |
-39.44% |
-35.75% |
|
2009 |
31.64 |
25.62 |
|
2010 |
12.53 |
15.15 |
|
2011 |
-4.35 |
-0.72 |
|
2012 |
12. |
17.25 |
Источник: performance.morningstar.com.
На основании приведенных выше данных сделайте следующее:
- Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
- Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
- Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.
Решение для части 1:
Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).
А. SLASX:
1. Среднее значение выборки:
\( \overline R \) = (-39.44 + 31.64 + 12.53 — 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.
2. Квадратичные отклонения от среднего значения:
(-39.44 — 2.64)2 = (-42.08)2 = 1,770. 73
73
(31.64 — 2.64)2 = (29.00)2 = 841.00
(12.53 — 2.64)2 = (9.89)2 = 97.81
(-4.35 — 2.64)2 = (-6.99)2 = 48.86
(12.82 — 2.64)2 = (10.18)2 = 103.63
3. Сумма квадратов отклонений от среднего составляет:
1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.
4. Разделим сумму квадратов отклонений от среднего на (n — 1):
2,862.03 / (5 — 1) = 2,862.03 / 4 = 715.51
B. PRFDX:
1. Среднее значение выборки:
\( \overline R \) = (-35.75 + 25.62 + 15.15 — 0.72 + 17.25)/5 = 21.55/5 = 4.31%.
2. Квадратичные отклонения от среднего значения:
(-35.75 — 4.31)2 = (-40.06)2 = 1,604.80
(25.62 — 4.31)2 = (21.31)2 = 454.12
(15.15 — 4.31)2 = (10.84)2 = 117.51
(-0.72 — 4.31)2 = (-5.03)2 = 25.30
(17. 25 — 4.31)2 = (12.94)2 = 167.44
25 — 4.31)2 = (12.94)2 = 167.44
3. Сумма квадратов отклонений от среднего составляет:
1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.
4. Разделим сумму квадратов отклонений от среднего на \((n — 1)\):
2,369.17/4 = 592.29
Решение для части 2:
Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.
A. Для SLASX, s = \( \sqrt {715.51} \) = 26.7%.
B. Для PRFDX, s = \( \sqrt {592.29} \) = 24.3%.
Решение для части 3:
Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.
|
Фонд |
Стандартное |
Среднее |
|---|---|---|
|
SLASX |
26. |
19.6 |
|
PRFDX |
24.3 |
18.0 |
Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат).
Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем среднее арифметическое и стандартное отклонение вместе при анализе данных.
Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.
В Таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.
Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.
|
Ставка доходности |
Геометрическое |
Среднее |
Стандартное отклонение |
|---|---|---|---|
|
S&P 500 (Годовая) |
9.84 |
11.82 |
20.18 |
|
S&P 500 (Месячная) |
0.79 |
0.94 |
5.50 |
Источник: Ibbotson.
1.5 — Дополнительные меры рассеивания
Общие меры рассеивания Раздел
Иногда также полезно иметь общую меру разброса данных. В этом показателе было бы хорошо включить все переменные одновременно, а не по одной. В прошлом мы рассматривали отдельные переменные и их дисперсии, чтобы измерить индивидуальные дисперсии. Здесь мы рассмотрим меры дисперсии всех переменных вместе, в частности, мы рассмотрим такие меры, которые рассматривают общую вариацию. 9{2}\) измеряет дисперсию отдельной переменной X j . Следующие два используются для измерения дисперсии всех переменных вместе.
- Общее изменение
- Обобщенная дисперсия
Чтобы понять общую вариацию, мы сначала должны найти след квадратной матрицы. Квадратная матрица — это матрица, имеющая равное количество столбцов и строк. Важные примеры квадратных матриц включают матрицы дисперсии-ковариации и корреляции. 92_п\)
Важные примеры квадратных матриц включают матрицы дисперсии-ковариации и корреляции. 92_п\)
Общая вариация представляет интерес для анализа основных компонентов и факторного анализа, и мы рассмотрим эти концепции позже в этом курсе.
Пример 1-6: Обследование здоровья женщин (дисперсия) Раздел
Давайте снова воспользуемся данными исследования здоровья женщин Министерства сельского хозяйства США, чтобы проиллюстрировать это. Мы взяли дисперсии для каждой из переменных из выходных данных программного обеспечения и поместили их в таблицу ниже.
| Переменная | Разница |
| Кальций | 157829.4 |
| Железо | 35,8 |
| Белок | 934,9 |
| Витамин А | 2668452.4 |
| Витамин С | 5416. 3 3 |
| Итого | 2832668.8 |
Общая вариация данных о потреблении питательных веществ определяется простым суммированием всех дисперсий для каждой из индивидуальных переменных. Общая вариация равна 2 832 668,8 . Это очень большое число.
Примечание ! Проблема с полной вариацией заключается в том, что она не принимает во внимание корреляции между переменными.
Интерпретация корреляции Раздел
На этих графиках показаны смоделированные данные для пар переменных с разными уровнями корреляции. В каждом случае дисперсии обеих переменных равны 1, так что общая вариация равна 2.
. сюжета.
Увеличивая корреляцию до r = 0,7, мы видим овальную фигуру. Обратите внимание, что точки не так широко рассредоточены.
Увеличивая корреляцию до r = 0,9, мы видим, что точки ложатся на 45-градусную линию, и еще меньше разбросаны.
Таким образом, дисперсия точек уменьшается с ростом корреляции. Но во всех случаях общая вариация одинакова. Общая вариация не учитывает корреляцию между двумя переменными.
Зафиксировав отклонения, разброс данных будет уменьшаться как \(| r | \rightarrow 1\).
Для учета корреляций между парами переменных предлагается альтернативная мера общей дисперсии. Эта мера принимает большое значение, когда различные переменные показывают очень небольшую корреляцию между собой. Напротив, эта мера принимает небольшое значение, если переменные демонстрируют очень сильную корреляцию между собой, как положительную, так и отрицательную. Эта конкретная мера дисперсии является обобщенной дисперсией. Чтобы определить обобщенную дисперсию, мы сначала определяем определитель матрицы.
Мы начнем с простой матрицы 2 x 2, а затем перейдем к более общим определениям для больших матриц.
Рассмотрим определитель матрицы 2 x 2 \(\mathbf{B}\) , как показано ниже. Здесь мы видим, что это произведение двух диагональных элементов за вычетом произведения недиагональных элементов.
\(|\textbf{B}| =\left|\begin{array}{cc}b_{11} & b_{12}\\ b_{21} & b_{22}\end{массив}\right |= b_{11}b_{22}-b_{12}b_{21}\)
Вот пример простой матрицы, состоящей из элементов 5, 1, 2 и 4. Вы получите определитель 18. Произведение диагонали 5 x 4 за вычетом элементов вне диагонали 1 x 2 дает ответ 18:
\(\left|\begin{array}{cc}5 & 1\\2 & 4\end{array}\right| = 5 \times 4 — 1\times 2= 20-2 = 18\)
- Определитель общей \(p\ x\ p\) матрицы \(\mathbf{B}\)
В более общем смысле определитель общего 9{th}\) степени, так что в основном у нас будут чередующиеся знаки плюс и минус в нашей сумме. Матрица \(B1_j\) получается удалением строки 1 и столбца j из матрицы \(\mathbf{B}\).
По определению, обобщенная дисперсия случайного вектора \(\mathbf{X}\) равна \(|\sum|\), определителю матрицы дисперсии/ковариации.
 Обобщенную дисперсию можно оценить, вычислив \(|S|\), определитель выборочной матрицы дисперсии/ковариации.
Обобщенную дисперсию можно оценить, вычислив \(|S|\), определитель выборочной матрицы дисперсии/ковариации.Дисперсия и стандартное отклонение
Научный метод
Было бы полезно иметь меру разброса, обладающую следующими свойствами:
- Мера должна быть пропорциональна разбросу данные (маленькие, когда данные сгруппированы вместе, и большие, когда данные сильно разбросаны).
- Мера не должна зависеть от количества значений в наборе данных (в противном случае, просто сделав больше измерений, значение увеличилось бы, даже если бы разброс измерений не был увеличивается).
- Мера не должна зависеть от среднего (поскольку теперь мы заинтересованы только в распространении данных, а не в их центральном тенденция).
Как дисперсия , так и стандартное отклонение соответствуют этим трем критериям для нормально распределенных (симметричных, «колоколообразных») наборов данных.

Дисперсия ( σ 2 ) является мерой того, насколько далеко каждое значение в наборе данных от среднего. Вот как это определяется:
- Вычтите среднее значение из каждого значения в данных. Это дает вам меру расстояния каждого значения от среднего.
- Возведите в квадрат каждое из этих расстояний (чтобы все они были положительными значениями) и сложите все квадраты вместе.
- Разделите сумму квадратов на количество значений в наборе данных.
Стандартное отклонение ( σ ) — это просто (положительный) квадратный корень из дисперсии.
Оператор суммирования
Чтобы написать уравнение, определяющее дисперсию, проще всего использовать оператор суммирования , Σ. Оператор суммирования — это просто сокращенный способ написать: «Возьмите сумму набора чисел». В качестве примера мы покажем, как использовать оператор суммирования для записи уравнения для вычисления среднего значения набора данных 1.
 Мы начнем с присвоения каждого числа переменной X 1 – X 6 , например:
Мы начнем с присвоения каждого числа переменной X 1 – X 6 , например:Подумайте о переменной ( X ) как измеренное количество из вашего эксперимента — например, количество листьев на растении — и думайте о нижнем индексе как о номере испытания (1–6). Чтобы вычислить среднее количество листьев на растении, мы сначала должны сложить значения из каждого из шести испытаний. Используя оператор суммирования, мы запишем это так:
, что эквивалентно:
или:
Очевидно, что сумма будет намного компактнее, если ее записать с помощью оператора суммирования. Вот уравнение для расчета среднего, μ x , нашего набора данных с использованием оператора суммирования:
Общее уравнение для вычисления среднего, μ , набора чисел, X 1 – X N
9 ,
9 будет записано так:
Иногда для простоты индексы опускаются, как мы сделали справа выше. Отказ от индексов делает уравнения менее загроможденными, но все же понятно, что вы суммируете все значения 9.
 0213 х .
0213 х .Уравнение, определяющее дисперсию
Теперь, когда вы знаете, как работает оператор суммирования, вы можете понять уравнение, определяющее дисперсию генеральной совокупности (см. , и какой из них вы должны использовать для своего научного проекта):
Дисперсия ( σ 2 ) определяется как сумма квадратов расстояний каждого члена в распределении от среднего ( μ ), деленное на количество слагаемых в раздаче ( N ).
Существует более эффективный способ расчета стандартного отклонения для группы чисел, показанный в следующем уравнении:
Вы берете сумму квадратов слагаемых в распределении и делите на количество слагаемых в распределении ( N ). Из этого вычесть квадрат среднего ( μ 2 ). Таким образом вычислить стандартное отклонение намного проще.
Легко доказать самому себе, что эти два уравнения эквивалентны.
 Начните с определения дисперсии (уравнение 1 ниже). Разверните выражение для возведения в квадрат расстояния термина от среднего (уравнение 2, ниже).
Начните с определения дисперсии (уравнение 1 ниже). Разверните выражение для возведения в квадрат расстояния термина от среднего (уравнение 2, ниже).Теперь разделите отдельные члены уравнения (оператор суммирования распределяет по членам в скобках, см. уравнение 3 выше). В конечном итоге сумма μ 2 / N , взятая N раз, равна всего Nμ 2 / N .
Затем мы можем упростить второе и третье слагаемые в уравнении 3. Во втором слагаемом вы можете видеть, что Σ X / N — это просто другой способ записи μ , среднее значение членов. Таким образом, второй член упрощается до −2 μ 2 (сравните уравнения 3 и 4 выше). В третьем члене N / N равно 1, поэтому третий член упрощается до μ 2 (сравните уравнения 3 и 4 выше).
Наконец, из уравнения 4 видно, что второе и третье слагаемые можно объединить, что даст нам результат, который мы пытались доказать в уравнении 5.

В качестве примера давайте вернемся к двум распределениям, с которых мы начали обсуждение с:
набор данных 1: 3, 4, 4, 5, 6, 8
набор данных 2: 1, 2, 4, 5, 7, 11 .Каковы дисперсия и стандартное отклонение каждого набора данных?
Мы составим таблицу для расчета значений. Вы можете использовать аналогичную таблицу, чтобы найти дисперсию и стандартное отклонение для результатов ваших экспериментов.
Хотя оба набора данных имеют одно и то же среднее значение ( μ = 5), дисперсия ( σ 2 ) второго набора данных, 11,00, немного больше, чем четырежды дисперсии первого набор данных, 2.67. Стандартное отклонение ( σ ) представляет собой квадратный корень из дисперсии, поэтому стандартное отклонение второго набора данных, 3,32, чуть больше , дважды умноженное на стандартного отклонения первого набора данных, 1,63.
Дисперсия и стандартное отклонение дают нам числовую меру разброса набора данных.
 Эти меры полезны для сравнения наборов данных, выходящих за рамки простых визуальных впечатлений.
Эти меры полезны для сравнения наборов данных, выходящих за рамки простых визуальных впечатлений.Дисперсия совокупности и дисперсия выборки
Уравнения, приведенные выше, показывают, как рассчитать дисперсию для всей совокупности. Однако при выполнении научного проекта у вас почти никогда не будет доступа к данным обо всем населении. Например, вы можете измерить рост всех в своем классе, но вы не можете измерить рост всех на Земле. Если вы запускаете шарик для пинг-понга с помощью катапульты и измеряете расстояние, которое он проходит, теоретически вы можете запускать мяч бесконечное количество раз. В любом случае ваши данные всего лишь выборка всего населения. Это означает, что вы должны использовать немного другую формулу для расчета дисперсии с членом N-1 в знаменателе вместо N :
Это известно как поправка Бесселя.
Моделирование того, как работает коллективный иммунитет
Создание зеркала бесконечности
Научные друзья: запуск спорового мешочка пилоболуса
Общий анализ максимального правдоподобия компонентов дисперсии в обобщенных линейных моделях
.
 1999 март; 55(1):117-28.
1999 март; 55(1):117-28.doi: 10.1111/j.0006-341x.1999.00117.x.
М Эйткин 1
принадлежность
- 1 Статистический факультет Университета Ньюкасла, Великобритания. Murray.Aitkin@newcastle.ac.uk
- PMID: 11318145
- DOI: 10.1111/j.0006-341x.1999.00117.x
М Эйткин. Биометрия. 1999 март
. 1999 март; 55(1):117-28.
doi: 10.
 1111/j.0006-341x.1999.00117.х.
1111/j.0006-341x.1999.00117.х.Автор
М Эйткин 1
принадлежность
- 1 Статистический факультет Университета Ньюкасла, Великобритания. Murray.Aitkin@newcastle.ac.uk
- PMID: 11318145
- DOI: 10.1111/j.0006-341x.1999.00117.х
Абстрактный
В этой статье описывается алгоритм EM для непараметрической оценки максимального правдоподобия (ML) в обобщенных линейных моделях со структурой компонентов дисперсии. Алгоритм обеспечивает альтернативный анализ для приближенного анализа MQL и PQL (McGilchrist and Aisbett, 1991, Biometrical Journal 33, 131-141; Breslow and Clayton, 1993; Journal of the American Statistical Association 88, 9).
 -25; McGilchrist, 1994, Журнал Королевского статистического общества, серия B 56, 61-69; Goldstein, 1995, Многоуровневые статистические модели) и анализу GEE (Liang and Zeger, 1986, Biometrika 73, 13-22). Алгоритм, впервые предложенный Хайндом и Вудом (1987, в Longitudinal Data Analysis, 110-126), представляет собой обобщение алгоритма для моделей со случайными эффектами для избыточной дисперсии в обобщенных линейных моделях, описанного в Aitkin (1996, Statistics and Computing 6, 251). -262). Алгоритм изначально получен как форма квадратуры Гаусса, предполагающая нормальное распределение смешивания, но с небольшими изменениями его можно использовать для совершенно неизвестного распределения смешивания, предоставляя прямой метод для полностью непараметрической оценки этого распределения ML. Это имеет значение, потому что оценки ML параметров GLM могут быть чувствительны к спецификации параметрической формы для распределения смешивания. Непараметрический анализ можно непосредственно распространить на общие модели случайных параметров с полной NPML-оценкой совместного распределения случайных параметров.
-25; McGilchrist, 1994, Журнал Королевского статистического общества, серия B 56, 61-69; Goldstein, 1995, Многоуровневые статистические модели) и анализу GEE (Liang and Zeger, 1986, Biometrika 73, 13-22). Алгоритм, впервые предложенный Хайндом и Вудом (1987, в Longitudinal Data Analysis, 110-126), представляет собой обобщение алгоритма для моделей со случайными эффектами для избыточной дисперсии в обобщенных линейных моделях, описанного в Aitkin (1996, Statistics and Computing 6, 251). -262). Алгоритм изначально получен как форма квадратуры Гаусса, предполагающая нормальное распределение смешивания, но с небольшими изменениями его можно использовать для совершенно неизвестного распределения смешивания, предоставляя прямой метод для полностью непараметрической оценки этого распределения ML. Это имеет значение, потому что оценки ML параметров GLM могут быть чувствительны к спецификации параметрической формы для распределения смешивания. Непараметрический анализ можно непосредственно распространить на общие модели случайных параметров с полной NPML-оценкой совместного распределения случайных параметров. Это может обеспечить значительную экономию вычислительных ресурсов по сравнению с полным численным интегрированием по заданному параметрическому распределению для случайных параметров. Описан простой метод получения правильных стандартных ошибок для оценок параметров при использовании EM-алгоритма. Обсуждается несколько примеров, включающих простую компоненту дисперсии и продольные модели, а также оценку малых площадей.
Это может обеспечить значительную экономию вычислительных ресурсов по сравнению с полным численным интегрированием по заданному параметрическому распределению для случайных параметров. Описан простой метод получения правильных стандартных ошибок для оценок параметров при использовании EM-алгоритма. Обсуждается несколько примеров, включающих простую компоненту дисперсии и продольные модели, а также оценку малых площадей.Похожие статьи
Стандартные ошибки для оценок EM в обобщенных линейных моделях со случайными эффектами.
Фридл Х., Кауэрманн Г. Фридл Х. и др. Биометрия. 2000 г., сен; 56 (3): 761-7. doi: 10.1111/j.0006-341x.2000.00761.x. Биометрия. 2000. PMID: 10985213
Метаанализ путем моделирования случайных эффектов в обобщенных линейных моделях.

Айткин М. Айткин М. Стат мед. 1999 г., 15–30 сентября; 18 (17–18): 2343–51. doi: 10.1002/(sici)1097-0258(199/30)18:17/183.0.co;2-3. Стат мед. 1999. PMID: 10474144
Сравнение подхода на основе обобщенного оценочного уравнения с методом максимального правдоподобия для повторных измерений.
Парк Т. Парк Т. Стат мед. 1993 г., 30 сентября; 12 (18): 1723-32. doi: 10.1002/sim.4780121807. Стат мед. 1993. PMID: 8248664
Об алгоритме EM для сверхдисперсных данных подсчета.
Маклахлан Г.Дж. Маклахлан Г.Дж. Статистические методы Med Res. 1997 март; 6(1):76-98. дои: 10.1177/096228029700600106. Статистические методы Med Res. 1997. PMID: 9185291 Обзор.
Расширение параметра для оценки ковариационных матриц уменьшенного ранга.

Мейер К. Мейер К. Генет Сель Эвол. 2008 г., январь-февраль; 40(1):3-24. дои: 10.1186/1297-9686-40-1-3. Epub 2007, 21 декабря. Генет Сель Эвол. 2008. PMID: 18096112 Бесплатная статья ЧВК. Обзор.
Посмотреть все похожие статьи
Цитируется
Полупараметрический факторный анализ данных о времени отклика на уровне элементов.
Лю Ю, Ван В. Лю Ю и др. Психометрика. 2022 июнь; 87 (2): 666-692. doi: 10.1007/s11336-021-09832-8. Epub 2022 31 января. Психометрика. 2022. PMID: 35098450
Модель гетероскедастической траектории с препятствиями латентного класса: закономерности приверженности пациентов с обструктивным апноэ во сне, получающих СРАР-терапию.

P Den Teuling NG, van den Heuvel ER, Aloia MS, Pauws SC. P Den Teuling NG, et al. БМС Мед Рез Методол. 2021 1 декабря; 21 (1): 269. doi: 10.1186/s12874-021-01407-6. БМС Мед Рез Методол. 2021. PMID: 34852769Бесплатная статья ЧВК.
Взаимосвязь между социальной поддержкой и проблемами психического здоровья во время беременности: систематический обзор и метаанализ.
Бедасо А., Адамс Дж., Пэн В., Сиббритт Д. Бедасо А. и др. Воспроизведение здоровья. 2021 28 июля; 18 (1): 162. doi: 10.1186/s12978-021-01209-5. Воспроизведение здоровья. 2021. PMID: 34321040 Бесплатная статья ЧВК. Обзор.
Перспектива нормы реакции на воспроизводимость.
Фёлькль Б., Вюрбель Х. Voelkl B, et al.
 Теория Биологии. 2021 июнь; 140(2):169-176. doi: 10.1007/s12064-021-00340-y. Epub 2021 25 марта.
Теория Биологии. 2021.
PMID: 33768464
Бесплатная статья ЧВК.
Теория Биологии. 2021 июнь; 140(2):169-176. doi: 10.1007/s12064-021-00340-y. Epub 2021 25 марта.
Теория Биологии. 2021.
PMID: 33768464
Бесплатная статья ЧВК.Рекомендации по размерам выборки для многоуровневых моделей скрытых классов.
Парк Дж, Ю ХТ. Парк Дж. и др. Educ Psychol Meas. 2018 окт; 78 (5): 737-761. дои: 10.1177/0013164417719111. Epub 2017 9 июля. Educ Psychol Meas. 2018. PMID: 32655168 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
термины MeSH
вещества
Дисперсия: простое определение, пошаговые примеры
Содержание:- Как рассчитать дисперсию?
- Вариант на TI-83
- Инструкции для Minitab
- Насколько сильно могут отличаться данные?
- Дисперсия биномиального распределения
- Дисперсия населения
- Образец дисперсии
Дисперсия измеряет, насколько далеко разбросан набор данных.
 Математически он определяется как среднее квадратов отличий от среднего.
Математически он определяется как среднее квадратов отличий от среднего.Посмотрите видео с примером того, как найти выборочную дисперсию.
Как вручную найти дисперсию и стандартное отклонение (для примера)
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Дисперсия для населения рассчитывается следующим образом:
- Нахождение среднего значения.
- Вычитание среднего значения из каждого числа в наборе данных и возведение результата в квадрат. Результаты возводятся в квадрат, чтобы сделать отрицательные числа положительными. В противном случае отрицательные числа отменили бы положительные на следующем шаге. Важно расстояние от среднего, а не положительные или отрицательные числа.
- Усреднение квадратов разностей.
Однако в статистике чаще всего находят дисперсию для выборки . Когда вы вычисляете его для выборки, разделите на размер выборки минус один ( Зачем использовать n-1? ) при расчете среднего квадрата разницы на шаге 3 выше. См.: Нахождение выборочной дисперсии.
См.: Нахождение выборочной дисперсии.Используйте наш онлайн-вар. и калькулятор стандартного отклонения, который показывает вам пошаговых расчетов для вашего индивидуального набора данных. Вы также можете рассчитать σ 2 в Minitab.
Нужна помощь с домашним заданием? Посетите нашу обучающую страницу!
Стандартное отклонение
Квадратный корень из дисперсии представляет собой стандартное отклонение. В то время как вар. дает вам приблизительное представление о разбросе, стандартное отклонение является более конкретным и дает вам точное расстояние от среднего значения.
Вернуться к началу
Посмотрите видео с шагами:
Дисперсия на TI 83
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Отклонение в обзоре TI-83
Вы можете найти стандартное отклонение для списка данных с помощью калькулятора TI 83 и возвести в квадрат результат, но вы не получите точного ответа, если не возведете в квадрат весь ответ, включая все значащих цифр.
 Есть «трюк» для получения дисперсии TI-83, и он включает в себя копирование стандартного отклонения на главный экран, а затем возведение его в квадрат, чтобы получить дисперсию.
Есть «трюк» для получения дисперсии TI-83, и он включает в себя копирование стандартного отклонения на главный экран, а затем возведение его в квадрат, чтобы получить дисперсию.Дисперсия на TI-83: Шаги
Пример задачи: Найдите дисперсию высот 12 верхних зданий в Лондоне, Англия. Высота (в футах): 800, 720, 655, 655, 625, 600, 590, 529, 513, 502, 502, 502.
Шаг 1: Введите приведенные выше данные в список. Нажмите кнопку STAT, а затем нажмите ENTER. Введите первое число (800) и нажмите клавишу ВВОД. Продолжайте вводить цифры, нажимая ENTER после каждого ввода.
Шаг 2: Нажмите СТАТ.
Шаг 3: Нажмите кнопку со стрелкой вправо (клавиши со стрелками расположены в верхней правой части клавиатуры), чтобы выбрать Calc .
Шаг 4: Нажмите ENTER, чтобы выделить 1-Var Stats .
Шаг 5: Нажмите ENTER еще раз, чтобы открыть список статистики.

Шаг 6: Нажмите VARS 5, чтобы вызвать список доступных статистических переменных.
Шаг 7: Нажмите 3, чтобы выбрать «Sx», которое является нашим стандартным отклонением.
Шаг 8: Нажмите x 2 , затем Enter, чтобы отобразить отклонение, которое равно 9326,628788 .
Вот как найти дисперсию на TI-83!
НаверхПотеряли путеводитель? Вы можете загрузить новый с веб-сайта Texas Instruments.
Посмотрите видео, чтобы найти образец отклонения:
Как найти отклонение в Minitab
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Как найти дисперсию в Minitab: шаги
Пример формулы дисперсии.Пример вопроса : Найдите дисперсию для следующей выборки: 12, 13, 24, 24, 25, 26, 34, 35, 38, 45, 46, 52, 53, 78, 78, 89
Шаг 1: Введите данные в столбец на листе Minitab.

Шаг 2: Нажмите «Статистика», затем нажмите «Основная статистика», затем нажмите «Описательная статистика».
Шаг 3: Щелкните переменные, для которых требуется найти дисперсию для , а затем щелкните «Выбрать», чтобы переместить имена переменных в правое окно.
Шаг 4: Нажмите «Статистика».
Шаг 5: Установите флажок «Отклонение» и дважды нажмите «ОК». Разница в Minitab будет отображаться в новом окне. Дисперсия для этого конкретного набора данных составляет 540,667.
Вот и все!
Наименьшая дисперсия равна нулю, но технически она может быть бесконечное число с числами в миллионы или даже миллиарды и выше.
Биномиальное распределение — это простой эксперимент, в котором есть «успех» или «неудача». Например, выбор выигрышного лотерейного билета может быть биномиальным экспериментом (вы либо выигрываете, либо проигрываете!). Подбрасывание монеты с целью выпадения орла также является биномиальным (выпадение орла — это «успех», а решки — «неудача»).
 Формула дисперсии биномиального распределения: n*p (1-p) или n*p*q. Эти две формулы эквивалентны, поскольку q = (1-p).
Формула дисперсии биномиального распределения: n*p (1-p) или n*p*q. Эти две формулы эквивалентны, поскольку q = (1-p).Пример задачи: Если вы подбросите монету 50 раз и попытаетесь получить решку, какова дисперсия биномиального распределения?
Шаг 1: Найдите «p». Первый шаг к решению этой проблемы — осознать, что вероятность выпадения орла составляет 50 процентов, или 0,5. Следовательно, «p» (вероятность) равен 0,5.
Шаг 2: Найдите «q» или 1-п. Эти два эквивалентны. Это вероятность того, что , а не выпадут орлом (другими словами, вероятность выпадения решки). 1 – 0,5 = 0,5. Следовательно, «q» (или 1 – p) = 0,5.
Шаг 3: Умножьте шаг 1 (p) на шаг 2 (q) на «n» (количество попыток). Мы подбрасываем монету 50 раз, поэтому число попыток равно 50 (n = 50).
Н * р * кв = 50 * 0,5 * 0,5 = 12,5.
Вар. биномиального распределения для подбрасывания монеты 50 раз равно 12,5.
Итак, что означает биномиальная дисперсия?
В сущности, немного! Дисперсия практически не используется, за исключением расчета стандартного отклонения.
 Например, стандартное отклонение для этого конкретного биномиального распределения:
Например, стандартное отклонение для этого конкретного биномиального распределения:
√12,5 = 3,54.
Вы будете использовать дисперсию для таких вещей, как вычисление z-показателей (это обычно происходит позже в классе статистики, после нормальных распределений), который имеет стандартное отклонение в нижней части формулы:Альтернативная форма z-показателя.
Вернуться к началуДисперсия генеральной совокупности является типом параметра . Если вы не уверены, что такое параметр, вы можете просмотреть:
В чем разница между статистикой и параметром?Формула:
Посмотрите видео, чтобы узнать, как найти дисперсию совокупности, или прочтите инструкции ниже:дисперсия совокупности
Посмотрите это видео на YouTube.
Как найти дисперсию населения.
Большую часть времени в статистике вам нужно найти выборочную дисперсию, а не дисперсию генеральной совокупности. Почему? Потому что в статистике обычно делают выводы на основе выборок, а не совокупности.
 Если бы у вас были все данные о населении, в статистике вообще не было бы необходимости! Тем не менее, между формулой дисперсии генеральной совокупности и формулой дисперсии выборки действительно очень мало различий. Если у вас есть образцы данных, вы все равно можете использовать эту формулу. Вам просто нужно будет вставить свои данные в столбцы вместо данных о населении. Если вы предпочитаете подставлять числа прямо в формулу, просто убедитесь, что вы используете среднее значение генеральной совокупности, а не среднее значение выборки(). Кроме того, наиболее распространенная формула выборочной дисперсии использует n-1 в знаменателе вместо n. 92 28 29 30 31 32
Если бы у вас были все данные о населении, в статистике вообще не было бы необходимости! Тем не менее, между формулой дисперсии генеральной совокупности и формулой дисперсии выборки действительно очень мало различий. Если у вас есть образцы данных, вы все равно можете использовать эту формулу. Вам просто нужно будет вставить свои данные в столбцы вместо данных о населении. Если вы предпочитаете подставлять числа прямо в формулу, просто убедитесь, что вы используете среднее значение генеральной совокупности, а не среднее значение выборки(). Кроме того, наиболее распространенная формула выборочной дисперсии использует n-1 в знаменателе вместо n. 92 28 29 30 31 32Шаг 2: Найдите среднее значение. Среднее значение для этого набора данных равно (28 + 29 + 30 + 31 + 32) / 5 = 30.
Шаг 3: Заполните столбец 2.
92 Этот столбец представляет собой ваше значение X минус среднее значение. Например, первая запись 28 – 30 = -2.
Этот столбец представляет собой ваше значение X минус среднее значение. Например, первая запись 28 – 30 = -2.28 -2 4 29 -1 1 30 0 0 31 1 1 32 2 4 Шаг 5: Сложите все числа в столбце 3 (это часть формулы суммирования):
4 + 1 + 0 + 1 + 4 = 10Шаг 6: Разделите на количество элементов в вашем наборе данных:
10 / 5 = 2
Дисперсия населения для этого набора данных равна 2.Вернуться к началу
Посетите наш канал YouTube, чтобы посмотреть сотни видео с пошаговой статистикой.
Ссылки
Kenney, JF и Keeping, E.S. Математика статистики, Pt. 2, 2-е изд. Принстон, Нью-Джерси: Ван Ностранд, 1951.
Папулис, А. Вероятность, случайные величины и случайные процессы, 2-е изд. Нью-Йорк: McGraw-Hill, стр. 144–145, 1984.
Нью-Йорк: McGraw-Hill, стр. 144–145, 1984.УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Дисперсия: простое определение, пошаговые примеры» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/variance/————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.  org
org+86 18163351462 (WhatsApp) 1655362766 Публикация бумаги WeChat Недавно опубликованные статьи Недавно опубликованные статьи Исследование привычек образа жизни, вызванных стрессом()
Фумихиро Омасу, Ай Кавано, Майко Нагаясу, Аска Ниси
Открытый журнал профилактической медицины Том 12 № 9, 27 сентября 2022 г.

DOI: 10.4236/ojpm.2022.129014 6 загрузок 57 просмотров
Выбор нового регулирующего права для траста с преимущественно английскими элементами: насколько просторна комната для маневра с точки зрения его применения в английском суде? ()
Зинат Бибиджон
Beijing Law Review Vol.13 No.3, 27 сентября 2022 г.
DOI: 10.4236/blr.2022.133042 5 загрузок 65 просмотров
Субпараневральная подмышечная блокада под ультразвуковым контролем в странах Африки к югу от Сахары: проспективное многоцентровое исследование и обзор литературы ()
Гислен Эджо Нкилли, Амилкар Гомбако, Николя Сомье, Рафаэль Окуэ Ондо, Стефан Оливейра, Ричард Обаме, Ромен Чуа
Открытый журнал анестезиологии Том 12 № 9, 27 сентября 2022 г.

DOI: 10.4236/ojanes.2022.129025 2 загрузки 34 просмотра
Защитный эффект премедикации пероральными стероидами: побочные реакции на неионогенные йодсодержащие контрастные вещества для компьютерной томографии ()
Нориказу Коори, Акико Маэда, Маюми Ясуи, Хироки Камекава, Юсуке Ёсида, Акари Нода, Юта Шираки, Казуя Ёкои, Юдай Сузуки, Казума Курата, Хироко Нишикава
Open Journal of Radiology Vol.12 No.3, 27 сентября 2022 г.
DOI: 10.4236/ojrad.2022.123012 5 загрузок 32 просмотров
Стратиграфия бассейна MSGBC в западной части Тиеса с помощью пикселизации и веб-моделирования (Сенегал, Западная Африка)()
Мохамаду Мустафа Тиам, Мумар Дийе, Адама Дионе, Абдул Азиз Ндиайе, Мапате Ндиайе, Салимата Нгом, Рафаэль Сарр
Открытый геологический журнал Том 12 № 9, 27 сентября 2022 г.

DOI: 10.4236/ojg.2022.129032 11 загрузок 55 просмотров
Микрохирургическая резекция медуллобластомы мостомозжечкового угла, клинический случай и обзор литературы()
Фадаль Алретими, Хешам Бен Хаял, Абдуссалам Абограра Саид, Лубна Аззуз, Амани Масуд
Открытый журнал современной нейрохирургии Том 12 № 4, 27 сентября 2022 г.
DOI: 10.4236/ojmn.2022.124020 7 загрузок 41 просмотр
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.org +86 18163351462 (WhatsApp) 1655362766 Публикация бумаги WeChat Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc.
верхний Все права защищены.
Все права защищены.Общий процесс отклонения | Мерсер-Айленд, Вашингтон,
В Едином кодексе землеустройства есть конкретные численные стандарты застройки, такие как отступы или высота зданий, которым должны соответствовать все застройки. Однако бывают случаи, когда строгое применение таких стандартов может оказаться неуместным из-за особых характеристик объекта. Процедура отклонения предназначена для того, чтобы разрешить незначительные корректировки правил застройки при наличии особых или чрезвычайных обстоятельств, применимых к земельному участку или зданию. Отклонение предоставляется только в том случае, если строгое соблюдение стандартов застройки применительно к конкретному участку создаст практические трудности в использовании имущества, а без отклонения имущество становится непригодным для использования [MICCC 19.15.020(G)(4)].
Чем обосновано отклонение?
Особые обстоятельства могут включать такие факторы, как размер, форма, топография, расположение участка, деревья, почвенный покров или другие физические условия участка и его окрестностей; или факторы, необходимые для успешной установки системы солнечной энергии, такие как особая ориентация здания для доступа к солнечным лучам.
 Корректировки, разрешенные отклонением, ограничены конкретными стандартами числового развития. Изменение использования не может быть разрешено процедурой отклонения (например, автосалон в жилой зоне). Кроме того, должно быть установлено, что предоставление отклонения не нанесет существенного ущерба общественному благополучию или ущербу имуществу или улучшениям в окрестностях и зоне, в которой расположено имущество. Предоставление отклонения не может ни изменить характер района, ни нанести ущерб надлежащему использованию или развитию прилегающей собственности.
Корректировки, разрешенные отклонением, ограничены конкретными стандартами числового развития. Изменение использования не может быть разрешено процедурой отклонения (например, автосалон в жилой зоне). Кроме того, должно быть установлено, что предоставление отклонения не нанесет существенного ущерба общественному благополучию или ущербу имуществу или улучшениям в окрестностях и зоне, в которой расположено имущество. Предоставление отклонения не может ни изменить характер района, ни нанести ущерб надлежащему использованию или развитию прилегающей собственности.Отклонения рассматриваются экспертом по слухам. Важно подчеркнуть, что отклонение может быть предоставлено только в том случае, если будет установлено особое обстоятельство, как описано ранее. Отклонение не может быть предоставлено просто для того, чтобы сделать строительство недвижимости менее затратным или расширить использование собственности.
Как подать заявление на отклонение?
Рассмотрение проекта
В начале рассмотрения потенциального проекта вам следует внимательно ознакомиться с Единым кодексом землеустройства, чтобы убедиться, что все правила соблюдены.
 Альтернативы должны быть тщательно исследованы, чтобы увидеть, есть ли способ достичь целей проекта, не запрашивая отклонения. Бремя доказывания лежит на заявителе, который должен продемонстрировать, что он соответствует применимым критериям отклонения, он рассмотрел альтернативы и объяснил, почему эти альтернативы неосуществимы, и ему необходимо отклонение, о котором он просит. (Примечание: заявка на отклонение требует значительного времени, затрат и риска для владельца собственности. Заявка не гарантирует одобрения. Сборы не возвращаются, если заявка отклонена; заявители действуют на свой страх и риск. (Нажмите здесь для тарифный план.)
Альтернативы должны быть тщательно исследованы, чтобы увидеть, есть ли способ достичь целей проекта, не запрашивая отклонения. Бремя доказывания лежит на заявителе, который должен продемонстрировать, что он соответствует применимым критериям отклонения, он рассмотрел альтернативы и объяснил, почему эти альтернативы неосуществимы, и ему необходимо отклонение, о котором он просит. (Примечание: заявка на отклонение требует значительного времени, затрат и риска для владельца собственности. Заявка не гарантирует одобрения. Сборы не возвращаются, если заявка отклонена; заявители действуют на свой страх и риск. (Нажмите здесь для тарифный план.)Консультация персонала
После ознакомления с применимыми правилами разработки, поскольку они относятся к вашему проекту, вы можете договориться о встрече со специалистом по планированию, чтобы обсудить предлагаемое вами заявление на отклонение, прежде чем подавать заявление на отклонение.
Подача заявки
Нажмите здесь для подачи заявки на отклонение.
 Только заполненные заявки принимаются Группой услуг по развитию. Ваша заявка будет рассмотрена, чтобы убедиться, что предоставлена вся необходимая информация. Имейте в виду, что материалы заявки, которые вы отправляете, являются общедоступной информацией и могут быть просмотрены представителями общественности, поэтому важна хорошая организация, а также четкое и краткое письменное описание запроса на отклонение и вашего ответа на применимые критерии отклонения.
Только заполненные заявки принимаются Группой услуг по развитию. Ваша заявка будет рассмотрена, чтобы убедиться, что предоставлена вся необходимая информация. Имейте в виду, что материалы заявки, которые вы отправляете, являются общедоступной информацией и могут быть просмотрены представителями общественности, поэтому важна хорошая организация, а также четкое и краткое письменное описание запроса на отклонение и вашего ответа на применимые критерии отклонения.После подачи полной заявки на проект ваша заявка передается специалисту по планированию персонала. Специалист по планированию персонала, назначенный для проекта, будет вашим основным контактным лицом и связующим звеном с персоналом на протяжении всего процесса. Заявка направляется любым необходимым внешним агентствам и сотрудникам города, которые будут вносить свой вклад в проект. В течение 28 дней после подачи заявки планировщик персонала, назначенный для проекта, уведомит вас о том, завершена ли заявка для обработки или требуется дополнительная информация.

Когда заявка будет считаться заполненной, заявка на отклонение будет отмечена в Бюллетене разрешений города.
Проверка персонала
Владельцы недвижимости в пределах 300 футов от объекта недвижимости будут уведомлены по почте о предлагаемом отклонении, и им будет предоставлено не менее 14 дней для предоставления письменных комментариев по проекту. Общественное замечание также может быть дано на публичных слушаниях. Заявитель несет ответственность за размещение публичного объявления о предлагаемом отклонении на видном месте на участке, видимом с улицы. В уведомлениях указывается характер отклонения и, если применимо, указывается время, дата и место любого публичного слушания.
За кем последнее слово?
Решение является окончательным, если только зарегистрированная сторона не подаст апелляцию. Апелляция должна быть подана в течение 14 дней после уведомления города о решении. Апелляция будет рассмотрена Комиссией по планированию, которая вынесет решение, подтверждающее, изменяющее или отменяющее административное решение.

Решение Комиссии по планированию является окончательным, если только зарегистрированная сторона* не подаст апелляцию. Апелляция должна быть подана в течение 14 дней после уведомления о решении. Решение Комиссии по планированию может быть обжаловано официальной стороной, имеющей правоспособность, путем подачи ходатайства о землепользовании в вышестоящий суд округа Кинг. Такая петиция должна быть подана в течение 21 дня после вынесения решения плановой комиссии.
*Подписной стороной является любое лицо, представившее письменный комментарий в течение объявленного периода представления комментариев или, в случае проведения публичных слушаний, давшее устные показания в ходе части слушания, посвященной общественному обсуждению.
Сколько времени займет этот процесс?
Приблизительное время обработки заявления на отклонение будет варьироваться в зависимости от сложности и масштаба изменения и рабочей нагрузки персонала. В течение 28 дней после подачи заявки вы будете уведомлены о том, определили ли сотрудники проектную заявку как полную или заявка требует дополнительной информации.


 Найти
несмещенную оценку генеральной
средней.
Найти
несмещенную оценку генеральной
средней.

 Г(A2:A11)
Г(A2:A11)

 82
82 7
7 Обобщенную дисперсию можно оценить, вычислив \(|S|\), определитель выборочной матрицы дисперсии/ковариации.
Обобщенную дисперсию можно оценить, вычислив \(|S|\), определитель выборочной матрицы дисперсии/ковариации.
 Мы начнем с присвоения каждого числа переменной X 1 – X 6 , например:
Мы начнем с присвоения каждого числа переменной X 1 – X 6 , например: 0213 х .
0213 х . Начните с определения дисперсии (уравнение 1 ниже). Разверните выражение для возведения в квадрат расстояния термина от среднего (уравнение 2, ниже).
Начните с определения дисперсии (уравнение 1 ниже). Разверните выражение для возведения в квадрат расстояния термина от среднего (уравнение 2, ниже).
 Эти меры полезны для сравнения наборов данных, выходящих за рамки простых визуальных впечатлений.
Эти меры полезны для сравнения наборов данных, выходящих за рамки простых визуальных впечатлений.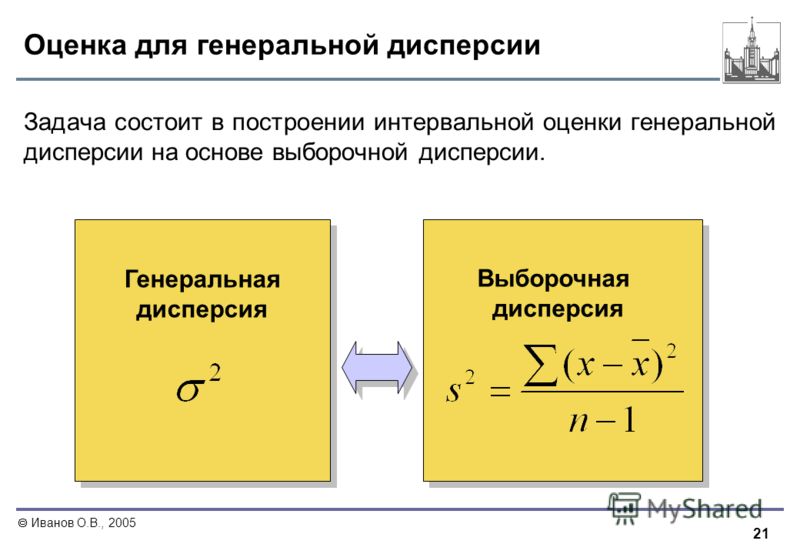 1999 март; 55(1):117-28.
1999 март; 55(1):117-28. 1111/j.0006-341x.1999.00117.х.
1111/j.0006-341x.1999.00117.х. -25; McGilchrist, 1994, Журнал Королевского статистического общества, серия B 56, 61-69; Goldstein, 1995, Многоуровневые статистические модели) и анализу GEE (Liang and Zeger, 1986, Biometrika 73, 13-22). Алгоритм, впервые предложенный Хайндом и Вудом (1987, в Longitudinal Data Analysis, 110-126), представляет собой обобщение алгоритма для моделей со случайными эффектами для избыточной дисперсии в обобщенных линейных моделях, описанного в Aitkin (1996, Statistics and Computing 6, 251). -262). Алгоритм изначально получен как форма квадратуры Гаусса, предполагающая нормальное распределение смешивания, но с небольшими изменениями его можно использовать для совершенно неизвестного распределения смешивания, предоставляя прямой метод для полностью непараметрической оценки этого распределения ML. Это имеет значение, потому что оценки ML параметров GLM могут быть чувствительны к спецификации параметрической формы для распределения смешивания. Непараметрический анализ можно непосредственно распространить на общие модели случайных параметров с полной NPML-оценкой совместного распределения случайных параметров.
-25; McGilchrist, 1994, Журнал Королевского статистического общества, серия B 56, 61-69; Goldstein, 1995, Многоуровневые статистические модели) и анализу GEE (Liang and Zeger, 1986, Biometrika 73, 13-22). Алгоритм, впервые предложенный Хайндом и Вудом (1987, в Longitudinal Data Analysis, 110-126), представляет собой обобщение алгоритма для моделей со случайными эффектами для избыточной дисперсии в обобщенных линейных моделях, описанного в Aitkin (1996, Statistics and Computing 6, 251). -262). Алгоритм изначально получен как форма квадратуры Гаусса, предполагающая нормальное распределение смешивания, но с небольшими изменениями его можно использовать для совершенно неизвестного распределения смешивания, предоставляя прямой метод для полностью непараметрической оценки этого распределения ML. Это имеет значение, потому что оценки ML параметров GLM могут быть чувствительны к спецификации параметрической формы для распределения смешивания. Непараметрический анализ можно непосредственно распространить на общие модели случайных параметров с полной NPML-оценкой совместного распределения случайных параметров. Это может обеспечить значительную экономию вычислительных ресурсов по сравнению с полным численным интегрированием по заданному параметрическому распределению для случайных параметров. Описан простой метод получения правильных стандартных ошибок для оценок параметров при использовании EM-алгоритма. Обсуждается несколько примеров, включающих простую компоненту дисперсии и продольные модели, а также оценку малых площадей.
Это может обеспечить значительную экономию вычислительных ресурсов по сравнению с полным численным интегрированием по заданному параметрическому распределению для случайных параметров. Описан простой метод получения правильных стандартных ошибок для оценок параметров при использовании EM-алгоритма. Обсуждается несколько примеров, включающих простую компоненту дисперсии и продольные модели, а также оценку малых площадей.

