Геометрическая прогрессия | umath.ru
Содержание
- Определение геометрической прогрессии
- Формула n-го члена геометрической прогрессии
- Сумма первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии
- Сумма бесконечно убывающей геометрической прогрессии
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.
То есть геометрическая прогрессия определяется рекуррентным соотношением
Примеры геометрических прогрессий.
- Последовательность — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем
Теорема 1. Пусть — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула
Пусть — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула
Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство. Из определения геометрической прогрессии
Следовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.
Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.
Решение. По условию
Выразим члены геометрической прогрессии через и : Тогда система запишется в виде
Разделив второе уравнение системы на первое, получим Следовательно,
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогресcии выражается формулой
(5)
Пример 3. Найдём сумму
Решение. — сумма бесконечно убывающей геометрической прогрессии с первым членом и знаменателем По формуле (5) получаем
То есть
Геометрическая прогрессия: определение, формулы, свойства
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Геометрическая прогрессия: определение, формулы, свойства
Геометрическая прогрессия – это числовая последовательность, в которой, начиная со второго числа, каждое последующее равняется предыдущему, умноженному на постоянный множитель.
- Общий вид геометрической прогрессии
- Свойства и формулы геометрической прогрессии
Общий вид геометрической прогрессии
b1, b1q, b2q, …, bn-1q
- q – знаменатель прогрессии; это и есть постоянный множитель.
- b ≠ 0, q ≠ 0
Члены прогрессии:
- b1
- b2 = b1q
- b3 = b2q = b1q2
- и т.д.
Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.
Виды прогрессии:
- возрастающая: b1 > 0 и q1 > 0;
- убывающая: 0 < q < 1;
- знакочередующаяся: q < 0;
- стационарная: q = 1.
Свойства и формулы геометрической прогрессии
1. Нахождение n-ого члена (bn)
Нахождение n-ого члена (bn)
- bn = bn-1q
- bn = b1qn-1
2. Знаменатель прогрессии
3. Характеристическое свойство
Последовательность чисел b1, b2, b3 … является геометрической прогрессией, если для любого ее члена справедливо следующее выражение:
При условии: 1 < i < n
Также данное свойство можно представить в таком виде:
4. Сумма первых членов прогрессии
Найти сумму n первых членов геометрической прогрессии можно, используя формулу ниже (если q ≠ 1):
Если q = 1, то Sn = nb1
5. Произведение первых членов прогрессии
6. Произведение членов прогрессии с k по n
7. Сумма всех членов убывающей прогрессии
Сумма всех членов убывающей прогрессии
При условии: |q| < 1, а значит, bn → 0 при n → + ∞.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
4. ..$
..$ , где r ≠ 0, r — обыкновенное отношение, а a — масштабный коэффициент (также первый член).
Примеры
Геометрическая прогрессия с знаменателем 2 и масштабным коэффициентом 1 равна
1, 2, 4, 8, 16, 32…
Геометрическая последовательность с знаменателем 3 и масштабным коэффициентом 4 равна
Геометрическая прогрессия с обыкновенным отношением -1 и масштабным коэффициентом 5 равна
5, -5, 5, -5, 5, -5,…
Формулы
Формула для n-го члена может быть определена как: 9{n-1}$
Формула обыкновенного отношения:
$r = \frac{a_k}{a_{k-1}}$
Если общее отношение:
- Отрицательный, результаты будут чередоваться между положительными и отрицательными .
Пример:
1, -2, 4, -8, 16, -32… — знаменатель равен -2, а первый член равен 1. - Больше 1, будет экспоненциальный рост до бесконечности (положительный) .

Пример :
1, 5, 25, 125, 625 … — обыкновенное отношение равно 5. - Меньше -1, будет экспоненциальный рост до бесконечности (положительный и отрицательный) .
Пример :
1, -5, 25, -125, 625, -3125, 15625, -78125, 3, -1953125 … — обычное отношение равно -5. - Между 1 и -1, будет экспоненциальное затухание к нулю .
Пример :
4, 2, 1, 0,5, 0,25, 0,125, 0,0625 … — обыкновенное отношение $\frac{1}{2}$
4, -2, 1, -0,5, 0,25, -0,125, 0,0625 … — обыкновенный коэффициент $-\frac{1}{2}$. 93 + \cdots = a\frac{1}{1-r}$, который действителен только тогда, когда |r| < 1.
a 1 — первое слагаемое.Калькулятор геометрической прогрессии
Задачи на геометрическую прогрессию
Задача 1.
Является ли последовательность 2, 4, 6, 8… геометрической прогрессией?
Решение: Нет, это не так. (2, 4, 8 — геометрическая прогрессия)
(2, 4, 8 — геометрическая прогрессия)Задача 2
Если 2, 4, 8… образуют геометрическую прогрессию. Что такое 10-й срок?Решение: Мы можем использовать формулуЗадача 3
. Найдите масштабный коэффициент и отношение команд геометрической прогрессии, если
a 5 — a 1 = 15
a 4 — a 2 = 6
Решение: есть две геометрические прогрессии. У первого есть масштабный коэффициент 1 и общее отношение = 2
второе решение равно -16, 1/2Дополнительные задачи:
Геометрическая прогрессия — задачи
Задачи на прогрессииГеометрические прогрессии на математическом форуме
Присоединяйтесь к нашему математическому форуму (регистрация не требуется!)
Форумы с прогрессами
- 10%-ная надбавка на предмет, что бы вы потратили за 100 лет
- Правила чисел
- Каким будет 560-е число?
- Трудная задача на арифметическую прогрессию
- Это АРИФМЕТИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ИЛИ ПРОГРЕССИВНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
- Телескопическая серия
- Прогрессия и серия, Комплексная задача, ПОМОГИТЕ!
- ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
- [Уровень AS] — Геометрические прогрессии.
 {-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
Расследуй!18
Для узоров из точек ниже нарисуйте следующий узор в последовательности.
 Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.
Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.Обратимся теперь к вопросу о нахождении замкнутых формул для отдельных типов последовательностей.
Арифметические последовательности
Если члены последовательности отличаются на константу, мы говорим, что последовательность является
Рекурсивное определение: \(a_n = a_{n-1} + d\) с \(a_0 = a\text{.}\)
Замкнутая формула: \(a_n = a + dn\text{.}\)
Откуда мы это знаем? Для рекурсивного определения нам нужно указать \(a_0\text{.}\) Затем нам нужно выразить \(a_n\) в терминах \(a_{n-1}\text{.}\) Если мы вызовем первый член \(a\text{,}\), затем \(a_0 = a\text{.}\) Для рекуррентного отношения по определению арифметической последовательности разница между последовательными терминами является некоторой константой, скажем, \ (d\text{.
\begin{уравнение*} a_0 = a \qquad a_n=a_{n-1}+d. \end{уравнение*} }\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,
}\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,Чтобы найти замкнутую формулу, сначала выпишите последовательность в общем виде:
\начать{выравнивать*} а_0 \амп = а\\ a_1 \amp = a_0 + d = a+d\\ a_2 \amp = a_1 + d = a+d+d = a+2d\\ a_3 \amp = a_2 + d = a+2d+d = a+3d\\ \amp\vdots \конец{выравнивание*}Мы видим, что для нахождения \(n\)-го члена нам нужно начать с \(a\), а затем добавить \(d\) несколько раз. Фактически, добавьте его \(n\) раз. Таким образом, \(a_n = a+dn\text{.}\)
Пример 2.2.1
Найдите рекурсивные определения и замкнутые формулы для приведенных ниже последовательностей. Предположим, что первый указанный термин равен \(a_0\text{.}\)
- \(2, 5, 8, 11, 14, \ldots\text{.}\)
- \(50, 43, 36, 29, \ldots\text{.}\)
Решение
Сначала мы должны проверить, что эти последовательности действительно являются арифметическими, взяв разности последовательных членов.
 Это покажет общую разницу \(d\text{.}\)
Это покажет общую разницу \(d\text{.}\)- \(5-2 = 3\text{,}\) \(8-5 = 3\text{,}\) и т. д. Чтобы перейти от каждого термина к следующему, мы добавляем три, так что \(d = 3\text{.}\) Таким образом, рекурсивное определение \(a_n = a_{n-1} + 3\) с \(a_0 = 2\text{.}\) Замкнутая формула \(a_n = 2 + 3n\text{.}\)
Здесь общая разница: \(-7\text{,}\), так как мы прибавляем \(-7\) к 50, чтобы получить 43, и так далее. Таким образом, у нас есть рекурсивное определение \(a_n = a_{n-1} — 7\) с \(a_0 = 50\text{.}\) Замкнутая формула \(a_n = 50 — 7n\text{.} \)
Как насчет таких последовательностей, как \(2, 6, 18, 54, \ldots\text{?}\) Это не арифметика, поскольку разница между членами не является постоянной. Однако отношение между последовательными членами остается постоянным. Мы называем такие последовательности 9{п}\текст{.}\)
Пример 2.2.2
Найдите рекурсивную и замкнутую формулу для приведенных ниже последовательностей.
. Опять же, первый указанный термин равен \(a_0\text{.}\)
Опять же, первый указанный термин равен \(a_0\text{.}\)- \(3, 6, 12, 24, 48, \ldots\)
- \(27, 9, 3, 1, 1/3, \ldots\)
Решение
Опять же, мы должны сначала проверить, действительно ли эти последовательности являются геометрическими, на этот раз путем деления каждого члена на его предыдущий член. Предполагая, что это отношение постоянно, мы нашли \(r\text{.}\)
9{п}\текст{.}\) Предположим, что автомат для конфет в настоящее время содержит ровно 650 кеглей, и каждый раз, когда кто-то вставляет четвертак, из автомата выходит ровно 7 кеглей.
Сколько кеглей останется в автомате после того, как будут вставлены 20 четвертаков?
Останется ли когда-нибудь в автомате ровно ноль Skittles? Объяснять.
Что, если автомат выдает 7 Skittles первому покупателю, положившему четвертак, 10 — второму, 13 — третьему, 16 — четвертому и т. д. Сколько Skittles выдал автомат после того, как было положено 20 четвертак в машину?
Что, если автомат выдает 4 кегли первому покупателю, 7 — второму, 12 — третьему, 19 — четвертому и т.
 д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?
д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?Дайте рекурсивное определение последовательности.

Приведите замкнутую формулу для \(n\)-го члена последовательности.
Является ли \(2013\) членом последовательности? Объяснять.
Сколько элементов содержит последовательность \(5, 9, 13, 17, 21, \ldots, 533\)?
9{th}\) член \(1, 6, 15, 28, 45, \ldots\text{,}\), где \(b_0 = 1\)
В приведенных выше примерах и формулах мы предполагали, что начальный термин был \(a_0\text{.}\). Если ваша последовательность начинается с \(a_1\text{,}\), вы можете легко найти термин, который было бы \(a_0\) и использовать это в формуле. Например, если мы хотим получить формулу для последовательности \(2, 5, 8,\ldots\) и настаиваем на том, что \(2= a_1\text{,}\), то мы можем найти \(a_0 = -1\) (поскольку последовательность арифметическая с общей разностью 3, имеем \(a_0 + 3 = a_1\)). Тогда замкнутая формула будет \(a_n = -1 + 3n\text{.
 }\)
}\)Подраздел Суммы арифметических и геометрических последовательностей
¶Расследуй!19
В вашем соседнем продуктовом магазине есть кондитерский автомат, полный Skittles.
Посмотрите на последовательность \((T_n)_{n\ge 1}\), которая начинается с \(1, 3, 6, 10, 15,\ldots\text{.}\) Это называется треугольных чисел. , так как они представляют количество точек в равностороннем треугольнике (представьте, как вы расположите 10 кеглей для боулинга: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).
Является ли эта последовательность арифметической? Нет, поскольку \(3-1 = 2\) и \(6-3 = 3 \ne 2\text{,}\) общего различия нет. Является ли последовательность геометрической? Нет. \(3/1 = 3\), но \(6/3 = 2\text{,}\), поэтому общего соотношения нет. Что делать?
Обратите внимание, что различия между терминами образуют арифметическую последовательность: \(2, 3, 4, 5, 6,\ldots\text{.}\) Это говорит о том, что \(n\)-й член последовательности \(1 ,3,6,10,15,\ldots\) — это сумма первых \(n\) членов последовательности \(1,2,3,4,5,\ldots\text{.
 }\ ) Мы говорим, что первая последовательность — это последовательность 90 216 частичных сумм 90 217 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.
}\ ) Мы говорим, что первая последовательность — это последовательность 90 216 частичных сумм 90 217 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.Это должно стать яснее, если мы напишем треугольные числа так:
\начать{выравнивать*} 1 \амп = 1\\ 3 \амп = 1+2\\ 6 \ампер = 1 + 2 + 3\\ 10 \ампер = 1+2 + 3+ 4\\ \vdots\amp\qquad\vdots\\ T_n \amp = 1 + 2 + 3 + \cdots + n. \конец{выравнивание*}Подумайте, как найти сумму первых 100 положительных целых чисел (то есть \(T_{100}\)). Вместо того, чтобы складывать их по порядку, мы перегруппируем и добавим \(1+100 = 101\text{.}\) Следующая пара для объединения: \(2+99 = 101\text{.}\) Затем \(3+ 98 = 101\text{.}\) Продолжайте. Это дает 50 пар, каждая из которых в сумме дает \(101\text{,}\), поэтому \(T_{100} = 101\cdot 50 = 5050\text{.
 }\) 1 Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.
}\) 1 Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.В общем случае, используя такую же перегруппировку, мы находим, что \(T_n = \frac{n(n+1)}{2}\text{.}\) Между прочим, это в точности то же самое, что и \({n +1 \выберите 2}\text{,}\), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий на вечеринке с \(n+1\) людьми: первый человек пожимает \ (n\) рук, следующий пожимает еще \(n-1\) рук и так далее.
Суть всего этого в том, что некоторые последовательности, хотя и не являются арифметическими или геометрическими, могут быть интерпретированы как последовательности частичных сумм арифметических и геометрических последовательностей. К счастью, есть методы, которые мы можем использовать для быстрого вычисления этих сумм.
Подподраздел Суммирование арифметических последовательностей: реверс и сложение
¶Вот метод, который позволяет нам быстро найти сумму арифметической последовательности.

Пример 2.2.4
Найдите сумму: \(2 + 5 + 8 + 11 + 14 + \cdots + 470\text{.}\)
Решение
Идея состоит в том, чтобы подражать тому, как мы нашли формулу для треугольных чисел. Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме дают 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Вызовите сумму \(S\text{.}\) Затем
\(S =\) \(2\) \(+\) \(5\) \(+\) \(8\) \(+ \cdots +\) \(467\) \(+\) 470 \(+ \quad S =\) \(470\) \(+\) \(467\) \(+\) \(464\) \(+ \cdots +\) \(5\) \(+\) 2 \(2S =\) \(472\) \(+\) \(472\) \(+\) \(472\) \(+ \cdots +\) \(472\) \(+\) \(472\) Чтобы найти \(2S\), мы прибавляем 472 к самому себе несколько раз.
 Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,
Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,\begin{уравнение*} 2S = 157\cdot 472 = 74104 \end{уравнение*}
Теперь легко найти \(S\text{:}\)
\begin{уравнение*} S = 74104/2 = 37052 \end{уравнение*}
Это будет работать для любой суммы арифметических последовательностей. Вызовите сумму \(S\text{.}\) в обратном порядке и добавьте. Это дает одно число, добавленное к самому себе много раз. Найдите количество раз. Умножить. Разделить на 2. Готово.
Пример 2.2.5
Найдите замкнутую формулу для \(6 + 10 + 14 + \cdots + (4n — 2)\text{.
 }\)
}\)Решение
Опять у нас есть сумма арифметической прогрессии. Нам нужно знать, сколько членов в последовательности. Ясно, что каждый член последовательности имеет вид \(4k — 2\) (о чем свидетельствует последний член). Но для каких значений \(k\)? Чтобы получить 6, \(k = 2\text{.}\) Чтобы получить \(4n-2\), возьмите \(k = n\text{.}\) Итак, чтобы найти количество терминов, нам нужно знать сколько целых чисел находится в диапазоне \(2,3,\ldots, n\text{.}\) Ответ: \(n-1\text{.}\) (есть \(n\) чисел от 1 в \(n\text{,}\), так что на единицу меньше, если мы начнем с 2.)
Теперь переверните и добавьте:
\(S =\) \(6\) \(+\) \(10\) \(+ \cdots +\) \(4н-6\) \(+\) \(4н-2\) \(+ \quad S =\) \(4н-2\) \(+\) \(4н-6\) \(+ \cdots +\) \(10\) \(+\) 6 \(2S =\) \(4n+4\) \(+\) \(4n+4\) \(+ \cdots +\) \(4n+4\) \(+\) \(4n+4\) Так как членов \(n-2\), мы получаем
\begin{уравнение*} 2S = (n-2)(4n+4)\qquad \mbox{ так} \qquad S = \frac{(n-2)(4n+4)}{2} \end{уравнение*}
Помимо нахождения сумм, мы можем использовать эту технику для нахождения замкнутых формул для последовательностей, которые мы распознаем как последовательности частичных сумм.

Пример 2.2.6
Используйте частичные суммы, чтобы найти замкнутую формулу для \((a_n)_{n\ge 0}\), которая начинается с \(2, 3, 7, 14, 24, 37,\ldots \ldots\)
Решение
Во-первых, если вы посмотрите на различия между терминами, вы получите последовательность различий: \(1,4,7,10,13, \ldots\text{,}\), которая является арифметической последовательностью. Написано по-другому:
\начать{выравнивать*} а_0 \ампер = 2\\ a_1 \амп = 2+1\\ a_2 \amp = 2+1+4\\ а_3 \амп = 2+1+4+7 \конец{выравнивание*}
и так далее. Мы можем записать общий член \((a_n)\) в терминах арифметической последовательности следующим образом:
\begin{уравнение*} a_n = 2 + 1 + 4 + 7 + 10 + \cdots + (1 + 3 (n-1)) \end{уравнение*}
(мы используем \(1+3(n-1)\) вместо \(1+3n\), чтобы правильно выровнять индексы; для \(a_3\) мы добавляем 7, что равно \ (1+3(3-1)\)).
Мы можем перевернуть и сложить, но начальная цифра 2 не соответствует нашему шаблону.
 Это просто означает, что нам нужно убрать 2 из обратной части:
Это просто означает, что нам нужно убрать 2 из обратной части:\(a_n =\) \(2\) \(+\) \(1\) \(+\) \(4\) \(+ \cdots +\) \(1+3(n-1)\) \(+ ~ a_n =\) \(2\) \(+\) \(1+3(n-1)\) \(+\) \(1+3(n-2)\) \(+ \cdots +\) \(1\) \(2a_n =\) \(4\) \(+\) \(2+3(n-1)\) \(+\) \(2+3(n-1)\) \(+ \cdots +\) \(2+3(n-1)\) Не считая первого члена (4), есть \(n\) слагаемых \(2+3(n-1) = 3n-1\), поэтому правая часть становится \(2+( 3n-1)n\text{.}\)
Наконец, найдя \(a_n\), мы получим
\begin{уравнение*} a_n = \d \frac{4+(3n-1)n}{2}. \end{уравнение*}
На всякий случай проверяем \(a_0 = \frac{4}{2} = 2\text{,}\) \(a_1 = \frac{4+2}{2} = 3\text{, }\) и т.
 д. Имеем правильную замкнутую формулу.
д. Имеем правильную замкнутую формулу.Подподраздел Суммирование геометрических последовательностей: умножение, сдвиг и вычитание
¶Чтобы найти сумму геометрической последовательности, мы не можем просто поменять местами и сложить. Вы понимаете, почему? Причина, по которой один и тот же термин добавлялся сам к себе много раз, заключается в том, что существовала постоянная разница. Таким образом, когда мы добавили эту разницу в одном направлении, мы вычли разницу в другом направлении, оставив постоянную сумму. Для геометрических сумм у нас есть другая техника.
Пример 2.2.7
Что такое \(3 + 6 + 12 + 24 + \cdots + 12288\text{?}\)
Решение
Умножьте каждый член на 2, обыкновенный коэффициент. Вы получаете \(2S = 6 + 12 + 24 + \cdots + 24576\text{.}\) Теперь вычтите: \(2S — S = -3 + 24576 = 24573\text{.}\) Так как \(2S — S = S\text{,}\) у нас есть ответ.

Чтобы лучше понять, что произошло в приведенном выше примере, попробуйте записать его так:
\(S=\) \(3\, +\) \(6 + 12 + 24 + \cdots + 12288\) \(-~2S=\) \(6 + 12 + 24 + \cdots + 12288\) \(+ 24576\) \(-S = \) \(3\, +\) \(0 + 0 + 0 + \cdots + 0 \) \(-24576\) Затем разделите обе части на \(-1\), и мы получим тот же результат для \(S\text{.}\) Идея состоит в том, что при умножении суммы на обыкновенное отношение каждый член становится следующим термином. Мы сдвигаем сумму, чтобы вычитание в основном сокращалось, оставляя только первый член и новый последний член. 9{n+1}}{-4}\)
Хотя это может показаться новой техникой, вы, вероятно, использовали ее раньше.
Пример 2.2.9
Выразите \(0,464646\ldotts\) в виде дроби.
Решение
Пусть \(N = 0,46464646\ldots\text{.
 }\) Рассмотрим \(0,01N\text{.}\) Получим:
}\) Рассмотрим \(0,01N\text{.}\) Получим:\(Н =\) \(0,4646464\ldotts\) \(-\) \(0,01Н =\) \(0,00464646\ldotts\) 906:30 \(0,99Н =\) \(0,46\) Итак, \(N = \frac{46}{99}\text{.}\) Что мы сделали? Мы рассматривали повторяющуюся десятичную дробь \(0,464646\ldots\) как сумму геометрической последовательности \(0,46, 0,0046, 0,000046, \ldots\). Обычное отношение равно \(0,01\text{.}\). Единственная реальная разница что мы теперь вычисляем бесконечную геометрическую сумму , у нас нет дополнительного «последнего» члена для рассмотрения. На самом деле, это результат ограничения, как если бы вы вычисляли 9 в математических вычислениях.n k = n!\text{.}\)
ПодразделУпражнения
¶1
Рассмотрим последовательность \(5, 9, 13, 17, 21, \ldots\) с \(a_1 = 5\)
- \(a_n = a_{n-1} + 4\) с \(a_1 = 5\text{.}\)
- \(a_n = 5 + 4(n-1)\text{.}\)
Да, поскольку \(2013 = 5 + 4(503-1)\) (так что \(a_{503} = 2013\)).
133
- \(\frac{538\cdot 133}{2} = 35777\text{.}\)
- \(b_n = 1 + \frac{(4n+6)n}{2}\text{.}\)
\(32\text{,}\), что равно \(26+6\text{.
 }\)
}\)- \(a_n = 8 + 6n\text{.}\)
- \(30500\text{.}\) Мы хотим \(8 + 14 + \cdots + 602\text{.}\) Перевернуть и сложить, чтобы получить 100 сумм 610, всего 61000, что в два раза больше суммы мы ищем.
Сколько членов (слагаемых) в сумме?
Подсчитать сумму. Не забудьте показать все свои работы.
36.
- \(\frac{253 \cdot 36}{2} = 4554\text{.}\)
Сколько элементов в последовательности?
Какой предпоследний член?
Найдите сумму всех членов последовательности.
- \(n+2\) членов, так как для получения 1 по формуле \(6n+7\) мы должны использовать \(n=-1\text{.
 }\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\).
}\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\). - \(6n+1\text{,}\), что на 6 меньше, чем \(6n+7\) (или подставьте \(n-1\) вместо \(n\)).
- \(\frac{(6n+8)(n+2)}{2}\text{.}\) Перевернуть и добавить. Каждая сумма дает константу \(6n+8\) и есть \(n+2\) терминов.
Создайте последовательность прямоугольников, используя это правило, начиная с прямоугольника \(1\times 2\).
 Затем выпишите последовательность из периметров прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).
Затем выпишите последовательность из периметров прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).На этот раз повторите описанную выше часть, начиная с прямоугольника \(1 \times 3\).
Найдите рекурсивные формулы для каждой из последовательностей периметров, которые вы нашли в частях (a) и (b). Не забудьте также указать начальные условия.
Являются ли последовательности арифметическими? Геометрический? Если нет, то являются ли они близкими к любому из этих (т. е. являются ли разности или отношения почти постоянными)? Объяснять.
Пусть \(t_n\) будет количеством зубочисток, необходимых для создания треугольной сетки размером \(n\). Выпишите первые 5 членов последовательности \(t_1, t_2, \ldots\text{.}\)
Найдите рекурсивное определение последовательности. Объясните, почему вы правы.
Является ли последовательность арифметической или геометрической? Если нет, то это последовательность частичных сумм арифметической или геометрической прогрессии? Объясните, почему ваш ответ правильный.
Используйте результаты из части (c), чтобы найти замкнутую формулу для последовательности.

Решение
2
Рассмотрим последовательность \((a_n)_{n \ge 0}\), которая начинается с \(8, 14, 20, 26, \ldots\text{.}\) 9{99}a_k\text{.}\)
Решение
3
Рассмотрим сумму \(4 + 11 + 18 + 25 + \cdots + 249\text{.}\)
Раствор
4
Рассмотрим последовательность \(1, 7, 13, 19, \ldots, 6n + 7\text{.}\)
Решение
5
Найти \(5 + 7 + 9 + 11+ \cdots + 521\text{.}\) 9{30}}\text{.}\)
8
Найдите \(x\) и \(y\) такие, что \(27, x, y, 1\) является частью арифметической прогрессии. Затем найдите \(x\) и \(y\) так, чтобы последовательность была частью геометрической прогрессии. (Предупреждение: \(x\) и \(y\) могут быть не целыми числами.)
9
Начав с любого прямоугольника, мы можем создать новый, больший прямоугольник, присоединив квадрат к более длинной стороне. Например, если мы начнем с прямоугольника \(2\x 5\), мы склеим квадрат \(5\x 5\), сформировав прямоугольник \(5 \x 7\):
10
Рассмотрим последовательность \(2, 7, 15, 26, 40, 57, \ldots\) (где \(a_0 = 2\)). Глядя на различия между членами, представить последовательность как последовательность частичных сумм. Затем найдите замкнутую формулу последовательности, вычислив \(n\)-ю частичную сумму. 9n (2+3k)\text{.}\) Чтобы найти замкнутую формулу, мы обращаем и складываем. Получаем \(a_n = \frac{(4+3n)(n+1)}{2}\) (там у нас \(n+1\), потому что в сумме есть \(n+1\) членов для\)).
9n (2+3k)\text{.}\) Чтобы найти замкнутую формулу, мы обращаем и складываем. Получаем \(a_n = \frac{(4+3n)(n+1)}{2}\) (там у нас \(n+1\), потому что в сумме есть \(n+1\) членов для\)).
11
Если у вас достаточно зубочисток, вы можете сделать большую треугольную сетку. Ниже представлены треугольные сетки размера 1 и размера 2. Для сетки размера 1 требуется 3 зубочистки, для сетки размера 2 требуется 9 зубочисток.


 (2, 4, 8 — геометрическая прогрессия)
(2, 4, 8 — геометрическая прогрессия) {-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
 Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.
Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне. }\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,
}\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами, Это покажет общую разницу \(d\text{.}\)
Это покажет общую разницу \(d\text{.}\) Опять же, первый указанный термин равен \(a_0\text{.}\)
Опять же, первый указанный термин равен \(a_0\text{.}\) }\)
}\) д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?
д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат? }\ ) Мы говорим, что первая последовательность — это последовательность 90 216 частичных сумм 90 217 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.
}\ ) Мы говорим, что первая последовательность — это последовательность 90 216 частичных сумм 90 217 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности. }\) 1 Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.
}\) 1 Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.
 Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,
Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом, }\)
}\)
 Это просто означает, что нам нужно убрать 2 из обратной части:
Это просто означает, что нам нужно убрать 2 из обратной части: д. Имеем правильную замкнутую формулу.
д. Имеем правильную замкнутую формулу.
 }\) Рассмотрим \(0,01N\text{.}\) Получим:
}\) Рассмотрим \(0,01N\text{.}\) Получим:
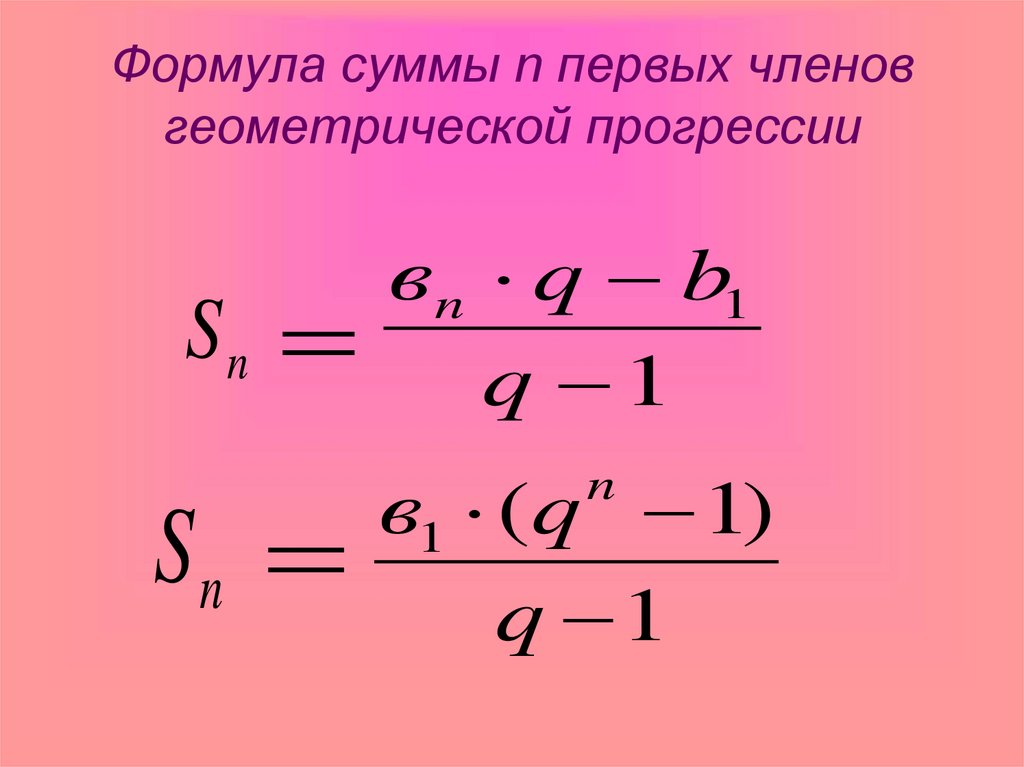 }\)
}\) }\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\).
}\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\). Затем выпишите последовательность из периметров прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).
Затем выпишите последовательность из периметров прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).