Как найти радиус окружности физика формула: Найти радиус окружности,по которой движется тело, если при линейной. скорости 40 м/с его центростремительное ускорение…

чему равен, как найти, формула, вокруг чего можно описать

Содержание:

• Описанная окружность — что из себя представляет
  • Вокруг чего можно описать
• Теорема, основные свойства, признаки
• Как найти радиус и диаметр описанной окружности, формула
  • Треугольник
  • Трапеция
  • Правильный многоугольник
  • Правильного шестиугольник
  • Прямоугольник
  • Квадрат

Содержание

• Описанная окружность — что из себя представляет
  • Вокруг чего можно описать
• Теорема, основные свойства, признаки
• Как найти радиус и диаметр описанной окружности, формула
  • Треугольник
  • Трапеция
  • Правильный многоугольник
  • Правильного шестиугольник
  • Прямоугольник
  • Квадрат

Описанная окружность — что из себя представляет

Решение задач по геометрии может быть проще, если при нахождении неизвестных пользоваться дополнительными сведениями и приемами. Одним из таких будет описание окружности вокруг фигуры.

Описанная окружность — окружность, которая описана вокруг многоугольника. Главным свойством описанной окружности будет тот факт, что она должна содержать все вершины многоугольника.

Точки окружности равноудалены от ее центра, а значит, также равноудалены будут и вершины многоугольника, вокруг которого описана окружность.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Вокруг чего можно описать

Окружность можно описать вокруг (или около):

• треугольника;
• трапеции;
• правильного многоугольника;
• правильного шестиугольника;
• прямоугольника;
• квадрата;
• многоугольника, чьи серединные перпендикуляры пересекаются в одной точке.

Теорема, основные свойства, признаки

Правило об описанной окружности

Около любой из вышеперечисленных фигур можно описать окружность, причем только одну.

Доказательством теоремы будет тот факт, что точка пересечения серединных перпендикуляров через медианы у любой фигуры будет только одна. Это точка будет является центром окружности, а значит, никакая другая окружность, которая при этом также захватывает все вершины фигуры, не может быть описана вокруг нее.

Теорема синусов

Теорема синусов позволяет найти двойной радиус или диаметр окружности по расчету формулы:

\(2R=d=\frac a{\sin\left(\angle A\right)}=\frac b{\sin\left(\angle B\right)}=\frac c{\sin\left(\angle C\right)},\)

где R — радиус,

d — диаметр,

a, b, c — стороны треугольника,

A, B, C — углы треугольника.

Соответственно, для того, чтобы найти радиус описанной окружности, необходимо знать величины любой стороны и противоположного ей угла.

Свойства описанной окружности:

• центр окружности лежит на пересечении всех серединных перпендикуляров фигуры;
• вершины фигуры, которая описана окружностью, будут равноудалены от центра и будут лежать на кривой окружности;
• в любом вписанном четырехугольнике сумма противоположных углов будет равна 180 градусам;
• вокруг любого треугольника можно описать окружность.

Главным признаком описанной окружности будет ее расположение вокруг фигуры, причем ни одна из ее вершин не должна выходить за пределы кривой окружности.

Как найти радиус и диаметр описанной окружности, формула

Треугольник

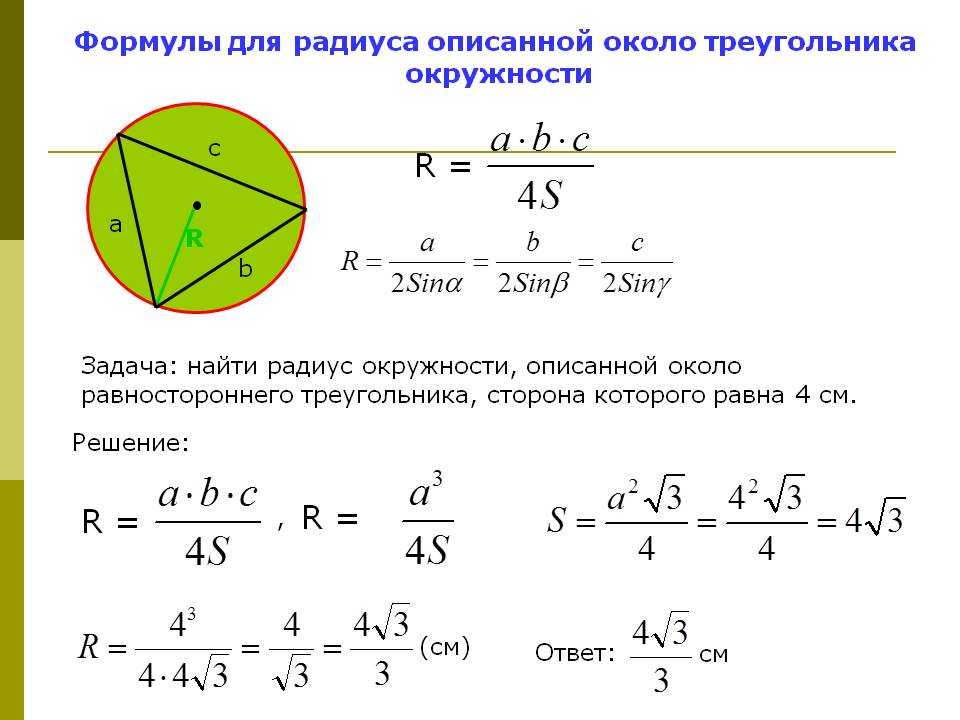
Формула нахождения радиуса описанной окружности вокруг треугольника:

\(R=\frac{a\times b\times c}{4\sqrt{p\times\left(p-a\right)\times\left(p-b\right)\times\left(p-c\right)}},\)

где R — радиус ,

a, b и c — стороны треугольника,

p — половина периметра, \(p=\frac{\left(a+b+c\right)}2.\)

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по стороне:

\(R=\frac a{\sqrt3},\)

где R — радиус,

а — сторона треугольника.

Формула нахождения радиуса описанной окружности вокруг равностороннего треугольника по высоте:

\(R=\frac{2h}3,\)

где R — радиус,

h — высота.

Формула нахождения радиуса описанной окружности вокруг равнобедренного треугольника по сторонам:

\(R=\frac{a^2}{\sqrt{4a^2-b^2}},\)

где R — радиус,

a и b — стороны. 2}}2=\frac d2,\)

где R — радиус,

a и b — стороны прямоугольника,

d — диагональ.

Квадрат

Формула нахождения радиуса описанной окружности вокруг квадрата:

\(R=\frac a{\sqrt2}=\frac d2,\)

где R — радиус,

d — диагональ.

Так как диаметр является суммой двух радиусов, при помощи вышеперечисленных формул можно найти диаметр просто умножив полученный результат на 2.

Насколько полезной была для вас статья?

Рейтинг: 2.25 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Линейная скорость | формула и расшифровка

3823

3

20.05.2022

3 мин. на чтение

Понимание любого понятия в физике предполагает расшифровку определения связанных терминов.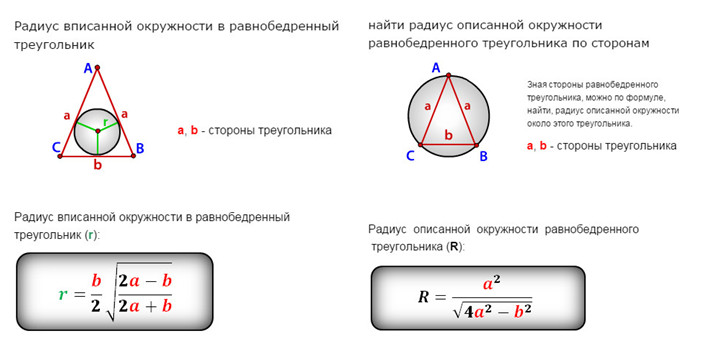 Таким образом, в случае линейной скорости становится необходимым определить линейную скорость и скорость по отдельности.

Линейная скорость относится к движению объекта по прямой линии или по заданной оси. С другой стороны, скорость означает расстояние, которое движущееся тело проходит в определенном направлении за определенное время. Таким образом, сочетание этих двух определений поможет вам понять основную концепцию линейной скорости.

Что такое скорость?

Термин «скорость» может использоваться в различных областях, включая физику, термодинамику, химию и т. д. Прежде чем мы перейдем к пониманию линейной и угловой скорости, мы сначала определим скорость как отдельный термин.

Скорость можно объяснить как скорость изменения положения объекта в течение определенного срока или диапазона времени, ее можно разделить на два типа: угловая скорость и линейная скорость. Чтобы определить скорость, мы возьмем пример, поэтому представьте, что вы едете по дороге и смотрите на приборную панель или любые вывески во время движения, спидометр показывает, что автомобиль движется со скоростью 65 км в час, тогда мы можем сказать, что скорость 65 км в час — это скорость, которая представляет собой скорость изменения км по отношению к часам, которые мы видим.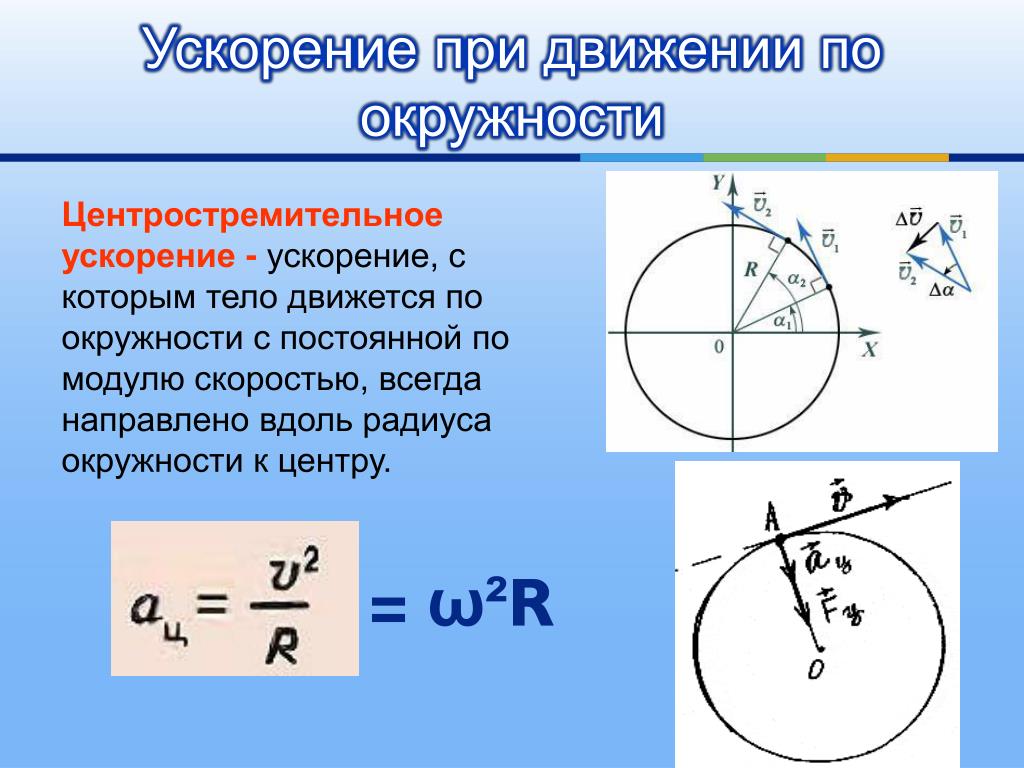 Формула скорости равна расстоянию, деленному на время, может рассчитать линейную скорость объекта. В формуле v обозначает линейную скорость, d обозначает пройденное расстояние, а t обозначает время.

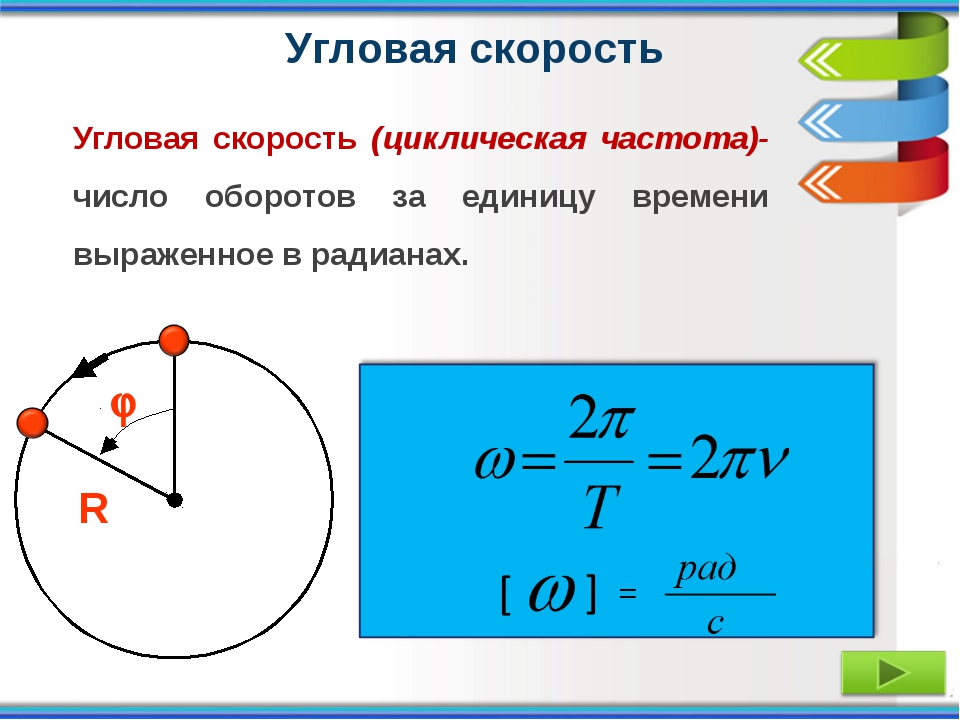
Теперь, возвращаясь к ее различным типам, линейная скорость — это просто скорость изменения положения объекта, который движется по прямому пути, поэтому любой движущийся объект имеет линейную скорость, с другой стороны, угловая скорость применяется только или может применяться к объектам, которые движутся по круговой траектории, а также может быть определена как скорость изменения углового смещения во времени. Угловая скорость, измеряемая в рад/с, которая также может быть преобразована в градусы, представляет собой изменение угла во времени. v=rω для расчета линейной скорости по угловой скорости.

V = ωr, где ω равно радианам в секунду, а r — радиус.

Если период вращения равен t, то ω=^2π/_t. Как результат, v=^2π∗r/_t.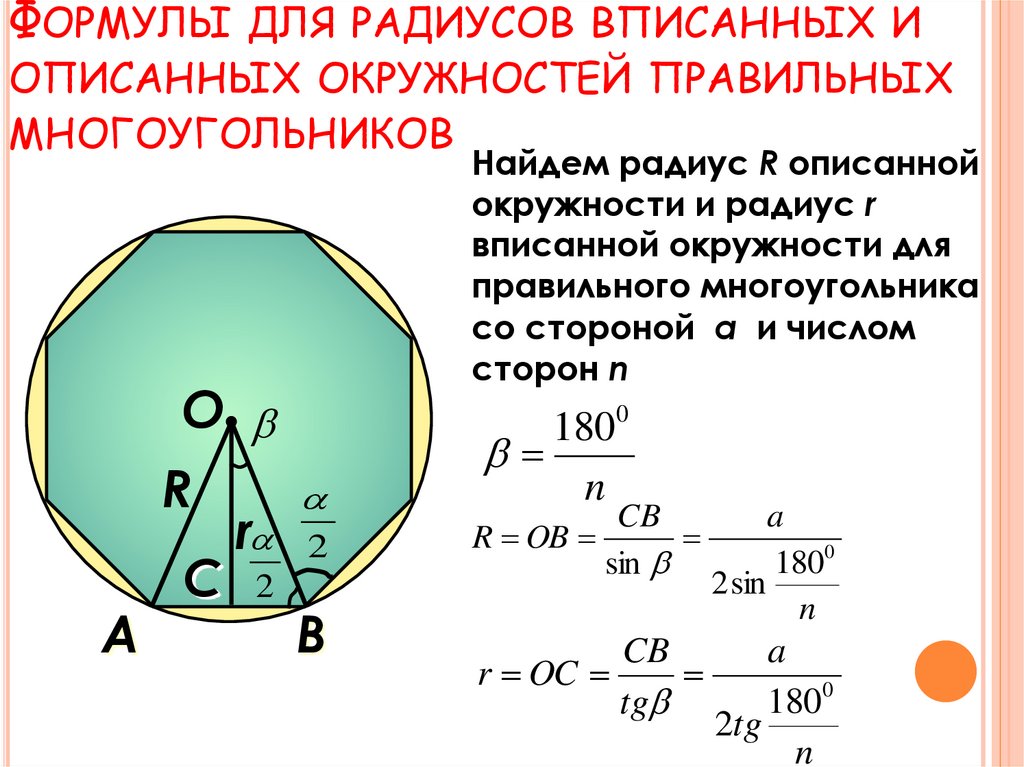

Линейную скорость можно испытать в повседневной жизни, поскольку мы видим так много движущихся объектов, которые имеют линейную скорость, таких как человек, идущий на прогулку, вождение, бег или езду на велосипеде, всегда может быть линейная скорость, которая может наблюдаться. Кроме того, бывают случаи, когда объект может двигаться по прямому пути с заданной постоянной скоростью, это можно сказать, что объект движется с постоянной линейной скоростью, проще говоря, мы можем сказать, что скорость Лены объекта не изменяется и, следовательно, постоянный. Линейная скорость, измеряемая в м/с, — это скорость по прямой.

Когда мы говорим об окружности, связь между дугой на окружности и углом, на который она опирается, измеренным в излучении, позволяет нам определить величины, связанные с движением по окружности, и благодаря этому также мы можем сказать, что объекты, движущиеся по круговой траектории, относятся к типу 2. скорости, когда линейна, а другая — угловая скорость, как упоминалось выше. В дополнение к этому мы также можем понимать равномерное круговое движение. Равномерное круговое движение может определять линейную скорость, которая измеряет изменение длины дуги с течением времени.

Когда мы говорим о круговом движении, мы также говорим о направлении линейной скорости. Теперь направление скорости частицы Салина является тангенциальным к круговому пути, который мы видим в любой данной точке этого кругового движения. Направление играет очень важную роль в определении изменения характеристик, скорость является физической векторной величиной, что означает, что для ее правильного определения требуются как величина, так и направление, поэтому, если происходит изменение скорости, направления или того и другого, меняется философия объекта, и тогда мы говорим, что объект является ускоренным движением или ускоряется.

Что такое линейная скорость? 

В самом основном смысле определение линейной скорости связано с измерением скорости объекта, когда он движется в определенном направлении. Следовательно, это относится к смещению объекта во времени. 

Однако объект должен двигаться по определенной прямой линии. Единицей линейной скорости в системе СИ является метр в секунду или м/с (мс- ¹ ). 

С другой стороны, размерная формула линейной скорости имеет вид M ⁰ L ¹ T ¹

Кроме того, вы должны знать, что это векторная величина, что указывает на то, что она имеет направленный характер. 

Какая формула линейной скорости? 

Нет никаких различий между обычной скоростью и линейной скоростью, поскольку обе они являются векторными величинами. 

Следовательно, формула линейной скорости –  ν = d/t

Например, предположим, что движущийся объект преодолевает расстояние 500 метров по прямой линии за 10 секунд. В этом случае линейная скорость объекта равна – 

ν = 500 метров/10 секунд = 50 м/с или 50 мс- ¹ . 

Логически говоря, линейная скорость также применяется к объекту, который движется в круговом направлении, следуя геометрическому месту.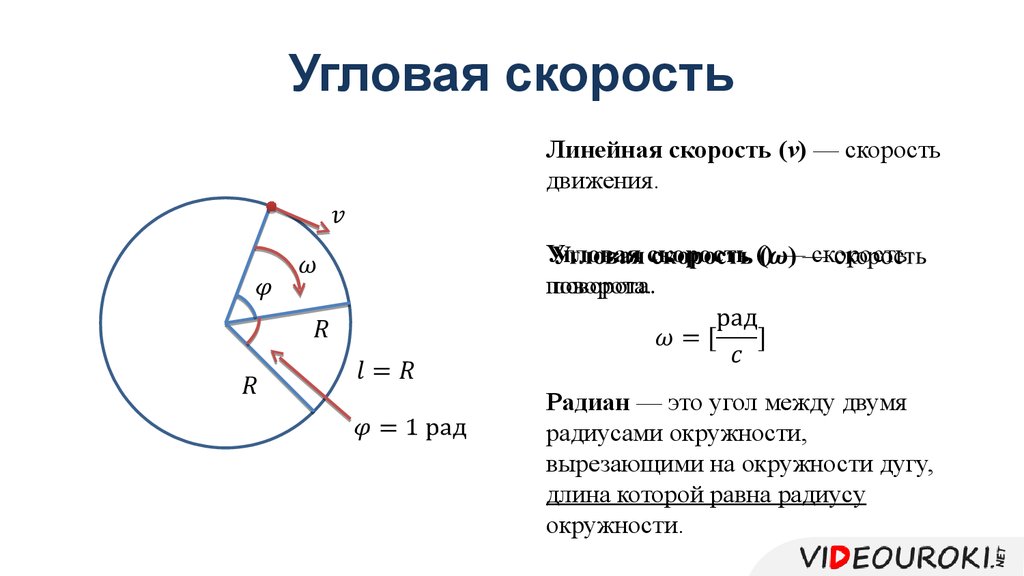 В этом случае она называется угловой скоростью. 

Криволинейное движение

электромагнетизм — Формула радиуса окружности пути заряженной частицы в однородном магнитном поле

спросил 5 лет, 11 месяцев назад

Изменено 1 год, 8 месяцев назад

Просмотрено 59 тысяч раз

$\begingroup$

Заряженная частица $q$ входит в однородное магнитное поле $\vec{B}$ со скоростью $\vec{v}$, образуя с ним угол $\theta$.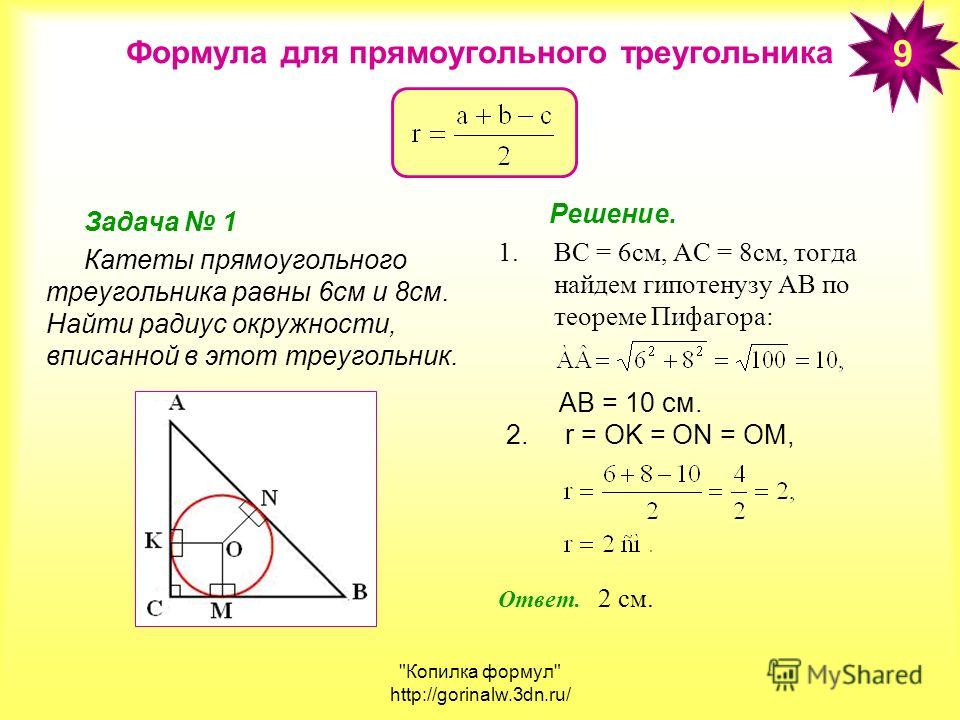 Поскольку сила Лоренца перпендикулярна скорости, частица будет двигаться по круговой траектории радиуса $r$, что 92}{r}=qvB \sin\theta$$ $$r=\frac{mv\sin\theta}{qB}.$$

Это должно быть потому, что мы учитываем только перпендикулярную составляющую скорости, когда вычисляем магнитную силу, и, следовательно, скорость, к которой перпендикулярна сила, является составляющая скорости, перпендикулярная $\vec{B}$, а не $\vec{v}$.

Какая формула правильная?

• электромагнетизм
• магнитные поля

$\endgroup$

$\begingroup$

Ваш вывод верен, и ваша книга неверна, если только $v$ в их уравнении не является составляющей скорости, перпендикулярной магнитному полю?
На приведенной ниже диаграмме предполагается положительный заряд.

Радиус кругового движения определяется уравнением $r=\dfrac{mv\sin\theta}{qB}$, а шаг спирали $p = \dfrac{2\pi mv\cos \тета}{qB}$

$\endgroup$

5

$\begingroup$

Легко видеть, что книжный ответ r = mv/qBsin θ верен.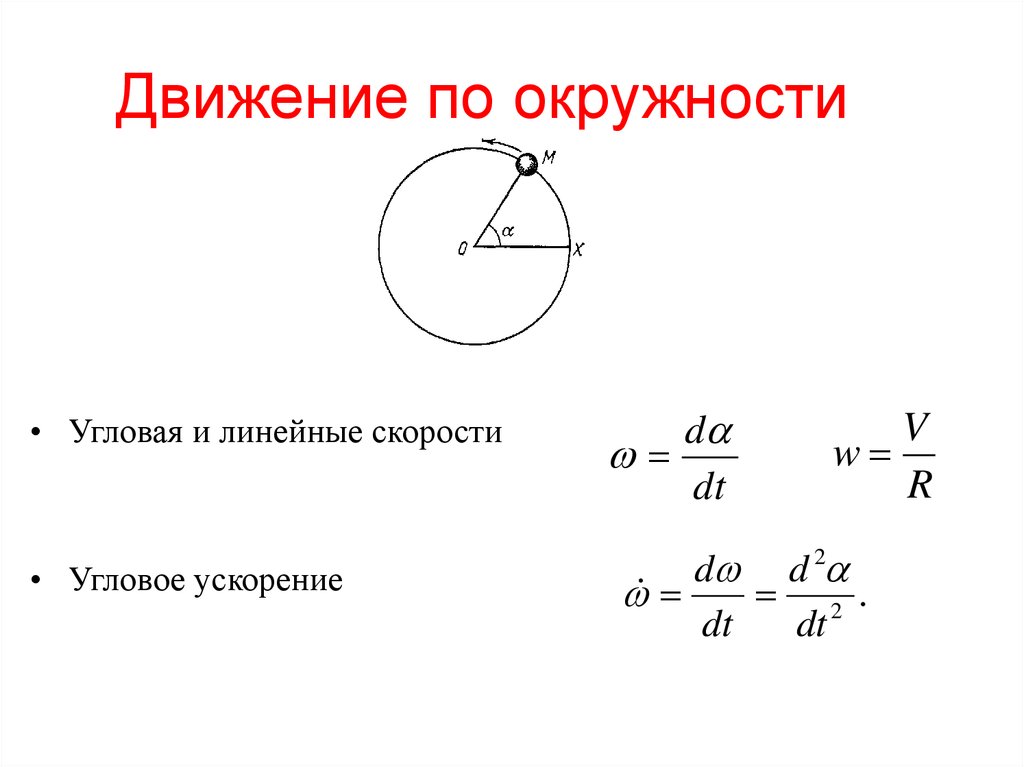

Спросите себя, что происходит с радиусом, когда сила магнитного поля уменьшается. Поскольку составляющая магнитного поля, воздействующая на заряд, меньше 1,0 для любого θ меньше 90 градусов, формула книги правильно описывает, что происходит для углов, отличных от 90 градусов.

Ошибка при умножении скорости на sin θ, а не на магнитное поле, заключается в том, что вы рассматриваете только ту составляющую скорости, которая перпендикулярна полю. Вы ошибочно проигнорировали влияние общей скорости на окружность круга.

Также коэффициент sin θ применяется только к силе, действующей на заряд, движущийся перпендикулярно магнитному полю. Это не относится к силе, необходимой для изменения направления движущейся массы, которая имеет заряд.

$\endgroup$

1

$\begingroup$

.это ответ на вопрос

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Равномерное круговое движение

Равномерное круговое движение

Обзор:

Объект, движущийся по окружности радиусом r с постоянной скоростью v ускоряется. направление вектора его скорости все время меняется, но величина вектор скорости остается постоянным. Вектор ускорения не может иметь компонента в направлении вектора скорости, так как такая компонента вызвать изменение скорости. Поэтому вектор ускорения должен быть перпендикулярно вектору скорости в любой точке окружности. Этот ускорение называется радиальным ускорением или центростремительное ускорение, и оно указывает к центру круга. Величина центростремительной вектор ускорения равен

с = v ² /r.

Какова сила при различных обстоятельствах?

Исследуя этот вопрос, решим несколько задач.

Проблема:

Груз массой 3 кг, прикрепленный к легкой нити, вращается по горизонтальной поверхности без трения. стол. Радиус окружности равен 0,8 м, а струна может выдержать массу 25 кг до разрыва. Какой диапазон скоростей может иметь масса перед струной перерывы?

Решение:

• Обоснование:
  Масса, прикрепленная к нити, вращается по горизонтали, стол без трения.
  Предположим, что масса вращается с постоянной скоростью. Это ускорение. Направление ускорения в сторону центр круга, а его величина v ² /r. В струне есть напряжение. Нить натягивает массу с силой F, направленной к центру окружности. Этот сила F отвечает за центростремительное ускорение, F = мв ² /р.
  Струна может выдержать до разрыва массу 25 кг, т.е. может позволить массе до 25 кг висеть на веревке рядом с поверхность земли. Максимальное натяжение струны поэтому F _max = mg = (25 кг)(9,8 м/с ² ) ^{= 245 Н.
  Учитывая F _max = 245 Н и F = mv 2 /r, мы можем найти v _max .}
• Детали расчета:
  v _max ² = F _макс.
  об/мин = (250 Н)(0,8 м)/(3кг). v _max = 8,1 м/с.

Проблема:

Монета, помещенная на расстоянии 30 см от центра вращающегося горизонтального поворотного стола когда его скорость 50 см/с.
а) Какая сила обеспечивает центростремительное ускорение, когда монета неподвижна? относительно поворотного стола?
б) Каков коэффициент статического трения между монетой и поворотным столом?

Решение:

• Обоснование:
  Когда монета покоится относительно вращающегося поворотного стола, сила статическое трение между монетой и поворотным столом обеспечивает центростремительное ускорение.
  Сила трения покоя имеет максимальное значение f _с = μ _с Н = μ _с мг.
  Настройка μ _с мг = mv ² /r, мы можем решить для μ _с .
• Детали расчета:
  (а) Сила трения покоя между монетой и поворотным столом обеспечивает центростремительное ускорение.
  (b) Величина максимального сила трения покоя равна f _с = μ _с Н. Это максимальная сила трения покоя равна mv ² /r при v = 0,5 м/с. Имеем µ _с N = µ _с mg = mv ² /r,
  или мк _с = v ² /(rg) = (0,5 м/с) ² /(0,3 м 9,8 м/с ² ) = 0,085.

Проблема:

Рассмотрим конический маятник с грузом массой 80 кг на 10-метровом проводе, образующем угол. θ = 5 ^o с вертикалью. Определить
(а) горизонтальная и вертикальная составляющая силы, действующей со стороны проволоки на маятник и
(b)  центростремительное ускорение боба.

Решение:

• Обоснование:
  Диаграмма свободного тела боба показана справа.
  Боб не меняет своего вертикального положения, y = константа, v _y = a _y = 0. Вертикальный компонент T должен иметь величина мг.
  Горизонтальная составляющая Т обеспечивает центростремительное (радиальное) ускорение а _р .
• Детали расчета:
  (a) Вертикальный компонент T должен иметь величина мг.
  Tcos(5 ^o ) = мг, T = (80 кг 9,8 м/с ² )/cos(5 ^или ) = 787 N
  Величина горизонтальной составляющей T равна Tsin(5 ^o ) = 68,6 Н. Горизонтальная составляющая силы направлена ​​к центру круг.

  (b) Tsin(5 ^o ) = ma _r , a _r = (68,6 Н)/(80 кг) = 0,857 м/с ² .
  Скорость боба находится из a _r = v ² /r, v = (a _r r) ^½ .
  Так как r = (10 м)*sin(5 ^o ), имеем v = 0,86 м/с.

Проблема:

Автомобиль массой 1800 кг преодолевает неровность на дороге, идущей по дуге окружности. радиусом 42 м.
а) С какой силой дорога действует на автомобиль при прохождении автомобиля? наивысшая точка горки, если автомобиль движется со скоростью 16 м/с?
б) С какой максимальной скоростью может двигаться автомобиль, проезжая через этот горб? потеря связи с дорогой?

Решение:

• Обоснование:
  Показана схема свободного кузова автомобиля.
  

  Единственными силами, действующими на автомобиль, движущийся с постоянной скоростью, являются сила тяжести и нормальная сила, действующая на дорогу. Если эти силы равны по величине, автомобиль не разгоняется. Если автомобиль движется по дуга окружности, то она ускоряется. Ускорение равно _r = v ² /р. Следовательно, гравитационная сила должна иметь большую величины, чем нормальная сила.

• Детали расчета:
  Нам нужно
  мг — n = mv ² /r, или n = m(g — v ² /r).
  n = (1800 кг)(9,8 м/с ² — (16 м/с) ² /(42 m)) = 6669 N

  (b) Автомобиль теряет контакт с дорогой, когда n становится равным нулю. Тогда дорога больше не поддерживает машину. Это происходит, когда g — v ² /r = 0, или v ² = gr = 411,6 м ² /с ² , v = 20,3 РС.

---

Модуль 5: Вопрос 1

Чувствуете ли вы, что вас бросает в обе стороны, когда вы преодолеваете поворот, который идеально накрен для скорости вашего автомобиля? Как направлена ​​сила, приложенная на вас возле автокресла?

Обсудите это со своими однокурсниками на форуме!

---

Гравитация

Массивные объекты обладают инерцией. Требуется сила, чтобы изменить их состояние движение. Все массивные объекты взаимодействуют через сила гравитации . Частица массой m ₁ действует с силой F ₁₂ на частицу массой m ₂ . Закон тяготения Ньютона дает эту силу как

F ₁₂ = (-G m ₁ m ₂ /r ₁₂ ² ) ( р ₁₂ / р ₁₂ ).
Здесь r ₁₂ — расстояние между частицами 1 и 2, и ( р ₁₂ /r ₁₂ ) является Единичный вектор , указывающий от частицы 1 к частице 2.
G — гравитационная постоянная, G = 6,67*10 ^-11 Нм ² /кг ² .

Сила F ₂₁ , действующая на частицу массой m ₂ действует на частицу массой m ₁ , равно — F ₁₂ , по третьему закону Ньютона. Сила тяжести всегда привлекательный.

Точка в объекте, от которой расстояние r ₁₂ равно измеряется его центр масс. Масса m ₁ тянет массу m ₂ , и масса m ₂ тянет за собой массу m ₁ . Центр масса каждого тела притягивается к центру масс другого объект.

Взвешивание земли

Радиус Земли R = 6368 км. Если вы подниметесь на гору высотой 1000 м, ваше расстояние от центра земли изменится на (1/6368) * 100 % = 0,016 % а величина гравитационной силы, действующей на вас, изменится на (1/6368) ² *100 % = 2,4*10 ^-6 %. Для всех объектов вблизи поверхности земли расстояние от центра почти постоянно, а величина Поэтому вектор гравитационной силы приблизительно постоянен. За малым расстояния, когда кривизной земной поверхности можно пренебречь, направление вектора гравитационной силы также почти постоянно. Это указывает прямо вниз к центру земли.
Сила тяжести, действующая на тело массой m на поверхности земли, равна величина F = мг. Используя закон всемирного тяготения Ньютона, мы пишем GMm/R ² = мг, где М — масса Земли. Таким образом, мы имеем M = gR ² /G.
Используя R = 6,4*10 ⁶ м, находим M = (9,8 м/с ² )(6,4*10 ⁶ м) ² /(6,67*10 ^-11 Н·м ² /кг ² ) = 6*10 ²⁴ кг.

На орбите

Гравитационное притяжение между объектом и землей притягивает объект к центру земли. Когда объект вращается вокруг Земли, направление силы тяжести на объекте постоянно меняется. радиус Земли настолько велик, что Земля кажется в некоторых местах плоской наблюдатель, стоящий на поверхности. Когда проблема касается только расстояний, которые намного меньше радиуса Земли, мы часто пренебрегаем кривизной земной поверхности и предположим, что сила гравитации направлена ​​в одну и ту же направление вниз везде.

Ссылка: Спутник как снаряд

Предположим, что вблизи поверхности земли в x-направление, как показано на рисунке выше. Первоначально он ускоряется только в Y-направление. Но по мере движения объекта направление ускорения изменения. Если начальная скорость объектов достаточно высока, мы должны принять изменение направления силы учитывать при расчете объектов траектория. Объект на круговой орбите вокруг Земли находится постоянно падает к центру земли. Это постоянно ускорение. Но пока он движется по криволинейной траектории, поверхность Земля изгибается в сторону от объекта так, что расстояние между Землей и объект остается постоянным.

Сила тяжести всегда направлена ​​к центру объекта. круговой орбите и отвечает за центростремительное ускорение объект.

F = mv ² /r

Для объекта вблизи поверхности земли F = mg и r = 6,4*10 ⁶ м. Скорость орбитального объекта находится из mg = mv ² /r, v ² = gr = (9,8 м/с ² )(6,4*10 ⁶ м). У нас v = 7919 м/с, или примерно 8000 м/с. Требуется объект t = 2πr/v = (6,28*6,4*10 ⁶ м)/(7919 м/с) = 5075 с = 84 мин, чтобы совершить полный оборот.

Если тот же объект двигался по круговой орбите с большим радиусом, сила силы тяжести на объекте будет меньше. Поскольку мы удваиваем расстояние от центра земли сила тяжести уменьшается в 1/4 раза. центростремительное ускорение v ² /r уменьшается в 1/4 раза. Этот означает, что v ² должен уменьшиться в 1/2 раза. Имеем v = 5600 м/с а для совершения оборота по орбите требуется 14355 с = 240 мин.

Объектов на геосинхронных орбитах совершить полный оборот за 24 часа или 86400 с. Следовательно, их скорость равна v = 2πr/(86400 с). Запись GMm/r ² = mv ² /r = m(2πr/(86400 с)) ² /r, или r ³ = GM(86400s) ² /(4π). мы можем решить это уравнение для радиуса геосинхронной орбиты. При М = 6*10 ²⁴ кг имеем r=42260 км. Геосинхронный спутник вращается вокруг 42260 км — 6400 км = 35860 км над поверхностью земли. Радиус его орбиты в 6,6 раза больше радиуса Земли.

Луна делает один оборот вокруг Земли за 27,3 дня. Мы можем найти расстояние до Луну таким же образом мы нашли расстояние до геосинхронного спутника. Расстояние от Земли до Луны 384400 км.

Проблема:

Когда падающий метеор находится на расстоянии над земной поверхностью в 3 раза больше Радиус Земли, каково ускорение ее свободного падения под действием силы тяжести приложенная к нему сила?

Решение:

• Обоснование:
  Сила, действующая на метеор, равна F = ma = GMm/r ² . Следовательно, a = GM/r ² .
• Детали расчета:
  a = GM/r ² , a = (6,67*10 ^-11 Н·м ² /кг ² )*(6*10 ²⁴ кг)/(4*6,4*10 ⁶ м) ² = 0,61 м/с ² .
  (Метеор находится на высоте 3 земных радиуса над поверхностью земли, значит, это 4 земных радиуса. от его центра.)

---

Для получения дополнительной информации о равномерном круговом движении изучите это материал из «Кабинета физики».