Геометрическая прогрессия что это: Геометрическая прогрессия — урок. Алгебра, 9 класс.

alexxlab / / Разное

Геометрическая прогрессия — определение и формулы

Геометрическая прогрессия – важное понятие в алгебре и в математике вообще, объясняется впервые в 9 классе. Обычно применяется при решении текстовых задач, связанных с экономикой или теорией вероятности, но может использоваться самостоятельно для усвоения понятия геометрической прогрессии. Арифметическую прогрессию мы изучали в предыдущих темах. Сейчас рассмотрим геометрическую прогрессию – дадим ей определение, рассмотрим основные формулы геометрической прогрессии и ее характеристики, разберем несколько примеров.

Содержание

Определение геометрической прогрессии

Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же не равное нулю число.

Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, то есть

Это число называется знаменателем геометрической прогрессии и обозначается обычно буквой .

Для того, чтобы задать геометрическую прогрессию , достаточно знать ее первый член и знаменатель . Например, условиями и можно задать геометрическую прогрессию: .

Монотонная последовательность

Если знаменатель геометрической прогрессии больше нуля , , то прогрессия называется монотонной последовательностью. Например, если прогрессия задана , тогда геометрическая прогрессия -2, -6, -18, … есть монотонно убывающая последовательность.

Если прогрессия с параметрами , при образует последовательность 4, -12, 36, -108 … . Такая прогрессия не является ни возрастающей, ни убывающей последовательностью.

Если , то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.

Свойство геометрической прогрессии

Характеристической свойство геометрической прогрессии – последовательность является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, то есть , где .

Формулы геометрической прогрессии

Формула n-го члена геометрической прогрессии

Формула для определения n-го члена геометрической прогрессии имеет вид: , где .

Формула суммы n первых членов геометрической прогрессии

Для определения суммы n первых членов геометрической прогрессии используется формула:

   

Если в эту формулу вместо подставить выражение по формуле для определения n-го члена геометрической прогрессии, то мы получим вот такой вариант формулы:

   

Произведение равноотстоящих членов геометрической прогрессии

Из определения знаменателя геометрической прогрессии следует, что

, то есть произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная.

Примеры на геометрическую прогрессию с решениями

Пример 1

В геометрической прогрессии , , найти и .

Решение: чтобы найти определяется по формуле: , подставляя в нее данные примера, получим:

.

Сумму восьми первых членов геометрической прогрессии находим по формуле

:

Ответ: 13122 и 19680.

Пример 2

Сумма первого и третьего членов геометрической прогрессии равна 15, а сумма второго и четвертого 30. Найти сумму первых десяти членов.

Решение: чтобы найти сумму первых десяти членов прогрессии нам нужно знать ее первый член и знаменатель. Для нахождения их составим систему уравнений.

   

   

Разделив почленно второе уравнение системы на первое уравнение системы, получим . Подставляя найденное значение . Подставляя найденное значение в первое уравнение, находим .

По формуле

  находим:

Ответ: 3069

Пример 3

Найдите четыре числа, составляющие геометрическую прогрессию, зная, что первое больше второго на 36, а третье больше четвертого на 4.

Решение:

По условию задачи имеем и .

Составим систему:

   

   

Разделим почленно второе уравнение системы на первое уравнение, получим , откуда , .

Если , то , , , .

Если , то  , , , .

Ответ: 54, 18, 6 и 2 или 27, -9, 3, -1.

Практическая бесконечность / Статьи — Математическая составляющая

Приложения: мир вокруг нас

Математика: геометрическая прогрессия

«Рас­тёт в геомет­ри­че­ской прогрес­сии» — это выраже­ние часто можно услышать от теле­ве­дущих и экс­пер­тов, его можно встре­тить на стра­ни­цах газет, в книгах по есте­ство­зна­нию, в усло­виях экза­ме­наци­он­ных задач. А что оно озна­чает?

После­до­ва­тель­ность чисел $\{b_1, b_2, b_3, …\}$, в кото­рой каж­дое число $b_n$ пере­хо­дит в соседа справа $b_{n+1}$ по пра­вилу $b_{n+1}=b_n q$, назы­ва­ется геомет­ри­че­ской прогрес­сией. Прогрес­сия опре­де­ля­ется двумя парамет­рами: чис­лом $b_1$, кото­рое назы­ва­ется пер­вым чле­ном геомет­ри­че­ской прогрес­сии, и посто­ян­ной $q$ — её знаме­на­те­лем. {n-1}$, а не по цепочке после­до­ва­тель­ных вычис­ле­ний $b_2=b_1q$, $b_3=b_2q$, …, $b_n=b_{n-1}q$. Прогрес­сия назы­ва­ется воз­рас­тающей, если $q>1$; убы­вающей, если $0<q<1$.

Позна­комимся с при­ме­рами, в кото­рых про­ис­хо­дящее можно опи­сать в терми­нах геомет­ри­че­ской прогрес­сии, и посмот­рим, насколько быстро может расти воз­рас­тающая геомет­ри­че­ская прогрес­сия, и, соот­вет­ственно, быстра ли в своём убы­ва­нии прогрес­сия убы­вающая.

I. ⁠В самой попу­ляр­ной из легенд о про­ис­хож­де­нии шахмат рас­ска­зы­ва­ется, что некогда в Древ­ней Индии муд­рец по имени Сесса при­думал пра­вила новой игры и препод­нёс игру в дар царю Шераму.

Царь был оча­ро­ван и пред­ложил созда­телю игры самому выбрать награду. Тот попро­сил у царя немного зерна: на первую клетку доски положить 1 пше­нич­ное зерно, на вто­рую — 2, на тре­тью — 4 и т. д. — на каж­дую сле­дующую клетку надо положить вдвое больше зёрен, чем на пред­ше­ствующую. Воз­ни­кает геомет­ри­че­ская прогрес­сия, в кото­рой $b_1=1$, $q=2$. «Скром­ная» просьба ока­за­лась невы­пол­нимой, пона­до­бился бы урожай, соби­ра­емый на всей Земле за тысячи лет.

II. Нево­об­ра­зимый рост геомет­ри­че­ской прогрес­сии можно ощу­тить и про­сто скла­ды­вая обыч­ный лист бумаги. После пер­вого скла­ды­ва­ния попо­лам толщина бумаги уве­ли­чится вдвое, после вто­рого — вчет­веро, и очень скоро прак­ти­че­ские возмож­но­сти будут исчерпаны. А если допу­стить, что уда­лось сложить лист 42 раза, то ока­за­лось бы, что «толщина» кон­струкции больше, чем рас­сто­я­ние от Земли до Луны.

III. При­меры, иллю­стри­рующие свойства убы­вающей прогрес­сии, впе­чат­ляют не меньше. Изго­то­вим цепочку из шесте­рё­нок, зацеп­лен­ных после­до­ва­тельно одна за другую так, чтобы каж­дая сле­дующая враща­лась в 5 раз мед­лен­нее преды­дущей. Таким обра­зом, угло­вые ско­ро­сти шесте­рё­нок обра­зуют геомет­ри­че­скую прогрес­сию, знаме­на­тель кото­рой равен $1/5$.

Предпо­ложим, что цепочка доста­точно длин­ная. t$, кото­рые назы­ваются экс­по­ненци­аль­ными. Отсюда и род­ствен­ный термин — экс­по­ненци­аль­ный рост.

В Европе в круг матема­ти­че­ских зна­ний легенда о про­ис­хож­де­нии шахмат попала в XVII веке, когда Джон Вал­лис (матема­тик, крип­тограф и один из осно­ва­те­лей Лон­дон­ского Коро­лев­ского обще­ства) опуб­ли­ко­вал пере­вод сочи­не­ния араб­ского исто­рика ас‐­Сафада (XIV век).

В после­дующие века исто­рия про Сессу и Шерама рас­про­стра­ни­лась по всей Европе; напри­мер, вели­кий Лео­нард Эйлер в книге «Элементы алгебры» при­во­дит задачу о прак­ти­че­ской оценке необ­хо­димого коли­че­ства зёрен.

Ещё один инте­рес­ный при­мер рас­тущей геомет­ри­че­ской прогрес­сии — после­до­ва­тель­ность частот нот рав­но­мерно темпе­ри­ро­ван­ного строя (см. ⁠«Музыкаль­ный строй»). Здесь знаме­на­тель прогрес­сии $q=\sqrt[12]{2}&approx; 1{,}06$ бли­зок к 1, но кла­виш доста­точно много — в кла­ви­а­туре стан­дарт­ного рояля их 88. И за эти 88 шагов про­бега­ется интер­вал, охва­ты­вающий более 7 октав ($88{=}7{\cdot }12{+}4$) и пред­став­ляющий почти весь диапа­зон зву­ков, комфорт­ных для чело­ве­че­ского уха.

С чис­лом 88 чита­тель может встре­титься в этой книге и в сюжете ⁠«Созвез­дия»: именно на такое число созвез­дий аст­ро­номы поде­лили звёзд­ное небо.

Геометрическая прогрессия — определение, примеры и вопросы

A Геометрическая прогрессия (Г.П.) — это последовательность, в которой каждый член получается путем умножения или деления предыдущего члена на фиксированное число или постоянное отношение(r) .

2, 4, 8, 16, 32, 64, … здесь первый член равен 2, а знаменатель равен 2. Мы можем получить последовательные члены, умножив число на 2. Таким образом, следующим членом после 64 будет 128.

Мы можем использовать это понятие, чтобы получить произвольный член, конечную или бесконечную сумму ряда, и применять их в различных контекстах, включая некоторые сложные проблемы.

История

Глиняная табличка раннего династического периода в Месопотамии , MS 3047, содержит геометрическую прогрессию с основанием 3 и множителем 1/2.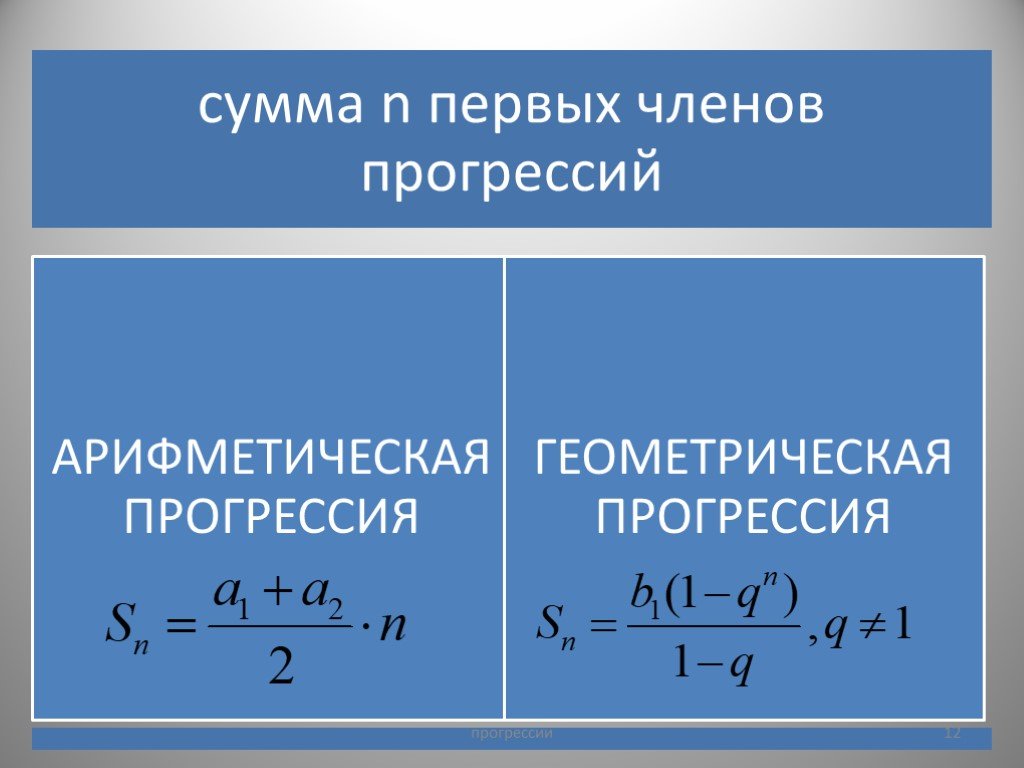 Было высказано предположение, что это шумерский из города Шуруппак.

Это единственная известная запись геометрической прогрессии до времен вавилонской математики .

 Вавилонская глиняная табличка YBC 7289 (Источник)

Согласно Боэция (510), арифметические и геометрические последовательности были известны ранним греческим писателям.

Бесконечная серия возникла в Индии к 14-му веку. Явная формула суммы бесконечного ( Anantya ) геометрического ряда дается Nilkantha в его Aryabhatyabhasya около 15 th -16 th век .

Геометрическая последовательность

Последовательность называется геометрической прогрессией или G.P . если 9{п – 1}\).

Здесь

a — первый член
r   — знаменатель
n — номер члена. 2\) 9n – 1)}{(r – 1)} \mbox{ (когда r>1) } \)

Среднее геометрическое (GM)

Среднее геометрическое любых двух чисел x и y (где ‘x ‘ — первый член, а y — последний) можно получить по формуле

G.M. = \(\sqrt{xy}\)

Это обобщенная формула для Г.М.

Сумма бесконечной геометрической прогрессии

Существует еще один тип геометрического ряда, бесконечный геометрический ряд . Бесконечный геометрический ряд представляет собой сумму бесконечной геометрической последовательности и может быть задан формулой 9{\frac{1}{2}}\) = 3 = RHS

Отсюда доказано.

Часто задаваемые вопросы

Что понимается под геометрической прогрессией?

Геометрическая прогрессия — это ряд чисел, в котором каждое число умножается или делится на фиксированное число, чтобы получить следующее, например, 1, 3, 9, 27, 81…

Почему геометрическая прогрессия называется так?

Выражение «геометрическая прогрессия» происходит от «среднего геометрического» (евклидово понятие) отрезков длины a и b: это длина стороны c квадрата, площадь которого равна площади прямоугольника сторон а и б.

Как узнать, является ли последовательность арифметической или геометрической?

В последовательности есть закономерность. Если последовательность имеет общую разность, то она арифметическая. Если у него есть общее отношение, то оно геометрическое.

Каково среднее геометрическое 2 и 32?

Среднее геометрическое дается формулой \(\sqrt{ab}\)
Следовательно, Г.М. = \(\sqrt{2*32}\) = 8.

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ определение | Кембриджский словарь английского языка

Переводы геометрической прогрессии

на китайском (традиционном)

幾何 數 ： ： 從 第一 項 開始 ， 以後 一 項 都 是 前 一 項 乘上 一 個 數 數 如 2, 6, 18…

См. Подробнее

на китайском (упрощенном)

几何 级 数 ： 从 项 开始 ， 以后 毎 一 项 都 是 它 一 项 乘上 一 固定 数 数 ， 2, 6, 18…

Увидеть больше

Нужен переводчик?

Получите быстрый бесплатный перевод!

Как произносится геометрическая прогрессия ?