Производная и ее приложения: § 2. Производная и ее приложения

§ 2. Производная и ее приложения

2.1. Производной функции называется предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:

.

Если этот предел конечный, то производная существует и функция называется дифференцируемой в точке . Производная обозначается также или . Процесс нахождения производной называется дифференцированием функции.

Правила дифференцирования функций. Пусть — постоянная, , — функции, имеющие производные.

1. .

2. = .

3. .

4. .

5. , .

6. Правило дифференцирования сложной функции. Если функция дифференцируемая по , а функция — по x, то сложная функция имеет производную .

Таблица производных элементарных функций

1. .

1а. . 1б. .

2. . 2а. .

3. . 3а. .

4. . 5. .

6. . 7. .

8. . 9. .

10. . 11. .

12. (вывод этой формулы дан ниже).

Производные второго порядка. Производной второго порядка (второй производной) от функции называется производная от ее производной, т. е.

.

Вторую производную также обозначают или . Производная от производной второго порядка называется производной третьего порядка и т. д. Производную -го порядка обозначают или .

Пример 1. Используя правила дифференцирования и таблицу производных, найдем производные следующих функций:

1) , 2) ,

3) , 4) ,

5) , 6) ,

7) .

Решение. 1) Перепишем данную функцию, записав слагаемые в виде степени: . Тогда

.

2) Записываем данную функцию в виде степени: и вычисляем: .

3) Применив формулу 4 правил дифференцирования, находим:

.

4) Дифференцируя функцию как сложную находим производную:

.

5) В соответствии с формулой 5 правил дифференцирования получаем:

.

6) По аналогии с примером 3 находим:

.

7) Так как данная функция — показательная, то, согласно формуле 2

Степенно — показательная функция. Выведем формулу для производной степенно — показательной функции , считая что и дифференцируемые функции и .

Решение. Логарифмируя равенство и дифференцируя обе части полученного равенства , находим: . Следовательно, . Таким образом, получили .

Замечание. Степенно – показательная функция дифференцируется как степенная плюс как показательная. Например, производная функции , равна

.

Теорема. Если кривая задана уравнением , то значение производной в точке , равно угловому коэффициенту касательной к кривой в точке : , где (см. рис 9).

Уравнение касательной к кривой в точке имеет вид:

или .

Определение. Углом между двумя кривыми в точке их пересечения называется угол между касательными к кривым в этой точке.

Угол между прямыми с угловыми коэффициентами и находится по формуле:

,

причем знак “плюс” соответствует острому углу θ, а знак “минус” – тупому.

Если , то касательные — взаимно перпендикулярны, а кривые называются ортогональными.

Пример2. Найти уравнение касательной к графику функции , которая параллельна прямой . Сделать чертеж.

Решение. График функции – парабола. Так как при , , то вершиной параболы является точка (2; –1). По условию, касательная к параболе и данная прямая с уравнением параллельны, значит, их угловые коэффициенты равны:

, , .

Следовательно, — абсцисса точки касания параболы и прямой , – ее ордината. Таким образом, уравнение касательной имеет вид:

или . (рис.10)

Производная и ее приложения — презентация онлайн

Похожие презентации:

Производная функции

Производная функции

Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций

Определение производной. Задачи, приводящие к понятию производной

Определение производной

Производная. Функции одной переменной. (Тема 3)

Приложение производной к исследованию функции

Понятие производной

Элементы дифференциального исчисления. Производые. Исследование (лекция 2)

Производная функции

1. Производная и ее приложения.

Приращение функции. Физический
смысл производной. Вычисление
производной по определению

2. Приращение функции

1) Сформулируйте определения
приращения
аргумента
и
приращения функции в данной точке
x0.
?
2) От чего зависит приращение
функции при каждом
фиксированном x0?
3) Что показывает на
графике отношение
f ( x 0 )
x

3. Физический смысл производной, рассмотрим падение тела с некоторой высоты

• рассмотрим промежуток t от момента t0 до t = t0 + t.
Тогда S(t0) = S(t0 + t) – S(t0) = … = gt0 t + g( t)2, то
есть, при фиксированном t0 S(t0) зависит только
от t ! Для рассматриваемой функции: t –
приращение аргумента в точке t0; S(t0) –
приращение функции в этой точке. Средняя скорость
S ( t 0 )
• движения на [t0; t0 + t] равна: Vср.
= gt0 + 1 g t
1
t
2
= V0 + 2 g t. Пусть t 0, тогда
1
lim Vс р. lim V0 g t V0
t 0
t 0
2
Таким образом, для каждого фиксированного
S (t 0 )
lim
V0
момента времени t0
t 0
t
–равен некоторому числу, которое называется мгновенной
скоростью падения тела в момент времени t0!

4. Определение

• Производной функции в точке x0
называется предел отношения
приращения функции к приращению
аргумента, если приращение
аргумента стремится к нулю.
f ( x 0 )
f ( x 0 x ) f ( x 0 )
f ‘( x 0 ) lim
lim
x 0
x 0
x
x

5. Определения.

• 1) Функция называется дифференцируемой в
точке x0, если f’(x0).
• 2) Функция называется дифференцируемой на
множестве I, если она дифференцируема в
каждой точке из этого множества.
• Пусть функция y = f(x) дифференцируема на I.
Тогда x0 I f’(x0). Соответствие {x0} {f’(x0)}
определяет новую функцию, которая
называется производной функции y = f(x) и
обозначается f’(x).
• В чем различие f’(x) и f’(x0)? [функция и число].
Операция вычисления производной функции
называется дифференцированием функции.

6. Вычисление производных по определению

• 1) f(x) = C.
f(x0) = f(x0 + x) – f(x0) = C – C = 0;
.
Таким
образом,.
f ( x 0 )
f ‘( x 0 ) lim
lim 0 0
(С)’ = 0
x 0
x 0
x
• 2) f(x) = kx + b.
• f(x0) = f(x0 + x) – f(x0) = k(x0 + x) – kx0 = k x;
f ( x 0 )
lim k k Таким образом,
• f ‘( x 0 ) lim
.
x 0
x 0
x
.
(kx + b)’ = k

7. Алгоритм нахождения производной:

• Зафиксировать значение х0 и найти f(x0)
• Дать аргументу х0 приращение х ,и найти
f(х0+ х)
• Найти приращение у= f(х0+ х) — f(х0)
• Составить отношение у/ х
• Вычислить
f ( x 0 )
f ( x 0 x ) f ( x 0 )
f ‘( x 0 ) lim
lim
x 0
x 0
x
x

8.

Вычислить по определению производные• 3) f(x) = ax2 + bx + c
• 4) f(x) =
x . f’(0) – не существует
.
(
x )’ =
1
2 x
(ax2 + bx + c)’ = 2ax + b

9. Рассмотрим функцию f(x) = |x| и ее график

• Докажем по определению, что
1, если x 0
f ‘( x )
1, если x 0
А) Пусть x0 > 0, тогда выберем x так, чтобы
x0 + x > 0. f(x0) = |x0 + x| – |x0| = x;
f ( x 0 )
f ‘( x 0 ) lim
lim 1 1
x 0
x 0
• .
x
Б) Пусть x0 < 0, тогда выберем x так, чтобы
x0 + x < 0. Аналогично получим, что . f ‘( x ) 1
0
В) Пусть x0 = 0, тогда f(x0) = |x0 + x| – |x0|=| x|.
f ( x 0 )
x
,
не существует, поэтому
lim
x 0
x
lim
x 0
x
• данная функция не дифференцируема в
нуле.
• F(x) = |x2 – 6x + 5|.
• А) Постройте график функции.
• Б) Найдите f’(2) и f’(6).
• B) (по вариантам) Докажите, что в точках
x0 = 1 и x0 = 5 функция не дифференцируема
x 6x 5, если x 1 или x 5
f (x )
2
x 6x 5, если 1 x 5
2
2 x 6, если x 1 или x 5
f ‘( x )
2 x 6, если 1 x 5
f’(2) = 2; f’(6) = 6
x 1 x 5
f ( x ) f (1)
lim
lim
x 1
x 1
x 1
x 1
lim
x 1 0
x 1 x 5
x 1
4
не существует, так как
lim
x 1 0
x 1 x 5
x 1
4
x 1 x 5
f ( x ) f ( 5)
lim
lim
x 5
x 1
x 5
x 5
не существует, так как
lim
x 5 0
x 1 x 5
x 5
4
lim
x 5 0
x 1 x 5
x 5
4

14.

Домашнее задание • Выучить стр163 п1,2,3 и записи
• Вып.№392 (3,5,7) №393(1,2)
• Cоставить таблицу производных.
Вопросы по теории:
1)Сформулируйте определение приращения функции и приращения аргумента.
2) определение производной функции в точке.
3)Физический смысл производной
4)Как называется операция нахождения производной?
5)Какая функция называется дифференцируемой в точке?.
6)Какая функция называется дифференцируемой на отрезке?
7)Алгоритм вычисления производной.
8) Вычислять по определению производные простейших функций.

English     Русский Правила

Применение производных — определение, применение, свойства, примеры

Применение производных разнообразно не только в математике, но и в реальной жизни. Чтобы привести пример, производные имеют различные важные приложения в математике, такие как определение скорости изменения количества, определение значения приближения, определение уравнения касательной и нормали к кривой, а также определение минимального и максимального значений.

алгебраических выражений.

Производные широко используются в таких областях, как наука, инженерия, физика и т. д. В этой статье мы узнаем о применении деривативов в реальной жизни. Давайте подробно узнаем об этих применениях деривативов.

1.	Применение производных в математике
2.	Производная скорости изменения количества
3.	Приблизительное значение
4.	Касательная и нормаль к кривой
5.	Максимум, минимум и точка перегиба
6.	Функции возрастания и убывания
7.	Решенные примеры
8.	Практические вопросы по применению производных
9.	Часто задаваемые вопросы о применении деривативов

Применение производных в математике

В математике широко используются производные. Они используются во многих ситуациях, таких как поиск максимумов или минимумов функции, поиск наклона кривой и даже точки перегиба. Несколько мест, где мы будем использовать производную, приведены ниже. И каждый из них подробно объясняется в следующих разделах. Наиболее распространенное использование производных наблюдается в:

• Нахождение скорости изменения величины
• Нахождение значения приближения
• Нахождение уравнения касательной и нормали к кривой
• Нахождение максимума и минимума и точки перегиба
• Определение возрастающих и убывающих функций

Производная скорости изменения количества

Производные используются для нахождения скорости изменения количества по отношению к другому количеству. Используя производные, мы можем найти приближенное изменение одной величины по отношению к изменению другой величины. Предположим, что у нас есть функция y = f(x), которая определена на интервале [a, a+h], тогда средняя скорость изменения функции на данном интервале равна

(f(a + h)-f(a))/h

Теперь, используя определение производной, мы можем написать

\(f′(a)=\lim_{h→0}\frac{f (a+h)−f(a)}{h}\)

, что также является мгновенной скоростью изменения функции f(x) в точке a.

Теперь для очень малого значения h мы можем записать

f'(a) ≈ (f(a+h) − f(a))/h

или

f(a+h) ≈ f(a) + f'(a)h

Это означает, что если мы хотим найти малое изменение функции, нам просто нужно найти производную функции в данной точке, и, используя данное уравнение, мы можем рассчитать изменение. Следовательно, производная дает мгновенную скорость изменения функции в заданных пределах и может использоваться для нахождения предполагаемого изменения функции f (x) для небольшого изменения другой переменной (x).

Приблизительное значение

Производная функции может использоваться для нахождения линейной аппроксимации функции при заданном значении. Метод линейной аппроксимации был дан Ньютоном, и он предложил найти значение функции в данной точке, а затем найти уравнение касательной для нахождения приблизительно близкого к функции значения. Уравнение функции тангенса:

L(x) = f(a) + f'(a)(x−a)

значение функции.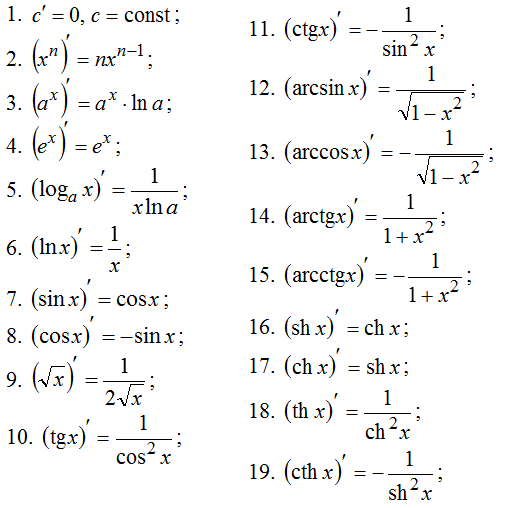 Давайте разберемся в этом на примере, мы можем оценить значение √9.1 с использованием линейного приближения. Здесь у нас есть функция: f(x) = y = √x. Мы найдем значение √9 и, используя линейное приближение, найдем значение √9,1.

Имеем f(x) = √x, тогда f'(x) = 1/(2√x)

Положив a = 9 в L(x) = f(a) + f'(a)(x −a), получаем

L(x) = f(9) + f'(9)(9,1−9)

L(x) = 3 + (1/6)0,1

L(x) ≈ 3,0167.

Это значение очень близко к фактическому значению √(9.1)

Следовательно, используя производные, мы можем найти линейную аппроксимацию функции, чтобы получить значение, близкое к функции.

Касательная и нормаль к кривой

Уравнение касательной и нормали к кривой функции можно вычислить с помощью производных. Если у нас есть кривая функции и мы хотим найти уравнение касательной к кривой в данной точке, то с помощью производной мы можем найти наклон и уравнение касательной. Касательная — это линия к кривой, которая касается кривой только в одной точке, а ее наклон равен производной кривой в этой точке.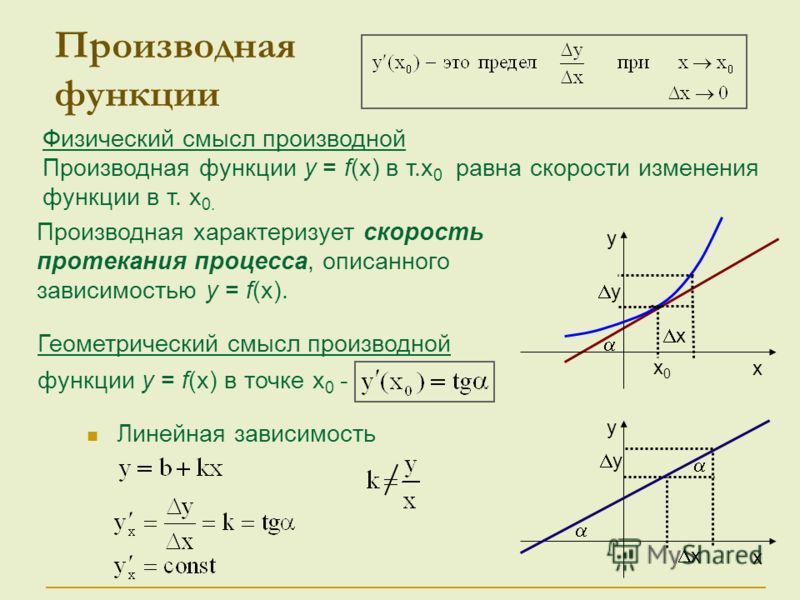 Наклон (m) касательной к кривой функции y = f (x) в точке \((x_1, y_1)\) получается путем взятия производной функции (m = f'(x)) .

Найдя наклон касательной к кривой и используя уравнение \(m = (y — y_1)/(x — x_1) \), мы можем найти уравнение касательной к кривой. Аналогично можно найти уравнение нормали к кривой функции в точке. Эта нормальная линия будет нормальной (перпендикулярной) к касательной. Следовательно, наклон нормальной линии к кривой функции y = f(x) в точке \((x_1, y_1)\) определяется следующим образом.

n = -1/m = — 1/ f'(x)

И с помощью уравнения \(-1/m = (y — y_1)/(x — x_1) \) мы можем найти уравнение нормальная линия к кривой.

Максимум, минимум и точка перегиба

Применение производных также полезно при нахождении максимумов, минимумов и точки перегиба кривой. Максимумы и минимумы — это пики и впадины кривой, тогда как точка перегиба — это часть кривой, где кривая меняет свой характер (с выпуклой на вогнутую или наоборот). Мы можем найти максимумы, минимумы и точку перегиба, используя критерий производной первого порядка. Согласно этому тесту сначала находим производную функции в данной точке и приравниваем ее к 0, т. е. f'(c) = 0, (здесь мы нашли наклон кривой равным 0, а значит, она это прямая, параллельная оси абсцисс). Теперь, если функция определена на данном интервале, то проверяем значение f'(x) в точках, лежащих левее и правее кривой, и проверяем характер f'(x) , то мы можем сказать, что данная точка является максимумом или минимумом на основе следующих условий.

• Максимум, когда наклон или f'(x) меняет знак с +ve на -ve при движении через точку c. А f(c) — максимальное значение.
• Минимум, когда наклон или f’(x) меняет знак с -ve на +ve при движении через точку c. А f(c) — минимальное значение.
• Точка C называется точкой перегиба, когда знак наклона или знак f’(x) не меняется при движении через c.

Функции возрастания и убывания

Используя производные, мы можем узнать, является ли функция возрастающей или убывающей функцией.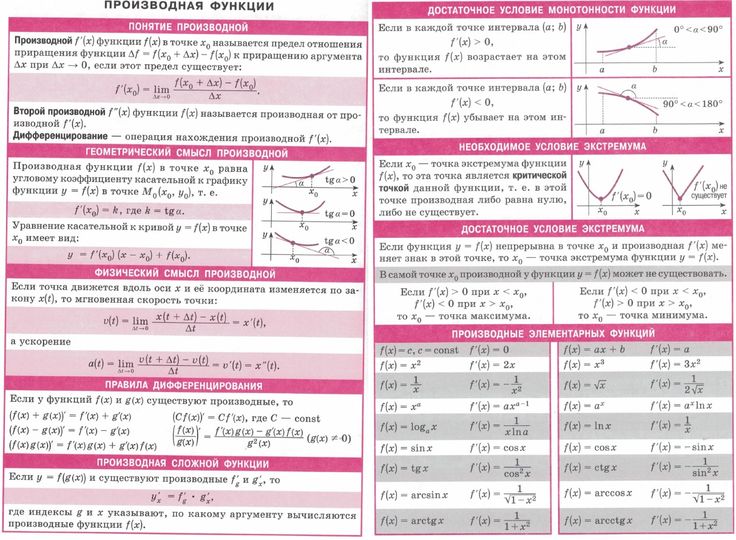 Возрастающая функция — это функция, которая, кажется, достигает вершины плоскости xy, тогда как убывающая функция кажется достигающей нижнего угла плоскости xy. Допустим, у нас есть функция f(x), дифференцируемая в пределах (a, b). Затем проверяем любые две точки на кривой функции.

• Если в любых двух точках \(x_1\) и \(x_2\) таких, что \(x_1\) < \(x_2\), существует отношение \(f(x_1)\) ≤ \(f( x_2)\), то данная функция является возрастающей функцией на данном интервале, а если \(f(x_1)\) < \(f(x_2)\), то данная функция является строго возрастающей функцией на данном интервале.
• И если в любых двух точках \(x_1\) и \(x_2\) таких, что \(x_1\) < \(x_2\), существует соотношение \(f(x_1)\) ≥ \(f( x_2)\), то данная функция является убывающей функцией на данном интервале, а если \(f(x_1)\) > \(f(x_2)\), то данная функция является строго убывающей функцией на данном интервале

Связанные темы по применению производных:

• Формула производной
• Исчисление
• Дифференциальные уравнения
• Интеграция
• Формулы интегрирования

Важные замечания по применению производных:

• Применение производных используется для нахождения скорости изменения количества по отношению к другому количеству.
• Уравнение касательной и нормали к кривой функции можно вычислить с помощью производных.
• Производную функции можно использовать для нахождения линейной аппроксимации функции при заданном значении.

Часто задаваемые вопросы о применении деривативов

Какое применение производных в математике?

В математике широко используются производные. Они используются во многих ситуациях, таких как поиск максимумов или минимумов функции, поиск наклона кривой и даже точки перегиба. Несколько мест, где мы будем использовать производную, приведены ниже, а затем объяснены по одному в следующих разделах. Наиболее распространенное использование применения производных наблюдается в следующих областях.

• Нахождение скорости изменения величины
• Нахождение значения приближения
• Нахождение касательной и нормали к кривой
• Нахождение максимума и минимума и точки перегиба
• Определение возрастающих и убывающих функций

Каково применение дифференциации в реальной жизни?

Дифференциация имеет широкое применение в реальной жизни. Вот несколько приложений:

• В бизнесе дифференциация используется для определения прибылей и убытков для будущих инвестиций с использованием графиков.
• Колебания температуры также рассчитываются с помощью дифференцирования.
• Используется для расчета скорости изменения расстояния движущегося тела во времени.

Каковы применения дифференциального исчисления?

Производные используются для нахождения скорости изменения количества по отношению к другому количеству. Уравнение касательной и нормали к кривой функции можно рассчитать с помощью производных. Производную функции можно использовать для нахождения линейного приближения функции при заданном значении. Производные также помогают найти максимумы, минимумы и точки перегиба кривой.

Какие темы подпадают под применение деривативов?

Следующие главы подпадают под действие производной:

• Скорость изменения количества.
• Приближения.
• Возрастающие и убывающие функции.
• Максимум и минимум.
• Касательные и нормали.
• Функция увеличения и уменьшения.

Почему производные важны в математике?

Производные представляют скорость изменения. В математике скорость изменения может быть применена ко многим обстоятельствам. Например, ускорение — это скорость изменения скорости. Следовательно, производная функция может использоваться для определения ускорения объекта, когда задана скорость во времени.

Изучите приложения на примерах

В математике производные имеют широкое применение. Они применяются во многих случаях, таких как вычисление наклона кривой, определение максимума или минимума функции, получение уравнения касательной и нормали к кривой, а также точек перегиба. В этой конкретной статье мы рассмотрим некоторые важные приложения производных, связанных формул и различных подобных концепций с решенными примерами и часто задаваемыми вопросами.

Каково применение деривативов?

Производные простыми словами понимаются как скорость изменения одной величины по отношению к другой и широко применяются в областях науки, техники, физики, математики и т. д. Ниже упомянуто несколько наиболее известных применений формул производных в математике, которые мы обсудим в следующих разделах:0072

Уравнение касательной и нормали к кривой

Максимум и минимум

Точка перегиба

Определение возрастающих и убывающих функций

 Узнайте больше о дифференциальном исчислении в этой статье.

Скорость изменения величин при применении производных

Если данное уравнение имеет форму y = f(x), это можно прочитать как «y» является функцией «x». Теперь, если мы скажем, что «y» изменяется, когда происходит некоторое изменение значения «x». Тогда скорость изменения «y» относительно «x» определяется по формуле:
\(\frac{Δy}{Δx}=\frac{y_2-y_1}{x_2-x_1}\)

Приведенная выше формула также читается как средняя скорость изменения функции.
Теперь, если мы рассмотрим случай, когда скорость изменения функции определяется при определенных значениях, то есть при определенном значении «x»,. {\prime}\left(x\right)\) обозначает скорость изменения y относительно x. 9{\prime}\left(x_1\right)\) обозначает скорость изменения y относительно x в определенной точке, т.е. \(x=x_{1}\).

Проще говоря, если y = f(x). Тогда \(\frac{dy}{dx}\) обозначает скорость изменения y относительно x, а его значение при x = a обозначается как:
\(\left[\frac{dy}{dx}\right] _{_{x=a}}\)

Теперь, если x = f(t) и y = g(t), предположим, что мы хотим найти скорость изменения y относительно x.

Тогда dy/dx можно записать как:
\(\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\left(\ frac{d y}{d t} \cdot \frac{d t}{d x}\right)\) с помощью цепного правила.

Узнайте о производных алгебраических функций здесь, в связанной статье.

Приближенное значение

Для расчета очень небольшой разницы или изменения количества мы можем использовать правила производных, чтобы получить приблизительное значение для того же самого. Это приблизительное значение интерпретируется дельтой △. Производная функции может также применяться для определения линейной аппроксимации функции в данной точке. Метод линейного приближения был предложен Ньютоном. Согласно ему, получите значение функции при заданном значении, а затем найдите уравнение касательной, чтобы получить примерно близкое значение функции. Уравнение функции тангенса задается уравнением. 9{\prime}(a)\ (x−a)\)

Мы можем прочитать приведенное выше уравнение как для данной функции f(x), уравнение касательной представляет собой L(x) в точке x=a .

Уравнение касательной и нормали к кривой

Далее следует применение производных для определения уравнения касательной и нормали к кривой. Касательная — это линия, проведенная к кривой, которая пересекается с кривой только в одном месте, а ее наклон эквивалентен производной кривой в этой точке. Нормаль – это прямая, перпендикулярная полученной касательной.

Уравнение касательной и нормали к кривой функции можно получить с помощью производных. Если задана кривая функции и задано уравнение касательной к кривой в данной точке, то, применяя производную, мы можем получить наклон и уравнение касательной. Точно так же мы можем получить уравнение нормальной линии к кривой функции в определенном месте.

Пусть y = f(x) уравнение кривой, тогда наклон касательной в любой точке, скажем, \(\left(x_1,\ y_1\right)\) определяется выражением: \(m=\ влево[\frac{dy}{dx}\right]_{_{\left(x_1,\y_1\\right)}}\)

Нормаль перпендикулярна касательной, поэтому наклон нормали в любой точке, скажем, определяется как:

\(-\frac{1}{\text{Наклон касательной в точке}\ \left(x_1,\ y_1 \ \right)}=-\frac{1}{m}=-\left[\frac{dx}{dy}\right]_{_{\left(x_1,\y_1\\right)}}\)

Уравнение касательной в любой точке, скажем, \((x_1, y_1)\) определяется как:

\(y-y_1=\left[\frac{dy}{dx}\right]_{_{\left (x_1,\ y_1\ \right)}}.\ \left(x-x_1\right)\)

Уравнение нормали в любой точке скажем \((x_1, y_1)\) определяется как:

\(y-y_1=-\left[\frac{dx}{dy}\right]_{_{\left(x_1,\ y_1\\right)}}. \ \left(x-x_1\right) )\)

Если касательная к кривой y = f (x) образует угол с осью x в положительном направлении, то;

\(\frac{dy}{dx}=\text{ наклон тангенса}=\tan \theta\)

Если вы читаете Приложения производных, вы можете прочитать о решении дифференциальных уравнений здесь.

Максимумы, минимумы и точки перегиба

Под этим заголовком приложений производных мы поймем концепцию максимальных или минимальных значений различных функций, используя концепцию производных. Для функции f, заданной на интервале I, максимумы или минимумы (или локальные максимумы, или локальные минимумы) в I зависят от заданного условия: f(x)≤ f(c) или f(x) ≥ f(c), ∀ x ∈ I и c — точка интервала I.

Это также можно прочитать как:

При x=c, если f(x)≤f(c) для каждого значения x в области, с которой мы работаем, то f(x) имеет абсолютный максимум; это также известно как глобальное максимальное значение.

Аналогично,

При x=c, если f(x)≤f(c) для каждого значения x на некотором открытом интервале, скажем, (r, s), то f(x) имеет относительный максимум; это также известно как локальное максимальное значение.

Таким же образом:

Мы можем утверждать, что при x=c, если f(x)≥f(c) для каждого значения x в области, с которой мы работаем, то f(x) имеет абсолютный минимум; это также известно как глобальное минимальное значение.

Аналогично, при x=c, если f(x)≥f(c) для каждого значения x на некотором открытом интервале, скажем, (r, s), то f(x) имеет относительный минимум; это также известно как локальное минимальное значение.

Узнайте о первых принципах производных здесь в связанной статье.

Мы также можем понять максимумы и минимумы с помощью наклона функции:

• Когда наклон функции изменяется от +ve до -ve при движении через точку c, тогда говорят, что это максимум.
• Когда наклон функции изменяется от -ve до +ve при движении через точку c, говорят, что она достигает минимума.

Точка перегиба

В рассмотренных выше условиях для максимумов и минимумов точка c обозначает точку перегиба, которую также можно заметить по изображениям максимумов и минимумов. Точка перегиба — это участок кривой, где кривая меняет свою природу с выпуклой на вогнутую или наоборот.

Возрастающие и убывающие функции в приложениях производных

Под этим заголовком мы будем использовать приложения производных и методы дифференцирования, чтобы определить, является ли функция возрастающей или убывающей, или никакая. Используя производные, мы можем определить, является ли данная функция возрастающей или убывающей функцией. Возрастающая функция — это функция, которая кажется касающейся верхней части плоскости xy, тогда как убывающая функция выглядит как перемещение нижнего угла плоскости xy. 9{\prime}}\left(x\right)=0\)

Узнайте больше о производных логарифмических функций здесь.

Применение производных в реальной жизни

• Применение производных используется для определения скорости изменения количества по отношению к другому количеству.
• Также применяется для определения прибыли и убытков на рынке с помощью графиков.
• Производные применяются для определения уравнений в физике и математике.
• Уравнение касательной и нормали к кривой функции можно определить, применяя производные.
• Производная функции также может использоваться для получения линейной аппроксимации функции в заданном состоянии.
• Производная далее находит применение в исследованиях сейсмологии для определения диапазона магнитуд землетрясений.
• Производная также находит применение для определения скорости пройденного расстояния, например миль в час, километров в час, для контроля за изменением температуры и т. д.

Решенные примеры применения производных

Хорошо знакомы с различными приложениями производных, давайте попрактикуемся в некоторых решенных примерах, чтобы понять их с помощью математического подхода.

Решено Пример 1: Найдите скорость изменения площади круга по отношению к его радиусу r при r = 6 см?

Решение:

Здесь мы должны найти скорость изменения площади круга по отношению к его радиусу r при r = 6 см. 2\), где r — радиус круга. 92+26\times1−10)=2\)

Итак, наклон касательной к данной кривой в точке (1, 3) равен 2.

Поскольку мы знаем, что уравнение касательной в любой точке говорит \(( x_1, y_1)\) определяется как: \(y−y_1=\left[\frac{dy}{dx}\right]_{_{(x_1,y_1)}}⋅(x−x_1)\)

Здесь \(x_1 = 1, y_1 = 3\) и \(\left[\frac{dy}{dx}\right]_{_{(1,3)}}=2\)

Подставляя эти значений в уравнении:

⇒y−3=2⋅(x−1)

⇒ 2x – y + 1 = 0

Отсюда уравнение касательной к заданной кривой в точке (1, 3) равно: 2x – y + 1 = 0 92}\)

⇒ f”(x) = – 2

Теперь оценим значение f”(x) при x = 12

⇒ f”(12) = – 2 < 0

Поскольку мы знаем, что по критерию второй производной, если f”(c) < 0, то x = c – точка максимумов

Итак, x = 12 – точка максимумов

Итак, когда x = 12, то 24 – x = 12

Следовательно, нужные числа 12 и 12

Если вы освоили применение производных, вы можете узнать об интегральном исчислении здесь.

92−x+6\) равно 1/2.

Ребро переменного куба увеличивается со скоростью 5 см/сек. С какой скоростью увеличивается объем куба, если длина ребра равна 10 см?

Понятие:

• Объем куба определяется как: a3, где a — длина каждой стороны куба.
• Если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x, ее значение при x = a обозначается: \({\left[ {\frac{{dy}}{ {dx}}} \right]_{x = a}}\)
• Убывающая скорость представлена ​​отрицательным знаком, тогда как возрастающая скорость представлена положительным знаком.
• Цепное правило:
• Пусть y = f(v) — дифференцируемая функция от v, а v = g(x) — дифференцируемая функция от x, тогда \(\frac{{dy}}{{dx}} = \ frac{{dy}}{{dv}} \cdot \frac{{dv}}{{dx}}\)

Расчет :

В любой момент t пусть длина каждой стороны куба быть x, а V — его объем.

Дано: dx/dt = 5 см/с

Как мы знаем, объем куба определяется как: a3, где a – длина каждой стороны куба.

93}/сек\)

Длина x прямоугольника уменьшается со скоростью 5 см/мин, а ширина у увеличивается со скоростью 4 см/мин. Найдите скорость изменения площади прямоугольника при x = 8 см и y = 6 см.

Концепция ;

• Площадь прямоугольника определяется как: a × b, где a – длина, а b – ширина прямоугольника.
• Если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x, ее значение при x = a обозначается: \({\left[ {\frac{{dy}}{ {dx}}} \right]_{x = a}}\)
• Убывающая скорость представлена ​​отрицательным знаком, а возрастающая скорость представлена положительным знаком.
• \(\frac{d}{{dx}}\left[ {f\left( x \right) \cdot g\left( x \right)} \right] = f\left( x \right) \ cdot \;\frac{{d\left\{ {g\left( x \right)} \right\}}}{{dx}}\; + \;\;g\left( x \right) \cdot \;\frac{{d\left\{ {f\left( x \right)} \right\}}}{{dx}}\)

​ Расчет:

В любой момент t пусть А — площадь прямоугольника, х — длина прямоугольника, у — ширина прямоугольника.

Дано: dx/dt = – 5 см/мин и dy/dt = 4 см/мин.

Как мы знаем, площадь прямоугольника определяется как: a × b, где a – длина, а b – ширина прямоугольника.

т.е. A = x × y

Как мы знаем, \(\frac{d}{{dx}}\left[ {f\left( x \right) \cdot g\left( x \right)} \right] = f\left( x \right) \cdot \;\frac{{d\left\{ {g\left( x \right)} \right\}}}{{dx}}\; + \ ;\;g\left( x \right) \cdot \;\frac{{d\left\{ {f\left( x \right)} \right\}}}{{dx}}\)

Теперь, дифференцируя A по t, мы получаем,

\(\Rightarrow \frac{{dA}}{{dt}} = \frac{{d\left( {x \times y} \right)}} {{dt}} = \frac{{dx}}{{dt}} \cdot y + x \cdot \frac{{dy}}{{dt}}\)

Теперь, подставив значение dx/dt и dy/dt в приведенном выше уравнении мы получаем,

\(\Rightarrow \frac{{dA}}{{dt}} = \left( { – \;5} \right) \cdot y + x \cdot 6 \)

Теперь подставьте x = 8 см и y = 6 см в приведенное выше уравнение, и мы получим

\(\Rightarrow \frac{{dA}}{{dt}} = \left( { – \;5} \справа) \cdot 6 + 8 \cdot 6 = 2\;c{м^2}/мин\)

Следовательно, площадь прямоугольника увеличивается со скоростью 2 см2/мин.

Сферический мыльный пузырь расширяется так, что его радиус увеличивается со скоростью 0,02 см/с. С какой скоростью увеличивается площадь поверхности, если ее радиус равен 5 см? (Возьмите π = 3,14)

Концепция ;

• Площадь поверхности сферы определяется как: 4πr2 где r – радиус сферы.
• Если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x, ее значение при x = a обозначается: \({\left[ {\frac{{dy}}{ {dx}}} \right]_{x = a}}\)
• Убывающая скорость представлена ​​отрицательным знаком, а возрастающая скорость представлена положительным знаком.
• Цепное правило:
• Пусть y = f(v) — дифференцируемая функция от v, а v = g(x) — дифференцируемая функция от x, тогда \(\frac{{dy}}{{dx}} = \ frac{{dy}}{{dv}} \cdot \frac{{dv}}{{dx}}\)

Вычисление :

Как мы знаем, мыльный пузырь имеет форму шара. Пусть в момент t его радиус равен r, а площадь поверхности равна S.

92}/сек\)

Камень брошен в тихий пруд, и волны ходят кругами. Если радиус круговой волны увеличивается со скоростью 8 см/с, какова скорость увеличения ее площади в тот момент, когда ее радиус равен 6 см?

Концепция ;

• Площадь круга определяется как: π ⋅ r2 где r — радиус круга.
• Если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x, ее значение при x = a обозначается: \({\left[ {\frac{{dy}}{ {dx}}} \right]_{x = a}}\)
• Убывающая скорость представлена ​​отрицательным знаком, а возрастающая скорость представлена положительным знаком.
• Цепное правило :
• Пусть y = f(v) — дифференцируемая функция от v, а v = g(x) — дифференцируемая функция от x, тогда \(\frac{{dy}}{{dx}} = \frac{{dy}}{{dv}} \cdot \frac{{dv}}{{dx}}\)

Расчет:

При падении камня в тихий пруд соответствующие волны генерируемые ходы в круговой форме.

Дано: \(\frac{{dr}}{{dt}} = 8см/\сек \)

Итак, здесь нужно найти скорость увеличения площади круговых волн, образовавшихся в момент, когда радиус r = 6 см.

Как мы знаем, площадь круга определяется как: π ⋅ r2 где r – радиус круга.

Пусть A = π ⋅ r2

Поскольку мы знаем, что если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x.

Итак, дифференцируя A по t, получаем:

\(\frac{{dA}}{{dt}} = \frac{{dA}}{{dr}} \cdot \frac{{dr }}{{dt}}\) ——— (Цепное правило) 92}/сек\)

Отсюда скорость увеличения площади круговых волн, образующихся в момент, когда ее радиус равен 6 см, составляет 96π см ²  /сек.

Найдите скорость изменения площади круга по отношению к его радиусу r при r = 6 см ?

Концепция ;

• Площадь круга определяется как: π ⋅ r ²  где r — радиус круга.
• Если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x, ее значение при x = a обозначается: \({\left[ {\frac{{dy}}{ {dx}}} \right]_{x = a}}\)
• Убывающая скорость представлена ​​отрицательным знаком, а возрастающая скорость представлена положительным знаком.

Расчет :

Здесь мы должны найти скорость изменения площади круга по отношению к его радиусу r при r = 6 см.

Как мы знаем, площадь круга определяется как: π ⋅ r2 где r – радиус круга.

Пусть A = π ⋅ r ²

Поскольку мы знаем, что если y = f(x), то dy/dx обозначает скорость изменения y по отношению к x. 92}} \right)}}{{dr}} = 2π r\)

Теперь нам нужно найти значение dA/dr при r = 6 см, т.е. \({\left[ {\frac{{dA} }{{dr}}} \right]_{r\; = 6}}\)

\(\Rightarrow {\left[ {\frac {{dA}}{{dr}}} \right]_{ r\; = 6}} = 2π \cdot 6 = 12π \;см\)

Следовательно, скорость изменения площади круга относительно его радиуса r при r = 6 см равна 12π см.

Если радиус круга увеличивается со скоростью 0,5 см/с, какова скорость увеличения его окружности?

Понятие:

Скорость изменения ‘x’  задается выражением \(\rm \frac {dx}{dt}\)

Длина окружности = 2πr

2

3 90:

Длина окружности, C = 2πr rm \frac {dC}{dt}\) = 2π \(\rm \frac {dr}{dt}\)

= 2π (0,5)

= π см/сек 92}}}\;\)

Цепное правило:

Пусть y = f(v) — дифференцируемая функция от v, а v = g(x) — дифференцируемая функция от x, тогда \(\frac{{dy} }{{dx}} = \frac{{dy}}{{dv}} \cdot \frac{{dv}}{{dx}}\)

Пусть f(x) — функция, заданная на интервале (a, b) эта функция называется строго возрастающей:

• Если x1 < x2, то f(x1) < f(x2) ∀ x1, x2 ∈ (a, b)
• Здесь \frac{{dy}}{{dx}} > 0\;или\;f’\left( x \right) > 0\) 92}}} \cdot \frac{{d\left( {\cos x + \sin x} \right)}}{{dx}}\)

  \(⇒ f’\left( x \right) = \frac{{\cos x – \sin x}}{{2 + \sin 2x}}\)

  Теперь, когда 0 < x < π/4, мы имеем cos x > sin x и sin 2x > 0

  ⇒ cos x – sin x > 0 и 2 + 2 sin 2x > 0

  ⇒ f'(x) > 0 ∀ x ∈ (0, π/4)

  Поскольку мы знаем, что для строго возрастающей функции f'( x) > 0 для всех x ∈ (a, b)

  Итак, заданная функция f(x) является строго возрастающей функцией на (0, π/4).

  Следовательно, вариант 3 верен.

  Что из следующего верно относительно f(x) = x – sin x ?

  Понятие :

  Пусть f(x) — функция, определенная на интервале (a, b), эта функция называется возрастающей:

  • Если x1 < x2, то f(x1) ≤ f (x2 f(x1) ≤ f(x2) ∀ x1, x2 ∈ (a, b)
  • Здесь \(\frac{{dy}}{{dx}} \ge 0\;or\;f’\ left( x \right) \ge 0\)

  Аналогично, f(x) называется убывающей функцией:

  • Если Если x1 < x2, то f(x1) ≥ f(x2) ∀ x1, x2 ∈ (a, b).
  • Здесь, \(\frac{{dy}}{{dx}} \le 0\;или\;f’\left( x \right) \le 0\)

  Расчет :

  Дано : f(x) = x – sin x

  Вычислим f'(x).

  ⇒ f'(x) = 1 – cos x

  Как мы знаем, – 1 ≤ cos x ≤ 1 ∀ x ∈ R

  ⇒ f'(x) = 1 – cos x ≥ 0 ∀ x ∈ R

  Поскольку мы знаем, что для возрастающей функции, скажем, f(x), имеем f'(x) ≥ 0

  Следовательно, данная функция f(x) является возрастающей функцией на R.

  Следите за обновлениями в приложении Testbook или посетите веб-сайт Testbook, чтобы узнать больше об обновлениях по похожим темам из математики, естественных наук и многих других предметов, а также можете проверить серию тестов, доступных для проверки ваших знаний относительно различных экзаменов.

  Часто задаваемые вопросы о применении производных

  В.1 Для чего используется дифференциальное исчисление?

  Ответ 1 Дифференциальное исчисление в математике применяется для определения скорости изменения одной величины относительно другой, для определения возрастания или убывания функции на графике, для определения максимума и минимума значение кривой.

  Q.2 Что вы понимаете под скоростью изменения количества?

  Ответ 2 Если функция y = f(x). Тогда \(\frac{dy}{dx}\) обозначает скорость изменения y относительно x, а его значение при x = a обозначается как:\(\left[\frac{dy}{dx}\right]_ {_{х=а}}\).

  Q.3 Каковы приблизительные значения при применении производных?

  Ответ 3 Чтобы найти очень маленькую модификацию или вариацию функции, применяются данные производные, чтобы получить приблизительное ее значение, и обозначается символом дельта △.

  No related posts.