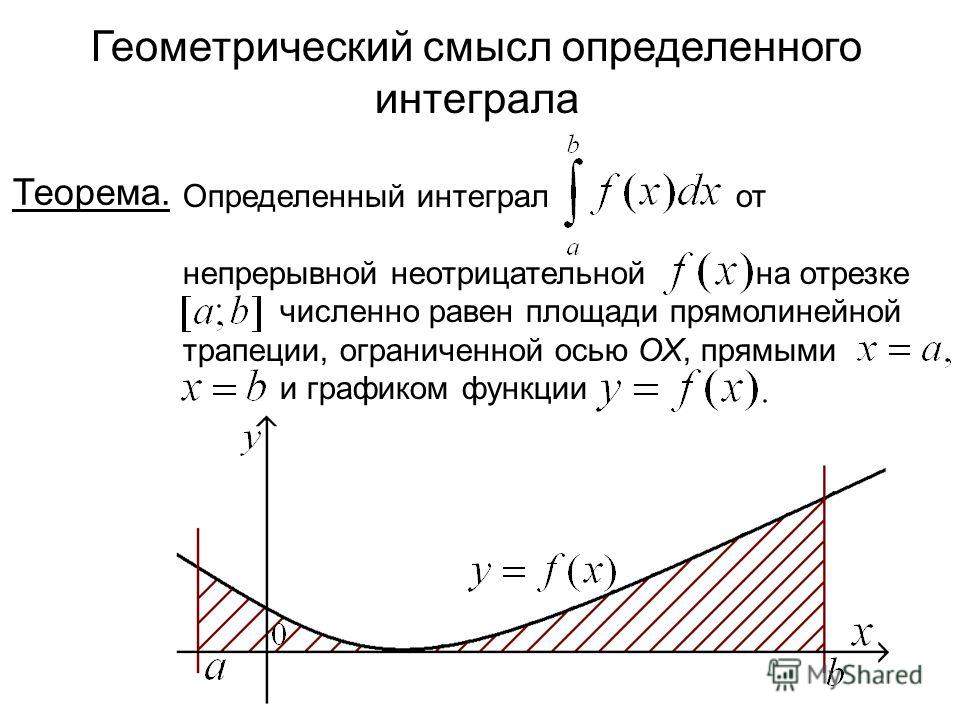
Геометрический смысл интеграл: Геометрический смысл определенного интеграла

Геометрический смысл определенного интеграла, выражение площади криволинейной трапеции

Вычисление площади является основным  в теории площадей. Возникает вопрос о ее нахождении, когда фигура имеет неправильную форму или необходимо прибегнуть к ее вычислению через интеграл.

Данная статья рассказывает о вычислении площади криволинейной трапеции по геометрическому смыслу.  Это позволяет выявлять связь между  интегралом и площадью криволинейной трапеции. Если дана функция f(x), причем непрерывная на интервале [a; b], знак перед выражением не меняется.

Криволинейная трапеция

Определение 1

Фигура, обозначенная как G, ограничена линиями вида y = f(x), y = 0, x = a и x = b, называется криволинейной трапецией. Она принимает обозначение S(G).

Рассмотрим на рисунке, приведенном ниже.

Для вычисления криволинейно трапеции необходимо разбить отрезок  [a; b] на количество n частей xi-1; xi, i=1, 2,…, n с точками, определенными на a=x0<x1<x2<. ..<xn-1<xn=b, причем дать обозначение λ=maxi=1, 2,…, nxi-xi-1 с точками xi, i=1, 2,…, n-1. Необходимо выбрать так, чтобы λ→0 при n→+∞, тогда фигуры, которые соответствуют нижней и верхней частям Дарбу, считаются входящей Р и объемлющей Q многоугольными фигурами для G. Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что P⊂G⊂Q, причем при увеличении количества точек разбиения n, получим неравенство вида S-s<ε, где ε является малым положительным числом, s и S являются верхними и нижними суммами Дабру из отрезка  [a; b]. Иначе это запишется как limλ→0S-s=0. Значит, при обращении к понятию определенного интеграла Дарбу, получим, что limλ→0S=limλ→0s=SG=∫abf(x)dx.

Из последнего равенства получим, что определенный интеграл вида ∫abf(x)dx является площадью криволинейной трапеции для заданной непрерывной функции вида y=f(x). Это и есть геометрический смысл определенного интеграла.

При вычислении ∫abf(x)dx получим площадь искомой фигуры, которая ограничивается линиями  y = f(x), y = 0, x = a и x = b.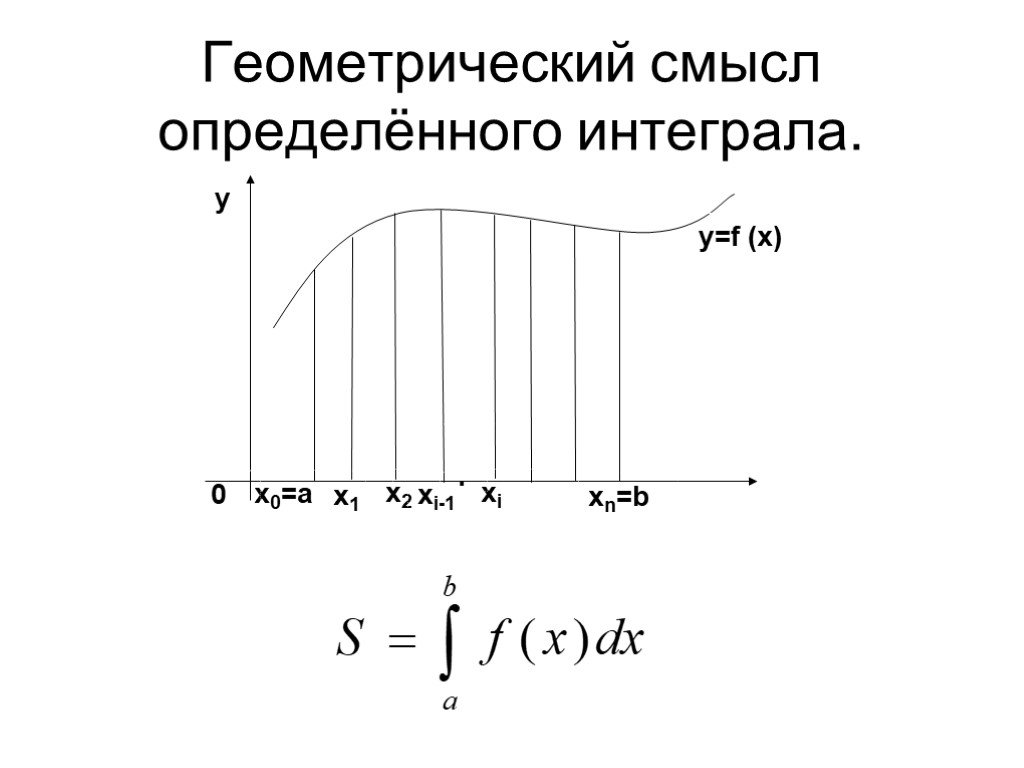

Замечание: Когда функция y=f(x) является неположительной из отрезка [a; b], тогда получаем, что площадь криволинейной трапеции вычисляется, исходя из формулы S(G)=-∫abf(x)dx.

Пример 1

Вычислить площадь фигуры, которая ограничена заданными линиями вида y=2·ex3, y=0, x=-2, x=3.

Решение

Для того, чтобы решить, необходимо для начал построить фигуру на плоскости, где имеется прямая y=0, совпадающая с Ох, с прямыми  вида x = -2 и x = 3, параллельными оси оу, где кривая y=2·ex3 строится при помощи геометрических преобразований графика функции y=ex. Построим график.

Отсюда видно, что необходимо найти площадь криволинейной трапеции. Вспоминая геометрический смысл интеграла, получаем, что искомая площадь и будет выражена определенным интегралом, который необходимо разрешить. Значит, необходимо применить формулу S(G)=∫-232·ex3dx. Такой неопределенный интеграл вычисляется, исходя из формулы Ньютона-Лейбница

S(G)=∫-232·ex3dx=6·ex3-23=6·e33-6·e-23=6·e-e-23

Ответ: S(G)=6·e-e-23

Замечание: Для нахождения площади криволинейной трапеции не всегда можно построить фигуру. Тогда решение выполняется следующим образом. При известной функции f(x) неотрицательной или неположительной на отрезке  [a; b], применяется формула вида SG=∫abf(x)dx или SG=-∫abf(x)dx.

Пример 2

Произвести вычисление площади, ограниченной линиями вида y=13(x2+2x-8), y=0, x=-2, x=4.

Решение

Для построения этой фигуры получим, что у=0 совпадает с Ох, а х=-2 и х=4 являются параллельными Оу. График функции y=13(x2+2x-8)=13(x+1)2-3 — это парабола с координатами точки (-1; 3), являющейся ее вершиной с направленными вверх ветвями. Чтобы найти точки пересечения параболы с Ох, необходимо вычислить:

13(x2+2x-8)=0⇔x2+2x-8=0D=22-4·1·(-8)=36×1=-2+362=2, x2=-2-362=-4

Значит, парабола пересекает ох в точках (4;0) и (2;0). Отсюда получим, что фигура, обозначенная как G, получит вид, изображенный на рисунке ниже.

Данная фигура не является криволинейной трапецией, потому как функция вида y=13(x2+2x-8) изменяет знак на промежутке [-2; 4]. Фигура G может быть представлена в виде объединений двух криволинейных трапеций G=G1∪G2, исходя из свойства аддитивности площади, имеем, что S(G)=S(G1)+S(G2).

Рассмотрим график, приведенный ниже.

Отрезок [-2; 4] считается неотрицательной областью параболы, тогда отсюда получаем, что площадь будет иметь вид SG2=∫2413(x2+2x-8)dx. Отрезок [-2; 2] неположительный для функции вида y=13(x2+2x-8), значит, исходя из геометрического смысла определенного интеграла, получим, что S(G1)=-∫-2213(x2+2x-8)dx. Необходимо произвести вычисления по формуле Ньютона-Лейбница. Тогда определенный интеграл примет вид:

S(G)=S(G1)+S(G2)=-∫-2213(x2+2x-8)dx+∫2413(x2+2x-8)dx==-13×33+x2-8x-22+13×33+x2-8×24==-13233+22-8·2—233+(-2)2-8·(-2)++13433+43-8·4-233+22-8·2==-1383-12+83-20+13643-16-83+12=1249

Стоит отметить, что нахождение площади не верно по принципу S(G)=∫-2413(x2+2x-8)dx=13×33+x2-8x-24==13433+43-8·4—233+-22-8·-2=13643-16+83-20=-4

Так как полученное число является отрицательным и представляет собой разность S(G2)-S(G1).

Ответ: S(G)=S(G1)+S(G2)=1249

Если фигуры ограничены линиями вида y=c, y= d, x=0 и x=g(y), а функция равна x=g(y), причем непрерывна и имеет неменяющийся знак на промежутке [c; d], то их называют криволинейными тарпециями.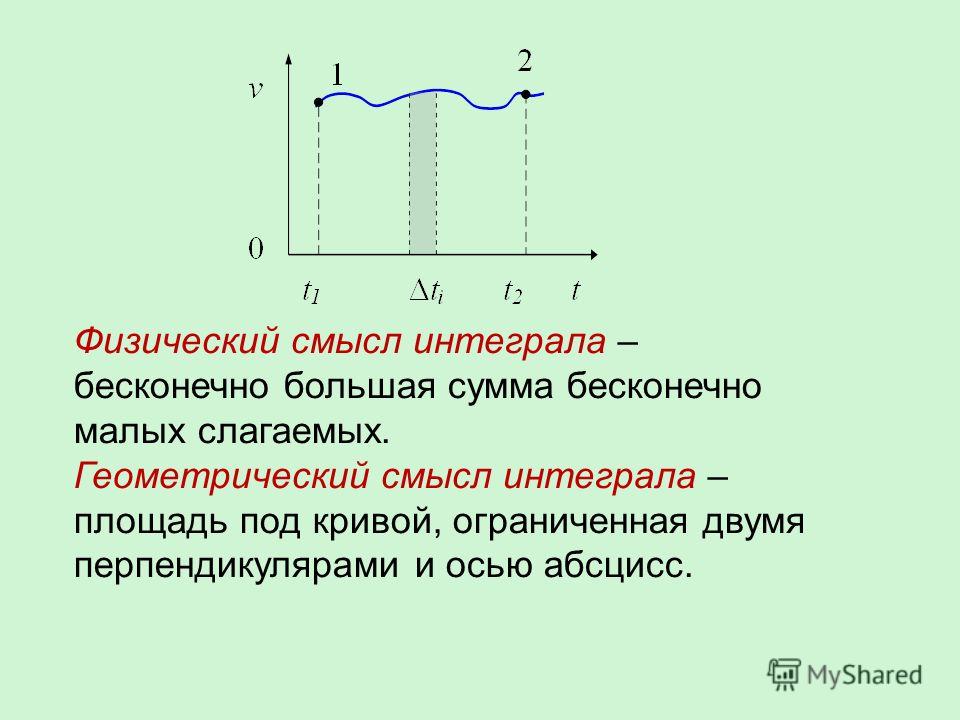 Рассмотрим на рисунке, приведенном ниже.

Геометрический смысл определенного интеграла

Определение 2

Геометрический смысл определенного интеграла ∫cdg(y)dy заключается в том, что его значением является площадь криволинейной трапеции для непрерывной и неотрицательной функции вида x=g(y), расположенной на интервале [c;d].

Справедливо считать, что S(G)=-∫cdg(y)dy имеет место быть для непрерывной и неположительной функции x=g(x), расположенном на отрезке  [c;d].

Пример 3

Произвести вычисление фигуры, которая ограничена осью ординат и линиями x=4ln yy+3, y=1, y=4.

Решение

Построение графика x=4ln yy+3 не является простым. Поэтому необходимо решить без чертежа. Вспомним, что функция определена для всех положительных значений y. Рассмотрим значения функции, имеющиеся на отрезке [1; 4]. По свойствам элементарных функций знаем, что логарифмическая функция возрастает на всей области определения. Тогда не отрезке [1; 4] является неотрицательной.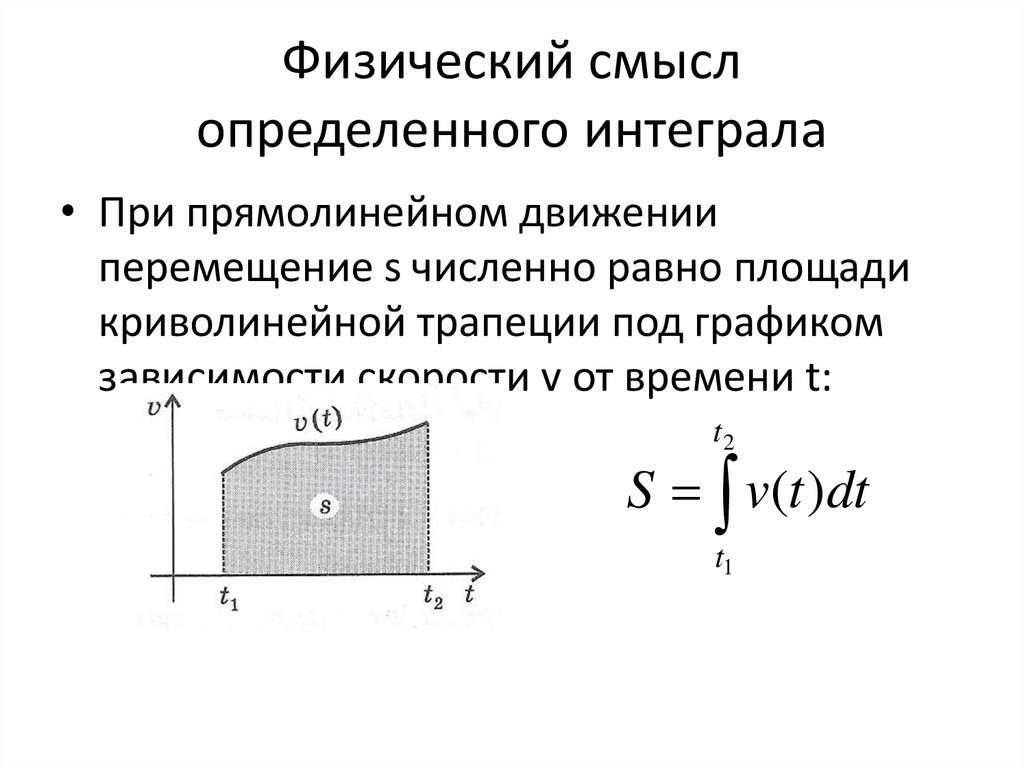

Значит имеем, что ln y≥0.  Имеющееся выражение ln yy, определенное на том же отрезке, неотрицательно. Можно сделать вывод, что функция x=4ln yy+3 является положительной на интервале, равном [1; 4]. Получаем, что фигура на этом интервале является положительной. Тогда ее площадь должна вычисляться по формуле S(G)=∫144ln yy+3dy.

Необходимо произвести вычисление неопределенного интеграла. Для этого необходимо найти первообразную функции x=4ln yy+3 и применить формулу Ньютона-Лейбница. Получаем, что

∫4ln yy+3dy=4∫ln yydy+3∫dy=4∫ln yd(ln y)+3y==4ln2y2+3y+C=2ln2y+3y+C⇒S(G)=∫144ln yy+3dy=2ln2+y+3y14==2ln24+3·4-(2ln21+3·1)=8ln22+9

Рассмотрим чертеж, приведенный ниже.

Ответ: S(G)=8ln22+9

Итоги

В данной статье мы выявили геометрический смысл определенного интеграла и изучили связь с площадью криволинейной трапеции. Отсюда следует, что мы имеем возможность вычислять площадь сложных фигур при помощи вычисления интеграла для криволинейной трапеции. В разделе нахождения площадей и фигур, которые ограниченными линиями y=f(x), x=g(y), данные примеры рассмотрены подробно.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.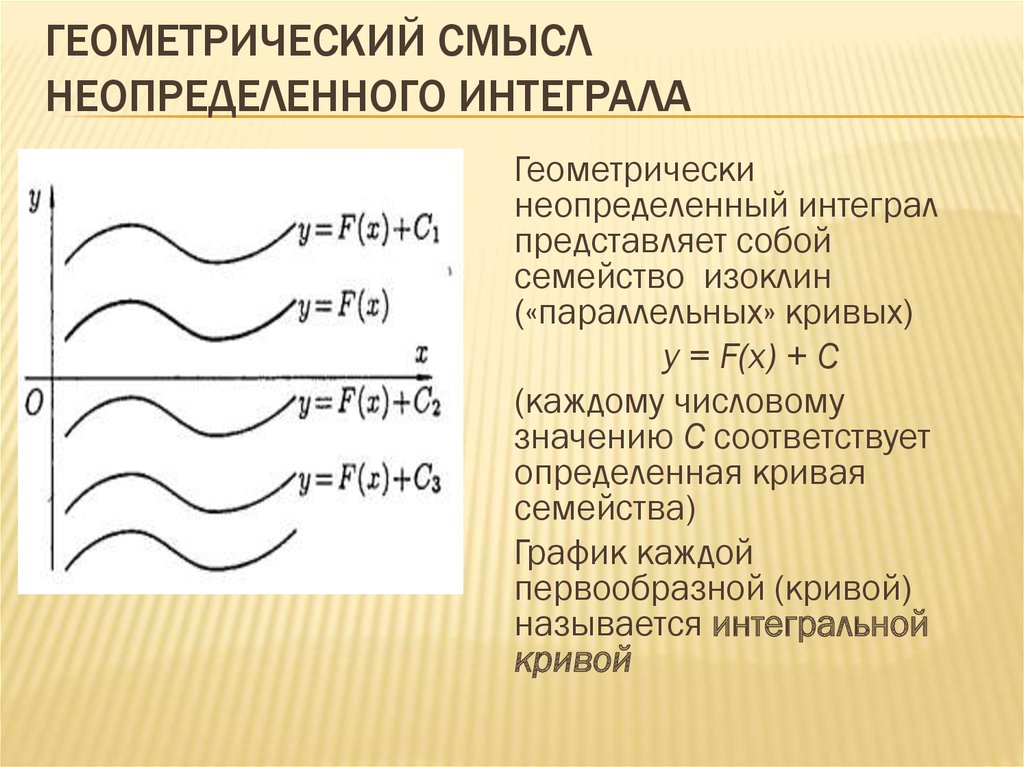

Геометрический смысл определенного интеграла

Геометрия способна помочь решать различные задачи, в том числе относительно вычисления площади, то, что является неотъемлемой частью теории площади. Достаточно легко и просто рассчитать площадь, когда она является легко распознаваемой и с виду представляет собой какую-ту известную геометрическую фигуру правильной формы. Совсем другое, когда речь о вычислении площади неправильных фигур и тогда на помощь можно позвать другие хитрости геометрии, в том числе использовать геометрический смысл определенного интеграла.

Интегральное вычисление позволяет рассчитать в точности площадь сложных фигур и это достаточно просто, если понять что собой представляет геометрический смысл определенного интеграла. Данные расчеты можно рассмотреть наглядно на примере криволинейной трапеции. Связь между интегралом и параметром площадь фигуры определенно существует, остается только научиться распознавать ее и использовать для расчета площади.

Для начала следует понять, что такое криволинейная трапеция, ведь именно от ее площади нужно отталкиваться при вычислении. Криволинейная трапеция это нечто иное как плоская фигура, чьи границы определяются функцией непрерывного неотрицательного типа и двумя прямыми и осью абсцисс. Согласно этому понятию можно суммировать значения функции y = f(x) и таким образом определить площадь фигуры. Значения, которые необходимо суммировать, важно учитывать через бесконечно малые промежутки по оси между точками а и b, которые определяют границы фигуры. Такой подход к расчету площади позволяет разбивать целую фигуру на бесконечное количество прямоугольников, что упрощает расчет всей площади. У каждого прямоугольника есть длина и ширина согласно значению ординаты f(x) и оси Ох через бесконечно малые промежутки.

Формула расчета площади криволинейной трапеции

Геометрический смысл определенного интеграла определение

Геометрический смысл определенного интеграла в ином понимании это площадь криволинейной трапеции для неотрицательной и непрерывной функции, которая расположена между двумя интервалами.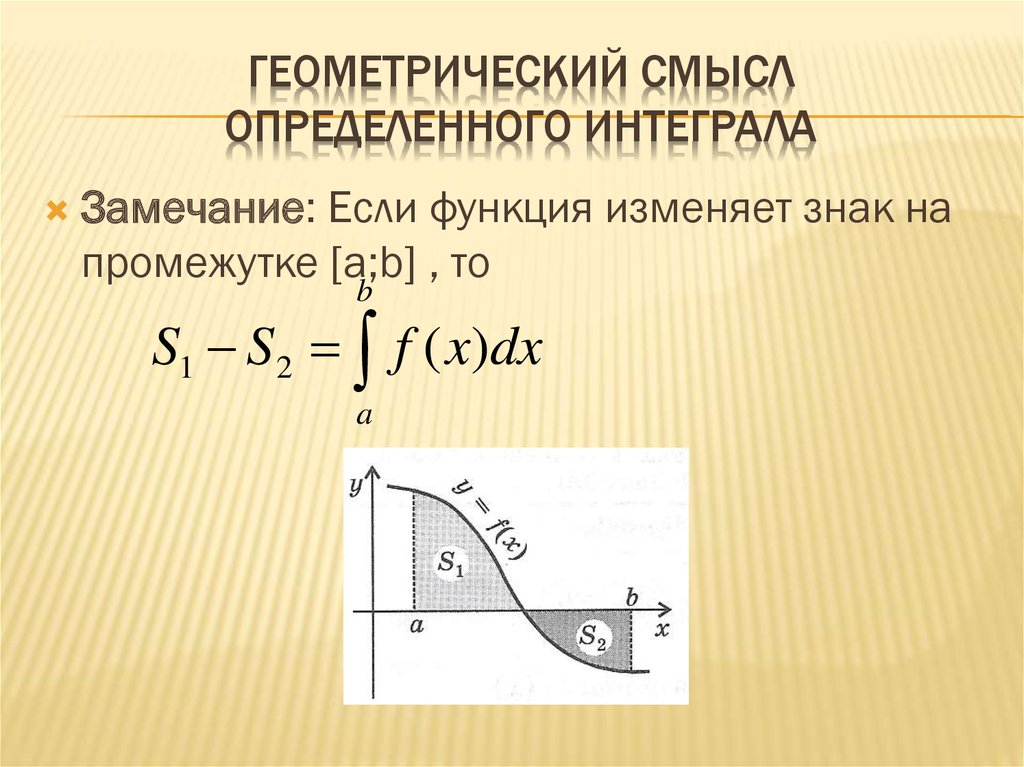 Так как криволинейную трапеции можно воспринимать как квадрируемую фигуру, то и подобный тип расчета площади является актуальным. Для того чтобы определенный интеграл мог существовать, очень важно, чтобы соблюдалось условие непрерывности функции.

Существует возможность определить, если заданная функция имеет определенный интеграл, но согласно общепринятой теореме в первую очередь рассматривается интегрируемость непрерывных функций. Изучение геометрического смысла определенного интеграла, как правило, всегда изучается в сочетание с определением площади для фигуры под названием криволинейная трапеция. Практическая польза данного понятия сводится к возможности расчета площади сложных фигур. Данные правила расчета актуальны для фигур с площадью в рамках линий x=g(y) и y=f(x).

Все очень просто, достаточно вычислить интеграл и площадь сложной фигуры станет известной. Любую фигуру созданную из несколько линий по типу y = f(x), x = a, y = 0, x = b может вычисляться таким образом. Расчет возможен при условии, что функция не является положительной на отрезке между а и b, только принцип расчета частично отличается.

Обобщая вышесказанное можно заявить, что каждая сложная фигура является по факту криволинейной трапецией, а это значит, все вышеперечисленные расчеты актуальны для них. Успешный расчет площади сложных фигур возможен, если начинать с расчета более простых примеров и постепенно совершенствовать свои навыки. Согласно всему вышесказанному становится понятно, что геометрический смысл определенного интеграла позволяет решать одну из сложных задач геометрии – вычисление площади сложных фигур. Это становится возможным за счет применения интеграла, то, что одновременно и упрощает и усложняет задачу. В мире математики все понятия между собой тесно связаны и поэтому в обучении не должно быть пробелов, если вы стремитесь к определенным успехам.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

{b} f(x) dx = F(b) — F(a)\]

В приведенной выше формуле a и b являются пределами, d/dx(F(x)) = f(x).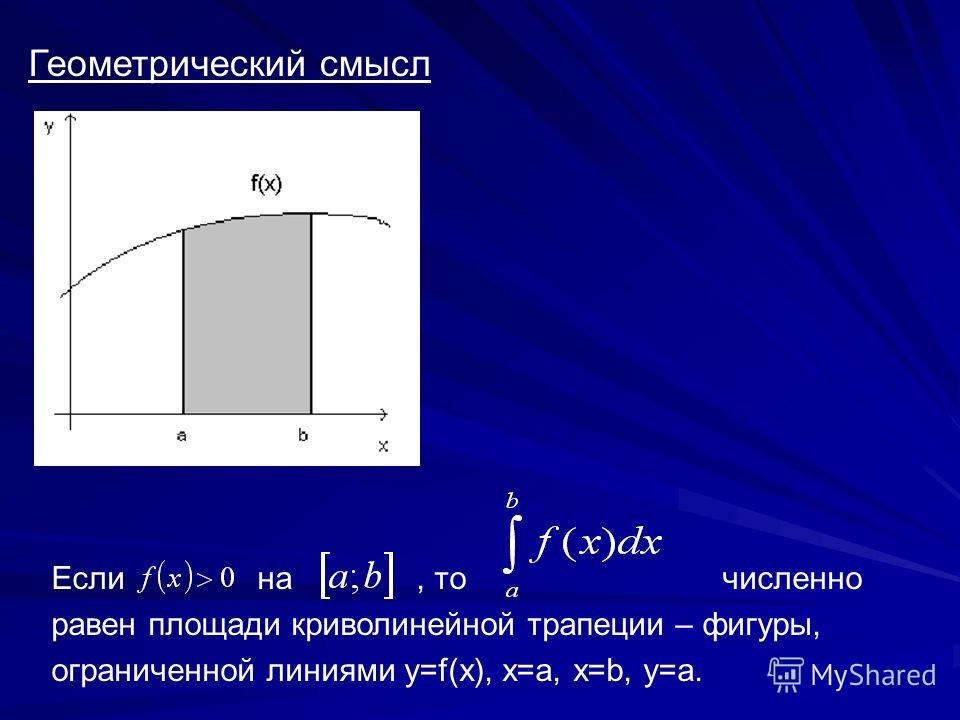

Существуют некоторые различия между определенным интегралом и неопределенным интегралом, давайте обсудим их:

Основу определенного интеграла составляет неопределенный интеграл.

Неопределенный интеграл определяет расчет неопределенной площади, тогда как площадь заданного предела рассчитывается с помощью определенного интеграла.

(изображение скоро будет загружено) 9{m} x dx\] = [(n — 1)(n — 3)(n — 5)….. 1 или 2][(m — 1)(m — 3)….1 или 2]. K/(m + n)(m + n — 2) …1 или 2),

Учитывая, что если m и n четны, то K = π/2

10. Правило Лейбница

Если g непрерывна на [a,b] и f1(x) и f2(x) — две дифференцируемые функции, значения которых лежат в [a,b], то d/dx ∫f2(x) f1(x) g( t) dt = g(f2(x)) f2′(x) — g(f1(x)) f1′(x).

Измерение определенного интеграла

Лучший способ найти определенный интеграл с помощью геометрической интерпретации — найти площадь, ограниченную осью X и кривой.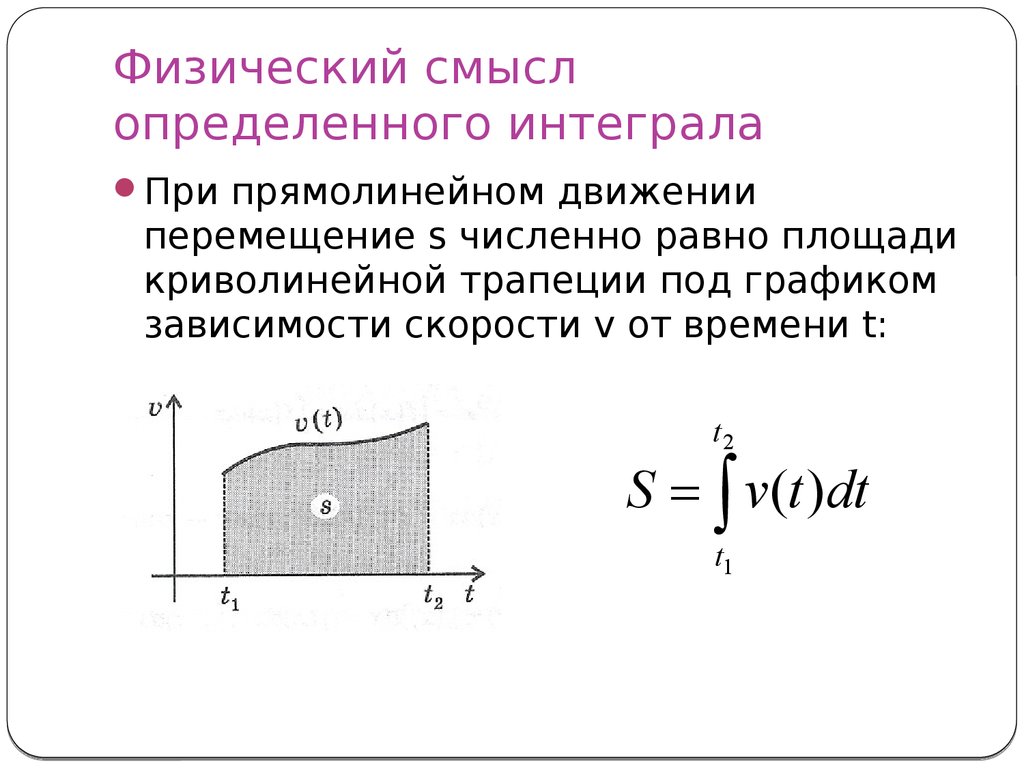 Определенный интеграл представляет собой сумму высоты функции и произведения длины интервалов, при этом высота интегрируется с интервалом, в который входит формула площади прямоугольника. 9{1}\] dx / √[1 + x ⁴ ] ≤ 1

Следовательно, [ 1 / √2, 1] — наименьший интервал, такой что I ∈ [ 1 / √2, 1].

линейная алгебра — Каков геометрический смысл этого интеграла?

спросил 8 лет, 4 месяца назад

Изменено 8 лет, 4 месяца назад

Просмотрено 776 раз 92 (mx) \ dx= \frac{2 m \pi+ \sin(2 m \pi)}{4 m} = \frac{\pi}{2}$$

Теперь моя книга просит меня интерпретировать результат геометрически с использованием таких терминов, как «точечный продукт» или «векторное пространство». Мне любопытно, каков ответ, но, к сожалению, мои познания в линейной алгебре весьма примитивны, и я не нашел никакого геометрического соотношения.

• линейная алгебра
• интегрирование

$\endgroup$

2 9\pi f(x)g(x)\,\mathrm{d}x.$$

Факт: $\varphi$ — скалярное произведение на $E$.

Чтобы доказать этот факт, нужно показать, что:

• $\varphi$ симметрична, т.е. для всех $f,g\in E$ $\varphi(f,g)=\varphi(g,f )$. Это очевидно.
• $\varphi$ положительно полуопределенно, т. е. для всех $f\in E$ $\varphi(f,f)\geq0$. Это тоже очевидно.
• $\varphi$ положительно определена, т. е. если $f\in E$ таково, что $\varphi(f,f)=0$, то $f=0$. Это легко доказать (вам должен использовать непрерывность $f$).

Итак, $\varphi$ — скалярное произведение на $E$.

Теперь для $n\in\mathbb{N}$ определим функцию $c_n$ на $[0,\pi]$ следующим образом: $$\forall x\in[0,\pi],\ c_n(x)=\cos(nx).$$ Ясно, что функции $c_n$ принадлежат $E$.

Вы показали следующее: $$\forall m,n\in\mathbb{N},\ \varphi(c_n,c_m)=\begin{cases}0&\text{if $m\neq n$}\\\pi/2&\text{ if $m=n\neq0$}\\\pi&\text{if $m=n=0$. }\end{cases}$$

Таким образом, ваш результат можно интерпретировать как:

Семейство $(c_n)_n$ является ортогональным семейством векторов $E$ (относительно скалярного произведения $\varphi$).

$\endgroup$

1

$\begingroup$

Определить последовательность функций $f_n(x)=\cos(nx)$.

Давайте придерживаться неотрицательных целых чисел, потому что $f_n(x)=f_{-n}(x)$.

Также задайте последовательность векторов с бесконечным числом компонентов: 92=π$. На самом деле, абстрактно $f_n$ — это векторов, а интеграл их произведений — это скалярное произведение .

$\endgroup$

$\begingroup$

Предположим, у вас есть пространство функций, скажем, например, $\mathcal(\mathbb{R}, \mathbb{R})$.