Первообразная. Геометрический смысл первообразной — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Первообразная. Геометрический смысл первообразной
1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ
ФУНКЦИИ
3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ
ПЕРВООБРАЗНЫХ
4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
2. 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ
Под дифференцированием функции f (х) мыпонимаем нахождение ее производной f ′(х).

Нахождение функции f (х) по заданной ее
производной f ′(х) называют операцией
интегрирования.
Таким образом, операция интегрирования
обратна операции дифференцирования.
Следовательно, операция интегрирования
состоит в том, что по заданной производной
f ′(х) находят (восстанавливают) функцию f (х).
Например, пусть f ′(х) = 4х3.
Следует найти f (х). Опираясь на правило
дифференцирования, нетрудно увидеть, что
f (х)=х4.
Действительно, (х4)’ = 4×3.
f (х) находится неоднозначно, ведь в качестве f (х)
могут быть использованы и такие функции, как
f (х) = х4 + 3,
f (х)= х4 — 6,
и др., так как производная каждой из данных
функций равна 4х3. Все эти функции отличаются
друг от друга только постоянным слагаемым.
Общее решение задачи можно записать в виде
f (х)= х4 +С,
где С — произвольное действительное число.
Любую из найденных функций f (х) называют
первообразной для функции f ‘(х) = 4х3.
Определение.
 Функция F называется
Функция F называетсяпервообразной для функции f на заданном
промежутке, если для всех х из этого промежутка,
если F ′(х)=f(x).
Например, функция F(x)=x2 есть первообразная
для функции f(x)=2x на промежутке (-∞,+∞), так
как для всех действительных х справедливо
равенство F ′(х)=(х2)′=2х
Множество всех первообразных для функции f(x)
можно представить в виде F(x)+С, где С – любое
действительное число.
6. Упражнение с решением
Доказать, что функция F (х) есть первообразнаядля функции f (х) на заданном промежутке, если
F (х)=3х4, f (х)=12х3, (-∞,+∞).
Решение. Так как F (x) = 3х4, то
F ′(х)= (3х4)’= 12х3 = f(x) для всех х,
что и требовалось доказать.
7. 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ
Теорема. Если функция F есть первообразная дляфункции f на промежутке X, то при любой
постоянной С функция F(x)+С также является
первообразной для функции f на промежутке X.
Любая первообразная функции f на промежутке X
может быть записана в виде F (х) + С.

Какую бы постоянную в этой формуле ни подставить
вместо С, получится первообразная для функции f .
Выражение F(x)+С называют общим видом
первообразных для функции f.
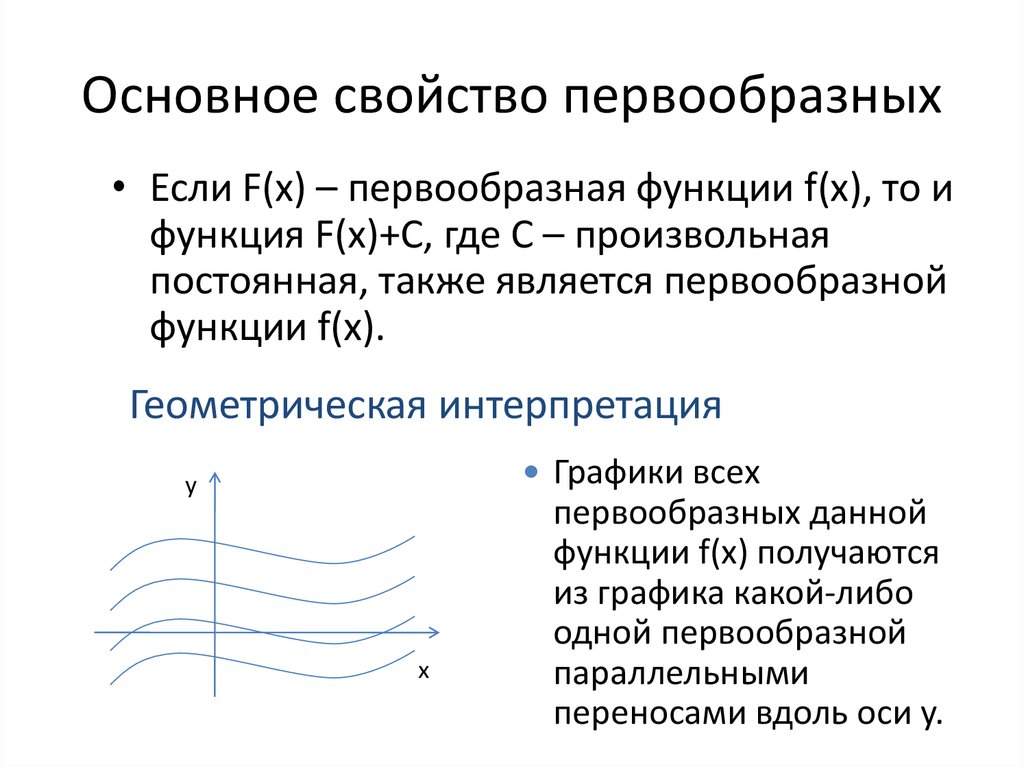
Геометрически основное свойство первообразных
можно интерпретировать так: графики всех
первообразных данной функции f (х) получаются из
любого из них путем параллельного переноса вдоль
оси Оу
9. Таблица первообразных для некоторых функций:
11. Упражнения с решениями
12. 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ
1. Если F есть первообразная для f ,a G — первообразная для g,
то F+G есть первообразная для f+g,
т. е.
(F + G)’ = f + g.
2. Если F есть первообразная для f,
a k — постоянная,
то kF есть первообразная для kf,
т. е. (kF)’ = kf.
16. Например y=sin(3x-4)
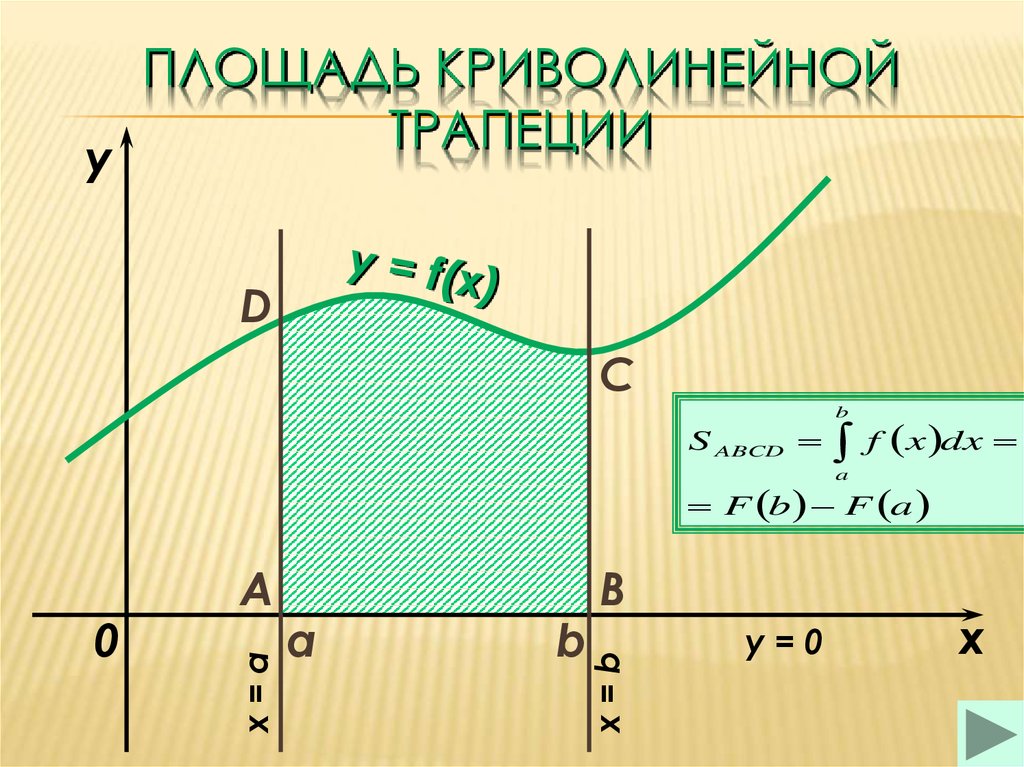
17. 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ
Криволинейной трапецией называется фигура,ограниченная графиком неотрицательной и
непрерывной на отрезке [a; b] функции f, осью
Ох и прямыми х = а и х = b.

Теорема. Пусть f – непрерывная и
неотрицательная на отрезке [a; b] функция,
а
S
–
площадь
соответствующей
криволинейной трапеции . Если F есть
первообразная для f па интервале,
содержащем отрезок [a; b] , то
S = F(b)— F (а).
19. упражнения с решениями
Вычислить площадь фигуры, ограниченной линиями:у = 2х — х2 и у = 0.
Решение. Для функции у = 2х — х2
первообразная есть F(x) = x2 –1/3 х3.
Найдем точки пересечения кривой 2х — х2 с
осью абсцисс: 2х — х2 = 0, х = 0, х = 2,
т. е. (0; 0) и (2; 0).
Значит, а = 0, b = 2.
Искомую площадь находим по формуле:
S = F(b)-F(a)=
=F (2)-F(0) = 4 – 8/3 – 0 + 0=4/3
English Русский Правила
3. Первообразная и неопределенный интеграл.
Первообразная:
Функция F(x) называется первообразной для функции f (x) на данном промежутке, если для любого х из данного промежутка F'(x)= f (x).
Основное свойство первообразных:
Если F(x) – первообразная функции f(x), то и функция F(x)+ C , где C –произвольная постоянная, также является
первообразной функции f(x) (т.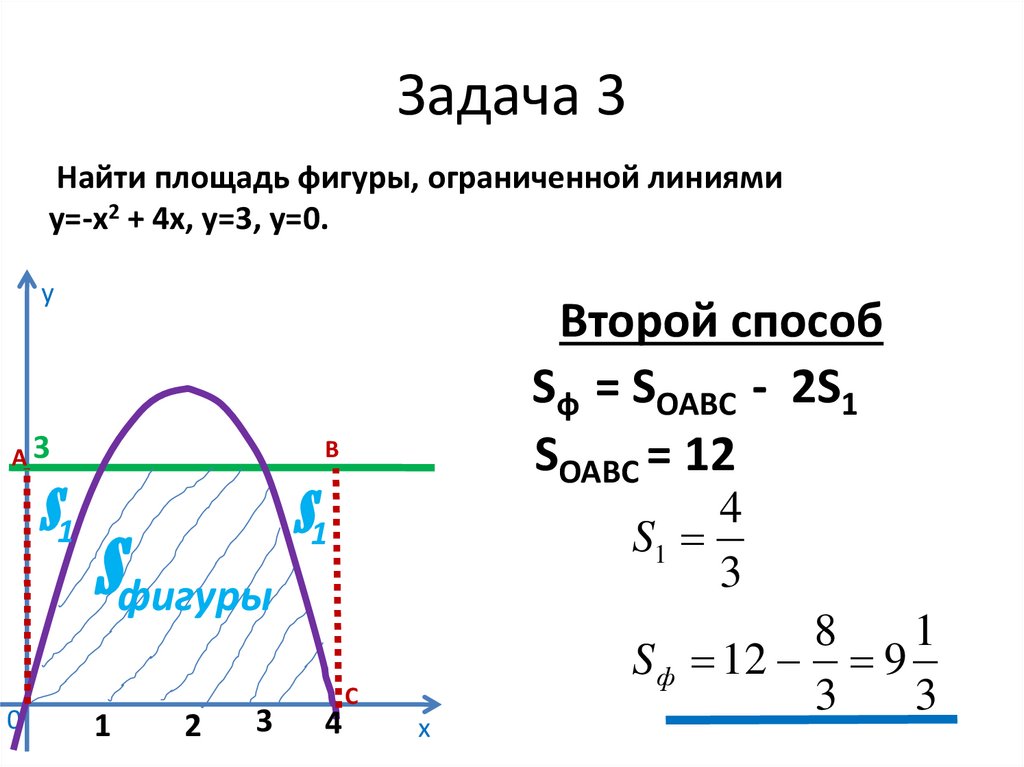 е. все
первообразные функции f(x) записываются
в виде F(x) + С ).
е. все
первообразные функции f(x) записываются
в виде F(x) + С ).
Геометрическая интерпретация:
Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.
Первообразная — это величина, обратная производной. Т.е. если мы знаем, что , то для первообразной будет . Еще первообразная связана с определенным интегралами формулой Ньютона-Лейбница. Т.е. по сути первообразная есть интеграл, геометрический смысл которого — площадь под кривой.
Производная от функции скорости есть ускорение (быстрота изменеия скорости), а первообразная от функции скорости характеризует пройденное расстояние при данной скорости.
Правила нахождения первообразных:
Пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x). Тогда:
F( x ) ± G( x ) – первообразная для f(x) ± g(x);
аF( x ) – первообразная для а f(x);
– первообразная для а f( kx + b ).

Примеры.
1. Выяснить, является ли функция первообразной для функции .
Решение: , т.е. F'(x) = f(x), следовательно,
Неопределенный интеграл:
Неопределенный интеграл данного выражения или данной функции называется наиболее общий вид его первообразной функции. Обозначается он . Постоянное слагаемое подразумевается включенным в это обозначение. Слово «неопределенный» подчеркивает, что в общее выражение первообразной функции входит постоянное слагаемое, которое можно взять по произволу.
Выражение называется подинтегральным выражением, а — подинтегральной функцией, переменная x – переменная интегрирования.
Более точное определение —
Пример:
;
;
Геометрический смысл неопределенного интеграла следует из геометрического смысла производной: уравнение y=F(x) +С на плоскости ХОY определяет семейство кривых (называемых интегральными кривыми), для которых в точке с абсциссой х угловой коэффициент касательных равен )
Физический смысл неопределенного
интеграла: т.
Свойства неопределенного интеграла:
Основные методы интегрирования:
Метод внедрения нового аргумента:
Если , то , где — непрерывно дифференцируемая функция
Метод разложения:
Если , то
Метод подстановки:
Если — непрерывна, то полагая , где непрерывна вместе со своей производной , получим
Метод интегрирования по частям:
Если u и v – некоторые дифференцируемые функции от x, то
Задача.
Билет №7
1. Теорема о среднем для определённого интеграла.
Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что .
Док-во.
 Тогда
.
Число заключено между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом,
существует точка
,
такая что
.
Тогда
.
Число заключено между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом,
существует точка
,
такая что
.Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
мягкий вопрос — Как «точка» в геометрии не определена? И что такое «математическое определение»?
Что касается вашего определения «точки» в геометрии, достаточно того, что немного O сказал в комментарии:
Вы заменили только один неопределенный термин другими неопределенными терминами.
Чтобы быть более точным, если вы определяете «точку» с точки зрения «местоположения», я бы просто попросил вас определить «местоположение» .
Это не относится к другим вашим вопросам.
Если это не определение, то как мы можем узнать, является ли некоторое утверждение определением или нет?
Неформально мы говорим, что правильное определение — это способ описания чего-то точного, который включает только ранее определенные понятия. Этого достаточно для неформальной математики, но на самом деле существует совершенно точное определение «действительных определений» в логике первого порядка, которое по-разному называют дефиниторным расширением или полным сокращением. Это правило в основном позволяет назвать и позже использовать любой символ-константу, символ-предикат или символ-функцию, которые могут быть однозначно представлены некоторой формулой первого порядка. Например, если вы работаете с арифметикой Пеано первого порядка плюс полная мощность аббревиатуры, вы можете определить:
$even(n) \overset{def}\equiv \exists k\ ( k+k = n )$.
И с этого момента вы можете рассуждать об объектах, которые удовлетворяют уже определенному предикату $even$, и можете доказывать связанные с ним теоремы, такие как:
$\forall n\ ( четное(n \times n) \до четного(n))$.
Достаточно сказать, что такое техническое устройство необходимо на практике, чтобы у нас не было бессмысленного дублирования контента. Конечно, приведенную выше теорему можно было бы записать простым арифметическим предложением без использования $even$, но очевидно, что это было бы намного длиннее и менее информативно.
Каковы характеристики определения в математике?
Вышеизложенное касается технических деталей того, как формально определить «действительное определение» в логике первого порядка и, следовательно, большей части математики (которая основана на теории множеств первого порядка, называемой ZFC). В любом случае, концепция мощности аббревиатуры легко распространяется на другие логические схемы. Но есть и вторая проблема различных видов определений в математике.
Первый вид предполагает определение концепций в рамках существующей структуры. Пример $even$ является одним из примеров этого.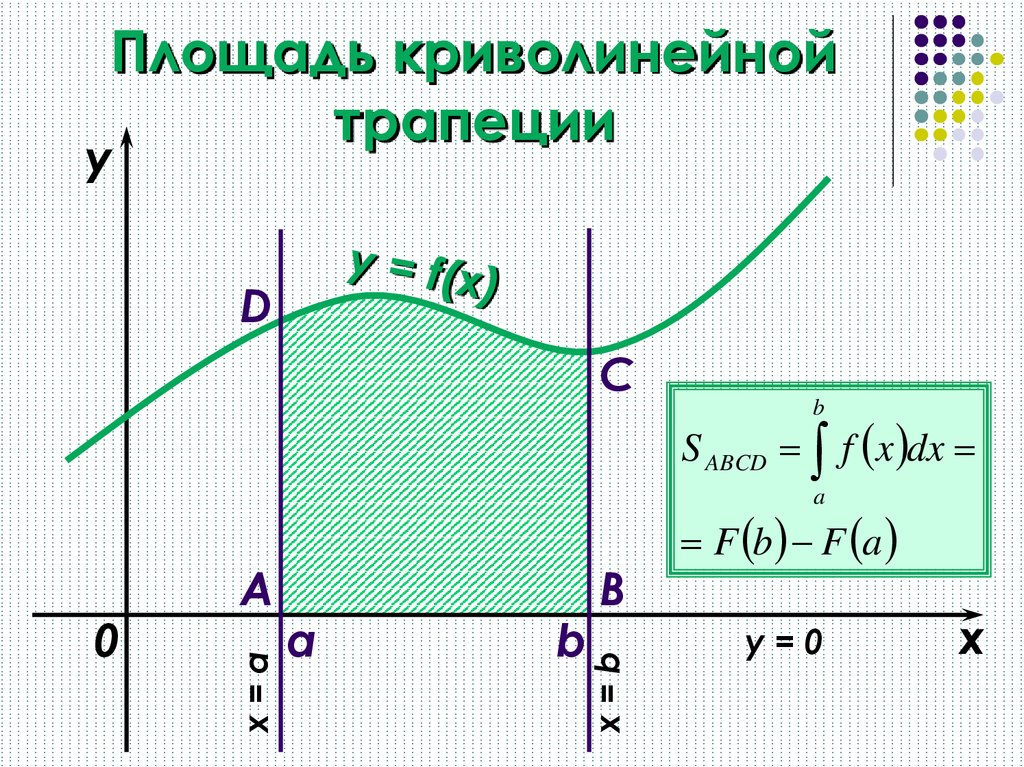 Второй вид предполагает определение всего фреймворка (как единой концепции)! Например, мы можем определить структура будет моделью для арифметики Пеано, если и только если она подчиняется всем
Второй вид предполагает определение всего фреймворка (как единой концепции)! Например, мы можем определить структура будет моделью для арифметики Пеано, если и только если она подчиняется всем
Точно так же в любой обычной аксиоматизации евклидовой геометрии не определяют, что такое точки, а скорее определяют, что структура является евклидовой геометрией тогда и только тогда, когда она состоит из линий и точек (и обычно чисел), которые вместе удовлетворяют определенным аксиомам.
Примитивы
| На этой странице |
|
Обзор ¶
В Houdini примитива относятся к единице геометрии, более низкому уровню, чем объект, но выше точек. Houdini поддерживает несколько различных типов примитивов:
Houdini поддерживает несколько различных типов примитивов:
- ,
- .
Многоугольная грань
Примитивы Packed, примитивы Packed Disk и примитивы Packed Disk Sequence
Упакованные примитивы USD
Полигон суп
Том
Тетраэдр
Поверхности Безье/NURBS
Многоугольник/Кривые Безье/NURBS
Метаболы
Существует также специальный примитив, называемый упакованным примитивом, который представляет собой упрощенную ссылку на геометрию, хранящуюся где-то еще.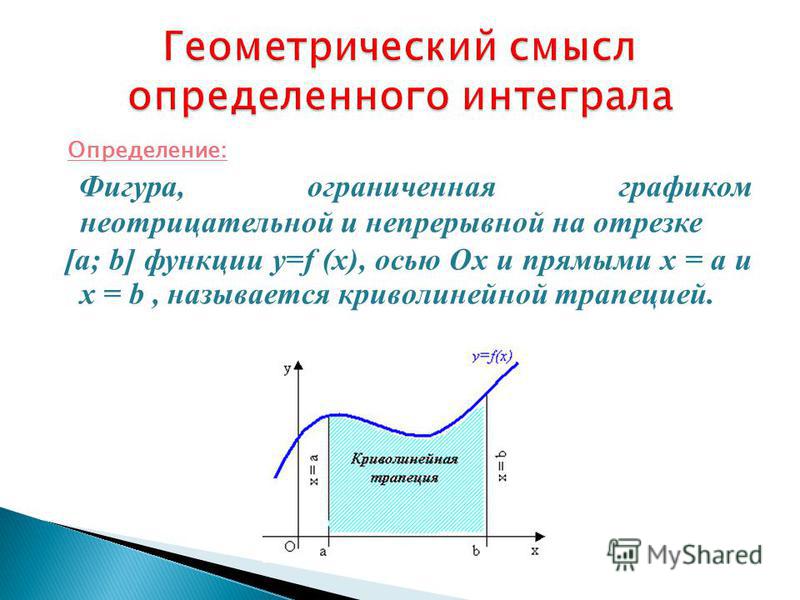 Это очень полезно для копирования/создания экземпляров и работы с тяжелой геометрией. Файлы Alembic представлены в Houdini в виде упакованных примитивов.
Это очень полезно для копирования/создания экземпляров и работы с тяжелой геометрией. Файлы Alembic представлены в Houdini в виде упакованных примитивов.
Существует также несколько типов квадратичных примитивов, которые математически представляют геометрические фигуры, а не многоугольные поверхности. Они могут быть полезны в качестве облегченной геометрии.
Окружность (определяется одной точкой, вращением и радиусом).
Сфера/эллипсоид (определяется одной точкой и радиусами).
Трубка/конус (определяется одной точкой, поворотом, радиусом и длиной).
Окружность, сфера и труба Гудини имеют параметры для выбора того, создают ли они, например, «примитивную сферу» или многоугольную сферу.
Вы можете преобразовать большинство типов геометрии между собой, используя Convert SOP.
Совет
Нажмите MMB на узле в геометрической сети, чтобы увидеть всплывающее окно с информацией о геометрии, проходящей через узел, включая количество/типы примитивов.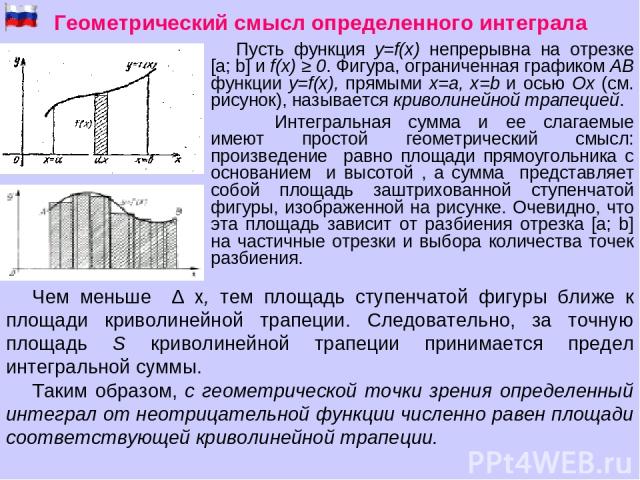
Полигоны и сетки ¶
Многоугольники — это фигуры, состоящие из ряда прямых ребер. Эти ребра определяются серией вершин. Полигоны идеально подходят для работы со сложными топологиями, которые выходят за рамки четырехсторонней сетки и NURBS-поверхностей.
Сетка представляет собой набор полигонов с гарантированным порядком. Это намного эффективнее, чем эквивалентные полигоны, и, в отличие от большинства обычных полигонов, вы можете преобразовать его напрямую в NURBS. Вы также можете использовать узел Преобразовать поверхность, чтобы преобразовать примитивы сетки в обычные многоугольники, если вам нужно красивое расположение полигонов в строках и столбцах.
Открыт/закрыт
Замкнутый многоугольник имеет общие первую и последнюю вершины и помечается внутри как «закрытый».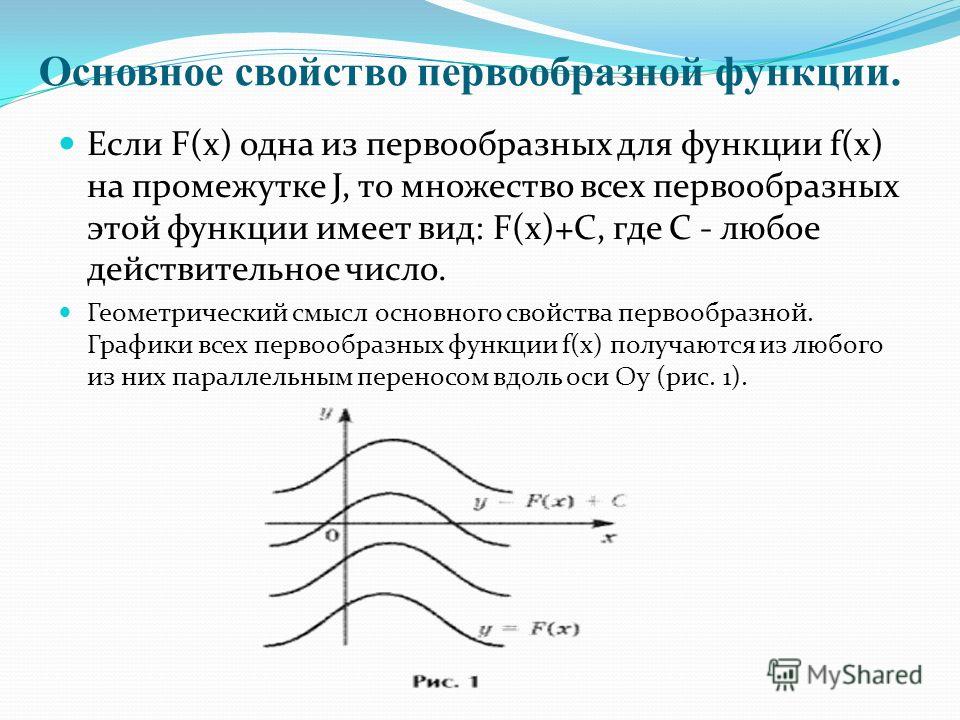 Закрашиваются только замкнутые полигоны.
Закрашиваются только замкнутые полигоны.
Плоский/неплоский
Вершины плоских многоугольников лежат в одной плоскости в трехмерном пространстве. Неплоские многоугольники имеют вершины, которые не все находятся на одной плоскости в трехмерном пространстве.
Выпуклая/вогнутая
Многоугольник выпуклый, если каждая бесконечная прямая в той же плоскости, что и он, пересекает его не более двух раз. Вогнутые многоугольники имеют более сложную форму с точками «вставки».
Используйте инструменты на вкладке полки Create для создания поверхностей и используйте Всплывающее меню примитива типа на панели инструментов управления операциями, чтобы установить новую поверхность, которая будет создана из полигонов.
Используйте инструменты на вкладке полки Polygon для редактирования и изменения формы граней и многоугольных поверхностей.
Упакованные примитивы ¶
См. упакованные примитивы.
упакованные примитивы.
Полигон суп ¶
Суп полигонов — это примитив, который хранит полигоны, используя компактное представление в памяти, и очень эффективно хранит грани, атрибуты примитивов которых совпадают. Его представление в памяти позволяет разделить почти всю память большого супа между узлами, работающими с супом, до тех пор, пока топология не изменится (где обычные полигоны требуют, чтобы каждый узел сохранял копию каждого полигона). Совместное использование также делает кэши памяти более эффективными, что означает, что многие операции моделирования и рендеринга будут выполняться быстрее, а также использовать меньше памяти.
Чем больше полигонов в супе, тем больше преимуществ перед обычными полигонами. Для простой геометрии с небольшим количеством полигонов накладные расходы на управление супами могут сделать их медленнее, чем обычные полигоны, хотя супы всегда будут использовать меньше памяти.
Вы можете преобразовать геометрию в полигональный суп, используя узел Polysoup.
Загрузка супа из файла может быть намного быстрее, чем загрузка обычных полигонов (как для Mantra, так и для Houdini). Вы можете загружать файлы Alembic как полигональные супы. Создание фигур сетки, сферы, трубы и тора происходит быстрее, если вы используете опцию для создания супов.
Наряду с узлами формы вы можете создавать супы с помощью Convert, Convert Meta, Convert VDB, Convert Volume, Iso Offset, Iso Surface, Point Cloud Iso, Subdivide и Tetra Surface, поддерживающих создание полигональных супов. Вы можете использовать узел Subdivide для разделения супов, если вы выберете один из методов OpenSubdiv .
Многие (но не все) узлы геометрии могут «нативно» работать с полисупами. Вы получаете преимущества совместного использования супа с операциями, которые изменяют атрибуты, такие как редактирование, преобразование, скульптура, перенос атрибута на точки, группировка точек, создание атрибута, обработка атрибутов, копирование атрибутов, вычисление нормалей точек с помощью Facet, точечный UV-проект, рисование , Partition, Point Connectivity и Ray, среди прочих.
Некоторые операции, изменяющие атрибуты вершин или примитивов, могут по-прежнему работать с супами полигонов, но могут иметь несколько иное значение, чем для полигонов. Например, каждый суп — это только один примитив, поэтому полигоны в супе не могут иметь свои собственные атрибуты примитивов. Кроме того, у полигональных супов часто не так много вершин, как у полигональных примитивов (они объединяют одинаковые вершины). Это означает, например, что UV Project не может правильно вычислить координаты текстуры вершины, а вершинная нормаль не поддерживается.
Большинство операций, изменяющих топологию полигонов, таких как Poly Extrude и Poly Split, не поддерживают супы, но некоторые поддерживают. Например, параметр Convex polygons на узле Divide будет выпуклым полигональным супом и позволит избежать добавления каких-либо дополнительных вершин, позволяя совместно использовать память для атрибутов вершин.
Для узлов, которые не поддерживают супы, вы можете использовать Convert для преобразования супа в обычные полигоны, а затем преобразовать полигоны обратно в суп с помощью Polysoup. Однако преимущества полигональных супов обычно перевешиваются стоимостью преобразования, поэтому в большинстве случаев вам следует просто использовать обычные полигоны. (Если вы выполняете этот тип преобразования туда и обратно в HDA, вы должны установить Выгрузить флаг на всех узлах, чьи выходные данные представляют собой полигоны, поэтому кэш SOP не будет удерживать полигоны дольше, чем необходимо.)
Однако преимущества полигональных супов обычно перевешиваются стоимостью преобразования, поэтому в большинстве случаев вам следует просто использовать обычные полигоны. (Если вы выполняете этот тип преобразования туда и обратно в HDA, вы должны установить Выгрузить флаг на всех узлах, чьи выходные данные представляют собой полигоны, поэтому кэш SOP не будет удерживать полигоны дольше, чем необходимо.)
См. ниже, когда использовать полигональные супы, упакованные примитивы или обычные полигоны.
Полигональный суп против упакованных примитивов против обычных полигонов ¶
См. также создание экземпляров с использованием упакованной геометрии и полигональных супов.
Редактирование | Правильные многоугольники поддерживаются всеми операциями в Houdini. Полигональные супы поддерживаются многими, но не всеми операциями в Houdini. Геометрия упакованных примитивов не редактируется и не деформируется . Однако вы можете преобразовать их и установить атрибуты для точек, представляющих упакованную геометрию. |
Использование памяти | Упакованные примитивы загружаются в память только по мере необходимости. Для упакованных примитивов, которые ссылаются на файл на диске, они передаются непосредственно на графическую карту для отображения и в модуль визуализации для визуализации. Текущее использование памяти упакованным примитивом часто может быть нулевым. Полигональные супы имеют гораздо более компактное представление в памяти, чем обычные полигоны. Правильные многоугольники используют больше всего памяти из трех. |
Советы | Для небольших частей геометрии используйте правильные многоугольники, чтобы избежать накладных расходов, связанных с набором полигонов. Если вам нужно использовать какие-либо операции, которые изменяют топологию или иным образом не поддерживают полигональные супы, используйте обычные полигоны на всем протяжении — стоимость преобразования обычно перевешивает любую выгоду от использования супа только для части цепочки узлов. Если у вас есть большая геометрия, которую нужно отредактировать или деформировать, используйте полигональные супы. Если вам нужно только отобразить и преобразовать геометрию, сохраните ее на диске и используйте упакованные примитивы. |
Интерпретация использования памяти ¶
Вы можете увидеть, сколько памяти использует узел, нажав MMB на узле. Появится всплывающее окно с различными способами измерения использования памяти узла:
Память
Общий объем памяти, на который ссылается конкретная деталь. Эта память может быть разделена с другим узлом (например, если вы используете полигональный суп), так что это не обязательно то, сколько памяти вы сэкономите, если удалите этот узел. Это скорее мера того, сколько материала проходит через узел.
Новый
Объем памяти, на который ссылается этот узел, на который не ссылается ни один из его входов. Это указывает, сколько памяти используется этим узлом. Это число не сообщается для узлов без входов (генераторов).
Уникальный
Память, на которую ссылается только этот узел (то есть на которую не ссылаются его входы или выходы). Это указывает, сколько памяти вы бы сэкономили, если бы вы включили флаг «Выгрузить» на этом узле.
Этот дисплей имеет некоторые ограничения:
Память, на которую ссылаются упакованные примитивы, еще не подсчитана из соображений производительности.
Диспетчер кэша SOP и Cache SOP еще неправильно отслеживают использование памяти.
Нажатие MMB в подсети (например, в цифровом активе) показывает только память, используемую самой подсетью, а не использование памяти сетью внутри подсети.
Упакованные примитивы в долларах США ¶
Как и упакованные примитивы Alembic, упакованные примитивы USD хранят сторонние данные (в данном случае геометрию USD) внутри примитива SOP.

Окно просмотра умеет отображать геометрию, закодированную в этих примитивах, но если вы хотите изменить данные внутри, вам сначала нужно распаковать это.
Точки в упакованном примитиве представляют собой примитивы в долларах США, а позиция точки и стандартные атрибуты создания экземпляров точек представляют преобразование каждого примитива. Вы можете изменить их, чтобы перемещать/вращать/масштабировать примитивы, не распаковывая их. (Это обычное дело при работе с симуляторами RBD.)
Используйте Unpack USD SOP для преобразования упакованной геометрии USD в геометрию SOP, чтобы вы могли изменять ее с помощью последующих узлов SOP.
Можно преобразовать геометрию USD в упакованные примитивы SOP или полигоны. Если вы не хотите использовать только SOP, которые работают непосредственно с упакованными примитивами, вам следует выбрать преобразование в полигоны.

Метаболы ¶
Metaballs создают неявную поверхность, вычисляемую вокруг набора точек. Меташары похожи на сферы, центрированные вокруг точек, но когда два меташара помещаются рядом друг с другом, их поверхности плавно сливаются.
Метаболы могут быть полезны для представления клякс или странных поверхностей. Вы также можете изменить способ вычисления поверхности, что может быть полезно для достижения некоторого эффекта:
NURBS и сплайны Безье ¶
NURBS — это аббревиатура от Non-Uniform Rational B-Spline. NURBS — это гладкие кривые и поверхности, определяемые управляющими вершинами (CV).
 См. определение в Википедии
Чтобы получить больше информации. Преимущество NURBS заключается в том, что перемещение CV изменяет форму окружающей кривой/поверхности, сохраняя непрерывность кривой/поверхности. Это позволяет вам «тянуть и тянуть» CV кривой или поверхности NURBS, чтобы создать желаемую форму, не вызывая перегибов или разрывов.
См. определение в Википедии
Чтобы получить больше информации. Преимущество NURBS заключается в том, что перемещение CV изменяет форму окружающей кривой/поверхности, сохраняя непрерывность кривой/поверхности. Это позволяет вам «тянуть и тянуть» CV кривой или поверхности NURBS, чтобы создать желаемую форму, не вызывая перегибов или разрывов.Кривые/поверхности Безье проще, чем NURBS. См. определение в Википедии Чтобы получить больше информации. Кривые Безье допускают разрывы в узлах, что упрощает создание углов, но затрудняет создание гладких непрерывных кривых/поверхностей.
Параметризация ¶
Форма кривой NURBS для заданного набора CV определяется относительным расстоянием между узлами.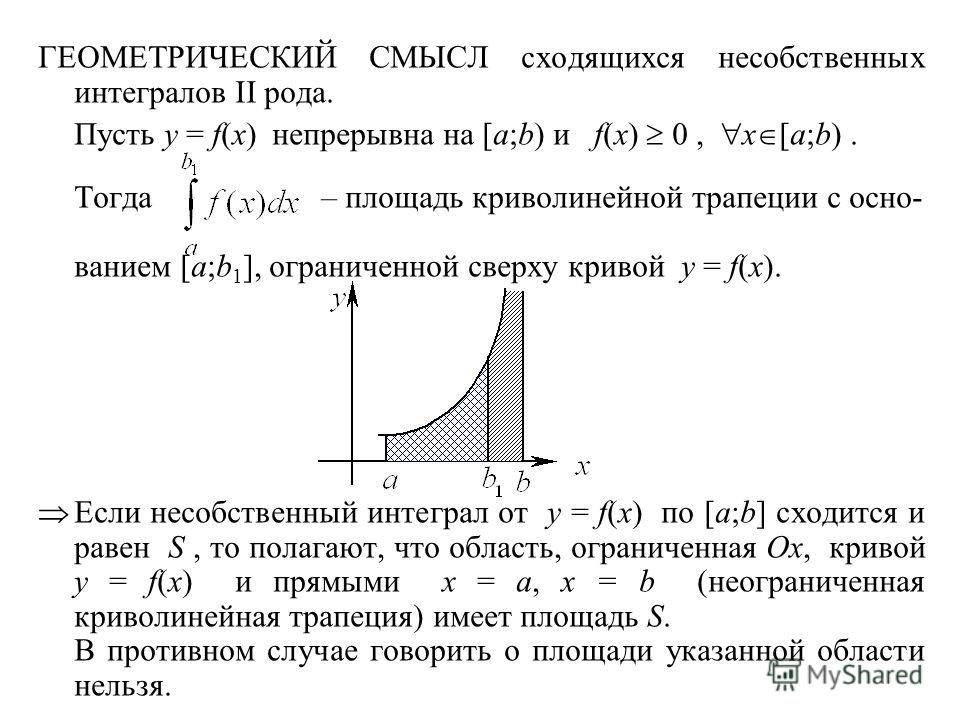 Существует два типа параметризации узла: равномерная и длина хорды .
Существует два типа параметризации узла: равномерная и длина хорды .
В однородной параметризации узлы расположены равномерно.
В параметризации длины хорды расстояния между узлами определяются расстояниями между последовательными CV. Унифицированная параметризация рекомендуется для правильных форм, тогда как длина хорды используется для форм произвольной формы. Третий тип параметризации, называемый «центростремительным», подобен длине хорды и лучше всего подходит для крутых кривых.
Орден/степень ¶
Сплайн-кривые имеют
заказ
, иногда обозначаемый как степени , что на единицу меньше порядка. Степень определяет потенциальную гладкость линии. Ломаная линия имеет степень 1 (или «второй порядок»). Кривая с одной контрольной точкой между узлами имеет степень 2 (она же «третий порядок» или «кубическая»). Знакомая кривая Безье с двумя контрольными точками между узлами имеет степень 3 (она же «четвертый порядок» или «квадратичная»).
Ломаная линия имеет степень 1 (или «второй порядок»). Кривая с одной контрольной точкой между узлами имеет степень 2 (она же «третий порядок» или «кубическая»). Знакомая кривая Безье с двумя контрольными точками между узлами имеет степень 3 (она же «четвертый порядок» или «квадратичная»).
Houdini поддерживает сплайны со степенями от 1 до 10. Для анимации и эффектов вы обычно обнаружите, что сплайны степени 2 (кубические) достаточно гладкие и хорошо себя ведут. Вам редко потребуется использовать другие степени.
Создание острой точки на NURBS-кривой ¶
Иногда требуется создать острый угол на NURBS-кривой. Это можно сделать тремя способами:
Измените вес выбранного CV в диалоговом окне Curve > Parameters в редакторе моделей на что-то большее, например 10 000.
 Это придает CV такую большую «притягательность», что кривая почти полностью проходит через него.
Это придает CV такую большую «притягательность», что кривая почти полностью проходит через него.Если вы перетащите две соседние CV кубической кривой на среднюю CV, она будет выглядеть как точка с острым углом. Это называется повышением Множественности CV. Максимальная множественность CV возникает, когда соседние CV «степени» перекрываются.
Сделать узлы «степень» идентичными. Когда это делается, это называется повышением кратности узла. Вы можете сделать это в разделе Refine, выбрав опцию Subdivision, или в редакторе моделей, выбрав состояние Refine и разделив его средней кнопкой мыши ( MMB ).
Квадратичные примитивные формы ¶
Houdini поддерживает примитивные сферы/эллипсоиды, круги/эллипсы и трубы/конусы.






 См. определение в Википедии
Чтобы получить больше информации. Преимущество NURBS заключается в том, что перемещение CV изменяет форму окружающей кривой/поверхности, сохраняя непрерывность кривой/поверхности. Это позволяет вам «тянуть и тянуть» CV кривой или поверхности NURBS, чтобы создать желаемую форму, не вызывая перегибов или разрывов.
См. определение в Википедии
Чтобы получить больше информации. Преимущество NURBS заключается в том, что перемещение CV изменяет форму окружающей кривой/поверхности, сохраняя непрерывность кривой/поверхности. Это позволяет вам «тянуть и тянуть» CV кривой или поверхности NURBS, чтобы создать желаемую форму, не вызывая перегибов или разрывов.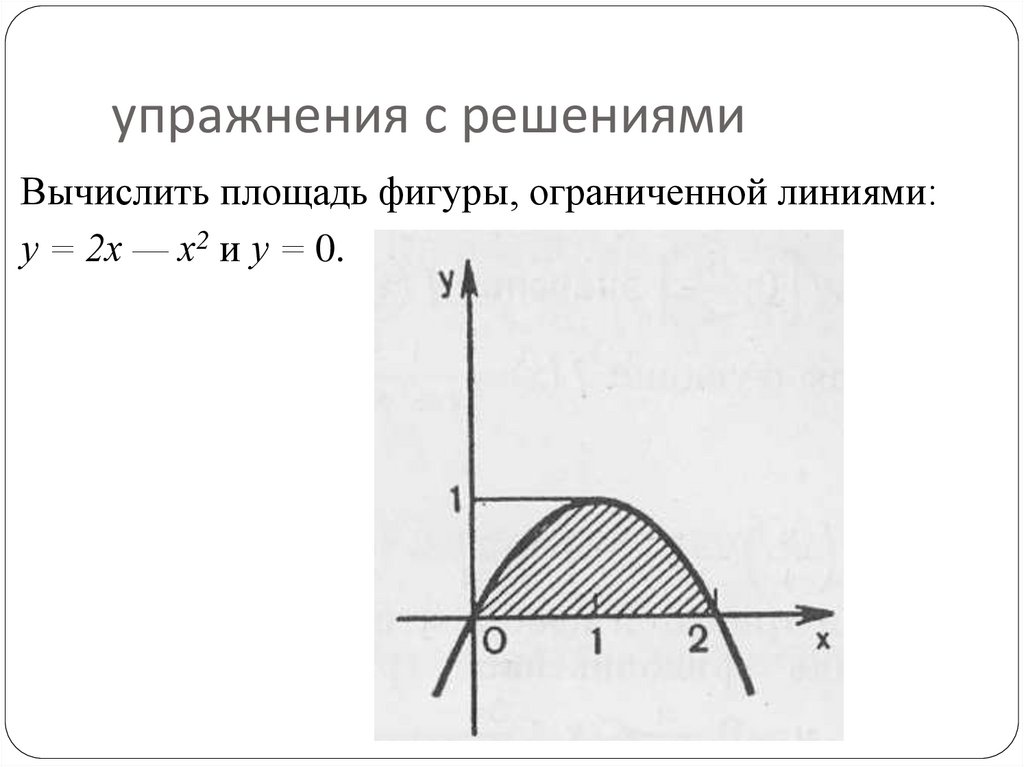 Это придает CV такую большую «притягательность», что кривая почти полностью проходит через него.
Это придает CV такую большую «притягательность», что кривая почти полностью проходит через него.