решение с синусом, косинусом, тангенсом, котангенсом
- Решение неравенств с синусом
- Решение неравенств с косинусом
- Решение неравенств с тангенсом
- Решение неравенств с котангенсом
- Примеры
п.1. Решение неравенств с синусом
Алгоритм решения неравенства \(sinx\gt a\)
Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой \(a\). Провести горизонталь \(y=a\), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение \(sinx=a\). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: \((arcsina+2\pi k;\ \pi-arcsin a+2\pi k)\)
Например:
$$ sin x\gt \frac12 $$ 1. 3. При обходе полученной дуги против часовой стрелки получаем интервал: \((\frac\pi6;\ \frac{5\pi}{6})\). Добавляем к концам интервала полный период. Ответ: \(\left(\frac\pi6;+2\pi k;\ \frac{5\pi}{6}+2\pi k\right)\) |
Алгоритм решения неравенства \(sinx\geq a\) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства \(sinx\lt a\) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью \(y=a\). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).
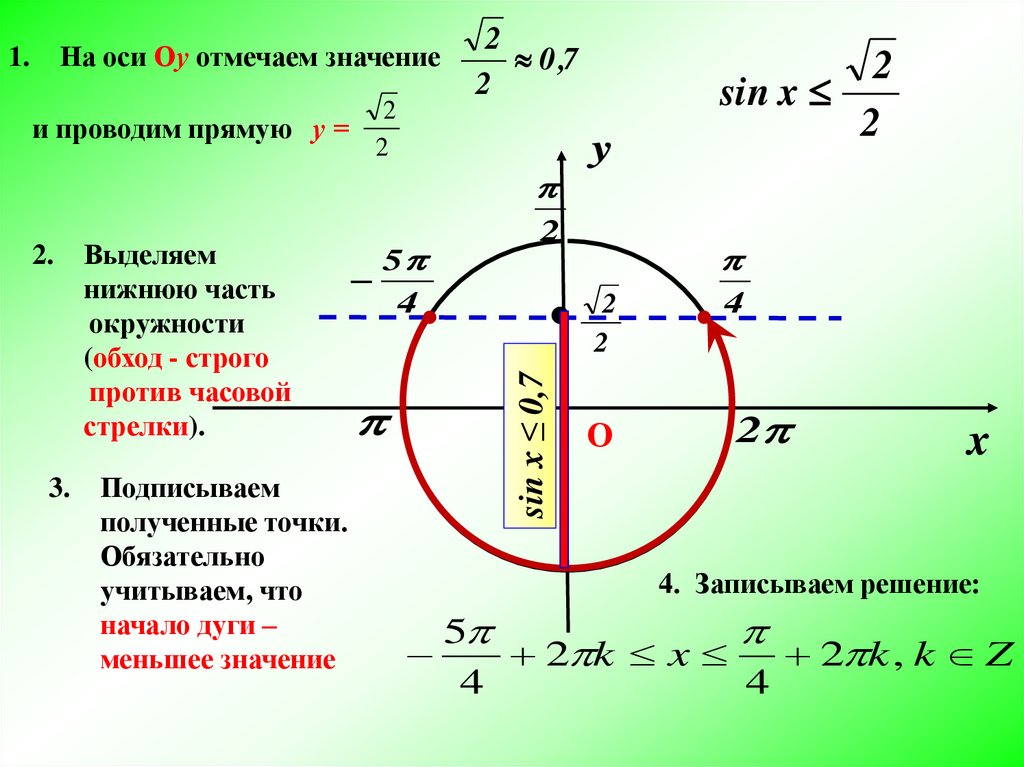
Наконец, в неравенстве \(sinx\leq a\) всё будет то же, что и в \(sinx\lt a\). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
3. При обходе полученной дуги против часовой стрелки получаем отрезок: \(\left[-\frac{3\pi}{4};-\frac{\pi}{4}\right]\). Добавляем к концам отрезка полный период.
Ответ: \(\left[-\frac{3\pi}{4}+2\pi k;-\frac{\pi}{4}+2\pi k\right]\)
п.2. Решение неравенств с косинусом
Алгоритм решения неравенства \(cosx\gt a\)
Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой \(a\). Провести вертикаль \(x=a\), отметить точки её пересечения с окружностью.
Шаг 2. Решить уравнение \(cosx=a\). Полученные базовые решения являются значениями точек пересечения, подписать их.
Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки.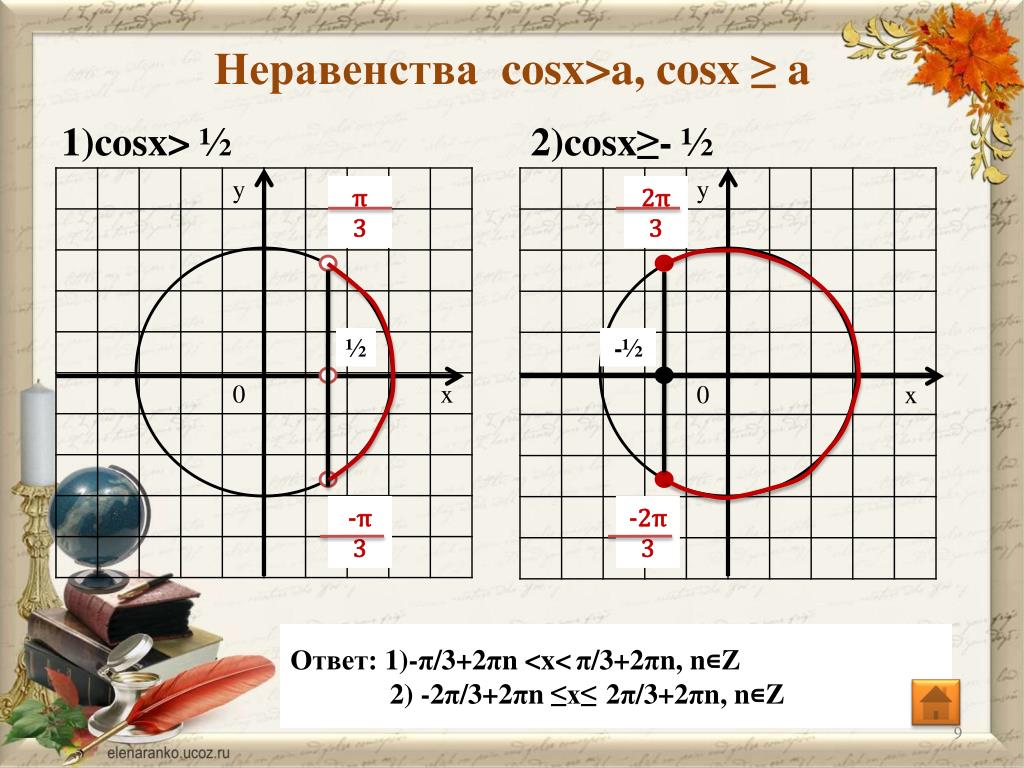
Добавить к концам полученного интервала полный период.
Решение имеет вид: \((-arccosa+2\pi k;\ arccosa+2\pi k)\)
Например:
| $$ cosx\gt \frac{\sqrt{3}}{2} $$ 1. Проводим вертикаль \(x=\frac{\sqrt{3}}{2}\), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое). 2. Решаем уравнение \(cosx=\frac{\sqrt{3}}{2}\) \begin{gather*} x=\pm\frac\pi6+2\pi k \end{gather*} Подписываем точку снизу \(-\frac\pi6\) и точку сверху \(\frac{\pi}{6}\). 3. При обходе полученной дуги против часовой стрелки получаем интервал: \(\left(-\frac\pi6;\frac\pi6\right)\). Добавляем к концам интервала полный период. Ответ: \(\left(-\frac\pi6;+2\pi k;\ \frac{\pi}{6}+2\pi k\right)\) |
Алгоритм решения неравенства \(cosx\geq a\) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).
Алгоритм решения неравенства \(cosx\lt a\) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали \(x=a\).
При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.
Наконец, в неравенстве \(cosx\leq a\) всё будет то же, что и в \(cosx\lt a\). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).
п.3. Решение неравенств с тангенсом
Алгоритм решения неравенства \(tgx\gt a\)
Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой \(a\). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.
Шаг 2. Решить уравнение \(tgx=a\). Полученное базовое решение является значением точки пересечения.
Шаг 3. Дуга числовой окружности от отмеченной точки до \(\frac\pi2\) (в которой \(tgx\rightarrow +\infty\)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: \(\left(arctga+\pi k;\ \frac\pi2+\pi k\right)\)
Например:
$$ tg x\gt -\frac{1}{\sqrt{3}} $$ 1. На оси тангенсов отмечаем точку \(-\frac{1}{\sqrt{3}}\). Проводим луч из начала координат через эту точку.2. Решаем уравнение \(tgx=-\frac{1}{\sqrt{3}}\) \begin{gather*} x=-\frac\pi6+\pi k \end{gather*} Подписываем точку снизу \(-\frac\pi6.\) Верхней границей интервала будет \(\frac\pi2\), угол, в котором \(tgx\rightarrow +\infty .\) 3. При обходе полученной дуги против часовой стрелки получаем интервал: \(\left(-\frac\pi6;\frac\pi2\right)\). Добавляем к концам интервала период для тангенса. Строго говоря, на числовой окружности длиной \(2\pi\) получим две дуги для тангенса с периодом \(\pi\). Ответ: \(\left(-\frac\pi6;+\pi k;\ \frac{\pi}{2}+\pi k\right)\) |
Алгоритм решения неравенства \(tgx\lt a\) будет отличаться тем, что в ответе нужно записывать дугу от точки \(-\frac\pi2\) (в которой \(tgx\rightarrow -\infty\)) до найденного арктангенса.
Для нестрогих неравенств будут получаться полуинтервалы, в которых точки \(\pm\frac\pi2\) (\(tgx\rightarrow \pm\infty\)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.
п.4. Решение неравенств с котангенсом
Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).
В неравенствах вида \(ctgx\gt a\) пределу \(ctgx\rightarrow +\infty\) соответствует угол 0.
В неравенствах вида \(ctgx\lt a\) пределу \(ctgx\rightarrow -\infty\) соответствует угол \(\pi\).
п.5. Примеры
Пример 1. Решите неравенства:
$$ x\in\left[-\frac{5\pi}{4}+2\pi k;\ \frac{\pi}{4}+2\pi k\right] $$ | б) \(cosx\lt -\frac{1}{2}\) $$ x\in\left(\frac{2\pi}{3}+2\pi k;\ \frac{4\pi}{3}+2\pi k\right) $$ |
| в) \(sinx\gt -\frac{\sqrt{3}}{2}\) $$ x\in\left(-\frac{\pi}{3}+2\pi k;\ \frac{4\pi}{3}+2\pi k\right] $$ | г) \(tgx\geq 1\) $$ x\in\left.\left(-\frac{\pi}{2}+\pi k;\ \frac{\pi}{4}+\pi k\right.\right] $$ |
Пример 2*.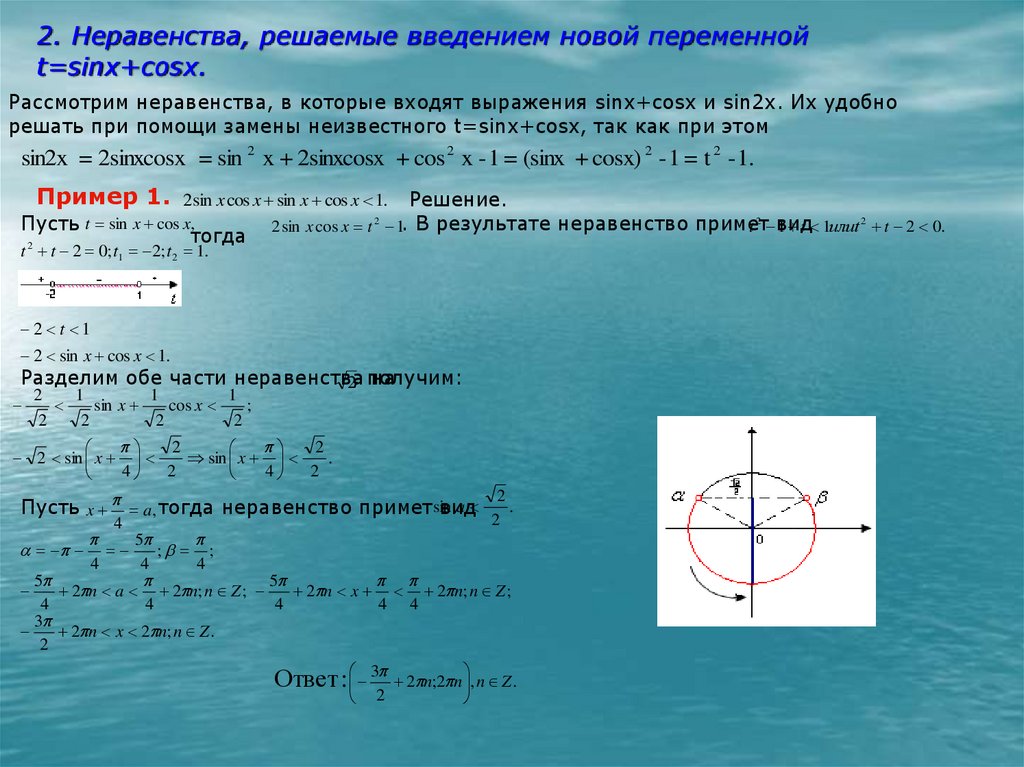
2\frac x2-3\leq 0\)
\(4\cdot \frac{1+cosx}{2}\leq 3\)
\(2+2cosx\leq 3\)
\(cosx\leq\frac12\)
Ответ: \(\left[\frac\pi3+2\pi k;\ \frac{5\pi}{3}+2\pi k\right]\)
в) \(-\sqrt{3}\lt tgx\leq 5\)
\(-arctg\sqrt{3}+\pi k\lt x\leq arctg5+\pi k\)
\(-\frac\pi3+\pi k\lt x\leq arctg5+\pi k\)
Ответ: \(\left.\left(-\frac{\pi}{3}+\pi k;\ arctg5+\pi k\right.\right]\)
г) \(tg\left(x-\frac\pi4\right)\gt\sqrt{3}\)
\(arctg\sqrt{3}+\pi k\lt x-\frac\pi4\lt\frac\pi2+\pi k\)
\(\frac\pi4+\frac\pi3+\pi k\lt x\lt\frac\pi4+\frac\pi2+\pi k\)
\(\frac{7\pi}{12}+\pi k\lt x\lt\frac{3\pi}{4}+\pi k\)
Ответ: \(\left(\frac{7\pi}{12}+\pi k;\ \frac{3\pi}{4}+\pi k\right)\)
Тригонометрическое неравенство и красивые примеры сложных задач
Анна Малкова (опыт преподавания математики 26 лет, автор книг для подготовки к ЕГЭ по математике).
Привет, дорогие друзья!
Все привыкли к тригонометрическим уравнениям, но иногда нам встречаются тригонометрические неравенства, и мы помним, что в ЕГЭ у нас есть задание № 15 «Неравенства». И неравенства там бывают самые разные: и показательные, и логарифмические, и алгебраические, и степенные, и даже тригонометрические. Причем тригонометрические неравенства я встречала и в сборниках задач ЕГЭ под редакцией Ященко, и даже в вариантах тренировочных работ ЕГЭ, которые старшеклассники пишут в течение учебного года.
У меня есть для вас замечательное тригонометрическое неравенство .
Оно такое короткое, такое безобидное, такое, на первый взгляд, милое, но на его примере я смогу показать, как вообще решаются тригонометрические неравенства. Это вам может пригодиться и в задаче 15, и в задаче с параметрами, и даже иногда в первой части, под № 10 есть задача с практическим содержанием, и там тоже встречаются тригонометрические неравенства. Кроме того, я покажу на примере этой задачи одну классную, абсолютно нетривиальную замену переменной, которая вам может помочь в задаче с параметрами и в олимпиадных задачах, а заодно и повторим, как решать иррациональные неравенства, то есть с корнями, а это тоже полезно.
Давайте начнем с самого простого, с области допустимых значений. Она здесь такая:
Обратите внимание, я могу оставить эту систему в таком виде, а могу сразу ее дорешать. Нарисую тригонометрический круг и отмечу те точки, где синус и косинус неотрицательны. Они находятся в первой четверти, от до + , где принадлежит множеству целых чисел.
И ведь в самом деле, подходят углы только первой четверти, потому что синус неотрицательный для углов из первой и второй четверти, а косинус неотрицательный для углов из первой и четвертой четверти, а и то и другое только в первой четверти.
ОДЗ мы записали, что же нам еще сделать?
Слева у нас сумма корней, а корни квадратной величины неотрицательные, значит, левая часть неотрицательная. И правая часть у нас тоже неотрицательная, значит, мы можем возвести обе части этого неравенства в квадрат, конечно, при условиях, что синус х и косинус х больше или равны 0. Мы имеем право возводить в квадрат, когда обе части неотрицательны.
Получаем .
Вы, конечно, узнали формулу .
Здесь же запишу, что и . Получаем
Теперь смотрим на первое неравенство и видим сумму синуса и косинуса и их произведение под корнем. И сейчас я покажу ту самую замену, о которой я говорила вначале.
Если у нас в уравнении или в неравенстве есть только сумма синуса и косинуса, а также произведение синуса и косинуса, а также всевозможные , или , , то мы можем сделать замену .
Эта замена, возможно, поможет вам в олимпиадных задачах и, возможно, в задаче 18, если там встретится тригонометрия, и вы захотите его решать аналитически. С минусом можно сделать точно так же.
А все остальное мы будем выражать через эту новую переменную t. Давайте так и сделаем.
— замена. И тогда все остальное выразим через эту t. Сейчас покажу, как это сделать.
Если , а мы сказали, что при этом и , то в этом уравнении можно обе части возвести в квадрат, тогда у нас .
.
Получается
Значит, первое неравенство примет вид: .
Давайте уединим корень .
У нас получилось стандартное иррациональное неравенство, про которое вам обещали, что на ЕГЭ 2021-го года их не будет. Но о том, что не будет тригонометрических неравенств, ничего не сказали.
Что же с этим делать? Конечно, хочется возвести обе части в квадрат, но мы знаем, что возводить обе части неравенства в квадрат можно только тогда, когда обе эти части неотрицательные. Если , мы можем возвести обе части в квадрат.
Получаем .
Обратите внимание, что при этом я могу не писать, что , потому что она уже больше, квадрат какого-то неотрицательного выражения больше неотрицательного выражения.
Но это еще не все. Есть второй случай, когда , ведь у нас тоже такое может быть. Тогда в квадрат возводить мы не можем. Но тогда неравенство просто будет выполняться, потому что слева корень, величина неотрицательная, а справа минус. И неравенство выполняется, когда t принадлежит области допустимых значений, когда .
Решаем полученную совокупность
Давайте для первой системы второе неравенство решим методом интервалов
Значит, мы получаем, что
.
Вернемся к переменной t.
Пронумеруем наши два неравенства и будем решать их по порядку
.
1 случай: ; .
Что-то здесь странное, ведь мы же знаем, что
а у нас даже сумма меньше -3. Такого не может быть.
Поскольку у меня
а я могу складывать неравенства с одинаковым знаком, отсюда следует, что .
Мы получаем, что у нашего неравенства нет решений.
— нет решений. Остался второй случай: .
Когда вам попадаются такие уравнения или неравенства, где есть сумма синуса и косинуса, равная какому-то числу, мы знаем, как их решать. Воспользуемся методом введения дополнительного угла. Я об этом уже рассказывала на онлайн-курсе, также об этом можно почитать на нашем сайте в материалах по математике. В простейшем случае, как сейчас у нас, этот метод дается в учебнике алгебры.
Умножаем левую и правую части этого неравенства на корень из 2/2, потому что это .
И у нас получается ; .
Узнаем формулу .
Сворачиваем по формуле и получаем .
Точно не нужно это тригонометрическое неравенство решать в уме, даже простейшие тригонометрические неравенства решать в уме не надо. Надо нарисовать тригонометрический круг.
Пусть у меня угол . И я решаю простейшее тригонометрическое неравенство .
Отмечаем на тригонометрическом круге на оси косинусов и точки, у которых такой косинус. В первой четверти будет угол или и все углы, которые отличаются от на целое число полных кругов. А в четвертой четверти это . А косинус у нас больше, чем
Осталось записать решение для угла , который , .
И последним действием мы находим х.
Значит, х – это углы из первой четверти, не включая точки, лежащие на осях. И для всех этих углов выполняется условие и . Мы решили это непростое тригонометрическое неравенство.
Мы сделали очень нетривиальную замену переменной, решили получившееся иррациональное неравенство, вспомнили, как решать тригономитрические неравенства с помощью единичной окружности. Но оказывается, есть более сложные неравенства, которые можно сделать с помощью не тригонометрических, а обратных тригонометрических функций.
Если вы хотите неравенства с обратными тригонометрическими функциями и заодно повторить, что такое арксинус и арккосинус, — ставьте лайки и подписывайтесь на мой канал!
Все видео по математике
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Тригонометрическое неравенство и красивые примеры сложных задач» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 07.04.2023
Основные тригонометрические неравенства
Неизвестная переменная (угол): x
Набор целых чисел: ℤ
Целое число: n
Набор действительных чисел: ℝ
Real number: a
Trigonometric functions: sin x , cos x , tan x , cot x
Inverse trigonometric functions: arcsin a , arccos a , arctan a , арккот и
Неравенство, включающее тригонометрические функции неизвестного угла, называется тригонометрическим неравенством.
Следующие \(16\) неравенства относятся к основным тригонометрическим неравенствам:
\[\sin x \gt a,\; \sin x \ge a,\; \sin x \lt a,\; \sin x \le a,\]
\[\cos x \gt a,\; \cos x \ge a,\; \cos x \lt a,\; \cos х \ле а,\]
\[\tan x \gt a,\; \тан х \ге а,\; \загар х \lt а,\; \загар х \ле а,\]
\[\cot x \gt a,\; \cot x \ge a,\; \кот х \lt а,\; \cot x \le a.\]
Здесь \(x\) неизвестная переменная, \(a\) может быть любым вещественным числом.
Неравенства вида \(\sin x \gt a,\) \(\sin x \ge a,\) \(\sin x \lt a,\) \(\sin x \le a\)
Неравенство \(\sin x \gt a\)
Если \(\left| a \right| \ge 1\), то неравенство \(\sin x \gt a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \lt -1\), то решением неравенства \(\sin x \gt a\) является любое действительное число: \(x \in \mathbb{R}.\)
При \(-1 \le a \lt 1\) решение неравенства \(\sin x \gt a\) выражается в виде
\[\arcsin a + 2\pi n \lt x \lt \pi — \arcsin a + 2\pi n, \;n \in \mathbb{Z}.
\]
Неравенство \(\sin x \ge a\)
Если \(a \gt 1\), то неравенство \(\sin x \ge a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \le -1\), то решением неравенства \(\sin x \ge a\) является любое действительное число: \(x \in \mathbb{R}.\)
Случай \(а = 1:\)
\[x = \pi/2 +2\pi n,\; n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\sin x \ge a\) включает граничные углы и имеет вид
\[\arcsin a + 2\pi n \le x \le \pi — \arcsin a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\sin x \lt a\)
Если \(a \gt 1\), то решением неравенства \(\sin x \lt a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \le -1\), то неравенство \(\sin x \lt a\) не имеет решений: \(x \in \varnothing.\)
При \(-1 \lt a \le 1\) решение неравенства \(\sin x \lt a\) лежит в интервале
\[-\pi — \arcsin a + 2\pi n \lt x \lt \arcsin a + 2\pi n,\;n \in \mathbb{Z}.
\]
Неравенство \(\sin x \le a\)
Если \(a \ge 1\), то решением неравенства \(\sin x \le a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \lt -1\), то неравенство \(\sin x \le a\) не имеет решений: \(x \in \varnothing.\)
Случай \(а = -1:\)
\[x = -\pi/2 + 2\pi n,\;n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\sin x \le a\) находится в интервале
\[-\pi — \arcsin a + 2\pi n \le x \le \arcsin a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\cos x \gt a,\) \(\cos x \ge a,\) \(\cos x \lt a,\) \(\cos x \le a\)
Неравенство \(\cos x \gt a\)
Если \(a \ge 1\), то неравенство \(\cos x \gt a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \lt -1\), то решением неравенства \(\cos x \gt a\) является любое действительное число: \(x \in \mathbb{R}.\)
При \(-1 \le a \lt 1\) решение неравенства \(\cos x \gt a\) имеет вид
\[-\arccos a + 2\pi n \lt x \lt \arccos a + 2\pi n,\;n \in \mathbb{Z}.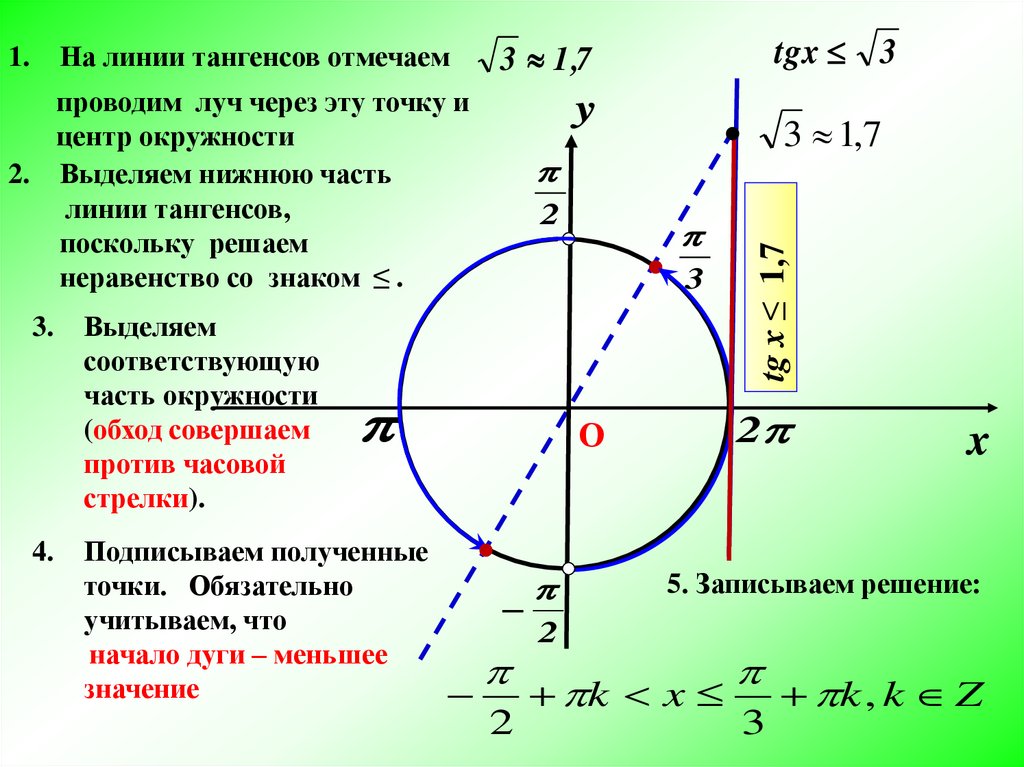
\]
Неравенство \(\cos x \ge a\)
Если \(a \gt 1\), то неравенство \(\cos x \ge a\) не имеет решений: \(x \in \varnothing.\)
Если \(a \le -1\), то решением неравенства \(\cos x \ge a\) является любое действительное число: \(x \in \mathbb{R}.\)
Случай \(а = 1:\)
\[x = 2\pi n,\;n \in \mathbb{Z}.\]
При \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\cos x \ge a\) выражается формулой
\[-\arccos a + 2\pi n \le x \le \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\cos x \lt a\)
Если \(a \gt 1\), то неравенство \(\cos x \lt a\) верно для любого действительного значения \(x\): \(x \in \mathbb{R}.\)
Если \(a \le -1\), то неравенство \(\cos x \lt a\) не имеет решений: \(x \in \varnothing.\)
При \(-1 \lt a \le 1\) решение неравенства \(\cos x \lt a\) записывается в виде
\[\arccos a + 2\pi n \lt x \lt 2\pi — \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Рис.
4.Неравенство \(\cos x \le a\)
Если \(a \ge 1\), то решением неравенства \(\cos x \le a\) является любое действительное число: \(x \in \mathbb{R}.\)
Если \(a \lt -1\), то неравенство \(\cos x \le a\) не имеет решений: \(x \in \varnothing.\)
Случай \(а = -1:\)
\[x = \pi + 2\pi n,\;n \in \mathbb{Z}.\]
Для \(-1 \lt a \lt 1\) решение нестрогого неравенства \(\cos x \le a\) записывается как
\[\arccos a + 2\pi n \le x \le 2\pi — \arccos a + 2\pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\tan x \gt a,\) \(\tan x \ge a,\) \(\tan x \lt a,\) \(\tan x \le a\)
Неравенство \(\tan x \gt a\)
Для любого действительного значения \(a\) решение строгого неравенства \(\tan x \gt a\) имеет вид
\[\arctan a + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
Рис. 5.Неравенство \(\tan x \ge a\)
Для любого действительного значения \(a\) решение неравенства \(\tan x \ge a\) выражается в виде
\[\arctan a + \pi n \le x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.
\]
Неравенство \(\tan x \lt a\)
При любом значении \(a\) решение неравенства \(\tan x \lt a\) записывается в виде
\[-\pi/2 + \pi n \lt x \lt \arctan a + \pi n,\;n \in \mathbb{Z}.\]
Рис. 6.Неравенство \(\tan x \le a\)
Для любого значения \(a\) неравенство \(\tan x \le a\) имеет следующее решение:
\[-\pi/2 + \pi n \lt x \le \arctan a + \pi n,\;n \in \mathbb{Z}.\]
Неравенства вида \(\cot x \gt a,\) \(\cot x \ge a,\) \(\cot x \lt a,\) \(\cot x \le a\)
Неравенство \(\cot x \gt a\)
При любом значении \(а\) решение неравенства \(\cot x \gt a\) имеет вид
\[\pi n \lt x \lt \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
Рис. 7.Неравенство \(\cot x \ge a\)
Нестрогое неравенство \(\cot x \ge a\) имеет аналогичное решение:
\[\pi n \lt x \le \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
Неравенство \(\cot x \lt a\)
При любом значении \(a\) решение неравенства \(\cot x \lt a\) лежит на открытом интервале
\[\text {arccot} a + \pi n \lt x \lt \pi + \pi n,\;n \in \mathbb{Z}.
\]
Неравенство \(\cot x \le a\)
При любом значении \(a\) решение нестрогого неравенства \(\cot x \le a\) находится в полуинтервале
\[\text {arccot} a + \pi n \le x \lt \pi + \pi n,\;n \in \mathbb{Z}.\]
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Решить неравенство
\[\sin x \ge -\frac{1}{2}.\]
Пример 2
Решить неравенство
\[\cos x \lt -\frac{\sqrt{2}}{2}.\]
Пример 3
Решите неравенство
\[\tan x \gt -\sqrt{3}. \]
Пример 4
Решить неравенство
\[\cot x \ge \frac{1}{\sqrt{3}}.\]
Пример 1.
Решить неравенство
\[\sin x \ge -\frac{1}{2}.\]
Раствор.
Отметить на оси \(y-\) точку \(y = -\frac{1}{2}.\) Найти углы, соответствующие данному значению синуса:
\[\sin x = -\frac{1}{2}, \стрелка вправо\]
\[x_1 = \arcsin{\left({-\frac{1}{2}}\right)} = — \ arcsin{\left({\frac{1}{2}}\right)} = — \фракция{\пи}{6};\]
\[x_2 = \pi — {x_1} = \pi — \left({-\frac{\pi}{6}}\right) = \pi + \frac{\pi}{6} = \frac{ 7\pi}{6}.
\]
Решение неравенства \(\sin x \ge -\frac{1}{2}\) на единичной окружности представляется в виде сектора \(\left[-\frac{\pi}{6} , \frac{7\pi}{6}\right].\) Не забудьте добавить в ответ периодические члены:
\[-\frac{\pi}{6} + 2\pi n \le x \le \frac{7\pi}{6} + 2\pi n,\;n \in \mathbb{Z}. \]
Пример 2.
Решить неравенство
\[\cos x \lt -\frac{\sqrt{2}}{2}.\]
Раствор.
Решая уравнение \(\cos x = -\frac{\sqrt{2}}{2}\) находим:
\[x = \pm\arccos\left({-\frac{\sqrt{2}}{2}}\right) + 2\pi n = \pm\left({\pi — \arccos{\frac {\ sqrt {2}} {2}}} \ справа) + 2 \ pi n = \ pm \ слева ({\ pi — \ frac {\ pi} {4}} \ справа) + 2 \ pi n = \ pm\frac{3\pi}{4} + 2\pi n,\;n \in \mathbb{Z}.\]
Обратите внимание, что угол \(-\frac{3\pi}{4}\) можно записать как \(\frac{5\pi}{4}.\) Следовательно, решение неравенства лежит в интервале \(\left[{\frac{3\pi}{4}, \frac{5\pi}{4}}\right].\)
Рисунок 10.Ответ дается
\[\frac{3\pi}{4} + 2\pi n \lt x \lt \frac{5\pi}{4} + 2\pi n,\;n \in \mathbb{Z}.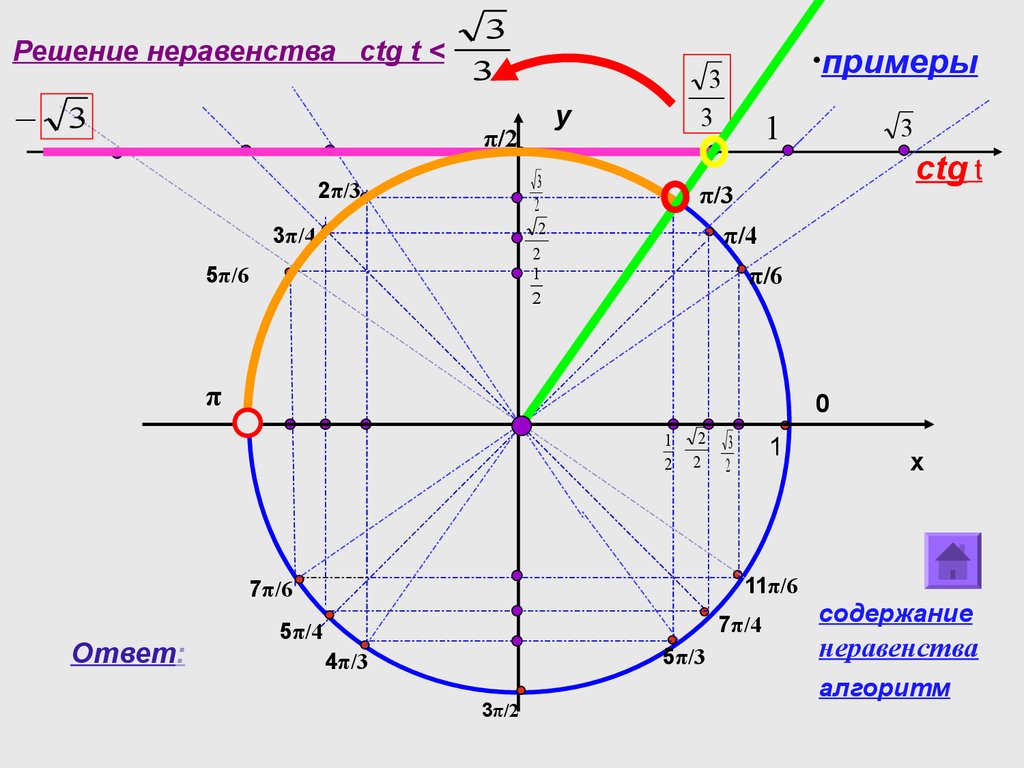
\]
Пример 3.
Решить неравенство
\[\tan x \gt -\sqrt{3}.\]
Раствор.
Решение неравенства \(\tan x \gt a\) записывается в виде
\[\arctan a + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
В нашем случае:
\[\arctan a = \arctan\left({-\sqrt{3}}\right) = — \arctan\sqrt{3} = -\frac{\pi}{3}.\]
Следовательно, имеем:
\[-\frac{\pi}{3} + \pi n \lt x \lt \pi/2 + \pi n,\;n \in \mathbb{Z}.\]
Рис. 11.Пример 4.
Решить неравенство
\[\cot x \ge \frac{1}{\sqrt{3}}.\]
Раствор.
Мы знаем, что решение нестрогого неравенства \(\cot x \ge a\) дается выражением
\[\pi n \lt x \le \text {arccot } a + \pi n,\;n \in \mathbb{Z}.\]
С
\[\text{arccot}\frac{1}{\sqrt{3}} = \frac{\pi}{3},\]
мы можем написать
\[\pi n \lt x \le \frac{\pi}{3} + \pi n,\;n \in \mathbb{Z}.\]
Рисунок 12.Решение тригонометрических уравнений и неравенств
Все ресурсы предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Precalculus Help » Тригонометрические тождества » Решение тригонометрических уравнений и неравенств
Используйте тригонометрические тождества, чтобы решить следующее уравнение для:
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте тригонометрические тождества, чтобы преобразовать sec в термины tan:
, следовательно,
Итак, мы имеем , что делает
Таким образом, решение для любого целого числа n.
Сообщить об ошибке
Что из следующего не является решением для
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с того, что приравняем правую часть уравнения к 0.
Уравнение может быть проще разложить на множители, используя следующую замену.
Это дает следующие
Это можно учитывать следующим образом
Следовательно,
Заменить наш заменитель между тремя ответами, поэтому мы получим три ответа.
когда
когда
Таким образом, единственным неверным выбором является
Сообщить об ошибке
Найдите одно возможное значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с выделения касательной стороны уравнения:
Затем возьмите арктангенс обеих сторон:
Разделите на пять, чтобы получить окончательный ответ:
Сообщить об ошибке
Используйте тригонометрические тождества для определения значения угла.
Возможные ответы:
Правильный ответ:
Объяснение:
Есть два способа решить эту проблему. Первый включает два тригонометрических тождества:
Второй метод позволяет использовать только первое тригонометрическое тождество:
Сообщить об ошибке
Используйте тригонометрические тождества для решения уравнения для значения угла.
Возможные ответы:
Правильный ответ:
Объяснение:
Самый простой способ решить эту задачу — использовать тождество двойного угла для косинуса.
Подстановка этого значения в исходное уравнение дает нам:
Сообщить об ошибке
Согласно тригонометрическим тождествам
Возможные ответы:
Правильный ответ:
Объяснение:
Тригонометрическое тождество важно запомнить.
Некоторые другие идентификаторы, которые важно знать:
Сообщить об ошибке
Если существует в домене от , решите следующее:0322 Возможные ответы:
Правильный ответ:
Объяснение:
Факторизация .
Приравняйте оба члена к нулю и решите.
Это значение не входит в домен.
Это единственное правильное значение в домене.
Сообщить об ошибке
Решите для в уравнении на интервале .
Возможные ответы:
Правильный ответ:
Объяснение:
Если вы замените, вы получите узнаваемое квадратное уравнение, которое можно решить для ,
.
Затем мы можем снова подключиться к нашему уравнению и использовать единичный круг, чтобы найти это
.
Сообщить об ошибке
Учитывая, что тета существует из , решите:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы правильно решить, не разделяйте на обе стороны. Эффект устранит один из корней этой триггерной функции.
Вычесть с обеих сторон.
Фактор левой части уравнения.
Приравняйте каждый член к нулю и найдите тета с ограничением .
Правильный ответ:
Сообщить об ошибке
Решить для
Возможные ответы:
3 Нет решения
Правильный ответ:
Решения нет.