Правильный треугольник – формулы
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
Обновлено 11 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
Обновлено 11 Января, 2021
Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.
Рис. 1. Правильный треугольник.Формулы правильного треугольника
Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.
Площадь
Начнем с формулы площади.
Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.
Рис. 2. Рисунок к доказательству.В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
$$Sin(ВАM)={ВM\over AB}$$
С другой стороны синус 60 градусов заранее известнее и равен $\sqrt{3} \over 2$ . Значит можно выразить значение АМ:
$$ВМ=АВ*sin(ВАM)=AB* {\sqrt{3}\over 2}$$
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
AB=AC=BC=a
Тогда формула будет выглядеть следующим образом:
$$ВМ=а*{\sqrt{3}\over2}$$
Теперь вспомним классическую формулу площади треугольника:
$S= {1\over2}h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию.
2*{\sqrt{3}\over4}$$
Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через значение одной стороны.
Периметр
Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:
Р=3а
Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.
В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.
Что мы узнали?
Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Иван Дарьин
5/5Василий Головин
5/5
Денис Каспер
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
А какая ваша оценка?
Треугольник, Произвольный треугольник это | matematicus.ru
Skip to content
Artman Планиметрия
Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника).
По сути это самый простой многоугольник.
Виды треугольников
Рассмотрим виды треугольника, в зависимости от их свойств.
Рисунок 1
Если все углы острые, то такой треугольник — остроугольный (рис.1).
Рисунок 2
Если один из углов прямой ∠С=900, а остальные ∠A
Рисунок 3
Если один из углов тупой — ∠A, а остальные ∠C и ∠B — острые, то треугольник — тупоугольный (рис.3).
Равносторонний (правильный) треугольник
Равнобедренный треугольник
Произвольный треугольник
Произвольный треугольник — это треугольник, у которого нет равных углов, сторон (как например у равностороннего или равнобедренного треугольника), отсутствует угол 900 (как например у прямоугольного треугольника).
Свойства треугольника
- Сумма углов треугольника равна 180°, то есть (рис. 4):
α+β+γ=180°
Рисунок 4
2. Внешний угол равен сумме двух внутренних не смежных с ним углов (рис. 5):
δ=α+β
Рисунок 5
3. Неравенство треугольника заключается в том, что любая сторона треугольника меньше суммы двух других сторон, но при этом больше их разности по модулю:
|a-b| < с <a+b
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, в точке M (рис.6). Эта точка называется ортоцентром.
- Высоты треугольника обратно пропорциональны сторонам и формула имеет вид (рис.6):
3. Формула для определения длины высоты к стороне a:
ha=b·sinC=c·sinB
или
где R — радиус описанной окружности (рис.9)
S — площадь Δ
Рисунок 6
Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.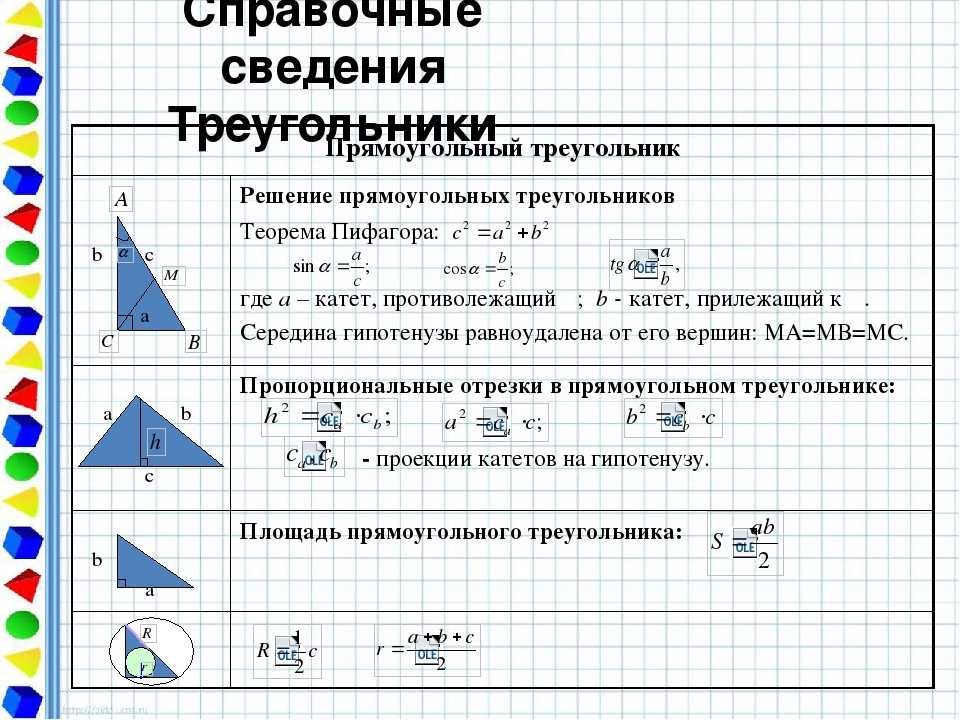
Рисунок 7
Формула для определения средней линии треугольника (рис.7):
Формула периметра треугольника:
P=a+b+c
Формула полупериметра треугольника:
Формулы для нахождения площади произвольного треугольника
Площадь треугольника по формуле Герона:
, где р — полупериметр.
Формула площади произвольного треугольника через две стороны и угла между ними (рис.8):
S=b·c·sinγ
Формула площади произвольного треугольника через высоту и основания (рис.8):
где hb – высота опущенная на сторону b
Рисунок 8
Площадь треугольника через радиусы (рис.9):
S=rp
где
R — радиус описанной окружности
r — радиус вписанной окружности
Радиус вписанной окружности в треугольник (рис.9):
Радиус описанной окружности в треугольник (рис.
2 \ frac {\ sin A \ sin B} {\ sin (A + B)}
\end{выравнивание*} 92\frac{\sin A \sin B}{\sin (A+B)}$$
Предположим, что $b$ = $c$.
Тогда $c\frac{\sin A \sin B}{\sin (A+B)} \equiv \frac{c}{\cot A + \cot B}$. Но $\cot A \equiv \frac{b \cos A}{h}$ и $\cot B \equiv \frac{a\cos B}{h}$. Следовательно, $\frac{c}{\cot A + \cot B} \equiv \frac{ch}{a\cos B + b\cos A}$. Поскольку $a\cos B + b\cos A \equiv c$, имеем $h \equiv \frac{ch}{c}$. $ч\экв ч$.
Я понял это после того, как отправил вопрос…
$\endgroup$
$\begingroup$
$$\triangle =\dfrac12bc\sin A=\dfrac12(2R\sin B)c\sin A\cdot\dfrac c{2R\sin C}$$
Теперь $A+B=\pi-C \подразумевает\sin(A+B)=\sin(\pi-C)=?$
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Геометрическое доказательство формулы Герона
Геометрическое доказательство формулы Герона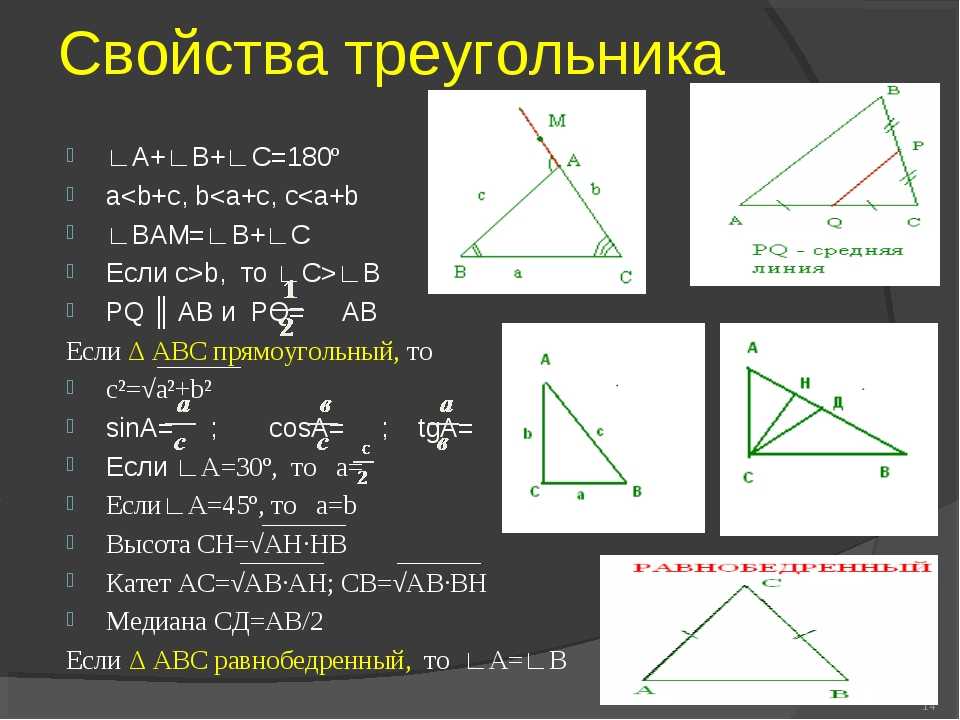
Это доказательство было адаптировано из схемы
доказательство на странице 194 в 6-м издании Дан треугольник ABC, длина отрезка BC равна a, длина отрезка AC равна b, а длина отрезка AB равна c.
Обратите внимание на периметр p треугольника ABC = a + b + c. Половина периметр называется полупериметром, s, и поэтому для треугольника ABC, s = (a + b + c)/2,
Пусть точка пересечения биссектрисы углов A, B и C назовем точкой I. Построим отрезки AI, BI и КИ.
Далее пусть точка пересечения перпендикуляра к стороны АС, проходящей через точку I, будем называть точкой D, точкой пересечения перпендикуляра к стороне ВС, проходящего через точку, которую я называю точка Е и точка пересечения перпендикулярной линии в сторону АВ через точку I, называемую точкой F.
По определению, точка I называется центром треуг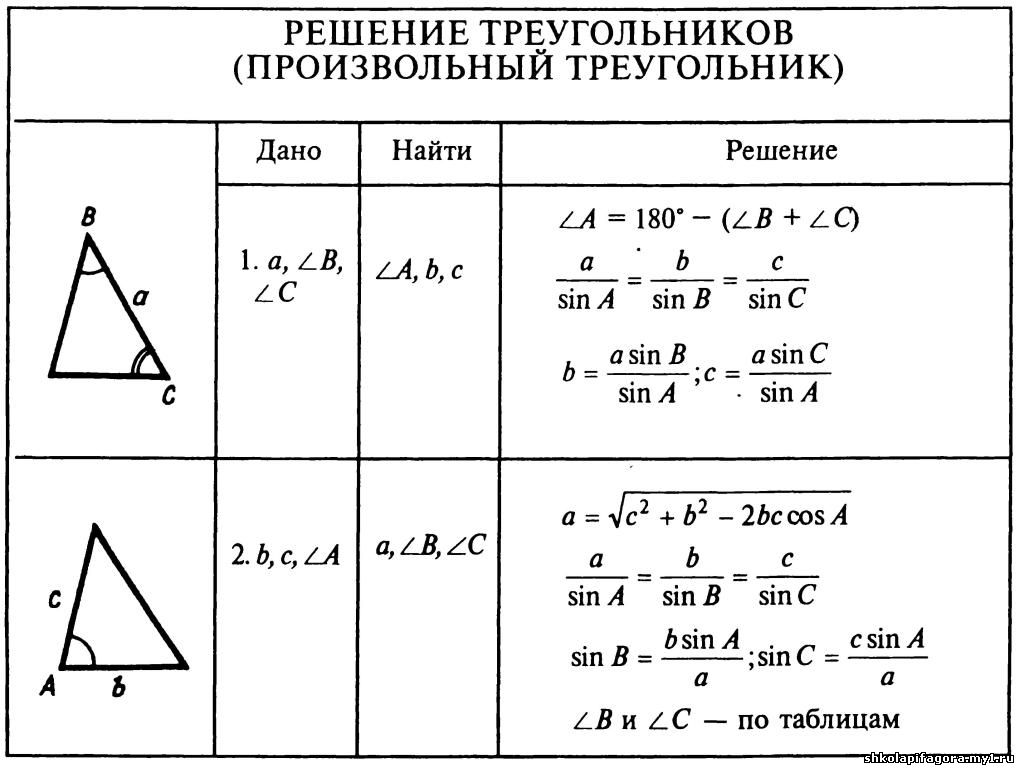ольника ABC.
Окружность с точкой I в центре, проходящая через
точки D, E и F называются вписанными окружностями треугольника ABC.
Теперь, поскольку отрезок IB является биссектрисой угла B, то углы IBF и IBE равны. Так как углы IFB и IEB прямые по построению, то они равны, а значит углы BIF и BIE равны (поскольку сумма всех углов треугольника равна 180 градусам). Обратите внимание, что отрезки IF и IE равны, так как оба являются радиусами тот самый круг. Следовательно, треугольники BIF и BIE (выделены красным) равны конгруэнтны по SAS.
Точно так же треугольники CID и CIE (зеленые) равны по САС.
Аналогично, треугольники AIF и AID (обозначены синим цветом) равны. по САС.
Поскольку соответствующие стороны конгруэнтных треугольников конгруэнтны,
следует, что отрезки BF и BE (выделены красным) равны, отрезки
CD и CE (зеленый) равны, а сегменты AD и AF (синий)
равны.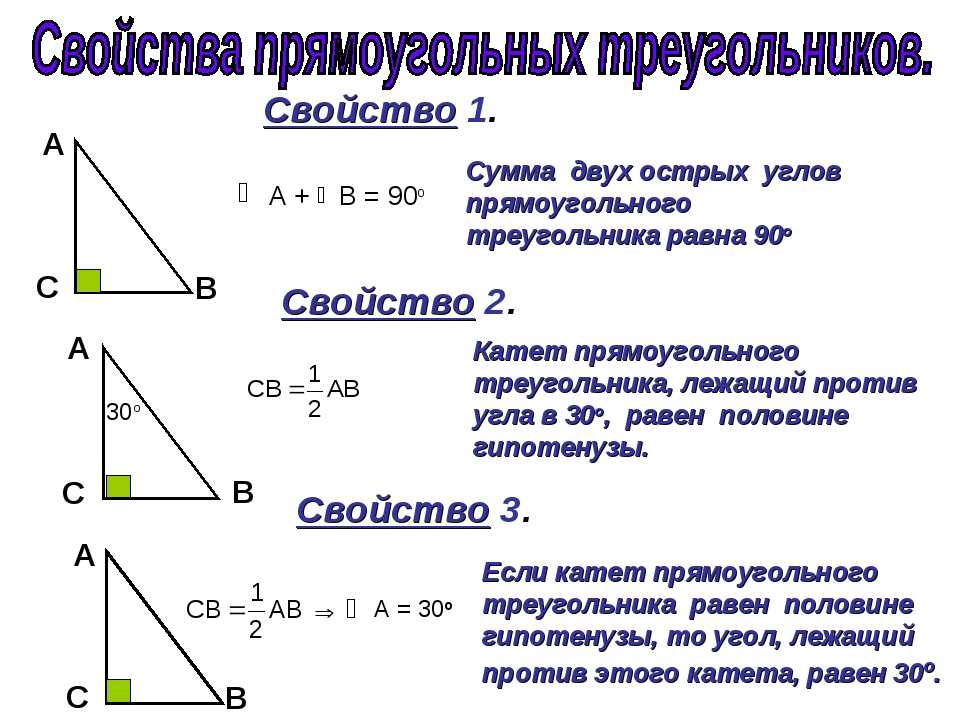
Используя формулу, которая утверждает, что площадь треугольника равна половина основания умноженная на высоту, площадь треугольника AIB = (1/ 2)*АВ*ЕСЛИ,…
…площадь треугольника BIC = (1/2)*BC*IE,…
…и площадь треугольника AIC = (1/2)*AC*ID.
Следовательно, площадь треугольника ABC равна сумме площадей треугольников AIB, BIC и AIC.
Подстановкой площадь треугольника ABC = (1/2)*AB*IF +
(1/2)*BC*IE + (1/2)*AC*ID. Поскольку сегменты IF, IE и ID
равны (все они являются радиусами одной и той же окружности), отсюда следует, что
немного алгебры, что площадь треугольника ABC = (1/2)*ID*(AB
+ ВС + АС). Но AB + BC + AC = a + b + c, так что эта сумма действительно
периметр треугольника АВС; поэтому площадь треугольника
ABC = (1/2)*ID*p. Поскольку (1/2)*p = s, полупериметр треугольника
ABC, то площадь треугольника ABC = ID*s.
Теперь постройте точку G так, чтобы G лежала на одной линии с отрезок AC, а отрезок CG равен отрезку BE. Помните р = а + b + c = AB + BC + AC, и, таким образом, добавлением и заменой отрезков, p = (BE + CE) + (CD + AD) + (AF + BF) = (BF + BE) + (CE + CD) + (АД + АФ). Кроме того, путем замены p = 2*BE + 2*CD + 2*AD = 2(BE + CD + AD). Снова подстановкой p = 2(CG + CD + AD). Но AG = AD + DC + CG добавлением сегмента и, следовательно, заменой, р = 2*АГ. Следовательно, s = AG.
Таким образом, подстановкой площадь треугольника ABC = ID*AG.
Построить линию перпендикулярно отрезку AI через точку I (розовый) и прямая, перпендикулярная отрезку AG, проходящая через точку С (светло-голубой). Пусть точка пересечения этих двух прямые назовем точкой H. Пусть точка пересечения отрезка IH и отрезок AG назовем точкой J. Построим отрезок AH (в желтый).
Так как углы AIH и ACH прямые (по построению), то
треугольники AIH и ACH прямоугольные.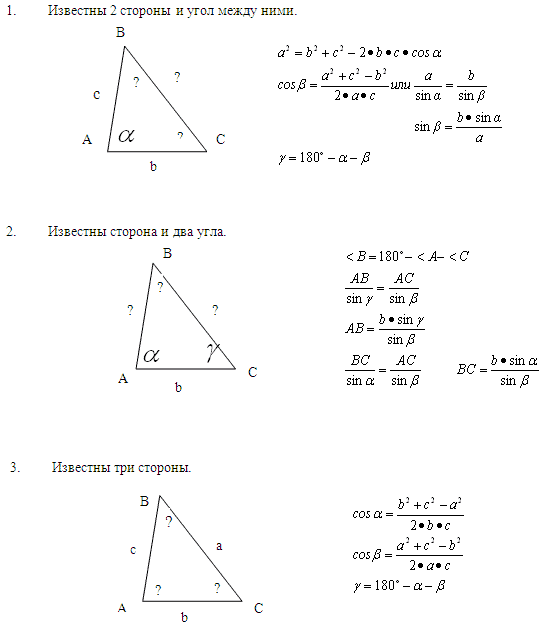
Обратите внимание, что треугольники имеют общий
гипотенуза, отрезок AH. Отсюда следует, что эти треугольники вписаны
в общей окружности с отрезком AH в качестве диаметра окружности.
Этот факт означает, что четырехугольник AICH вписанный, а значит, противоположный углы AIC и AHC являются дополнительными.
Так как сумма углов в точке I равна 360 градусов, по углу сложение, (угол BIF + угол BIE) + (угол CIE + угол CID) + (угол AID + угол AIF) = 360 градусов. Подстановкой 2*(угол BIE) + 2*(угол CID) + 2*(угол AID) = 360 градусов, т. е. угол BIE + угол CID + угол AID = 180 градусов. Но угол CID + угол AID = угол AIC путем сложения углов, таким образом, угол BIE + угол AIC = 180 градусов, поэтому углы BIE и AIC являются дополнительными.
Поскольку углы BIE и AHC являются дополнительными к одному и тому же углу, отсюда следует, что угол BIE = углу AHC.
Так как углы BIE и AHC равны, а углы BEI и ACH
равны (оба прямоугольны по построению), то треугольники BIE
и AHC подобны подобием AA.
Подстановка AC/CG = AC/BE. Тогда по определению подобные треугольники, AC/BE = HC/IE.
Теперь, поскольку углы IJD и HJC являются вертикальными углами, они равный. Также равны углы IDJ и HCJ (оба прямые по построению). Следовательно, треугольники IJD и HJC подобны по АА-подобию.
Путем замены HC/IE = HC/ID. Тогда по определению подобные треугольники, HC/ID = CJ/DJ.
Таким образом, по транзитивности AC/CG = CJ/DJ.
Следующие несколько шагов доказательства потребуют некоторых алгебраических приемов.
Поскольку AC/CG = CJ/DJ, то AC/CG + 1 = CJ/DJ + 1.
Итак, AC/CG + CG/CG = CJ/DJ + DJ/DJ.
Отсюда следует, что (AC + CG)/CG = (CJ + DJ)/DJ.
Но при добавлении сегментов AC + CG = AG, а CJ + DJ = CD.
Следовательно, подстановкой AG/CG = CD/DJ.
Ну тогда AG/CG * 1 = CD/DJ * 1.
Итак, AG/CG * AG/AG = CD/DJ * AD/AD.
Затем AG 2 /CG*AG = CD*AD/DJ*AD.