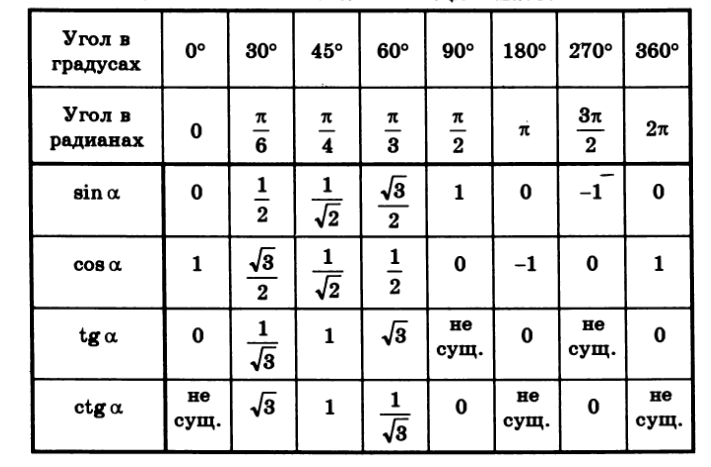
Вычисление тригонометрических функций
Вычисление тригонометрических функцийЭто совершенно необязательная страница. Нет необходимости знать, как вычислять триггерные функции и их обратные, чтобы использовать их. Тем не менее, многих интересует, как вычислялись значения этих функций до и после изобретения калькуляторов и компьютеров. Если вам интересно, то читайте дальше. В противном случае переходите к следующему разделу о косых треугольниках.
До компьютеров: таблицы
Птолемей (100–178) создал одну из первых таблиц для тригонометрии в своей работе, Альмагест , , и он включил математику, необходимую для разработки этой таблицы. Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами. Вместо того, чтобы повторять то, что он сделал для аккордов, давайте посмотрим, как создавать таблицы для синусов и косинусов, используя его методы.
Во-первых, на основе теоремы Пифагора и подобных треугольников можно напрямую вычислять синусы и косинусы определенных углов. В частности, вы можете напрямую найти синусы и косинусы для углов 30°, 45° и 60°, как описано в разделе о косинусах. Птолемей знал еще два угла, которые можно построить, а именно 36° и 72°. Эти углы были построены Евклидом в предложении IV.10 его
Имейте в виду, что если известен синус угла θ , то известен и косинус дополнительного угла 90° – θ ; аналогично, если вы знаете косинус угла θ , то вы знаете синус дополнительного угла 90° – θ :
Таким образом, у вас также есть триггерные функции для 18° и 54°.
Далее вы можете использовать формулы половинного угла для синусов и косинусов, чтобы вычислить значения половины угла, если вы знаете значения угла.
Используя их, из значений 18°, 30° и 54° можно найти значения 27°, 15° и 9° и, следовательно, их дополнения 63°, 75° и 81°.
С помощью формул суммы и разности
Вы можете найти синус и косинус для 3° (от 30° до 27°), а затем заполнить таблицы для синуса и косинуса для углов от 0° до 90° с шагом 3°.
Опять же, используя формулы половинного угла, вы можете создать таблицу с шагом 1,5° (то есть 1° 30′), затем 0,75° (что составляет 45′) или даже 0,375° (что составляет 22′ 30′). «). Но как получить таблицу с шагом в 1°? Птолемей признал, что не существует евклидовой конструкции, позволяющей разделить угол в 3° на три части, чтобы получить угол в 1°, но поскольку функция синуса почти линейна для малых углов, вы можете аппроксимировать sin 1°, просто интерполируя треть пути между значениями sin 0,75° и sin 1,5°. С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с приращением в 1°.
На протяжении столетий создавались лучшие триггерные таблицы. Например, Улугбек (15 век) построил таблицы синусов и тангенсов для каждой угловой минуты с точностью до девяти знаков!
| Улугбек (1394–1449) | |||
|---|---|---|---|
| Обсерватория Улугбека, Самарканд, Узбекистан | |||
Между прочим, если у вас есть таблица синусов, вы можете прочитать ее в обратном порядке, чтобы вычислить арксинус, поэтому для обоих нужна только одна таблица.
После компьютеров: серия Power
Хотя компьютеры и калькуляторы могут просто хранить триггерные таблицы в своей памяти, они также могут напрямую вычислять триггерные функции, что они обычно и делают.
В конце 17 века Ньютон и другие математики разработали степенные ряды. Степенной ряд подобен многочлену неограниченной степени. Для различных триггерных функций эти математики нашли степенные ряды. Вот степенные ряды для синуса и косинуса (где x — это угол, измеренный в радианах):
Три точки … означают, что выражение должно продолжаться бесконечно, добавляя новый термин, затем вычитая термин и т. д. Восклицательный знак ! следует читать как «факториал», и это означает, что вы перемножаете целые числа от 1 до заданного числа. Например, 5!, «факториал пяти», равно 1 умножить на 2 умножить на 3 умножить на 4 умножить на 5, что равно 120, и, следовательно, 6! = 720.
Эти степенные ряды имеют бесконечно много членов, но они так быстро становятся маленькими, что только первые несколько членов дают большой вклад.
Предположим, вы хотите вычислить синус 45°, с точностью до некоторого числа разрядов, используя этот степенной ряд.
Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение
- 0,78539816 0,78539816 3 /3! + 0,78539816 5 0,78539816 7 /7! +…
- 0,78539816 =
0,78539816
0,70465265 = 0,78539816 0,78539816 3 /3!
0,70714304 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5!
0,70710647 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5! 0,78539816 7 /7!
0,70710678 = 0,78539816 0,78539816 3 /3! + 0,78539816 5 /5! 0,78539816 7 /7! + 0,78539816 9 /9!
Требуется небольшой анализ, чтобы определить, сколько членов степенного ряда необходимо для достижения желаемой точности. Кроме того, для ускорения вычислений можно использовать некоторые другие приемы. В любом случае основная идея состоит в том, чтобы использовать первые несколько членов степенного ряда для вычисления триггерных функций.
Степенные ряды для остальных триггерных функций и степенные ряды для обратных триггерных функций можно найти в большинстве книг по математическому анализу, в которых обсуждаются степенные ряды.
Тригонометрический стол | Функции, таблица соотношений и шаги
Введение в тригонометрию
Тригонометрия — это математическая дисциплина, изучающая отношения между углами и сторонами треугольников. Слово «тригонометрия» происходит от греческих слов «треугольник» (τρίγωνος) и «мера» (μέτρος). Эти отношения представлены набором из шести отношений, называемых тригонометрическими функциями: синус, косинус, тангенс, косеканс, секанс и котангенс.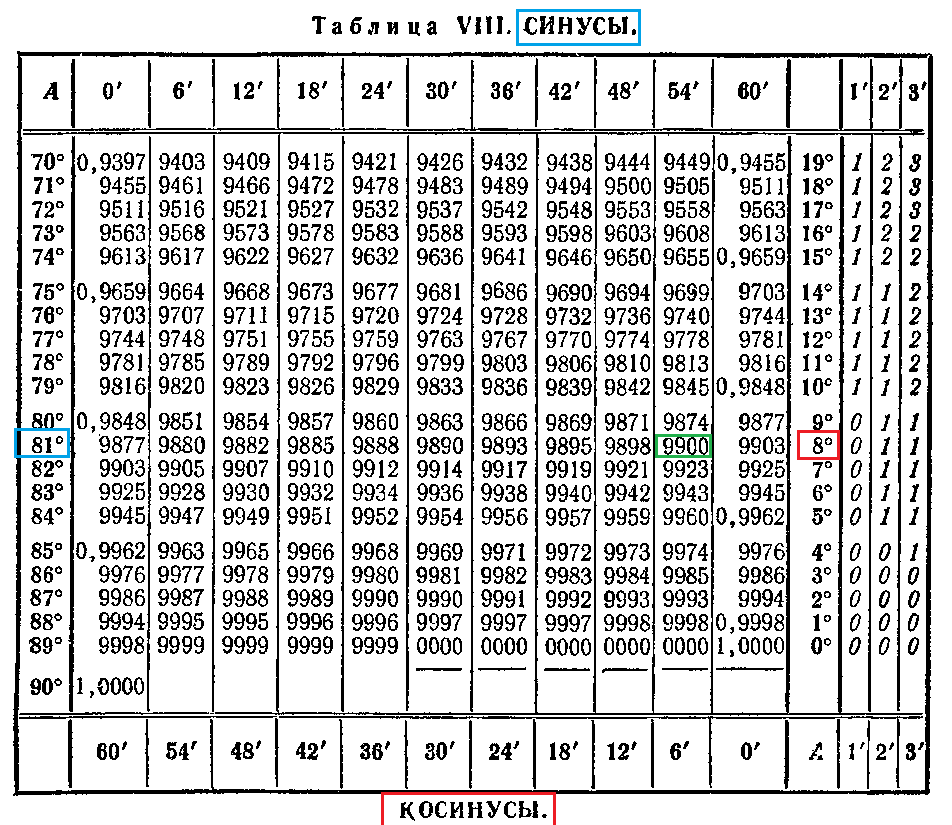
В этой статье светятся знания, покажите Тригонометрическая таблица , Тригонометрические функции , Таблица тригонометрических отношений и Этапы создания тригонометрической таблицы .
Тригонометрические функции можно использовать для решения задач в различных областях, включая астрономию, инженерию и физику. Кроме того, эти функции можно использовать для вычисления свойств фигур, таких как многоугольники и круги.
В следующей таблице перечислены значения шести тригонометрических функций для углов, измеренных в градусах.
Значение функции
- синесин (θ) = противоположный / гипотенуза
- Cosinecos (θ) = Addacent / Hypotenus
- Secantsec(θ) = гипотенуза /
Тригонометрические функции
Тригонометрические функции являются одними из самых важных функций в математике. Они возникают во многих различных контекстах, от геометрии до физики.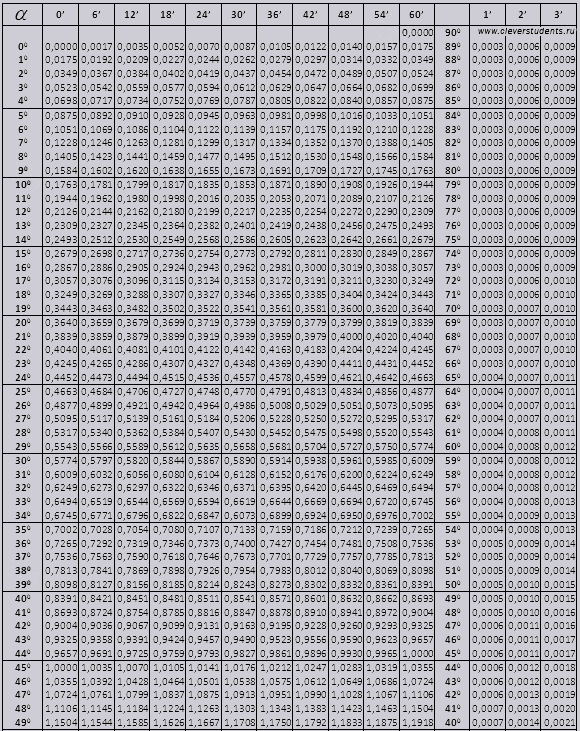
В этом сообщении блога мы рассмотрим, что такое тригонометрические функции и как их можно использовать.
Тригонометрические функции — это функции угла. Наиболее простой тригонометрической функцией является функция синуса, которая дает отношение длины стороны, противоположной углу в прямоугольном треугольнике, к длине гипотенузы. Две другие основные тригонометрические функции — это функции косинуса и тангенса, которые дают отношения двух других сторон прямоугольного треугольника к длине гипотенузы.
Эти три функции могут использоваться для решения задач в различных областях математики и физики. Например, их можно использовать для вычисления длин и углов в треугольниках, для понимания волнового движения и для решения задач, связанных с движением снарядов.
Существует множество других тригонометрических функций, которые можно определить в зависимости от того, что вы хотите с ними делать. Однако в общем случае все эти функции будут определены в терминах трех основных тригонометрических функций.
Таблица тригонометрии
Если вы изучаете тригонометрию, то вы знаете, что большая часть предмета заключается в запоминании большого количества информации. Таблицы тригонометрии могут очень помочь, когда дело доходит до запоминания, и в этом посте блога мы дадим вам таблицу тригонометрии, чтобы помочь вам. Мы также объясним некоторые шаги, связанные с использованием таблицы тригонометрии.
Во-первых, давайте взглянем на таблицу тригонометрии. В этой таблице перечислены шесть наиболее распространенных тригонометрических функций и их значения для различных углов.
Angle (degrees) 0 30 45 60 90
- sin 0 0.5 0.7 0.8 1
- cos 1 0.8 0.7 0.5 0
- tan 0 0.6 1.0 1.7 –
- sec 1 1.7 1,0 0,6 –
- csc – 1,0 1/6 – –
- кроватка – 1/6 1,0 – –
Как видите, в этой таблице перечислены шесть тригонометрических функций: синус (sin), косинус (cos),
Таблица тригонометрических соотношений
Таблица тригонометрических соотношений (показана ниже) представляет собой ссылка на триггерные функции и соответствующие им угловые измерения.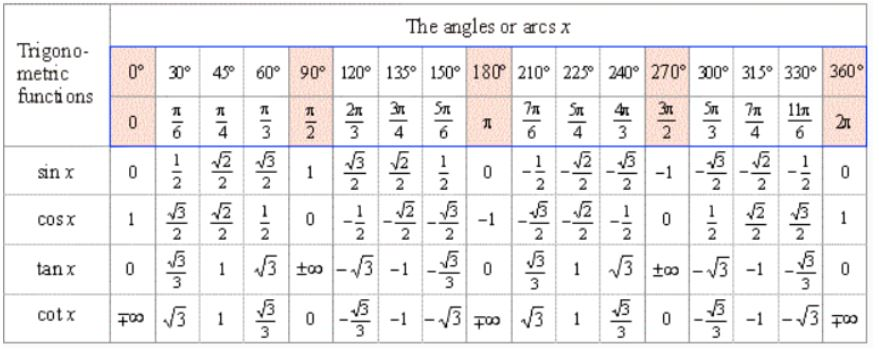
Измерения углов также известны как «тригонометрические функции», и вы можете использовать их для определения значения треугольника на основе его сторон.
Тригонометрические коэффициенты Таблица
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Углы (в радианах) | 0° | №/6 | №/4 | №/3 | №/2 | № | 3π/2 | 2π |
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | 0 | |
| 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 | |
| желтовато-коричневый | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| сек | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Как пользоваться таблицей тригонометрии
Таблица тригонометрии — отличный инструмент для быстрого нахождения значений общих тригонометрических функций.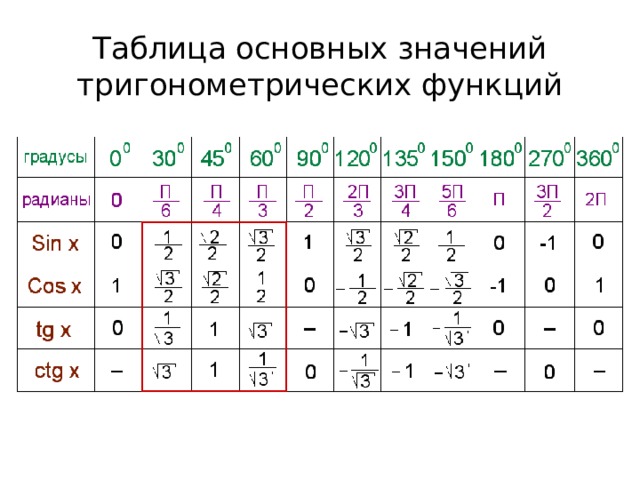
Чтобы использовать таблицу, просто найдите интересующий вас угол в левой части, а затем найдите интересующую вас функцию в верхней строке. Значение на пересечении вашего угла и функции будет значением, которое вы ищете. 9{i*60} равно 0,5+0,86603i.
Этапы поиска значений в тригонометрической таблице
1. Найдите угол, с которым вы работаете, на внешней стороне таблицы.
2. Найдите в таблице строку, соответствующую этому углу.
3. Найдите в таблице столбец, соответствующий искомой функции (синус, косинус, тангенс и т. д.).
4. Значение на пересечении этой строки и столбца является ответом на вашу проблему.
Советы по запоминанию таблицы тригонометрии
Память поможет легче запомнить таблицу тригонометрии. Если вы знаете формулы тригонометрии, то очень легко запомнить таблицу тригонометрии. Таблица отношений тригонометрии зависит от формул тригонометрии, поскольку они составляют эту таблицу.
Вот несколько шагов для запоминания таблицы тригонометрии.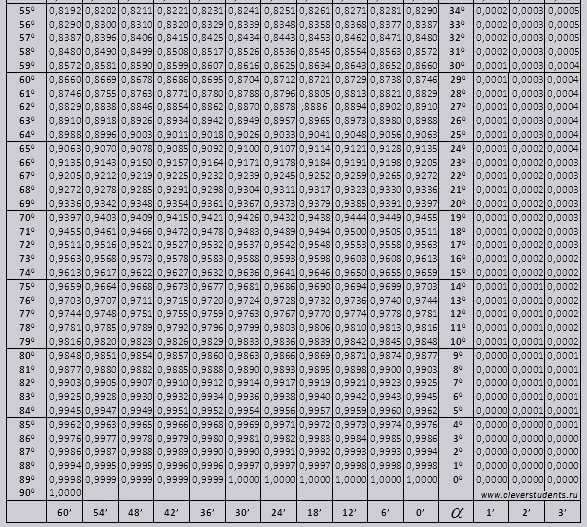
Прежде чем начать, постарайтесь запомнить приведенные ниже формулы тригонометрии.
- sin x = cos (90° – x)
- cos x = sin (90° – x)
- tan x = cot (90° – x)
- cot x = tan (90° – x)
- sec x = cosec (90° – x)
- cosec x = sec (90° – x)
- 1/sin x = cosec x
- 1/cos x = sec x
- 1/tan x = cot x
- 1/cot x = 1/sec x
Шаги по созданию тригонометрической таблицы
Тригонометрическая таблица охватывает значения тригонометрических соотношений для всех основных углов в диапазоне от 0º до 360º.
Шаг 1: Создайте таблицу, в верхней строке которой перечислены углы.
, например 0°, 30°, 45°, 60°, 90°, а затем запишите все тригонометрические функции в первый столбец, такие как sin, cos, tan, cosec, sec, cot.
Шаг 2: Определение значения sin: запишите углы 0°, 30°, 45°, 60°, 90° в порядке возрастания и присвойте им значения 0, 1, 2, 3, 4 в соответствии с порядком .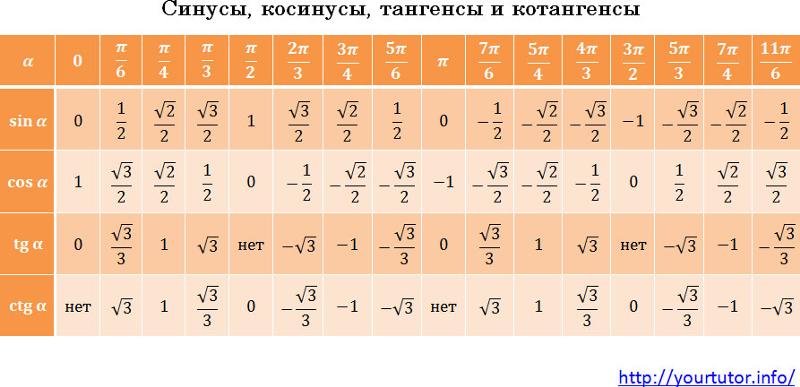
Итак, 0° ⟶ 0; 30° ⟶ 1; 45° ⟶ 2; 60° ⟶ 3; 90° ⟶ 4.
Затем разделите значения на 4 и извлеките из них квадратный корень. 0° ⟶ √0/2; 30° ⟶ 1/2; 45° ⟶ 1/ √2; 60° ⟶ √3/2; 90° ⟶ √(4/4).
Это дает значения синуса для этих 5 углов. Now for the remaining three use:
| Angles (In Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Шаг 3: . .
Используйте эту формулу для вычисления значений cos x. Например, cos 45° = sin (90° – 45°) = sin 45°. Аналогично, cos 30° = sin (90° – 30°) = sin 60°.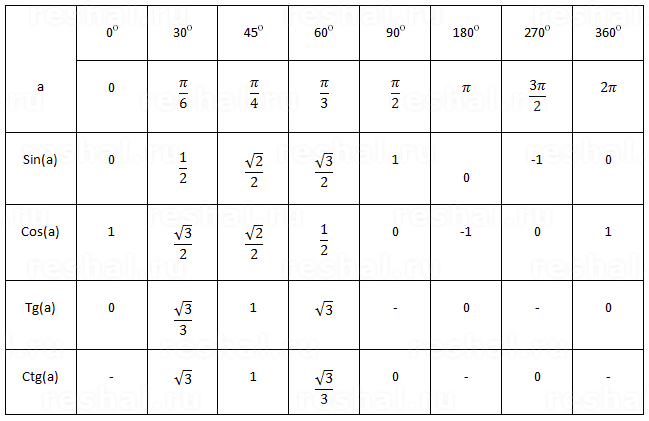
Используя это, вы можете легко узнать значение функции cos как
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
Step 4: Determining the value of tan: ( тангенс x = sin x/cos x). Следовательно, значение функции тангенса может быть сгенерировано как
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Шаг 5: Определение значения cot: (cot x = 1/tan x).
Use the relation to generate the cot function as,
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90 ° | 180° | 270° | 360° |
| ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ | |
4. x)
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Step 7: Determining the value of sec: (sec x = 1/cos x)
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
Заключение
Тригонометрическая таблица является очень полезным инструментом для решения задач, связанных с тригонометрическими функциями.