математическая гипербола. Как построить гиперболу?
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой \(y=\frac{k}{x}\), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции \(y=\frac{k}{x}\) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти
2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=\frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$y\neq\color{red} {\frac{1}{x}}+0$$
\(\frac{1}{x}\) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=\frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=\color{red} {\frac{1}{x+2}}-1$$
Дробь \(\color{red} {\frac{1}{x+2}}\) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Пример №3:
$$\begin{align*}
&y=\frac{2+x}{1+x} \\\\
&y=\frac{\color{red} {1+1}+x}{1+x} \\\\
&y=\frac{1}{1+x}+\frac{1+x}{1+x}\\\\
&y=\frac{1}{1+x}+1\\\\
&y=\frac{1}{\color{red} {1+x}}+1
\end{align*}$$
Находим первую асимптоту.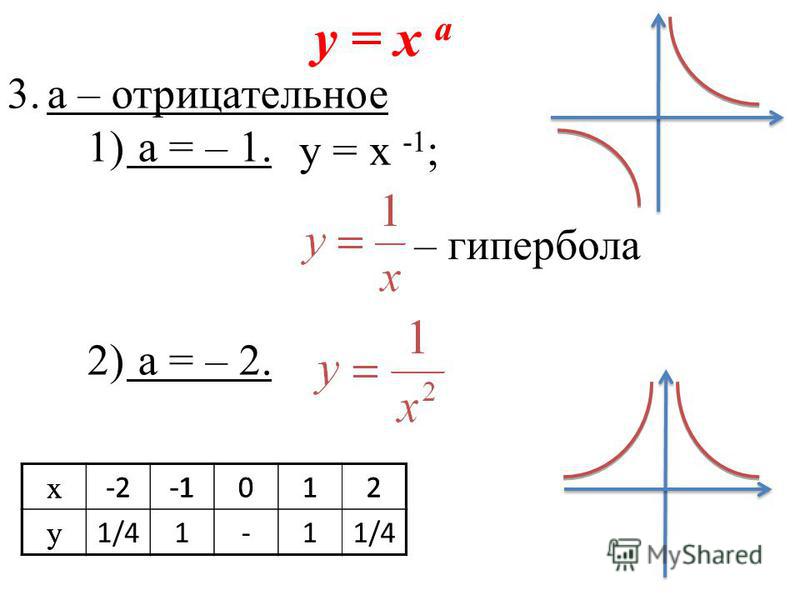
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red}{\frac{1}{1+x}}+1$$
\(\color{red}{\frac{1}{1+x}}\) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=\frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
$$y=\frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.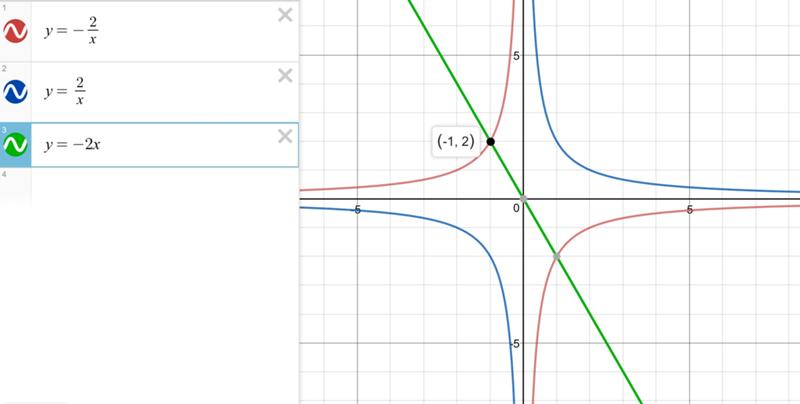
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
$$f(-x)=\frac{1}{-x}=-\frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=\frac{-1}{x-1}-1$$
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=\color{red} {\frac{-1}{x-1}}-1$$
Дробь \(\color{red} {\frac{-1}{x-1}}\) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
2
Эллипс и гипербола. Пошаговое решение математических задач. Теперь рассмотрим другой тип — эллипс.
ЭЛЛИПСЫ Определение эллипса также основано на расстоянии.
ЭЛЛИПСЫ Эллипс – это множество всех точек на плоскости, сумма расстояний которых от двух фиксированных точек постоянна. Две неподвижные точки называются фокусами эллипса.
Рисунок 3.37
Например. эллипс на рис. 3.37 имеет фокусы в точках F и F ‘. По определению эллипс состоит из всех точек P таких, что сумма d(P, F) + d(RF ‘) постоянна. Эллипс на рис. 3.37 имеет центр в начале координат. Точки V и V’ являются вершинами эллипса, а отрезок, соединяющий V и V’, является большой осью. Фокусы всегда лежат на большой оси. Отрезок линии от B до B’ является малой осью. Большая ось имеет длину 2а, а малая ось имеет длину 2b. 92) = 1, домен [-a, a] и диапазон [-b, b]. Обратите внимание, что эллипс на рис.
3.37 симметричен относительно оси x, оси y и начала координат. В более общем смысле каждый эллипс симметричен относительно своей большой оси, малой оси и своего центра.
Эллипсы имеют множество полезных применений. Когда Земля совершает годичное путешествие вокруг Солнца, она описывает эллипс. Космические корабли летают вокруг Земли по эллиптическим орбитам, а планеты вращаются по эллиптическим орбитам вокруг Солнца. Интересным недавним применением является использование эллиптической ванны для нехирургического удаления камней в почках. 92)/4=1
Этот эллипс с центром в начале координат с точками пересечения по оси x 3 и -3 и точками пересечения по оси y 2 и -2. Дополнительные упорядоченные пары, которые удовлетворяют уравнению эллипса, могут быть найдены и построены по мере необходимости (калькулятор с ключом квадратного корня будет полезен). Область определения этого отношения равна -3,3. а диапазон -2,2. График показан на рисунке 3.38.
Рисунок 3.
Давайте посмотрим, как наш математический решатель генерирует график для этой и подобных задач. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров. 92 имеет центр в точке (h, k). Аналогичным образом можно переместить эллипс так, чтобы его центр находился вдали от начала координат.
ПРОСТО
Одним из самых полезных свойств эллипса является его свойство рефлексии. если луч проецируется из одного фокуса на эллипс, он отразится в другом фокусе. Эта функция помогла ученым разработать литограф, машину, которая использует ударные волны для дробления камней в почках. Волны исходят из одного фокуса и, отражаясь, достигают камня в почке, расположенного во втором фокусе. 92/16=1,
. Члены в числителях дробей в левой части, однако. указывают, что это отношение представляет собой эллипс с центром в (2, -1). Нарисуйте эллипс, используя тот факт, что a = 3 и b = 4. Станьте в точке (2.-1) и найдите две точки на расстоянии 3 единиц от (2.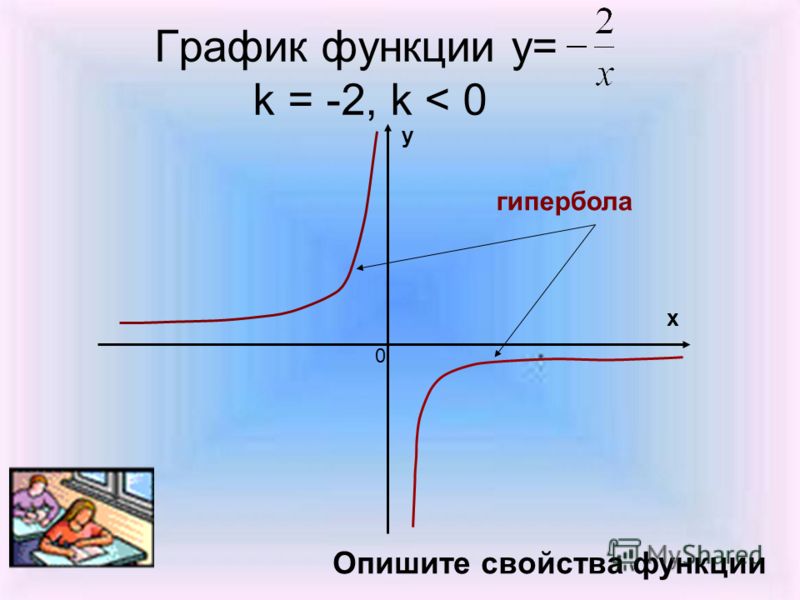
-1) на горизонтальной линии, одну справа от (2.-1) и одну слева. Найдите две другие точки на вертикальной линии, проходящей через (2. -1), одну на 4 единицы вверх и одну на 4 единицы вниз. Так как b > a, вершины находятся на
вертикальная линия через центр. Вершины (2.3) и (2.-5). При необходимости найдите дополнительные точки. Окончательный график показан на рис. 3.39. Как следует из графика, домен равен -1,5, а диапазон -5,3.
Давайте посмотрим, как наш математический решатель генерирует график для этой и подобных задач. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решите аналогичную задачуВведите свою задачу
ГИПЕРБОЛА Определение эллипса требует, чтобы сумма расстояний от двух фиксированных точек была постоянной. Определение гиперболы включает в себя разность, а не сумму.
Некоторые применения гипербол даны в упражнениях.
Как и в случае с эллипсами, уравнение гиперболы можно найти из формулы расстояния и определения гиперболы. (См. упражнение 45.)
УРАВНЕНИЯ ГИПЕРБОЛ
92=180/16=45/4 Умножить на 9; самые низкие условия.
y=+-(3root(5))/(2)≈ +-3,4. Возьми квадратный корень и воспользуйся калькулятором.
График включает точки (6,3.4) и (6, -3.4). Если x = -6, y ≈ +-3,4, то точки (-6, 3,4) и (-6, -3,4) также есть на графике. Эти точки, наряду с другими точками на графике, использовались, чтобы набросать окончательный график, показанный на рис. 3.40. Из графика следует, что область определения этой гиперболы равна (-∞,-4) {объединению} (4,∞), а диапазон равен (-∞,∞). Использование тестов на симметрию показало бы, что эта гипербола симметрична относительно оси x, оси y и начала координат. 92/49=1.
Рис. Используйте точки пересечения x: если x = 5, то y = (+-7/5)(5) = +-7, а если x = -5, y = 17.
Эти четыре точки (5, 7), (5, -7), (-5, 7) и (-5, -7) ведут к прямоугольнику, показанному на рис. 3.41. Расширенные диагонали этого прямоугольника являются асимптотами гиперболы. Гипербола имеет точки пересечения x 5 и -5. Домен (-∞,-5) {объединение} (5,∞), а диапазон (-∞,∞). Окончательный график показан на рис. 3.41. 92/4=1,
за исключением того, что он находится в центре (-3, -2). См. Рисунок 3.42.
Давайте посмотрим, как наш математический решатель генерирует график для этой и подобных задач. Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить похожую задачуВведите свою задачу
Пример 7
ПОИСК УРАВНЕНИЯ ГИПЕРБОЛЫ
Напишите уравнение гиперболы с центром в точке (-2, 1) и вершиной в точке (-2,3), и с равным половине b.
92+Dy+{Эпсилон}=0,, где либо A, либо C должны быть отличны от нуля. Особенности каждого из конических сечений приведены ниже.
УРАВНЕНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
| C Коническое сечение | Характеристика | Пример |
| Парабола | Либо A=0, либо C=0, но не оба одновременно. |