Тест на функция `y=k/x` (гипербола) по алгебре за 9 класс
Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!
Вопросов в тесте: 12
Среднее время прохождения: ~10:00
Зарегистрируйся и получи персональный план прокачки знаний до 100%!
Как работает платформа Skills4u
Тестирование по предмету за класс
Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения
Персональный план обучения
План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету
Закрепление темы на 100%
Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%
Проработка слабых тем с предыдущих классов
Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем
Почему нужно пройти общее тестирование по алгебре за 9 класс, а не по отдельной теме «Функция `y=k/x` (гипербола)»
Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.
Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.
Зарегистрироваться и пройти тестирование
Как растут результаты учеников
после занятий на тренажерах Skills4u
Занятия
на Skills4u
Занятия
с учебником
Успеваемость
Мотивация
Внимательность
Скорость
Самостоятельность
Запоминание
Первичный Тест «Функция `y=k/x` (гипербола)» по алгебре за 9 класс онлайн и бесплатно предоставляется всем желающим.
Советуем пройти тестирование за весь 9 класс по алгебре, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.
После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.
Зарегистрироваться и пройти тестирование
А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам
Ученик
Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!
Родитель
Наслаждайтесь прогрессом вашего ребенка в школе и на платформе
Учитель/
репетитор
Задавайте и проверяйте домашние задания прямо на платформе
Зарегистрироваться и пройти тестирование
65127
учеников уже занимаются с нами
Алгебра 7-9 класс. Гипербола — math200.ru
Skip to contentАлгебра 7-9 класс. Гиперболаadmin2022-10-07T19:18:53+03:00
Скачать файл в формате pdf. 2} + x}}\) и определите, при каких значениях m прямая \(y = m\) не имеет с графиком общих точек.
2} + x}}\) и определите, при каких значениях m прямая \(y = m\) не имеет с графиком общих точек.
Ответ
ОТВЕТ: -4; -3.
Ответ
ОТВЕТ: \(\left( {4;0} \right).\)
ОТВЕТ: \(\left( { — 4;0} \right).\)
Ответ
ОТВЕТ: \(\left( {2;3} \right).\)
 Найдите координаты точки касания.
Найдите координаты точки касания.Ответ
ОТВЕТ: \(\left( { — 3;2} \right).\)
Реклама
Поддержать нас
Гипербола | безграничная алгебра |
Введение в гиперболу
Гиперболы являются одним из четырех конических сечений и описываются определенными уравнениями.
Цели обучения
Соедините уравнение гиперболы с формой ее графика
Ключевые выводы
Ключевые точки
- Гипербола образуется пересечением плоскости, перпендикулярной основаниям двойного конуса.
- Все гиперболы имеют значение эксцентриситета больше
111
. - Все гиперболы имеют две ветви, каждая из которых имеет вершину и фокус.
- Все гиперболы имеют асимптоты — прямые линии, образующие букву X, к которой гипербола приближается, но никогда не касается.
Ключевые термины
- гипербола : Одно из конических сечений.

- эллипс : Одно из конических сечений.
- вершин : точка поворота кривой функции. Каждая гипербола имеет две вершины.
- фокальная точка : Точка не на гиперболе, вокруг которой кривая гиперболы.
Гипербола может быть определена несколькими способами. Гиперболой является:
- Пересечение прямого кругового двойного конуса с плоскостью под углом, большим, чем наклон конуса (например, перпендикулярно основанию конуса)
- Множество всех точек, для которых разница расстояний до двух фокусных точек постоянна
- Набор всех точек, для которых отношение расстояния до одной фокусной точки к расстоянию до прямой (направляющей) больше единицы
Давайте посмотрим, как это второе определение дает нам то, что называется стандартной формой уравнения гиперболы.
Диаграмма гиперболы: Гипербола, показанная синим цветом, имеет центр в начале координат, два фокуса в
(−c,0)(-c,0)(−c,0)
и
(c,0)(c,0)(c,0)
+a+a+a
и
-a-a-a
на оси
xxx
.
Начнем с двух фокусов,
F1F_1F1
и
F2F_2F2
, расположенных на оси
xxx
-c (0,010)0 )(c,0)
и
(−c,0)(-c,0)(−c,0)
(возможны другие варианты). Нам нужен набор всех точек, имеющих одинаковые разница между расстояниями до этих точек. Центр этой гиперболы является началом координат
(0,0)(0,0)(0,0)
.
Представьте, что мы берем точку на красной кривой гиперболы, называемую
PPP
, и принимаем эту точку за значение
+a+a+a
на оси
xxx
. Тогда разница расстояний между
PPP
и двумя фокальными точками составляет:
(P→F2)−(P→F1)=(c+a)−(c−a)=2a\displaystyle{ \начать{выравнивать} (P \rightarrow F_2) — (P \rightarrow F_1) &= (c+a) — (c — a)\\ &= 2а \end{выравнивание} }(P→F2)−(P→F1)=(c+a)−(c−a)=2a 92} = 1}a2x2+b2y2=1
Сходство не случайно. Эллипс может быть определен как все точки, которые имеют постоянную сумму расстояний до двух фокусных точек, а гипербола определяется как все точки, которые имеют постоянную разность расстояний до двух фокусных точек.
Эллипс может быть определен как все точки, которые имеют постоянную сумму расстояний до двух фокусных точек, а гипербола определяется как все точки, которые имеют постоянную разность расстояний до двух фокусных точек.
Существует еще одна распространенная форма уравнения гиперболы, которая на первый взгляд выглядит совсем иначе:
y=1x\displaystyle{y = \frac{1}{x}}y=x1
или
xy= 1ху = 1ху=1 9\circ45∘
. Чтобы доказать, что это то же самое, что и стандартная гипербола, вы можете сами проверить, что у нее две фокусные точки и что все точки имеют одинаковую разность расстояний. Другой способ доказать это алгебраически — построить повернутую систему координат
xxx
—
yyy
.
Части гиперболы
Свойства гиперболы можно определить из ее уравнения.
Цели обучения
Опишите части гиперболы и выражения для каждой
Ключевые выводы
Ключевые моменты
Гипербола – это одно из четырех конических сечений. Все гиперболы имеют общие черты, и можно определить особенности любой гиперболы из определяющего ее уравнения.
Стандартная форма
Схема гиперболы: Все гиперболы имеют общие черты. Гипербола состоит из двух кривых, каждая из которых имеет вершину и фокус. Поперечная ось — это ось, проходящая через обе вершины и фокусы, а сопряженная ось перпендикулярна ей. Гипербола также имеет асимптоты, которые пересекаются через «х». Две ветви гиперболы находятся на противоположных сторонах креста асимптот. Вершины и асимптоты можно использовать для формирования прямоугольника с вершинами в центрах двух противоположных сторон и углами на асимптотах. Центры двух других сторон вдоль сопряженной оси называются ко-вершинами. Место, где асимптоты гиперболы пересекаются, называется центром. 92} = 1}a2(y−k)2−b2(x−h)2=1
Место, где асимптоты гиперболы пересекаются, называется центром. 92} = 1}a2(y−k)2−b2(x−h)2=1
Мы будем использовать гиперболу с осями
xxx
, чтобы продемонстрировать, как определять характеристики гиперболы, поэтому что
aaa
связан с координатами
xxx
, а
bbb
связан с координатами
yyy
. Для гиперболы оси
yyy
ассоциации обратные.
Центр
Центр имеет координаты
(ч,к)(ч,к)(ч,к)
.
Вершины
Вершины имеют координаты
(h+a,k)(h + a,k)(h+a,k)
и
(h−a,k)(h-a,k)(h−a,k) )
. Линия, соединяющая вершины, называется поперечной осью.
Линия, соединяющая вершины, называется поперечной осью.
Со-вершины
Ковершины соответствуют
bbb
, «длине малой полуоси», и имеют координаты
(h,k+b)(h,k+b)(h,k+b)
и
(ч,к-б)(ч,к-б)(ч,к-б)
.
Асимптоты
Большая и малая оси
aaa
и
bbb
в качестве вершин и ко-вершин описывают прямоугольник, который имеет тот же центр, что и гипербола, и имеет размеры
2a×2b2a \times 2b2a×2b.
. Асимптоты гиперболы – это прямые линии, являющиеся диагоналями этого прямоугольника. Поэтому мы можем использовать углы прямоугольника, чтобы определить уравнение этих линий:
y=±ab(x−h)+k\displaystyle{y = \pm \frac{a}{b}(x — h) + k}y=±ba(x−h)+k
Сам прямоугольник также полезен для рисования графика гиперболы вручную, так как он содержит вершины. Рисуя гиперболу, сначала нарисуйте прямоугольник. Затем нарисуйте асимптоты в виде расширенных линий, которые также являются диагоналями прямоугольника. Наконец, нарисуйте кривую гиперболы, следуя асимптоте внутрь, изгибаясь внутрь, чтобы коснуться вершины прямоугольника, а затем следуя другой асимптоте наружу. Повторите для другой ветки. 92c2=a2+b2
Рисуя гиперболу, сначала нарисуйте прямоугольник. Затем нарисуйте асимптоты в виде расширенных линий, которые также являются диагоналями прямоугольника. Наконец, нарисуйте кривую гиперболы, следуя асимптоте внутрь, изгибаясь внутрь, чтобы коснуться вершины прямоугольника, а затем следуя другой асимптоте наружу. Повторите для другой ветки. 92c2=a2+b2
Прямоугольная гипербола
Прямоугольные гиперболы, определяемые как
(x−h)(y−k)=m\left(xh\right)\left(yk\right) = m(x−h)(y−k)=m
для некоторые константы
ммм
гораздо проще анализировать, чем гиперболы стандартной формы.
Прямоугольная гипербола: Эта прямоугольная гипербола имеет центр в начале координат и также является графиком функции
f(x)=1x\displaystyle{f(x) = \frac{1}{x}} f(x)=x1
.
Центр
Центр прямоугольной гиперболы имеет координаты
(h,k)(h,k)(h,k)
.
Вершины и ковершины
Прямоугольная гипербола очень симметрична. Значения его большой и малой осей равны, так что
a=b=2ma = b = \sqrt{2m}a=b=2m
. Вершины имеют координаты
(h+2m,k+2m)(h+\sqrt{2m},k+\sqrt{2m})(h+2m
,k+2m
)
и 9.
Ковершины имеют координаты
(h−2m,k+2m)(h-\sqrt{2m},k+\sqrt{2m})(h−2m
,k+2m
) .
Асимптоты
Асимптоты прямоугольной гиперболы равны
ххх
— и
92c2=a2+b2как и раньше. Имея
a=b=2ma = b = \sqrt{2m}a=b=2m
, мы находим, что
c=±2mc = \pm 2\sqrt{m}c=±2m
. Следовательно, фокусные точки расположены в
Следовательно, фокусные точки расположены в
(h+2m,k+2m)(h+2\sqrt{m},k+2\sqrt{m})(h+2m
,k+2m
)
и
(h−2m,k−2m)(h-2\sqrt{m},k-2\sqrt{m})(h−2m
,k−2m
)
.
Применение гипербол
Гипербола — это незамкнутая кривая с двумя ответвлениями и разрезом через обе половины двойного конуса, который не обязательно параллелен оси конуса.
Цели обучения
Обсудите применение гиперболы в реальных задачах
Ключевые выводы
Ключевые моменты
- Гиперболы применяются в ряде различных систем и задач, включая солнечные часы и трилатерацию.
- Гиперболы можно увидеть на многих солнечных часах.
 В любой день солнце вращается по кругу на небесной сфере, и его лучи, попадающие в точку на солнечных часах, очерчивают световой конус. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение.
В любой день солнце вращается по кругу на небесной сфере, и его лучи, попадающие в точку на солнечных часах, очерчивают световой конус. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение. - Гипербола является основой для решения задач трилатерации, задачи определения местоположения точки по разности ее расстояний до заданных точек или, что то же самое, по разнице времен прихода синхронизированных сигналов между точкой и заданными точками.
Ключевые термины
- трилатерация : Определение местоположения точки на основе ее расстояния от трех других точек.
- гипербола : Коническое сечение, образованное пересечением конуса с плоскостью, которая пересекает основание конуса и не касается конуса.
- коническое сечение : Любая из четырех различных форм, являющихся точками пересечения конуса с плоскостью, а именно круг, эллипс, парабола и гипербола.

Применение и решение проблем
Как мы уже должны знать, гипербола — это незамкнутая кривая с двумя ответвлениями, пересечение плоскости с обеими половинами двойного конуса. Плоскость может быть или не быть параллельной оси конуса.
Гипербола : Гипербола — открытая кривая с двумя ветвями, пересечение плоскости с обеими половинами двойного конуса. Плоскость может быть или не быть параллельной оси конуса.
Вот несколько примеров гипербол в реальном мире.
Солнечные часы
Гиперболы можно увидеть на многих солнечных часах. Каждый день солнце вращается по кругу на небесной сфере, и его лучи, попадающие в точку на солнечных часах, очерчивают световой конус. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение. Угол между плоскостью земли и солнечным конусом зависит от того, где вы находитесь, и от наклона оси Земли, который меняется в зависимости от сезона. В большинстве населенных широт и в большинстве времен года это коническое сечение представляет собой гиперболу.
В большинстве населенных широт и в большинстве времен года это коническое сечение представляет собой гиперболу.
Солнечные часы работают, отбрасывая тень вертикального маркера, иногда называемого гномоном, на циферблат на горизонтальной поверхности. Угол между солнечным светом и землей будет таким же, как угол, образованный линией, соединяющей кончик гномона с концом его тени.
Если мы отметим, куда в течение дня падает конец тени, линия, проведенная тенью, образует на земле гиперболу (этот путь называется линией склонения ). Форма этой гиперболы меняется в зависимости от географической широты и времени года, поскольку эти факторы влияют на угол конуса солнечных лучей относительно горизонта.
Параметры прослеживаемой гиперболы, такие как ее асимптоты и эксцентриситет, связаны с конкретными физическими условиями, которые ее создали, а именно с углом между солнечным светом и землей и широтой, на которой находятся солнечные часы.
Гиперболы и солнечные часы: Гиперболы как линии склонения на солнечных часах.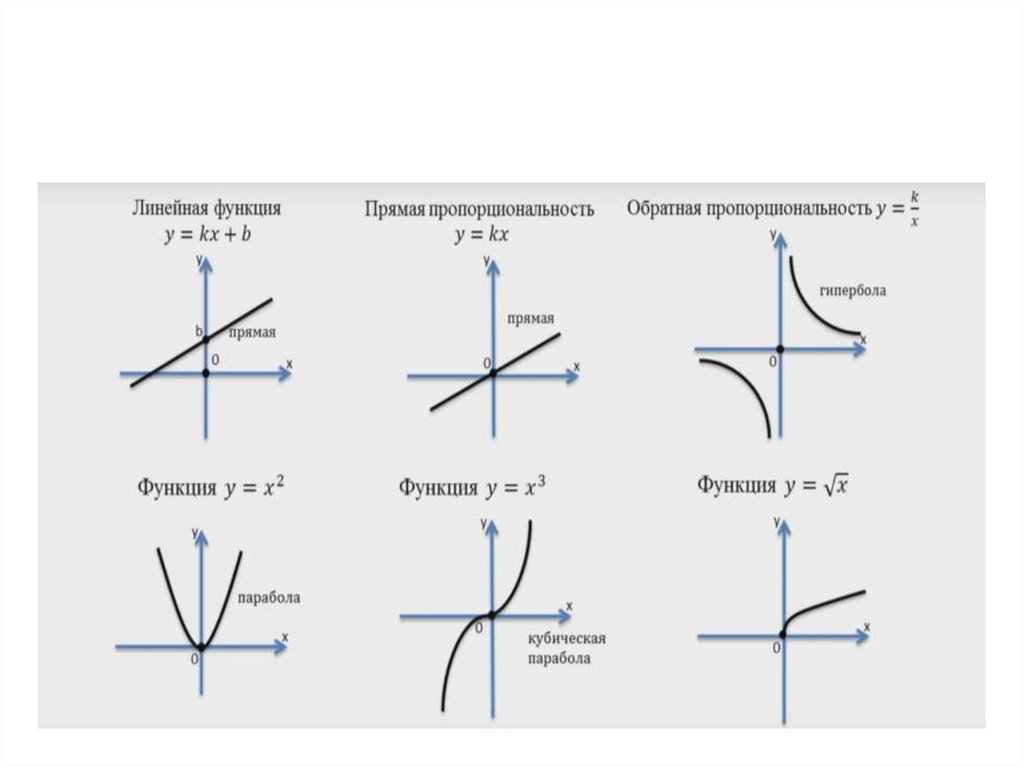
Трилатерация
Трилатерация — это метод определения точного местоположения с использованием его расстояний до заданных точек. Его также можно охарактеризовать как разницу во времени прихода синхронизированных сигналов между желаемой точкой и известными точками. Эти типы проблем возникают в навигации, в основном морской. Корабль может определить свое местоположение, используя время прибытия сигналов от передатчиков GPS. В качестве альтернативы самонаводящийся радиомаяк можно определить, сравнив время прихода его сигналов на две отдельные приемные станции. Это можно использовать для отслеживания людей, мобильных телефонов, интернет-сигналов и многого другого.
В случае, когда корабль или другой объект, который необходимо определить, знает только разницу расстояний между ним и двумя известными точками, кривая возможных местоположений представляет собой гиперболу. Один из способов определения гиперболы заключается именно в этом: кривая точек такая, что абсолютное значение разности расстояний до двух фокусных точек остается постоянным.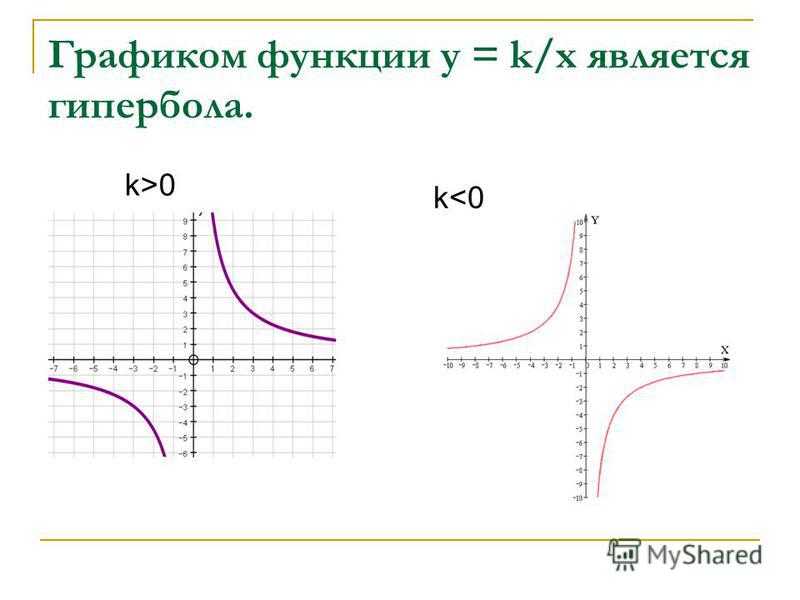
Итак, если мы назовем эту разницу расстояний
2a2a2a
, гипербола будет иметь вершины, разделенные одинаковым расстоянием
2a2a2a
, а фокусами гиперболы будут две известные точки.
Орбита частиц Кеплера
Орбита Кеплера — это путь, по которому движется любое вращающееся тело. Это может быть применено к частице любого размера, пока гравитация является единственной силой, определяющей орбитальную траекторию. В зависимости от свойств орбиты, включая размер и форму (эксцентриситет), эта орбита может иметь любое из четырех конических сечений. В частности, если эксцентриситет e орбиты больше
111
, путь такой частицы представляет собой гиперболу. На рисунке синей линией показана гиперболическая орбита Кеплера. В общем случае гравитационной орбиты массивный объект является одним из фокусов гиперболы (или другого конического сечения).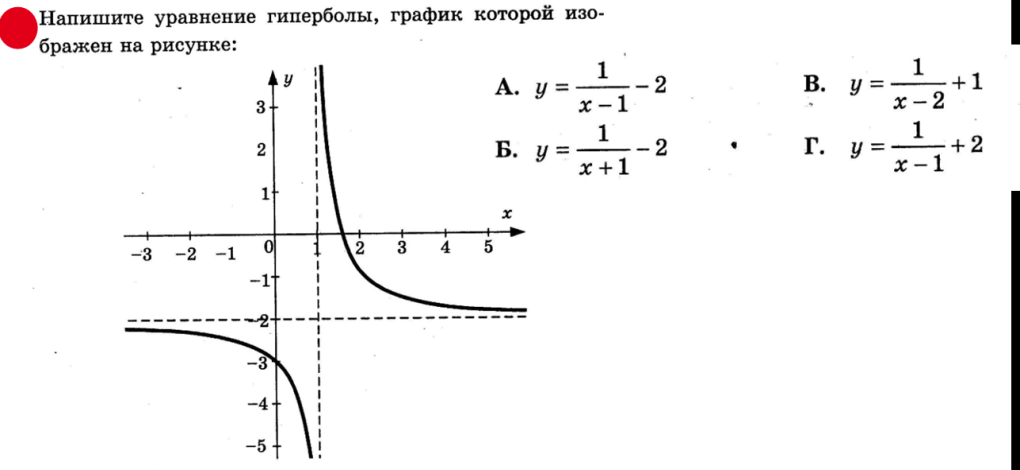
Орбиты Кеплера: Схема различных форм орбиты Кеплера и их эксцентриситетов. Синий — гиперболическая траектория (
e>1e > 1e>1
). Зеленый — параболическая траектория (
е=1е = 1е=1
). Красный — эллиптическая орбита (
e<1e < 1e<1
). Серый — это круговая орбита (
e=0e = 0e=0
).
Физически другой способ понять гиперболические орбиты — это использовать энергию орбитальной частицы. Орбиты, которые являются круговыми или эллиптическими, являются связанными орбитами, то есть объект никогда не выходит за пределы своего замкнутого пути вокруг одной из фокусных точек. Это связано с полной энергией частицы
EEE
меньше минимальной энергии, необходимой для побега, поэтому в этих случаях
EEE
считается отрицательным.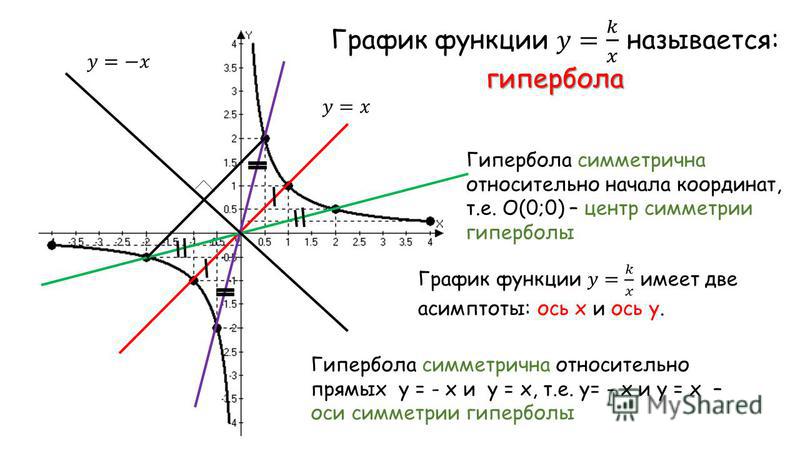
При параболической траектории частица покидает систему. Однако это совершенно особый случай, когда полная энергия
EEE
является в точности минимальной энергией убегания, поэтому
EEE
в этом случае считается равным нулю.
Если к минимальному (нулевому) значению добавляется какая-либо дополнительная энергия, траектория станет гиперболической, и поэтому
EEE
положительно в случае гиперболической орбиты.
Лицензии и авторство
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Автор: : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Гипербола. Предоставлено : Википедия. Расположен по адресу : https://en.
 wikipedia.org/wiki/Hyperbola. Лицензия : CC BY-SA: Attribution-ShareAlike
wikipedia.org/wiki/Hyperbola. Лицензия : CC BY-SA: Attribution-ShareAlike - OpenStax CNX. Предоставлено : Гипербола. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
- CNX_Precalc_Figure_10_02_013.jpg. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Rectangular_hyperbola.svg. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Гипербола. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Атрибуция
- Википедия. Предоставлено : Гипербола. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_10_02_013.
 jpg. Предоставлено : OpenStaxCNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
jpg. Предоставлено : OpenStaxCNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution - Rectangular_hyperbola.svg. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- CNX_Precalc_Figure_10_02_003.jpg. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
- Rectangular_hyperbola.svg. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Hyperbola. Лицензия : Общественное достояние: Нет данных Copyright
- Орбита Кеплера. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Гипербола. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- гипербола. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- трилатерация. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- коническое сечение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- CNX_Precalc_Figure_10_02_013.jpg. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
- Rectangular_hyperbola.svg. Предоставлено : Википедия.
 Лицензия : Общественное достояние: неизвестно Авторские права
Лицензия : Общественное достояние: неизвестно Авторские права - CNX_Precalc_Figure_10_02_003.jpg. Предоставлено : OpenStax CNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
- Rectangular_hyperbola.svg. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Гипербола. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OrbitalEccentricityDemo. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Гипербола (PSF). Предоставлено : Википедия. Лицензия : Общественное достояние: Не известно Авторские права
Математические слова: Гипербола
Математические слова: Гипербола
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 В любой день солнце вращается по кругу на небесной сфере, и его лучи, попадающие в точку на солнечных часах, очерчивают световой конус. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение.
В любой день солнце вращается по кругу на небесной сфере, и его лучи, попадающие в точку на солнечных часах, очерчивают световой конус. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение.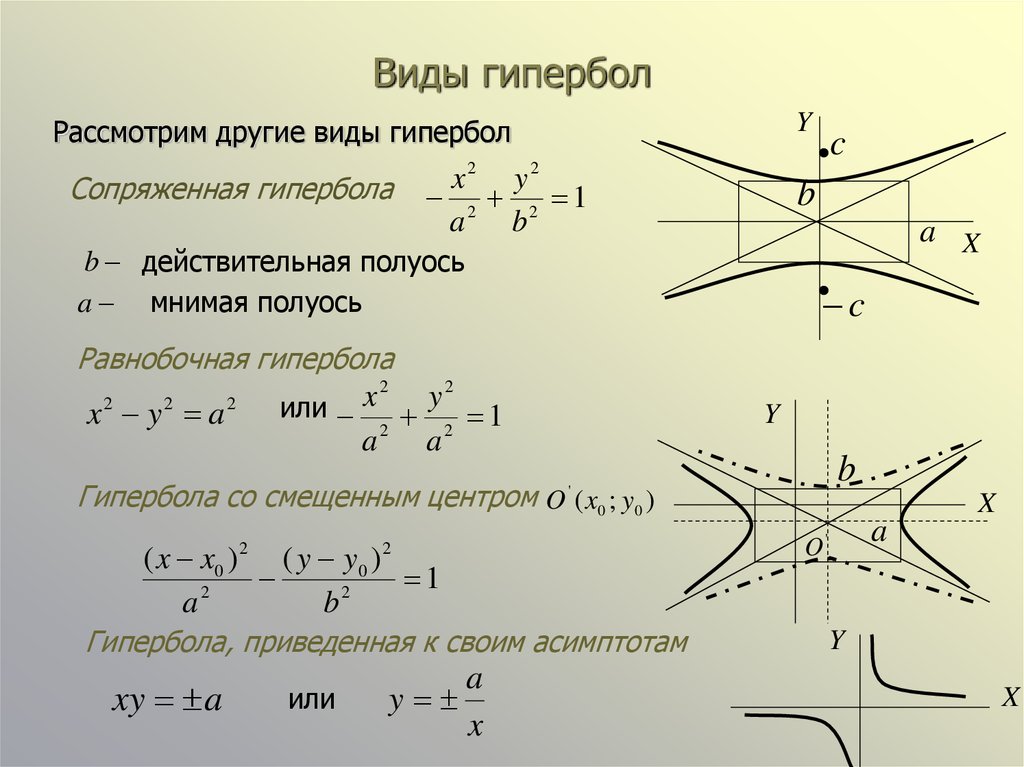
 wikipedia.org/wiki/Hyperbola. Лицензия : CC BY-SA: Attribution-ShareAlike
wikipedia.org/wiki/Hyperbola. Лицензия : CC BY-SA: Attribution-ShareAlike  jpg. Предоставлено : OpenStaxCNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution
jpg. Предоставлено : OpenStaxCNX. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/12-2-the-hyperbola. Лицензия : CC BY: Attribution 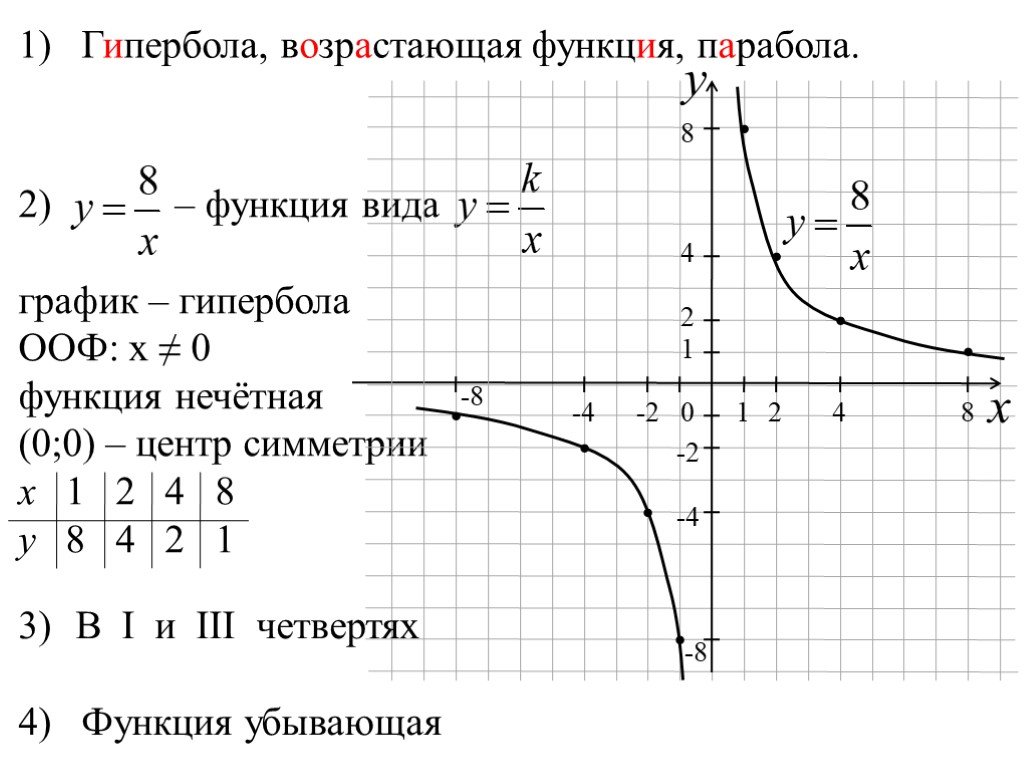 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : Общественное достояние: неизвестно Авторские права
Лицензия : Общественное достояние: неизвестно Авторские права