Зачем модуль? Заметим, что в левую часть равенства можно подставлять вместо \(b\) все числа \(b\ne 0\). Если в правой части не поставить модуль (т.е. \(\log_3b\)), то вместо \(b\) можно подставлять только \(b>0\). Таким образом, теряется часть возможных значений числа \(b\).
2) В формулах (4): \[\log_a{bc}=\log_a{|b|}+\log_a{|c|} \ \ \ \ \ \ \text{и}
\ \ \ \ \ \ \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\] аналогичная причина: в левую часть равенств можно подставлять как одновременно положительные \(b\) и \(c\), так и одновременно отрицательные (так как произведение двух отрицательных чисел является положительным числом). А вот в правые части, если в них убрать модули, отрицательные \(b\) и \(c\) уже подставлять будет нельзя (так как аргумент логарифма – всегда положительное выражение). Таким образом, не поставив модули, мы значительно сузим возможные значения для \(b\) и \(c\).
Пример:
Если не поставить модули, а записать, например, \(\log_2{bc}=\log_2b+\log_2c\), то значения \(b=-1\) и \(c=-1\) не удовлетворяют равенству.
Свойства логарифмов и примеры их решений. Исчерпывающий гид (2020)
(от греческого λόγος — «слово», «отношение» и ἀριθμός — «число») числа b по основанию a (log α b ) называется такое число c , и b = a c , то есть записи log α b =c и b=a c эквивалентны. Логарифм имеет смысл, если a > 0, а ≠ 1, b > 0.
Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени , в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).
Из данной формулировки вытекает, что вычисление x= log α b , равнозначно решению уравнения a x =b.
Например:
log 2 8 = 3 потому, что 8=2 3 .
Выделим, что указанная формулировка логарифма дает возможность сразу определить значение логарифма , когда число под знаком логарифма выступает некоторой степенью основания.
И в правду, формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа .
Вычисление логарифма именуют логарифмированием . Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей трансформируется в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов трансформируются в произведение сомножителей.
Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).
На данном этапе целесообразно рассмотреть образцы логарифмов log 7 2, ln√ 5, lg0.0001.
А записи lg(-3), log -3 3.
2, log -1 -4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число , во второй — отрицательное число в основании, а в третьей — и отрицательное число под знаком логарифма и единица в основании.
Условия определения логарифма.
Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма . Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = log α b , называемое основным логарифмическим тождеством , которое напрямую следует из данного выше определения логарифма.
Возьмем условие a≠1 . Поскольку единица в любой степени равна единице, то равенство x=log α b может существовать лишь при b=1 , но при этом log 1 1 будет любым действительным числом . Для исключения этой неоднозначности и берется a≠1 .
Докажем необходимость условия a>0 . При a=0 по формулировке логарифма может существовать только при b=0 .
И соответственно тогда log 0 0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0 . А при a нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0
И последнее условие b>0 вытекает из неравенства a>0 , поскольку x=log α b , а значение степени с положительным основанием a всегда положительно.
Особенности логарифмов.
Логарифмы характеризуются отличительными особенностями , которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов. При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ — область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться.
Почему так?
Начнем с простого: допустим, что. Тогда, например, число не существует, так как в какую бы степень мы не возводили, всегда получается. Более того, не существует ни для какого.
Но при этом может равняться чему угодно (по той же причине — в любой степени равно). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае: в любой положительной степени — это, а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение.
Вспомним определение: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна, а произведение. Легко подобрать, это числа и.
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
Это явно неверно, так как основание не может быть отрицательным, то есть корень — «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и, сразу отбросим корень, и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно):
Найдите корень уравнения. Если корней несколько, в ответе укажите меньший из них.
Решение:
В первую очередь напишем ОДЗ:
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание, чтобы получить аргумент? Во вторую. То есть:
Казалось бы, меньший корень равен.
Но это не так: согласно ОДЗ корень — сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .
Ответ: .
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо логарифм:
Это равенство называется основным логарифмическим тождеством . Хотя по сути это равенство — просто по-другому записанное определение логарифма :
Это степень, в которую нужно возвести, чтобы получить.
Например:
Реши еще следующие примеры:
Пример 2.
Найдите значение выражения.
Решение:
Вспомним правило из раздела : , то есть, при возведении степени в степень показатели перемножаются. Применим его:
Пример 3.
Докажите, что.
Решение:
Свойства логарифмов
К сожалению, задачи не всегда такие простые — зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение.
Это проще всего сделать, зная свойства логарифмов . Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1:
Доказательство:
Пусть, тогда.
Имеем: , ч.т.д.
Свойство 2: Сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: .
Доказательство:
Пусть, тогда. Пусть, тогда.
Пример: Найдите значение выражения: .
Решение: .
Только что выученная формула помогает упростить сумму логарифмов, а не разность, так что сразу эти логарифмы не объединить. Но можно сделать наоборот — «разбить» первый логарифм на два:А вот обещанное упрощение:
.
Зачем это нужно? Ну например: чему равно?
Теперь очевидно, что.
Теперь упрости сам:
Задачи:
Ответы:
Свойство 3: Разность логарифмов:
Доказательство:
Все точно так же, как и в пункте 2:
Пусть, тогда.
Пусть, тогда. Имеем:
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: . Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению — такое сразу не упростить.
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это — . Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов :
Ответ для проверки:
Упрости сам.
Примеры
Ответы.
Свойство 4: Вынесение показателя степени из аргумента логарифма:
Доказательство: И здесь тоже используем определение логарифма:пусть, тогда. Имеем: , ч.т.д.
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения.
Решение: .
Реши сам:
Примеры:
Ответы:
Свойство 5: Вынесение показателя степени из основания логарифма:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6: Вынесение показателя степени из основания и аргумента логарифма:
Или если степени одинаковые: .
Свойство 7: Переход к новому основанию:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Свойство 8: Замена местами основания и аргумента логарифма:
Доказательство: Это частный случай формулы 7: если подставить, получим: , ч.
т.д.
Рассмотрим еще несколько примеров.
Пример 4.
Найдите значение выражения.
Используем свойство логарифмов № 2 — сумма логарифмов с одинаковым основанием равна логарифму произведения:
Пример 5.
Найдите значение выражения.
Решение:
Используем свойство логарифмов № 3 и № 4:
Пример 6.
Найдите значение выражения.
Решение:
Используем свойство № 7 — перейдем к основанию 2:
Пример 7.
Найдите значение выражения.
Решение:
Как тебе статья?
Если ты читаешь эти строки, значит ты прочитал всю статью.
И это круто!
А теперь расскажи нам как тебе статья?
Научился ты решать логарифмы? Если нет, то в чем проблема?
Пиши нам в комментах ниже.
И, да, удачи на экзаменах.
На ЕГЭ и ОГЭ и вообще в жизни
Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание.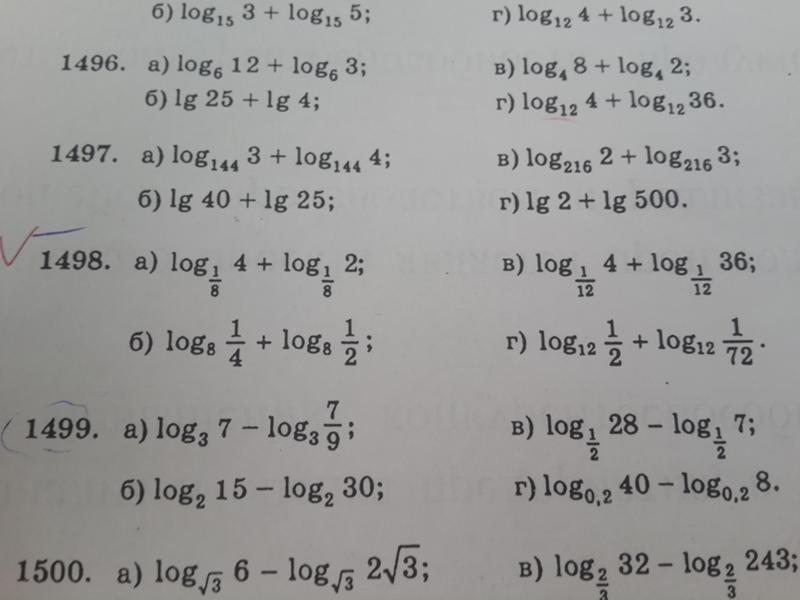
Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Содержание
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 | 0 |
| Область значений | — ∞ | — ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | — ∞ | |
| — ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом :
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Логарифмирование — это математическая операция взятия логарифма.
При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b
,
имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a .
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e .
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n
— целое,
то будет одним и тем же числом при различных n .
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См.
также:
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6, поскольку 2 6 = 64.
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко.
Например, попробуйте найти log 2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5, log 3 8, log 5 100.
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1, т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется.
Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача.
Вычислите логарифм: log 5 25
Вычислите логарифм: log 5 25- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Составим и решим уравнение:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Получили ответ: 2.
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.
е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459.
..
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Йоост Бюрги | Швейцарский математик
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю. - Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Факты и сопутствующий контент
Викторины
- Числа и математика
Формула логарифма: объяснение, формула, примеры решений и важные часто задаваемые вопросы Математически логарифмы выражаются следующим образом: m — это логарифм n по основанию b, если bm = n, что также можно записать как m = logb n.
Например, 43 = 64; следовательно, 3 — это логарифм 64 по основанию 4, или 3 = log464. Точно так же мы знаем, что 103 = 1000, тогда 3 = log101000. Логарифмы с основанием 10 обычно известны как обычные или бриггсовские логарифмы и просто записываются как log n. В этой статье мы обсудим, что такое логарифм, формулы логарифмов, основные формулы логарифмов, правило изменения основания, правила и формулы логарифмов, для чего используется логарифм и т. д.
Правила логарифмирования
Существует 7 правил логарифмирования, которые полезны при расширении логарифмов, сокращении логарифмов и решении логарифмических уравнений. Семь правил логарифмов обсуждаются ниже:
1. Правило произведения
\[\log_{b}{(P \times Q)} = \log_{b}{P} + \log_{b}{Q} \]
Логарифм произведения равен сумме логарифмов факторов.
2. Частное правило
\[\log_{b}{(\frac{P}{Q})} = \log_{b}{P} — \log_{b}{Q}\] 9{y}} = y \]
Правило логарифмирования основания в степени утверждает, что логарифм b с рациональным показателем равен показателю степени, умноженному на его логарифм.
6. Основание степени логарифма Правило
b log y = y
Приведенное выше правило гласит, что возведение логарифма числа в основание логарифма равно числу.
7. Правило идентификации
\[\log_{y}{y} = 1 \]
Аргумент логарифма (в скобках) аналогичен основанию. Поскольку основание равно аргументу, y может быть больше 0, но не может быть равен 0.
Формулы логарифмирования
Ниже приведены некоторые из различных формул логарифмирования, которые помогают решать уравнения логарифмирования.
Основная формула логарифма
Некоторые из различных основных формул логарифма приведены ниже:
\[\log_{b}{(m \times n)} = \log_{b}{m} + \ log_{b}{м}\] 9{n})} \]
Сложение и вычитание
Изменение базовой формулы
.
\[\log_{n}{m} = \frac{\log_{d}{m}}{\log_{d}{n}}\]
Решенные примеры
1. Решить Следующее: 2 log429
Решение:
Дано,
\[2 \log_{4}{29} \]
Используя замену формулы основания n, получаем 9{2}\] \]
\[75x = 90\]
\[X = \frac {90}{75}\]
\[X = \frac {6}{5}\]
В математике характеристики логарифма используются для решения задач логарифмирования. Многим алгебраическим характеристикам, таким как коммутативные, ассоциативные и дистрибутивные, нас учили в начальной школе. Есть пять основных особенностей логарифмических функций.
Логарифмическое число связано с показателем степени и степенью, таким образом, если xn = m, то logxm = n. В результате мы также должны понимать экспоненциальный закон. Например, логарифм 10000 по основанию 10 равен 4, потому что 4 — это степень, в которую нужно возвести десять, чтобы получить 10000 : 104 = 10000, поэтому log1010000 = 4,9.
0128
Мы можем представить логарифм произведения как сумму логарифмов, логарифм частного как разность логов и логарифм мощности как произведение, используя эти функции.
Вещественное число Логарифмы видны только в положительных действительных числах; отрицательные и комплексные числа имеют комплексные логарифмы.
Применение логарифмов
Логарифмы имеют широкий спектр применений как в математике, так и за ее пределами. Давайте рассмотрим несколько примеров того, как логарифмы используются в повседневной жизни:
Они используются для расчета магнитуды землетрясения.
Логарифмы используются для расчета уровня шума в децибелах, например звука колокола.
Логарифмы используются в химии для определения кислотности или уровня pH.
Они используются для расчета прироста денежной массы при заданной процентной ставке.
Логарифмы обычно используются для расчета времени, необходимого для распада или экспоненциального развития чего-либо, например роста бактерий или радиоактивного распада.
Их также можно использовать в вычислениях, требующих преобразования умножения в сложение или наоборот.
Вместо простого вычисления мы можем использовать таблицу логарифмов, чтобы получить логарифм целого числа. Прежде чем вычислять логарифм числа, мы должны сначала понять его характеристическую и мантиссу части.
Характеристическая часть — Характеристический компонент — это целая часть числа. Любое число больше единицы имеет положительную характеристику, а если оно на единицу меньше, чем количество цифр слева от десятичной точки в данном целом числе, оно имеет отрицательную характеристику.
Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.
Часть мантиссы. Часть мантиссы представляет собой десятичную часть логарифмического числа, которая всегда должна быть положительной. Если часть мантиссы имеет отрицательное значение, превратите ее в положительное значение.
Как вы используете таблицу журнала?
Процесс определения логарифмического значения числа с помощью логарифмической таблицы показан ниже. Во-первых, вы должны понять, как использовать таблицу журнала. Таблица журнала предоставляется как ресурс для определения значений.
Шаг 1. Понимание идеи логарифма. Каждая таблица журнала может использоваться только на определенной основе. Логарифмическая база 10 — наиболее часто используемая форма таблицы логарифмов.
Шаг 2: Определить характеристику числа и часть мантиссы.
Например, чтобы получить значение log1015,27, сначала разделите характеристику и часть мантиссы.
Часть характеристики = 15
Часть мантиссы = 27
Шаг 3. Используйте общую таблицу журнала. Теперь используйте строку 15, чтобы проверить столбец 2 и записать соответствующее значение. В итоге получается 1818.
Шаг 4. Вычислите среднюю разницу, используя таблицу логарифмов. Проведите пальцем по столбцу средней разницы 7 и строке 15 и запишите соответствующее значение как 20.
Шаг 5. Объедините значения, полученные на шагах 3 и 4. Это равно 1818 + 20 = 1838. В результате значение 1838 представляет часть мантиссы.
Шаг 6. Найдите отличительный признак. Поскольку число находится в диапазоне от 10 до 100 (от 101 до 102), отличительным признаком должен быть 1.
Шаг 7: Наконец, объедините часть характеристики и мантиссы, чтобы получить 1,1838.
Пример
Вот пример использования таблицы логарифмов для получения значения логарифмической функции.
Определите значение log102,872.
Решение:
Шаг 1. Характеристический компонент равен 2, а часть мантиссы равна 872.
Шаг 2. Изучите строки 28 и 7 в таблице. В итоге получается значение 4579.
Шаг 3. Изучите значение средней разницы для строки 28 и среднюю разницу в столбце 2. Значение, связанное со строкой и столбцом, равно 3. получаем 4582. Это сечение мантиссы.
Шаг 5: Поскольку количество цифр слева от десятичной части равно единице, характеристическая часть меньше единицы. В результате характеристический участок равен 0
Шаг 6: Наконец, соедините характеристики и части мантиссы. В результате получается 0,4582.