определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
- Определение и функция гиперболы
- Алгоритм построения гиперболы
- Пример 1
- Пример 2
Определение и функция гиперболы
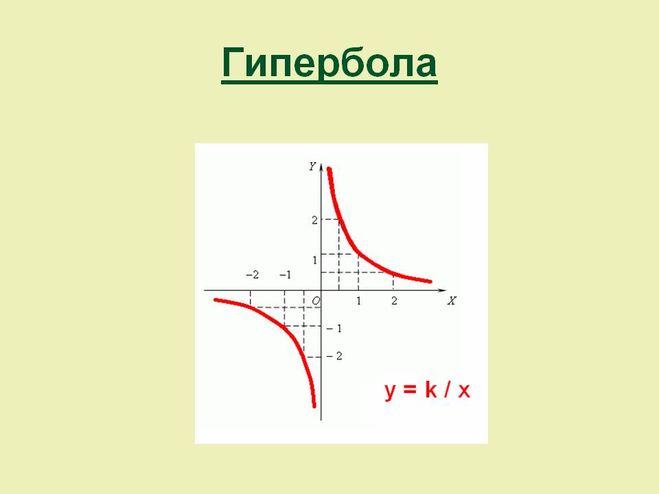
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Здесь:
- x – независимая переменная;
- k ≠ 0;
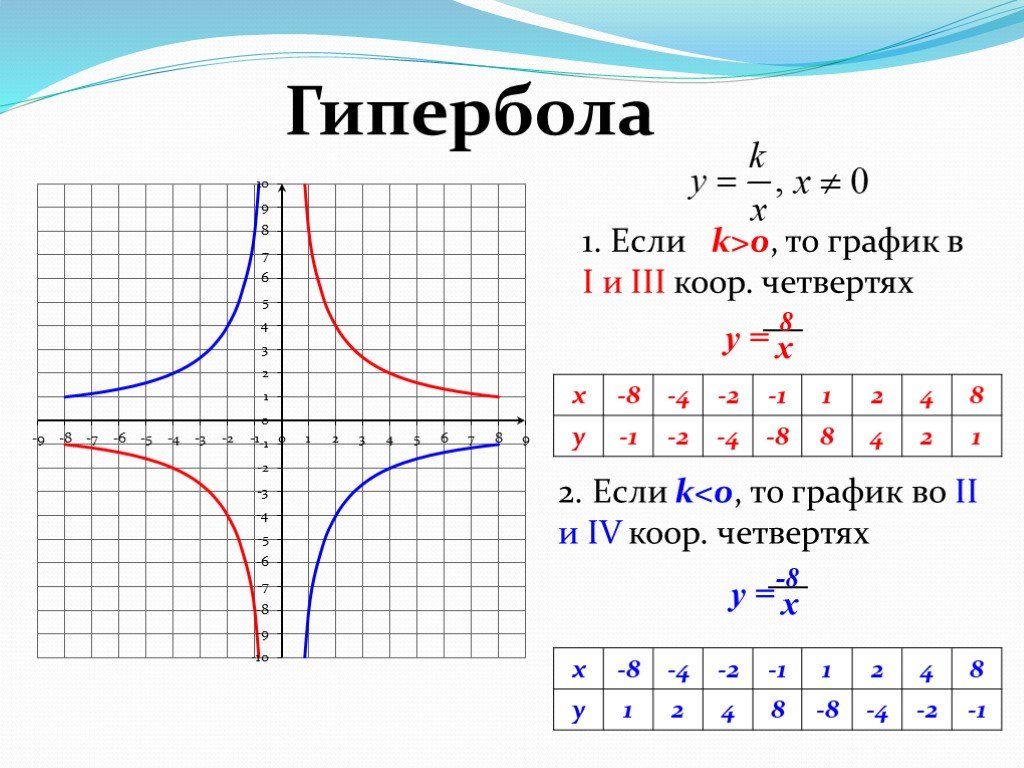
- при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
- при k < 0 график находится во II и IV четвертях.
На рисунке ниже изображен пример гиперболы.
- Линии графика (зеленым цветом) называются его
- Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
- Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)
Смещение асимптот
Допустим у нас есть функция, заданная формулой:
В этом случае:
- x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
- y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.
Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):
Алгоритм построения гиперболы
Пример 1
Дана функция y = 4/x. Построим ее график.
Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| x | y | Расчет y |
| 0,5 | 8 | 4 / 0,5 = 8 |
| 1 | 4 | 4 / 1 = 4 |
| 2 | 2 | 4 / 2 = 2 |
| 4 | 1 | 4 / 4 = 1 |
| 8 | 0,5 | 4 / 8 = 0,5 |
Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат.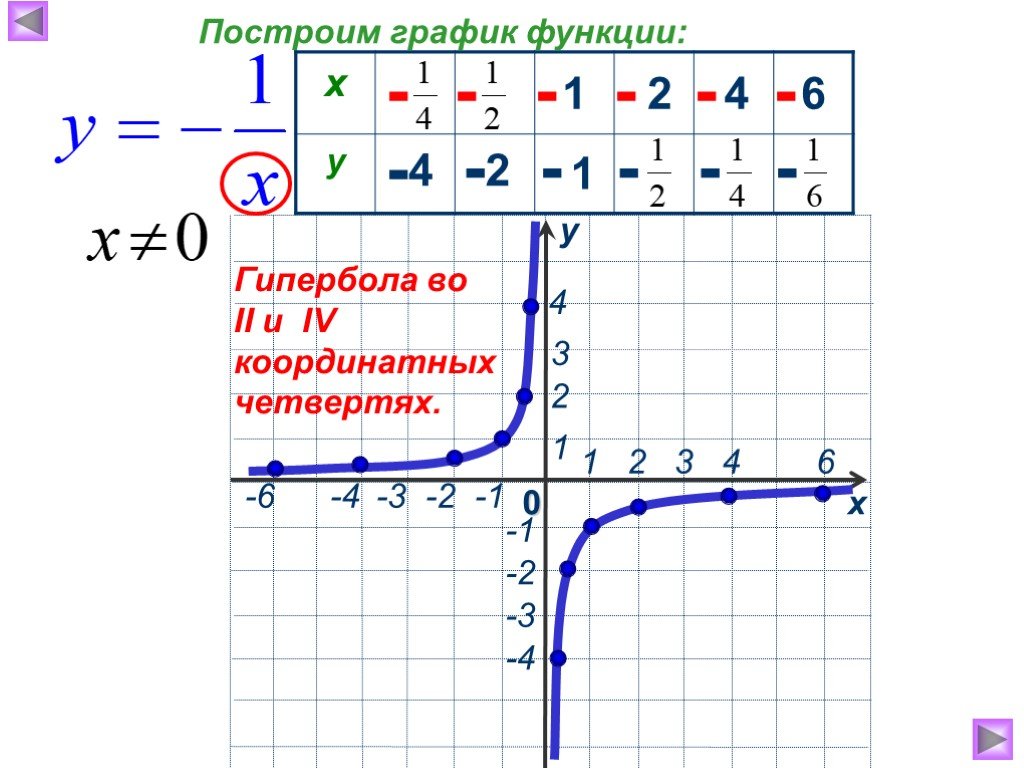 В итоге получится ветвь гиперболы, расположенная в первой четверти.
В итоге получится ветвь гиперболы, расположенная в первой четверти.
Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.
| x | y | Расчет y |
| -0,5 | -8 | 4 / -0,5 = -8 |
| -1 | -4 | 4 / -1 = -4 |
| -2 | -2 | 4 / -2 = -4 |
| -4 | -1 | 4 / -4 = -1 |
| -8 | -0,5 | 4 / -8 = -0,5 |
Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.
На этом построение гиперболы завершено.
Пример 2
Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:
Решение
Так как k < 0, график будет располагаться во второй и четвертой четвертях.
Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).
Составим таблицу соответствия значений x и y.
| </sub></em></nobr>» data-order=»<nobr><em>x<sub> II четв.</sub></em></nobr>»>x II четв. | y II четв. | x IV четв. | </sub></em></nobr>»>y IV четв. |
| -1 | 4,5 | 3,5 | 0 |
| 1 | 5 | 4 | 2 |
| 2 | 6 | 5 | 3 |
| 2,5 | 8 | 7 | 5″ data-order=»3.5″>3.5 |
Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.
Гипербола
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная, не равная 0 и меньшая расстояния между фокусами.
Каждая гипербола
характеризуется положением своих
фокусов и тем числом, которому равен
модуль (постоянной!) разности расстояний
от точек эллипса до его фокусов. Так
же, как и в случае эллипса, для получения
уравнения гиперболы выберем подходящую
систему координат. Пусть точки и
на плоскости − фокусы эллипса, обозначим
через
половину расстояния между ними. Как и
для эллипса, ось
(фокальную ось) направим вдоль этого отрезка, начало
системы координат расположим на середине
отрезка
,
а ось
− перпендикулярно к этому отрезку (см.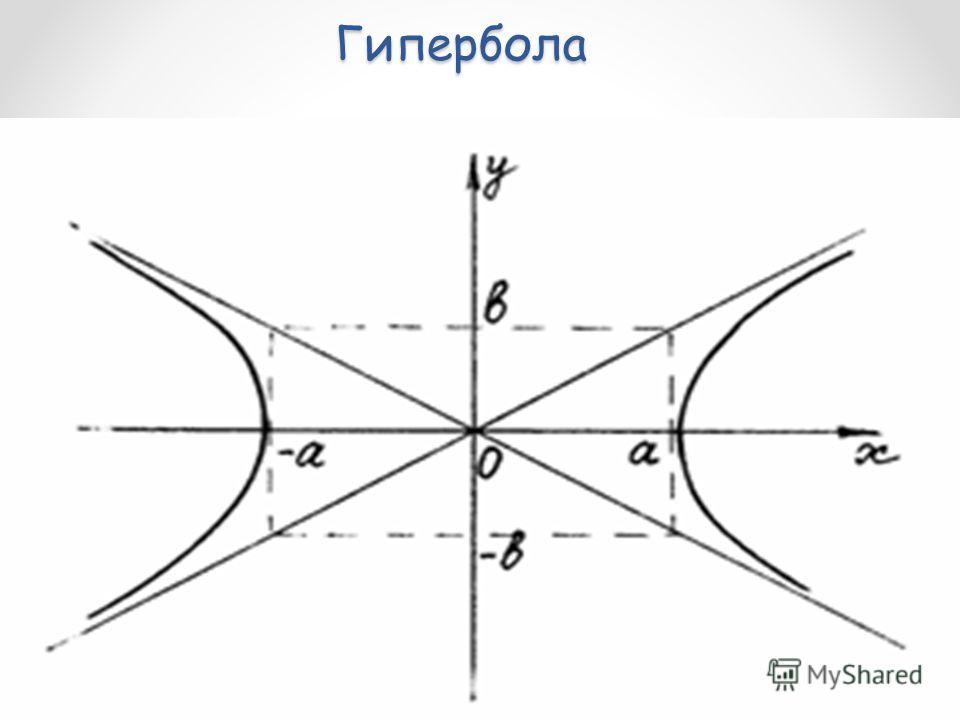 рисунок).
Это и будет подходящая система координат
для данной гиперболы. Найдем ее уравнение
в этой системе координат. Пусть
− произвольная точка на гиперболе.
Найдем соотношение, которому в этом
случае должны удовлетворять координаты
и
этой точки. Обозначим буквой
(постоянный!) модуль
рисунок).
Это и будет подходящая система координат
для данной гиперболы. Найдем ее уравнение
в этой системе координат. Пусть
− произвольная точка на гиперболе.
Найдем соотношение, которому в этом
случае должны удовлетворять координаты
и
этой точки. Обозначим буквой
(постоянный!) модуль
(1) ,
где новый параметр определен формулой
( 2) .
Под корнем в (2) опять число положительное, так как . Уравнение (1) называется каноническим уравнением гиперболы. Из этого уравнения (аналогично случаю эллипса) следует симметрия гиперболы относительно выбранных осей координат, а ее вид в первой четверти легко установить, выразив из (1) через :
(3) .
Часть гиперболы, заключенная в (1) четверти, есть график функции (3). Функция в (3), очевидно, определена и возрастает при , причем . Методами математического анализа легко также установить наличие так называемой асимптоты, т.е. прямой, к которой безгранично приближается (снизу, не пересекая) график функции (3) при безграничном удалении точки графика в бесконечность. Уравнение этой прямой : , поэтому она проходит через начало координат. Сказанное позволяет начертить график функции (3), который является частью гиперболы, заключенной в 1 четверти (см. рисунок).
Используя указанную
выше симметричность гиперболы относительно
осей координат, можно теперь восстановить
форму всей гиперболы (см. рисунок).
Пунктирными линиями о
бозначены асимптоты
гиперболы − прямые с уравнениями и ,
к которым безгранично примыкают ветви
гиперболы Точки пересечения гиперболы,
заданной каноническим уравнением, с
фокальной осью
называются  Отрезок оси ординат между точками с
координатами и называется мнимой осью.
Числа
и
называются соответственно действительной и мнимой полуосями гиперболы. Начало координат
называется ее центром.
Отрезок оси ординат между точками с
координатами и называется мнимой осью.
Числа
и
называются соответственно действительной и мнимой полуосями гиперболы. Начало координат
называется ее центром.
Из сказанного следует следующий способ построения гиперболы по заданному ее каноническому уравнению (1). Прежде всего, из уравнения определяются числа и . Затем числа и наносятся на ось , а числа и наносятся на ось . Затем по этим точкам строится так называемый основной прямоугольник, который на рисунке изображен пунктиром. Затем проводятся диагонали этого прямоугольника и продолжаются за его границы – это асимптоты гиперболы. Затем рисуются ветви гиперболы, исходящие из ее вершин и приближающиеся к асимптотам.
Как видно из
рисунка, форма гиперболы зависит от
соотношения сторон
и
в основном прямоугольнике, т.е. от
отношения
. Если
мало (близко к 0),
то число
мало по сравнению с числом
. В этом случае основной прямоугольник
вытянут вдоль фокальной оси Ох,
а потому ветви гиперболы «прижаты» к
этой оси. Если же
велико (намного больше 1), то число
мало по сравнению с числом
.
В этом случае основной прямоугольник
вытянут вдоль оси Оу,
а потому ветви гиперболы «прижаты» к
этой оси. Однако, как и в случае эллипса,
в качестве параметра, характеризующего
форму гиперболы, берут не
, а отношение
, которое тесно связано с отношением
.
В этом случае основной прямоугольник
вытянут вдоль фокальной оси Ох,
а потому ветви гиперболы «прижаты» к
этой оси. Если же
велико (намного больше 1), то число
мало по сравнению с числом
.
В этом случае основной прямоугольник
вытянут вдоль оси Оу,
а потому ветви гиперболы «прижаты» к
этой оси. Однако, как и в случае эллипса,
в качестве параметра, характеризующего
форму гиперболы, берут не
, а отношение
, которое тесно связано с отношением
.
Величина
называется  В частности,
при мы получим равностороннюю гиперболу, известную из школьного курса
математики. Ее уравнение примет знакомый
вид ,
если взять ,
а систему координат выбрать не ту,
которую выбрали ранее (подходящую), а
оси координат направить по ее асимптотам
(т.е. по биссектрисам четвертого и первого
координатных углов первоначальной
подходящей системы координат − см.
рисунок).
В частности,
при мы получим равностороннюю гиперболу, известную из школьного курса
математики. Ее уравнение примет знакомый
вид ,
если взять ,
а систему координат выбрать не ту,
которую выбрали ранее (подходящую), а
оси координат направить по ее асимптотам
(т.е. по биссектрисам четвертого и первого
координатных углов первоначальной
подходящей системы координат − см.
рисунок).
Пример. Построить гиперболу , найти ее фокусы и эксцентриситет.
Решение. Приведем исходное уравнение к каноническому уравнению гиперболы , разделив обе его части на 4. Получим . Таким образом, получаем каноническое уравнение гиперболы с полуосями а=1 и b=2. Определяем . Поэтому координаты фокусов . Эксцентриситет .
О
тметим,
что если уравнение кривой имеет вид ,
то это тоже уравнение гиперболы, у
которой действительная и мнимая ось
меняются местами (фокусы, в частности,
расположены на оси
),
а потому ветви гиперболы вытянуты вдоль
оси
. Например, гипербола с уравнением имеет вид как на рисунке.
Например, гипербола с уравнением имеет вид как на рисунке.
Как график гипербола в 5 этапах
БА: Ян Куанг и Эллин Казе и
Обновлено: 04-18-2017
Тригонометрическая рабочая книга для Dummies
Исследуйте покупку книг на Amazon
, когда график а гипербола, вы можете думать о ней как о соединении двух парабол, каждая из которых является идеальным зеркальным отражением другой, и каждая из которых расходится друг от друга. Математическое определение гиперболы — это множество всех точек, где разница в расстоянии от двух фиксированных точек (называемых
Горизонтальная и вертикальная гипербола, рассеченные для вашего удовольствия.
Уравнение горизонтальной гиперболы
Уравнение вертикальной гиперболы:
Чтобы построить гиперболу, как в этом примере,
выполните следующие простые шаги:
Отметьте центр.

Поскольку это уравнение относится к вертикальной гиперболе, вы обнаружите, что центр ( h , v ) этой гиперболы равно (–1, 3). Помните, что знаки чисел в скобках противоположны знакам координат центра. Также помните, что h находится внутри круглых скобок с x, и v находится внутри круглых скобок с y. В этом примере количество с y в квадрате идет первым, но h и v не меняются местами. h и v всегда остаются верными своим соответствующим переменным, х и г.
Из центра на шаге 1 найдите поперечную и сопряженную оси.
Пройдите вверх и вниз по поперечной оси на расстояние 4 (потому что 4 2 меньше y ), а затем пройдите вправо и влево 3 (потому что 3 2 меньше x ). Но не соединяйте точки, чтобы получить эллипс! До сих пор этапы рисования гиперболы были точно такими же, как и для рисования эллипса, но здесь все по-другому: точки, отмеченные вами как и (на поперечной оси) — ваши вершины.

Используйте эти точки, чтобы нарисовать прямоугольник, который поможет определить форму вашей гиперболы.
Поскольку вы поднялись вверх, а вниз на 4, высота вашего прямоугольника равна 8; движение влево и вправо 3 дает ширину 6.
Проведите диагональные линии через центр и углы прямоугольника, выходящие за пределы прямоугольника.
Этот шаг дает вам две линии, которые будут вашими асимптотами.
Нарисуйте кривые.
Начиная с каждой вершины отдельно, нарисуйте кривые, которые приближаются к асимптотам по мере удаления от вершин. График приближается к асимптотам, но никогда не касается их.
Создание прямоугольника для построения гиперболы с асимптотами.
На этом рисунке показана готовая гипербола.
Эту статью можно найти в рубрике:
- Предварительное исчисление,
Гипербола эллиптической геометрии (и 14 других математических карикатур) – Математика с плохими рисунками
Эти карикатуры появлялись в Твиттере и Фейсбуке в течение февраля 2018 года и хранятся здесь, как в музее, для потомков и/или людей, которые слишком круты для соцсетей.
Смешной против попытки быть забавным
С тех пор мне говорили, что Эмили Дикинсон на самом деле забавная. Я поддерживаю этот мультфильм в противном случае.
«Хартия» Мысли
Четыре года я преподавал в чартерной школе. Этот опыт не позволяет рассматривать хартийное движение как демона или как панацею. Я вижу в них больше, чем новую тип школы, я рассматриваю их в основном как отдельные новые школы , склонные к таким же амбициозным шагам и ошибкам, которых можно избежать, как и любое новое учреждение.
Многовариантные беды
Иногда погоня за изюминкой приводит к тому, что вы придаете удару больше силы, чем на самом деле заслуживает ваша жертва.
Наверное, это не тот случай.
Как назвать вашу математическую группу
Пользователи Twitter и Facebook внесли свои предложения. Мой фаворит принадлежит @SpinVector: кавер-группе Partial Derivative. Если название группы не будет занято к концу недели, то кавер-группы не так уж и интересны, как я думал.
Мой фаворит принадлежит @SpinVector: кавер-группе Partial Derivative. Если название группы не будет занято к концу недели, то кавер-группы не так уж и интересны, как я думал.
Обучение статистике
Когда дело доходит до обучения статистике, я обнаруживаю прискорбное несоответствие между возможностью и практикой. Я обвиняю себя и здесь — временами я привносил слишком много «чисто математического» мышления ( давайте докажем некоторые теоремы, детишки! ) в дисциплину со своим характерным стилем мышления.
Ангел Смерти
Ангел Смерти приходит за всеми нами. Спасения нет.
Еще мой начальник ответил на этот мультфильм: «ЭТО ТЫ. ВЫ ДЕЛАЛИ ЭТО ВСЕ ВРЕМЯ», что теперь абсолютно точно будет на моих визитных карточках.
Романтическое предложение
Как вы можете догадаться по старомодному фото с доски, это относится к самым ранним дням существования этого блога.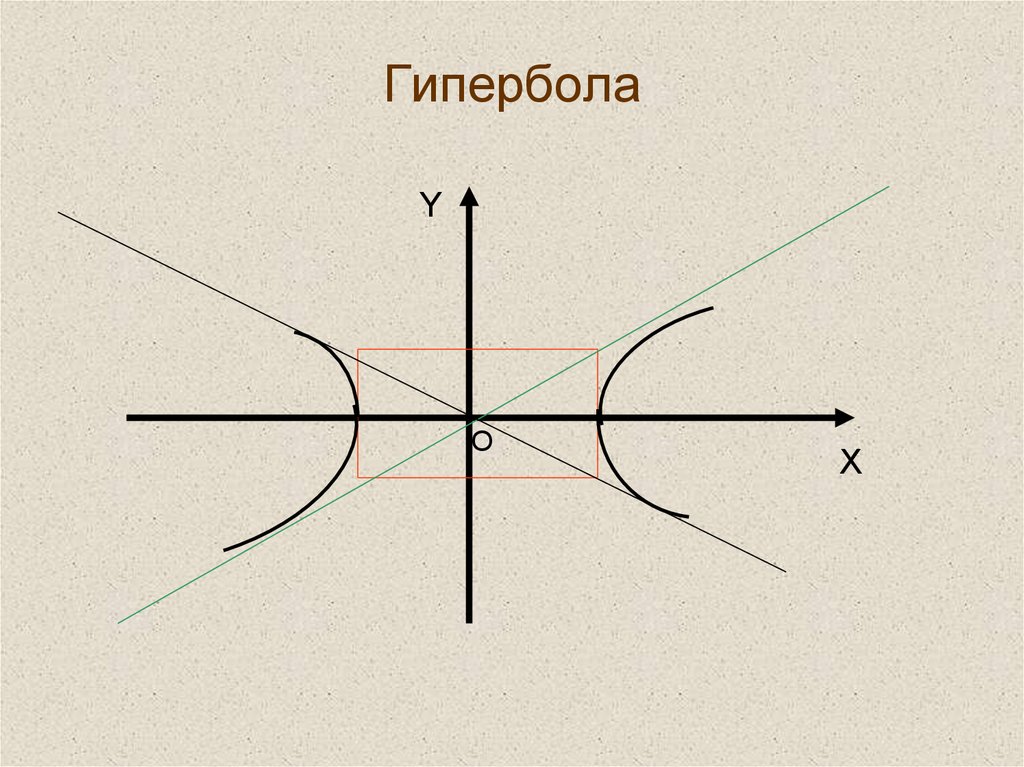 Я возродил его здесь, потому что (A) он посвящен Дню святого Валентина, и (B) Ханна Фрай сказала, что ей понравилось, и нет лучшего способа вывести из себя моих британских друзей, чем притвориться, что я лучший друг Ханны Фрай.
Я возродил его здесь, потому что (A) он посвящен Дню святого Валентина, и (B) Ханна Фрай сказала, что ей понравилось, и нет лучшего способа вывести из себя моих британских друзей, чем притвориться, что я лучший друг Ханны Фрай.
Гипербола и многоточие
Не изображено: плоские утверждения евклидовой геометрии (например, «евклидова геометрия — это форма геометрии, получившая свое название от Евклида»).
«Линейная алгебра»
Я воспользуюсь этой возможностью, чтобы добавить превосходную серию видеороликов 3Blue1Brown, дающих геометрическую визуализацию линейной алгебры.
Я могу смотреть 3Blue1Brown весь день.
И под «мог бы» я подразумеваю некоторую комбинацию «сделал» и «сделаю снова».
Туман замешательства
Туман очень сложно нарисовать, хорошо?
Этот мультфильм является эквивалентом тех скетчей SNL, где первая строка персонажа должна быть: «Привет, это я! Роберт Мюллер!» потому что вы не смогли бы понять шутку, если бы она была менее явной.
Байесовцы на испытании
Как только люди узнают меня достаточно хорошо, они даже не ждут кульминации; вместо этого они вздыхают с покорностью, как только начинается установка.
Десерт с супердобавкой
Я нахожусь в постоянном поиске комбинаций продуктов, вызывающих супераддитивность. Один из моих любимых: к традиционной для кесадильи комбинации тортилья + расплавленный чеддер добавить куркуму + нарезанный сельдерей. Невероятно хорошо.
Эпистемология трудна
У меня противоречивые чувства по отношению к философам-рационалистам (Декарт, Лейбниц, Спиноза, типа Гоббса). С одной стороны, мне нравится эстетика аргументов: ясное, аксиоматическое развитие по образцу математики.
С другой стороны, это кажется очень глупым способом попытаться понять мир. Вселенная очень запутана и никогда не бывает такой, какой вы могли бы догадаться. «Некоторое знание» настолько неуловимо, что это, по сути, оксюморон.
«Некоторое знание» настолько неуловимо, что это, по сути, оксюморон.
Я считаю, что я рационалист по наклонностям, но мой рационализм приводит к выводу, что эмпиризм — единственный разумный путь.
Тривиальное дело
С нетерпением жду моего графического романа «Жизнь и времена тривиального дела», который будет состоять из 400 страниц этого зеленого эльфа с разным текстом на каждой странице, как в комиксах о динозаврах.
Club Obvi
«Очевидность» в глазах смотрящего, верно?
НЕПРАВИЛЬНО. Если это в глазах смотрящего, то это недостаточно очевидно!
Наконец, быстрое объявление результатов Пула Оскара Незнайки!
- 219 человек заполненных бюллетеня.
- Ultimate Visionary , учитель математики по имени Кин , набрал 33,1 (из возможных 47,1) во всех категориях. Кин в основном придерживался фаворитов, за одним мастерским исключением: выбрав «Небеса — это пробка на 405-й дороге», которая стала самым большим проигравшим вечером.