Сколько различных цепочек можно составить из двух частей решение: ГДЗ учебник по математике 2 класс Петерсон. Урок 1. Цепочки Номер 1

Комбинаторика. Правила и формулы — презентация онлайн

1. Комбинаторика

Правила и формулы

2. Правило суммы

• Если элемент x можно выбрать
способами nx и если элемент y можно
выбрать ny способами, то выбор «либо
x, либо y» можно осуществить
способами nx+ ny.
Любой цвет
Выбираем один шар
Nx=4
Ny=5
Nx +Ny=4+5=9
способов

3. Правило суммы

• Правило суммы используется тогда,
когда варианты соединяются словом
«ИЛИ»

4. Пример 1

• Сколько различных символов можно
закодировать, используя код Морзе
длиной не менее 5 и (или) не более 6
сигналов(точек и тире)?
• Одновременно это никак не может
произойти.

5. Правило произведения

• Если элемент x можно выбрать nx
способами и если после его выбора
элемент y можно выбрать ny
способами, то выбор упорядоченной
пары (x, y) можно осуществить nx∙ ny
способами.
Синий и рыжий
Выбираем пару шаров
Nx=4
Ny=5
Nx ∙Ny=4∙5=20
способов
• Пример 2. Номер автомобиля состоит из шести
мест, на первом – буква, затем – три цифры, за ними
еще две буквы. Сколько существует автомобильных
номеров ?
• Могут быть использованы любые из 33 букв русского
алфавита, кроме «ь», «ъ» и «й».
• Решение. На первое место можно поставить любую
из 30 букв. На второе, третье, четвертое – любую из
10-ти цифр. На пятое, шестое место можно
поставить любую из 30-ти букв. По правилу
умножения имеем:
30*10*10*10*30*30=27*106
• Такое количество номеров автомобилей может быть
выдано ГАИ в Саратовской области

7. Формулы комбинаторики

Перестановки
Размещения
Сочетания

8. Два главных вопроса

1. В задаче требуется переставить все
элементы или требуется выбрать
несколько из них? (все элементы –
перестановки, выбрать несколько
– сочетания или размещения).
2. Если нужен выбор, то важен ли
порядок? Если важен – размещения,
если не важен – сочетания.

9. Перестановки

Используются все элементы
Порядок элементов важен

10.

Перестановки без повторений• Перестановками без повторений из n
различных элементов называются все
возможные последовательности этих n
элементов. Число перестановок без
повторений из n элементов равняется
Pn n! 1 2 3 … n
по определению
0! 1

11. Перестановки без повторений

n 3
6 различных
перестановок
P3 1 2 3 6

12. Пример 4.Сколькими способами можно расставить на полке 4 книги ? (Обозначим их А, В, С,D ).

• Основным различием этих размещений
служит порядок объектов; изменение
порядка дает другое размещение.
• 4*3*2*1=24

13. Пример 5

• По следствию должны пройти пять
человек: A, B, C, D, E.
• Cколько вариантов того, что в списке
из этих пяти человек, составленном
случайным образом B будет следовать
сразу после A?

14. Решение

АВ??? — таких вариантов Р3=3!=6
?АВ??
??АВ?
???АВ
Всего вариантов М=6*4=24

15. Перестановки с повторениями

• Перестановки с повторением из n
элементов k типов (k n)
k
• число элементов 1-го типа n1;
число элементов 2-го типа n2; ni n
i 1
число элементов k-го типа nk,
• все возможные последовательности
исходных n элементов.
• Число перестановок с повторениями
обозначают Pn n1 n2 … nk
подсчитывают так:
Pn n1 n2 … nk
n!
n1! n2 !…nk !

16. Перестановки с повторениями

n=n1+n2=2+1=3
n1=2
n2=1
3 различные
перестановки
3!
6
P3 2 1
3
2! 1! 2
Пример 6. Сколько чисел можно создать
из двух цифр «2» и двух цифр «1»?
1122
1212
1221
2211
2121
2112
4!/2!/2!=6

18. Пример 7.

• Существует конечное число неэквивалентных
друг другу логических функций, зависящих от
трех аргументов. Среди них есть функции,
для каждой из которых существует только
два набора значений аргументов, при
которых функция становится тождественно
равна значению «Истина» (для всех
остальных наборов значений аргументов
такая функция тождественно равна значению
«Ложь»). Сколько существует таких функций?
В ответе укажите целое число.

19. Решение

8!/(2!*6!)=23

20. Размещения

(выборки)
Используются не все
элементы
Порядок элементов важен

21.

Размещения без повторений• Размещениями без повторений из n
различных элементов по m элементов
называются все такие последовательности m
различных элементов, выбранных из
исходных n, которые отличаются друг от
друга или порядком следования элементов,
или составом элементов.
• Число размещений без повторений из n
элементов по m обозначается символом
n!
A
(n m)!
m
n
( m n)

22. Размещения без повторений

Выбираем два шара
n=3
Порядок выбора важен!
m=2
3!
6
A
6
(3 2)! 1
2
3
6 различных
выборок

23. Пример 8

• В фирме работают 8 человек
одинаковой квалификации, среди них
Иванов, Петров, Сидоров. Сколькими
способами можно случайно выбрать
трех из восьми?

24. Решение

• Всего вариантов — выбрать три из
восьми без повторения, т.к. один и тот
же не может выполнять две работы
8!
8!
N A
8 * 7 * 6 336
(8 3)! 5!
3
8

25.

Размещения с повторениями• Размещения с повторениями из элементов k
типов по m элементов (k и m могут быть в
любых соотношениях) называются все такие
последовательности m элементов,
принадлежащих исходным типам, которые
отличаются друг от друга или порядком
следования элементов, или составом
элементов.
m
m
k
A k

26. Размещения с повторениями

n=3
k=2
A 2 8
3
2
3
8 вариантов
выборок

27. Пример 9

Замок камеры хранения имеет четыре диска,
каждый из которых разделен на 10 секторов; на
секторах каждого из дисков написаны цифры 0, 1,
…, 9.
• Какова вероятность открыть закрытую камеру для
человека:
1. забывшего все, что он набрал на дисках, закрывая
камеру;
2. помнящего только цифру, набранную на первом
диске;
3. помнящего только, что ни на втором, ни на третьем,
ни на четвертом, диске не набирал цифру 6?

28. Решение

1) Всего вариантов
2) Всего вариантов
N A104 K m 10 4
N A103 K m 10 3
3) Всего вариантов N=10*9*9*9

29.

СочетанияИспользуются не все
элементы
Порядок элементов не важен

30. Сочетания без повторений

• Сочетаниями без повторений из n
различных элементов по m элементов
называются все такие
последовательности m различных
элементов, выбранных из исходных n,
которые отличаются друг от друга
составом элементов.
n!
C
m!(n m)!
m
n
( m n)

31. Сочетания без повторений

Выбираем два шара
n=3
Порядок выбора не важен!
m=2
3!
6
C
3
2!(3 2)! 2
2
3
3 сочетания

32. Пример 10

• В чемпионате по шахматам
участвовало 40 спортсменов. Каждый с
каждым сыграл по одной партии.
Сколько всего партий было сыграно?

33. Решение

C
2
40
40!
39 * 40
780
2!*38!
2

34. Сочетания с повторениями

• Сочетаниями с повторениями из
элементов k типов по m элементов (m и
k могут быть в любых соотношениях)
называются все такие
последовательности m элементов,
принадлежащих исходным типам,
которые отличают друг от друга
составом элементов.
(k m 1)!
C
m!(k 1)!
m
k

35. Сочетания с повторениями

m=3
4 варианта
сочетаний
k=2
(2 3 1)! 4!
C
4
3!(2 1)! 3!
3
2

36. Пример 11

• Имеется 2 типа цветов, количество
цветов не ограничено. Сколько
различных букетов можно составить из
3-х цветов?
• 111
• 222
• 122
• 211
• Всего 4 различных букета

37. Пример 12

• Имеется 5 типов цветов, количество
цветов не ограничено. Сколько
различных букетов можно составить из
3-х цветов?

38. Решение

• Сочетание с повторением:
(5+3-1)!/(3!*(5-1) !)=35
Формулы
комбинаторики
Перестановки
Используются все элементы
Порядок элементов важен
Размещения
Используются не все элементы
Порядок элементов важен
Сочетания
Используются не все элементы
Порядок элементов не важен
• Пример 13. Сколькими способами можно выбрать
четырех студентов, которые будут получать
стипендию, из восьми.
Решение.
Мы выбираем четырех из восьми, следовательно,
это не «перестановки», а «сочетания» или
«размещения».
Так как студенты все разные, и один студент не
может получать две или более стипендий, то должна
использоваться формула «без повторений».
Так как по условию задачи не сказано, что стипендии
разные по величине, то порядок отбора нам не
важен. Следовательно, нам нужна формула
«сочетания без повторений».
Всего студентов: n=8 , количество выбираемых: m=4 .
8!/4!/(8-4)!=70 вариантов.
Пример 14. Паша, Сережа, Андрей и Антон думают надеть ли на торжественный
вечер галстуки или бабочки. Они хотят одеться так, чтобы количество бабочек было
нечетным. Перечислите все способы так одеться.
Решение.
Хотя нас и не спрашивают, сколько вариантов, давайте найдем их количество, чтобы
потом проверить себя.
Если бабочек должно быть нечетное число, то бабочка может быть или одна, или
три.
Найдем, сколько вариантов может быть, если бабочка одна.
Воспользуемся формулой сочетания без повторений. Всего ребят четверо n=4,
выбираем одного, кто оденет бабочку m=1 .
4!/1!/(4-1)!=4
Теперь найдем количество вариантов, когда бабочек будет три.
4!/3!/(4-3)!=4,
Найдем общее количество вариантов одеваний, воспользовавшись правилом суммы
4+4=8.
Теперь собственно сделаем то, что требовалось в задаче.
Паша
1Галстук
2Галстук
3Галстук
4Бабочка
5Галстук
6Бабочка
7Бабочка
8Бабочка
Сережа
Галстук
Галстук
Бабочка
Галстук
Бабочка
Бабочка
Бабочка
Галстук
Андрей
Галстук
Бабочка
Галстук
Галстук
Бабочка
Бабочка
Галстук
Бабочка
Антон
Бабочка
Галстук
Галстук
Галстук
Бабочка
Галстук
Бабочка
Бабочка

42. Задача1

Световое табло состоит из лампочек.
Каждая лампочка может находиться в
одном из трех состояний («включено»,
«выключено» или «мигает»). Какое
наименьшее количество лампочек
должно находиться на табло, чтобы с
его помощью можно было передать 18
различных сигналов?

43.

Задача 2• Для передачи сигналов на флоте
используются специальные сигнальные
флаги, вывешиваемые в одну линию
(последовательность важна). Какое
количество различных сигналов может
передать корабль при помощи четырех
сигнальных флагов, если на корабле
имеются флаги трех различных видов
(флагов каждого вида неограниченное
количество)?

44. Задача 3

Вася и Петя передают друг другу
сообщения, используя синий, красный и
зеленый фонарики. Это они делают,
включая по одному фонарику на
одинаковое короткое время в некоторой
последовательности. Количество вспышек в
одном сообщении – 3 или 4, между
сообщениями – паузы. Сколько различных
сообщений могут передавать мальчики?

45. Задача 4

Для кодирования 300 различных
сообщений используются 5
последовательных цветовых вспышек.
Вспышки одинаковой длительности,
для каждой вспышки используется
одна лампочка определенного цвета.
Лампочки скольких цветов должны
использоваться при передаче
(укажите минимально возможное
количество)?

46.

Задача 5• Сколько существует четырехзначных
чисел, в записи которых все цифры
различны?

47. Задача 6

• Виктор хочет купить пять разных книг,
но денег у него хватает только на три
(любые) книги. Сколькими способами
Виктор может выбрать три книги из
пяти?

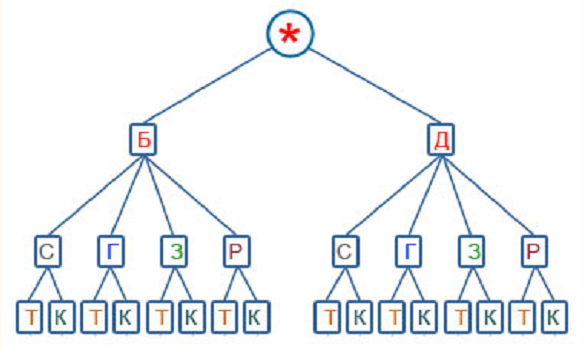
48. Задача 7

• Цепочка из трех бусин формируется по
следующему правилу: На первом месте
в цепочке стоит одна из бусин А, Б, В.
На втором – одна из бусин Б, В, Г. На
третьем месте – одна из бусин А, В, Г,
не стоящая в цепочке на первом или
втором месте. Сколько всего есть таких
цепочек?

Занятие для преподавателей «Комбинаторика»

Методическое онлайн-занятие для преподавателей «Комбинаторика на ЕГЭ по информатике»!

Приветствуем, дорогие коллеги, учителя и репетиторы информатики!

В субботу, 8 октября, в 12:00 состоится методический мастер-класс Лады Есаковой «Комбинаторика на ЕГЭ по информатике».

Это специфическая тема. И даже если вы отлично разбираетесь в комбинаторике как математик, нужно знать, как ее правила применяются в задачах по информатике.

ОНЛАЙН-КУРС ДЛЯ ПРЕПОДАВАТЕЛЕЙ

 

Комбинаторика на ЕГЭ

Для того, чтобы решать задачи по информатике № 7, 8, 11, 27, нужна одна-единственная формула комбинаторики.

Вот она: N = Ai.

Это формула для количества способов N, которыми можно расставить на i мест А символов.

Например, сколькими способами можно заполнить 5 клеточек нулями и единицами?

Очевидно, это 25 способов. Здесь i = 5, А = 2 (ноль и единица, 2 символа), N = 32.

В информатике это формулируется так:

Количество цепочек (N) длинной i, которые можно составить из символов алфавита мощностью A, равно A в степени i.

Мы посмотрим, как применяется эта формула. Однако ее понимания не достаточно для решения всех типов задач.

Например, рассмотрим обычную задачу №11:

Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация.

Личный код состоит из 13 символов, каждый из которых может быть одной из 12 допустимых заглавных букв или одной из 10 цифр.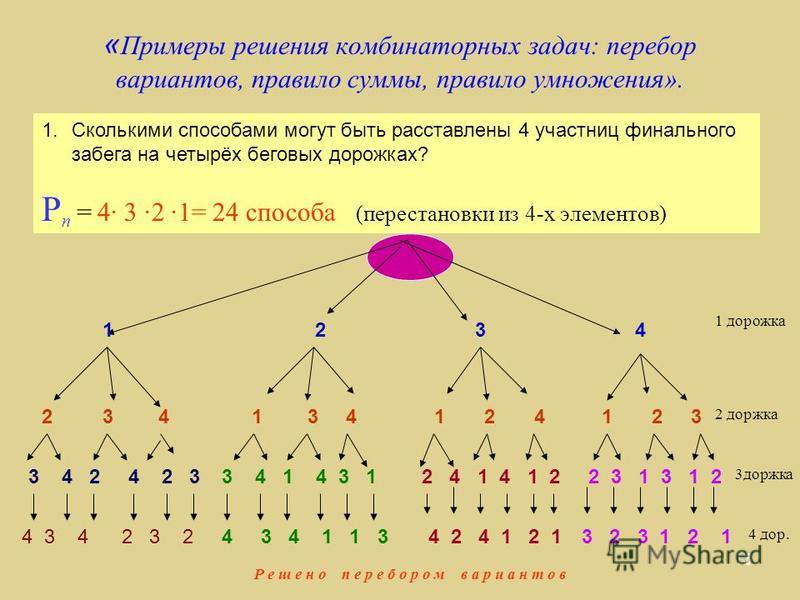

Для записи личного кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит. Код подразделения состоит из двух натуральных чисел, не превышающих 1000, каждое из которых кодируется как двоичное число и занимает минимально возможное целое число бит.

Личный код и код подразделения записываются подряд и вместе занимают минимально возможное целое число байт. Всего на пропуске хранится 32 байт данных.

Сколько байт выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байт.

Получилось в ответе 21? Но почти все ученики скажут, что 19.

А вот задача №8:

Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква А должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Андрей?

Можно решить эту задачу программным способом. Но что будет, если увеличить длину слова до 12? Сколько времени это займет? На ЕГЭ точно не будет возможности так долго ждать результата, а аналитически задача решается за секунды.

На Мастер-классе для учителей и репетиторов вместе с Ладой Борисовной Есаковой разберем основные приемы решения. Научимся обходить ловушки, расставленные составителями задач.

Ждем в субботу, 8 октября, в 12.00 по московскому времени.

Присоединиться к онлайн-курсу для преподавателей

Онлайн-курс для учителей и репетиторов

Этот курс поможет вам подготовить учеников к ЕГЭ по информатике на 90+ баллов. Вы первыми узнаете обо всех новинках ЕГЭ-2023.

В Онлайн-курс для преподавателей включены:

— 36 Мастер-классов каждую неделю, по всем темам и задачам ЕГЭ. С возможностью обсудить решения, задать вопросы (каждую неделю по воскресеньям).

— 10 Мастер-классов для учитилей по методике преподавания

— Онлайн-учебник и тренажер с задачами по всем темам ЕГЭ. 25 тем, в каждой не менее 15 задач. К каждой задаче – подробное решение. Задачи в онлайн-тренажере сгруппированы по разделам и расположены по нарастанию сложности. Набор задач пополняется постоянно.

— Готовые проверочные работы по каждой теме. Просто распечатайте их и используйте на своих занятиях.

— Домашние задания с проверкой.

— Специально для учителей и репетиторов: варианты мини-зачетов по каждой задаче ЕГЭ.

— Пробные ЕГЭ раз в месяц. Авторские варианты с проверкой и полным видеоразбором.

И самое интересное: методические мастер-классы для учителей и репетиторов. Они будут проходить каждый месяц.

Методика подготовки на максимальные баллы. Темы и лайфхаки, которых не найти в учебнике или интернете.

Заказать курс для преподавателей!

Вот некоторые темы:

— Особенности ЕГЭ по информатике. Методика подготовки на максимальный балл.

— Основы комбинаторики на ЕГЭ по информатике.

— Булева алгебра (алгебра логики). От основ до сложных задач.

— Выбор способа решения задач (аналитический, программный, Excel).

— Тонкости использования различных языков программирования (С++, Pascal, Python).

Онлайн-курс по информатике для учителей и репетиторов ведет Лада Борисовна Есакова – автор 3 книг для подготовки к ЕГЭ, в том числе «Авторского курса для подготовки к ЕГЭ по информатике».

Присоединиться!

Что получают участники курса

На Онлайн-курсе разбираем все типы задач, встречавшихся в демоверсиях, работах Статграда, в вариантах досрочных и основных ЕГЭ за последние 5-6 лет.

Вся необходимая теория, методы и секреты решения. Вы получите различные способы решения задач.

Это даст возможность подготовить ученика, который не силен в программировании, на 80 – 85 баллов.

При этом 51 балл можно получить, вообще не прикасаясь к компьютеру.

А для сильных учеников представлены решения и разборы самых сложных задач 24, 25, 26, 27.

Программное решение задач предоставлено на трех языках программирования (C++, Pascal, Python)!!! Такой подборки вы не найдете нигде!

И наконец, вы получите видеоразборы и тексты программ для решения самой сложной, самой интересной задачи № 27. По статистике всего 1,6% учеников правильно решают оба пункта этой задачи.

Увы, преподавателям непросто собрать воедино все типы этой красивейшей задачи и тем более решить ее на разных языках программирования.

Лада Борисовна – признанный специалист в решении этой непростой задачи. Хотите увеличить процент звездных учеников? Скачивайте задания, смотрите видеоразборы, учитесь сами и готовьте своих учеников!

Заказать курс для преподавателей!

Онлайн-курс для абитуриентов

Полный онлайн-курс для подготовки к ЕГЭ по информатике. Подробно изучаем все темы с нуля и до самых сложных заданий. А также, формат экзамена, распространенные ошибки и правила оформления. Не зубрим алгоритмы (которые меняют каждый год), а учимся понимать задачу. Это спасает от неожиданностей на экзамене. Контролируем знания регулярными пробными ЕГЭ.

— Подробный учебник для ЕГЭ по информатике.

— Тренажер задач (актуальные задания 2022-23 г.).

— 60+ ч. онлайн-занятия каждое воскресенье (18:00 по Мск).

— Много практики.

— ДЗ с разбором.

— 6 репетиционных ЕГЭ.

Заказать курс

Занятия построены следующим образом:

1. Вы читаете тему во встроенном учебнике.

2. Переходите к тренажеру задач тестовой части.

3. По воскресеньям (в 14:00 по мск, кроме ближайшего занятия в субботу) у вас онлайн-занятия. Вы разбираете с преподавателем тему по авторской методике и выполняете самостоятельные задания в течение занятия.

— Занятие длится 120 минут.

— Все онлайн-занятия будут доступны в личном кабинете.

— После занятия вы получаете ДЗ.

4. В течение года вы пишете 6 репетиционных ЕГЭ онлайн. В личном кабинете будет доступен вариант. Вы его решаете, фотографируете и присылаете нам. Получаете полный разбор работы.

Ведет курс Есакова Лада Борисовна. Окончила МГУ им. Ломоносова, факультет ВМиК (1988 г.). Автор книги «Информатика. Полный курс подготовки к ЕГЭ». Репетиторская деятельность с 2001 года (работа как со слабыми учениками, так и с претендующими на 90 баллов и выше).

Лучшие результаты 2022 года: 97, 92, 88, 86, 86, 82, 80. Пример программы курса (100 баллов) 22/23 уч.г., бесплатный демодоступ для ознакомления с устройством курса здесь.

Доступ до 1 июля 2023 г. и полный возврат средств, если получите 100 баллов!

Заказать курс

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Занятие для преподавателей «Комбинаторика»» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из Рубрики: Новости.

Публикация обновлена: 07.02.2023

комбинаторика — Количество различных ожерелий с черными и белыми бусами по 2$

Задавать вопрос

спросил 3 года 10 месяцев назад

Изменено 3 года, 10 месяцев назад

Просмотрено 2к раз

$\begingroup$

Это не домашний вопрос, я готовлюсь к вступительному тесту.

Сколько разных ожерелий можно составить из черных и 6 долларов белых бусин?

Мой подход: мы можем расположить белые бусины в ожерелье по $1$, потому что все они белые. Затем черные бусины снова можно разместить в любом месте способом $1$, как только черная бусина размещена, теперь она действует как ссылка, и я могу разместить последнюю черную бусину либо рядом с первой черной, либо с промежутком в $1,2. ,3$ белых бусинок, что дало мне комбинации по 4$ как, wbbwwwww, wbwbwwww, wbwwbwww, wbwwwbww.

Есть ли другой лучший подход для этого? Я пытался следовать этому пути: сколько разных ожерелий можно составить из белых и красных бус за 6 долларов? но я получаю дробные значения,

$$\frac{7!}{6! \кдот 2! \cdot 2}$$
Почему так происходит? Разве мы не можем использовать эту логику формулы во всех случаях?

• комбинаторика
• дискретная математика
• перестановки
• ожерелья-браслеты

$\endgroup$

4

$\begingroup$

Вы правы, что есть четыре ожерелья, состоящие из 2$ черных и 6$ белых бусин, так как две черные бусины могут быть разделены белыми бусинами по $0$, $1$, $2$ или $3$.

Мы можем сделать ожерелье, расположив восемь бусин в ряд и соединив концы. Если мы поместим черную бусину на левый конец, есть семь способов разместить другую черную бусину.

Однако, поскольку есть две неразличимые черные бусины, мы посчитали каждое такое ожерелье дважды, за одним исключением — средний ряд — поскольку ряды $j$ и $7-j$ дают одно и то же ожерелье, когда их концы соединяются. Так как средний ряд был подсчитан только один раз, мы должны добавить $1$ перед делением на $2$, иначе мы будем считать его $1/2$ раза. Следовательно, есть $$\фракция{7 + 1}{2} = 4$$ ожерелья, которые могут быть сформированы из черных бусин за 2$ и белых бусин за 6$.

Обратите внимание, что средний ряд соответствует симметричному ожерелью внизу справа вверху, в котором черные бусины расположены напротив друг друга.

В качестве альтернативы мы можем выбрать две из восьми позиций в круге для черных бусин $\binom{8}{2}$ способами. Если мы затем разделим на $8$, чтобы учесть повороты, которые сохраняют относительный порядок бусинок, мы получим $$\frac{1}{8}\binom{8}{2} = \frac{1}{8} \frac{8!}{2!6!} = \frac{7!}{2!6 !}$$ что не является целым числом.

Причиной этого является симметричное ожерелье внизу справа вверху. У него всего четыре различимых оборота, поэтому мы посчитали его $4/8 = 1/2$ раза. Добавив $1/2$ к нашему расчету выше, чтобы учесть этот доход $$\frac{7!}{2!6!} + \frac{1}{2} = \frac{7}{2} + \frac{1}{2} = 4$$ как указано выше.

$\endgroup$

2

$\begingroup$

Зафиксируйте ожерелье $N$ как вершины восьмиугольника. Путем вращения мы можем предположить, что верхняя бусина черная. Проведите линию между черными бисеринками. Это делит ожерелье на два подмножества белых бусин. При необходимости размышляя вдоль линии, мы можем предположить, что меньшее подмножество $L_N$ (возможно, оба равны, это не проблема) находится слева от верхней вершины. Теперь количество бусин слева определяет ожерелье, потому что этот процесс обратим, и, зная количество белых бусин одной стороны, определяется другое.

Следовательно, каждое ожерелье является выбором для $L_N$. Обратите внимание, что у нас не может быть $|L_N| > 3$, потому что это будет «большое» подмножество. Следовательно, у нас есть четыре возможных случая, соответствующих $|L_N| = 0,1,2,3$.

Если вам нужен формальный ответ, можно определить ожерелья как классы эквивалентности $8$-множеств $\{B,W\}$ по модулю поворота, а затем дать биекцию с $\{0,1,2 ,3\}$, сопоставив каждому ожерелью $N$ соответствующее подмножество $L_N$.

Если вам интересно и вы знаете основы групповых действий, Теорема перечисления Полиа является результатом комбинаторики, которая подсчитывает возможные ожерелья, которые можно составить из определенного количества бусин и цветов.

$\endgroup$

2

SudokuWiki.org — XY-цепочки

XY-цепочка пример 1 : Пример загрузки или : С самого начала

Цепочки Y-Wing фактически являются частью более широкой стратегии, называемой XY-Chains. Общность заключается в том же клешнеподобном нападении на кандидатов, которое видят оба конца, и в том, что цепочка состоит из двузначных ячеек. В Y-цепочках петля была расширена до цепочки идентичных ячеек с двойным значением, но в XY-цепочке они могут быть разными — до тех пор, пока есть один кандидат на создание всех связей. «X» и «Y» в названии представляют эти два значения в каждом звене цепи.

Примером здесь является очень простая XY-цепочка длины 4, в которой удалены все 5, выделенные желтым цветом. Концы цепи — 5 A7 и C2 — так что все ячейки, которые могут видеть оба этих элемента, находятся под огнем. Можно начать с любого конца, но давайте последуем примеру из A7. Мы можем рассуждать следующим образом:

• Если A7 равно 5, то A3/C7/C9 не может быть.
  
• если A7 НЕ 5, то это 9, поэтому A5 должно быть 2, что заставляет A1 быть 6. Если A1 равно 6, то C2 равно 5.
  

Какой бы ни был выбор в A7, 5 в A3/C7/C9 не могут быть 5.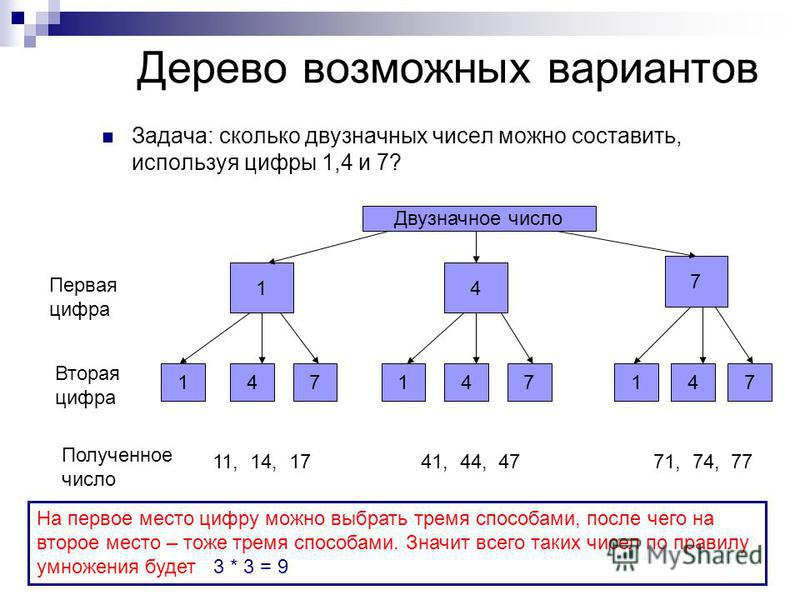 Та же логика прослеживается от C2 до A7, так что стратегия является двунаправленной, говоря жаргонным языком.

Пример цепи XY 2 : Пример загрузки или : С самого начала

Следующая головоломка судоку содержит занимательную серию цепочек XY, начиная с этой прямоугольной. Это доказывает, что 8 должно быть либо в ячейке B3, либо в ячейке B8, и поэтому мы можем удалить остальные три восьмерки в строке B. Начнем с B3, если эта ячейка равна 8 или 6. Если это 6, то D3 должно быть 4, что подталкивает 2 к D8. что, в свою очередь, делает B8 равным 8. Вы можете проследить это от B8 назад для того же эффекта. Хорошая короткая XY-цепочка, но, как показывает следующий пример, эти четыре ячейки представляют собой богатый шов.

Одинаковые ячейки — разные XY-цепочки : Пример загрузки или : С самого начала

Глядя на точно такую ​​же начальную ячейку, кажется, что мы можем сделать дальнейшие исключения, на этот раз 6s в столбце 3.