Линейные неравенства с одной переменной
Как решать линейные неравенства с одной переменной вида ax+b>cx+d?
Для этого используем всего два правила.
1) Слагаемые можно переносить из одной части неравенства в другую с противоположным знаком. Знак неравенства при этом не меняется.
2) Обе части неравенства можно разделить на число, стоящее перед иксом (или другой переменной). При делении на положительное число знак неравенства не меняется. При делении на отрицательное число знак неравенства изменяется на противоположный.
В общем виде решение линейного неравенства с одной переменной
можно изобразить так:
1) Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:
2) Если число перед иксом не равно нулю (a-c≠0), обе части неравенства делим на a-c.
Если a-c>0, знак неравенства не изменяется:
Если a-c<0, знак неравенства изменяется на противоположный:
Если a-c=0, то это — частный случай.
Частные случаи решения линейных неравенств рассмотрим отдельно.
Примеры.
Это — линейное неравенство. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -2<0, знак неравенства изменяется на противоположный:
Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой. Штриховка от 10 влево, на минус бесконечность.
Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой.
Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как 10>0, знак неравенства при этом не изменяется:
Так как неравенство нестрогое, -2,3 на числовой прямой отмечаем закрашенной точкой.
Штриховка от -2,3 идёт вправо, на плюс бесконечность.
Так как неравенство строгое и точка закрашенная, -2,3 в ответ записываем с квадратной скобкой.
Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположным знаком.
Обе части неравенства делим на число, стоящее перед иксом. Поскольку 3>0, знак неравенства при этом не изменяется:
Так как неравенство строгое, x=2/3 на числовой прямой изображаем выколотой точкой.
Так как неравенство строгое и точка выколотая, в ответ 2/3 записываем с круглой скобкой.
Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -4 — отрицательное число, знак неравенства при этом изменяется на противоположный:
Поскольку неравенство нестрогое, -2,25 на числовой прямой отмечаем закрашенной точкой.
Так как неравенство нестрогое и точка закрашенная, -2,25 включаем в ответ, то есть записываем с квадратной скобкой.
Ответ:
Решать линейные неравенства с одной переменной в алгебре приходится не только в виде отдельных примеров, но также при нахождении области определения функций, области допустимых значений выражений, решении уравнений и более сложных неравенств. Вот почему важно вовремя понять эту тему и научиться применять её.
Рубрика: Линейные неравенства | КомментарииЛинейные неравенства с одной переменной
ОпределениеВыражение с одной переменной, содержащее знак неравенства, называется неравенством с одной переменной. Например:
23х+11<11x+5; 6x–10; х>9
Неравенства такого вида называют линейными неравенствами с одной переменной, так как х в них в первой степени.
Вспомним, что в зависимости от знака неравенства, их называют строгие знаки (< и >) или нестрогие знаки (≤ и ≥).
Решением неравенства с одной переменной является значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
При решении неравенства с одной переменной пользуются следующими свойствами.
Свойства неравенств- Если из одной части неравенства перенести слагаемое в другую часть, поменяв при этом знак слагаемого на противоположный, то получится равносильное ему неравенство;
- Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится равносильное ему неравенство.
Рассмотрим решение линейных неравенств с одной переменной на примерах.
Пример №1. Решить неравенство:
6х–13<x–3
Перенесем слагаемые из одной части в другую, изменяя знаки у слагаемых, которые будем переносить, на противоположные:
6х–x < –3+13
Теперь приведем подобные слагаемые в каждой части неравенства: 5х<10. Дальше разделим обе части неравенства на число 5 (коэффициент при х), получим: х<2. Множество решений данного неравенства состоит из всех чисел, которые меньше минус двух. Ответ можно записать в виде неравенства х<2, либо в виде числового промежутка (–∞;-2). Вспомним, что около знака «бесконечность» всегда ставится круглая скобка, а так как неравенство строгое (знак «меньше»), то и у числа два также ставится «круглая» скобка). Это множество чисел можно показать на числовом луче (точка, которая показывает число 2, будет «выколотая», так как неравенство строгое):
Пример №2.
Решить неравенство:
12–2х≤х–6
Выполним перенос слагаемых:
–х–2х–6–12
Приведем подобные слагаемые: –3х–18. Разделим обе части неравенства на минус три и изменим знак неравенства на противоположный: х≥6. Значит, множество решений данного неравенства – это все числа, которые больше или равны 6. Ответ можно записать, как в виде нестрогого (знак «больше или равно») неравенства х≥6, так и в виде числового промежутка [6;+), (видим около числа 6 «квадратную» скобку), показав его на числовом луче, где точка, обозначающая число 6, закрашена, ее называют «приколотой» точкой, так как неравенство нестрогое.
В рассмотренных примерах мы получали неравенства, у которых коэффициент при переменной не равен нулю. Но есть случаи, когда получается неравенство вида 0•х>a или 0•х<a (возможны и нестрогие знаки). В этом случае неравенство либо не имеет решений, либо решением является любое число.
Пример №3. Решить неравенство:
3х–15<3x–56
Выполняя перенос слагаемых и приведение подобных, получим неравенство:
0х<–41
Данное неравенство при любом значении х будет иметь вид 0<–41, что является неверным. Значит, оно не имеет решений, следовательно, и данное по условию неравенство не имеет решений.
Пример №4. Решить неравенство:
5х+24>5x+14
Выполним все необходимые действия, получим:
0х>–10
Данное неравенство при любом значении х будет иметь вид 0>–10, а это верное неравенство, значит х – любое число. Следовательно, ответ в данном неравенстве – «х – любое число».
Алла Василевская | Просмотров: 3.7k
6.1 – Линейные неравенства с одной переменной
Цели обучения
- (6.1.1) – Использование свойств сложения и умножения для решения алгебраических неравенств
- (6.1.2) — Решать линейные неравенства и выражать решения с помощью интервальной записи и в виде неравенства
- (6. 1.3) — Упростить и решить алгебраические неравенства, используя распределительное свойство
1.3) — Упростить и решить алгебраические неравенства, используя распределительное свойствоКогда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как и с равенствами, но не совсем так. Мы можем использовать добавление свойства и свойство умножения , чтобы помочь нам решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число; при этом символ неравенства переворачивается.
Существует три способа представления решений неравенств: интервал, график и неравенство. Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства. Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как и с равенствами, но не совсем так.
A Общее примечание: свойства неравенств
[latex]\begin{array}{ll}\text{Свойство сложения}\hfill& \text{Если }a< b,\text{ then }a+c< b+ c.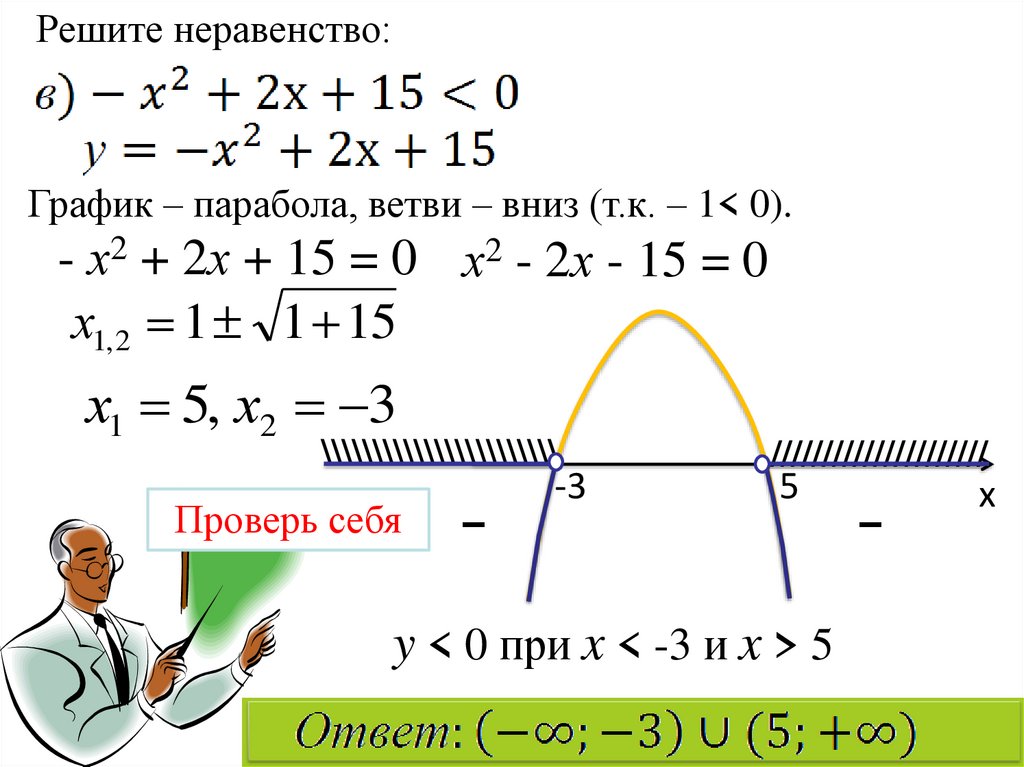
\hfill \\ \hfill & \hfill \\ \text{Свойство умножения}\hfill & \text{Если }a< b\text{ и }c> 0,\text{, то }ac< bc.\hfill \\ \hfill & \text{Если }a< b\text{ и }c< 0,\text{, то }ac> bc.\hfill \end{array}[/latex]
Эти свойства также применимы к [ латекс]a\le b[/латекс], [латекс]a>b[/латекс] и [латекс]a\ge b[/латекс].
В следующей таблице показано, как свойство умножения применяется к неравенствам и как умножение на отрицание обращает неравенство:
| Начать с | Умножить на | Окончательное неравенство |
| [латекс]а> | [латекс]с[/латекс] | [латекс]ac>bc[/латекс] |
| [латекс]5>3[/латекс] | [латекс]3[/латекс] | [латекс]15>9[/латекс] |
| [латекс]а>б[/латекс] | [латекс]-с[/латекс] | [латекс]-ac<-bc[/латекс] |
| [латекс]5>3[/латекс] | [латекс]-3[/латекс] | [латекс]-15<-9[/латекс] |
В следующей таблице показано, как свойство деления применяется к неравенствам и как деление на минус меняет неравенство на противоположное:
| Начать с | Разделить на | Окончательное неравенство |
| [латекс]а>б[/латекс] | [латекс]с[/латекс] | [латекс] \displaystyle \frac{a}{c}>\frac{b}{c}[/latex] |
| [латекс]4>2[/латекс] | [латекс]2[/латекс] | [латекс] \displaystyle \frac{4}{2}>\frac{2}{2}[/latex] |
| [латекс]а>б[/латекс] | [латекс]-с[/латекс] | [латекс] \displaystyle -\frac{a}{c}<-\frac{b}{c}[/latex] |
| [латекс]4>2[/латекс] | [латекс]-2[/латекс] | [латекс] \displaystyle -\frac{4}{2}<-\frac{2}{2}[/latex] |
В первом примере мы покажем, как применить свойства умножения и деления равенства для решения некоторых неравенств.
Пример: демонстрация свойства сложения
Проиллюстрируйте свойство сложения для неравенств, решая каждое из следующих действий:
- [латекс]х — 15<4[/латекс]
- [латекс]6\ge x — 1[/латекс]
- [латекс]x+7>9[/латекс]
Раствор
Попробуйте
Решите [латекс]3x — 2<1[/латекс].
Решение
Пример: демонстрация свойства умножения
Проиллюстрируйте свойство умножения для неравенств, решая каждое из следующих действий:
- [латекс]3x<6[/латекс]
- [латекс]-2x — 1\ge 5[/латекс]
- [латекс]5-x>10[/латекс]
Решение
Попробуйте
Решите [латекс]4x+7\ge 2x — 3[/латекс].
Решение
ОПРЕДЕЛЕНИЕ
Определение: Линейное неравенство — это неравенство с одной переменной, которое может быть записано в одной из следующих форм, где [latex]a[/latex] и [latex]b[/latex] являются действительными числами, а [латекс]а \neq 0[/латекс]:
[латекс]а +bx <0[/латекс]; [латекс]a+bx \leq 0[/латекс]; [латекс]а+bx>0[/латекс]; [латекс]a+bx \geq 0[/латекс]
Как показали примеры, мы можем выполнять одни и те же действия с обеими частями неравенства точно так же, как и с уравнениями; мы объединяем подобные термины и выполняем операции.
Чтобы решить, мы изолируем переменную.
Пример: Алгебраическое решение неравенства
Решите неравенство: [latex]13 — 7x\ge 10x — 4[/latex].
Решение
Попробуйте
Решите неравенство и запишите ответ, используя интервальную запись: [латекс]-x+4<\frac{1}{2}x+1[/latex].
Решение
Пример. Решение неравенства с дробями
Решите следующее неравенство и запишите ответ в виде интервалов: [latex]\displaystyle -\frac{3}{4}x\ge -\frac{5}{8}+ \frac{2}{3}x[/латекс].
Решение
Попробуйте
Решите неравенство и запишите ответ в интервальной записи: [латекс]\displaystyle -\frac{5}{6}x\le \frac{3}{4}+\frac{8}{3 }х[/латекс].
Решение
Как и в случае с уравнениями, свойство дистрибутивности можно применять для упрощения выражений, являющихся частью неравенства. После того, как скобки будут очищены, решение неравенства будет простым.
Попробуйте
Математический обзор линейных неравенств с одной переменной
Математический обзор линейных неравенств с одной переменной https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
Обзор
Линейные неравенства с одной переменной можно решать аналогично линейным уравнениям с одной переменной. Свойства, которые справедливы для линейных неравенств, включают свойства сложения, вычитания, умножения и деления, а также те, которые связаны с отношениями между отрицательными числами.
Свойства неравенств
Есть четыре свойства неравенств, которые справедливы для действительных чисел. Дополнительным свойством равенства в символьной форме является: если a > b, то a + c > b + c. Точно так же для вычитания, если a > b, то a – c > b –c. Для свойств умножения и деления c должно быть больше 0. Если a > b и c > 0, то ac > bc. Аналогично, если a > b и c > 0, то a/c > b/c. Предположим, что неравенство x -5 > -2. Переменную можно изолировать в левой части уравнения, чтобы решить его, так что x > -2 + 5 или x > 3. Кроме того, a > b означает то же самое, что и b < a.
Рисунок 1: Свойства неравенства в символьной форме.
Умножение на отрицательные числа
Свойства неравенств для умножения и деления указывают, что действительное число c больше 0, чтобы отношение сохранялось. Что произойдет, если c — отрицательное число? Предположим, что неравенство 5 > 3, и обе части умножены на -4. 5(-4) равно -20 и 3(-4) равно -12. Соотношение -20 < -12, поэтому направление знака меняется.
Точно так же предположим, что 100 > 80, и обе части были разделены на -10. 100/-10 равно -10, а 80/-10 = -8. Соотношение -10 < -8, поэтому направление знака также меняется при делении.
Неравенства с переменной по обе стороны от знака
Неравенства с переменной по обе стороны от знака решаются аналогично уравнениям с переменной по обе стороны от знака равенства. Предположим, что выражение -5q + 9 < -2q + 6. Чтобы решить неравенство, -5q + 2q + 9 < -2q + 2q + 6, или -3q + 9 < +6, или -3q < 6 - 9, или -3q < -3. Поскольку деление на -3 изменит знак, q > 1.
Рис. 2: Процесс решения неравенств, когда переменная находится по обе стороны от знака.
Линейные неравенства со всеми решениями или без решений
Подобно уравнениям, в которых все действительные числа являются набором решений, некоторые неравенства имеют все действительные числа в качестве набора решений. Предположим, что неравенство 2(x + 3) ≤ 5x -3x + 8. Его можно упростить как 2x + 6 ≤ 2x + 8 или 6 ≤ 8.