Гиперболические функции комплексного числа
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Гиперболическая функция — frwiki.
 wiki
wikiПолупрямая, проходящая через начало координат, пересекает гиперболу уравнения x 2 — y 2 = 1 в точке (ch a , sh a ) , где a вдвое больше алгебраической площади поверхности, ограниченной полуправами, гипербола и х- ось . См. Также анимированную версию этой диаграммы со сравнением с тригонометрическими функциями.
В математике мы называем функции гиперболическими функциями гиперболическим косинусом , гиперболическим синусом и касательной гиперболическими . Названия «синус», «косинус» и «касательная» происходят от их сходства с тригонометрическими функциями (называемыми «круговыми», потому что по отношению к единичной окружности x 2 + y 2 = 1 ), а термин «гиперболический» происходит от их отношения с гиперболой уравнения x 2 — y 2 = 1 .
Они используются в анализе для интегрального исчисления , разрешения дифференциальных уравнений, а также в гиперболической геометрии .
Резюме
- 1 рассказ
- 2 Определения
- 2.1 Гиперболический синус
- 2.2 Гиперболический косинус
- 2.3 Гиперболический тангенс
- 2.4 Гиперболический котангенс
- 2.5 Гиперболический секанс
- 2.6 Гиперболический косеканс
- 2.7 Таблица вариаций
- 3 свойства
- 4 Взаимные заявки
- 4.1 аргумент гиперболического синуса
- 4.2 аргумент гиперболического косинуса
- 4.3 Аргумент гиперболического тангенса
- 4.4 Аргумент гиперболического котангенса
- 4.5 аргумент гиперболического секанса
- 4.6 аргумент гиперболического косеканса
- 4.7 Демонстрация этих результатов
- 5 Связь между гиперболическими и круговыми функциями
- 6 Использование в гиперболической геометрии
- 7 Примечания и ссылки
- 8 См. Также
- 8.1 Связанная статья
- 8.2 Внешняя ссылка
История
Гиперболические функции были изобретены иезуитом Винченцо Риккати в 1760-х годах, когда он и его коллега Саладини пытались вычислить площадь под гиперболой уравнения x 2 — y 2 = 1 . Геометрический метод, который он тогда использовал, был очень похож на тот, который можно использовать для вычисления площади круга по уравнению x 2 + y 2 = 1 . Для вычисления площади круга используются классические тригонометрические функции, которые Риккати назвал круговыми косинусами и синусами. По аналогии он затем вызвал только что созданные функции гиперболическими косинусами и синусами. Это был удачный выбор, потому что это сходство не ограничивается методом вычисления площади, но также и всеми тригонометрическими формулами. Однако, зная о работах своего современника Эйлера , он не использовал экспоненциальную функцию для их определения, а только из геометрических соображений. Другой великий математик, изучавший гиперболические функции, — Жан-Анри Ламберт , который полностью изучил их в 1770 году. Эта квазиодновременность означает, что Ламберту иногда приписывают отцовство гиперболических функций, хотя работы Риккати были написаны несколькими годами ранее.
Геометрический метод, который он тогда использовал, был очень похож на тот, который можно использовать для вычисления площади круга по уравнению x 2 + y 2 = 1 . Для вычисления площади круга используются классические тригонометрические функции, которые Риккати назвал круговыми косинусами и синусами. По аналогии он затем вызвал только что созданные функции гиперболическими косинусами и синусами. Это был удачный выбор, потому что это сходство не ограничивается методом вычисления площади, но также и всеми тригонометрическими формулами. Однако, зная о работах своего современника Эйлера , он не использовал экспоненциальную функцию для их определения, а только из геометрических соображений. Другой великий математик, изучавший гиперболические функции, — Жан-Анри Ламберт , который полностью изучил их в 1770 году. Эта квазиодновременность означает, что Ламберту иногда приписывают отцовство гиперболических функций, хотя работы Риккати были написаны несколькими годами ранее.
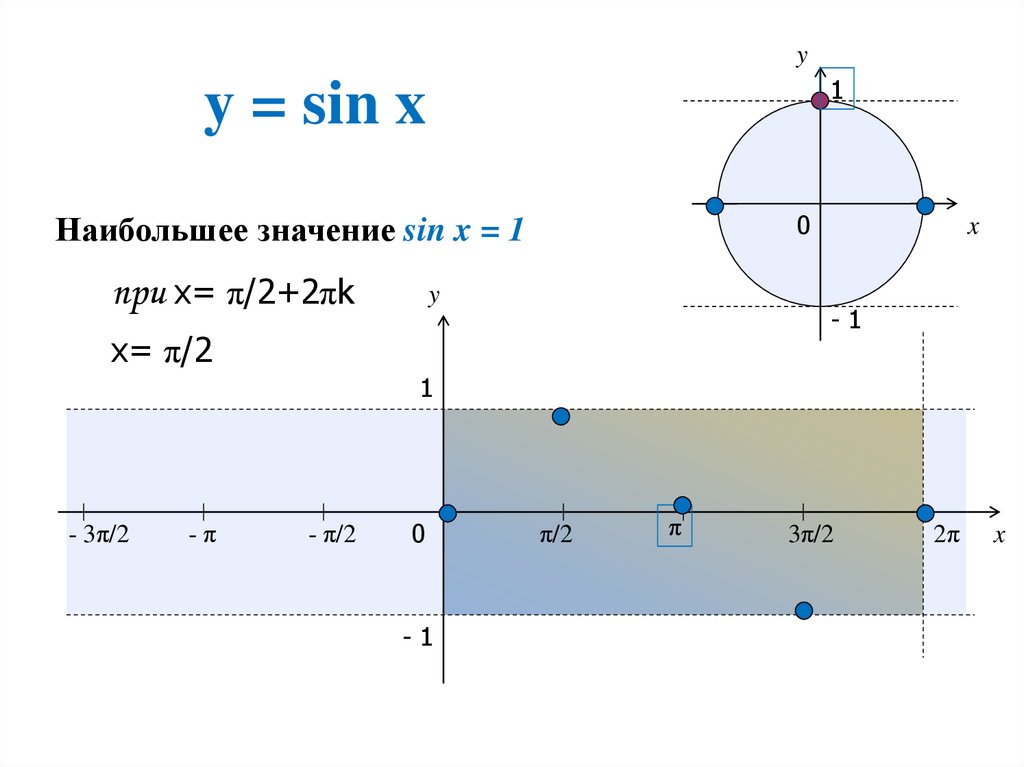
Точно так же, как точки (cos x , sin x ) описывают окружность, когда x пересекает ℝ, точки (cosh x , sinh x ) описывают ветвь гиперболы .
Параметр x нельзя интерпретировать как угол или длину дуги ; гиперболические функции периодичны , но имеют чисто мнимый период .
Функция cosh допускает минимум 1 в 0.
Функция sinh нечетная, поэтому sinh (0) = 0 .
Гиперболические функции удовлетворяют соотношениям, очень похожим на тригонометрические тождества. Фактически, Правило Осборна гласит, что можно преобразовать любое тригонометрическое тождество в гиперболическое, полностью расширив его, используя целые степени синуса и косинуса, заменив sin на sinh и cos на cosh и заменив знак каждого члена, который содержит произведение два синуса в свою противоположность.
Это позволяет получить, например, формулы сложения и вычитания:
- грех(Икс+y)знак равногрех(Икс)шуш(y)+шуш(Икс)грех(y){\ displaystyle \ operatorname {sinh} (x + y) = \ operatorname {sinh} (x) \, \ operatorname {cosh} (y) + \ operatorname {cosh} (x) \, \ operatorname {sinh} (y )}
- шуш(Икс+y)знак равношуш(Икс)шуш(y)+грех(Икс)грех(y){\ displaystyle \ operatorname {cosh} (x + y) = \ operatorname {cosh} (x) \, \ operatorname {cosh} (y) + \ operatorname {sinh} (x) \, \ operatorname {sinh} (y )}
- грех(Икс-y)знак равногрех(Икс)шуш(y)-шуш(Икс)грех(y){\ displaystyle \ operatorname {sinh} (xy) = \ operatorname {sinh} (x) \, \ operatorname {cosh} (y) — \ operatorname {cosh} (x) \, \ operatorname {sinh} (y)}
- шуш(Икс-y)знак равношуш(Икс)шуш(y)-грех(Икс)грех(y){\ displaystyle \ operatorname {cosh} (xy) = \ operatorname {cosh} (x) \, \ operatorname {cosh} (y) — \ operatorname {sinh} (x) \, \ operatorname {sinh} (y)}
и «формулы половинного угла» (второй действителен, если x положителен или равен нулю):
- шуш(Икс2)знак равношуш(Икс)+12{\ displaystyle \ operatorname {cosh} \ left ({\ frac {x} {2}} \ right) = {\ sqrt {\ frac {\ operatorname {cosh} (x) +1} {2}}}}
- грех(Икс2)знак равношуш(Икс)-12{\ displaystyle \ operatorname {sinh} \ left ({\ frac {x} {2}} \ right) = {\ sqrt {\ frac {\ operatorname {cosh} (x) -1} {2}}}}
Из этих выражений мы выводим следующие формулы, относящиеся к гиперболическому тангенсу:
1-танх2(Икс)знак равно1шуш2(Икс),танх(Икс+y)знак равнотанх(Икс)+танх(y)1+танх(Икс)танх(y),танх(Икс2)знак равношуш(Икс)-1шуш(Икс)+1. {2}}} + 1}} \ right)}.
{2}}} + 1}} \ right)}.
Демонстрации этих результатов
Явное вычисление этих логарифмических форм сводится к решению, например, уравнения sinh t = x ; полагая e t = T , мы попадаем в квадратное уравнение T 2 — 2 xT –1 = 0 , единственное положительное решение которого T = x + √ 1 + x 2, но может быть проще заметить, что, поскольку ch 2 t — sinh 2 t = 1 , имеем e t = sh t + ch t = x + √ 1 + x 2 .
Отношения между гиперболическими и круговыми функциями
Из формул Эйлера сразу выводим:
- потому что(Икс)знак равношуш(яИкс){\ Displaystyle \ соз (х) = \ OperatorName {соз} (\ mathrm {я} х)}
- ягрех(Икс)знак равногрех(яИкс){\ displaystyle \ mathrm {i} \ sin (x) = \ operatorname {sinh} (\ mathrm {i} x)}
Или же :
- шуш(Икс)знак равнопотому что(яИкс){\ Displaystyle \ OperatorName {сш} (х) = \ соз (\ mathrm {я} х)}
- грех(Икс)знак равно-ягрех(яИкс).
 {\ displaystyle \ operatorname {sinh} (x) = — \ mathrm {i} \, \ sin (\ mathrm {i} x).}
{\ displaystyle \ operatorname {sinh} (x) = — \ mathrm {i} \, \ sin (\ mathrm {i} x).}
Другие отношения между гиперболическими и круговыми функциями задаются функцией Гудермана или Гудермана. Их идентифицировал математик Кристоф Гудерманн . Гудерманиан θ функции t может быть определен как sinh t = tan θ . Мы выводим из этого множества соотношений между тригонометрическими функциями от θ и гиперболическими функциями от t . Например :
- 1шуш(т)знак равнопотому чтоθ{\ displaystyle {\ frac {1} {\ operatorname {cosh} (t)}} = \ cos \ theta}
- танх(т)знак равногрехθ.{\ displaystyle \ operatorname {tanh} (t) = \ sin \ theta.}
- dтзнак равноdθпотому чтоθ{\ displaystyle dt = {\ frac {d \ theta} {\ cos \ theta}}}
Использование в гиперболической геометрии
Формулы сферической тригонометрии остаются в силе в гиперболической геометрии при замене везде cos на cosh, sin на sinh и tan на tanh, и не забывая менять знаки, соответствующие произведениям четного числа функций sin или tan.
Примечания и ссылки
- ↑ (in) Эрик В. Вайстейн , « Правило Осборна » на MathWorld .
- ↑ Стандарт ISO 31-11 рекомендует использовать обозначение «арсинь» для этой функции.
- ↑ Стандарт ISO 31-11 рекомендует использовать обозначение «arcosh» для этой функции.
- ↑ Стандарт ISO 31-11 рекомендует использовать обозначение «artanh» для этой функции.
- ↑ Стандарт ISO 31-11 рекомендует использовать обозначение «arcoth» для этой функции.
Смотрите также
Связанная статья
- Примитивы взаимных гиперболических функций
- Закон гиперболического секанса
Внешняя ссылка
(ru) » Винсент Риккати, SJ (1707 — 1775) и его гиперболические функции »
Обычные математические функции | |
|---|---|
| Рациональная алгебраическая функция |
|
| Иррациональная алгебраическая функция |
|
| Трансцендентная функция |
|
Тригонометрия | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Круговая тригонометрия |
| ||||||||
| Гиперболическая тригонометрия |
| ||||||||
| |||||||||
<img src=»https://fr.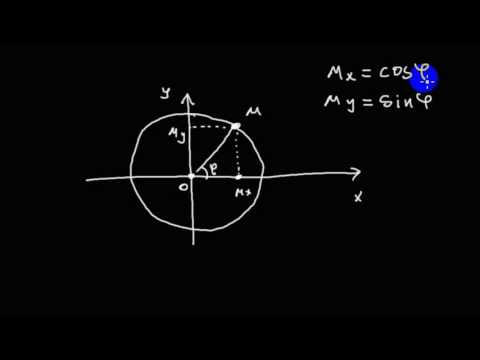 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Таблица гиперболических косинусов. Гиперболические функции. Интегралы от sh x, ch x, th x, cth x
В математике и её приложениях к естествознанию и технике находят широкое применение показательные функции. Это, в частности, объясняется тем, что многие изучаемые в естествознании явления относятся к числу так называемых процессов органического роста, в которых скорости изменения участвующих в них функций пропорциональны величинам самих функций.
Если обозначить через функцию, а через аргумент, то дифференциальный закон процесса органического роста может быть записан в виде где некоторый постоянный коэффициент пропорциональности.
Интегрирование этого уравнения приводит к общему решению в виде показательной функции
Если задать начальное условие при, то можно определить произвольную постоянную и, таким образом, найти частное решение которое представляет собой интегральный закон рассматриваемого процесса.
К процессам органического роста относятся при некоторых упрощающих предположениях такие явления, как, например, изменение атмосферного давления в зависимости от высоты над поверхностью Земли, радиоактивный распад, охлаждение или нагревание тела в окружающей среде постоянной температуры, унимолекулярная химическая реакция (например, растворение вещества в воде), при которой имеет место закон действия масс (скорость реакции пропорциональна наличному количеству реагирующего вещества), размножение микроорганизмов и многие другие.
Возрастание денежной суммы вследствие начисления на неё сложных процентов (проценты на проценты) также представляет собой процесс органического роста.
Эти примеры можно было бы продолжать.
Наряду с отдельными показательными функциями в математике и её приложениях находят применение различные комбинации показательных функций, среди которых особое значение имеют некоторые линейные и дробно-линейные комбинации функций и так называемые гиперболические функции. Этих функций шесть, для них введены следующие специальные наименования и обозначения:
Этих функций шесть, для них введены следующие специальные наименования и обозначения:
(гиперболический синус),
(гиперболический косинус),
(гиперболический тангенс),
(гиперболический котангенс),
(гиперболический секанс),
(гиперболический секанс).
Возникает вопрос, почему даны именно такие названия, причём здесь гипербола и известные из тригонометрии названия функций: синус, косинус, и т. д.? Оказывается, что соотношения, связывающие тригонометрические функции с координатами точек окружности единичного радиуса, аналогичны соотношениям, связывающим гиперболические функции с координатами точек равносторонней гиперболы с единичной полуосью. Этим как раз и оправдывается наименование гиперболических функций.
Функции, заданные формулами называют соответственно гиперболическим косинусом и гиперболическим синусом.
Эти функции определены и непрерывны на, причем — четная функция, а — нечетная функция.
Рисунок 1.1 — Графики функций
Из определения гиперболических функций и следует, что:
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
Функция определена и непрерывна на, а функция определена и непрерывна на множестве с выколотой точкой; обе функции — нечетные, их графики представлены на рисунках ниже.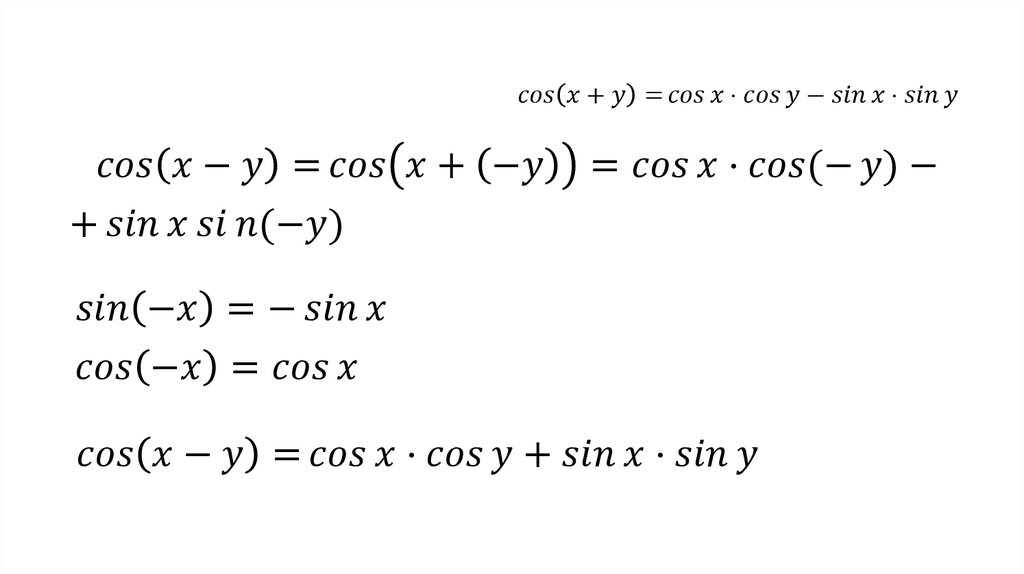
Рисунок 1.2 — График функции
Рисунок 1.3 — График функции
Можно показать, что функции и — строго возрастающие, а функция — строго убывающая. Поэтому указанные функции обратимы. Обозначим обратные к ним функции соответственно через.
Рассмотрим функцию, обратную к функции, т.е. функцию. Выразим ее через элементарные. Решая уравнение относительно, получаем Так как, то, откуда
Заменяя на, а на, находим формулу для функции, обратной для гиперболического синуса.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Гиперболические синус (sh x) и косинус (сh x) определяются следующими равенствами:
Гиперболические тангенс и котангенс определяются по аналогии с тригонометрическими тангенсом и котангенсом:
Аналогично определяются гиперболические секанс и косеканс:
Имеют место формулы:
Свойства гиперболических функций во многом аналогичны свойствам (см.). Уравнения х=соs t, у=sin t определяют окружность х²+у² = 1; уравнения х=сh t, у=sh t определяют гиперболу х² — у²=1.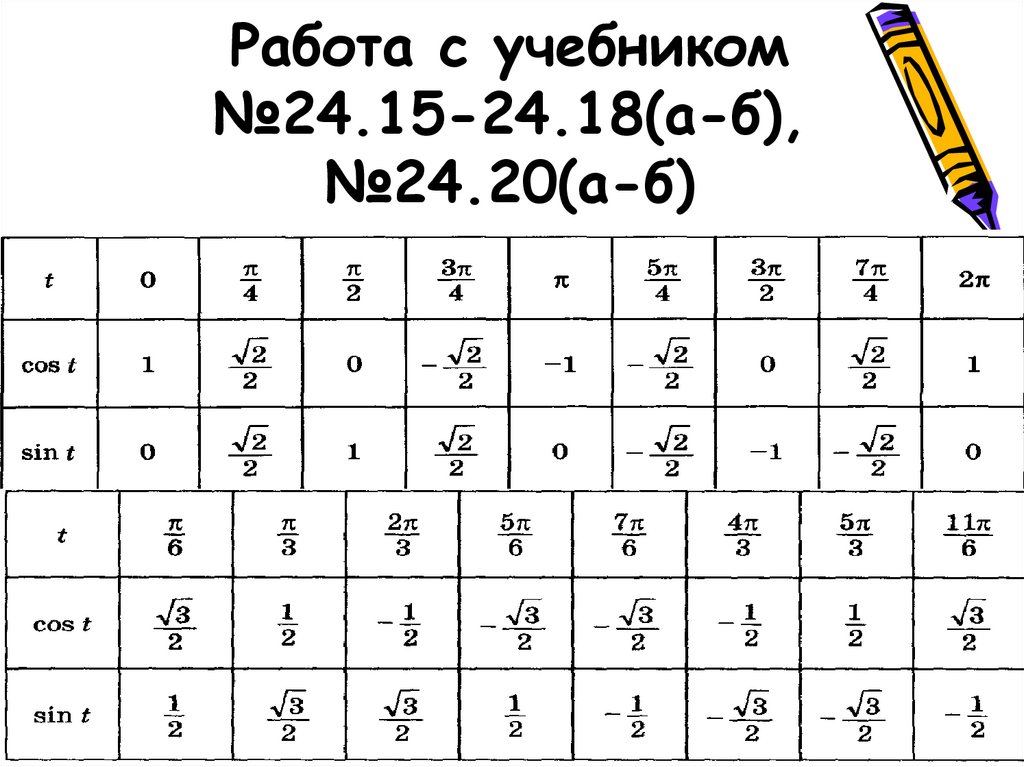 Как тригонометрические функции определяются из окружности единичного радиуса, так и гиперболические функции определяются из равнобочной гиперболы х² — у²=1. Аргумент t есть двойная площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48), аналогично тому как для круговых (тригонометрических) функций аргумент t численно равен удвоенной площади криволинейного треугольника ОКЕ (рис. 49):
Как тригонометрические функции определяются из окружности единичного радиуса, так и гиперболические функции определяются из равнобочной гиперболы х² — у²=1. Аргумент t есть двойная площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48), аналогично тому как для круговых (тригонометрических) функций аргумент t численно равен удвоенной площади криволинейного треугольника ОКЕ (рис. 49):
для круга
для гиперболы
Теоремы сложения для гиперболических функций аналогичны теоремам сложения для тригонометрических функций:
Эти аналогии легко усматриваются, если за аргумент х принять комплексное переменное г. Гиперболические функции связаны с тригонометрическими функциями следующими формулами: sh x = — i sin ix, ch x = cos ix,где i — одно из значений корня √-1
. Гиперболические функции sh х, а также и сh x: могут принимать сколько, угодно большие значения (отсюда, естественно, и большие единицы) в отличие от тригонометрических функций sin х, соs х, которые для действительных значений не могут быть по модулю больше единицы.
Гиперболические функции играют роль в геометрии Лобачевского (см. ), используются при изучении сопротивления материалов, в электротехнике и других отраслях знаний. Встречаются в литературе также обозначения гиперболических функций такие sinh x; соsh х; tgh x.
, страница 6
11 Основные функции комплексной переменной
Напомним определение комплексной экспоненты – . Тогда
Разложение в ряд Маклорена. Радиус сходимости этого ряда равен +∞, значит комплексная экспонента аналитична на всей комплексной плоскости и
(exp z)»=exp z; exp 0=1. (2)
Первое равенство здесь следует, например, из теоремы о почленном дифференцировании степенного ряда.
11.1 Тригонометрические и гиперболические функции
Синусом комплексного переменного называется функция
Косинус комплексного переменного есть функция
Гиперболический синус комплексного переменного определяется так:
Гиперболический косинус комплексного переменного — это функция
Отметим некоторые свойства вновь введеных функций.
A. Если x∈ ℝ , то cos x, sin x, ch x, sh x∈ ℝ .
Б. Имеет место следующая связь тригонометрических и гиперболических функций:
cos iz=ch z; sin iz=ish z, ch iz=cos z; sh iz=isin z.
В. Основные тригонометрическое и гиперболическое тождества :
cos 2 z+sin 2 z=1; ch 2 z-sh 2 z=1.
Доказательство основного гиперболического тождества.
Основное тригонометрическое тождество следует из оновного гиперболического тождества при учете связи тригонометрических и гиперболических функций (см. свойство Б)
Г Формулы сложения :
В частности,
Д. Для вычисления производных тригонометрических и гиперболических функций следует применить теорему о почленном дифференцировании степенного ряда. Получим:
(cos z)»=-sin z; (sin z)»=cos z; (ch z)»=sh z; (sh z)»=ch z.
Е. Функции cos z, ch z четны, а функции sin z, sh z нечетны.
Ж. (Периодичность) Функция e z периодична
с периодом 2π i. Функции cos z, sin z периодичны с периодом 2π , а функции ch
z, sh z периодичны с периодом 2πi. Более того,
Функции cos z, sin z периодичны с периодом 2π , а функции ch
z, sh z периодичны с периодом 2πi. Более того,
Применяя формулы суммы, получаем
З . Разложения на действительную и мнимую части :
Если однозначная аналитическая функция f(z) отображает биективно область D на область G, то D называется областью однолистности.
И. Область D k ={ x+iy | 2π k≤ y
Доказательство. Из соотношения (5) следует инъективность отображения exp:D k → ℂ . Пусть w — любое ненулевое комплексное число. Тогда, решая уравнения e x =|w| и e iy =w/|w| с действительными переменными x и y (y выбираем из полуинтеравала }
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение. Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 Гиперболические функции встречаются в механике, электротехнике и других технических дисциплинах.
Формулы для гиперболических функций 1. . Доказательство. Рассмотрим искомую разность . Соединяя начало и конец, получим доказываемое равенство: .
2. . Доказательство. Рассмотрим произведение . Соединяя начало и конец, получим доказываемое равенство: .
3. . Доказательство. Рассмотрим произведение . Рассмотрим произведение . Сложим два произведения и приведем подобные: . Соединяя начало и конец, получим доказываемое равенство: . Ещё много других свойств гиперболических функций похожих на свойства тригонометрических функций, которые доказываются аналогично. Докажем формулы для производных гиперболических функций. 1. Рассмотрим гиперболический синус . При нахождении производной константу выносим за знак производной. Далее применяем свойство о производной разности двух функций и . Находим производную функции по таблице производных: . Производную функции ищем как производную сложной функции . Поэтому, производная . Соединяя начало и конец, получим доказываемое равенство: . 2. Рассмотрим гиперболический косинус . Полностью применяем предыдущий алгоритм, только вместо свойства о производной разности двух функций и применяем свойство о производной суммы двух этих функций. . Соединяя начало и конец, получим доказываемое равенство: . 3. Рассмотрим гиперболический тангенс . Находим производную по правилу отыскания производной дроби. . 4. Производную гиперболического котангенса можно найти как производную сложной функции . Соединяя начало и конец, получим доказываемое равенство: .
Дифференциал функции Пусть функция – дифференцируема в точке , тогда её приращение этой функции в точке , соответствующее приращению аргумента , может быть представлено в виде , (8.1) где – некоторое число, не зависящее от , а – функция аргумента , которая является бесконечно малой при . Таким образом, приращение функции представляет собой сумму двух бесконечно малых слагаемых и . Было показано, что второе слагаемое является бесконечно малой функцией более высокого порядка, чем т.е. (см. 8.1). Поэтому первое слагаемое является главной линейной частью приращения функции . В замечании 8.1. получена другая формула (8. Определение 8.3.Дифференциаломфункции в точке называется главная линейная частью её приращения, равная произведению производной в этой точке на произвольное приращение аргумента , и обозначается (или ): (8.4) Дифференциал функции называют также дифференциалом первого порядка. Под дифференциалом независимой переменной понимается любое, независящее от , число. Чаще всего, в качестве этого числа берётся приращение переменной , т.е. . Это согласуется с правилом(8.4) нахождения дифференциала функции Рассмотрим функцию и найдем её дифференциал. , т.к. производная . Таким образом, получили: и дифференциал функции можно находить по формуле . (8.4.1) Замечание 8.7.Из формулу (8.4.1) следует, что. Таким образом, запись можно понимать не только как обозначение для производной , но и как отношение дифференциалов зависимого и независимого переменных.
8.7. Геометрический смысл дифференциала функции Пусть к графику функции проведена (см. рис. 8.1) касательная . Точка находится на графике функции и имеет абсциссу – . Даем произвольное приращение , такое, чтобы точка не вышла из области определения функции .
Рисунок 8.1 Изображение графика функции
Точка имеет координаты . Отрезок . Точка лежит на касательной к графику функции и имеет абсциссу – . Из прямоугольного следует, что , где угол – угол между положительным направлением оси и касательной, проведенной к графику функции в точке . По определению дифференциала функции и геометрического смысла производной функции в точке , делаем вывод, что . Таким образом, геометрический смысл дифференциала функции заключается в том, что дифференциал представляет собойприращение ординаты касательной к графику функции в точке . Замечание 8.8.Дифференциал и приращение для произвольной функции , вообще говоря, не равны между собой. На рисунке 8.1точка лежит на графике функции и имеет координаты . Отрезок . На рисунке 8.1 выполнено неравенство , т.е. . Но возможны случаи, когда справедливо противоположное неравенство . Это выполняется для линейной функции и для выпуклой вверх функции.
⇐ Предыдущая12 Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Гиперболические и обратные им функции MatLab
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
Наряду с тригонометрическими
функциями в математических расчетах часто используются и гиперболические функции.
Ниже приводится список таких функций, определенных в системе MATLAB. Функции
вычисляются для каждого элемента массива. Входной массив допускает комплексные
значения. Все углы в тригонометрических функциях измеряются в радианах.
Все углы в тригонометрических функциях измеряются в радианах.
acosh(X) — возвращает гиперболический арккосинус для каждого элемента X. Пример:
»Y= acosh (0.7)
Y =
0 + 0.7954i
acoth(X) — возвращает гиперболический арккотангенс для каждого элемента X. Пример:
»Y = acoth (0.1)
Y=
0.1003 + 1.5708i
acsch(X) — возвращает гиперболический арккосеканс для каждого элемента X. Пример:
» Y = acsch(1)
Y =
0. 8814
8814
asech(X) — возвращает гиперболический арксеканс для каждого элемента X. Пример:
» Y = asech(4)
Y =
0 + 1.3181i
asinh(X) — возвращает гиперболический арксинус для каждого элемента X. Пример:
» Y = asinh (2.456)
Y =
1.6308
atanh(X)
— возвращает гиперболический арктангенс для каждого элемента X. Пример:
» Х=[0.84 0.16 1.39];
» atanh (X)
ans =
1. 2212
0.1614 0.9065 + 1.5708i
2212
0.1614 0.9065 + 1.5708i
cosh(X) — возвращает гиперболический косинус для каждого элемента X. Пример:
» Х=[1 23];
» Cosh(X)
ans =
1.5431
3.7622 10.0677
coth(X)
— возвращает гиперболический котангенс для каждого элемента X. Пример:
» Y = coth(3.987)
Y =
1.0007
csch(x) — возвращает гиперболический косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csch(X)
Y =
0. 2757
0.0186 0.0135
2757
0.0186 0.0135
0.8656
0.8509 0.0998
sech(X) — возвращает гиперболический секанс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sech(X)
ans =
0.3985 0.7549 0.8770 0.0863
sinh(X) — возвращает гиперболический синус для каждого элемента X. Пример:
»
X=[pi/8 pi/7 pi/5 pi/10];
» sinh(X)
ans =
0.4029 0.4640 0.6705 0.3194
tanh(X)
— возвращает гиперболический тангенс для каждого элемента X. Пример:
Пример:
» X=[pi/2 pi/4 pi/6 pi/10];
»tanh(X)
ans =
0.9172
0.6558 0.4805 0.3042
Следующий m-файл-сценарий строит графики ряда гиперболических функций:
syms x
subplot(2,2,l).ezplot(sinh(x).[-4 4]).xlabel(«).grid on
subplot(2,2.2).ezplot(cosh(x).[-4 4]).xlabel(»).grid on
subp1ot(2.2,3).ezplot(tanh(x).[-4 4]).grid on
subplot(2.2.4).ezplot(sech(x).[-4 4]).grid on
Нетрудно заметить,
что гиперболические функции в отличие от тригонометрических не являются периодическими. Выбранные для графического представления функции дают примеры характерных нелинейностей.
Выбранные для графического представления функции дают примеры характерных нелинейностей.
В другом файле использованы команды для построения графиков ряда обратных гиперболических функций:
syms x
subplot(2,2.1).ezplot(asinh(x).[-4 4]).xlabel(«).grid on
subplot(2.2.2),ezp1ot(acosh(x).[0 4]).xlabel(«).grid on
subplot(2,2.3),ezplot(atanh(x).[-l l]).grid on
subplot(2.2.4).ezplot(asech(x).[0 l]).grid on
На этих графиках хорошо видны особенности данного класса функций. Такие функции, как обратный гиперболический синус и тангенс, «ценятся» за симметричный вид их графиков, дающий приближение к ряду типовых нелинейностей.
Нравится
Твитнуть
Гиперболические функции формулы.
 Справочные данные по гиперболическим функциям – свойства, графики, формулы
Справочные данные по гиперболическим функциям – свойства, графики, формулыЕго можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название).
Обозначим y= b·sht , тогда х2 / а2=1+sh3t =ch3t . Откуда x=± a·cht .
Таким образом мы приходим к следующим параметрическим уравнениям гиперболы:
У= в ·sht , –
Рис. 1.
Знак «»+»» в верхней формуле (6) соответствует правой ветви гиперболы, а знак «»– «» — левой (см. рис. 1). Вершинам гиперболы А(– а; 0) и В(а; 0) соответствует значение параметра t=0.
Для сравнения можно привести параметрические уравнения эллипса, использующие тригонометрические функции:
X=а·cost ,
Y=в·sint , 0 t 2p . (7)
3. Очевидно, что функция y=chx является четной и принимает только положительные значения. Функция y=shx – нечетная, т.к. :
Функции y=thx и y=cthx являются нечетными как частные
четной и нечетной функции. Отметим, что в отличие
от тригонометрических, гиперболические функции
не являются периодическими.
4. Исследуем поведение функции y= cthx в окрестности
точки разрыва х=0:
Таким образом ось Оу является вертикальной
асимптотой графика функции y=cthx . Определим
наклонные (горизонтальные) асимптоты:
Следовательно, прямая у=1 является правой горизонтальной асимптотой графика функции y=cthx . В силу нечетности данной функции ее левой горизонтальной асимптотой является прямая у= –1. Нетрудно показать, что эти прямые одновременно являются асимптотами и для функции y=thx. Функции shx и chx асимптот не имеют.
2) (chx)»=shx (показывается аналогично).
4)
Здесь так же прослеживается определенная аналогия с тригонометрическими функциями. Полная таблица производных всех гиперболических функций приведена в разделе IV.
Тангенс, котангенс
Определения гиперболических функций, их области определений и значений
sh
x
— гиперболический синус
,
-∞ ch
x
— гиперболический косинус
,
-∞ th
x
— гиперболический тангенс
,
-∞ cth
x
— гиперболический котангенс
,
x ≠ 0
; y +1
.
Графики гиперболических функций
График гиперболического синуса y = sh x
График гиперболического косинуса y = ch x
График гиперболического тангенса y = th x
График гиперболического котангенса y = cth x
Формулы с гиперболическими функциями
Связь с тригонометрическими функциями
sin
iz = i sh
z ; cos
iz = ch
z
sh
iz = i sin
z ; ch
iz = cos
z
tg
iz = i th
z ; ctg
iz = — i cth
z
th
iz = i tg
z ; cth
iz = — i ctg
z
Здесь i
— мнимая единица, i 2 = -1
.
Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.
Четность
sh(-x) = — sh x
;
ch(-x) = ch x
.
th(-x) = — th x
;
cth(-x) = — cth x
.
Функция ch(x) — четная. Функции sh(x) , th(x) , cth(x) — нечетные.
Разность квадратов
ch 2 x — sh 2 x = 1 .
Формулы суммы и разности аргументов
sh(x ± y) = sh
x ch
y ± ch
x sh
y
,
ch(x ± y) = ch
x ch
y ± sh
x sh
y
,
,
,
sh 2
x = 2 sh
x ch
x
,
ch 2
x = ch 2
x + sh 2
x
= 2 ch 2
x — 1 = 1 + 2 sh 2
x
,
.
Формулы произведений гиперболического синуса и косинуса
,
,
,
,
,
.
Формулы суммы и разности гиперболических функций
,
,
,
,
.
Связь гиперболического синуса и косинуса с тангенсом и котангенсом
,
,
,
.
Производные
,
Интегралы от sh x, ch x, th x, cth x
,
,
.
Разложения в ряды
Обратные функции
Ареасинус
При — ∞ ,
.
Ареакосинус
При 1
≤ x ,
.
Вторая ветвь ареакосинуса расположена при 1 ≤ x .
Ареатангенс
При — 1 ,
В математике и её приложениях к естествознанию и технике находят широкое применение показательные функции. Это, в частности, объясняется тем, что многие изучаемые в естествознании явления относятся к числу так называемых процессов органического роста, в которых скорости изменения участвующих в них функций пропорциональны величинам самих функций.
Если обозначить через функцию, а через аргумент, то дифференциальный закон процесса органического роста может быть записан в виде где некоторый постоянный коэффициент пропорциональности.
Интегрирование этого уравнения приводит к общему решению в виде показательной функции
Если задать начальное условие при, то можно определить произвольную постоянную и, таким образом, найти частное решение которое представляет собой интегральный закон рассматриваемого процесса.
К процессам органического роста относятся при некоторых упрощающих предположениях такие явления, как, например, изменение атмосферного давления в зависимости от высоты над поверхностью Земли, радиоактивный распад, охлаждение или нагревание тела в окружающей среде постоянной температуры, унимолекулярная химическая реакция (например, растворение вещества в воде), при которой имеет место закон действия масс (скорость реакции пропорциональна наличному количеству реагирующего вещества), размножение микроорганизмов и многие другие.
Возрастание денежной суммы вследствие начисления на неё сложных процентов (проценты на проценты) также представляет собой процесс органического роста.
Эти примеры можно было бы продолжать.
Наряду с отдельными показательными функциями в математике и её приложениях находят применение различные комбинации показательных функций, среди которых особое значение имеют некоторые линейные и дробно-линейные комбинации функций и так называемые гиперболические функции. Этих функций шесть, для них введены следующие специальные наименования и обозначения:
(гиперболический синус),
(гиперболический косинус),
(гиперболический тангенс),
(гиперболический котангенс),
(гиперболический секанс),
(гиперболический секанс).
Возникает вопрос, почему даны именно такие названия, причём здесь гипербола и известные из тригонометрии названия функций: синус, косинус, и т. д.? Оказывается, что соотношения, связывающие тригонометрические функции с координатами точек окружности единичного радиуса, аналогичны соотношениям, связывающим гиперболические функции с координатами точек равносторонней гиперболы с единичной полуосью. Этим как раз и оправдывается наименование гиперболических функций.
Этим как раз и оправдывается наименование гиперболических функций.
Функции, заданные формулами называют соответственно гиперболическим косинусом и гиперболическим синусом.
Эти функции определены и непрерывны на, причем — четная функция, а — нечетная функция.
Рисунок 1.1 — Графики функций
Из определения гиперболических функций и следует, что:
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
Функция определена и непрерывна на, а функция определена и непрерывна на множестве с выколотой точкой; обе функции — нечетные, их графики представлены на рисунках ниже.
Рисунок 1.2 — График функции
Рисунок 1.3 — График функции
Можно показать, что функции и — строго возрастающие, а функция — строго убывающая. Поэтому указанные функции обратимы. Обозначим обратные к ним функции соответственно через.
Рассмотрим функцию, обратную к функции, т.е. функцию. Выразим ее через элементарные. Решая уравнение относительно, получаем Так как, то, откуда
Решая уравнение относительно, получаем Так как, то, откуда
Заменяя на, а на, находим формулу для функции, обратной для гиперболического синуса.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Гиперболические синус (sh x) и косинус (сh x) определяются следующими равенствами:
Гиперболические тангенс и котангенс определяются по аналогии с тригонометрическими тангенсом и котангенсом:
Аналогично определяются гиперболические секанс и косеканс:
Имеют место формулы:
Свойства гиперболических функций во многом аналогичны свойствам (см.). Уравнения х=соs t, у=sin t определяют окружность х²+у² = 1; уравнения х=сh t, у=sh t определяют гиперболу х² — у²=1. Как тригонометрические функции определяются из окружности единичного радиуса, так и гиперболические функции определяются из равнобочной гиперболы х² — у²=1. Аргумент t есть двойная площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48), аналогично тому как для круговых (тригонометрических) функций аргумент t численно равен удвоенной площади криволинейного треугольника ОКЕ (рис.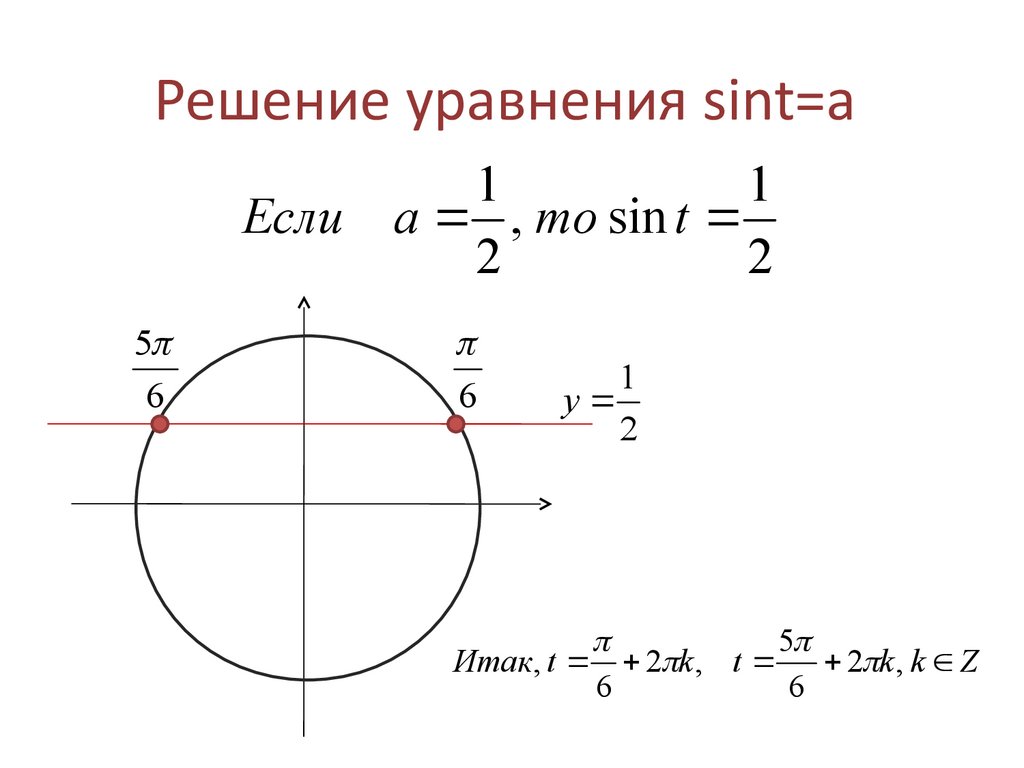 49):
49):
для круга
для гиперболы
Теоремы сложения для гиперболических функций аналогичны теоремам сложения для тригонометрических функций:
Эти аналогии легко усматриваются, если за аргумент х принять комплексное переменное г. Гиперболические функции связаны с тригонометрическими функциями следующими формулами: sh x = — i sin ix, ch x = cos ix,где i — одно из значений корня √-1
. Гиперболические функции sh х, а также и сh x: могут принимать сколько, угодно большие значения (отсюда, естественно, и большие единицы) в отличие от тригонометрических функций sin х, соs х, которые для действительных значений не могут быть по модулю больше единицы.
Гиперболические функции играют роль в геометрии Лобачевского (см. ), используются при изучении сопротивления материалов, в электротехнике и других отраслях знаний. Встречаются в литературе также обозначения гиперболических функций такие sinh x; соsh х; tgh x.
Определение 4. 2 x = 1$.
92 t-1}=\pm\sinh t$. Так что для некоторых
подходящие $t$, $\cosh t$ и $\sinh t$ — координаты типичного
точка на гиперболе. На самом деле получается, что $t$ в два раза больше
площадь, показанная на первом графике
рисунок 4.11.2. Даже
это аналогично тригонометрии; $\cos t$ и $\sin t$ – это
координаты типичной точки на единичной окружности, а $t$ дважды
площадь, показанная на втором графике рисунка 4.11.2.
2 x = 1$.
92 t-1}=\pm\sinh t$. Так что для некоторых
подходящие $t$, $\cosh t$ и $\sinh t$ — координаты типичного
точка на гиперболе. На самом деле получается, что $t$ в два раза больше
площадь, показанная на первом графике
рисунок 4.11.2. Даже
это аналогично тригонометрии; $\cos t$ и $\sin t$ – это
координаты типичной точки на единичной окружности, а $t$ дважды
площадь, показанная на втором графике рисунка 4.11.2.
Рисунок 4.11.2. Геометрические определения sin, cos, sinh, ch: $t$ в два раза больше заштрихованного площади на каждом рисунке. 9{-x }\over 2} =\cosh x$. $\qed$
Поскольку $\cosh x > 0$, $\sinh x$ возрастает и, следовательно, инъективен, поэтому
У $\sinh x$ есть обратный $\arcsinh x$. Кроме того, $\sinh x > 0$, когда
$x>0$, поэтому $\cosh x$ инъективен на $[0,\infty)$ и имеет (частичный)
обратный, $\arccosh x$. Другие гиперболические функции имеют обратные
также, хотя $\arcsech x$ является лишь частично обратным.
Мы можем вычислить производные этих функций, поскольку у нас есть другие
обратные функции. 2}}$.
92+1})$.)
2}}$.
92+1})$.)
Пример 4.11.2 Вычислите следующие пределы:
а. $\ds \lim_{x\to \infty} \cosh x$
б. $\ds \lim_{x\to \infty} \sinh x$
в. $\ds \lim_{x\to \infty} \tanh x$
д. $\ds \lim_{x\to \infty } (\cosh x -\sinh x)$
(отвечать)
Пример 4.11.3 Покажите, что диапазон $\tanh x$ равен $(-1,1)$. какая являются диапазонами $\coth$, $\sech$ и $\csch$? (Используйте тот факт, что они являются обратными функциями.) 92 х$. Вычислить производные остальных гиперболических функций.
Пример 4.11.8 Каковы области определения шести обратных гиперболических функции?
Пример 4.11.9 Нарисуйте графики всех шести обратных гиперболических функции.
Гиперболические тригонометрические функции | Brilliant Math & Science Wiki
Джефф Пиллинг, сэр Хайек, Арьен Фройгденхил, а также
способствовал
Содержимое
- Вывод экспоненциальных форм
- Список гиперболических тригонометрических функций
- Связь с уравнениями для единичного круга
- Гиперболические тригонометрические тождества
- Форма подвесного моста
- Смотрите также
Одной из ключевых характеристик, которая мотивирует гиперболические тригонометрические функции, является поразительное сходство с тригонометрическими функциями, которое можно увидеть из формулы Эйлера: ,sinθ=eiθ−e−iθ2i. {-i\тета}}{2i}.
\end{align}e±iθcosθ=cosθ±isinθ=2eiθ+e−iθ,sinθ=2ieiθ−e−iθ. 9{\pm a} = \cosh a \pm \sinh a,e±a=cosha±sinha,
{-i\тета}}{2i}.
\end{align}e±iθcosθ=cosθ±isinθ=2eiθ+e−iθ,sinθ=2ieiθ−e−iθ. 9{\pm a} = \cosh a \pm \sinh a,e±a=cosha±sinha,
, что эквивалентно формуле Эйлера для гиперболических функций. □ _\квадрат□
Билли Тангент наивно полагал, что функция гиперболического косинуса и функция стандартного косинуса одинаковы. Чтобы убедиться, он попробовал одно реальное значение и действительно получил тот же результат.
Какое значение он пробовал?
Если вы считаете, что это сработает для нескольких значений, введите в качестве ответа 99999. 9{-x}}{2}coshx=2ex+e−x
Здесь показаны их графические изображения:
Графики шести тригонометрических гиперболических функций
y=sech x y=\text{sech}\, xy=sechx y=csch x y=\text{csch}\, xy=cschx у = шишх у = \ шиш ху = шишх y=tanhxy=\tanhxy=tanhx y = sinhx y = \ sinh xy = sinhx y=cothxy=\coth xy=cothx
Какой из следующих гиперболических тригнометрических графов лучше всего «аппроксимируется» выражением y=1x?y = \frac{1}{x}?y=x1?
Параметрические уравнения для единичного круга задаются как
- x=costx = \cos tx=cost
- y=sinty = \sin ty=sint.

Когда ttt идет от 0→2π0 \стрелка вправо 2\pi0→2π, xxx и yyy очерчивают единичную окружность:
Аналогично, параметрические уравнения для единичной гиперболы задаются как
Синяя линия для положительного xxx показывает линию, которую вычерчивает этот параметрический набор уравнений: 9{-2x}}{2}\\\\ &= \кош (2x).\ _\квадрат \end{align}cosh3x+sinh3x=4e2x+2+e−2x+4e2x−2+e−2x=2e2x+e−2x=cosh(2x). □
грех\грех кос\коскос загар\тантан детская кроватка\раскладушка сек\сексек csc\csccsc Ни один из 6 вышеперечисленных Более одного из 6 выше
Чарли Брайанс играл со следующими 6 тригонометрическими функциями:
- sin\sinsin
- кос\коскос
- коричневый\тантановый
- кроватка\кроватка
- сек\сексек
- csc\csccsc.

Он заметил, что для одного из них, если он приравняет его гиперболическому аналогу — sinh, ch, tanh, coth, sech, \sinh, \cosh, \tanh, \coth, \text{ sech},sinh,cosh,tanh,coth,sech или csch,\text{csch},csch соответственно — он пересекается ровно в четырех точках.
Предполагая, что мы имеем дело только с действительными числами, какую триггерную функцию он выбрал?
Вдохновение: Brian Charlesworth
Часто возникает вопрос, является ли форма висячего моста контактной или параболой.
Теперь, если вы держите кусок веревки или цепь, поддерживаемую с обоих концов, она образует цепную связь (y=λcoshxλ).\big(y =\lambda \cosh \frac{x}{\lambda }\big).(y=λcoshλx). Таким образом, можно сделать вывод, что подвесной мост принимает такую форму.
Однако трос моста отличается от цепи тем, что трос моста выдерживает не только собственный вес, но и вес самого моста. Итак, рассмотрим два примера:
- , где вес моста пренебрежимо мал по сравнению с тросом;
- , где вес опорного троса незначителен по сравнению с весом моста.

Найдите форму троса подвесного моста (на фото выше), принимая вес мост пренебрежимо мал по сравнению с весом кабелей .
Если это так, то проблема аналогична болтающейся цепи.
Пусть функцией формы является y(x)y(x)y(x), а WLOG определяет, что нижняя точка цепи находится в начале координат.
Определите следующее:
- μ=\mu =μ= вес на единицу длины кабеля
- T=T =T= натяжение троса.
Определите следующее для заданной точки P:
- F = сила вдоль троса, направление которой будет представлять уклон троса в точке P
- T = горизонтальная составляющая натяжения троса
- W = вес кабеля.
Ясно, что наклон в точке P будет определяться выражением Уклон=WT=dydx=y′.\text{Уклон}= \frac{W}{T} = \frac{dy}{dx} = y’.Slope=TW=dxdy=y′.
{-1}(y’) = \frac{\mu x}{T}.sinh−1(y′)=Tµx. (\big((Постоянная интегрирования отсутствует, поскольку самая нижняя точка троса находится в начале координат, поэтому y′(0)=0.)y'(0) =0.\big)y′(0)=0 .)
Следовательно, y′=sinh(µxT) ⟹ y=Tµcosh(µxT)+Cy’ = \sinh \left(\frac{\mu x}{T}\right)\имеет y = \frac{T}{\mu } \cosh\left(\frac{\mu x}{T}\right) + C. y′=sinh(Tµx)⟹y=µTcosh(Tµx)+C. Опять же, нет константы интегрирования, поскольку y (0) = 0, y (0) = 0, y (0) = 0, что означает y=Tµcosh(µxT).y = \frac{T}{\mu} \cosh\left(\frac{\mu x}{T}\right).y=µTch(Tµx). Это можно упростить, установив λ=Tµ\lambda =\frac{T}{\mu}λ=µT: у=λкошxλ. □y=\lambda \cosh \frac{x}{\lambda}.\ _\squarey=λcoshλx. □
Между прочим, если вы когда-нибудь предполагали, что кривая оборванной цепи является параболической, вы не одиноки, так как часто говорят, что Галилей также предполагал параболическую форму. Это неудивительно, так как на этом рисунке показано сравнение двух кривых:
Теперь рассмотрим форму подвесного троса, предполагая, что вес троса пренебрежимо мал по сравнению с весом моста. Это немного легче решить, так как вес моста теперь однороден в направлении xxx, тогда как выше он менялся в зависимости от наклона цепи.
Это немного легче решить, так как вес моста теперь однороден в направлении xxx, тогда как выше он менялся в зависимости от наклона цепи.
Найдите форму троса подвесного моста (на фото выше), считая, что вес троса пренебрежимо мал по сравнению с весом моста .
Давайте определим те же переменные, что и раньше:
- μ=\mu =μ= вес на единицу длины кабеля
- T=T =T= натяжение троса
- F = сила вдоль троса, направление которой будет представлять наклон троса в точке P
- T = горизонтальная составляющая натяжения троса
- W = вес кабеля.
Как и в примере выше,
Уклон=WT=y′.\text{Уклон} = \frac{W}{T} = y’.Slope=TW=y′.
Но на этот раз плотность массы не зависит от уклона, и мы будем считать, что плотность моста постоянна для всего его пролета. Итак,
WT=μ dxy′=μxT⇒y=μ2Tx2+C.\begin{выровнено} \frac{W}{T} &= \mu\, dx\\ y ‘&= \ гидроразрыва {\ mu x} {T} \\ \Стрелка вправо y &= \frac{\mu}{2T}x^2 +C.
\end{выровнено} TWy′⇒y=µdx=Tµx=2Tµx2+C. 92}{2\лямбда}.\ _\squarey=2λx2. □
Итак, в заключение, мы видим, что если трос поддерживает только собственный вес, как канат, удерживаемый в двух точках, он образует форму контактной сети . Однако, если он имеет незначительный вес относительно моста, который он поддерживает, он принимает форму параболы .
Если вы повесите цепочку, как показано на рисунке выше, она образует функцию гиперболического косинуса.
Допустим следующие значения:
- Δh=6\Delta h = 6Δh=6 дюймов
- Δx=2\Дельта x = 2Δx=2 фута.
Какое расстояние от левой (нижней) стороны до самой нижней точки цепи в дюймах?
Дайте ответ до 222 знаков после запятой.
Если вы считаете, что ответ не может быть определен, введите 99999.
Цитировать как: Гиперболические тригонометрические функции. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/hyperbolic-trigonometric-functions/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/hyperbolic-trigonometric-functions/
Производные гиперболических функций
9\prime = — \text{sech}\,x\tanh x.\]Производные обратных гиперболических функций
Рассмотрим теперь производные \(6\) обратных гиперболических функций. Соответствующие формулы дифференцирования можно вывести с помощью теоремы об обратной функции.
Возьмем, например, функцию \(y = f\left( x \right) \) \(= \text{arcsinh}\,x\) (обратный гиперболический синус). Вместе с функцией \(x = \varphi \left( y \right) \) \(= \sinh y\) они образуют пару взаимно обратных функций. Тогда производная обратного гиперболического синуса равна 92}}}\;\;\left( {\left| x \right| \gt 1} \right).\]
Как видите, производные функций \(\text{arctanh}\,x\) и \(\text{arccoth}\,x\) совпадают, но определяются при разных значениях \( х.\) Ограничения области для аркгиперболического тангенса и котангенса следуют из области значений функций \(у = \th х\) и \(у = \coth х,\) соответственно.
Мы также выводим производные аркгиперболического секанса и косеканса, хотя эти функции встречаются редко. 92}} }},\;\;x \in \left( {0,1} \right).\]
Аналогично можно найти производную обратного гиперболического косеканса. Предположим, что \(y = f\left( x \right) \) \(= \text{arccsch}\,x\) \(\left( {x \in \mathbb{R},\;x \ne 0 } \right)\) и \(x = \varphi \left( y \right) \) \(= \text{csch}\,y\) \(\left( {y \ne 0} \right). \)
Сначала рассмотрим ветвь \(x \gt 0\). В этом случае переменная \(y\) принимает значения \(y \gt 0.\) Производная обратного гиперболического косеканса выражается как 92}} }}\;\;\left( {x \ne 0} \right).\]
Таблица производных гиперболических функций
Для удобства соберем формулы дифференцирования всех гиперболических функций в одну таблицу:
См. решенные проблемы на стр. 2,3.
Исчисление I. Производные гиперболических функций
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Производные
/ Производные гиперболических функций
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. {\mbox{2}}}\влево(x\вправо)\end{ множество}\]
{\mbox{2}}}\влево(x\вправо)\end{ множество}\]
Вы заметите, что они похожи, но не совсем одинаковы, на некоторые из наиболее распространенных триггерных тождеств, поэтому будьте осторожны, чтобы не спутать представленные здесь тождества со стандартными триггерными функциями.
Поскольку гиперболические функции определяются в терминах экспоненциальных функций, найти их производные довольно просто, если вы уже прочитали следующий раздел. Однако мы этого не сделали, поэтому нам понадобится следующая формула, которую можно легко доказать после того, как мы рассмотрим следующий раздел. 92}}}\]
6.9 Вычисление гиперболических функций — Вычисление, том 1
Цели обучения
- 6.9.1 Примените формулы для производных и интегралов гиперболических функций.
- 6.9.2 Примените формулы для производных обратных гиперболических функций и связанных с ними интегралов.
- 6.9.3
Опишите общие прикладные условия контактной кривой.

Мы познакомились с гиперболическими функциями в разделе «Введение в функции и графики» вместе с некоторыми их основными свойствами. В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.
Производные и интегралы гиперболических функций
Напомним, что гиперболический синус и гиперболический косинус определяются как
sinhx=ex-e-x2andcoshx=ex+e-x2.sinhx=ex-e-x2andcoshx=ex+e-x2.
Другие гиперболические функции затем определяются через sinxsinhx и chx.coshx. Графики гиперболических функций показаны на следующем рисунке.
Рисунок 6,81 Графики гиперболических функций.
Легко вывести формулы дифференцирования для гиперболических функций. Например, глядя на sinxsinhx, мы имеем
ddx(sinhx)=ddx(ex-e-x2)=12[ddx(ex)-ddx(e-x)]=12[ex+e-x]=coshx.ddx(sinhx)=ddx(ex- e−x2)=12[ddx(ex)−ddx(e−x)]=12[ex+e−x]=chx.
Аналогично, (d/dx)coshx=sinhx.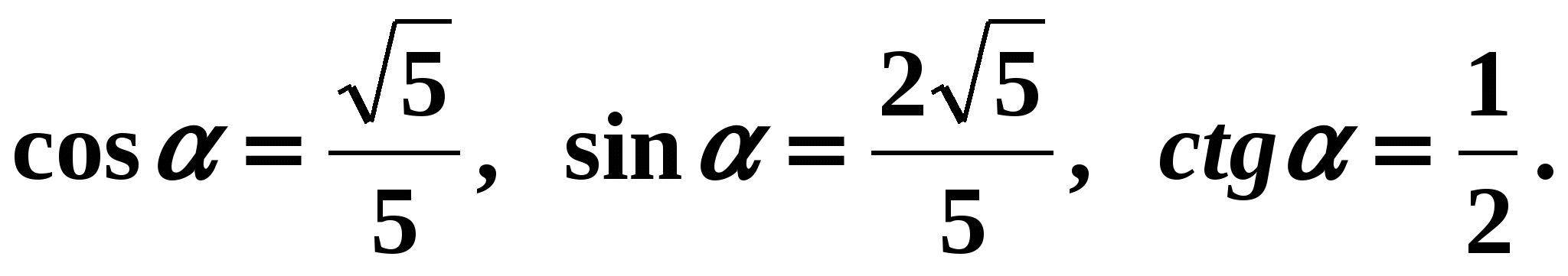 (d/dx)coshx=sinhx. Мы суммируем формулы дифференцирования для гиперболических функций в следующей таблице.
(d/dx)coshx=sinhx. Мы суммируем формулы дифференцирования для гиперболических функций в следующей таблице.
| ф(х)ф(х) | ddxf(x)ddxf(x) |
|---|---|
| синхсинхх | кошхкошх |
| кошхкошх | sinxsinx |
| танкстанкс | sech3xsech3x |
| коткскоткс | -csch3x-csch3x |
| sechxsechx | −sechxtanx−sechxtanx |
| cschxcschx | -cschxcothx-cschxcothx |
Стол
6. 2
Производные гиперболических функций
2
Производные гиперболических функций
Давайте на минутку сравним производные гиперболических функций с производными стандартных тригонометрических функций. Сходства много, но и различий тоже. Например, производные функций синуса совпадают: (d/dx)sinx=cosx(d/dx)sinx=cosx и (d/dx)sinhx=coshx.(d/dx)sinhx=coshx. Однако производные функций косинуса различаются по знаку: (d/dx)cosx=-sinx, (d/dx)cosx=-sinx, но (d/dx)chx=sinhx.(d/dx)coshx= синх. Продолжая изучение гиперболических функций, мы должны помнить об их сходствах и различиях со стандартными тригонометрическими функциями.
Эти формулы дифференцирования для гиперболических функций непосредственно приводят к следующим интегральным формулам.
cothu+C∫coshudu=sinhu+C∫sechutanhudu=−sechu+C∫sech3udu=tanhu+C∫cschucothudu=−cschu+C
Пример 6,47
Дифференцирование гиперболических функций
Оценить следующие производные:
- ддх(ш(х2))ддх(ш(х2))
- ddx(кошх)2ddx(кошх)2
Решение
Используя формулы из таблицы 6. 2 и цепное правило, мы получаем
2 и цепное правило, мы получаем
- ddx(sinh(x2))=ch(x2)·2xddx(sinh(x2))=ch(x2)·2x
- ddx(coshx)2=2coshxsinhxddx(coshx)2=2coshxsinhx
Контрольно-пропускной пункт 6,47
Оценить следующие производные:
- ddx(tanh(x2+3x))ddx(tanh(x2+3x))
- ddx(1(sinx)2)ddx(1(sinx)2)
Пример 6,48
Интегралы, включающие гиперболические функции
Вычислите следующие интегралы:
- ∫xcosh(x2)dx∫xcosh(x2)dx
- ∫tanhxdx∫tanhxdx
Решение
Мы можем использовать u -замену в обоих случаях.
- Пусть u=x2.u=x2. Тогда du=2xdxdu=2xdx и
∫xcosh(x2)dx=∫12coshudu=12sinhu+C=12sinh(x2)+C.∫xcosh(x2)dx=∫12coshudu=12sinhu+C=12sinh(x2)+C .
- Пусть u=coshx.u=coshx. Тогда du=sinhxdxdu=sinhxdx и
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln|coshx|+C.
 ∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
Обратите внимание, что chx>0coshx>0 для всех x,x, поэтому мы можем убрать знаки абсолютного значения и получить∫tanhxdx=ln(chx)+C.∫tanhxdx=ln(chx)+C.
Контрольно-пропускной пункт 6,48
Вычислите следующие интегралы:
- ∫sinh4xcoshxdx∫sinh4xcoshxdx
- ∫sech3(3x)dx∫sech3(3x)dx
Расчет обратных гиперболических функций
Глядя на графики гиперболических функций, мы видим, что при соответствующих ограничениях диапазона все они имеют обратные значения. Большинство необходимых ограничений диапазона можно различить при внимательном рассмотрении графиков. Области и диапазоны обратных гиперболических функций приведены в следующей таблице.
| Функция | Домен | Диапазон |
|---|---|---|
| sin-1xsin-1x | (-∞,∞)(-∞,∞) | (-∞,∞)(-∞,∞) |
| кош-1хкош-1х | [1,∞)[1,∞) | [0,∞)[0,∞) |
| tanh-1xtanh-1x | (−1,1)(−1,1) | (-∞,∞)(-∞,∞) |
| ткань-1x ткань-1x | (−∞,−1)∪(1,∞)(−∞,−1)∪(1,∞) | (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) |
| сек-1кссек-1х | (0, 1] (0, 1] | [0,∞)[0,∞) |
| csch-1xcsch-1x | (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) | (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) |
Стол
6. 3
Области и диапазоны обратных гиперболических функций
3
Области и диапазоны обратных гиперболических функций
Графики обратных гиперболических функций показаны на следующем рисунке.
Рисунок 6,82 Графики обратных гиперболических функций.
Чтобы найти производные обратных функций, мы используем неявное дифференцирование. У нас есть
y=sinh-1xsinhy=xddxsinhy=ddxxcoshydydx=1.y=sinh-1xsinhy=xddxsinhy=ddxxcoshydydx=1.
Напомним, что ch3y-sinh3y=1, cosh3y-sinh3y=1, поэтому coshy=1+sinh3y.coshy=1+sinh3y. Тогда
dydx=1coshy=11+sinh3y=11+x2.dydx=1coshy=11+sinh3y=11+x2.
Аналогичным образом можно вывести формулы дифференцирования для других обратных гиперболических функций. Эти формулы дифференцирования сведены в следующую таблицу.
| ф(х)ф(х) | ddxf(x)ddxf(x) |
|---|---|
| sin-1xsin-1x | 11+x211+x2 |
| кош-1хкош-1х | 1×2-11×2-1 |
| tanh-1xtanh-1x | 11-x211-x2 |
| ткань-1x ткань-1x | 11-x211-x2 |
| сек-1кссек-1х | −1×1−x2−1×1−x2 |
| csch-1xcsch-1x | −1|x|1+x2−1|x|1+x2 |
Стол
6. 4
Производные обратных гиперболических функций
4
Производные обратных гиперболических функций
Обратите внимание, что производные от tanh-1xtanh-1x и coth-1xcoth-1x одинаковы. Таким образом, когда мы интегрируем 1/(1−x2),1/(1−x2), нам нужно выбрать правильную первообразную на основе области определения функций и значений x.x. Формулы интегрирования, включающие обратные гиперболические функции, резюмируются следующим образом.
∫11+u2du=sinh−1u+C∫1u1−u2du=−sech−1|u|+C∫1u2−1du=ch−1u+C∫1u1+u2du=−csch−1|u|+C∫ 11−u2du={tanh−1u+Cif|u|<1coth−1u+Cif|u|>1∫11+u2du=sinh−1u+C∫1u1−u2du=−sech−1|u|+C∫1u2 −1du=ch−1u+C∫1u1+u2du=−csch−1|u|+C∫11−u2du={tanh−1u+Cif|u|<1coth−1u+Cif|u|>1
Пример 6,49
Дифференцирование обратных гиперболических функций
Вычисление следующих производных:
- ddx(sinh-1(x3))ddx(sinh-1(x3))
- ddx(tanh-1x)2ddx(tanh-1x)2
Решение
Используя формулы из таблицы 6.4 и цепное правило, мы получаем следующие результаты: =19+x2
Контрольно-пропускной пункт 6,49
Оценить следующие производные:
- ddx(cosh-1(3x))ddx(cosh-1(3x))
- ddx(coth-1x)3ddx(coth-1x)3
Пример 6.
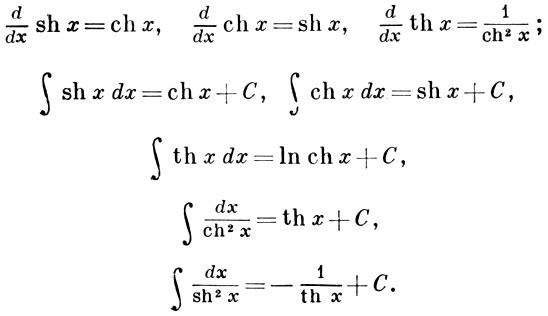 50
50Интегралы, включающие обратные гиперболические функции
Вычислить следующие интегралы:
- ∫14×2−1dx∫14×2−1dx
- ∫12×1−9x2dx∫12×1−9x2dx
Решение
Мы можем использовать u-подстановкуu-подстановку в обоих случаях.
- Пусть u=2x.u=2x. Тогда du=2dxdu=2dx и имеем
∫14×2−1dx=∫12u2−1du=12cosh−1u+C=12cosh−1(2x)+C.∫14×2−1dx=∫12u2−1du=12cosh−1u+ С=12кош-1(2х)+С.
- Пусть u=3x.u=3x. Тогда du=3dxdu=3dx и мы получаем
∫12×1−9x2dx=12∫1u1−u2du=−12sech−1|u|+C=−12sech−1|3x|+C.∫12×1−9x2dx=12∫1u1 −u2du=−12sech−1|u|+C=−12sech−1|3x|+C.
Контрольно-пропускной пункт 6.50
Вычислить следующие интегралы:
- ∫1×2−4dx,x>2∫1×2−4dx,x>2
- ∫11−e2xdx∫11−e2xdx
Приложения
Одно из физических применений гиперболических функций включает подвесные кабели.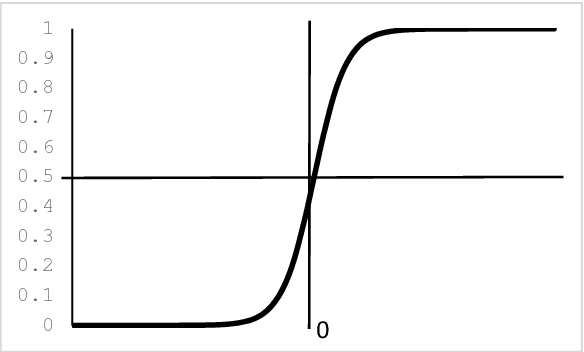 Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.
Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.
Рисунок 6,83 Цепи между этими столбами имеют форму контактной сети. (кредит: модификация работы OKFoundryCompany, Flickr)
Гиперболические функции могут использоваться для моделирования контактных сетей. В частности, функции вида y=acosh(x/a)y=acosh(x/a) являются контактными. На рис. 6.84 показан график y=2cosh(x/2).y=2cosh(x/2).
Рисунок 6,84 Функция гиперболического косинуса образует контактную сеть.
Пример 6,51
Использование контактной сети для определения длины кабеля
Предположим, что висящий кабель имеет вид 10cosh(x/10)10cosh(x/10) для −15≤x≤15, −15≤x≤15, где xx измеряется в футах. Определите длину кабеля (в футах).
Определите длину кабеля (в футах).
Решение
Напомним из Раздела 2.42.4, что формула для длины дуги такова:
Длина дуги=∫ab1+[f′(x)]2dx. Длина дуги=∫ab1+[f′(x)]2dx.
Имеем f(x)=10cosh(x/10),f(x)=10cosh(x/10), поэтому f′(x)=sinh(x/10).f′(x)=sinh( х/10). Тогда
Длина дуги=∫ab1+[f′(x)]2dx=∫−15151+sinh3(x10)dx. Длина дуги=∫ab1+[f′(x)]2dx=∫−15151+sinh3(x10)dx .
Теперь вспомним, что 1+sinh3x=cosh3x,1+sinh3x=cosh3x, поэтому мы имеем
Длина дуги=∫−15151+sinh3(x10)dx=∫−1515cosh(x10)dx=10sinh(x10)|−1515 =10[sinh(32)−sinh(−32)]=20sinh(32)≈42,586 футов. Длина дуги=∫−15151+sinh3(x10)dx=∫−1515cosh(x10)dx=10sinh(x10)|− 1515=10[sinh(32)−sinh(−32)]=20sinh(32)≈42,586 фута.
Контрольно-пропускной пункт 6,51
Предположим, что висящий трос имеет форму 15cosh(x/15)15cosh(x/15) для −20≤x≤20,−20≤x≤20. Определите длину кабеля (в футах).
Раздел 6.9 Упражнения
377.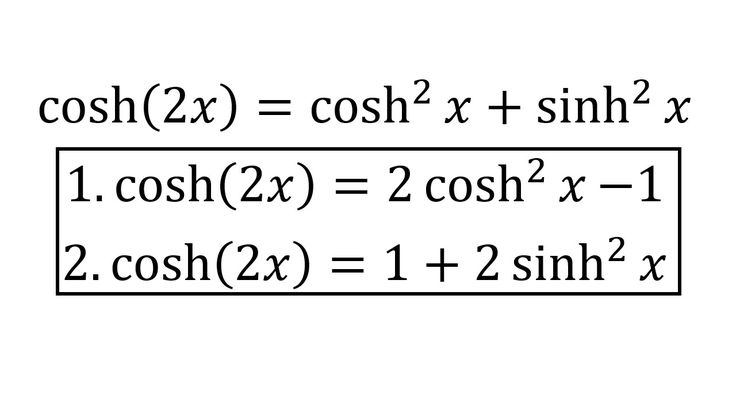
[T] Найдите выражения для coshx+sinhxcoshx+sinx и coshx-sinhx.coshx-sinhx. Используйте калькулятор, чтобы построить график этих функций и убедиться, что ваше выражение правильное.
378.
Из определений ch(x)ch(x) и sh(x),sinh(x) найдите их первообразные.
379.
Покажите, что ch(x)ch(x) и sh(x)sinh(x) удовлетворяют условию y″=y.y″=y.
380.
Используйте правило частных, чтобы проверить, что tanh(x)′=sech3(x).tanh(x)′=sech3(x).
381.
Выведите ch3(x)+sinh3(x)=ch(2x)cosh3(x)+sinh3(x)=cosh(2x) из определения.
382.
Возьмите производную от предыдущего выражения, чтобы найти выражение для sinh(2x).sinh(2x).
383.
Докажите, что sinh(x+y)=sinh(x)ch(y)+cosh(x)sinh(y)sinh(x+y)=sinh(x)ch(y)+cosh(x)sin(y) ), заменив выражение экспонентами.
384.
Возьмите производную от предыдущего выражения, чтобы найти выражение для cosh(x+y).cosh(x+y).
В следующих упражнениях найдите производные заданных функций и постройте график вместе с функцией, чтобы убедиться, что ваш ответ правильный.
385.
[T] ш(3х+1)ш(3х+1)
386.
[T] ш(х2)ш(х2)
387.
[Т] 1шт(х)1шт(х)
388.
[T] зв(лн(х)) зв(лн(х))
389.
[T] cosh3(x)+sinh3(x)cosh3(x)+sinh3(x)
390.
[Т] cosh3(x)−sinh3(x)cosh3(x)−sinh3(x)
391.
[T] танх(х2+1)танх(х2+1)
392.
[T] 1+tanh(x)1−tanh(x)1+tanh(x)1−tanh(x)
393.
[Т] sin6(x)sin6(x)
394.
[T] пер(сек(х)+танг(х)) пер(сек(х)+танг(х))
Для следующих упражнений найдите первообразные для заданных функций.
395.
кош(2x+1)кош(2x+1)
396.
танх(3x+2)танх(3x+2)
397.
ксош(х2)кскош(х2)
398.
3x3tanh(x4)3x3tanh(x4)
399.
cosh3(x)sinh(x)cosh3(x)sinh(x)
400.
tanh3(x)sech3(x)tanh3(x)sech3(x)
401.
грех(х)1+кош(х)зп(х)1+кош(х)
402.
Кот (х) Кот (х)
403.
кош(х)+шп(х)ш(х)+шп(х)
404.
(ш(х)+шп(х))п(ш(х)+шп(х))п
Для следующих упражнений найдите производные функций.
405.
tanh−1(4x)tanh−1(4x)
406.
sinh-1 (x2) sinh-1 (x2)
407.
sinh−1(ch(x)) sinh−1(ch(x))
408.
кош-1(х3) кош-1(х3)
409.
tanh−1(cos(x))tanh−1(cos(x))
410.
esinh-1(x)esinh-1(x)
411.
пер(танг-1(х)) пер(танг-1(х))
Для следующих упражнений найдите первообразные функций.
412.
∫dx4−x2∫dx4−x2
413.
∫dxa2−x2∫dxa2−x2
414.
∫dxx2+1∫dxx2+1
415.
∫xdxx2+1∫xdxx2+1
416.
∫-dxx1-x2∫-dxx1-x2
417.
∫exe2x-1∫exe2x-1
418.
∫−2xx4−1∫−2xx4−1
В следующих упражнениях используйте тот факт, что падающее тело с трением, равным квадрату скорости, подчиняется уравнению dv/dt=g−v2.dv/dt=g−v2.
419.
Покажите, что v(t)=gtanh((g)t)v(t)=gtanh((g)t) удовлетворяет этому уравнению.
420.
Получите предыдущее выражение для v(t)v(t) путем интегрирования dvg-v2=dt.dvg-v2=dt.
421.
[T] Оцените, как низко упало тело за 1212 секунд, найдя площадь под кривой v(t).v(t).
Для следующих упражнений используйте этот сценарий: Канат, висящий под собственным весом, имеет наклон S=dy/dxS=dy/dx, удовлетворяющий условию dS/dx=c1+S2. dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению.
dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению.
422.
Покажите, что S=sinh(cx)S=sinh(cx) удовлетворяет этому уравнению.
423.
Интегрируйте dy/dx=sinh(cx)dy/dx=sinh(cx), чтобы найти высоту троса y(x)y(x), если y(0)=1/c.y(0)=1/c.
424.
Нарисуйте кабель и определите, насколько он провисает при x=0.x=0.
Для следующих упражнений решите каждую задачу.
425.
[T] Цепь свисает с двух столбов на расстоянии 22 м друг от друга, образуя контактную сеть, описываемую уравнением y=2cosh(x/2)−1.y=2cosh(x/2)−1. Найдите уклон контактной сети у левого столба забора.
426.
[T] Цепь свисает с двух столбов на расстоянии четырех метров друг от друга, образуя контактную сеть, описываемую уравнением y=4cosh(x/4)−3. y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).
y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).
427.
[T] Высоковольтная линия электропередачи представляет собой контактную сеть, описываемую формулой y=10cosh(x/10).y=10cosh(x/10). Найдите отношение площади под контактной сетью к длине ее дуги. Что ты заметил?
428.
Телефонная линия — контактная сеть, описываемая формулой y=acosh(x/a).y=acosh(x/a). Найдите отношение площади под контактной сетью к длине ее дуги. Подтверждает ли это ваш ответ на предыдущий вопрос?
429.
Докажите формулу производной y=sinh-1(x)y=sinh-1(x) путем дифференцирования x=sinh(y).x=sinh(y). ( Подсказка: Используйте гиперболические тригонометрические тождества.)
430.
Докажите формулу производной y=ch-1(x)y=ch-1(x) путем дифференцирования x=ch(y). x=ch(y).
x=ch(y).
( Подсказка: Используйте гиперболические тригонометрические тождества.)
431.
Докажите формулу производной от y=sech-1(x)y=sech-1(x) путем дифференцирования x=sech(y).x=sech(y). ( Подсказка: Используйте гиперболические тригонометрические тождества.)
432.
Докажите, что (ch(x)+sinh(x))n=ch(nx)+sinh(nx).(ch(x)+sinh(x))n=ch(nx)+sinh(nx).
433.
Докажите выражение для sinh-1(x).sinh-1(x). Умножьте x=sinh(y)=(1/2)(ey+e−y)x=sinh(y)=(1/2)(ey+e−y) на 2ey2ey и найдите y.y. Соответствует ли ваше выражение тому, что написано в учебнике?
434.
Докажите выражение для ch−1(x).cosh−1(x). Умножьте x=ch(y)=(1/2)(ey-e-y)x=cosh(y)=(1/2)(ey-e-y) на 2ey2ey и найдите y.y. Соответствует ли ваше выражение тому, что написано в учебнике?
Сходства гиперболических и тригонометрических функций
Между гиперболическими функциями и тригонометрическими функциями существует большое сходство. Давайте сначала определим гиперболическую функцию, как она есть на самом деле. Гиперболические функции являются экспоненциальными функциями и отличаются от тригонометрических аналогов, которые являются периодическими функциями.
Давайте сначала определим гиперболическую функцию, как она есть на самом деле. Гиперболические функции являются экспоненциальными функциями и отличаются от тригонометрических аналогов, которые являются периодическими функциями.
Ниже приведены графики сравнения функций.
Гиперболический косинус выглядит как парабола, но отличается от параболы, так как гиперболический косинус растет экспоненциально. Обе функции демонстрируют линейную симметрию относительно и -ось.
Гиперболический синус напоминает многочлен третьей степени. Обе функции являются нечетными функциями и демонстрируют точечную симметрию относительно начала координат. В отличие от полиномиальных функций, на гиперболическом синусе нет точки, где наклон равен 0.
Когда гиперболический синус и косинус изображаются вместе, мы видим, что они асимптотичны на положительной оси x . Поэтому мы ожидаем, что гиперболический тангенс будет иметь горизонтальную асимптоту. x\). 92}\) ( x < –1 или x > 1)
x\). 92}\) ( x < –1 или x > 1)
Производная от tanh –1 x и coth –1 x одинакова. Это прекрасное время для изучения их графиков.
Синяя кривая — гиперболический арктангенс. Поскольку гиперболический тангенс имеет горизонтальные асимптоты, его обратный имеет вертикальные асимптоты. Следовательно, домен tanh –1 x равен –1 < x < 1,
92 = 1\). Параллельность в знаках заслуживает внимания. Мы можем параметризовать уравнение окружности с помощью синуса и косинуса. Параметрическое уравнение окружности имеет вид \((\cos t, \sin t)\). Точно так же параметрическое уравнение гиперболы имеет вид \((\ch t, \sinh t)\). Для круга t представляет собой угол, созданный началом координат и точкой на круге относительно оси x , когда мы движемся против часовой стрелки по кругу. Поскольку t увеличивается и проходит 2 π , получаем периодичность тригонометрических функций. Для гиперболических функций при увеличении t расстояние точки гиперболы от начала координат просто экспоненциально увеличивается, и оно не представляет собой угол, создаваемый началом координат и точкой гиперболы.
Для гиперболических функций при увеличении t расстояние точки гиперболы от начала координат просто экспоненциально увеличивается, и оно не представляет собой угол, создаваемый началом координат и точкой гиперболы.
На изображении выше показаны две коники, точки на окружности и гипербола для данного t . Для круга вы можете суммировать квадраты x и y в точке C, и вы получите 1. Для гиперболы вы можете вычесть квадраты x и y в точке H, и вы получите 1.
Обратите внимание, что параметр t , хотя и может иметь одно и то же значение, не даст точек на окружности и гиперболе, коллинеарных с началом координат. Следовательно, t от 1, который является мерой радиана для окружности или угла AOC, дает точку C на окружности; тогда как т of 1 (не мера радиана и не мера угла AOH) для гиперболы дает точку H, где точки C и H не совпадают с началом координат.
Формула аналогичной площади
Интересной параллелью является площадь, заметаемая параметром t .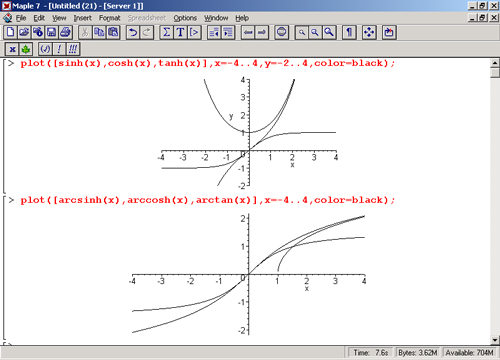 Для круга площадь, создаваемая сектором, равна \(\frac{1}{2}t\). Помните, что t представляет угол или длину дуги окружности, поскольку это единичная окружность. Следовательно, есть скрытая π в этой формуле.
Для круга площадь, создаваемая сектором, равна \(\frac{1}{2}t\). Помните, что t представляет угол или длину дуги окружности, поскольку это единичная окружность. Следовательно, есть скрытая π в этой формуле.
Для гиперболы площадь, ограниченная гиперболой, отрезок от начала координат до точки на гиперболе и ось x равна \(\frac{1}{2}t\).
На изображении ниже показан сектор круга, заданный углом t . Площадь легко вычислить. Отношение дуги, образованной углом t , к длине окружности равно отношению площади сектора к площади всей окружности: \(\frac{t}{2\pi} = \ frac{\text{площадь сектора}}{\text{площадь всего круга}}\) или \(\text{площадь сектора} = \frac{t\pi}{2\pi} = \frac{1 {2}т\).
Теперь сосредоточимся на гиперболическом секторе.
Область, заштрихованная синим цветом выше, представляет собой область, ограниченную сегментом OH, гиперболой и осью x . Самый простой способ — найти площадь A H под кривой путем интегрирования параметрического уравнения, а затем вычитания этой площади из площади A T треугольника OHC.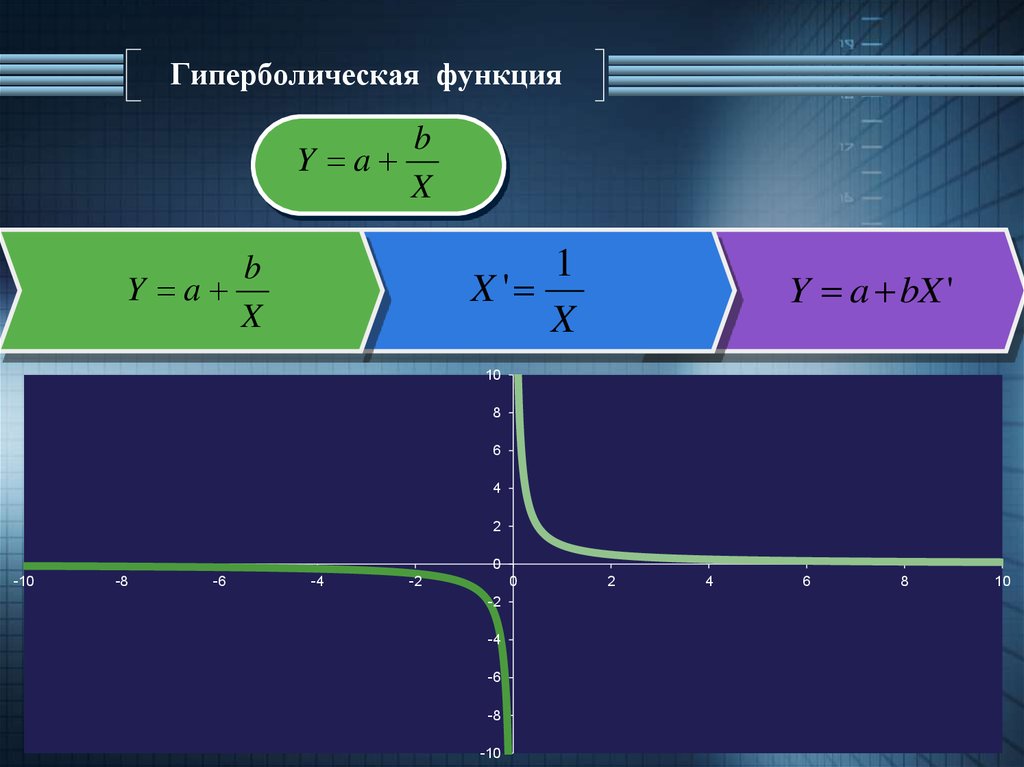 Это устраняет беспорядочные вычисления, которые мы все равно сделаем позже, чтобы доказать, что эта площадь растет с логарифмической скоростью по отношению к 9.{t_1}=\) \(A_H = \frac{\sinh(2t_1)}{4}-\frac{1}{2}t_1\).
Это устраняет беспорядочные вычисления, которые мы все равно сделаем позже, чтобы доказать, что эта площадь растет с логарифмической скоростью по отношению к 9.{t_1}=\) \(A_H = \frac{\sinh(2t_1)}{4}-\frac{1}{2}t_1\).
Мы можем просто заменить t 1 на t и сказать, что площадь под гиперболой от t = 0 до t = t равна \(\fract){\sinh {4}-\frac{1}{2}t\).
Площадь треугольника равна \(A_T = \frac{1}{2}(\sinh t)(\cosh t)\). Используя тождество «двойного угла», это равно \(A_T = \frac{1}{4}\sinh(2t)\). Итак, площадь заштрихованной области:
(iii) \(A = \frac{1}{4}\sinh(2t) — \left(\frac{\sinh(2t)}{4}-\frac{1}{2}t\right) = \) \(\frac{1}{2}t\).
Скорость роста гиперболического сектора
Прежде чем мы продолжим, отметим, что формулы для кругового и гиперболического секторов одинаковы и дают одну и ту же площадь для любого данного t . Для круга, когда t достигает 2 π , та же область просто повторяется, и область трассируется.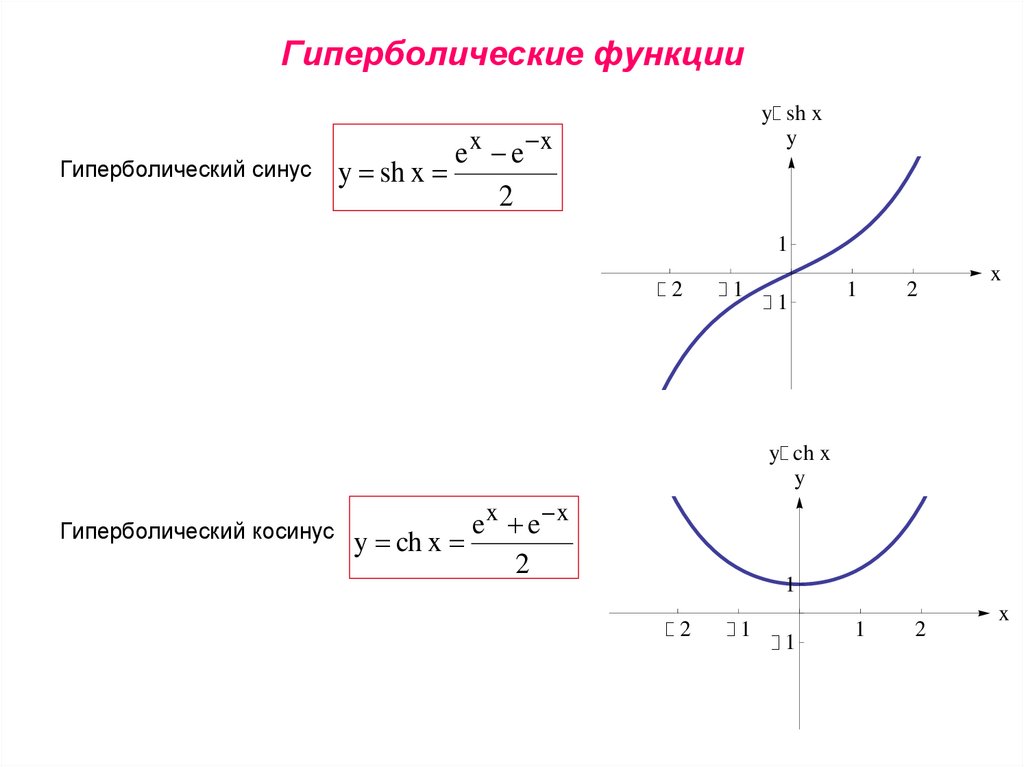 Таким образом, площадь увеличивается из-за ретрейсинга, а не потому, что область увеличивается, хотя и очень медленно. Для гиперболы этого никогда не происходит. Как t увеличивается до бесконечности, площадь области фактически увеличивается. Таким образом, площади совпадают с увеличением t . Это также приводит нас к следующему вопросу: насколько быстро растет площадь в гиперболическом секторе?
Таким образом, площадь увеличивается из-за ретрейсинга, а не потому, что область увеличивается, хотя и очень медленно. Для гиперболы этого никогда не происходит. Как t увеличивается до бесконечности, площадь области фактически увеличивается. Таким образом, площади совпадают с увеличением t . Это также приводит нас к следующему вопросу: насколько быстро растет площадь в гиперболическом секторе?
Если мы посмотрим на скорость изменения, основанную на параметре t , то она просто растет с постоянной скоростью 1/2, поскольку площадь равна t /2. Но давайте найдем скорость, исходя из координаты x . Нам нужно интегрировать, используя прямоугольное уравнение, как мы упоминали ранее о беспорядочных вычислениях. Площадь, 92} + x \right) \ приблизительно \frac{1}{2}\ln (2x) \). Следовательно, площадь растет с логарифмической скоростью. Это наблюдение согласуется с площадью под кривой функции \(f(x) = \frac{1}{x}\), которая представляет собой единичную гиперболу, повернутую на 45°.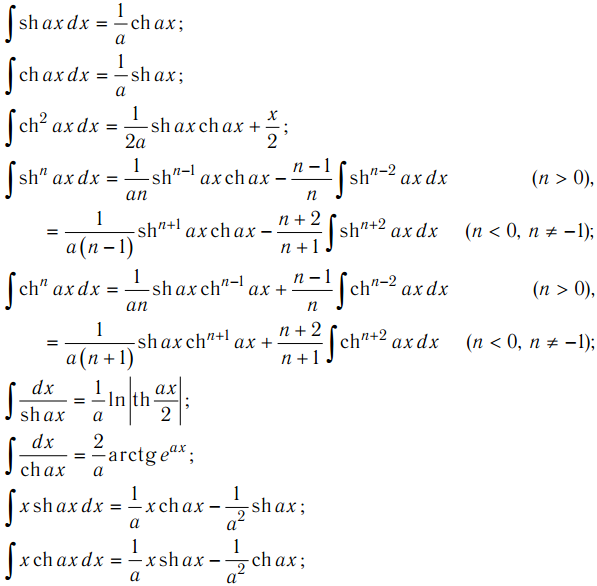 Площадь под этой кривой равна \(\ln x\).
Площадь под этой кривой равна \(\ln x\).
Приложения
Катящаяся парабола
Есть несколько интересных вещей, которые могут происходить с гиперболическими функциями. Например, фокус параболы, катящейся по оси x , описывает цепную связь или гиперболическую косинусную кривую. Ниже приведено задание Geogebra, с которым вы можете поиграть, чтобы увидеть его в действии.
У меня есть полное доказательство того, что этот фокус параболы отслеживает контактную сеть: Доказательство того, что фокус параболы движется по контактной сети.
Катящийся квадрат
Еще одним интересным свойством контактной сети является то, что если квадрат катится по контактной сети, центр квадрата следует прямолинейному пути. Это можно увидеть в следующем упражнении Geogebra.
Вы можете изменить форму контактной сети, увеличив или уменьшив коэффициент a . Длина стороны квадрата будет 2 и . Обратите внимание, что в какой-то момент квадрат больше не касается контактной сети; однако его центр остается на оси x .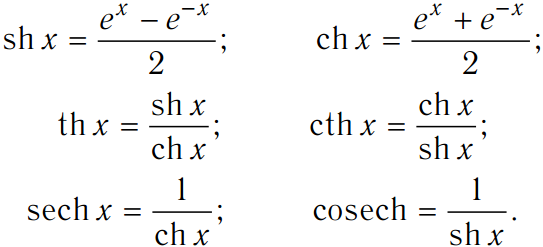 2}\text{}dx\). Для нашей контактной сети уравнение имеет вид \(y = -a\cosh\frac{x}{a}\). Производная равна \(\frac{dy}{dx} = -\sinh\frac{x}{a}\). Найдем длину дуги, 9{t}\cosh\frac{x}{a}\text{ }dx =\) \( a\sinh\frac{t}{a}\)
2}\text{}dx\). Для нашей контактной сети уравнение имеет вид \(y = -a\cosh\frac{x}{a}\). Производная равна \(\frac{dy}{dx} = -\sinh\frac{x}{a}\). Найдем длину дуги, 9{t}\cosh\frac{x}{a}\text{ }dx =\) \( a\sinh\frac{t}{a}\)
Это приятный сюрприз. Следовательно, длина дуги от вершины до точки P (после замены нашего фиктивного t на x ) равна a sh( x / a ). Это равно HP, так как квадрат катится по контактной сети. Мы уже знаем, что OP равно — ch( x / ). Нам нужно найти О. Если OH равно a , то мы знаем, что оно должно лежать на 9-м2\)
Следовательно, точки OH и OP имеют общую точку, лежащую на оси x . Это позволяет найти середину стороны квадрата, катящегося по контактной сети. Если кто-то хочет найти точку H, вот шаги:
- Сначала выберите точку P на контактной сети.
- Проведите касательную в точке P.
- Нарисуйте перпендикуляр к оси x в точке P.
- Проведите перпендикуляр к касательной, проходящей через точку O.


 pozitiv-r.ru
pozitiv-r.ru Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн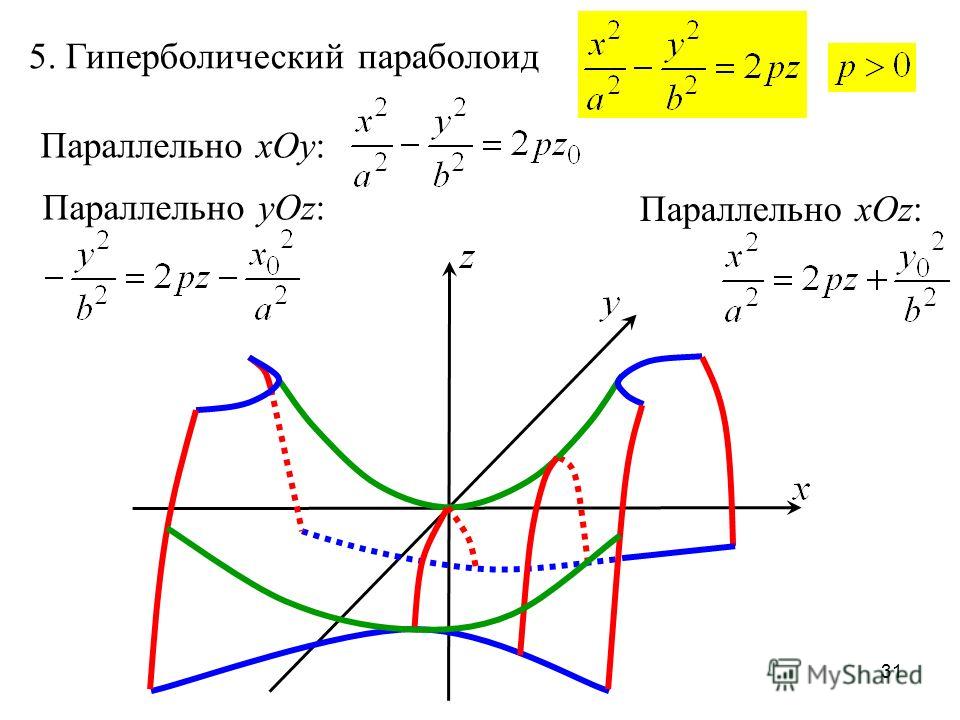 {\ displaystyle \ operatorname {sinh} (x) = — \ mathrm {i} \, \ sin (\ mathrm {i} x).}
{\ displaystyle \ operatorname {sinh} (x) = — \ mathrm {i} \, \ sin (\ mathrm {i} x).}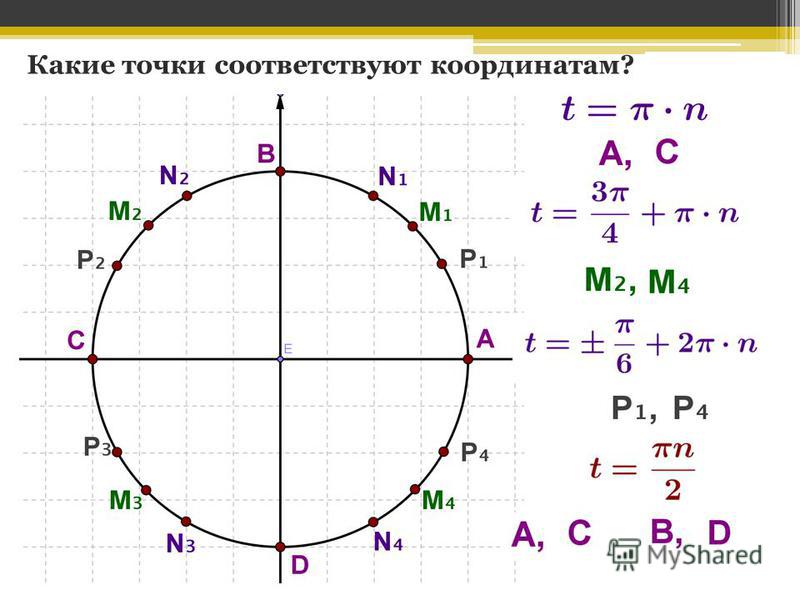 ..
.. Многие формулы для гиперболических функций похожи на формулы для тригонометрических функций, кроме свойства ограниченности.
Многие формулы для гиперболических функций похожи на формулы для тригонометрических функций, кроме свойства ограниченности.
 1.1) для приращения функции , а именно: . (8.1.1)
1.1) для приращения функции , а именно: . (8.1.1)
 В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1следует, что , т.е. .
В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1следует, что , т.е. . ..
..

 {-1}(y’) = \frac{\mu x}{T}.sinh−1(y′)=Tµx.
(\big((Постоянная интегрирования отсутствует, поскольку самая нижняя точка троса находится в начале координат, поэтому y′(0)=0.)y'(0) =0.\big)y′(0)=0 .)
{-1}(y’) = \frac{\mu x}{T}.sinh−1(y′)=Tµx.
(\big((Постоянная интегрирования отсутствует, поскольку самая нижняя точка троса находится в начале координат, поэтому y′(0)=0.)y'(0) =0.\big)y′(0)=0 .) \end{выровнено} TWy′⇒y=µdx=Tµx=2Tµx2+C. 92}{2\лямбда}.\ _\squarey=2λx2. □
\end{выровнено} TWy′⇒y=µdx=Tµx=2Tµx2+C. 92}{2\лямбда}.\ _\squarey=2λx2. □
 ∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.