Семь нерешенных задач тысячелетия: Семь задач тысячелетия

Проект «Задачи тысячелетия» | Образовательная социальная сеть

Задачи, задачи… Мы сталкиваемся с ними каждый день. Некоторые мы решаем легко и не задумываясь, а над некоторыми нам приходится поломать голову несколько дней, а есть задачи, на решение которых уходят десятки лет.

На II Международном математическом Конгрессе, проходившем в Париже в 1900 году, немецкий математик Давид Гильберт представил список из 23 математических проблем в самых разных областях.

 Среди них проблемы, охватывающие алгебру, геометрию, математическую физику, теорию чисел, теорию вероятностей, топологию и дифференциальные уравнения.

Данные задачи определенным образом определили развитие математики 20 века.

  Сейчас из данных проблем полностью решены только 16. Остальные же либо не имеют четкого решения, либо имеют, но лишь для некоторых случаев.

Например 8 проблема, проблема размещения простых чисел
Долгое время люди пытались выстроить закономерность в размещении простых чисел, однако эти попытки не увенчались успехом, исследовалась функция распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например для 4 — 2 простых числа, для 10 — уже 4 числа. Свою гипотезу выдвинул

Гипотеза Римана как раз предполагает свойства данной функции распределения.

В совокупности с гипотезой Римана включена под

номером 8 в список проблем Гильберта проблема Гольдбаха

Гольдбах в истории математики более всего известен проблемой, которую в 1742 году предложил в письме Леонарду Эйлеру. Помимо прочего,

поступив в 1742 году на службу в министерство иностранных дел Российской империи занимался дешифровкой корреспонденции европейских послов в Санкт-Петербурге.

Проблему Гольдбаха сейчас разделяют на две отдельных. В 1742 году Христиан Гольдбах написал письмо известному математику Леонарду Эйлеру, в котором предположил следующее: Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел. Данное предположение называют тернарной (то есть состоящий из трех элементов) проблемой Гольдбаха.

                   Например

                  177=131+3+3

                  645=419+223+3

                  87=83+2+2 или 61+23+3

                  33=11+11+11 или 33=19+11+3

Прочитав письмо Гольдбаха, Эйлер выдвинул следующую гипотезу: Любое четное число больше двух можно представить в виде суммы двух простых чисел. Эту гипотезу назвали бинарной  (двойной) проблемой Гольдбаха, иногда она обозначается как проблема Эйлера.

Пример:

42 = 23+19 или 11+31

360= 349+11 или 179+181

22=19+3 или 11+11

184=181+3 или 131 +53

И хоть кажется, что так будет действительно со всеми четными числами, доказать это еще не удалось. На данный момент бинарная гипотеза Гольдбаха была проверена для всех чётных чисел, не превышающих 4×1018. Вопрос о верности данной гипотезы стоит и по сей день.

До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау на Пятом Международном математическом конгрессе

• Гипотеза Гольдбаха: Можно ли любое целое чётное число, большее 2, записать в виде суммы двух простых?

 42 = 23+19 или 11+31

• Гипотеза о числах-близнецах: Бесконечно ли число простых p таких, что p + 2 тоже простое?

 (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101,    103), (107, 109)

• Гипотеза Лежандра: Всегда ли существует по меньшей мере одно простое число, лежащее между двумя последовательными полными квадратами?

1≤3≤4, 4≤5≤9, 9≤11≤16, 16≤17≤25

• Существует ли бесконечно много простых чисел p, для которых p − 1 является полным квадратом?

5-1=4, 17-1=16, 37-1=36,…

Все четыре проблемы на 2018 год остаются открытыми.

Проблемы Смейла — список из восемнадцати нерешённых математических проблем, предложенный Стивеном Смейлом в 2000 году 

Смейл составил свой список по просьбе Владимира Арнольда, занимавшего в 1995–1998 годах пост вице-президента международного математического союза. Идею этого списка Владимир Арнольд взял из списка проблем Гильберта.

  Всего проблем Смейла 18, некоторые из них взяты из списка проблем Гильберта, а некоторые вошли и в список задач тысячелетия.

Теперь о математических проблемах тысячелетия .

Задачи тысячелетия составляют семь математических задач, охарактеризованных как «важные классические задачи, решение которых не найдено вот уже в течение многих лет». За решение каждой из этих задач институтом Клэя предложено вознаграждение в 1 000 000 долларов США. Анонсируя награду, институт Клэя провёл параллель со списком проблем Гильберта, представленным в 1900 году и оказавшим существенное влияние на математику XX века. Из 23 проблем Гильберта только одна — гипотеза Римана — вошла в список задач тысячелетия.

По состоянию на 2018 год только одна из семи задач тысячелетия (гипотеза Пуанкаре) решена

1. Равенство классов P и NP

Так квадратные уравнения решаются через дискриминант. Решение этой задачи относится к классу P (Polynomial time) — для нее существует быстрый алгоритм решения
Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно проверить по определенному алгоритму. Например проверка методом перебора компьютером.

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей.
Данная проблема имеет большое значение для самых различных областей знаний, но решить ее не могут уже более 40 лет.

2.  Гипотеза Ходжа
В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучение. Сейчас учеными придуман и применяется подход, основная идея которого заключается в том, чтобы вместо самого изучаемого объекта использовать простые «кирпичики» с уже известными свойствами, которые склеиваются между собой и образуют его подобие 
Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.

3. Гипотеза Римана — закономерность в размещении простых чисел
   

4. Теория Янга — Миллса

Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействий. Теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается не решенной.

5. Существование и гладкость решений уравнений Навье — Стокса

Течение жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как уравнения Навье — Стокса. Для некоторых частных случаев уже найдены решения, но в общем виде решения этих уравнений неизвестны

6. Гипотеза Бёрча — Свиннертон-Дайера

Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых эллиптических кривых

7. Гипотеза Пуанкаре

Чаще всего встречается такая расшифровка как «резиновую ленту натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедлива для гипотезы Тёрстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман. 

Пуанкаре утверждал, что всякое трехмерное тело,  трёхмерный «объект», обладающий некоторыми свойствами трёхмерной сферы, обязан быть сферой с точностью до деформации. В 2002-2003 годах российский математик Григорий Перельман в трех интернет-статьях опубликовал свое решение данной проблемы. В 2006 году его доказательство было проверено и утверждено. В 2006 году Григорию Перельману за решение гипотезы Пуанкаре присуждена международная премия «Медаль Филдса», однако он отказался от нее. Также Григорий Яковлевич отказывался и от денежного вознаграждения.

Сейчас Перельман ведет замкнутый образ жизни и не контактирует с прессой.

Заключение: мы за несколько минут рассказали вам о задачах тысячелетия в математике. Наверняка кто-нибудь из вас открыл для себя что-то новое. Решайте задачи, преодолевайте трудности! Спасибо за внимание!

Проблемы тысячелетия, важнейшие математические проблемы

Называемый проблемы тысячелетия, всего семь математических задач. Конечно, в данном случае ее разрешение еще не обнаружено. Более того, если бы вы это сделали, вы бы получили по миллиону долларов за каждого из них. Так что все дело в попытках, если ты думаешь, что сможешь это сделать.

Надо сказать, что в 2006 г. одна из семи проблем тысячелетия была решена. Так что это хорошая мотивация, чтобы заставить других тоже быть расшифрованными. Хотите знать, из чего они состоят?

Индекс

• 1 Какие проблемы тысячелетия? 
• 2 Гипотеза Пуанкаре
• 3 P против NP
• 4 Гипотеза Ходжа
• 5 Гипотеза Римана
• 6 Существование Янга-Миллса и массовый скачок
• 7 Уравнения Навье-Стокса 
• 8 Гипотеза Берча и Суиннертона-Дайера 

Какие проблемы тысячелетия? 

Как мы уже продвинулись, когда мы говорим о проблемах тысячелетия, мы должны говорить о серия предположений или математических утверждений. Все они имеют доказательства полной правды. Но соответствующее математическое доказательство пока не известно. Хотя мы уже знаем, что один из них добился этой демонстрации и что мы сейчас увидим. Как немаловажный факт, надо сказать, что есть много нерешенных проблем. Поскольку есть не только проблемы тысячелетия, но и проблемы Гильберта полностью не решены. Тем не менее, мы останемся на первом.

Гипотеза Пуанкаре

Это единственная проблема, которая пока решена. Это так называемая гипотеза Пуанкаре. Математик Григорий Перельман решил это. После своего разрешения это стало теоремой о трехмерной сфере. Далее он говорит, что сфера четвертого измерения — единственное компактное многообразие, в котором каждый замкнутый круг может быть преобразован в точку. Более века это была одна из самых больших нерешенных проблем. Хотя Перельман объявил, что решил эту задачу в 2002 году, только в 2006 году он получил медаль Филдса, которую отверг.

P против NP

Очевидно, математика, которую мы знаем сегодня, не способна различать Задачи типа P и NP. Потому что для этого пришлось бы разработать сложные алгоритмы. По этой причине, чтобы решить эту проблему, нужно решить, действительно ли включение между классами сложности (то есть набором задач решения связанной сложности) P и NP действительно строгим.

Гипотеза Ходжа

Еще одна математическая проблема — это гипотеза Ходжа. В этом случае он сообщает нам, что для проективных алгебраических многообразий циклы ходжа они представляют собой линейную и рациональную комбинацию алгебраических циклов. Поэтому можно сказать, что это проблема алгебраической геометрии. В нем связана алгебраическая топология комплексного неособого многообразия, а также подмногообразия. Но это также то, что эта гипотеза добавляет, что некоторые группы Когомологии де Рама они алгебраические. Итак, это суммы двойственностей Пуанкаре. Теперь вам просто нужно это доказать!

Гипотеза Римана

Эта гипотеза говорит нам, что все нетривиальные нули в дзета-функции Римана имеют действительную часть ½. Это было впервые сформулирован в 1859 году Бернхардом Риманом. Благодаря их связи с распределением простых чисел в множестве натуральных чисел, они делают эту гипотезу еще одной из проблем тысячелетия.

Хотя многие считают, что эта гипотеза верна, похоже, что есть математики, которые расходятся с этой идеей. В то время говорили, что проблема решена, но Институт Клэя это опроверг.

Существование Янга-Миллса и массовый скачок

Если мы начнем с поля Ян-Миллс Надо сказать, что это физическое поле, которое используется в квантовой теории поля. Эта теория использовалась для описания квантовой хромодинамики, объясняющей структуру протонов и нейтронов. Точно так же и степень устойчивости атомного ядра. Сложность возникает, когда необходимо объяснить, каким образом связанное состояние приобрело массу.

Уравнения Навье-Стокса 

Движение жидкостей и газов описывается так называемыми уравнениями Навье-Стокса. Они были сформулированы в XNUMX веке и до сих пор не известны все их значения. Это связано с нелинейностью их уравнений и связанных членов. Вы должны придумать теорию гидродинамики. Было бы необходимо продемонстрировать, если при некоторых начальных условиях ламинарной жидкости решение потока также является ламинарным для всех моментов времени.

Гипотеза Берча и Суиннертона-Дайера 

В этом случае, Гипотеза Берча и Суиннертона-Дайера относится к типу уравнения. Он отвечает за определение эллиптических кривых на рациональных. Кажется, что сама гипотеза говорит нам, что есть способ узнать, имеют ли эти уравнения бесконечное или, возможно, бесконечное количество рациональных решений. Его сформулировали в 1965 году два английских математика: Брайан Берч и Питер Суиннертон-Дайер. Утверждение гипотезы связывает арифметические данные, связанные с арифметической кривой E, над числовым полем, которым будет K.

Есть Институт Клэя, целью которого является повышение знаний по математике, а также его большое распространение. Помимо различных мероприятий и проектов, они также прославились поддержкой задач тысячелетия или этих не совсем простых математических задач. Некоторые задачи имеют двойную цель: с одной стороны, окончательное решение одного и того же, а с другой — такой сочный экономический приз, который они предлагают.

Задачи тысячелетия . Владивостокский государственный университет экономики и сервиса ВВГУ

Важные классические задачи, решение которых не найдено вот уже в течение многих лет

Задачи тысячелетия (Millennium Prize Problems) составляют семь математических проблем, охарактеризованных как «важные классические задачи, решение которых не найдено вот уже в течение многих лет». За решение каждой из этих проблем институтом Клэя предложен приз в 1 000 000 долларов США. Анонсируя приз, институт Клэя провёл параллель со списком проблем Гильберта, представленным в 1900 году и оказавшим существенное влияние на математику XX века. Из 23 проблем Гильберта большинство уже решены, и только одна — гипотеза Римана — вошла в список задач тысячелетия.

По состоянию на 2014 год только одна из семи проблем тысячелетия (гипотеза Пуанкаре) решена (Филдсовская премия за её решение была присуждена Григорию Перельману, который отказался от неё) и о решении ещё одной заявлено Мухтарбаем Отелбаевым (существование и гладкость решений уравнений Навье — Стокса).

Список проблем

Равенство классов P и NP

Если положительный ответ на какой-то вопрос можно быстро (за полиномиальное время) проверить (используя некоторую вспомогательную информацию, называемую сертификатом), то верно ли, что и сам ответ (вместе с сертификатом) на этот вопрос можно быстро найти? Задачи первого типа относятся к классу NP, второго — классу P. Проблема равенства этих классов является одной из важнейших проблем теории алгоритмов.

Гипотеза Ходжа

Важная проблема алгебраической геометрии. Гипотеза описывает классы когомологий на комплексных проективных многообразиях, реализуемые алгебраическими подмногообразиями.

Гипотеза Пуанкаре (доказана)

Считается наиболее известной проблемой топологии. Говоря более просто, она утверждает, что всякий трёхмерный «объект», обладающий некоторыми свойствами трёхмерной сферы (например, каждая петля внутри него должна быть стягиваема), обязан быть сферой с точностью до деформации.

Премия за доказательство гипотезы Пуанкаре присуждена российскому математику Г. Я. Перельману, опубликовавшему в 2002 году серию работ, из которых следует справедливость гипотезы Пуанкаре.

Гипотеза Римана

Гипотеза гласит, что все нетривиальные (то есть имеющие ненулевую мнимую часть) нули дзета-функции Римана имеют действительную часть 1/2. Её доказательство или опровержение будет иметь далеко идущие последствия для теории чисел, особенно, в области распределения простых чисел. Гипотеза Римана была восьмой в списке проблем Гильберта. В случае публикации контрпримера к гипотезе Римана, учёный совет института Клэя вправе решить, можно ли считать данный контрпример окончательным решением проблемы, или же проблема может быть переформулирована в более узкой форме и оставлена открытой (в последнем случае автору контрпримера может быть выплачен небольшой приз).

Квантовая теория Янга — Миллса

Задача из области физики элементарных частиц. Требуется доказать, что для любой простой компактной калибровочной группы квантовая теория Янга — Миллса для пространства существует и имеет ненулевой дефект массы. Это утверждение соответствует экспериментальным данным и численному моделированию, однако доказать его до сих пор не удалось.

Существование и гладкость решений уравнений Навье — Стокса

Уравнения Навье — Стокса описывают движение вязкой ньютоновской жидкости и являются основой гидродинамики. Численные решения уравнений Навье — Стокса используются во многих практических приложениях и научных работах. Однако в аналитическом виде решения этих уравнений найдены лишь в некоторых частных случаях, поэтому нет полного понимания свойств уравнений Навье — Стокса. В частности, решения уравнений Навье — Стокса часто включают в себя турбулентность, которая остаётся одной из важнейших нерешённых проблем в физике, несмотря на её огромную важность для науки и техники.

Гипотеза Бёрча — Свиннертон-Дайера

Бёрч и Свиннертон-Дайер в начале 1960-х годов предпoложили, что ранг эллиптической кривой над решений равен порядку нуля дзета-функции Хассе — Вейля

в точке . Более детально, гипотеза утверждает, что существует ненулевой предел , где значение зависит от тонких арифметических инвариантов кривых.

Наиболее ярким частным результатом по состоянию на 2011 год остается доказанное в 1977 году Джоном Коутсом и Эндрю Уайлсом утверждение, справедливое для большого класса эллиптических кривых о том, что если кривая содержит бесконечно много рациональных точек, то .

Гипотеза является единственным относительно простым общим способом вычисления ранга эллиптических кривых.

Источник: Википедия

уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия

Нерешаемые задачи — это 7 интереснейших математических проблем. Каждая из них была предложена в свое время известными учеными, как правило, в виде гипотез. Вот уже много десятилетий над их решением ломают головы математики во всем мире. Тех, кто добьется успеха, ждет вознаграждение в миллион американских долларов, предложенное институтом Клэйя.

Предыстория

В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.

Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:

• проблема непротиворечивости арифметических аксиом;
• общий закон взаимности на пространстве любого числового поля;
• математическое исследование физических аксиом;
• исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
• проблема строгого обоснования исчислительной геометрии Федора Шуберта;
• и пр.

Неисследованными являются: проблема распространения на любую алгебраическую область рациональности известной теоремы Кронекера и гипотеза Римана.

Институт Клэйя

Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.

В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.

Задачи тысячелетия

В список института Клэйя изначально входили:

• гипотеза о циклах Ходжа;
• уравнения квантовой теории Янга — Миллса;
• гипотеза Пуанкаре;
• проблема равенства классов Р и NP;
• гипотеза Римана;
• уравнения Навье Стокса, о существовании и гладкости его решений;
• проблема Берча — Свиннертон-Дайера.

Эти открытые математические проблемы представляют огромный интерес, так как могут иметь множество практических реализаций.

Что доказал Григорий Перельман

В 1900 году известный ученый-философ Анри Пуанкаре предположил, что всякое односвязное компактное 3-мерное многообразие без края гомеоморфно 3-мерной сфере. Ее доказательство в общем случае не находилось в течение века. Лишь в 2002-2003 годах петербургский математик Г. Перельман опубликовал ряд статей с решением проблемы Пуанкаре. Они произвели эффект разорвавшейся бомбы. В 2010 году гипотеза Пуанкаре была исключена из списка «Нерешенные задачи» института Клэйя, а самому Перельману было предложено получить полагающееся ему немалое вознаграждение, от которого последний отказался, не объяснив причин своего решения.

Самое понятное объяснение того, что удалось доказать российскому математику, можно дать, представив, что на бублик (тор), натягивают резиновый диск, а затем пытаются стянуть края его окружности в одну точку. Очевидно, что это невозможно. Другое дело, если произвести этот эксперимент с шаром. В таком случае вроде бы трехмерная сфера, получившаяся из диска, окружность которого стянули в точку гипотетическим шнуром, будет трехмерной в понимании обычного человека, но двумерной с точки зрения математики.

Пуанкаре предположил, что трехмерная сфера является единственным трехмерным «предметом», поверхность которой можно стянуть в одну точку, а Перельману удалось это доказать. Таким образом, список «Нерешаемые задачи» сегодня состоит из 6 проблем.

Теория Янга-Миллса

Эта математическая проблема была предложена ее авторами в 1954-м году. Научная формулировка теории имеет следующий вид: для любой простой компактной калибровочной группы квантовая пространственная теория, созданная Янгом и Милльсом, существует, и при этом имеет нулевой дефект массы.

Если говорить на языке, понятном для обычного человека, взаимодействия между природными объектами (частицами, телами, волнами и пр.) делятся на 4 типа: электромагнитное, гравитационное, слабое и сильное. Уже много лет физики пытаются создать общую теорию поля. Она должна стать инструментом для объяснения всех этих взаимодействий. Теория Янга-Миллса — это математический язык, с помощью которого стало возможно описать 3 из 4-х основных сил природы. Она не применима к гравитации. Поэтому нельзя считать, что Янгу и Миллсу удалось создать теорию поля.

Кроме того, нелинейность предложенных уравнений делает их крайне сложными для решения. При малых константах связи их удается приближенно решить в виде ряда теории возмущений. Однако пока непонятно, как можно решить эти уравнения при сильной связи.

Уравнения Навье-Стокса

С помощью этих выражений описываются такие процессы, как воздушные потоки, течение жидкостей и турбулентность. Для некоторых частных случаев аналитические решения уравнения Навье-Стокса уже были найдены, однако сделать это для общего пока никому не удалось. В то же время, численное моделирование для конкретных значений скорости, плотности, давления, времени и так далее позволяет добиться прекрасных результатов. Остается надеяться, что у кого-нибудь получится применить уравнения Навье-Стокса в обратном направлении, т. е. вычислить с их помощью параметры, либо доказать, что метода решения нет.

Задача Берча — Свиннертон-Дайера

К категории «Нерешенные задачи» относится и гипотеза, предложенная английскими учеными из Кембриджского университета. Еще 2300 лет назад древнегреческий ученый Эвклид дал полное описание решений уравнения x2 + y2 = z2.

Если для каждого из простых чисел посчитать количество точек на кривой по его модулю, получится бесконечный набор целых чисел. Если конкретным образом «склеить» его в 1 функцию комплексной переменной, тогда получится дзета-функция Хассе-Вейля для кривой третьего порядка, обозначаемая буквой L. Она содержит информацию о поведении по модулю всех простых чисел сразу.

Брайан Берч и Питер Свиннертон-Дайер выдвинули гипотезу относительно эллиптических кривых. Согласно ей, структура и количество множества ее рациональных решений связаны с поведением L-функции в единице. Недоказанная на данный момент гипотеза Берча — Свиннертон-Дайера зависит от описания алгебраических уравнений 3 степени и является единственным сравнительно простым общим способом расчета ранга эллиптических кривых.

Чтобы понять практическую важность этой задачи, достаточно сказать, что в современной криптографии на эллиптических кривых основан целый класс асимметричных систем, и на их применении основаны отечественные стандарты цифровой подписи.

Равенство классов p и np

Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.

Гипотеза Римана

Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных. Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.

Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.

Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.

Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др. Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.

Гипотеза о циклах Ходжа

Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.

Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.

Семь задач тысячелетия или как заработать миллион.: moris_levran — LiveJournal

Математики из американского института Клэя пошли на невиданную щедрость. Умную мысль они готовы оценить в $1 млн. А чтобы задать направление мыслительной деятельности, ученые составили список из семи задач тысячелетия — Millennium Prize Problems. Если у вас в школе по математике была пятерка, можете смело браться за карандаш. Полный вариант условий — на сайте www.claymath.org.
Математический институт Клэя был основан в Кембридже в 1998 году американским бизнесменом, учредителем и руководителем компании East Hill Management LLC (Бостон, США) Ланданом Клэем. Математик по образованию, он долгое время руководил известной корпорацией ADE Corporation, занимающейся производством систем контроля качества для компьютерных плат. Основными задачами созданного им некоммерческого института Клэй назвал распространение математических знаний, поддержку молодых и одаренных математиков, а также стимулирование решения основных математических проблем. Ради достижения последней цели институт и учредил семь премий Millennium Prize Problems

По сравнению с прошлым столетием количество таких проблем сократилось почти в четыре раза. Когда в самом начале XX века знаменитый немецкий математик Давид Гильберт выступил на международном математическом конгрессе в Париже, оглашенный им список математических и логических задач, которые предстояло решить в ближайшие сто лет, насчитывал 23 позиции. Плюс еще три проблемы, с которых он начал свою речь,- они не вошли в список, поскольку необхо-димость их решения казалась ученому сама собой разумеющейся,- итого 26.
К концу века математики выполнили 20 заданий. Последним павшим бастионом стала знаменитая теорема Ферма. Две из оставшихся проблем были решены частично, две ждут своих «героев» до сих пор. Проблема математического описания физических аксиом признана нематематической. Задача о прямой как кратчайшем соединении двух точек была объявлена слишком расплывчатой: невозможно было понять, решена она или нет (вряд ли эти математики прощают такие отговорки своим студентам!).
Составленный уже в начале этого века новый список проблем насчитывает всего семь пунктов. Коренное отличие нынешнего списка, названного Millennium Prize Problems («Призовые задачи тысячелетия»), состоит в том, что за решение каждой из них Математическим институтом Клэя назначена премия в $1 млн. Вернее сказать, наоборот: проблем было выбрано именно семь по числу выделенных на их решение миллионов. Решение задач Гилберта никакого вознаграждения, кроме вечной научной славы и глубокого научного же удовлетворения, не приносило.

• Гипотеза Пуанкаре.
Введение
Гипотеза Пуанкаре — одна из тех задач, даже ошибочные решения которых приводят к появлению новых областей математики; в этом с ней может соперничать разве что великая теорема Ферма.
Сходство с теоремой Ферма есть и еще в одном важном аспекте: общедоступности формулировки[Параллели с теоремой Ферма продолжаются и дальше: история доказательства обеих гипотез весьма схожа: гениальный одиночка на несколько лет полностью посвящает себя решению проблемы и добивается успеха].
Пончики, бублики и прочие сласти
Многочисленные книги по занимательной математике, мимо которых вы, читатели, вряд ли прошли в детстве, любят рассказывать о топологии, странной науке, в которой два предмета сравниваются только по количеству дырок в них: чайная чашка ничем не отличается от бублика, а апельсин — от Солнца. На самом деле, конечно, топология — очень глубокая наука, и объекты и свойства, которые она изучает, весьма многочисленны и разнообразны. Но прелесть в том, что для понимания сути гипотезы Пуанкаре нам ничего, кроме этих наивных представлений, и не потребуется!
Будем чуточку более формальны. Говорят, что поверхность k-связна, если на ней можно провести k-1 замкнутую кривую, которые не делят ее на две части. Сфера (поверхность апельсина) односвязна: как ни проводи на ней замкнутую кривую, кусочек вырежется; а вот поверхность бублика двусвязна — ее можно, например, разрезать поперек, превратив в цилиндр, но сохранив целостность (а вот повторно разрезать цилиндр уже не получится). Для поверхностей в трехмерном пространстве это свойство как раз и означает, что в поверхности есть k-1 «дырка». В общем случае поверхность односвязна, если на ней любую замкнутую кривую можно непрерывной деформацией стянуть в точку. Интуивно очевидно, например, что поверхность бублика этим свойством не обладает (меридиан или параллель в точку не стягиваются).

Другое важное понятие — гомеоморфизм — также уже встречается в рассуждениях о неразличимости чашки и бублика. Именно в этой неразличимости и дело: гомеоморфизм — это непрерывное преобразование, деформация, которой можно подвергнуть множество, сохранив при этом его топологические свойства (например, k-связность). Чашку легко непрерывным преобразованием превратить в бублик, а апельсин — в Солнце. При этом преобразовании сохраняются важнейшие топологические инварианты (об инвариантах я уже рассказывал в статье, посвященной гипотезе Ходжа), такие, как число k. Два множества, которые можно гомеоморфизмом превратить друг в друга, с топологической точки зрения считаются эквивалентными.
Гипотеза Пуанкаре состоит в том, что каждая односвязная трехмерная поверхность гомеоморфна трехмерной сфере. Хочу обратить особое внимание на то, что «трехмерная поверхность» может размещаться в пространстве, чья размерность как минимум 4! Трехмерная сфера — это поверхность четырехмерного шара (привычная нам двухмерная сфера — поверхность трехмерного шара).
Ошибка на ошибке: история вопроса
Все началось с исследований, которые Пуанкаре вел в области алгебраической геометрии. Он работал над одним из краеугольных камней этой науки — теорией гомологий, особого класса топологических инвариантов. В 1900 году он опубликовал статью, в которой доказывал, что если у трехмерной поверхности гомология совпадает с гомологией сферы, то и сама поверхность — сфера; на самом деле это утверждение даже более сильное, чем утверждение гипотезы Пуанкаре.
Однако в его рассуждения вкралась ошибка, которую он сам и нашел, к 1904 году разработав важнейшее понятие фундаментальной группы и построив на его базе контрпример к собственной теореме. Тогда же он наконец-то поставил вопрос правильно.
Достаточно долго на гипотезу не обращали внимания. Интерес к ней пробудил Генри Уайтхед[Джон Генри Константин Уайтхед (J.H.C. Whitehead, 1904–1960) — выдающийся английский математик, один из основателей теории гомотопий. Не следует его путать с его собственным дядей Альфредом Уайтхедом, тоже математиком, но специализировавшимся на логике и алгебре, соавтором Бертрана Рассела по знаменитой книге Principia Mathematica], который в 1930-е годы объявил о том, что нашел доказательство. Как вы уже догадались, его доказательство также было неверным. Однако в процессе поиска и попыток исправить свои неточности он обнаружил интереснейшие классы трехмерных поверхностей и значительно продвинул теорию, которая позднее получила название топологии малых (или низших) размерностей. В пятидесятые и шестидесятые годы всплеск интереса к проблеме вновь породил несколько ошибочных заявлений о том, что теорему удалось доказать, и после этого математики наконец-то поняли, что гипотезу Пуанкаре так просто не возьмешь: с шестидесятых годов и до работ Григория Перельмана ложные доказательства предъявляли только любители (таких всегда достаточно; не присоединяйтесь к их числу).
Топология низших размерностей стала отдельной ветвью математики по удивительной причине — в многомерном случае все гораздо проще! Уже в 50-е и 60-е годы утверждения, аналогичные гипотезе Пуанкаре, были доказаны для более высоких размерностей. Трехмерный же случай продолжал оставаться камнем преткновения.
Доказательство Григория Перельмана (см. врезку) основано на идеях, которые развил в начале 1980-х годов Ричард Гамильтон (Richard Hamilton). Эти идеи неожиданным образом выводят топологические заключения из фактов о дифференциальных уравнениях — так называемых потоках Риччи (Ricci flows), обобщающих уравнения термодинамики. Впрочем, в доказательстве Перельмана долгое время не могли разобраться ведущие топологи мира, и вряд ли оно когда-нибудь станет темой популярной статьи.
Алгоритмическая версия
К теме этой статьи примыкает интересная для компьютерщиков область математики — вычислительная топология. Вычислительные и распознавательные задачи есть, оказывается, и в этой абстрактной науке. С одной из таких задач связана и предпринятая в 1974 году очень интересная попытка решения проблемы Пуанкаре в ее алгоритмической версии.
Каждая трехмерная поверхность задается некоторым (не будем вдаваться в подробности) дискретным кодом — конечным набором символов. Одна и та же поверхность имеет бесконечное число различных кодировок. Естественный вопрос: существует ли алгоритм, определяющий по заданному кодовому слову, задает ли оно трехмерную сферу («алгоритмическая проблема Пуанкаре»). Именно эту задачу атаковали в 1974 году А. Фоменко (тот самый), И. Володин и В. Кузнецов [Володин И.А., Кузнецов В.Е., Фоменко А.Т., «О проблеме алгоритмического распознавания стандартной трехмерной сферы», Успехи математических наук, 1974, т. 29, N 5, с. 71-168.]. Они предположили, что определенное свойство кода (оно было названо «волной») дает критерий «сферичности». Однако строго доказать им удалось только, что наличие «волны» гарантирует — перед нами сфера. Доказать же, что в любом коде, задающем сферу, имеется «волна» никак не получалось. Тогда авторы сделали весьма стильный по тем временам ход — провели масштабный компьютерный эксперимент. Была написана программа для машины БЭСМ-6, которая случайным образом генерировала коды, задающие трехмерную сферу, и проверяла наличие в них «волны». В эксперименте, потребовавшем весьма длительного счета, был проверен миллион таких случайных представлений сферы — и во всех обнаружилась волна! С точки зрения здравого смысла — веский аргумент в пользу корректности предложенного алгоритма. Но авторы, будучи серьезными математиками, разумеется, воздерживались от поспешных заявлений. И не напрасно — спустя пару лет один из бывших учеников Фоменко обнаружил контрпример…
Спустя двадцать лет алгоритм распознавания 3-сферы (за экспоненциальное время) был построен[Abigail Thompson. Thin position and the recognition problem for S3. Math. Res. Lett., 1(5):613–630, 1994.]. Общая же проблема алгоритмического распознавания поверхностей размерности 3 открыта, она активно изучается и сегодня. Для более высоких размерностей давно известна ее неразрешимость, для размерности 2 она была решена еще раньше, а вот в нашем родном трехмерье все почему-то невероятно сложно устроено.

Анри Пуанкаре
Анри Пуанкаре — один из самых блистательных представителей французской науки. Он родился в 1854 году в семье, занимавшей весьма почтенное положение в обществе: достаточно упомянуть, что Анри приходился двоюродным братом Раймону Пуанкаре, пять раз занимавшему пост премьер-министра Франции, а с 1913 по 1920 годы, в тяжелое время Первой мировой войны, — пост президента страны.
За свою жизнь Анри Пуанкаре успел поработать во многих областях науки: комплексном анализе, небесной механике, алгебраической геометрии, теории чисел и, конечно, топологии, в которой он и сформулировал носящую его имя гипотезу. Не все знают, что Пуанкаре стоял у истоков теории относительности: долгое время он сотрудничал с Хендриком Лоренцом (кстати, преобразования Лоренца получили имя великого голландца именно с легкой руки Пуанкаре) и еще в 1898 году, задолго до Эйнштейна, в работе «Измерение времени» сформулировал принцип относительности, а затем даже ввел четырехмерное пространство-время, теорию которого в сотрудничестве с Эйнштейном позднее разработал Герман Минковский. Примечательно, что сам Эйнштейн очень долго отрицал всякое знакомство с трудами Пуанкаре и не ссылался на него вплоть до начала двадцатых годов (!), однако впоследствии все же признал заслуги французского математика.
Философия и методы работы Пуанкаре тоже заслуживают внимания: он категорически не принимал набирающих в то время силу формалистических взглядов Рассела, Фреге и Гильберта, для которых математика была частью логики. Пуанкаре считал, что основа работы математика — интуиция, а сама наука не допускает полного аналитического обоснования. В своих привычках он следовал этой философии: Пуанкаре всегда сначала полностью решал задачи в голове, а затем записывал решения. Он обладал феноменальной памятью и мог слово в слово цитировать прочитанные книги и проведенные беседы (память, интуиция и воображение Анри Пуанкаре даже стали предметом настоящего психологического исследования). Кроме того, он никогда не работал над одной задачей долгое время, считая, что подсознание уже получило задачу и продолжает работу, даже когда он размышляет о других вещах — вряд ли он смог бы повторить подвиг Григория Перельмана или Эндрю Уайлса, которые долгие годы посвящали себя одной задаче[Говорю это не для того, чтобы умалить достоинства Анри Пуанкаре — возможно (хотя весьма сомнительно), обладай он тем же математическим аппаратом, что Уайлс с Перельманом, он решил бы обе задачи за завтраком]. В его трудах неоднократно обнаруживались ошибки, но и в своих ошибках он был гениален: вовремя замеченная неточность Пуанкаре в знаменитом труде о проблеме трех тел привела к развитию теории хаоса, а другая — топологическая — к той самой гипотезе, которой и посвящена эта статья.

Григорий Перельман и гипотеза Пуанкаре
Григорий Яковлевич Перельман родился и вырос в Ленинграде, учился в знаменитой 239-й школе. В 1982 году выиграл Международную математическую олимпиаду, набрав максимально возможное количество баллов. Степень кандидата наук получил в СПбГУ, затем некоторое время работал в Петербургском отделении математического института РАН; в конце восьмидесятых уехал в США, где работал до середины девяностых, а затем вернулся в Россию; сейчас снова работает в ПОМИ.
История доказательства гипотезы Пуанкаре напоминает историю доказательства теоремы Ферма: как и Эндрю Уайлс, Перельман на долгих семь лет (с возвращения в Россию до 2002 года) практически перестал публиковаться и вообще почти ничем не напоминал о себе. Никто не знал, над чем он работал. Затем, как гром среди ясного неба, — препринт (предварительная версия статьи, обычно предшествующая публикации и нужная для того, чтобы установить приоритет и довести свои результаты до научного сообщества), помещенный Перельманом на популярный препринт-сервер arXiv [Вот ссылки на препринты Перельмана на этом сервере, содержащие доказательство гипотезы Пуанкаре: http://arxiv. org/abs/math.DG/0211159 , http://arxiv.org/abs/math.DG/0303109 ] в ноябре 2002 года. В препринте содержалось доказательство более общего геометрического факта, из которого, в частности, вытекала гипотеза Пуанкаре.
В 2003 году Григорий Яковлевич дополнил первый препринт еще одним, в котором подробнее изложил технические подробности доказательства. Кроме того, он выступил с лекциями, где комментировал свои идеи. Казалось бы, больше ничего не нужно: проверяйте доказательство и платите миллион. Однако одним из условий фонда Clay Mathematics Institute была публикация результата в реферируемых изданиях, а этого Перельман почему-то делать не хотел. Он вообще старался (и до сих пор старается) избегать любых контактов с прессой; создается впечатление, что приз Григория Яковлевича не интересует, а неразрывно связанная с ним слава — тяготит.
Текущее положение дел таково: множество экспертов тщательнейшим образом проверили детали доказательства. Опубликованы много сотен страниц пояснений и комментариев к двум препринтам Перельмана[См. , например, http://www.math.lsa.umich.edu/research/ricciflow/perelman.html]. Пока ошибок не найдено, и большинство экспертов склоняются к мысли, что задача действительно решена. Что же касается обязательных публикаций, то представители Clay Mathematics Institute уже выступили с заявлением о том, что могут пересмотреть условия присуждения приза.

А вот шесть еще не решенных задач…

• Гипотеза Ходжа (сформулирована в 1941 году)
Чем сложнее объект, тем труднее исследовать его. Поэтому математики обычно сначала пытаются разложить такой объект на более простые составляющие (анализ). Но иногда при этом возникают новые части, неизвестно откуда взявшиеся и непонятно что собой представляющие. Либо, наоборот, при более детальном исследовании выясняется, что каких-то деталей явно не хватает. Например, исследуя просто кирпичи, мы не можем себе представить, каков составленный из них дом. Для этого нужно как минимум учесть еще и заключенное между кирпичами пустое пространство — комнаты. Профессор Кембриджа Уильям Ходж в своих трудах описал правила ана-лиза, при которых, как ему кажется, такие метаморфозы с лишними или недостающими частями не должны возникать. В этом случае любое геометрическое тело можно исследовать как алгебраическое уравнение. Ни доказать его предположение, ни опровергнуть его ученые не могут уже более 60 лет.

• Уравнения Янга-Миллза (сформулированы в 1954 году)
Свои квантовые уравнения американские физики Чжэнь-Нин Янг и Роберт Миллз составили, наблюдая за движением элементарных частиц. Выведенные на основе практически одной только интуиции, они тем не менее замечательно описывают почти все виды взаимодействия этих объектов. С помощью уравнений даже было предсказано открытие новых частиц, которые потом действительно были найдены физиками-ядерщиками крупнейших мировых лабораторий — Брукхейвенской, Стэнфордской и европейской CERN. Правда, с помощью теории Янга-Миллза невоз¬можно правильно предсказать массу частиц, однако, несмотря на это, уравнениями смело пользуются почти все ядерщики мира. Хотя до сих пор непонятно, как они работают и так ли уж они верны. Из всех вышеперечисленных уравнений эти — наиболее сложные, поэтому мы их приводить не будем. Но если вам не хватит пяти миллионов, которые можно получить за решение предыдущих пяти проблем, никто не запретит решить еще и эту.

• Гипотеза Берча и Суиннертон-Дайера (сформулирована в I960 году)
«Философским камнем» математики можно назвать уравнения вида х в степени n + у в степени n + z в степени n +….= t в степени n . Наиболее простое — х в степени 2 + у в степени 2 = z в степени 2 — полностью исследовал еще за 300 лет до рождества Христова Евклид. Самое знаменитое из подобных уравнений стало основой для теоремы Ферма. А одно из самых больших решений (в докомпьютерную эпоху) предложил в 1769 Году Эйлер. Методом подстановки ему удалось соорудить следующее равенство:
2 682 4404 + 15 365 6394 + 18 796 7604 = 20 615 6734. Однако универсального метода вычисления для подобных уравнений не существует. Известно, что у каждого из них может быть либо конечное, либо бесконечное число решений. Математики Берч и Суиннертон-Дайер создали метод, по которому каждое такое уравнение можно свести к более простому, называемому дзета-функцией. Согласно их предположению, обоснованному экспериментально, но теоретически недоказанному, если эта функция в точке 1 будет равна О, то число решений будет бесконечным. В противном случае их либо вообще не будет, либо будет какое-то ограниченное число. Ни доказать, ни опровергнуть это утверждение пока никто не смог.

• Проблема решения-проверки (проблема Кука-Левина, сформулирована в 1971 году)

Если перед человеком ставят задачу найти в лесу закопанный там в прошлом веке клад, он может потратить на поиски и год, и два, и десятилетие, а то и всю жизнь. Все происходит гораздо быстрее, когда ему говорят: «Клад зарыт под единственной в лесу осиной. Пойди и проверь». Примерно то же происходит при решении любой задачи: на проверку решения уходит меньше вре-мени, чем на само решение. Но очевидность этого факта математиков не убеждает. Поэтому они задались вопросом: существует ли задача, проверка правильности решения которой будет занимать больше времени, чем само решение? Положительный ответ на этот вопрос приведет, например, к появлению нового поколения систем шифрования. Ведь частью взлома шифра является проверка правильности взлома, а сформулировать задачу, решение которой проверяется дольше, чем ищется,- значит сформулировать принципы составления такого шифра, чей ключ будет проверятся дольше, чем искаться.

• Гипотеза Римана (сформулирована в 1859 году)
Среди всей массы чисел особое место занимают числа, которые невозможно разделить на что-то более мелкое, чем они сами (не считая единицы): 2,3,5,7,11, 13,17 и так далее. Такие числа называ-ются простыми. Как они распределяются по числовому ряду — пока известно одному богу. Проверить, является ли число простым, можно, только разделив его на все меньшие числа. Самое большое из известных на сегодняшний день простых чисел было найдено в марте этого года и состоит из 7 816 230 цифр. Риман же нашел метод, по которому можно определить максимальное количество простых чисел, не превышающих некое заданное число. На сегодня математики проверили этот метод с полутора триллионами простых. Сбоев пока не было. Однако это вовсе не говорит о том, что метод не споткнется на первом после полутора триллионов простом числе. А поскольку гипотеза Римана, перешедшая в новый список еще из списка Гилберта, активно используется для расчета систем безопасности передачи данных, в сотовых сетях, в интернете, ее доказательство имеет заметный практический смысл. И миллион здесь платить есть за что.

• Уравнения Навье-Стокса (сформулированы в 1822 году)

Когда вы плывете по озеру на лодке, от нее разбегаются волны. Вслед за летящим самолетом или мчащимся автомобилем возникают турбулентные потоки. Все эти явления описываются уравнениями Навье-Стокса. Проблема заключается в следующем: несмотря на то, что уравнения созданы уже достаточно давно, как их решать, до сих пор никто не знает. Мало того, никто пока даже не знает, существует ли вообще способ их решения. В то же время ими весьма активно пользуются не только математики, но и конструкторы самолетов, автомобилей и кораблей. Правда, использовать их можно пока только «в одну сторону»: подставлять полученные в ходе аэродинамических испытаний значения скорости, времени, давления, плотности и т. д. и вычислять по ним неизвестные характеристики, например, летательного аппарата. Если кто-нибудь из математиков найдет решение, пользоваться уравнениями можно будет и в противоположном направлении, вычисляя всё необходимые параметры без испытаний.

Комментарий эксперта. Анатолий Фоменко, математик, академик РАН:
«В наше время назначение денежных премий будет безусловно способствовать более быстрому решению „проблем тысячелетия». Сейчас занимающаяся наукой молодежь интересуется не только научными, но и довольно прагматичными вопросами. И назначение таких премий для науки — благо. Эти проблемы довольно сложны, и ситуация, какая получилась с теоремой Ферма, когда решить ее пытались все, кому не лень, здесь возникнуть не должна. Непрофессионал за такую работу просто не возьмется: он ее не поймет. Вообще, выбор проблем в призовом списке довольно случаен. Есть много очень интересных вопросов. И мода на них постоянно меняется. Какие-то вопросы были интересны раньше, какие-то стали интересными только сейчас. Однако на авторитет клэевских задач работает фактор времени. Проблемы сформулированы давно, считаются до сих пор актуальными, поэтому дело это полезное. И потом, значение имеет даже не сам факт решения проблемы, а методы, которые при этом возникают. Поэтому для математики, для науки сам факт наличия такого списка очень важен».

p.s.
На самом деле то, что мы более трех веков называли «теоремой Ферма», получило право называться таковой лишь 10 лет назад. После того, как было официально доказано профессором Принстона Эндрю Уайлсом. До того времени теорема, будучи недоказанной, должна была именоваться гипотезой. Запись о том, что выражение х в степени п + y в степени n = z в степени n не имеет решения в целых числах при п > 2, Пьер Ферма оставил на полях книги Диофанта «Арифметика» в 1637 году. Тут же он написал, что знает, как доказать это, но для доказательства слишком мало места на полях. Больше трех веков над секретом бились не только ученые математики, но и студенты, инженеры, учителя и даже люди, совсем далекие от науки, настолько простой и красивой казалась задача. Еще большей популярности теоремы способствовала назначенная в 1908 году за ее доказательство премия в 100 тыс. немецких марок (около $1,5 млн по-современному).

ПО МАТЕРИАЛАМ
1. СЕРГЕЙ НИКОЛЕНКО ОПУБЛИКОВАНО В ЖУРНАЛЕ «КОМПЬЮТЕРРА» №1-2 ОТ 18 ЯНВАРЯ 2006 ГОДА
2. ЖУРНАЛ Ё 14 – 20 НОЯБРЯ 2005Г.
Дополнения http://www.tphs.info/lib/exe/fetch.php/wiki:autor:serov:2010_07_topology.pdf

английский математик утверждает, что решил проблему тысячелетия // Смотрим

• Профиль

Математика и её применения 25 сентября 2018, 15:52

• Гипотеза Римана включена в список семи величайших задач, из которых пока решена только одна.

  Фото Global Look Press.

• Фото YouTube.

• Фото YouTube.

• Гипотеза Римана включена в список семи величайших задач, из которых пока решена только одна.

  Фото Global Look Press.

• Фото YouTube.

• Фото YouTube.

Знаменитый учёный Майкл Атья выступил с доказательством гипотезы Римана, включённой в список шести величайших нерешённых задач. В случае успеха исследователю достанется миллион долларов США.

Знаменитый учёный Майкл Атья, лауреат Филдсовской премии, выступил с доказательством гипотезы Римана. Эта проблема включена в список шести величайших нерешённых задач. В случае успеха исследователю достанется миллион долларов США.

«Решите гипотезу Римана, и вы станете знаменитым. Если вы уже известны, вы становитесь пресловутыми, – говорит Атья в материале New Scientist. во время разговора. – Никто не верит никакому доказательству гипотезы Римана, потому что эта задача так сложна. Никто не доказал её, так с чего бы кому-нибудь доказать её сейчас? Если, конечно, у вас нет совершенно новой идеи».

Чтобы объяснить, в чём состоит гипотеза Римана, придётся начать издалека. Вспомним, что целое число называется простым, если без остатка делится только на себя и на единицу (но само не является единицей). Например, 2, 3, 5, 7, 11 – простые числа, а 4, 6, 8, 9 – нет.

Простые числа издавна привлекают внимание математиков. Дело в том, что любое целое число либо само является простым, либо может быть получено из простых путём их перемножения. Например, 8 = 2×2×2, а 9 = 3×3. Таким образом, простые числа являются «кирпичиками», из которых строятся все целые числа с помощью операции умножения.

 

Есть у этого математического явления и практическая сторона. Перемножить несколько простых чисел – куда более лёгкая задача, чем произвести обратный процесс: взять результат и рассчитать, произведением каких простых чисел он является. Перебор всех возможных кандидатов – слишком долгое дело. Каждый может убедиться в этом на опыте, попытавшись выяснить с помощью калькулятора, на какие простые множители раскладывается, скажем, 1059811.

Если простые множители достаточно велики, то найти их по произведению – задача, непосильная даже современным компьютерам. И на этом строятся алгоритмы шифрования, защищающие, скажем, наши финансовые счета. Ключ состоит из нескольких очень больших простых чисел. Компьютер перемножает их. Если произведение сходится с тем, которое хранится в базе данных, ему предоставляется доступ к информации. Зная же только произведение, найти его множители (подобрать ключ) невозможно ни за какой разумный срок.

Наши счета защищает тот факт, что не известно (и, возможно, не существует) никакого быстрого алгоритма, позволяющего найти все простые числа от единицы до заданного числа x. Однако если мы не можем узнать, какие это числа, можем ли мы, по крайней мере, выяснить, сколько их?

Функция, задающая количество простых чисел от единицы до данного числа x называется функцией распределения простых чисел. Для неё никакой удобной формулы тоже не найдено, однако математики с интересом исследуют её свойства.

Фото YouTube.

В 1859 году великий математик Бернхард Риман сформулировал гипотезу, которая позже была названа его именем. Если эта гипотеза верна, то верно и множество интереснейших утверждений о распределении простых чисел.

Как она формулируется? Здесь нам придётся немного коснуться высшей математики. Все числа, которые изучаются в школьной программе – положительные, отрицательные и нуль, целые и дробные, рациональные и иррациональные – математики объединяют под названием действительных. Однако существуют ещё и комплексные числа.

Такое число представляет собой сумму a + i×b, где a, b – действительные числа, i – так называемая мнимая единица. Она определяется формулой i² = -1. Если b = 0, то комплексное число – это просто действительное число a. Таким образом, действительные числа есть лишь частный случай комплексных.

Понятно, что никакое действительное число в квадрате не может быть отрицательным. Поэтому математикам и понадобилась мнимая единица и комплексные числа. Они позволяют решать задачи, которые при оперировании только действительными числами выглядят попросту бессмысленными. А вот с помощью этого инструмента такие задачи зачастую изящно решаются, и эти решения, кстати, находят многочисленные применения в физике и инженерии. Так что в том, что человечество сумело изобрести, скажем, компьютеры, есть «заслуга» комплексных чисел.

Риман придумал функцию, которая сегодня так и называется дзета-функцией Римана ζ(x). Её определения мы с позволения читателя приводить не будем: оно громоздко и требует введения ещё нескольких математических понятий. Отметим лишь два факта. Во-первых, эта функция тесно связана с распределением простых чисел. Во-вторых, её аргумент – комплексное число.

Фото YouTube.

По определению дзета-функции, если её аргумент – отрицательное чётное число (напомним, что целые числа – тоже комплексные), то ζ(x) = 0. Другими словами, ζ(-2) = ζ(-4) = ζ(-6) = … = 0. Вопрос заключается в том, в каких ещё числах эта функция обращается в нуль.

Гипотеза Римана звучит так: если ζ(a + ib) = 0 и a + ib не является отрицательным чётным (которые рассмотрены выше), то a = ½.

Такое на первый взгляд простое утверждение пытались доказать многие великие математики, но никому это не удалось. Математический институт имени Клэя (Clay Mathematics Institute) включил эту гипотезу в число семи проблем тысячелетия, за решение которых было назначено вознаграждение в один миллион долларов США. Заметим, что пока из этого списка решена только одна задача. Это гипотеза Пуанкаре, доказанная российским математиком Григорием Перельманом.

Атья утверждает, что доказал гипотезу Римана. Препринт доказательства, опубликованный в виде PDF-файла, занимает всего пять страниц. Как уточняет New Scientist, оно основано на результатах великих математиков XX века Джона фон Неймана и Фридриха Хирцебруха. Воспользовавшись их теоремами, Атья доказал гипотезу Римана от противного: он предположил, что она неверна, и пришёл к противоречию.

«Это чудесно, – говорит Атья, – но я утверждаю, что вся тяжелая работа была выполнена 70 лет назад».

Впрочем, работа математика, разумеется, нуждается в тщательной проверке. Никто не застрахован от ошибки в таком трудном деле, как математическое доказательство, тем более когда речь идёт о проблемах тысячелетия. Попытки доказательства гипотезы Римана разными авторами неоднократно публиковались, но каждый раз оказывались ошибочными. Возможно, в этот раз человечеству наконец повезёт.

Напомним, что «Вести.Наука» (nauka.vesti.ru) ранее писали о других выдающихся математических работах, в том числе выполненных российскими учёными.

• новости

Весь эфир

Проблемы тысячелетия: семь величайших нерешенных математических загадок нашего времени

В мае 2000 года Математический институт Клэя поднял семь давних открытых математических задач до статуса «Задач тысячелетия», наградив каждую из них наградой в миллион долларов. приз. Семь конкретных задач были выбраны отчасти из-за их сложности, но в большей степени из-за их центральной важности для современной математики. Задачи и соответствующие им общие области математики таковы.

1	Гипотеза Римана	Теория чисел
2	Существование Янга-Миллса и массовый разрыв	Математическая физика
3	Проблема P и NP	Информатика
4	Существование и гладкость Навье-Стокса	Математическая физика
5	Гипотеза Пуанкаре	Топология
6	Гипотеза Берча и Суиннертона-Дайера	Теория чисел
7	Гипотеза Ходжа	Алгебраическая геометрия

Уравнения Навье-Стокса были впервые записаны в начале 1820-х гг., Риман выдвинул свою гипотезу в статье 1859 г., а гипотеза Пуанкаре восходит к 19 г.04. Остальные проблемы возникли в период 1950-1971 гг.

В Проблемы тысячелетия, Кит Девлин стремится донести суть этих семи проблем до широкой читательской аудитории. Конечно, это очень амбициозная цель. Предисловие разъясняет основные правила Девлина. Сначала он предполагает только «хорошее школьное знание математики». Во-вторых, он пишет «не для тех, кто хочет заняться одной из проблем, а для читателей — как математиков, так и нематематиков, — которым любопытно текущее состояние на переднем крае древнейшего массива научных знаний человечества». Ему ясно, что читательская аудитория определяет уровень книги, так что не всегда будут даны точные формулировки проблем. Скорее, цель состоит в том, чтобы «предоставить предысторию каждой проблемы, описать, как она возникла, объяснить, что делает ее особенно сложной, и дать … некоторое представление о том, почему математики считают ее важной».

После короткого предисловия в книге есть интересная глава 0, а затем по одной главе для каждой задачи в указанном выше порядке. Эти семь глав построены аналогично. Большинство из них имеют длинную историческую составляющую, обычно включающую биографическую информацию о человеке или людях, в честь которых названа гипотеза. Каждый из них содержит существенную справочную математическую информацию, с темами, варьирующимися от комплексных чисел в главе 1 и теории групп в главе 2 до конгруэнтностей в главе 6 и алгебраических многообразиях в главе 7. По возможности особое внимание уделяется приложениям. Хорошая тема глав 2 и 4 заключается в том, что математики отстают от физиков и инженеров и просто пытаются их догнать. Каждая глава завершается обсуждением самой проблемы тысячелетия.

Глава 5 иллюстрирует, как Девлин связывает различные части главы в связное повествование. Он начинается с четырех страниц о жизни и творчестве Анри Пуанкаре. Он переходит к введению «геометрии резинового листа» с точки зрения того, как карты метро и электрические схемы холодильников не соответствуют геометрически верным физическим объектам, которые они представляют, но, тем не менее, четко фиксируют всю необходимую информацию. Этот модуль важен, так как он заставит читателей почувствовать, что топология естественна, а не странна. Затем в главе 5 вводятся понятия вершин, ребер, граней и, наконец, эйлеровой характеристики в терминах проблемы Кенигсбергского моста. Он вводит неориентируемые поверхности и делает естественным введение объемлющего четырехмерного пространства, поскольку оно необходимо для вложения бутылки Клейна. Он топологически классифицирует замкнутые поверхности сначала грубо с точки зрения их ориентируемости, а затем полностью с точки зрения нарисованных на них сетей и эйлеровой характеристики этих сетей. Это дает очень привлекательный пример двух, казалось бы, связанных колец, которые на самом деле могут быть разорваны. Этот пример показывает читателю, что не все геометрически очевидно, и таким образом подчеркивает полезность алгебраических инвариантов, которые могут строго подтвердить, что два объекта топологически различны. В нем обсуждается, как обычная двухсфера характеризуется среди всех замкнутых поверхностей тем, что обладает свойством, что любая петля на ней может непрерывно сжиматься в точку. Наконец, посредством этой двумерной аналогии обсуждается фактическая трехмерная гипотеза Пуанкаре.

Время от времени естественным образом проявляется напряжение, связанное с необходимостью донести все семь проблем тысячелетия до широкой читательской аудитории. В главе о Навье-Стоксе, например, представленная фоновая математическая информация представляет собой исчисление и, в частности, дифференцирование. Читатели проинструктированы, что «dy/dx» следует читать как «dee-wye by dee-ex». Примерно через семь страниц представлены сами уравнения Навье-Стокса. Это четыре связанных нелинейных дифференциальных уравнения в частных производных с четырьмя независимыми переменными. Изложение мягкое, но читатели, плохо знакомые с исчислением, поймут его только на поверхностном уровне. Напряжение несколько больше ощущается в главе 6 и особенно в главе 7. Но эти различные напряжения неизбежны, и я думаю, что в целом Девлин проделал очень хорошую работу, дав обычным читателям представление о проблемах семи тысячелетий.

Проблемы тысячелетия концентрируется на прошлом и настоящем проблем, но также естественно задумываться об их будущем! Можем ли мы ожидать, что какие-то призы будут розданы еще при нашей жизни? Девлин поднимает этот вопрос в конце различных глав, но всегда уклончиво. Его упоминание о «двадцать пятом веке» в предисловии может склонить некоторых читателей к пессимизму. Лично я считаю, что есть веские причины для оптимизма. Я воспользуюсь этой возможностью, чтобы высказать свое предположение о том, что бурный темп математического прогресса в 21 веке будет включать в себя решение по крайней мере двух задач тысячелетия до 2020 года и по крайней мере пяти до конца века. Когда решения проблем тысячелетия действительно придут, было бы хорошо, если бы широкая общественность признала их за монументальные достижения, которыми они станут. Такие книги, как «9» Кита Девлина.0077 Проблемы тысячелетия очень поможет.

---

Часть интересной Главы 0 появляется в слегка переработанной форме в ноябрьском выпуске 2002 года Угол Девлинса , Недоступность современной математики.

Дополнительную информацию о задачах тысячелетия, включая официальные формулировки задач, можно получить в Математическом институте Клэя. Девлин в своем предисловии ссылается также на предстоящую официальную книгу CMI, в которой он будет участвовать.

Есть несколько более коротких вводных статей по проблемам семи тысячелетий на несколько более продвинутом уровне, чем книга Девлина. Один из них написан Барри Сипра в томе, рассмотренном MAA Online. Хотя книга Девлина в целом свободна от ошибок, а книга Чипра была особенно хорошо отредактирована, обе они допускают одну и ту же ошибку в отношении уже доказанной гипотезы Пуанкаре о многомерности. Односвязное компактное многообразие в размерности четыре и более может иметь большую топологическую сложность. Только после того, как предполагается, что группы гомологий также тривиальны в степенях один через размерность минус один, такое многообразие гарантированно будет гомеоморфным сфере.

---

Дэвид Робертс — доцент математики Миннесотского университета в Моррисе.

семь величайших нерешенных математических головоломок нашего времени в каталоге SearchWorks

Ответственность

Кит Девлин.

Выходные данные

Нью-Йорк: Basic Books, c2002.

Физическое описание

х, 237 р. : больной. ; 24 см.

Доступно онлайн

В библиотеке

Научная библиотека (Ли и Ма)

Стеки

Предметы в стопках

Телефонный номер	Статус
КА93 .Д47 2002	edu/requests/new?barcode=36105111813304&item_id=5461585&origin=SCIENCE&origin_location=STACKS»> Неизвестный

Описание

Создатели/Соавторы

Автор/Создатель

Девлин, Кит Дж.

Содержание/Резюме

Библиография

Включает библиографические ссылки (стр. [229]-230) и предметный указатель.

Содержимое

• Гипотеза Римана
• Теория Янга-Миллса и гипотеза разрыва масс
• Проблема P и NP
• Уравнения Навье-Стокса
• Гипотеза Пуанкаре
• Гипотеза Берча и Суиннертона-Дайера
• Гипотеза Ходжа.

Резюме издателя

Окончательный отчет непрофессионального читателя об Эверестах математики — семи нерешенных проблемах, которые определяют состояние искусства в современной математике. В 2000 году Кембриджский фонд Клэя, штат Массачусетс, объявил исторический конкурс: тот, кто сможет решить любую из семи чрезвычайно сложных математических задач и добиться признания решения экспертами правильным, получит призовой фонд в размере 1 миллиона долларов США. Для этого был некоторый прецедент: в 1900 Дэвид Гильберт, один из величайших математиков своего времени, предложил двадцать три проблемы, теперь известные как проблемы Гильберта, которые определили большую часть повестки дня математики в двадцатом веке. Проблемы тысячелетия, вероятно, приобретут такой же статус, и их решение (или его отсутствие), вероятно, сыграет важную роль в определении курса математики в текущем столетии. Кит Девлин, известный толкователь математики, рассказывает здесь, что представляют собой семь задач, как они возникли и что они означают для математики и естественных наук. Эти проблемы — медные кольца, протянутые сегодняшним математикам, блестящие и недоступные. В руках Кейта Девлина, «Математика» из «Выпуска выходного дня» NPR, каждая Проблема тысячелетия становится увлекательным окном в самые глубокие и сложные вопросы в этой области. Для математиков, физиков, инженеров и всех, кто интересуется новейшими достижениями математики, «Проблемы тысячелетия» — исчерпывающее изложение предмета, у которого будет очень долгая жизнь.
(источник: данные книги Нильсена)

Резюме издателя

Окончательный отчет об Эверестах математики — семи нерешенных проблемах, которые определяют состояние дел в современной математике. В 2000 году Фонд Клэя объявил исторический конкурс: тот, кто сможет решить любую из семи чрезвычайно сложных математических задач и добиться признания решения экспертами правильным, получит призовой фонд в размере 1 миллиона долларов США. Для этого был некоторый прецедент: в 1900 математик Дэвид Гильберт предложил двадцать три проблемы, которые определили большую часть повестки дня математики в двадцатом веке. Проблемы тысячелетия, выбранные комитетом ведущих математиков мира, скорее всего, приобретут такой же статус, и их решение (или его отсутствие), вероятно, сыграет важную роль в определении курса математики в двадцатом веке. -первый век. Кит Девлин, известный толкователь математики и один из авторов официального описания проблем Института Клэя, дает здесь окончательный отчет для интересующегося математикой читателя.
(источник: данные книги Нильсена)

Субъекты

Субъекты

Математика > Популярные произведения.

Математика > Исследовательская работа > Популярные произведения.

Просмотр связанных элементов

Начните с номера телефона:

Посмотреть всю страницу

Библиотечный вид | Кошка: 5461585

Самые сложные математические задачи в мире — журнал непредвиденных обстоятельств

Решение одной из неуловимых и сложных задач тысячелетия стоит 1 миллион долларов.

Вот почему.

Алисса Оурслер и Карл Рот

24 мая 2000 года знаменитые математики сэр Майкл Атья и Джон Тейт вошел в лекционный зал Коллеж де Франс в Париже. Там они сделал объявление, которое поставило сложную математику в необычно основное внимание. Первый человек или команда, взломавшая любой из семи наиболее сложные нерешенные математические задачи будут награждены крутым призом в 1 миллион долларов. Проблемы премии тысячелетия, как их называют, создали коллективную 7-долларовую миллион призовых денег — денег, предназначенных для поощрения величайших умов к поиску ответы на некоторые из самых давних загадок математики.

За столетие до этого в Париже произошло очень похожее событие. На втором Международном конгрессе математиков немецкий математик Дэвид Гильберт представил 23 наиболее важных нерешенных математических проблемы того времени — проблемы, призванные продвинуть мир вперед, в 20-е век. Эти 23 проблемы стали известны как проблемы Гильберта. Чтобы решить один проблемы Гильберта обеспечили бы немедленную известность в области математика — стимул, которого оказалось достаточно. ^[1] К моменту Проблемы тысячелетия родились 100 лет спустя, все, кроме одной из проблем Гильберта. проблемы были решены.

Как сказано в заголовке журнала Scientific American , « Гильберт Ходил, чтобы Математический институт Клэя мог работать». ^[2] Лэндон Клей был успешным предпринимателем из Кембриджа, штат Массачусетс, и, что более важно, источник денежного приза за «Проблемы тысячелетия». Было бы легко предположим, что Клей тоже был математиком. На самом деле он был английским майором. из Гарварда, сколотивший состояние на паевых инвестиционных фондах и в бизнес-секторе. Этот тем не менее, это не помешало Клэю поддерживать область математики. За год до до объявления «Проблем тысячелетия» Клэй основал некоммерческую посвящен исследованиям в этой области. Его творчески назвали «Глина». Математический институт (CMI). CMI выбрал Проблемы Премии Тысячелетия и наблюдает за соревнованиями.

С объявлением задач тысячелетия, Клэй удалось и воздать должное Гильберту, и вновь привнести некоторую энергию в математическому сообществу, поскольку «Задачи тысячелетия» предоставили поле с долгожданным вниманием. ^[3] Каждая из семи задач имеет годами терзали умы выдающихся математиков, и решить хотя бы одну принесет пользу не только области математики, но и смежным областям, таким как физика, химия и информатика.

Проще говоря, ответы на Проблемы Тысячелетия позволяют нам глубже понять мир, который мы открыли и построили вокруг себя, вводя нас в малоизученные аспекты. Имея это в виду, давайте рассмотрим каждую проблему. В качестве примечания, некоторые из них будут связаны со сложной математикой, хотя мы стараемся оставаться на поверхности и делать это максимально простым. Если в какой-то момент вы обнаружите, что заблудились, просто помните: эти задачи ставили в тупик и величайшие математические умы!

Гипотеза Римана

Из 23 проблем, поставленных в Париже более 100 лет назад, только одна остается нерешенной. Эта давняя проблема Гильберта называется гипотезой Римана и вполне логично превратилась в проблему тысячелетия. Что касается последней оставшейся проблемы, то легко понять, почему CMI чувствовал необходимость сохранить ее в глобальном обсуждении.

Сама задача была впервые предложена в 1859 г. Германом математик Бернхард Риман. По существу, Риман пытался ответить на давний вопрос о структуре простых чисел и их распределение среди всех счетных чисел. Это было с его собственным пониманием и использование дзета-функции, позже известной как дзета-функция Римана, что Риман смог построить свою гипотезу.

Говоря простым языком, Риман обнаружил, что использование его дзета-функция будет давать сумму 0 для определенных входных данных, теперь известных как дзета нули. Некоторые дзета-нули считаются тривиальными; на самом деле, любое отрицательное число слева от четного нуля (–2, –4, –6, –8…) даст сумму нулей при помещении в дзета-функцию. Но это нетривиальные нули, которые вызвало большое любопытство на протяжении многих лет.

Нетривиальные нули создают уникальный шаблон, и это узор действует как центральный мотив гипотезы Римана. Все эти нетривиальные нули лежат в области, называемой критической полосой, которая по сути является пространством между 0 и 1. Риман доказал, что существует бесконечное количество нулей, которые нужно обнаружить в этой полосе. Его гипотеза по существу утверждает, что все эти нули существуют на прямой, проходящей через середину критическая полоса — непосредственно на ½.

Почему подтверждение или опровержение этой гипотезы гарантирует 1 доллар миллионная награда? И где эта теория пересекается с теорией простых чисел? Гипотеза Римана породила открытие волны на комплексной плоскости. Риман обнаружил, что дзета-нули — это именно то, что ему нужно, чтобы найти совпадение между его использованием дзета-функции и распределением простых числа вдоль бесконечной линии подсчета чисел. Однажды Риман увидел связь между использованием каждого дзета-ноль и создаваемыми ими гармониками, это по существу предсказывало бы точку каждого простого числа вдоль бесконечного линия.

Чтобы доказать эту гипотезу, мы получили бы все необходимое. знать о распределении простых чисел. Как Insider подвел итог «10 000 000 000 000 простых чисел были проверены и непротиворечивы. с уравнением, но нет доказательства того, что все простых чисел следуют за шаблон.» ^[4] Доказав, что все простых чисел следуют шаблону, мы может укрепить многие математические неопределенности.

Многие современные методы факторинга основаны на концепции что гипотеза Римана верна. Таким образом, доказательство этой гипотезы не только укрепляют текущие методы, но позволяют нам развивать указанные методы с большей уверенность. Его влияние также распространится за пределы теоретической математики на все времена. путь в области, которые в значительной степени зависят от большого количества числовых факторингов, таких как кибербезопасность или шифрование. И последнее, но не менее важное: гипотеза Римана даже помочь действовать как объединение между математикой и квантовой физикой.

Сэр Майкл Атья, математик, который помог представить общественности «Задачи тысячелетия», в 2018 году заявил, что доказал гипотезу Римана. Хотя его нынешние утверждения все еще расследуются, многие лидеры в этой области признали, что Атия действительно сделал это. Если это так, Алия положит конец этой давней проблеме , а заработает себе заслуженный 1 миллион долларов всего через несколько десятилетий после объявления приза.

Теория Янга-Миллса и гипотеза массового разрыва

Уже давно существует связь между миром математика и мир физики. Проще говоря, оба поля существуют для того, чтобы помочь нам познать окружающий мир. Но хотя прогресс в обеих областях было сделано, было сделано несколько прорывов в физике, для которых математике еще предстоит наверстать упущенное — большинство вращается вокруг открытия квантовых физика.

Святой Грааль физики давно провозглашен Открытие теории великого объединения. Эта теория будет служить связующим звеном между известные силы Вселенной: гравитация, электромагнетизм, сильное ядерное сила и слабое ядерное взаимодействие. В настоящее время в зависимости от сферы деятельности физика использует, физика понимается в любой относительной теории (для таких, как астрофизики, изучающие Вселенную в больших масштабах), или квантовые теория (для тех, кто, подобно физикам элементарных частиц, смотрит на мельчайшие масштабы). Все текущие попытки объединить обе теории ни к чему не привели, так как все уравнения в математической сфере дают бесконечные ответы, делая их пустыми и бессмысленный.

Однако около 80 лет назад в физике произошел сдвиг — и родилась квантовая физика.

Физики начали открывать множество различных типов частицы помимо трех, о которых они уже знали: протоны, нейтроны и электроны. Было принято, что эти три типа частиц составляют материю. в то время как фотоны были безмассовыми частицами, которые, как считалось, действовали как метод транспорт налегке.

С открытием новых частиц возникло много путаницы, так как многие бросили вызов тому, что считалось правдой в отношении поведения существующих частицы. Введите теорию Янга-Миллса: попытку организовать появление этот новый мир. Теория Янга-Миллса впервые была предложена в 19 в.50-е и представляет собой базу для построения стандартной модели: новый метод организация вновь открытых частиц с использованием структур, которые также встречаются в геометрия.

С момента своего появления теория Янга-Миллса стала фундамент для большого количества теории элементарных частиц. Таким образом, это представляет собой начальный шаг к теории великого объединения. Это потому, что в с точки зрения непрофессионала, Янг-Миллс позволяет физикам вывести уравнения для обоих классические и квантовые параметры. В рамках концепции Янга-Миллса возникает еще одна проблема. Возникает: гипотеза массового разрыва.

Сама проблема заключается просто в том, что ни у кого нет был в состоянии математически решить любое из уравнений Янга-Миллса. Теория предлагает. Как писал Кит Девлин в своей книге «Проблемы тысячелетия », «Самая точная научная теория, которую когда-либо видел мир, построена на уравнения, которые никто не может решить». Таким образом, конкурс «бросает вызов математическое сообщество для решения этой проблемы, — пишет Девлин, — сначала найдя решение уравнений Янга-Миллса, а во-вторых, установление технического свойство решения, называемое гипотезой массового разрыва». ^[5]

В то время как физики продолжают использовать уравнения для сбора цифры, которые на самом деле пугающе точны, приближения, что. Как резюмировал Девлин, «эта вторая часть проблемы гарантирует, что математика останется совместимой с компьютерным моделированием и наблюдения, сделанные физиками в лаборатории». ^[6]

Как было сказано ранее, для решения этой проблемы тысячелетия потребуется оказать огромное влияние на области физики и математика. В физике решение теории Янга-Миллса и гипотезы массового разрыва было бы важным прорыв в области теоретической физики, доказывающий существование теорий не опасаясь, что они развалятся под математическим контролем.

Кроме того, как писал Эдвард Вриттен в книге «Физические законы и Поиски математического понимания», это «пролило бы свет на фундаментальный аспект природы, который физики до сих пор не понимают должным образом». ^[7] В математике квантовая теория поля была бы принята в качестве совершенно новой теории. математической теории, в отличие от той, которая существует непосредственно в сфере физика.

Задача P vs. NP

И снова задачи на премию тысячелетия уходят корнями в математику но сильно пересекаются с другими областями. Для этого следующего вопроса мы оставляем мир физики, чтобы прийти в мир вычислительной математики и Информатика. Третья задача премии тысячелетия — P против NP Проблема — говорит о нашей способности вычислять сложные уравнения и об ограничениях изложенные компьютерами.

В 1971 году Стивен Кук опубликовал основополагающую статью под названием «Сложность процедур доказательства теорем». Изучив теорию сложности, которая «анализирует вычислительные процессы, чтобы увидеть, насколько эффективно они могут выполняться out» — Кук ввел термин NP-полнота . ^[8] NP означает недетерминированные процессы с полиномиальным временем. Проблема — это проблема NP, согласно Девлину, «если она может быть решена или завершена за полиномиальное время с помощью недетерминированный компьютер, способный делать случайный выбор между диапазоном альтернатив и, более того, делает это с большой удачей». ^[9]

Этот случайный выбор, сделанный с «совершенной удачей», помогает оптимизировать компьютерные функции, делая адаптированные, но «случайные» вычислительные выбор — в основном в интересах экономии вычислительного времени. Как более люди изучали теорию Кука, они начали понимать, что многие из самых важные установленные проблемы NP были, по сути, NP-полными. Если проблема НП считается завершенным, это означает, что будет невероятно сложно найти полиномиальная процедура для ее решения. Таким образом, большой объем вычислительных процессы увязли в обработке данных без метода различения где разместить свои вычислительные усилия.

Вот почему P vs. NP считается значительным и достойным член Проблемы Премии Тысячелетия. Проблема заключается в том, является ли некоторые проблемы стоят вычислительных усилий, необходимых для их обработки. К определить это, кто-то должен доказать, что P равно NP — или что это не так.

В настоящее время шифрование данных теоретически считается проблема, основанная на концепции, что для обработки достаточного количества возможностей для расшифровать длинное шифрование, потребуются годы и достаточно вычислительной способность взять на себя задачу (не говоря уже о правильном полиномиальном времени процедура). Однако задача найти способ взломать этот код считается NP-задачей.

Если бы мы обнаружили, что P и NP одно и то же, сделать наши методы шифрования полностью включенными. Теоретически они бы быть открытым для атак, если у злоумышленника достаточно времени и вычислительных ресурсов возможность достичь результата взлома кода. Между тем, теоретически выяснив то, что P равно NP, также делает всю концепцию Кука NP-полноты совершенно бессмысленно.

С другой стороны, чтобы доказать, что P и NP на самом деле другой приходит со своей тяжелой задачей. Для этого нужно «показать что не может быть процедуры, которая решает задачу за полиномиальное время». ^[10] Это означает процедуры как сейчас, так и в будущем. Нужно не только доказать их различия с известными доступными процедурами, но с любыми теоретическими процедуры еще не обнаружены. В этом плане никто даже близко не подошел.

Как математика породила информатику

До появления компьютеров математики уже рассматривали теорию, лежащую в основе того, что требуется для решения любой конкретной набор уравнений. В 1930 году Курт Гёдель обнаружил, что «в любой части математика, включающая в себя элементарную арифметику (то есть практически любую отдаленно полезная часть математики), сколько бы аксиом вы ни записали, всегда будут некоторые истинные утверждения, которые нельзя доказать из тех аксиомы». ^[11]

Аксиома – это математическое утверждение, представленное достаточно прямолинейно, чтобы считаться истинным. Таким образом, аксиомы представляют собой теоретическая основа, на которой можно проводить дальнейшие уравнения и получать результаты основано на предположении, что аксиома действительно верна. Открытие Геделя, вскоре получившая название теоремы Гёделя о неполноте, высветила тот факт, что при аксиоматизированной системы наверняка будут некоторые функции, которые не могут решить или обработать. Эта теория была первоначальной концепцией того, что мы теперь знаем как вычислимую функцию.

Гёдель вдохновил других математиков начать изучение понятие о том, какие функции в области математики можно даже вычислить, и какие функции не могли. Теперь, когда вычислимость стала достойной областью изучения, вскоре появятся и сами компьютеры. Но пока это поле создало потребность в компьютерах и во многом способствовала их появлению, компьютеры (которые могли предложить только инструмент для обработки данных и больших вычислений) были мало беспокойства для многих математиков, чья работа перекочевала в более теоретическая практика.

В то время как многие математики быстро потеряли интерес, другие заинтересовались возможностями компьютеров и их использованием в области математики. Именно благодаря их интересу и размышлениям возникли такие области, как теория приближения, теория динамических систем и численный анализ. Эти исследования превратились в то, что мы сейчас называем информатикой, и служат строительными блоками для современных компьютерных разработок, таких как искусственный интеллект.

Уравнения Навье-Стокса

Легко не заметить обыденное. Что-то вроде потока воды кажется нам настолько естественным, что мы часто забываем о скрытой сложности (простите за каламбур) под поверхностью. Интерес Клода Луи Мари Анри Навье в таких природных сложностях — вот что привело нас к следующей проблеме тысячелетия: Уравнения Навье-Стокса.

Навье, французский ученый и уважаемый инженер, сделал он привлек внимание общественности благодаря своим проектам и работе строителем мостов. Однако у Навье были страсть и образование математика. Во время его преподавая в Ecole des Ponts et Chaussées в 1800-х годах, Навье начал рассматривая математику текущих жидкостей. ^[12]

Ньютон впервые представил этот предмет в 1687 году, выпустив из Philosophiae Naturalis Principia Mathematica , в котором он выдвинул свои законы движения и навсегда изменил научный мир. Его второй Закон движения представляет собой основу природы движущихся жидкостей (жидкости состоящих как из жидкостей, так и из газов). ^[13]

Вскоре математики начнут глубже погружаться в предмет. Во-первых, адаптация исчисления Давидом Бернулли помогла жидкости движутся и действуют, когда на них действует множество сил. Леонхард Эйлер развил эту концепцию, построив систему уравнений, которые попытались для описания движения гипотетической невязкой жидкости. Далее, в 1822 г. Навье вступил в разговор, переработав уравнения Эйлера, чтобы учесть некоторое измеримое количество вязкости. ^[14]

По мере нарастания темпов изучения предмета, математическому вундеркинду Джорджу Габриэлю Стоксу понадобилось всего несколько лет, чтобы обнаружить, что математические рассуждения Навье были, к сожалению, неточными, но уравнения, на которые хирургическим путем наткнулся Навье, были правильными! Стоукс был с самого начала своей карьеры увлекался потоком жидкости и использовать свои передовые знания в области исчисления, чтобы заново открыть уравнения, которые Навье были найдены около 20 лет назад — только на этот раз он найдет их с правильным рассуждения. Это свяжет их вместе в истории и установит набор уравнения, известные как уравнения Навье-Стокса.

Стоукс добился больших успехов в своей карьере, и изучение поток жидкостей имел такое же поступательное движение. Очень уж показалось хотя математики были близки к созданию полной теории жидкости поток. Но в конце концов они остановились. Для того, чтобы рассмотреть поток жидкостей, действующих в непрерывном состоянии движения, математики должны были справиться два набора бесконечно малых: последовательность «неподвижных кадров» (где движение рассматривается как последовательность статических ситуаций) и бесконечно малая геометрическая вариация между двумя выбранными точками в последовательности (и как они следуют друг за другом на дорожка).

Проблема, как резюмировал Девлин, заключается в том, что «когда мы пытаемся фиксировать движение жидкости в любой точке с точки зрения ее движения в каждом из направления x, y и z, мы излишне усложняем жизнь себя». ^[15] Проще говоря, формула, которая на самом деле решает Уравнения Навье-Стокса остались неуловимыми, и никто не смог показать, существует ли вообще такое решение математически. Это очевидно для глаз, что природа работает такие уравнения. Но можно ли получить понимание такого явления в мире математики? Ответь на это вопрос, и вы станете миллионером.

В настоящее время предлагаются различные решения для упрощенные версии уравнений Навье-Стокса, но ни одна из них еще не объясняет явления, найденные в третьем измерении без невероятного количества ограничения. Таким образом, эти предлагаемые решения были сочтены неполными.

Решение этих уравнений дало бы нам невероятно глубокую понимание природных сил, с которыми мы ежедневно взаимодействуем. Например, быть способный рассчитать поток воздуха глубоким, глубоким, математическим способом, совершить революцию в авиаперевозках. Решение будет распространяться на сферу цифровых технологий. также СМИ; уравнения могут быть использованы, чтобы помочь нашей компьютерной визуализации естественного жидкости в цифровых ландшафтах, которые можно найти в видеоиграх и фильмах.

Гипотеза Берча и Суиннертона-Дайера

В начале 1960-х годов компьютеры все еще находились на самой ранней стадии развития. На самом деле в то время в мире существовало всего несколько компьютеров, в том числе один в Кембриджском университете в Англии. Брайан Берч и Питер Суиннертон-Дайер, два математика факультета, воспользовались своим доступом к Cambridge EDSAC, как назывался компьютер, чтобы собрать данные о массиве полиномиальных уравнений. При этом их внимание привлек определенный набор паттернов — паттерны, известные как эллиптические кривые. Используя свои данные, полученные в результате изучения таких математических закономерностей, Берч и Суиннертон-Дайер разработали гипотезу, которая составляет пятую проблему премии тысячелетия.

Это сложная штука, так что потерпите. Береза ​​и Гипотеза Суиннертона-Дайера — это утверждение об эллиптических кривых. Эллиптический кривые отличаются от эллипсов; они находятся при вычислении дуги длина эллипсов. На этих кривых математики нашли рациональные точки иметь какое-то существенное значение. Рациональные точки — это точки на кривой, где обе координаты оказываются рациональными. Они примечательны тем, что большинство числа, входящие в указанные уравнения, внутренне связаны свойствами высших математические функции. Именно эти рациональные моменты позволяют математикам лучше понимать эллиптические кривые и, в свою очередь, изучать более глубокие области, такие как Диофантовы уравнения и нули многочленов. ^[16]

В 1922 г. Луи Морделл обнаружил, что можно различать каждую рациональную точку на эллиптической кривой, если это было сделано из конечное подмножество. Это может показаться очевидным, так как некоторые эллиптические кривые имеют только конечное число рациональных точек. Но эллиптические кривые с бесконечным числом рациональных точек тоже существуют. Теорема Морделла оказалась вполне важно для прогресса в этой области. Однако не всегда полезный. Когда рациональные точки по своей природе велики, найти их невероятно сложно. сложное задание. Чтобы облегчить бремя такой задачи, математики создали L-функцию: «удобный инструмент для связывания различные виды объектов друг к другу, например, эллиптические кривые и модульные формы», как кратко подытожил кто-то на StackExchange. ^[17]

Гипотеза Берча и Суиннертона-Дайера ставит вопрос о специфические свойства этой L-функции относительно ранга эллиптического изгиб. Используя теорию Морделла для создания рациональных точек вдоль кривой, Ранг позволяет определить, сколько из этих рациональных точек появится бесконечное число рациональных точек. Конечно, это невероятно упрощенная версия не только того, что представляет собой эта гипотеза, но и математика нужна, чтобы понять это. В некотором смысле это может быть даже оскорбительно настоящим математикам! Если ваш интерес пробудился, и вы все еще с нами, определенно копать немного глубже. ^[18]

Доказательство истинности этой гипотезы дало бы некоторые важные достижения в технологии, которую мы уже упоминали: шифрование. В настоящее время мы используем метод шифрования данных, называемый шифрованием RSA. С дальнейшим пониманием эллиптических кривых, криптография на основе эллиптических кривых может стать следующим стандартом шифрования данных. Это было бы полезно, так как длина ключа намного короче, его гораздо быстрее хранить, и он использует меньше памяти и энергии процессора.

Гипотеза Ходжа

Пока что мы получили представление о степени математика выходит за рамки тех основ, которым многие из нас научились в детстве. Погружение в мир математики означает погружение в огромный мир, который связан с многочисленными другие области, но крайне абстрактные. Следующая проблема, гипотеза Ходжа, пожалуй, самый абстрактный из всех. Фактически это поставило в тупик математическое сообщество способами, которые были бы слишком сложными, чтобы копаться здесь!

Чтобы получить хотя бы элементарное представление о том, что Гипотеза Ходжа утверждает, что мы должны вернуться к рождению геометрии. Математики изучали и собирали данные о природе геометрические формы, и многие из них исключительным образом продвинулись в этой области. Будь то Пифагор около 500 г. до н.э. или работа Паскаля середины 1600-х гг. , акт сбора форм будет продолжаться годами. Но это была работа Декарта. в 1647 году, который заложил основу для того, что позже превратилось в Ходжа Гипотеза.

Декарт размышлял (и, в конце концов, с его картезианской системы координат, доказали), что существует неотъемлемая связь между геометрической линии и числа, найденные из системы уравнений. ^[19] Этот мост между алгеброй и геометрией вдохновил своего рода математический ренессанс. Математикам наскучила идея изучения только прямых, и они перешли на более сложные понятия.

Одной из таких концепций было введение более сложных уравнения, которые использовались для исследования форм, которые можно было представить только в алгебраический мир. Проще говоря, эти формы бросают вызов традиционной геометрии. один воображение было бы исчерпано, чтобы понять их. Однако в мир алгебры, они очень реальны. Математики переименовали эти фигуры затем алгебраические циклы создали различия, получившие название алгебраических разновидностей, для отличать природу одних форм от других.

Одна очень специфическая, но чрезвычайно важная алгебраическая разновидность является многообразием. Это описание используется, когда алгебраический цикл имеет гладкую поверхности и кривые, существующие без особой точки. Алгебраисты и Топологи одинаково начали играть с концепцией рисования фигур поверх многообразия, и могут ли эти формы быть математически перерисованы в другие формы. Это предложило новый вопрос: как мы описываем любое новое, случайное фигура, нарисованная на многообразии как четкий, чистый алгебраический цикл?

Гипотеза шотландского математика Уильяма Ходжа попытаться ответить на этот вопрос. Сама догадка пришла бы в результате его работы с 1930 по 1940 год. ^[20] Как резюмирует сайт CMI, « Гипотеза Ходжа утверждает, что для особенно хороших типов пространств, называемых проективных алгебраических многообразий, части, называемые циклами Ходжа, на самом деле (рациональные линейные) комбинации геометрических фигур, называемые алгебраическими циклами». ^[21]

Эта гипотеза могла бы стать фундаментальным ориентиром принцип, говорящий нам, что в этой области следует считать истинным, а что даже стоит доказать. Эти алгебраические циклы — невероятно сложные объекты. которые существуют в двух пространствах: интегралах периодов и представлениях Галуа. Доказательства Гипотеза Ходжа соединила бы эти два пространства и позволила бы нам разделить информацию из одного математического пространства в другое с помощью алгебраических циклов. Хотя последствия гипотезы Ходжа в реальном мире не распространяются на больших высот, его влияние на передовую теоретическую математику было бы огромный.

Гипотеза Пуанкаре

Математика состоит из теории, гипотезы и очень сложное предположение, что определенные теории, хотя, возможно, недоказанные, все еще на самом деле верны. Мы накладываем эти теории друг на друга, слишком. Таким образом, многие из проблем Премии тысячелетия (если не все) имеют породили бесчисленное количество новых математических полей, даже оставаясь недоказанными. Гипотеза Пуанкаре, тем не менее, является единственной задачей премии тысячелетия, в которой имеет был решено.

18 марта 2010 года — почти десять лет со дня, когда конкурс был объявлен в Париже — CMI официально заявил, что д-р Григорий Перельман из Санкт-Петербурга, Россия разрешила эту догадку. Гипотеза Пуанкаре была сформулирована французским математиком Анри Пуанкаре в 1904 году. интерес к космическому пространству в конце концов привел его к топологии, новому виду математики, который некоторые называют форму «ультрагеометрией». ^[22] Топология — это изучение форм всех размеров. Согласно профессору Паскалю Ламбрехтсу, Гипотезу Пуанкаре можно резюмировать следующим вопросом: «Какая форма может ли трехмерное пространство иметь?» ^[23]

Более конкретно, гипотеза рассматривает пространство, которое «локально выглядит как обычное трехмерное пространство, но связно, конечно по размеру и не имеет границ». Помните коллекторы из предыдущего раздела? Это пространство также известно как замкнутое трехмерное многообразие. ^[24] Гипотеза является ключом к пониманию трехмерных форм. Как профессор Хайам Рубинштейн резюмировал для The Conversation:

«Хороший способ визуализировать гипотезу Пуанкаре — исследовать граница шара (двухмерная сфера) и граница бублика (называемый тором). Любую петлю нити на 2-сфере можно сжать до точку, удерживая ее на сфере, тогда как если петля огибает отверстие в пончик, его нельзя уменьшить, не оставив поверхности пончика». ^[25]

Решение Перельмана этой гипотезы, основанное на разработанной программе потока Риччи профессор Ричард С. Гамильтон. По существу, Гамильтон сформулировал «динамическую процесс» для геометрического искажения 3-многообразия. Это геометрический аналог как тепло распространяется в материале. ^[26] И все же никто не смог доказать этому процессу не «мешали бы развивающиеся сингулярности» — до Перельмана. ^[27] Доказательство Перельмана продемонстрировало полное понимание формирования сингулярности в Поток Риччи, а также множество других новых элементов.

Перельман не мечтал решить проблему премии тысячелетия хотя бы за деньги. Он не представил свои корректуры в CMI; вместо этого он просто загрузил их на общедоступный веб-сайт ArXiv.org в 2002 году с окончательным версия размещена на том же сайте примерно четыре года спустя. В том году, Наука признал его «Прорывом года». ^[28] В 2008 г., Перельман также опубликовал свое решение гипотезы Пуанкаре в журнале Geometry. и Топология . Когда CMI предложила ему 1 миллион долларов за решение первой Два года спустя «Проблема тысячелетия» он отказался. Как BBC поставил, Перельман был «фактически отшельником». Он не хотел ни славы, ни богатства, ни внимания. ^[29]

Хотя Перельман, возможно, физически избегал внимания, такое монументальное достижение не будет забыто, и его имя не потеряно к истории. «Это крупное достижение в истории математики, которое еще долго будет помнить», — сказал Джеймс Карлсон, президент CMI, в 2010 году. «Его идеи и методы уже нашли новые применения в анализе и геометрии; конечно будущее принесет гораздо больше». ^[30] Через несколько месяцев после предложения ему миллион долларов, CMI и Институт Анри Пуанкаре провели конференцию, чтобы праздновать решение гипотезы. Это было, конечно, в Париже.

Алисса Оурслер — аспирант и отмеченный наградами журналист. Карл Рот — писатель и музыкант из Миннеаполиса.

Примечания

[1]          Проблемы тысячелетия: семь величайших нерешенных математических загадок нашего времени Время. Кевин Девлин. 2002.

[2]          «Гильберт Ходил, чтобы Математический институт Клэя мог работать». Научный американец. Эвелин Лэмб. 17 октября 2019 г. (https://blogs.scientificamerican.com/roots-of-unity/hilbert-walked-so-the-clay-mathematics-institute-could-run/)

[3]          Devlin, Стр. 2.

[4]          «Верх. математик говорит, что решил «самую важную открытую проблему» в математике через 160 лет». Инсайдер. Билл Босток. 24 сентября 2018 г.

[5]          Девлин, стр. 94.

[6]          Девлин, стр. 94.

[7]          «Физические Закон и поиски понимания». Бюллетень. Эдвард Виттен. 2002. (https://www.ams.org/journals/bull/2003-40-01/S0273-0979-02-00969-2/S0273-0979-02-00969-2.pdf)

[8]          Девлин, стр. 111.

[9]          Девлин, стр. 124.

[10]        Девлин, стр. 128.

[11]       Девлин, стр. 108.

[12]        Девлин, стр. 131–132.

[13]        «Миллениум Приз: проблема существования и единственности Навье-Стокса». Беседа. Джим Деньер. 16 ноября 2011 г. (https://theconversation.com/millennium-prize-the-navier-stokes-existence-and-uniqueness-problem-4244)

[14]        Девлин, стр. 132.

[15]        Девлин, стр. 154.

[16] «Премия тысячелетия: Береза и гипотеза Суиннертона-Дайера». Разговор. Даниэль Далбурго. 30 ноября 21:00. (https://theconversation.com/millennium-prize-the-birch-and-swinnerton-dyer-conjecture-4242)

[17]        «Почему важны ли L-функции L ? Обмен стеками. (https://math.stackexchange.com/questions/1857980/why-are-l-functions-a-big-deal)

[18]        См., для пример: «Самая сложная математическая задача, о которой вы никогда не слышали — Берч и Суиннертон-Дайер». Гипотеза. Кинерция. (www.youtube.com/watch?v=R9FKN9MIHlE)

[19]        «Выиграйте миллион долларов с математикой, № 4: Гипотеза Ходжа». Хранитель. Мэтт Паркер. 8 марта 2011 г. (https://www.theguardian.com/science/blog/2011/mar/01/million-dollars-maths-hodge-conjecture)

[20]        «Миллениум Приз: гипотеза Ходжа» The Conversation. Арун Рам. 21 ноября 2011 г. (https://theconversation.com/millennium-prize-the-hodge-conjecture-4243)

[21]        «Ходж Гипотеза. CMI. (https://www.claymath.org/millennium-problems/hodge-conjecture)

[22]        Делвин. Стр. 160.

[23]        Гипотеза Пуанкаре и форма Вселенной». Паскаль Ламбрехтс. Маршировать 2009. (https://www.wellesley.edu/sites/default/files/assets/lambrechts-colloq.pdf)

[24]        «Зарабатывайте 1 000 000 долларов с математикой? Проблемы Премии Тысячелетия». Середина. Марк Доддс. апреля 18, 2019. (https://medium.com/@marktdodds/the-millennium-prize-problems-bce6c3b50222)

[25]        «Миллениум Приз: гипотеза Пуанкаре». Разговор. Хайам Рубинштейн. нояб. 28, 2011. (https://theconversation.com/millennium-prize-the-poincare-conjecture-4245)

[26]        Рубинштейн.

[27]        «Григорий Перельман». Энциклопедия всемирного наследия. (http://www.self.gutenberg.org/articles/Grigori_Perelman)

[28]        «Научные прорыв года — Теорема Пуанкаре». ЮрекОсторожно! Американец Ассоциация содействия развитию науки, 21 декабря 2006 г. (https://www.eurekalert.org/pub_releases/2006-12/aaft-bo121506.php#)

[29]        «Русский гения математики призвали выиграть приз в 1 миллион долларов». Би-би-си. 24 марта 2010 г. (http://news.bbc.co.uk/2/hi/europe/8585407.stm#).

[30]        «Первая глина Премия тысячелетия Института математики объявлена ​​сегодня» CMI. 18 мая 2010 г. (https://www.claymath.org/sites/default/files/millenniumprizefull. pdf)

Семь задач премии тысячелетия

Около ста лет назад Давид Гильберт немецкий математик возмутился двадцатью тремя математическими головоломками, чтобы Международный конгресс математиков . Сегодня только три остаются нераскрытыми. К ним добавились еще четыре неразрешимые проблемы. Одна решена, но шестеро сопротивлялись, все попытки решить перечислены здесь:

1. Гповс PINCARE [Решено в 2002 году] ,
2. Берез и СВИННРТОН-ДИЕР ГОРОДА ,
3. . известный),
4. P Vs. NP Задача ,
5. Гипотеза Ходжа ,
6. Существование Янга-Миллса и массовый разрыв .

Многие эксперты считают, что решение этих задач приведет к выдающимся достижениям в физике, медицине и многих других неизвестных областях мира математики.

24 мая 2000 г. Математический институт Клэя предложил приз в размере 1 000 000 долларов США за решение одной из семи задач премии тысячелетия.

Гипотеза Пуанкаре

Гипотеза Пуанкаре — это теорема о характеристике 3-сферы, которая представляет собой гиперсферу, ограничивающую единичный шар в четырехмерном пространстве. Гипотеза гласит: каждое односвязное замкнутое трехмерное многообразие гомеоморфно трехмерной сфере. Эту проблему решил Перельман ¹ в 2002 г.

Анри Пуанкаре (1854-1912)

Гипотеза Берча и Суиннертона-Дайера

. Это открытая проблема в области теории чисел, широко признанная одной из самых сложных математических задач. Он назван в честь математиков Брайана Джона Берча и Питера Суиннертона-Дайера, 9 лет.0249, который разработал эту гипотезу в первой половине 1960-х годов с помощью машинных вычислений.

Сэр Генри Питер Фрэнсис Суиннертон-Дайер (1927-2018) и Брайан Джон Берч (1931- ) вещества, названные в честь французского инженера и физика Клода-Луи Навье и англо-ирландского физик и математик Джордж Габриэль Стоукс . Они разрабатывались в течение нескольких десятилетий постепенного построения теорий, с 1822 г. ( Навье ) до 1842–1850 гг. ( Стокс ). Уравнения Навье – Стокса математически выражают сохранение импульса и сохранение массы для ньютоновских жидкостей.

Клод Луи Навье (1785-1836) и Джордж Габриэль Стоукс (1819-1903)

Гипотеза Римана

Гипотеза Римана — это предположение о том, что дзета-функция Римана имеет нули только в отрицательных четных целых и комплексных числах с действительной частью 1/2. Многие считают ее самой важной нерешенной проблемой чистой математики. Он представляет большой интерес для теории чисел, поскольку из него вытекают результаты о распределении простых чисел. Он был предложен Бернхардом Риманом (1859 г.), в честь которого и назван.

Бернхард Риман (1826-1866)

Проблема P и NP

Проблема P и NP является основной нерешенной проблемой в информатике. Он спрашивает, можно ли быстро решить каждую проблему, решение которой можно быстро проверить. Используемый здесь неофициальный термин быстро означает существование алгоритма, решающего задачу, которая выполняется за полиномиальное время ² , так что время выполнения задачи зависит от размера входных данных алгоритма. (в отличие, скажем, от экспоненциального времени).

Гипотеза Ходжа

Гипотеза Ходжа является основной нерешенной проблемой в алгебраической геометрии и комплексной геометрии, которая связывает алгебраическую топологию неособого комплексного алгебраического многообразия с его подмногообразиями.
Или, проще говоря, гипотеза Ходжа утверждает, что базовую топологическую информацию, такую ​​как количество дыр в определенных геометрических пространствах, комплексных алгебраических многообразиях, можно понять, изучая возможные красивые формы, расположенные внутри этих пространств, которые выглядят как нулевые наборы полиномиальные уравнения. Последние объекты можно изучать с помощью алгебры и исчисления аналитических функций, и это позволяет косвенно понять широкую форму и структуру часто многомерных пространств, которые иначе не могут быть легко визуализированы.

Проблема существования Янга–Миллса

и проблемы массового разрыва

Проблема существования Янга–Миллса и массового разрыва является нерешенной проблемой математической физики и математики. Задача формулируется следующим образом: доказать, что для любой компактной простой калибровочной группы G нетривиальная квантовая теория Янга–Миллса существует на R ⁴ и имеет массовую щель ∆ > 0. Где R ⁴ — это евклидово 4-пространство, а массовая щель Δ — это масса наименее массивной частицы, предсказанная теорией.

¹ Григорий Яковлевич Перельман родился 13 июня 1966 года и является российским математиком, известным своим вкладом в области геометрического анализа, римановой геометрии и геометрической топологии.
22 декабря 2006 г. научный журнал Science признал доказательство Перельмана гипотезы Пуанкаре научным « прорывом года », что стало первым таким признанием в области математики.

² Запуск алгоритма может потребовать некоторого вычислительного времени. В основном это зависит от сложности алгоритма. Ученые-компьютерщики нашли способ классифицировать алгоритм на основе его поведения и того, сколько операций ему нужно выполнить (конечно, чем больше операций, тем больше времени). Один из этого класса показывает полиномиальную временную сложность. Операционная сложность пропорциональна n ^c , где n — размер ввода, а c — некоторая константа. Очевидно, название происходит из-за 9.0248 n ^c , который является многочленом.

4 ноября 2021 г. 15 февраля 2022 г. JosWP

Наука, тексты на английском языке/Энгельс Дэвид Гильберт, Семь задач премии тысячелетия

Предыдущая

Следующая

Задачи тысячелетия — Объяснение, типы и часто задаваемые вопросы

Задачи семи тысячелетий являются наиболее известными и важными нерешенными задачами в математике. Частный некоммерческий фонд Clay Mathematics Institute, занимающийся математическими исследованиями, бросил вызов математическому сообществу в 2000 году, решив эти уникальные семь задач, и за решение каждой из семи задач была установлена ​​награда в размере 1 000 000 долларов США. Из семи задач, поставленных на премию «Миллениум», одна решена, а остальные шесть представляют собой большую часть текущих исследований.

На рубеже веков объявление задач премии тысячелетия было данью уважения известному выступлению знаменитого Давида Гильберта на Международном конгрессе математиков в 1900 году в Париже. 23 нерешенные проблемы, поставленные Гильбертом, изучались бесчисленным количеством математиков 20-го века, что привело не только к решению некоторых из этих сложных проблем, но также привело к развитию новых идей, а также к новым темам исследований. Некоторые проблемы Гильберта до сих пор остаются открытыми, а именно знаменитая гипотеза Римана.

Эти семь задач охватывают разнообразную группу тем, которые включают теоретическую информатику и физику, а также темы чисто математических областей, таких как теория чисел, алгебраическая геометрия, а также темы топологии.

7 Задачи премии тысячелетия

1. Янга-Миллса и массовый разрыв

Компьютерное моделирование, а также различные эксперименты предполагают существование «массового разрыва» в решении квантовых версий уравнений Янга-Миллса. Но никаких доказательств этого свойства не известно. Известно, что теория Янга-Миллса представляет собой теорию квантовой физики, которая представляет собой обобщение работы Максвелла об электромагнитных взаимодействиях как для сильных, так и для слабых ядерных взаимодействий. Это ключевой компонент Стандартной модели физики элементарных частиц. Утверждается, что эта Стандартная модель обеспечивает основу для объяснения электромагнитных и ядерных сил, а также для классификации субатомных частиц.

В частности, успешное применение теории в экспериментах, а также в упрощенных моделях включало «массовый разрыв», который можно формально определить как разницу между энергией по умолчанию в вакууме, а также энергией в следующем наименьшем энергетическое состояние. Так что эта величина также известна как масса легчайшей частицы в теории. Решение проблемы тысячелетия будет включать как набор формальных аксиом, характеризующих теорию, так и демонстрацию ее внутренней логической непротиворечивости.

2. Гипотеза Римана

Теорема о простых числах определяет среднее распределение простых чисел. Тогда как гипотеза Римана в основном описывает отклонение от среднего. Он был сформулирован в статье Римана 1859 года, в которой утверждается, что все «неочевидные» нули дзета-функции являются комплексными числами с действительной частью 1/2.

3. Задача P vs NP

Если легко проверить правильность решения задачи, можете ли вы сказать, что решить задачу также легко? Говорят, что это точная суть вопроса NP против вопроса P. Типичной для NP-проблем является задача о гамильтоновом пути: предположим, что есть N городов, которые нужно посетить, как можно это сделать, не посещая город дважды? Если вы дадите мне решение, я легко проверю правильность задачи, но найти решение сложно.

4. Уравнение Навье-Стокса

Уравнение Навье-Стокса называется уравнением, которое управляет потоками жидкостей, таких как вода и воздух. Однако нет доказательств для самых основных вопросов, которые можно задать: существуют ли решения и являются ли они уникальными? Зачем требовать доказательства? Потому что доказательство дает не только уверенность, но и доказательство дает понимание.

5. Гипотеза Ходжа

Гипотеза Ходжа, ответ на которую определяет, какая часть топологии множества решений системы алгебраических уравнений может быть определена в терминах дальнейших алгебраических уравнений. Гипотеза Ходжа проявляется в некоторых частных случаях, например, когда размерность множества решений меньше четырех. Но в четвертом измерении это неизвестно.

Эта гипотеза также известна как утверждение о геометрических фигурах, вырезанных полиномиальными уравнениями над комплексными числами. Они также известны как комплексные алгебраические многообразия. Чрезвычайно полезным инструментом при изучении этих многообразий было построение групп, также известных как группы когомологий, которые содержали информацию о строении многообразий.

6. Гипотеза Пуанкаре

Французский математик Анри Пуанкаре в 1904 году задался вопросом, характеризуется ли трехмерная сфера как единственное односвязное трехмерное многообразие. Гипотеза Пуанкаре известна как частный случай гипотезы геометризации Терстона. Это доказательство гипотезы Пуанкаре говорит нам, что каждое трехмерное многообразие строится из набора стандартных частей, каждая из которых имеет одну из восьми хорошо понятных геометрий.

7. Гипотеза Берча и Суиннертона-Дайера

Эта гипотеза z в основном подтверждается многими экспериментальными данными, которые связывают число точек на эллиптической кривой по модулю p с рангом группы рациональных точек.

В поисках решения проблем тысячелетия · LRB 22 июля 2004 г.

В мае 2000 г. Математический институт Клэя объявил, что предлагает семь призов по 1 миллиону долларов каждый за решение семи математических задач, которые были определены группа всемирно известных математиков как семь самых сложных и самых важных нерешенных математических проблем дня. Они стали известны как «Проблемы тысячелетия».

Объявление имело как историческое, так и математическое значение. Ровно за сто лет до этого математик Давид Гильберт прочитал лекцию, в которой он определил то, что он считал (23 в его случае) наиболее важными нерешенными математическими проблемами своего времени. Проблемы Гильберта послужили толчком для некоторых из самых продуктивных математических исследований 20-го века. К 2000 г. все они, кроме одного, были либо решены, либо продемонстрированы некоторые особенности, исключающие определенное решение. Оставшаяся проблема сохранилась как одна из проблем тысячелетия.

В своей превосходной новой книге Кит Девлин знакомит с задачами непрофессиональную аудиторию, единственной квалификацией которой должно быть «хорошее школьное знание математики» и «достаточный интерес к теме».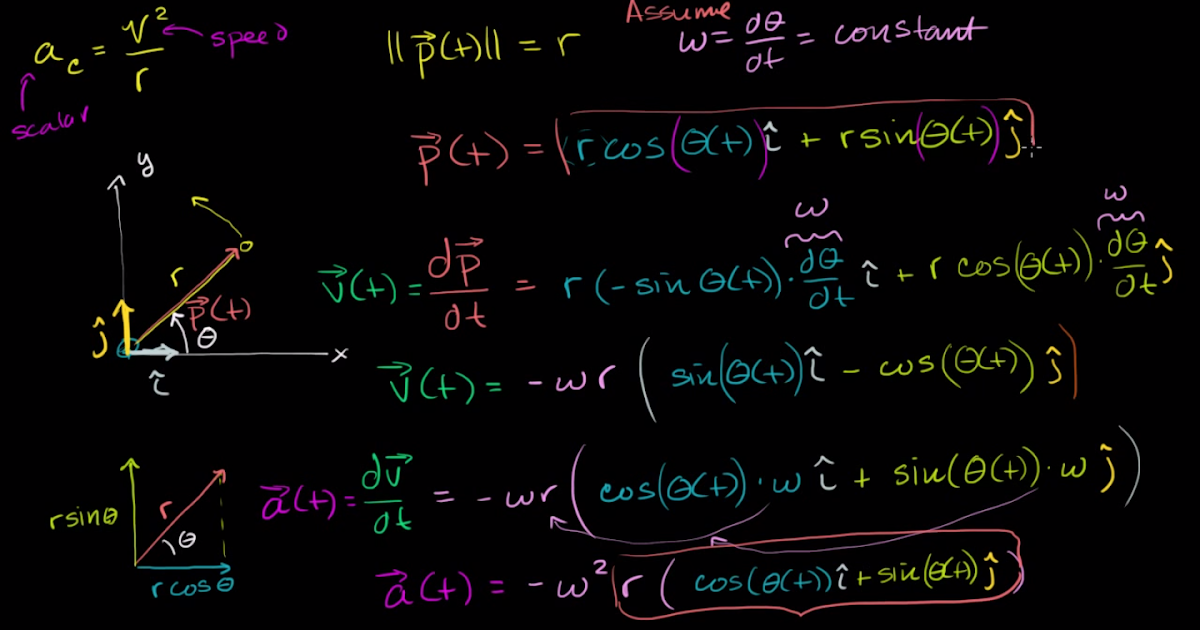 Он с самого начала ясно дает понять, что проблемы слишком глубоки и сложны, чтобы можно было сделать их полностью доступными для предполагаемой аудитории. Так, в предпоследней главе он обезоруживающе говорит: «Хотя я был профессиональным математиком более тридцати лет… . . это потребовало от меня значительных усилий, растянувшихся на несколько недель, чему способствовали обсуждения с экспертами. . . прежде чем я достаточно понял [эту] проблему, чтобы написать эту главу. Я бы даже не пытался ее решить». И в последней главе, посвященной тому, что он описывает как «наименее доступную» из проблем, он пишет: «Это очень технический вопрос, погребенный глубоко в лесу В высшей степени абстрактная передовая математика, известная немногим профессиональным математикам». Девлин стремится «предоставить предысторию каждой проблемы, описать, как она возникла, объяснить, что делает ее особенно трудной, и дать… . . какое-то понимание того, почему математики считают это важным». Ему это удается превосходно.

Первая проблема, сохранившаяся из списка Гильберта, заключается в том, верна ли гипотеза Римана. Сформулированная в 1859 году Бернхардом Риманом, гипотеза касается распределения простых чисел среди положительных целых чисел. (Простым числом является любое положительное целое число, отличное от 1, которое делится только на себя и на 1. Первые десять простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29.) Существует бесконечное число много простых чисел, но они становятся все реже и реже по мере того, как последовательность натуральных чисел расширяется все дальше и дальше. Таким образом, из первых восьми натуральных чисел половина — простые, но из первой сотни — только четверть, а из первого миллиона — только одно из тринадцати. В связи с этим возникает вопрос, можно ли сказать что-либо существенное о том, каким именно образом пропорция постепенно уменьшается. И ранний образец простых чисел, и то, что мы знаем о более поздних образцах, обескураживает. Например, промежутки между первыми десятью простыми числами равны 1, 2, 2, 4, 2, 4, 2, 4 и 6, ряду, который не демонстрирует какой-либо очевидной регулярности. Кроме того, по словам Девлина, «независимо от того, как далеко вы продвинулись по [целым положительным числам], вы можете найти кластеры из нескольких простых чисел, близких друг к другу, а также участки сколь угодно большой длины, в которых простых чисел вообще нет». Распределение простых чисел — это часть математики, в которой ощущается наибольшая случайность: кажется, что простые числа возникают случайно, как камни, разбросанные по бесплодному ландшафту. Тем не менее, математики достигли некоторого понимания того, как уменьшается доля простых чисел. (Это понимание опирается на раздел математики, который, по-видимому, совершенно не связан с теорией натуральных чисел, а вместо этого занимается непрерывным изменением одной величины по отношению к другой.) Однако остаются существенные пробелы и доказательство того, что Верная гипотеза Римана помогла бы их восполнить. Это также может иметь последствия как для физики, так и для коммуникационных технологий.

Вторая проблема, которая может быть наиболее доступной, называется проблемой P против NP. Ученые-компьютерщики различают два типа задач, которые может выполнять компьютер. Задачи типа P можно выполнять «эффективно». Задачи типа E, напротив, требуют определенного количества непреодолимого труда: компьютер не может выполнить даже очень простую задачу типа E, не сделав больше шагов, чем атомов в известной Вселенной. Но есть и третий тип задач, тип NP, который включает в себя большинство крупных задач, которые промышленность и коммерция хотели бы, чтобы компьютеры могли выполнять. Задача типа NP может эффективно выполняться компьютером, если на определенных критических этапах, когда компьютеру требуется ответ на вопрос, он получает ответ, а не прорабатывает его самостоятельно. (Конечно, это представляет в первую очередь теоретический интерес. На практике всегда возникнет вопрос, откуда взялся ответ.) Если бы компьютер был наделен такой возможностью, значительно ли увеличился бы спектр задач, которые он мог бы эффективно решать? ? Можно было бы так подумать. Но, возможно, нет. Возможно, все задачи типа NP на самом деле относятся к типу P. То есть, возможно, эффективность, которую можно было бы извлечь из этих готовых вычисленных ответов, можно получить в любом случае из-за достаточно умного программирования. Проблема P против NP состоит в том, чтобы определить, так это или нет. Доказательство того, что это так, будет иметь последствия для промышленности, торговли и интернет-безопасности.

Третья проблема касается гипотезы Пуанкаре, выдвинутой Анри Пуанкаре в начале 20 века. Предположим, у вас есть резинка, яблоко и кольцевой пончик. Если вы натянете резинку вокруг яблока, то вы сможете сжать ее до точки, катая ее по поверхности яблока — как бы от экватора к полюсу — не порвав его и не оставив его. поверхность. Но если бы резинка была натянута вокруг поверхности пончика, то не было бы способа сжать резинку до точки вдоль поверхности пончика, не порвав ни резинку, ни сам пончик. Пуанкаре предположил, что нечто подобное происходит в четырехмерном пространстве (где идее «пространства» с более чем тремя измерениями дается подходящее математическое определение). Впоследствии математики доказали, что нечто подобное действительно происходит в пространстве с более чем четырьмя измерениями, но остается неизвестным, верна ли первоначальная гипотеза. Если вопрос будет решен, решение может иметь последствия для разработки и производства различных электронных устройств.

На этом уровне мало что можно сказать о четырех оставшихся проблемах. Один занимается теорией, описывающей взаимодействие элементарных частиц; другой, с уравнениями, описывающими движение жидкостей; другой, с гипотезой, связанной с гипотезой Римана, которая также имеет последствия в отношении простых чисел; и последнее, с другой гипотезой, относящейся к пространствам, имеющим более трех измерений.

Теперь предположим, что охотник за славой сказал вам, что он заинтересован в решении всех семи проблем одновременно. Ваша первая мысль может состоять в том, чтобы расценить это как полное безумие. Правда, некоторые проблемы, как известно, связаны. И это знакомая черта математической жизни, как часто проблемы, считавшиеся несвязанными, впоследствии оказываются таковыми. (Гипотеза Римана свидетельствует об этом.) Так что было бы безрассудно настаивать на том, что никакие достижения в математике не могут быть связаны более чем с одной из этих семи проблем. Факт остается фактом: они лежат в разных областях дисциплины и не дают никакой очевидной перспективы быть использованными для прояснения друг друга.

Тем не менее, стремление охотника за славой добиться одновременного прогресса на всех семи фронтах может быть не таким безумным, как кажется. Возможно, он надеется, что, обратив свое внимание на теорию доказательств, раздел математики, занимающийся набором приемов и методов, используемых для решения задач такого рода, он сможет найти в наборе инструментов математиков что-то, что укажет, как продвинуться от подведение каждой из этих семи проблем к ее решению. На самом деле, у него могла быть еще более амбициозная надежда, чем эта, — найти святой Грааль всей математики: единый алгоритм для решения любой заданной математической задачи; другими словами, единая процедура, которой можно было следовать строго шаг за шагом, которая не требовала ни проницательности, ни изобретательности и которая гарантированно за конечное число шагов приводила к решению рассматриваемой проблемы. . Очевидно ли, что это была бы безнадежная надежда?

Нет. Но даже в этом случае это будет заброшено. И то, что это было бы так, само по себе является очень глубоким фактом о математике. Существуют фундаментальные принципиальные причины, согласно которым, когда дело доходит до решения математических вопросов, оставшихся без ответа, мы никогда не сможем отказаться от гадания и вдохновения в пользу механического применения правил. (Но даже если бы Святой Грааль существовал и даже если бы мы его нашли, он мог бы представлять чисто теоретический интерес. Его реализация при решении той или иной задачи могла бы быть задачей типа Е. Какое практическое значение имел бы алгоритм? было бы, если бы оно позволило нам определить, верна ли гипотеза Римана, но только если бы мы были в состоянии потратить на решение проблемы в триллион раз больше времени, чем потребуется, чтобы Земля была поглощена солнцем? )

Чтобы понять, почему не может быть единого алгоритма для решения всех математических задач, нам нужно обратиться к двум определениям и принять две вещи как должное. (Не потому, что они являются символами веры: каждое из них может быть доказано. Просто доказать их в этих пределах невозможно. Так уж вышло, что каждое из них достаточно правдоподобно и без доказательства.)

Первое определение это. Набор положительных целых чисел равен арифметическому , если его можно охарактеризовать с помощью таких стандартных арифметических терминов, как «плюс» и «умножение». Таким образом, множество простых чисел является арифметическим. Так же и набор квадратов. То же самое относится и к множеству положительных целых чисел, меньших 1. (Конечно, это последнее множество не имеет членов: это «пустое» множество.)

Второе определение таково. Множество положительных целых чисел является разрешимым , если существует алгоритм для определения того, принадлежит ли ему какое-либо данное положительное целое число. Все три набора, упомянутые выше, снова могут служить примерами. Это может привести нас к предположению, что множество положительных целых чисел является арифметическим тогда и только тогда, когда оно разрешимо.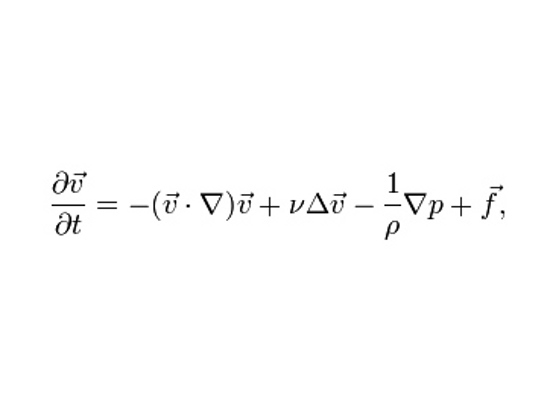 Но предположение было бы опрометчивым. Пока еще нет никаких оснований для исключения арифметического множества, которое не является разрешимым, или для исключения разрешимого множества, которое не является арифметическим.

Это подводит нас к первой из двух вещей, которые мы должны принять как должное, — назовем ее леммой 1. Лемма 1 состоит в том, что вторую из них можно на самом деле исключить: другими словами, каждое разрешимое множество является арифметическим.

Лемма 2 состоит в том, что существует алгоритмический способ перечисления всех арифметических множеств. Грубо говоря, набор с наименее сложной характеристикой указывается первым, набор со второй наименее сложной характеристикой — вторым и так далее. Однако единого способа измерения сложности не существует. Одним из очевидных критериев является количество символов, участвующих в характеристике, но для этого все же требуется какой-то способ различения характеристик, включающих одинаковое количество символов. В различных точках приходится принимать произвольные решения. Все, что имеет значение, что касается леммы 2, это то, что существует алгоритм, который позволяет нам, при задании любого положительного целого числа, определить, какое множество появляется в этой позиции в списке, и при задании любого арифметического множества — или более именно, когда дана какая-либо характеристика арифметического множества — определить, в какой позиции в списке появляется это множество, охарактеризованное таким образом. Поскольку наборы могут иметь более одной характеристики — например, множество, кратное 9также является набором положительных целых чисел, цифры которых в десятичной записи в сумме кратны 9 — они также могут появляться более чем в одной позиции в списке.

Лемму 2 можно использовать для задания множества положительных целых чисел, не являющихся арифметическими. Предположим, что у нас есть алгоритмический список всех арифметических множеств. И скажем, что натуральное число несовместимо с , когда оно не принадлежит соответствующему ему множеству. (Для иллюстрации предположим, что множество, указанное под номером 243, — это множество квадратов. Тогда число 243, которое не является квадратом, несовместимо. И предположим, что множество, указанное под номером 811, — это множество простых чисел. , не нелепо.) Пусть теперь S — множество несовместимых положительных целых чисел. Тогда S не является арифметическим. Ибо если бы это было так, то оно появилось бы в какой-то позиции и в списке. Но тогда для i несоответствие означало бы, что оно не принадлежит S. Это означает, что i принадлежало бы S тогда и только тогда, когда оно не принадлежало бы S . И это, очевидно, было бы противоречием.

Теперь предположим, что существует единый алгоритм решения всех математических задач. Затем, среди прочего, этот алгоритм можно было бы использовать для определения того, принадлежит ли любое данное натуральное число любому заданному арифметическому набору. Например, его можно использовать для определения того, является ли 809принадлежит множеству простых чисел; и его можно использовать, чтобы определить, принадлежит ли 2 множеству положительных целых чисел, которые точно делят другое число, не являющееся суммой двух простых чисел. (Ответ в первом случае был бы утвердительным; каким был бы ответ во втором случае, в настоящее время неизвестно.) Это, в свою очередь, означает, что алгоритм можно использовать для определения того, принадлежит ли любое заданное положительное целое число S . Ведь мы могли бы сначала определить, какое множество соответствует целому числу, затем использовать алгоритм, чтобы определить, принадлежит ли целое число этому множеству, а затем вынести противоположный вердикт о том, принадлежит ли целое число 9.0248 С . Таким образом, по определению S разрешимо. Следовательно, по лемме 1 S также будет арифметическим. Но мы только что доказали, что S не является арифметическим. Единственный возможный вывод состоит в том, что единого алгоритма решения всех математических задач все-таки не существует.

Это блокирует один конкретный путь к получению всех семи миллионов долларов. Кажется, нет другой альтернативы, кроме как вернуться к каждой из семи разных чертежных досок.