Иррациональные числа в других системах счисления : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| zm_sansan |
| ||
26/08/12 |
| ||
| |||
| migmit |
| |||
10/08/09 |
| |||
| ||||
| |
| ||
26/08/12 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| zm_sansan |
| ||
26/08/12 |
| ||
| |||
| Xaositect |
| |||
|
| |||
| ||||
| Urnwestek |
| ||
03/10/13 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| Neos |
| ||
246 |
| ||
| |||
| zm_sansan |
| ||
26/08/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Билет 4 Определение иррационального числаИррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби , где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа . Множество иррациональных чисел обычно обозначается заглавной латинской буквой «i» в полужирном начертании без заливки — . Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел. Если множество
рациональных чисел дополнить множеством
иррациональных чисел, то вместе они
оставят множество действительных чисел.
Множество действительных чисел обычно
обозначают буквой R; используют также
символическую запись (-∞, +∞) или (-∞,
∞). Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа. Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное соответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая. Вдумайтесь
в этот термин: не кажется ли он вам
противоестественным? Ведь число —
объект алгебры, а прямая — объект
геометрии. Нет ли тут «смешения жанров»?
Нет, все логично, все продумано. Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности. Рассмотрим
пример. Дана координатная прямая, на ее
единичном отрезке построен квадрат
(рис. 100), диагональ квадрата OB отложена
на координатной прямой от точки О вправо,
получилась точка D. Чему равна координата
точки D? Она равна длине диагонали
квадрата, т. е. . Это число, как мы теперь
знаем, не целое и не дробь. Значит, ни в
5-м, ни в 6-м, ни в 7-м классе координату
точки D вы бы найти не смогли. Потому мы
до сих пор и говорили «координатная
прямая», а не «числовая прямая». Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать любые допустимые действительные значения. Например, в тождестве в роли a и b могут выступать любые числа, не обязательно рациональные. Этим мы уже пользовались в конце предыдущего урока. Этим же мы пользовались и в уроке 18 «Преобразование выражений, содержащих операцию извлечения квадратного корня»— в частности, в примерах 6, 7, 8 из этого урока. Для действительных чисел a, b, c выполняются привычные законы: и т.д. Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число; произведение (частное) двух отрицательных чисел — положительное число; произведение
(частное) положительного и отрицательного
числа — отрицательное число. Действительные числа можно сравнивать друг с другом, используя следующее определение. Определение. Говорят, что действительное число a больше (меньше) действительного числа b, если их разность а — b — положительное (отрицательное) число. Пишут a > b (a < b). Из этого определения следует, что всякое положительное число a больше нуля (поскольку разность a — 0 = a — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b — 0 = b — отрицательное число). Итак, a > 0 означает, что a — положительное число; a < 0 означает, что a — отрицательное число; a > b означает, что a — b — положительное число, т. е. a — b > 0; a < b означает, что a — b — отрицательное число, т.е. a — b < 0. Наряду со знаками строгих неравенств (>, <) используют знаки нестрогих неравенств:
a-b>=0 a<=b означает, что a меньше или равно b, т. е. a — b — неположительное число, или что a не больше b; . a-b<=0 Например, для любого числа a верно неравенство ; для любых чисел a и b верно неравенство . Впрочем, для
сравнения действительных чисел
необязательно каждый раз составлять
их разность и выяснять, положительна
она или отрицательна. Можно сделать
соответствующий вывод, сравнивая записи
чисел в виде десятичных дробей.
Геометрическая модель множества
действительных чисел, т. е. числовая
прямая, делает операцию сравнения чисел
особенно наглядной: из двух чисел a, b
больше то, которое располагается на
числовой прямой правее. Иррациональные числа: Корень из двухНесложно заметить: число √2 встречается там, где речь идёт о квадратах или удвоении площади. И где же это происходит? Начнём, пожалуй, с вещей, которые ежедневно попадают нам в руки. Таких, как бумага в принтере. Формат бумаги — стандартизованный размер бумажного листа. Все страны мира, кроме Канады и США, пользуются международным стандартом ISO 216. Все форматы бумаги ISO имеют одно и то же соотношение сторон, равное 1 ÷ √2, так называемому отношению Лихтенберга (немецкий учёный Георг Лихтенберг в 1768 году первый заметил преимущества использования бумажного листа с таким отношением сторон).
Интересно следующее: поскольку отношение большей стороны к меньшей постоянно, при последовательном разрезании листа А0 на меньшие форматы левый нижний край, правый верхний и точки, в которых сходятся три разреза, согласно теореме Фалеса, будут лежать на одной прямой. Этот формат был создан в 1975 году на основе немецкого стандарта DIN 476 и отличается от него только бо́льшими допустимыми погрешностями. Базовый лист бумаги (А0) имеет площадь в 1 м² и соотношение сторон 1 ÷ √2. Все остальные размеры получаются разрезанием длинной стороны на две равные части, то есть площадь следующего листа равна половине площади предыдущего. Такое соотношение сторон сохраняется для всех последующих меньших форматов. Арифметически это связано с равенством . А именно: пусть стороны листа были x и √2x. Уменьшая вторую сторону в два раза и оставляя первую неизменной, мы уменьшаем площадь прямоугольника в два раза. Стороны стали x и . Найдём теперь отношение меньшей стороны к большей:
У фотографов тоже есть причина использовать число √2. Рассмотрим круг радиусом R. Его площадь равна πR². Если мы хотим построить круг вдвое большей площади, как вы думаете, на какое число необходимо умножить радиус? А если вдвое меньшей — на какое разделить? Опять нас ждёт встреча с числом √2.
Как это связано с фотографией? Когда мы снимаем в ручном режиме, то настраиваем фокус и экспозицию. Последняя определяется выдержкой и диафрагмой объектива — отверстием переменного радиуса, которое позволяет регулировать поток света, попадающего через объектив на плёнку или матрицу фотоаппарата. Если свет яркий, отверстие диафрагмы уменьшают, чтобы не засветить кадр. Если же света мало — пасмурный день или вообще ночное время, — отверстие диафрагмы увеличивают, иначе кадр получится слишком тёмным. Размеры диафрагмы имеют фиксированное значение: при закрытии на одно деление площадь отверстия уменьшается вдвое, ну а радиус, соответственно, в √2 раз. Делениям на шкале диафрагмы соответствуют так называемые диафрагменные числа: 2; 2,8; 4; 5,6; 8; 11; 16; 22 и так далее. Закономерность неочевидна, но на самом деле это не что иное, как приближённые значения степеней числа √2 (округлённые почему-то не по математическим законам):
Это связано с тем, что если мы хотим получить ряд кругов площадью каждый вдвое меньше предыдущего, то радиус исходного круга мы должны будем последовательно делить на √2. Поиск гармонииПифагорейцы изучали связь между гармонией природы и математикой, поэтому они искали числовые пропорции во всех окружающих явлениях. И, надо сказать, преуспели в этом. Например, выяснилось, что гармонические соотношения между нотами соответствуют определённым отношениям целых чисел (стоит ли говорить, что частоту звука можно напрямую связать с длиной струны — геометрической величиной). Число √2 как пропорциональное отношение часто встречается в архитектуре: оно есть во всех квадратах, которые только можно начертить. Поэтому корень из двух занимает почётное место в искусстве, прежде всего в архитектуре и дизайне.
В барселонском
парке Гуэль, спроектированном великим Антонио Гауди, вместо чётких прямых линий мы наблюдаем очертания различной кривизны; центральным элементом паркового ансамбля является терраса, поддерживаемая греческими колоннами. Слабость к правильному восьмиугольнику питали архитекторы разных эпох. Купол кафедрального флорентийского собора Санта-Мария-дель-Фьоре, Башня Ветров в Афинах, замок Кастель-дель-Монте на юге Италии, Капелла Карла Великого в немецком Ахене и многие другие постройки, всех не перечислить, имеют форму октагона.
Возможно, корень из двух не самое примечательное иррациональное число. Есть множество иррациональных чисел (π, экспонента е) и соотношений (например, золотое сечение), о которых можно рассказать больше интересного. Иррациональные числа презентация, доклад, проектРаботу выполнил ученик: Куликов Дмитрий Иррациональные числа-общие сведения(3-7 ) Содержание Определение Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби m/n , где m — целое число, n — натуральное число. http://gorinalw.3dn.ru/sprav/8klasse-algebra/Koll-sistematika.doc История Иррациональные числа были неявным образом восприняты индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены. Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о ее существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. Свойства Всякое вещественное число может быть записано бесконечной десятичной дробью, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями. http://image.newsru.com/pict/id/large/494379_1039170217.gif Число «пи» -это одно из множества представителей иррациональных чисел http://www.sensator.ru/images/0000/c/o/content/photo/2007/1/1169734700.26545_5326911.jpg Трансцендентность π — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Транцендентность числа π была доказана в 1882 году профессором Кенигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году. http://moikompas.ru/img/compas/2008-07-05/irrational_number_pi/29424127.jpg Соотношения Известно много формул числа π: Формула Валлиса: Ряд Лейбница: Тождество Эйлера: Т. Интегральный синус: История Впервые обозначением этого числа греческой буквой воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.История числа π шла параллельно с развитием всей математики. Некоторые авторы разделяют весь процесс на 3 периода: древний период, в течение которого π изучалось с позиции геометрии, классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке, и эра цифровых компьютеров. http://www.horoshienovosti.com.ua/images/slon/21_11.jpg Архимед, возможно, первым предложил математический способ вычисления π. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. http://upload.wikimedia.org/wikipedia/commons/thumb/e/e7/Domenico-Fetti_Archimedes_1620.jpg/200px-Domenico-Fetti_Archimedes_1620.jpg Около 265 года н. э. математик Лю Хуэй из царства Вэй предоставил простой и точный итеративный алгоритм (англ.) с любой степенью точности. Он самостоятельно провёл вычисление для 3072-угольника и получил приближённое значение для π по следующему принципу: http://www-groups.dcs.st-and.ac.uk/~history/Thumbnails/Liu_Hui.jpg Позднее Лю Хуэй придумал быстрый метод вычисления π и получил приближённое значение 3,1416 только лишь с 96-угольником, используя преимущества того факта, что разница в площади следующих друг за другом многоугольников формирует геометрическую прогрессию со знаменателем 4. http://thenews.kz/static/news/b/c/bcpIUb4T.jpg Нерешённые проблемы Неизвестно, являются ли числа π и e алгебраически независимыми. История вычисления В 1997 году Дэйвид Бэйли, Питер Боруэйн и Саймон Плуфф открыли способ (англ.) быстрого вычисления произвольной двоичной цифры числа π без вычисления предыдущих цифр, основанный на формуле Мнемонические правила
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть. Подсчитайте количество букв в каждом слове в нижеприведенных фразах (без учёта знаков препинания) и запишите эти цифры подряд — не забывая про десятичную запятую после первой цифры «3», разумеется. Получится приближенное число Пи: http://im5-tub.yandex.net/i?id=11258320-03 Если соблюдать стихотворный размер, можно довольно быстро запомнить: Дополнительные факты
Неофициальный праздник «День числа пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3. Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле http://img11.nnm.ru/c/f/d/2/5/97d0bdb2780f8e951969da99b1c_prev.jpg Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» (англ. Pi Approximation Day), так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π. http://uchitel56.rusedu.net/gallery/1409/chislo_Pi.jpg А вам слабо? 17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор Андрей Слюсарчук установил мировой рекорд, запомнив 30 миллионов знаков числа Пи, которые были напечатаны в 20 томах текста. Хочешь понастоящему развить память? Запомни и расскажи хотя бы до второго кольца!!! Удачи!!! ☺ ☺ http://s41.radikal.ru/i094/0811/7d/5ba48b5a68fc.jpg ЧИСЛО «Е» Число «е» -это еще одно число из множества представителей иррациональных чисел e — математическая константа, основание натурального логарифма, трансцендентное число. http://www.expert.ru/images/russian_reporter/2008/19/rep_49_064_1.jpg Способы определения Число e может быть определено несколькими Как сумма ряда: Как единственное число a, для которого выполняется Как единственное положительное число a, для которого верно Свойства Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция , где c — произвольная константа. http://image.newsru.com/pict/id/large/1107811_1224161687.gif Число e трансцендентно. Число e разлагается в бесконечную цепную дробь следующим образом: то есть Представление Каталана: http://ru.wikipedia.org/wiki/http://ru.wikipedia.org/wiki/Каталан,_Евгений-Шарль История Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен Константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела: Мнемоника Мнемо́ника (греч. Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Интересные факты В IPO компании Google в 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленное число представляет собой первые 10 цифр известной математической константы. http://ru.wikipedia.org/wiki/http://ru.wikipedia.org/wiki/Иррациональные_числа Скачать презентацию Теги
Не все десятичные числа являются дробями · Границы для юных умовАннотация Легенда гласит, что первый человек в Древней Греции, открывший существование чисел, которые нельзя записать в виде дробей, был выброшен за борт корабля. Спустя столетия, хотя мы регулярно используем числа, которые нельзя записать в виде дробей, те числа, которые можно записать в виде дробей, остаются мощными инструментами. В понедельник утром ваш друг Джордан подходит к вам и говорит: «Я думаю о числе от 1 до 100». Будучи хорошим игроком, вы подыгрываете и угадываете 43. «Нет, слишком мало!» Джордан заявляет. «Хорошо, как насчет 82?» ты спрашиваешь. «Слишком высоко!» Джордан отвечает. Вы продолжаете гадать. 60 это слишком мало. 76 слишком много. 70 это слишком мало. Радуясь тому, что приближаетесь, вы спрашиваете: «Как насчет 75?» «Ты понял!» Джордан отвечает, и вы с триумфом маршируете на свой первый урок. Но после урока вы снова сталкиваетесь с Джорданом, который, видимо, думает о том, как поставить вас в тупик: зачем придерживаться положительных чисел? Что, если вы также разрешите отрицательные числа? «Сейчас я думаю о числе от минус 100 до 100, — радостно говорит Джордан. Однако во время этого занятия вы поняли, что предполагали, что Джордан всегда будет выбирать целое число. Что делать, если дроби разрешены? Предположим, Джордан выбирает число от 0 до 1, например 322. Вам нужно угадать число где-то вдоль числовой строки от 0 до 1. Вы пытаетесь начать точно с середины и угадываете 12. Джордан говорит вам, что ваше предположение высокое, поэтому вы знаете, что ответ находится где-то на числовой прямой между 0 и 12.
Новая стратегия: десятичные расширения Давайте взглянем на эти числа по-другому и вместо этого будем думать о них как о десятичных дробях. Мы можем превратить дробь в десятичную, разделив числитель на знаменатель. Для первого шага деления мы спрашиваем, сколько 16 в числе 70. (На самом деле мы спрашиваем, сколько 1,6 в 7,0, но это эквивалентно на вопрос, сколько 16 в числе 70). Поскольку 16 × 4 = 64, мы пишем 4 над 0 в 7.0. Затем мы вычитаем 64 из 70 и получаем 6 оставшихся. В этом случае 6 называется остатком. Для следующего шага сбиваем очередной 0 с 7.00. Затем мы спрашиваем, сколько 16 в числе 60. Поскольку 16 × 3 = 48, мы пишем 3 над вторым 0. Затем мы вычитаем 48 из 60, чтобы получить остаток 12. Продолжаем этот процесс, опуская нули после каждого остатка и спрашивая, сколько 16 в полученном числе. После того, как мы сделали это четыре раза, мы получаем остаток 0, в котором нет 16-х. На этом мы закончили деление в длинную сторону и можем сказать, что 716=0,4375. Если вы играете в игру «угадай число», вы можете получить эту десятичную версию числа 716 за несколько коротких шагов. В таблице ниже показан возможный способ, которым это может произойти. Поскольку десятичная дробь числа 716 заканчивается, вы можете получить точное число, угадывая по одной цифре десятичной дроби за раз. Это происходит для всех дробей? Давайте посмотрим на десятичное число 322. Следуя тому же процессу деления, мы получаем 1 сверху с остатком 8, 3 сверху с остатком 14, 6 сверху с остатком 8 , 3 сверху с остатком 14 … но подождите! Мы уже видели эти остатки и знаем, что следующее сверху число — 6 с остатком снова 14. Поскольку мы продолжаем делить, два повторяющихся остатка 8 и 14 дают нам повторяющиеся 3 и 6 в десятичной записи числа 322. Это означает, что если вы попытаетесь угадать число 322 по одному десятичному знаку за раз, вы будет гадать навсегда! Рациональные числа Все числа, которые мы рассмотрели до сих пор, называются рациональными числами . Рациональное число — это любое число, которое мы можем записать в виде дроби ab двух целых чисел (целых чисел или их отрицательных чисел), a и b . Мы видели, что некоторые рациональные числа, такие как 716, имеют на конце десятичные расширения. Мы называем эти числа , заканчивая десятичными дробями . Другие рациональные числа, такие как 322, имеют десятичные расширения, которые продолжаются бесконечно. Но мы знаем, что даже десятичные расширения, которые не заканчиваются, повторяются, поэтому мы называем их повторяющимися десятичными числами . Для любого рационального числа ab единственными остатками, которые мы можем получить при вычислении десятичной дроби, являются числа 0, 1, 2, 3, …, b − 2, b − 1. Мы можем пойти в обратном направлении и заменить десятичные дроби тоже! Когда у нас есть конечное десятичное расширение, такое как 4,132, мы можем изменить его на дробь, используя разрядное значение. Двойка числа 4,132 находится в тысячном разряде, поэтому 4,132=41321000. Если мы начинаем с повторяющейся десятичной дроби, нам нужно проделать немного больше работы, чтобы найти соответствующую дробь. У нас есть 99 A = 35, поэтому, когда мы делим на 99, мы получаем A = 3599. Для любой повторяющейся десятичной дроби мы можем использовать тот же процесс, чтобы найти соответствующую дробь. Мы умножаем на 10, 100, 1000 или на то, что необходимо, чтобы переместить десятичную точку достаточно далеко, чтобы десятичные цифры выровнялись. Затем мы вычитаем и используем результат, чтобы найти соответствующую дробь. Это означает, что каждое повторяющееся десятичное число является рациональным числом! Иррациональные числа Что делать, если у нас есть десятичное расширение, которое не заканчивается, но цифры не повторяются? Например, посмотрите на 0,101001000100001…. Возвращаясь к нашей игре, все иррациональные и рациональные числа вместе заполняют нашу числовую строку от 0 до 1. Предположим, ваш друг Джордан может выбрать любое число от 0 до 1 и выбрать иррациональное число, которое вы должны угадать. Давайте изменим игру, чтобы вы могли победить! Джордан выбирает три вещи: число, которое вы должны угадать, диапазон чисел, в котором находится это число, и насколько точно должно быть ваше предположение. С этими новыми правилами Джордан выбирает число 9.0043 π и говорит вам: «Я думаю о числе от 2 до 10. Посмотрим, сможешь ли ты угадать мое число с точностью до 0,01». В этой ситуации игра могла бы выглядеть следующим образом: В этой новой версии игры, даже если Джордан изменит расстояние, на которое вам нужно угадать, вы всегда сможете в конце концов оказаться на расстоянии π . Вам просто нужно правильно указать целую часть числа и определенное количество знаков после запятой. Например, чтобы быть в пределах 0,1 от π , вам нужно только правильно указать первый десятичный разряд. Как мы видели ранее, каждое десятичное число, которое заканчивается, является рациональным числом. Если мы используем этот процесс приближения к иррациональному числу, угадывая все больше и больше знаков после запятой числа, мы можем получить рациональное число, которое будет настолько близко к нашему целевому иррациональному числу, насколько нам захочется. В нашей игре это означает, что независимо от того, какое иррациональное число выберет Джордан и насколько точно вам придется его угадывать, вы всегда сможете найти рациональное число, отвечающее требованиям. В этой игре вы всегда можете выиграть! Заключение Это происходит потому, что рациональные числа являются плотными в действительных числах. Но зачем вообще нужно приближать иррациональное число к рациональному? Предположим, вы строите деревянную раму для треугольной грядки в форме половины квадрата на рисунке 2. Вам нужно вырезать кусок дерева длиной 2 фута. Как вы измерите эту длину? Поскольку 2 — иррациональное число, вы не можете точно измерить его с помощью рулетки! Вместо этого вы выберете рациональное число, которое приблизительно равно 2. Вы можете выбрать количество десятичных цифр, которое нужно включить в ваше разложение, чтобы получить кусок дерева по длине настолько близким, насколько вы хотите, к 2, точно так же, как вы выбрали свое рациональное число.
Аппроксимация рациональными числами — очень мощный инструмент для выполнения вычислений, измерения материалов в строительстве и для многих других приложений. Тот факт, что рациональные числа плотны в вещественных числах, позволяет нам использовать этот инструмент! ГлоссарийРациональное число : ↑ Вещественное число, которое можно записать в виде дроби двух целых чисел ab. Десятичные расширения для рациональных чисел могут быть либо завершающими, либо повторяющимися десятичными знаками. Завершающее десятичное число : ↑ Десятичное расширение, которое имеет только конечное число ненулевых десятичных цифр. Например, 3,125 является завершающим десятичным числом. Повторяющееся десятичное число : ↑ Десятичное расширение, в котором цифры повторяются. Иррациональное число : ↑ Вещественное число, которое нельзя записать в виде дроби двух целых чисел ab. Десятичные расширения для иррациональных чисел — это бесконечные десятичные дроби, которые не повторяются. Плотный : ↑ Набор чисел является плотным в действительных числах, если для любых двух различных действительных чисел существует число из множества между ними. Например, целые числа не являются плотными в действительных числах, потому что между 2,1 и 2,2 нет целых чисел. Конфликт интересовАвторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Новое доказательство решает 80-летнюю проблему с иррациональными числами Большинство людей редко имеют дело с иррациональными числами — это было бы, ну, иррационально, поскольку они бесконечны, а для их точного представления требуется бесконечное количество места. Многие люди осмысливают иррациональные числа, округляя их до дробей или десятичных знаков: оценка π как 3,14, что эквивалентно 157/50, приводит к повсеместному празднованию Дня Пи 14 марта. Тем не менее, с другим приближением, 22/7, легче спорить, и оно ближе к π. Это вызывает вопрос: есть ли предел тому, насколько простыми и точными могут быть эти приближения? И можем ли мы выбрать дробь в любой форме, которую захотим? В 1941 году физик Ричард Даффин и математик Альберт Шеффер предложили простое правило для ответа на эти вопросы. Рассмотрим задачу аппроксимации различных иррациональных чисел. Обычно большие знаменатели связаны с меньшими ошибками. Если это верно и существует бесконечно много знаменателей, которые можно использовать для приближения числа с точностью до соответствующей ошибки, то, увеличивая знаменатель, приближение можно делать все лучше и лучше. Если выбранные ошибки в совокупности достаточно малы, случайно выбранное иррациональное число x будет иметь лишь ограниченное число хороших приближений: оно может попасть в промежутки между приближениями с определенными знаменателями. Но если ошибки достаточно велики, будет бесконечно много знаменателей, образующих хорошую аппроксимирующую дробь. В этом случае, если ошибки также уменьшаются по мере увеличения знаменателя, то вы можете выбрать аппроксимацию настолько точно, насколько вы хотите. Недоказано В результате либо вы можете сколь угодно точно приблизить почти каждое число, либо почти ни одно из них. «Существует поразительная дихотомия, — говорит Димитрис Кукулопулос, математик из Монреальского университета. Более того, вы можете выбирать ошибки по своему усмотрению, и пока они достаточно велики в совокупности, большинство чисел можно аппроксимировать бесконечным числом способов. Хотя кажется логичным, что небольшие ошибки затрудняют аппроксимацию чисел, Даффин и Шеффер не смогли доказать свою гипотезу, как и никто другой. Доказательство оставалось «знаковой открытой проблемой» в теории чисел, говорит Кристоф Эйстлейтнер, математик из Технологического университета Граца в Австрии, изучавший эту проблему. То есть до этого лета, когда Кукулопулос и его соавтор Джеймс Мейнард объявили о своем решении в статье, размещенной на сервере препринтов arXiv.org. Гипотеза Даффина-Шеффера «имеет волшебную простоту в области математики, которая обычно исключительно трудна и сложна», — говорит Мейнард, профессор Оксфордского университета. Он наткнулся на эту проблему случайно — он теоретик чисел, но не в той же области, что и большинство экспертов Даффин-Шеффера. (Обычно он изучает простые числа — те, которые делятся только на себя и на 1. Мейнард и Кукулопулос знали, что предыдущая работа в этой области сводила проблему к проблеме простых множителей знаменателей — простых чисел, которые при умножении дают знаменатель . Мейнард предложил рассматривать задачу как закрашивание чисел: «Представьте, что на числовой прямой раскрасьте все числа, близкие к дробям со знаменателем 100». Гипотеза Даффина-Шеффера гласит, что если ошибки достаточно велики и сделать это для каждого возможного знаменателя, то почти каждое число будет окрашено бесконечно много раз. Для любого конкретного знаменателя будет закрашена только часть числовой прямой. Если бы математики могли показать, что для каждого знаменателя закрашены достаточно разные области, они обеспечили бы закрашивание почти каждого числа. Если бы они также могли доказать, что эти участки перекрываются, они могли бы сделать вывод, что это происходило много раз. Один из способов уловить идею о разных, но перекрывающихся областях — доказать, что области, окрашенные разными знаменателями, не имеют ничего общего друг с другом — они независимы. Но на самом деле это не так, особенно если у двух знаменателей много общих простых множителей. Например, возможные знаменатели 10 и 100 делят коэффициенты 2 и 5, а числа, которые можно аппроксимировать дробями вида n/10 , обнаруживают разочаровывающие совпадения с теми, которые могут быть аппроксимированы дробями n/100 . Графическое представление задачи Мейнард и Кукулопулос решили эту головоломку, переформулировав проблему в терминах сетей, которые математики называют графами — набором точек, некоторые из которых соединены линиями (называемыми ребрами). Использование графиков позволило двум математикам по-новому визуализировать проблему. «Одно из самых важных открытий, которое вам нужно, — это забыть обо всех неважных частях проблемы и просто сосредоточиться на одном или двух факторах, которые делают ее особенной», — говорит Мейнард. Использование графиков, по его словам, «не только позволяет вам доказать результат, но и дает вам структурную информацию о том, что происходит в задаче». Мейнард и Кукулопулос пришли к выводу, что графы с множеством ребер соответствуют конкретной, строго структурированной математической ситуации, которую они могут анализировать по отдельности. Решение дуэта стало неожиданностью для многих в этой области. Другим экспертам может потребоваться несколько месяцев, чтобы понять все детали. «Теперь доказательство длинное и сложное», — говорит Эйстлейтнер. «Недостаточно просто иметь одну поразительную, блестящую идею. Есть много, много частей, которые нужно контролировать». На 44 страницах плотной технической математики даже ведущим математическим умам нужно время, чтобы окунуться в статью. Однако сообщество настроено оптимистично. Говорит Ваалер: «Это прекрасная бумага. Я думаю, это правильно». Являются ли отрицательные дроби рациональными числами? Числа – это математические значения или цифры, используемые для измерения или вычисления величин. Рациональные числа имеют форму p/q, где p и q являются целыми числами и q ≠ 0. Из-за лежащей в основе структуры чисел, формы p / q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3,-3, 4,-4, 5 и т. д. являются некоторыми примерами рациональных чисел, поскольку они могут быть представлены дробью как 3/1, 4/1 и 5/1. Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Преобразование дроби в рациональное число Чтобы преобразовать дробное число в рациональное число, выполните следующие действия: Шаг 1: Если дробь является смешанным числом, замените ее неправильной дробью. Шаг 2: Разделите числитель на знаменатель. Пример 1: 2 1/4 можно преобразовать смешанной дробью в рациональное число? Решение:
Пример 2. Преобразование 6/4 в рациональное число. Решение: Являются ли отрицательные дроби рациональными числами? Ответ: Похожие вопросы Вопрос 1: Определите, является ли -10/11…. является рациональным числом. Ответ:
Вопрос 2: Определите, является ли -8/4 рациональным или иррациональным числом. Ответ:
Вопрос 3: -5/14 является рациональным числом или нет? Ответ:
Вопрос 4: Является ли -8/13 иррациональным числом или нет? Ответ:
Вопрос 5. Является ли -7/11 иррациональным числом или нет? Ответ:
Вопрос 6: Является ли – 15/3 иррациональным числом или нет? Ответ:
Вопрос 7: Является ли – 10/4 иррациональным числом или нет? Ответ:
Определение рациональных и иррациональных чиселРезультаты обучения
Теперь еще раз взглянем на типы чисел, с которыми мы работали на всех предыдущих уроках. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа. И мы будем практиковаться в их использовании так, как будем использовать при решении уравнений и выполнении других процедур в алгебре. Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел? | ||||||||
| счет чисел | [латекс]1,2,3,4\точки [/латекс] | |||||||
| целые числа | [латекс]0,1,2,3,4\точки[/латекс] | |||||||
| целых | [латекс]\точки -3,-2,-1,0,1,2,3,4\точки [/латекс] |
Рациональные числа
Какой тип чисел вы бы получили, если бы начали со всех целых чисел, а затем включили все дроби? Числа, которые вы получили бы, образуют множество рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональные числа
Рациональное число — это число, которое можно записать в виде [латекс]{\большой\разрыв{р} {q}}[/латекс], где [латекс]р[/латекс] и [ latex]q[/latex] — целые числа, а [latex]q\ne o[/latex].
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров
Несколько примеров
[латекс]\Large\frac{4}{5}\normalsize,-\Large\frac{7}{8}\normalsize,\Large\frac{13}{4}\normalsize,\text{and} -\Large\frac{20}{3}[/latex]
Каждый числитель и каждый знаменатель являются целыми числами.
Нам нужно просмотреть все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы рассмотрим счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Являются ли целые числа рациональными числами? Чтобы решить, является ли целое число рациональным, мы пытаемся записать его как отношение двух целых чисел. Самый простой способ сделать это — записать дробь со знаменателем один.
[латекс]3=\Large\frac{3}{1}\normalsize ,\space-8=\Large\frac{-8}{1}\normalsize ,\space0=\Large\frac{0}{ 1}[/latex]
Поскольку любое целое число можно представить как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.
Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.
Как насчет десятичных знаков? Являются ли они рациональными? Давайте рассмотрим несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа являются рациональными числами. Целое число [латекс]-8[/латекс] можно записать как десятичное число [латекс]-8.0[/латекс]. Итак, ясно, что некоторые десятичные дроби рациональны.
Подумайте о десятичной дроби [латекс]7.3[/латекс]. Можем ли мы записать это как отношение двух целых чисел? Поскольку [latex]7.3[/latex] означает [latex]7\Large\frac{3}{10}[/latex], мы можем записать его в виде неправильной дроби: [latex]\Large\frac{73}{10 }[/латекс]. Итак, [латекс]7,3[/латекс] — это отношение целых чисел [латекс]73[/латекс] и [латекс]10[/латекс]. Это рациональное число.
В общем, любое десятичное число, которое заканчивается после нескольких цифр, таких как [латекс]7.3[/латекс] или [латекс]-1. 2684[/латекс], является рациональным числом. Мы можем использовать разрядное значение последней цифры в качестве знаменателя при записи десятичной дроби.
2684[/латекс], является рациональным числом. Мы можем использовать разрядное значение последней цифры в качестве знаменателя при записи десятичной дроби.
пример
Запишите каждое как отношение двух целых чисел:
1. [латекс]-15[/латекс]
2. [латекс]6.81[/латекс]
3. [латекс]-3\Large \frac{6}{7}[/latex]
Решение:
| 1. | |
| [латекс]-15[/латекс] | |
| Запишите целое число в виде дроби со знаменателем 1. | [латекс]\большой\фрак{-15}{1}[/латекс] |
| 2. | |
| [латекс]6.81[/латекс] | |
| Запишите десятичную дробь как смешанное число. | [латекс]6\большой\фрак{81}{100}[/латекс] |
| Затем преобразуйте его в неправильную дробь. | [латекс]\большой\фрак{681}{100}[/латекс] |
попробуй
Давайте посмотрим на десятичную форму известных нам рациональных чисел. Мы видели, что каждое целое число является рациональным числом, поскольку [latex]a=\Large\frac{a}{1}[/latex] для любого целого числа [latex]a[/latex]. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Целое [латекс]-2,-1,0,1,2,3[/латекс]
Десятичное число [латекс]-2.0,-1.0,0.0,1.0,2.0,3.0[/латекс]
Эти десятичные числа цифры останавливаются.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму дробей, которые мы только что рассмотрели.
Отношение целых чисел [latex]\Large\frac{4}{5}\normalsize ,\Large\frac{7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\ frac{20}{3}[/latex]
Десятичные формы [latex]0,8,-0,875,3,25,-6,666\ldots,-6. \overline{66}[/latex]
\overline{66}[/latex]
Эти десятичные дроби либо останавливаются, либо повторяются.
О чем говорят вам эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассмотрели, выраженные в виде отношения целых чисел и десятичных дробей.
| Рациональные числа | ||
|---|---|---|
| Дроби | Целые числа | |
| Номер | [латекс]\Large\frac{4}{5}\normalsize,-\Large\frac{7}{8}\normalsize,\Large\frac{13}{4}\normalsize,\Large\frac{- 20}{3}[/латекс] | [латекс]-2,-1,0,1,2,3[/латекс] |
| Отношение целого числа | [латекс]\Large\frac{4}{5}\normalsize ,\Large\frac{-7}{8}\normalsize ,\Large\frac{13}{4}\normalsize ,\Large\frac{- 20}{3}[/латекс] | [латекс]\Large\frac{-2}{1}\normalsize ,\Large\frac{-1}{1}\normalsize ,\Large\frac{0}{1}\normalsize ,\Large\frac{ 1}{1}\normalsize ,\Large\frac{2}{1}\normalsize ,\Large\frac{3}{1}[/latex] |
| Десятичное число | [латекс]0,8,-0,875,3,25,-6. \overline{6}[/латекс] \overline{6}[/латекс] | [латекс]-2.0,-1.0,0.0,1.0,2.0,3.0[/латекс] |
Иррациональные числа
Существуют ли десятичные дроби, которые не заканчиваются и не повторяются? Да. Число [латекс]\пи [/латекс] (греческая буква пи, произносится как «пирог»), очень важное для описания кругов, имеет десятичную форму, которая не заканчивается и не повторяется.
[латекс]\pi =\text{3.141592654…….}[/латекс]
Точно так же десятичные представления квадратных корней чисел, которые не являются полными квадратами, никогда не останавливаются и никогда не повторяются. Например,
[латекс]\sqrt{5}=\текст{2.236067978…..}[/латекс]
Десятичное число, которое не заканчивается и не повторяется, не может быть записано как отношение целых чисел. Мы называем такие числа иррациональными числами.
Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не прерывается и не повторяется.
Давайте обобщим метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
- останавливается или повторяется, число является рациональным.
- не останавливается и не повторяется, число иррациональное.
пример
Определите каждое из следующего как рациональное или иррациональное:
1. [латекс]0,58\overline{3}[/латекс]
2. [латекс]0,475[/латекс]
3. [латекс]3,605551275\ точки [/латекс]
Показать решение
попробуйте
Давайте теперь подумаем о квадратных корнях. Квадратные корни из полных квадратов всегда являются целыми числами, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются идеальными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.
пример
Определите каждое из следующего как рациональное или иррациональное:
1. [латекс]\sqrt{36}[/латекс]
[латекс]\sqrt{36}[/латекс]
2. [латекс]\sqrt{44}[/латекс]
Показать решение
попробуйте
В следующем видео мы покажем больше примеров того, как определить, является ли число иррациональным или рациональным.
1.3 Рациональные и иррациональные числа | Алгебраические выражения
1.3 Рациональные и иррациональные числа (EMA4)
- Рациональный номер
Рациональное число (\(\mathbb{Q}\)) — это любое число, которое можно записать как:
\[\ гидроразрыва{а}{б}\], где \(a\) и \(b\) — целые числа, а \(b \ne 0\).
Все следующие числа являются рациональными числами:
\[\frac{10}{1} \; ; \; \фракция{21}{7} \; ; \; \фракция{-1}{-3} \; ; \; \фракция{10}{20} \; ; \; \фракция{-3}{6}\] Мы видим, что все числители и все знаменатели целые числа.
Это означает, что все целые числа являются рациональными числами, потому что их можно записать со знаменателем \(\текст 1}\).
- Иррациональные числа
Иррациональные числа (\(\mathbb{Q}’\)) — это числа, которые нельзя записать в виде дроби с числитель и знаменатель как целые числа.
Примеры иррациональных чисел:
\[\sqrt{2} \; ; \; \sqrt{3} \; ; \; \sqrt[3]{4} \; ; \; \Пи \; ; \; \frac{1 + \sqrt{5}}{2}\]Это не рациональные числа, потому что либо числитель, либо знаменатель не являются целыми числами.
Десятичные числа (EMA5)
Все целые числа и дроби с целыми числителями и ненулевыми целыми знаменателями рациональны числа. Помните, что если знаменатель дроби равен нулю, то дробь не определена.
Вы можете записать любое рациональное число как десятичное число, но не все десятичные числа являются рациональными числами. Эти типы десятичных чисел являются рациональными числами:
Эти типы десятичных чисел являются рациональными числами:
Десятичные числа, которые заканчиваются (или заканчиваются). Например, дробь \(\frac{4}{10}\) может быть записывается как \(\text{0,4}\).
Десятичные числа, содержащие повторяющуюся одиночную цифру. Например, дробь \(\frac{1}{3}\) может записываться как \(\text{0,}\dot{3}\) или \(\text{0,}\overline{3}\). Обозначения с точками и штрихами эквивалентны, и оба представляют повторяющиеся символы \(\text{3}\), т. е. \(\text{0,}\dot{3} = \text{0,}\overline{3} = \text{0,333…}\).
Десятичные числа, которые имеют повторяющийся шаблон из нескольких цифр. Например, дробь \(\frac{2}{11}\) также можно записать как \(\text{0,}\overline{18}\).
 Бар представляет собой
повторяющийся шаблон \(\text{1}\) и \(\text{8}\), т. е. \(\text{0,}\overline{18} =
\text{0,181818…}\).
Бар представляет собой
повторяющийся шаблон \(\text{1}\) и \(\text{8}\), т. е. \(\text{0,}\overline{18} =
\text{0,181818…}\).
Вы можете увидеть точку вместо запятой, используемой для обозначения десятичного числа. Итак, число \(\text{0,4}\) также можно записать как 0,4
Обозначение: Вы можете использовать точку или черту над повторяющимися цифрами, чтобы указать, что decimal — повторяющееся десятичное число. Если полоса покрывает более одной цифры, то все цифры под чертой повторяются.
Если вас попросят определить, является ли число рациональным или иррациональным, сначала напишите число в
десятичная форма. Если число заканчивается, то оно рационально. Если это будет продолжаться вечно, то ищите
повторяющийся рисунок цифр. Если нет повторяющегося шаблона, то число иррациональное.
Когда вы записываете иррациональные числа в десятичной форме, вы можете продолжать записывать их для многих, многих десятичных чисел. места. Однако это не удобно и часто приходится округлять.
Округление иррационального числа делает его рациональным числом, приближающимся к иррациональному. количество.
Рабочий пример 1: Рациональные и иррациональные числа
Какие из следующих чисел не являются рациональными?
\(\pi =\text{3,14159265358979323846264338327950288419716939937510…}\)
\(\текст{1,4}\)
\(\текст{1,618033989…}\)
\(\текст{100}\)
\(\текст{1,7373737373.
 ..}\)
..}\)\(\text{0,}\overline{02}\)
Иррациональное, десятичное число не заканчивается и не имеет повторяющегося шаблона.
Рациональное, десятичное завершение.
Иррациональное, десятичное число не заканчивается и не имеет повторяющегося шаблона.
Рационально, все целые числа рациональны.
Рациональное, десятичное число повторяется.
Рациональное, десятичное число повторяется.

Преобразование конечных десятичных знаков в рациональные числа (EMA6)
Десятичное число состоит из целой и дробной частей. Например, \(\text{10,589}\) имеет целое число часть \(\text{10}\) и дробная часть \(\text{0,589}\), потому что \(10 + \text{0,589знак равно \текст{10,589}\).
Каждая цифра после запятой представляет собой дробь со знаменателем в возрастающих степенях \(\текст{10}\).
Например:
\(\text{0,1}\) равно \(\frac{1}{\text{10}}\)
\(\text{0,01}\) равно \(\frac{1}{\text{100}}\)
\(\text{0,001}\) равно \(\frac{1}{\text{1 000}}\)
Это означает, что
\начать{выравнивать*} \text{10,589} & = 10 + \frac{5}{10} + \frac{8}{100} + \frac{9}{\text{1 000}}\\ & = \frac{\text{10 000}}{\text{1 000}} + \frac{\text{500}}{\text{1 000}} + \frac{80}{\text{1 000}} + \frac{9}{\text{1 000}}\\ & = \frac{\text{10 589}}{\text{1 000}} \end{выравнивание*} Следующие два видеоролика объясняют, как преобразовать десятичные дроби в рациональные числа.
Часть 1
Видео: 2DBJ
Часть 2
Видео: 2DBK
Преобразование повторяющихся десятичных знаков в рациональные числа (EMA7)
Когда десятичная дробь является повторяющейся десятичной дробью, требуется немного больше усилий для записи дробной части числа. десятичное число как дробь.
Рабочий пример 2: Преобразование десятичных чисел в дроби
Запишите \(\text{0,}\dot{3}\) в виде \(\frac{a}{b}\) (где \(a\) и \(b\) — целые числа).
Определение уравнения
\[\text{Пусть } x = \text{0,33333…}\]Умножить на \(\text{10}\) с обеих сторон
\[10x = \текст{3,33333…}\]Вычесть первое уравнение из второго уравнения
\[9x = 3\]Упрощение
\[x = \frac{3}{9} = \frac{1}{3}\] температура текстРабочий пример 3: Преобразование десятичных чисел в дроби
Запишите \(\text{5,}\dot{4}\dot{3}\dot{2}\) в виде рациональной дроби.
Определение уравнения
\[х=\текст{5,432432432…}\]Умножить на \(\text{1 000}\) с обеих сторон
\[\text{1 000}x=\text{5 432,432432432…}\]Вычесть первое уравнение из второго уравнения
\[\text{999}x = \text{5 427}\]Упрощение
\[x = \frac{\text{5 427}}{\text{999}} = \frac{\text{201}}{\text{37}} = \text{5}\frac{\text{16}}{\text{37}}\] температура текстВ первом примере десятичная дробь умножалась на \(\text{10}\), а во втором десятичная дробь было умножено на \(\text{1 000}\). Это потому, что повторялась только одна цифра (т. \(\text{3}\)) в первом примере, в то время как в второй пример.
В общем, если у вас повторяется одна цифра, умножьте на \(\text{10}\). Если у вас две цифры
повторяющиеся, затем умножьте на \(\text{100}\). Если у вас есть повторяющиеся три цифры, то умножьте на
\(\text{1 000}\) и т. д.
Если у вас две цифры
повторяющиеся, затем умножьте на \(\text{100}\). Если у вас есть повторяющиеся три цифры, то умножьте на
\(\text{1 000}\) и т. д.
Не все десятичные числа можно записать как рациональные числа. Почему? Иррациональные десятичные числа, такие как \(\sqrt{2}=\text{1,4142135…}\) нельзя записать с целым числителем и знаменателем, потому что у них нет шаблона повторяющихся цифр, и они не заканчиваются.
Учебник Упражнение 1.1
Где на диаграмме место числа \(-\frac{12}{3}\)?
Сначала упростим дробь: \(-\frac{12}{3} = -4\)
\(-\text{4}\) является целым числом, поэтому оно попадает в множество \(\mathbb{ Z}\).
В следующем списке есть два ложных утверждения и одно верное утверждение. Который из утверждений верно ?
- Каждое целое число является натуральным.

- Каждое натуральное число является целым числом.
- В целых числах нет десятичных знаков.
Внимательно рассмотрите каждый вариант:
- Существуют целые числа, не попадающие в натуральные числа (все отрицательные номера), так что это неверно.
- Натуральные числа равны \(\left\{1; 2; 3; \ldots\right\}\), а целые числа \(\left\{0; 1; 2; 3; \ldots\right\}\) (круг \(\mathbb{N}\) находится внутри \(\mathbb{N}_{0}\)) поэтому, если число является натуральным числом, оно должно быть целым количество. Это верно.
- Целые числа \(\left\{0; 1; 2; 3; \ldots\right\}\) увеличиваются только с шагом 1, поэтому
в целых числах не может быть десятичных чисел, что делает это ложным.

Итак, верно только (ii).
Где на диаграмме место числа \(- \frac{1}{2}\)?
\(- \frac{1}{2}\) находится в простейшей форме, поэтому не находится в \(\mathbb{N}\), \(\mathbb{N}_0\) или \(\mathbb{Z}\). находится в пространстве между прямоугольником и \(\mathbb{Z}\).
В следующем списке есть два ложных утверждения и одно верное утверждение. Который заявлений правда ?
- Каждое целое число является натуральным.
- Каждое целое число является целым числом.
- В целых числах нет десятичных знаков.
Внимательно рассмотрите каждый вариант:
- Существуют целые числа, не попадающие в натуральные числа (все отрицательные
номера), так что это неверно.

- Целые числа равны \(\left\{\ldots; -3; -2; -1; 0; 1; 2; 3; \ldots\right\}\) и все числа равны \(\left\{0; 1; 2; 3; \ldots\right\}\) (круг \(\mathbb{Z}\) находится внутри \(\mathbb{N}_{0}\)) поэтому, если число является целым, оно должно быть целым числом. Это верно.
- Целые числа \(\left\{0; 1; 2; 3; 4; \ldots \right\}\) возрастают только шагами 1, поэтому в целых числах не может быть десятичных чисел, что делает ЛОЖЬ.
Итак, верно только (ii).
\(-\sqrt{3}\)
\(-\sqrt{3}\) не имеет знака минус под квадратным корнем (минус вне корня) и на ноль не делится, значит, оно реально.
\(\dfrac{0}{\sqrt{2}}\)
\(\dfrac{0}{\sqrt{2}}\) не имеет знака минус под корнем квадратным (минус снаружи
корень) и на ноль не делится, значит, оно вещественное.
\(\sqrt{-9}\)
\(\sqrt{-9}\) имеет знак минус под квадратным корнем, поэтому оно не является реальным.
\(\dfrac{-\sqrt{7}}{0}\)
\(\dfrac{-\sqrt{7}}{0}\) имеет деление на ноль, поэтому оно не определено.
\(-\sqrt{-16}\)
\(-\sqrt{-16}\) имеет отрицательное число под квадратным корнем, поэтому оно не является действительным.
\(\sqrt{2}\)
\(\sqrt{2}\) не имеет минуса под корнем квадратным (минус вне корня), есть не делится на ноль, значит, оно действительно.
\(-\frac{1}{3}\)
\(-\frac{1}{3}\) рационально. Доля целых чисел является рациональным числом.
\(\text{0,651268962154862…}\)
\(\text{0,651268962154862…}\) иррационально. Его нельзя упростить до дроби целых чисел.
\(\dfrac{\sqrt{9}}{3}\)
\(\dfrac{\sqrt{9}}{3}\) является рациональным, целым, целым числом и натуральным числом.
Целое число является рациональным числом. 97\) рационально, целое число, целое число и
натуральное число. Его можно записать как целое число.
97\) рационально, целое число, целое число и
натуральное число. Его можно записать как целое число.
\(\pi + 3\)
\(\pi\) иррационально. \(\text{3}\) рационально (это целое число). Любое рациональное число, добавленное к любому иррациональному числу, является иррациональным.
Следовательно, \(\pi + 3\) иррационально.
\(\pi + \text{0,858408346}\)
\(\pi\) иррационально. \(\text{0,858408346}\) рационально (это завершающий десятичный). Любое рациональное число, добавленное к любому иррациональному числу, является иррациональным.
Следовательно, \(\pi + \text{0,858408346}\) иррационально.
\(\dfrac{5}{6}\)
\(\frac{5}{6}\) рационально.
\(\dfrac{a}{3}\)
Поскольку \(a\) является целым числом, \(\frac{a}{3}\) рационально.
\(\dfrac{-2}{b}\)
Поскольку \(b\) является целым числом, \(\frac{-2}{b}\) рационально.
Обратите внимание, что \(b\) не может быть \(\text{0}\), так как это делает дробь неопределенной.
\(\dfrac{1}{c}\)
Поскольку \(c\) иррационально, \(\frac{1}{c}\) иррационально.
\(\text{1}\)
\(\frac{a}{14} = \frac{1}{14}\) рационально.
\(-\text{10}\)
\(\frac{a}{14} = \frac{-10}{14}\) рационально.
\(\sqrt{2}\)
\(\frac{a}{14} = \frac{\sqrt{2}}{14}\) иррационально.
\(\text{2,1}\)
\(\frac{a}{14} = \frac{\text{2,1}}{14}\) рационально.
натуральные числа
Проверить, какие числа входят в набор \(\left\{1; 2; 3; 4;\ldots\right\}\). Поэтому \(\text{7}\) и \(\text{11}\) — натуральные числа.
иррациональные числа
Помните, что рациональные числа можно записать как \(\frac{a}{b}\), где \(a\) и
\(b\) являются целыми числами. Также помните, что рациональные числа включают в себя завершающие десятичные дроби. числа. Поэтому \(-\sqrt{8} \; ; \; \text{3,3231089…} \; ; \; 3+\sqrt{2} \; ;
\; \pi\) все иррациональны.
числа. Поэтому \(-\sqrt{8} \; ; \; \text{3,3231089…} \; ; \; 3+\sqrt{2} \; ;
\; \pi\) все иррациональны.
недействительные числа
Любое число, являющееся квадратным корнем из отрицательного числа, является недействительным. Поэтому только \(\sqrt{-1}\) ненастоящий.
рациональные числа
Помните, что рациональные числа можно записать в виде \(\frac{a}{b}\), где \(a\) и \(b\) являются целыми числами. Также помните, что рациональные числа включают в себя завершающие десятичные дроби. числа. Поэтому \(-3 \; ; \; 0 \; ; \; -8\frac{4}{5} \; ; \; \frac{22}{7} \; ; \; 7\; ; \; \text{1,}\overline{34} \; ; \; 9\разрыв{7}{10} \; ; \; 11\) все рациональны числа.
целых чисел
Проверить, какие числа входят в набор \(\left\{\ldots; -3; -2; -1; 0; 1; 2;
3;\ldots\справа\}\). Следовательно, \(-3 \; ; \; 7 \; ; \; 11\) — целые числа.
Следовательно, \(-3 \; ; \; 7 \; ; \; 11\) — целые числа.
undefined
Любая дробь, разделенная на \(\text{0}\), не определена. Поэтому только \(\frac{14}{0}\) неопределенный.
\(\text{1,1}\dot{5}\)
\(\text{2,121314…}\)
Номер не завершается (обозначается символом \(\ldots\)). Есть также нет указания на повторяющийся рисунок цифр, поскольку нет точки или черту над любым из чисел. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя это выглядит так, будто в цифрах есть закономерность, которую мы не знаем если эта схема продолжится.
Иррационально, нет повторяющегося шаблона.

\(\text{1,242244246…}\)
Номер не завершается (обозначается символом \(\ldots\)). Есть также нет указания на повторяющийся рисунок цифр, поскольку нет точки или черту над любым из чисел. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя это выглядит так, будто в цифрах есть закономерность, которую мы не знаем если эта схема продолжится.
Иррационально, нет повторяющегося шаблона.
\(\text{3,324354. ..}\)
..}\)
Номер не завершается (обозначается символом \(\ldots\)). Есть также нет указания на повторяющийся рисунок цифр, поскольку нет точки или черту над любым из чисел. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя это выглядит так, будто в цифрах есть закономерность, которую мы не знаем если эта схема продолжится.
Иррационально, нет повторяющегося шаблона.
\(\text{3,3243}\dot{5}\dot{4}\)
\(\text{0,1}\)
\(\text{0,1}=\frac {1}{10}\)
\(\text{0,12}\)
\begin{align*} \text{0,12} & = \frac{1}{10} + \frac{2}{100} \\ & = \frac{10}{100} + \frac{2}{100} \\ & = \фракция{12}{100} \\ & = \фракция{3}{25} \end{выравнивание*}
\(\text{0,58}\)
\begin{align*} \text{0,58} & = \frac{5}{10} + \frac{8}{100} \\ & = \frac{50}{100} + \frac{8}{100} \\ & = \ гидроразрыв {58} {100} \\ & = \фракция{29}{50} \end{выравнивание*}
\(\text{0,2589}\)
\begin{выравнивание*} \text{0,2589} & = \frac{2}{10} + \frac{5}{100} + \frac{8}{\text{1 000}} + \фракция{9}{\текст{10 000}} \\ & = \frac{\text{2 000}}{\text{10 000}} + \frac{500}{\text{10 000}} + \frac{80}{\text{10 000}} + \frac{9}{\text{10 000}} \\ & = \frac{\text{2 589}}{\text{10 000}} \end{align*}
\(\text{0,1111111. ..}\)
..}\)
Мы видим, что повторяется только цифра \(\text{1}\), поэтому мы можем записать это как: \(\текст{0,}\точка{1}\).
\(\text{0,1212121212…}\)
Существует повторяющийся шаблон \(\text{12}\), поэтому мы можем записать это число как: \(\text{0,}\overline{12}\)
\(\text{0,123123123123…}\)
Существует повторяющийся шаблон \(\text{123}\) и т.д. мы можем записать это число как: \(\text{0,}\overline{123}\)
\(\text{0,11414541454145…}\)
Шаблон 4145 повторяется, поэтому мы можем записать это число как: \(\text{0,11}\overline{4145}\). 9{25}\текст{00}} &= \текст{5} \text{ остаток } \text{25} \\ \frac{\text{25}}{\text{45}} &= \text{0,}\text{5 555} \ldots \\ &= \текст{0,}\точка{\текст{5}} \end{align*}
\(\dfrac{\text{10}}{\text{18}}\)
\begin{align*} \text{18}|\overline{\text{10,0000}} &= \text{0} \text{остаток} \text{10} \\ \text{18}|\overline{\text{10,}^{10}\text{0 000}} &= \text{5} \text{остаток} \текст{10} \\ \text{18}|\overline{\text{10,}^{10}\text{0}^{10}\text{000}} &= \text{5} \text{ остаток } \text{10} \\ \text{18}|\overline{\text{10,}^{10}\text{0}^{10}\text{0}^{10}\text{00}} &= \text{5} \text{ остаток } \text{10} \\ \frac{\text{10}}{\text{18}} &= \text{0,}\text{5 555} \ldots \\ &= \текст{0,}\точка{\текст{5}} \end{выравнивание*} 97\текст{00}} &= \текст{2} \текст{ остаток } \text{4} \\ \frac{\text{7}}{\text{33}} &= \text{0,}\text{2 121} \ldots \\ &= \text{0,}\dot{\text{2}}\dot{\text{1}} \end{align*}
\(\dfrac{2}{3}\)
\begin{align*}
\frac{2}{3} &= 2\left(\frac{1}{3}\right) \\
&= 2(\текст{0,333333. ..}) \\
&= \текст{0,666666…} \\
&= \текст{0,}\точка{6}
\end{выравнивание*}
..}) \\
&= \текст{0,666666…} \\
&= \текст{0,}\точка{6}
\end{выравнивание*}
\(1\dfrac{3}{11}\)
\begin{align*} 1\frac{3}{11} &= 1 + 3\left(\frac{1}{11}\right) \\ &= 1 + 3(\text{0,0
…})\\ &= 1 + \text{0,27272727…} \\ &= \text{1,}\overline{27} \end{align*}
\(4\dfrac{5}{6}\)
\begin{align*} 4\frac{5}{6} &= 4 + 5\left(\frac{1}{6}\right) \\ &= 4+ 5(\text{0,1666666…}) \\ &= 4 + \text{0,833333…} \\ & = \текст{4,8}\точка{3} \end{выравнивание*}
\(2\dfrac{1}{9}\)
\begin{align*}
2\frac{1}{9} &= 2 + \text{0,1111111. ..} \\
& = \текст{2,}\точка{1}
\end{align*}
..} \\
& = \текст{2,}\точка{1}
\end{align*}
\(\text{0,}\dot{5}\)
\begin{align*} х&=\текст{0,55555…} \текст{ и} \\ 10x &= \text{5,55555…} \\ 10x — x &= (\text{5,55555…}) — (\text{0,55555…}) \\ \текст{9}x &= \text{5} \\ \поэтому x&=\frac{5}{9} \end{align*}
\(\text{0,6}\dot{3}\)
\begin{align*} 10x &= \text{6,3333…} \text{ и}\\ 100x &= \text{63,3333…} \\ 100x — 10x &= (\text{63,3333…}) — (\text{6,3333…}) \\ \text{99}x &= \text{57} \\ \поэтому x&=\frac{57}{90} \end{align*}
\(\text{0,}\dot{4}\)
\begin{align*}
х & = \текст{0,4444. ..} \текст{ и} \\
\text{10}x & = \text{4,4444…} \\
10x — x &= (\text{4,4444…}) — (\text{0,4444…}) \\
\text{9}x &= \text{4} \\
\следовательно, x & = \frac{\text{4}}{\text{9}}
\end{выравнивание*}
..} \текст{ и} \\
\text{10}x & = \text{4,4444…} \\
10x — x &= (\text{4,4444…}) — (\text{0,4444…}) \\
\text{9}x &= \text{4} \\
\следовательно, x & = \frac{\text{4}}{\text{9}}
\end{выравнивание*}
\(\text{5,}\overline{31}\)
\begin{align*} х &= \текст{5,313131…} \текст{ и} \\ 100x & = \text{531,313131…}\\ 100x — x &= (\text{531,313131…}) — (\text{5,313131…}) \\ \текст{99}х &= \текст{526} \\ \поэтому x&=\frac{526}{99} \end{align*}
\(\text{4,}\overline{\text{93}}\)
\begin{выравнивание*}
х &= \текст{4,939393…} \текст{ и} \\
100x &= \text{493,939393. ..} \\
100x — x &= (\text{493,939393…}) — (\text{4,939393…}) \\
\текст{99}х &= \текст{489} \\
\следовательно, x &= \frac{\text{163}}{\text{33}}
\end{align*}
..} \\
100x — x &= (\text{493,939393…}) — (\text{4,939393…}) \\
\текст{99}х &= \текст{489} \\
\следовательно, x &= \frac{\text{163}}{\text{33}}
\end{align*}
\(\text{3,}\overline{\text{93}}\)
\begin{выравнивание*} х &= \текст{3,939393…} \текст{ и} \\ 100x &= \text{393,939393…} \\ 100x — x &= (\text{393,939393…}) — (\text{3,939393…}) \\ \текст{99}х &= \текст{390} \\ \следовательно, x &= \frac{\text{130}}{\text{33}} \конец{выравнивание*}
Представление рациональных чисел дробями Python — Real Python
Модуль дробей в Python, возможно, является одним из наиболее недоиспользуемых элементов стандартной библиотеки. Несмотря на то, что он может быть малоизвестным, это полезный инструмент, который стоит иметь под рукой, потому что он может помочь устранить недостатки арифметики с плавающей запятой в двоичном формате. Это важно, если вы планируете работать с финансовыми данными или если вам требуется бесконечная точность для расчетов.
Несмотря на то, что он может быть малоизвестным, это полезный инструмент, который стоит иметь под рукой, потому что он может помочь устранить недостатки арифметики с плавающей запятой в двоичном формате. Это важно, если вы планируете работать с финансовыми данными или если вам требуется бесконечная точность для расчетов.
В конце этого урока вы увидите несколько практических примеров, в которых дроби являются наиболее подходящим и элегантным выбором. Вы также узнаете об их слабостях и о том, как наилучшим образом их использовать.
В этом уроке вы узнаете, как:
- Преобразовывать между десятичной и дробной записью
- Выполнение арифметики рациональных чисел
- Приблизительные иррациональные числа
- Точное представление дробей с бесконечной точностью
- Знать, когда выбрать
Дробная частьвместоДесятичнаяилиПлавающая
Большая часть этого руководства проходит через Fractions , который сам по себе не требует глубоких знаний Python, кроме понимания его числовых типов. Однако вам будет удобно работать со всеми приведенными ниже примерами кода, если вы знакомы с более сложными концепциями, такими как встроенный в Python модуль
Однако вам будет удобно работать со всеми приведенными ниже примерами кода, если вы знакомы с более сложными концепциями, такими как встроенный в Python модуль collections , модуль itertools и генераторы. Вы уже должны быть знакомы с этими темами, если хотите извлечь максимальную пользу из этого руководства.
Бесплатный бонус: 5 Thoughts On Python Mastery — бесплатный курс для Python-разработчиков, который показывает вам дорожную карту и образ мышления, который вам понадобится, чтобы вывести свои навыки Python на новый уровень.
Десятичное и дробное представление
Давайте пройдемся по закоулкам памяти, чтобы вернуть ваши школьные знания о числах и избежать возможной путаницы. Здесь задействованы четыре концепции:
- Типы чисел в математике
- Системы счисления
- Обозначения чисел
- Числовые типы данных в Python
Теперь вы получите краткий обзор каждого из них, чтобы лучше понять назначение типа данных Fraction в Python.
Удалить рекламу
Классификация номеров
Если вы не помните классификацию чисел, вот краткое напоминание:
Типы чиселВ математике существует гораздо больше типов чисел, но эти наиболее актуальны в повседневной жизни. В самом верху вы найдете комплексные числа, которые включают мнимые и действительные числа. Действительные числа, в свою очередь, состоят из рациональных и иррациональных чисел. Наконец, рациональные числа содержат целые и натуральные числа.
Системы счисления и обозначения
На протяжении веков существовали различные системы визуального представления чисел. Сегодня большинство людей используют позиционную систему счисления, основанную на индийско-арабских символах. Вы можете выбрать любое основание или систему счисления для такой системы. Однако, в то время как люди предпочитают десятичную систему (основание 10), компьютеры лучше всего работают в двоичной системе (основание 2).
Внутри самой десятичной системы вы можете представлять некоторые числа, используя альтернативные обозначения:
- Десятичный: 0,75
- Дробный: ¾
Ни один из них не лучше и не точнее другого. Выражение числа в десятичной системе счисления, возможно, более интуитивно понятно, потому что оно напоминает процент. Сравнение десятичных дробей также более просто, поскольку у них уже есть общий знаменатель — основа системы. Наконец, десятичные числа могут сообщать о точности, сохраняя конечные и начальные нули.
С другой стороны, дроби удобнее выполнять символическая алгебра вручную, поэтому они в основном используются в школе. Но можете ли вы вспомнить, когда в последний раз использовали дроби? Если вы не можете, то это потому, что в наши дни десятичная система счисления занимает центральное место в калькуляторах и компьютерах.
Дробная запись обычно связана только с рациональными числами . В конце концов, само определение рационального числа гласит, что вы можете выразить его как частное или дробь двух целых чисел, если знаменатель отличен от нуля. Однако это еще не все, если учесть бесконечные цепные дроби, которые могут аппроксимировать иррациональные числа:
В конце концов, само определение рационального числа гласит, что вы можете выразить его как частное или дробь двух целых чисел, если знаменатель отличен от нуля. Однако это еще не все, если учесть бесконечные цепные дроби, которые могут аппроксимировать иррациональные числа:
Иррациональные числа всегда имеют бесконечное и неповторяющееся десятичное расширение. Например, в десятичной записи числа пи (π) никогда не заканчиваются цифры, которые кажутся случайными. Если бы вы построили их гистограмму, то каждая цифра имела бы примерно одинаковую частоту.
С другой стороны, большинство рациональных чисел имеют конечное десятичное расширение. Однако некоторые могут иметь бесконечное повторяющееся десятичное расширение с одной или несколькими цифрами, повторяющимися в течение периода. Повторяющиеся цифры обычно обозначаются многоточием (0,33333…) в десятичной системе счисления. Независимо от их десятичной записи, рациональные числа, такие как число, представляющее одну треть, всегда выглядят элегантно и компактно в дробной записи.
Числовые типы данных в Python
Числа с бесконечным десятичным расширением вызывают ошибки округления при сохранении в виде данных с плавающей запятой в памяти компьютера, которая сама по себе конечна. Что еще хуже, часто невозможно точно представить числа с , заканчивающимся десятичным расширением , в двоичном формате!
Это известно как ошибка представления с плавающей запятой, которая затрагивает все языки программирования, включая Python. С этой проблемой рано или поздно сталкивается каждый программист. Например, вы не можете использовать с плавающей запятой в таких приложениях, как банковское дело, где числа должны храниться и действовать без потери точности.
Python Fraction — одно из решений этих препятствий. Хотя оно представляет рациональное число , имя Rational уже представляет абстрактный базовый класс в модуле чисел . Модуль чисел определяет иерархию абстрактных числовых типов данных для моделирования классификации чисел в математике:
Fraction является прямым и конкретным подклассом Rational , который обеспечивает полную реализацию рациональных чисел в Python. Целочисленные типы, такие как
Целочисленные типы, такие как int и bool , также являются производными от Rational , но они более специфичны.
Разобравшись с этой теоретической базой, пришло время создать свою первую фракцию!
Удалить рекламу
Создание фракции Python из разных типов данных
В отличие от int или float дроби не являются встроенным типом данных в Python, а это означает, что для их использования необходимо импортировать соответствующий модуль из стандартной библиотеки. Однако, как только вы пройдете этот дополнительный шаг, вы обнаружите, что дроби просто представляют другой числовой тип, который вы можете свободно смешивать с другими числами и математическими операторами в арифметических выражениях.
Примечание: Фракции реализованы на чистом Python и намного медленнее, чем числа с плавающей запятой, которые могут работать непосредственно на вашем оборудовании. В большинстве случаев, требующих большого количества вычислений, производительность важнее точности. С другой стороны, если вам нужна как производительность, так и точность, рассмотрите возможность замены дробей, называемой quicktions, которая может в некоторой степени повысить скорость выполнения.
В большинстве случаев, требующих большого количества вычислений, производительность важнее точности. С другой стороны, если вам нужна как производительность, так и точность, рассмотрите возможность замены дробей, называемой quicktions, которая может в некоторой степени повысить скорость выполнения.
Существует несколько способов создания дроби в Python, и все они включают использование класса Fraction . Это единственное, что вам нужно импортировать из дроби модуль. Конструктор класса принимает ноль, один или два аргумента различных типов:
>>>
>>> из фракций импорт Фракция >>> напечатать(Дробь()) 0 >>> печать (Дробь (0,75)) 3/4 >>> печать (Дробь (3, 4)) 3/4
Когда вы вызываете конструктор класса без аргументов, он создает новую дробь, представляющую число ноль. Вариант с одним аргументом пытается преобразовать значение другого типа данных в дробь. Передача второго аргумента заставляет конструктор ожидать числитель и знаменатель , которые должны быть экземплярами класса Rational или его потомков.
Обратите внимание, что вы должны print() дробь показать ее удобное для человека текстовое представление с символом косой черты ( / ) между числителем и знаменателем. Если вы этого не сделаете, он вернется к несколько более явному строковому представлению, состоящему из фрагмента кода Python. Позже в этом руководстве вы узнаете, как преобразовывать дроби в строки.
Рациональные числа
Когда вы вызываете конструктор Fraction() с двумя аргументами, оба они должны быть рациональными числами, такими как целые числа или другие дроби. Если числитель или знаменатель не рациональное число, то вы не сможете создать новую дробь:
>>>
>>> Дробь (3, 4.0)
Traceback (последний последний вызов):
...
поднять TypeError("оба аргумента должны быть "
TypeError: оба аргумента должны быть экземплярами Rational
Вместо этого вы получаете TypeError . Хотя 4. является рациональным числом в математике, Python не считает его таковым. Это связано с тем, что значение хранится как тип данных с плавающей запятой, который является слишком широким и может использоваться для представления любого действительного числа. 0
0
Примечание: Тип данных с плавающей запятой не может хранить иррациональные числа в памяти компьютера именно из-за их бесконечного и неповторяющегося десятичного представления. На практике, однако, это не имеет большого значения, потому что их 9Обычно достаточно приближения 0041 к . Единственный по-настоящему надежный способ сделать это потребовал бы использования символьных вычислений для обычных символов, таких как π.
Точно так же нельзя составить дробь со знаменателем, равным нулю, потому что это привело бы к делению на ноль , что не определено и не имеет смысла в математике:
>>>
>>> Дробь (3, 0) Traceback (последний последний вызов): ... поднять ZeroDivisionError('Дробь (%s, 0)' % числитель) ZeroDivisionError: Фракция (3, 0)
Python вызывает ошибку ZeroDivisionError . Однако, когда вы укажете действительный числитель и действительный знаменатель, они будут автоматически нормализованы для вас, если у них есть общий делитель:
>>>
>>> Дробь(9, 12) # НОД(9, 12) = 3 Фракция (3, 4) >>> Дробь(0, 12) # НОД(0, 12) = 12 Фракция (0, 1)
Обе величины упрощаются с помощью их наибольшего общего делителя (НОД), который равен трем и двенадцати соответственно. Нормализация также учитывает знак минус, когда вы определяете отрицательные дроби :
>>>
>>> -Дробь(9, 12) Дробь (-3, 4) >>> Дробь (-9, 12) Дробь (-3, 4) >>> Дробь(9, -12) Дробь (-3, 4)
Независимо от того, ставите ли вы знак минус перед конструктором или перед любым из аргументов, для согласованности Python всегда будет связывать знак дроби с ее числителем. В настоящее время существует способ отключить это поведение, но он не задокументирован и может быть удален в будущем.
В настоящее время существует способ отключить это поведение, но он не задокументирован и может быть удален в будущем.
Обычно вы определяете дроби как частное двух целых чисел. Всякий раз, когда вы вводите только одно целое число, Python преобразует это число в неправильную дробь , предполагая, что знаменатель равен 1 :
>>>
>>> Дробь(3) Дробь(3, 1)
И наоборот, если вы пропустите оба аргумента, числитель будет 0 :
>>>
>>> Дробь() Фракция (0, 1)
Однако не всегда нужно указывать целые числа в качестве числителя и знаменателя. В документации указано, что это могут быть любые рациональные числа, в том числе и другие дроби:
>>>
>>> одна_треть = дробь (1, 3) >>> Дробь (одна_треть, 3) Фракция (1, 9) >>> Дробь (3, одна_треть) Дробь(9, 1) >>> Дробь (одна_треть, одна_треть) Фракция (1, 1)
В каждом случае вы получите в результате дробь, хотя иногда они представляют целые значения, такие как 9 и 1. Позже вы увидите, как преобразовывать дроби в другие типы данных.
Позже вы увидите, как преобразовывать дроби в другие типы данных.
Что произойдет, если вы дадите конструктору Fraction единственный аргумент, который также окажется дробью? Попробуйте этот код, чтобы узнать:
>>>
>>> Дробь (одна_треть) == одна_треть Истинный >>> Дробь (одна_треть) равна одной_трети ЛОЖЬ
Вы получаете то же значение, но это отдельная копия входной дроби. Это связано с тем, что вызов конструктора всегда создает новый экземпляр, что совпадает с тем фактом, что дроби неизменяемы , как и другие числовые типы в Python.
Удалить рекламу
Числа с плавающей запятой и десятичные числа
До сих пор вы использовали только рациональные числа для создания дробей. В конце концов, версия конструктора Fraction с двумя аргументами требует, чтобы оба числа были экземплярами Rational . Однако это не относится к конструктору с одним аргументом, который с радостью примет любое действительное число и даже нечисловое значение, такое как строка.
Однако это не относится к конструктору с одним аргументом, который с радостью примет любое действительное число и даже нечисловое значение, такое как строка.
Двумя основными примерами типов данных вещественных чисел в Python являются float и decimal. Decimal . Хотя только последний может точно представлять рациональные числа, оба могут прекрасно аппроксимировать иррациональные числа. В связи с этим, если вам интересно, Fraction похож на Decimal в этом отношении, поскольку он является потомком Real .
В отличие от float или Fraction , класс Decimal формально не зарегистрирован как подкласс чисел . Real , несмотря на реализацию его методов:
>>>
>>> из чисел импортировать Real >>> issubclass(плавающая, вещественная) Истинный >>> из дробей импорт дроби >>> issubclass(Дробь, Вещественное) Истинный >>> из десятичного импорта Decimal >>> issubclass(десятичный, действительный) ЛОЖЬ
Это сделано намеренно, поскольку десятичные числа с плавающей запятой плохо сочетаются со своими двоичными аналогами:
>>>
>>> from decimal import Decimal
>>> Десятичный ("0,75") - 0,25
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: неподдерживаемые типы операндов для -: 'decimal. Decimal' и 'float'
Decimal' и 'float'
С другой стороны, замена Decimal эквивалентным Fraction даст результат float в приведенном выше примере.
До Python 3.2 вы могли создавать дроби только из действительных чисел, используя методы класса .from_float() и .from_decimal() . Хотя они и не устарели, сегодня они избыточны, поскольку конструктор Fraction может напрямую принимать оба типа данных в качестве аргумента:
>>>
>>> из десятичного импорта Десятичный
>>> Дробь(0,75) == Дробь(Десятичная("0,75"))
Истинный
Создаете ли вы объекты Fraction из объектов float или Decimal , их значения одинаковы. Вы уже видели дробь, созданную из значения с плавающей запятой:
>>>
>>> печать (Дробь (0,75)) 3/4
Результатом является то же число, выраженное в дробной форме. Однако этот код работает так, как ожидалось, только по стечению обстоятельств. В большинстве случаев вы не получите ожидаемого значения из-за ошибки представления, влияющей на
Однако этот код работает так, как ожидалось, только по стечению обстоятельств. В большинстве случаев вы не получите ожидаемого значения из-за ошибки представления, влияющей на числа с плавающей запятой чисел, рациональные они или нет:
>>>
>>> печать (Дробь (0,1)) 3602879701896397/36028797018963968
Ого! Что здесь случилось?
Давайте рассмотрим это в замедленной съемке. Предыдущее число, которое может быть представлено либо как 0,75, либо как ¾, также может быть выражено как сумма ½ и ¼, которые являются отрицательными степенями двойки и имеют точное двоичное представление. С другой стороны, число ⅒ может быть только 90 171 приблизительно равным 9.0172 с непрерывным повторяющимся расширением двоичных цифр:
Поскольку двоичная строка в конечном итоге должна закончиться из-за конечной памяти, ее конец округляется. По умолчанию Python показывает только самые значащие цифры, определенные в sys. , но вы можете отформатировать число с плавающей запятой с произвольным количеством цифр, если хотите: float_info.dig
float_info.dig
>>>
>>> стр(0,1) «0,1» >>> формат(0.1, ".17f") «0,10000000000000001» >>> формат(0.1, ".18f") «0,1000000000000000006» >>> формат(0.1, ".19е") «0,10000000000000000056» >>> формат(0.1, ".55f") '0,1000000000000000055511151231257827021181583404541015625'
Когда вы передаете число float или Decimal конструктору Fraction , он вызывает их метод .as_integer_ratio() для получения кортежа из двух неприводимых целых чисел, отношение которых дает точно такое же десятичное представление, что и входные данные. аргумент. Эти два числа затем присваиваются числителю и знаменателю вашей новой дроби.
Примечание: Начиная с Python 3.8, Fraction также реализует .as_integer_ratio() для дополнения других числовых типов. Например, это может помочь преобразовать вашу дробь в кортеж.
Например, это может помочь преобразовать вашу дробь в кортеж.
Теперь вы можете собрать воедино, откуда взялись эти два больших числа:
>>>
>>> Дробь (0,1) Дробь(3602879701896397, 36028797018963968) >>> (0.1).as_integer_ratio() (3602879701896397, 36028797018963968)
Если вы вытащите свой карманный калькулятор и введете эти числа, то в результате деления вы получите обратно 0,1. Однако, если вы разделите их вручную или воспользуетесь таким инструментом, как WolframAlpha, вы получите те же пятьдесят пять знаков после запятой, которые вы видели ранее.
Существует способ найти близкое приближение вашей дроби, имеющее более приземленные значения. Например, вы можете использовать .limit_denominator() , о котором вы узнаете подробнее позже в этом руководстве:
>>>
>>> одна_десятая = дробь (0,1) >>> один_десятый Дробь(3602879701896397, 36028797018963968) >>> один_десятый.предел_знаменателя() Дробь(1, 10) >>> one_tenth.limit_denominator(max_denominator=int(1e16)) Дробь(1000000000000000, 9999999999999999)
Однако это не всегда может дать вам наилучшее приближение. Суть в том, что вы не должны никогда не пытаться создавать дроби прямо из действительных чисел, таких как float , если вы хотите избежать ошибок округления, которые, вероятно, возникнут. Даже класс Decimal может быть восприимчив к этому, если вы не будете достаточно осторожны.
Во всяком случае, дроби позволяют наиболее точно передать десятичную запись строкой в их конструкторе.
Удалить рекламу
Строки
Конструктор Fraction принимает два строковых формата, которые соответствуют десятичному и дробному обозначениям:
>>>
>>> Дробь ("0,1")
Дробь(1, 10)
>>> Дробь ("1/10")
Дробь(1, 10)
Обе записи могут иметь знак плюс ( + ) или минус ( - ), а десятичная может дополнительно включать показатель степени, если вы хотите использовать научное обозначение :
>>>
>>> Дробь ("-2e-3")
Дробь (-1, 500)
>>> Дробь("+2/1000")
Дробь(1, 500)
Единственная разница между двумя результатами заключается в том, что один отрицательный, а другой положительный.
При использовании дробной записи нельзя использовать пробельные символы вокруг косой черты ( / ):
>>>
>>> Дробь ("1/10")
Traceback (последний последний вызов):
...
поднять ValueError('Неверный литерал для дроби: %r' %
ValueError: недопустимый литерал для дроби: «1/10»
Чтобы узнать, какие именно строки допустимы, а какие нет, вы можете изучить регулярное выражение в исходном коде модуля. Не забудьте создать дроби из строки или правильно созданного объекта Decimal , а не из числа с плавающей запятой , чтобы сохранить максимальную точность.
Теперь, когда вы создали несколько дробей, вам может быть интересно, что они могут сделать для вас, кроме двух групповых чисел. Это отличный вопрос!
Проверка фракции Python
Абстрактный базовый класс Rational определяет два атрибута только для чтения для доступа к числителю дроби и знаменателю :
>>>
>>> из фракций импорт Фракция >>> половина = дробь (1, 2) >>> половина.числитель 1 >>> половина знаменателя 2
Так как дроби неизменяемы , вы не можете изменить их внутреннее состояние:
>>>
>>> половина числителя = 2 Traceback (последний последний вызов): Файл "", строка 1, в AttributeError: невозможно установить атрибут
Если вы попытаетесь присвоить новое значение одному из атрибутов дроби, то получите ошибку. На самом деле, вы должны создавать новую фракцию каждый раз, когда хотите изменить ее. Например, чтобы инвертировать вашу дробь, вы можете вызвать .as_integer_ratio() , чтобы получить кортеж, а затем использовать синтаксис среза, чтобы инвертировать его элементы:
>>>
>>> Fraction(*half.as_integer_ratio()[::-1]) Дробь(2, 1)
Оператор унарной звезды ( * ) распаковывает ваш инвертированный кортеж и передает его элементы конструктору Fraction .
Еще один полезный метод, используемый для каждой дроби, позволяет найти ближайшее рациональное приближение к числу, заданному в десятичной системе счисления. Это метод .limit_denominator() , которого вы уже касались ранее в этом руководстве. Вы можете дополнительно запросить максимальный знаменатель для вашего приближения:
>>>
>>> число пи = дробь ("3,141592653589793")
>>> пи
Дробь(3141592653589793, 1000000000000000)
>>> pi.limit_denominator(20_000)
Фракция (62813, 19994)
>>> pi.limit_denominator(100)
Дробь(311, 99)
>>> pi.limit_denominator(10)
Дробь(22, 7)
Начальное приближение может быть не самым удобным в использовании, но оно самое точное. Этот метод также может помочь вам восстановить рациональное число , хранящееся как тип данных с плавающей запятой. Помните, что число с плавающей запятой может не точно представлять все рациональные числа, даже если они имеют завершающие десятичные расширения:
>>>
>>> пи = дробь (3,141592653589793) >>> пи Дробь (8842797155, 281474976710656) >>> pi.limit_denominator() Дробь(3126535, 995207) >>> pi.limit_denominator(10) Дробь(22, 7)
Вы заметите другой результат в выделенной строке по сравнению с предыдущим блоком кода, хотя экземпляр float выглядит так же, как строковый литерал, который вы передали конструктору ранее! Позже вы изучите пример использования .limit_denominator() для нахождения аппроксимаций иррациональных чисел.
Удаление рекламы
Преобразование дроби Python в другие типы данных
Вы научились составлять дроби из следующих типов данных:
-
ул -
внутр. -
поплавок -
десятичный. Десятичный -
дроби. Дробь
А наоборот? Как вы конвертируете 9Экземпляр 1204 Fraction вернулся к этим типам? Вы узнаете в этом разделе.
Числа с плавающей запятой и целые числа
Преобразование между собственными типами данных в Python обычно включает вызов одной из встроенных функций, таких как int() или float() для объекта. Эти преобразования работают до тех пор, пока объект реализует соответствующие специальные методы, такие как
Эти преобразования работают до тех пор, пока объект реализует соответствующие специальные методы, такие как .__int__() или .__float__() . Дробям случается наследовать только последнее от Rational абстрактный базовый класс:
>>>
>>> из фракций импорт Фракция >>> three_четверти = Дробь (3, 4) >>> с плавающей запятой (три_четверти) 0,75 >>> three_quarters.__float__() # Не вызывайте специальные методы напрямую 0,75 >>> три_четверти.__int__() Traceback (последний последний вызов): Файл "", строка 1, в AttributeError: объект «Дробь» не имеет атрибута «__int__»
Вы не должны вызывать специальные методы для объектов напрямую, но это полезно для демонстрационных целей. Здесь вы заметите, что дроби реализуют только .__float__() , а не .__int__() .
Когда вы исследуете исходный код, вы заметите, что метод .__float__() удобно делит числитель дроби на его знаменатель, чтобы получить число с плавающей запятой:
>>>
>>> три_четверти.числитель / три_четверти.знаменатель 0,75
Имейте в виду, что превращение экземпляра Fraction в экземпляр с плавающей запятой , скорее всего, приведет к преобразование с потерями , что означает, что вы можете получить число, которое немного отличается:
>>>
>>> с плавающей точкой (дробь (3, 4)) == дробь (3, 4) Истинный >>> float(Дробь(1, 3)) == Дробь(1, 3) ЛОЖЬ >>> float(Дробь(1, 10)) == Дробь(1, 10) ЛОЖЬ
Хотя дроби не обеспечивают реализацию целочисленного преобразования, все действительные числа могут быть усеченными , что является запасным вариантом для функции int() :
>>>
>>> дробь = дробь (14, 5) >>> целое(доля) 2 >>> импортировать математику >>> math.trunc(доля) 2 >>>fraction.__trunc__() # Не вызывайте специальные методы напрямую 2
Несколько других связанных методов вы найдете позже в разделе об округлении дробей.
Десятичные числа
Если вы попытаетесь создать число Decimal из экземпляра Fraction , вы быстро обнаружите, что такое прямое преобразование невозможно:
>>>
>>> из десятичного импорта Десятичный >>> Десятичный (Дробь (3, 4)) Traceback (последний последний вызов): Файл "", строка 1, в TypeError: преобразование из дроби в десятичную не поддерживается
При попытке получить TypeError . Однако, поскольку дробь представляет собой деление , вы можете обойти это ограничение, заключив только одно из чисел в Decimal и разделив их вручную:
>>>
>>> дробь = дробь (3, 4)
>>> дробь.числитель / десятичная(дробь.знаменатель)
Десятичный ('0,75')
В отличие от float , но аналогично Fraction , тип данных Decimal свободен от ошибки представления с плавающей запятой. Итак, когда вы конвертируете рациональное число, которое не может быть точно представлено в двоичном формате с плавающей запятой, вы сохраните точность числа:
Итак, когда вы конвертируете рациональное число, которое не может быть точно представлено в двоичном формате с плавающей запятой, вы сохраните точность числа:
>>>
>>> дробь = дробь (1, 10) >>> десятичная = дробь.числитель / десятичная (дробь.знаменатель) >>> дробь == десятичная Истинный >>> дробь == 0,1 ЛОЖЬ >>> десятичное == 0,1 ЛОЖЬ
В то же время, рациональные числа с неконечным повторяющимся десятичным представлением будут приводить к потере точности при преобразовании из дробного представления в десятичное:
>>>
>>> дробь = дробь (1, 3)
>>> десятичная = дробь.числитель / десятичная (дробь.знаменатель)
>>> дробь == десятичная
ЛОЖЬ
>>> десятичный
Десятичный ('0,33333333333333333333333333333')
Это потому, что в десятичном разложении одной трети есть бесконечное количество троек, или Fraction(1, 3) , в то время как тип Decimal имеет фиксированную точность. По умолчанию он хранит только двадцать восемь знаков после запятой. Вы можете настроить его, если хотите, но, тем не менее, он будет конечным.
По умолчанию он хранит только двадцать восемь знаков после запятой. Вы можете настроить его, если хотите, но, тем не менее, он будет конечным.
Удалить рекламу
Строки
Строковое представление дробей раскрывает их значения, используя знакомую дробную запись, в то время как их каноническое представление выводит фрагмент кода Python, состоящий из вызова Фракция конструктор:
>>>
>>> одна_треть = дробь (1, 3) >>> ул(одна_треть) «1/3» >>> repr(одна_треть) «Дробь (1, 3)»
Независимо от того, используете ли вы str() или repr() , результатом будет строка, но их содержимое разное.
В отличие от других числовых типов дроби не поддерживают форматирование строк в Python:
>>>
>>> из десятичного импорта Десятичный
>>> формат(Десятичный("0.333333333333333333333333333333"), ". 2f")
«0,33»
>>> формат(Дробь(1, 3), ".2f")
Traceback (последний последний вызов):
Файл "
2f")
«0,33»
>>> формат(Дробь(1, 3), ".2f")
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: строка неподдерживаемого формата передана в Fraction.__format__
Если вы попытаетесь, то получите TypeError . Это может быть проблемой, если вы хотите сослаться на экземпляр Fraction в строковом шаблоне, например, для заполнения заполнителей. С другой стороны, вы можете быстро исправить это, преобразовав дроби в числа с плавающей запятой, тем более что вам не нужно заботиться о точности в таком сценарии.
Если вы работаете в Jupyter Notebook, возможно, вы захотите отображать формулы LaTeX на основе ваших дробей вместо их обычного текстового представления. Для этого вы должны залатать 9 обезьян.1204 Тип данных Fraction путем добавления нового метода ._repr_pretty_() , который Jupyter Notebook распознает:
из фракций импорт Фракция из отображения импорта IPython.display, Math Fraction._repr_pretty_ = лямбда-выражение, *аргументы: \ display(Math(rf"$$\frac{{{self.numerator}}}{{{self.denominator}}}"))
Он заключает фрагмент разметки LaTeX в объект Math и отправляет его на расширенный дисплей вашего ноутбука, который может отображать разметку с помощью библиотеки MathJax:
В следующий раз, когда вы будете оценивать ячейку записной книжки, содержащую экземпляр Fraction , она нарисует красивую математическую формулу вместо печати текста.
Выполнение арифметики рациональных чисел на дробях
Как упоминалось ранее, вы можете использовать дроби в арифметических выражениях, состоящих из других числовых типов. Дроби будут взаимодействовать с большинством числовых типов, за исключением decimal.Decimal , который имеет свой собственный набор правил. Более того, тип данных другого операнда, независимо от того, находится ли он слева или справа от вашей дроби, будет определять тип результата вашей арифметической операции.
Дополнение
Вы можете сложить две или более дроби, не задумываясь о приведении их к общему знаменателю:
>>>
>>> из фракций импорт Фракция >>> Дробь (1, 2) + Дробь (2, 3) + Дробь (3, 4) Дробь(23, 12)
Результатом является новая дробь, представляющая собой сумму всех введенных дробей. То же самое произойдет, если вы сложите целые числа и дроби:
>>>
>>> Дробь (1, 2) + 3 Дробь(7, 2)
Однако, как только вы начнете смешивать дроби с нерациональными числами, то есть с числами, которые не являются подклассами чисел . Рациональные , ваша дробь будет сначала преобразована в этот тип, прежде чем добавляться:
>>>
>>> Дробь (3, 10) + 0,1 0,4 >>> float(Дробь(3, 10)) + 0,1 0,4
Вы получите тот же результат независимо от того, используете ли вы явно float() . Это преобразование может привести к некоторой потере точности, поскольку ваша дробь, а также результат теперь хранятся в представлении с плавающей запятой. Хотя число 0,4 кажется правильным, оно не совсем равно дроби 4/10.
Хотя число 0,4 кажется правильным, оно не совсем равно дроби 4/10.
Удалить рекламу
Вычитание
Вычитание дробей ничем не отличается от их сложения. Python найдет для вас общий знаменатель:
>>>
>>> Дробь (3, 4) - Дробь (2, 3) - Дробь (1, 2) Дробь (-5, 12) >>> Дробь(4, 10) - 0,1 0,30000000000000004
На этот раз потеря точности настолько значительна, что это видно с первого взгляда. Обратите внимание на длинный поток нулей, за которым следует цифра 4 9.1205 в конце десятичной записи. Это результат округления значения, для которого в противном случае потребовалось бы бесконечное количество двоичных разрядов.
Умножение
При умножении двух дробей их числители и знаменатели умножаются поэлементно, а полученная дробь при необходимости автоматически уменьшается:
>>>
>>> Дробь(1, 4) * Дробь(3, 2) Фракция (3, 8) >>> Fraction(1, 4) * Fraction(4, 5) # Результат 4/20 Фракция (1, 5) >>> Дробь (1, 4) * 3 Фракция (3, 4) >>> Дробь (1, 4) * 3,0 0,75
Опять же, в зависимости от типа другого операнда, в результате вы получите другой тип данных.
Подразделение
В Python есть два оператора деления, и дроби поддерживают оба из них:
- Истинное деление:
/ - Этажность:
//
Истинное деление приводит к другой дроби, в то время как деление по полу всегда возвращает целое число с усеченной дробной частью:
>>>
>>> Дробь (7, 2) / Дробь (2, 3) Дробь(21, 4) >>> Дробь(7, 2) // Дробь(2, 3) 5 >>> Дробь (7, 2) / 2 Дробь(7, 4) >>> Дробь(7, 2) // 2 1 >>> Дробь (7, 2) / 2.0 1,75 >>> Фракция (7, 2) // 2.0 1,0
Обратите внимание, что результат деления этажей не всегда является целым числом! В результате может получиться с плавающей запятой в зависимости от того, какой тип данных вы используете вместе с дробью. Дроби также поддерживают оператор по модулю ( % ), а также функцию divmod() , которая может помочь в создании смешанных дробей из неправильных:
>>>
>>> по определению смешанный (дробь): ... пол, остальное = divmod (доля.числитель, дробь.знаменатель) ... вернуть f"{пол} и {Дробь(остаток, дробь.знаменатель)}" ... >>> смешанный (Дробь (22, 7)) «3 и 1/7»
Вместо создания строки, как в приведенном выше выводе, вы можете обновить функцию, чтобы она возвращала кортеж, состоящий из целой части и дробного остатка. Идите вперед и попробуйте изменить возвращаемое значение функции, чтобы увидеть разницу.
Возведение в степень
Вы можете возводить дроби в степень с помощью двоичного оператора возведения в степень ( ** ) или встроенной функции pow() . Вы также можете использовать сами дроби в качестве показателей степени. Вернитесь к интерпретатору Python и начните изучать, как возводить дроби в степень:
>>>
>>> Дробь(3, 4) ** 2 Дробь(9, 16) >>> Дробь(3, 4) ** (-2) Дробь(16, 9) >>> Дробь(3, 4) ** 2.0 0,5625
Вы заметите, что можете использовать как положительные, так и отрицательные значения экспоненты. Если показатель степени не является числом
Если показатель степени не является числом Rational , ваша дробь автоматически преобразуется в число с плавающей запятой , прежде чем продолжить.
Все становится сложнее, когда экспонента представляет собой экземпляр Fraction . Поскольку дробные степени обычно дают иррациональные числа, оба операнда преобразуются в число с плавающей запятой , если основание и показатель степени не являются целыми числами:
>>>
>>> 2 ** Дробь (2, 1) 4 >>> 2,0 ** Дробь (2, 1) 4.0 >>> Дробь (3, 4) ** Дробь (1, 2) 0,8660254037844386 >>> Дробь (3, 4) ** Дробь (2, 1) Дробь(9, 16)
Единственный раз, когда вы получаете дробь в результате, это когда знаменатель показателя степени равен единице, и вы поднимаете экземпляр Fraction .
Удалить рекламу
Округление дроби Python
Существует множество стратегий округления чисел в Python и еще больше в математике. Вы можете использовать тот же набор встроенных глобальных функций и функций уровня модуля для дробей и десятичных чисел. Они позволят вам присвоить целое число дроби или создать новую дробь, соответствующую меньшему количеству знаков после запятой.
Вы можете использовать тот же набор встроенных глобальных функций и функций уровня модуля для дробей и десятичных чисел. Они позволят вам присвоить целое число дроби или создать новую дробь, соответствующую меньшему количеству знаков после запятой.
Вы уже узнали о грубом методе округления, когда преобразовывали дроби в целое число , которое усекало дробную часть, оставляя только целую часть, если она есть:
>>>
>>> из фракций импорт Фракция >>> int(Дробь(22, 7)) 3 >>> импортировать математику >>> math.trunc(Дробь(22, 7)) 3 >>> math.trunc(-Дробь(22, 7)) -3
В этом случае вызов int() эквивалентен вызову math.trunc() , который округляет положительные дроби вниз и отрицательные дроби вверх. Эти две операции известны как пол и потолок соответственно. Вы можете использовать оба напрямую, если хотите:
>>>
>>> math.floor(-Дробь(22, 7)) -4 >>> math.floor(Дробь(22, 7)) 3 >>> math.ceil(-Дробь(22, 7)) -3 >>> math.ceil(Дробь(22, 7)) 4
Сравните результаты math.floor() и math.ceil() с вашими предыдущими вызовами math.trunc() . Каждая функция имеет различное смещение округления, которое может повлиять на статистические свойства округленного набора данных. К счастью, существует стратегия округления от половины до четных , которая менее предвзята, чем усечение, пол или потолок.
По сути, он округляет вашу дробь до ближайшего целого числа, предпочитая ближайшее четное число для равноудаленных половин. Вы можете позвонить по номеру round() , чтобы воспользоваться этой стратегией:
>>>
>>> раунд(Дробь(3, 2)) # 1.5 2 >>> раунд(Дробь(5, 2)) # 2.5 2 >>> раунд(Дробь(7, 2)) # 3.5 4
Обратите внимание, как эти дроби округляются в большую или меньшую сторону в зависимости от того, где находится ближайшее четное число? Естественно, это правило применяется только к ничьим, когда расстояние до ближайшего целого числа слева такое же, как и справа. В противном случае направление округления основано на кратчайшем расстоянии до целого числа, независимо от того, четное оно или нет.
В противном случае направление округления основано на кратчайшем расстоянии до целого числа, независимо от того, четное оно или нет.
При желании вы можете предоставить функции round() второй параметр, который указывает, сколько знаков после запятой вы хотите сохранить. Когда вы это сделаете, вы всегда получите Дробь , а не целое число, даже если вы запрашиваете нулевые цифры:
>>>
>>> дробь = дробь (22, 7) # 3.142857142857143 >>> раунд(доля, 0) Дробь(3, 1) >>> раунд(доля, 1) # 3.1 Дробь(31, 10) >>> раунд(дробь, 2) # 3.14 Дробь(157, 50) >>> раунд(дробь, 3) # 3.143 Дробь(3143, 1000)
Однако обратите внимание на разницу между вызовами round(fraction) и round(fraction, 0) , которые дают то же значение, но используют другой тип данных:
>>>
>>> круглый(дробный) 3 >>> раунд(доля, 0) Дробь(3, 1)
Если вы опустите второй аргумент, round() вернет ближайшее целое число. В противном случае вы получите уменьшенную дробь, знаменатель которой изначально был степенью десяти, соответствующей запрошенному вами количеству десятичных цифр.
В противном случае вы получите уменьшенную дробь, знаменатель которой изначально был степенью десяти, соответствующей запрошенному вами количеству десятичных цифр.
Сравнение дробей в Python
В реальной жизни сравнение чисел, записанных в дробной форме, может оказаться более сложным, чем сравнение чисел, записанных в десятичной системе счисления, потому что дробная запись состоит из двух значений, а не из одного. Чтобы понять эти числа, вы обычно приводите их к общему знаменателю и сравниваете только их числители. Например, попробуйте расположить следующие дроби в порядке возрастания их значения:
- 2/3
- 5/8
- 13.08.
Не так удобно, как с десятичной системой счисления. Еще хуже обстоят дела со смешанными обозначениями. Однако, если вы приведете эти дроби к общему знаменателю, их сортировка станет простой:
.- 208/312
- 195/312
- 192/312
Наибольший общий делитель чисел 3, 8 и 13 равен 1. Это означает, что наименьший общий знаменатель для всех трех дробей равен их произведению 312. После того, как вы преобразовали все дроби, чтобы использовать их наименьший общий знаменатель, вы можете игнорировать знаменатель и сосредоточиться на сравнении числителей.
Это означает, что наименьший общий знаменатель для всех трех дробей равен их произведению 312. После того, как вы преобразовали все дроби, чтобы использовать их наименьший общий знаменатель, вы можете игнорировать знаменатель и сосредоточиться на сравнении числителей.
В Python это работает за кулисами, когда вы сравниваете и сортируете объекты Fraction :
>>>
>>> из фракций импорт Фракция >>> Дробь (8, 13) < Дробь (5, 8) Истинный >>> отсортировано ([Дробь (2, 3), Дробь (5, 8), Дробь (8, 13)]) [Дробь (8, 13), Дробь (5, 8), Дробь (2, 3)]
Python может быстро сортировать объекты Fraction , используя встроенную функцию sorted() . К счастью, все операторы сравнения работают как положено. Вы даже можете использовать их против других числовых типов, кроме комплексных чисел:
>>>
>>> Дробь (2, 3) < 0,625
ЛОЖЬ
>>> из десятичного импорта Decimal
>>> Дробь (2, 3) < десятичная ("0,625")
ЛОЖЬ
>>> Фракция (2, 3) < 3 + 2j
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: '<' не поддерживается между экземплярами 'Fraction' и 'complex'
Операторы сравнения работали с числами с плавающей запятой и десятичными знаками, но вы получаете ошибку при попытке с комплексным числом 3 + 2j . Это связано с тем, что комплексные числа не определяют естественного отношения порядка, поэтому их нельзя ни с чем сравнивать, включая дроби.
Это связано с тем, что комплексные числа не определяют естественного отношения порядка, поэтому их нельзя ни с чем сравнивать, включая дроби.
Удалить рекламу
Выбор между
Дробная , Десятичная и Плавающая Если вам нужно выбрать только одну вещь, которую нужно запомнить при чтении этого руководства, то это должно быть то, когда следует выбирать Дробное число вместо Десятичное число и Число с плавающей запятой . У всех этих числовых типов есть свои варианты использования, поэтому полезно понимать их сильные и слабые стороны. В этом разделе вы кратко рассмотрите, как числа представлены в каждом из этих трех типов данных.
Двоичные числа с плавающей запятой:
float Тип данных float должен быть вашим выбором по умолчанию для представления действительных чисел в большинстве ситуаций. Например, он подходит для науки, техники и компьютерной графики, где скорость выполнения важнее точности. Вряд ли какая-либо программа требует более высокой точности, чем вы можете получить с плавающей запятой.
Например, он подходит для науки, техники и компьютерной графики, где скорость выполнения важнее точности. Вряд ли какая-либо программа требует более высокой точности, чем вы можете получить с плавающей запятой.
Примечание: Если вам нужно использовать только целые числа, то int будет еще более эффективным по скорости и памяти типом данных.
Беспрецедентная скорость арифметики с плавающей запятой обусловлена ее аппаратной, а не программной реализацией. Практически все математические сопроцессоры соответствуют стандарту IEEE 754, который описывает, как представлять числа в виде двоичных чисел с плавающей запятой . Обратной стороной использования двоичной системы, как вы уже догадались, является печально известная ошибка представления.
Однако, если у вас нет особой причины использовать другой числовой тип, вы должны просто придерживаться float или int , если возможно.
Десятичное число с плавающей и фиксированной точкой:
Десятичное число Бывают случаи, когда использование двоичной системы не обеспечивает достаточной точности для действительных чисел. Одним из примечательных примеров являются финансовые расчеты , которые включают в себя работу с очень большими и очень маленькими числами одновременно. Они также имеют тенденцию повторять одну и ту же арифметическую операцию снова и снова, что может привести к значительной ошибке округления.
Вы можете хранить действительные числа, используя десятичную арифметику с плавающей запятой, чтобы смягчить эти проблемы и устранить ошибку двоичного представления. Он похож на с плавающей запятой , поскольку он перемещает десятичную точку, чтобы приспособить большие или меньшие величины. Однако он работает в десятичной системе , а не в двоичной.
Еще одна стратегия повышения числовой точности — арифметика с фиксированной точкой, которая выделяет определенное количество цифр для десятичного представления. Например, для точности до четырех знаков после запятой потребуется хранить дроби в виде целых чисел, увеличенных в 10 000 раз. Чтобы восстановить исходные дроби, они должны быть соответствующим образом уменьшены.
Например, для точности до четырех знаков после запятой потребуется хранить дроби в виде целых чисел, увеличенных в 10 000 раз. Чтобы восстановить исходные дроби, они должны быть соответствующим образом уменьшены.
Десятичный тип данных Python . Десятичный тип данных представляет собой гибрид десятичных представлений с плавающей запятой и фиксированной запятой под капотом. Он также соответствует этим двум стандартам:
- Общая спецификация десятичной арифметики (IBM)
- Независимая от системы счисления арифметика с плавающей запятой (IEEE 854-1987)
Они эмулируются программно, а не аппаратно, что делает этот тип данных гораздо менее эффективным с точки зрения времени и пространства, чем float . С другой стороны, он может представлять числа с произвольный но конечная точность , которую вы можете настроить. Обратите внимание, что вы все еще можете столкнуться с ошибкой округления , если арифметическая операция превышает максимальное количество знаков после запятой.
Однако буфер безопасности, обеспечиваемый фиксированной точностью сегодня, завтра может оказаться недостаточным. Подумайте о гиперинфляции или работе с несколькими валютами, курс которых сильно различается, например, биткойн (0,000029 BTC) и иранский риал (42 105,00 IRR). Если вам нужна бесконечная точность, используйте Фракция .
Рациональное число бесконечной точности:
Дробь Оба типа Fraction и Decimal имеют несколько общих черт. Они устраняют ошибку двоичного представления, они реализованы в программном обеспечении, и вы можете использовать их для денежных приложений. Тем не менее, дроби в основном используются для представления рациональных чисел , поэтому они могут быть менее удобными для хранения денег, чем десятичные дроби.
Примечание: Хотя тип данных Fraction реализован на чистом Python, большинство дистрибутивов Python содержат скомпилированную динамически подключаемую библиотеку для типа Decimal . Если он недоступен для вашей платформы, то Python также вернется к чистой реализации Python. Однако даже скомпилированная версия не будет использовать преимущества аппаратного обеспечения так, как
Если он недоступен для вашей платформы, то Python также вернется к чистой реализации Python. Однако даже скомпилированная версия не будет использовать преимущества аппаратного обеспечения так, как float .
Существует два преимущества использования Дробное число по сравнению с Десятичное число . Первый - бесконечная точность ограничена только вашей доступной памятью. Это позволяет вам представлять рациональные числа с непрерывающимся и повторяющимся десятичным расширением без потери информации:
>>>
>>> из фракций импорт Фракция >>> одна_треть = дробь (1, 3) >>> напечатать(3 * одна_треть) 1 >>> из десятичного импорта Decimal >>> одна_треть = 1 / десятичная (3) >>> напечатать(3 * одна_треть) 0,99999999999999999999999999999
Умножение 1/3 на 3 дает ровно 1 в дробном представлении, но результат округляется в десятичном представлении. Он имеет двадцать восемь знаков после запятой, что является точностью по умолчанию для типа Decimal .
Еще раз взгляните на еще одно преимущество дробей, о котором вы уже узнали ранее. В отличие от Decimal дроби могут взаимодействовать с двоичными числами с плавающей запятой:
>>>
>>> Дробь("0.75") - 0.25
0,5
>>> Десятичный ("0,75") - 0,25
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: неподдерживаемые типы операндов для -: 'decimal.Decimal' и 'float'
Когда вы смешиваете дроби с числами с плавающей запятой, в результате вы получаете число с плавающей запятой. С другой стороны, если вы попытаетесь смешать дроби с типом данных Decimal , вы столкнетесь с TypeError .
Удалить рекламу
Изучение фракции Python в действии
В этом разделе вы познакомитесь с несколькими забавными и практическими примерами использования типа данных Fraction в Python. Вы можете быть удивлены, насколько удобными могут быть дроби и в то же время насколько они недооценены. Приготовьтесь нырнуть прямо в воду!
Вы можете быть удивлены, насколько удобными могут быть дроби и в то же время насколько они недооценены. Приготовьтесь нырнуть прямо в воду!
Аппроксимация иррациональных чисел
Иррациональные числа играют важную роль в математике, поэтому они касаются многих подполей, таких как арифметика, исчисление и геометрия. Вот некоторые из самых известных из них, о которых вы, возможно, уже слышали: 9.0005
- Квадратный корень из двух (√2)
- Постоянная Архимеда (π)
- Золотое сечение (φ)
- Число Эйлера ( e )
В истории математики число пи (π) было особенно интересным, что привело к многочисленным попыткам найти для него точные приближения.
В то время как древним философам приходилось идти на многое, сегодня вы можете использовать Python, чтобы найти довольно хорошие оценки числа пи, используя методы Монте-Карло , например игла Бюффона или аналогичная. Однако в большинстве повседневных задач достаточно грубого приближения в виде удобной дроби. Вот как можно определить частное двух целых чисел, которое постепенно дает более точное приближение к иррациональному числу:
Вот как можно определить частное двух целых чисел, которое постепенно дает более точное приближение к иррациональному числу:
из фракций импорт Фракция
из счетчика импорта itertools
приблизительное определение (число):
история = установить ()
для max_denominator в count(1):
дробь = дробь (число). предел_знаменатель (максимальный_знаменатель)
если дробь не в истории:
история.добавить(дробь)
доля выхода
Функция принимает иррациональное число, преобразует его в дробь и находит другую дробь с меньшим количеством десятичных знаков. Набор Python предотвращает получение повторяющихся значений, сохраняя исторические данные, а итератор count() модуля itertools считает до бесконечности.
Теперь вы можете использовать эту функцию, чтобы найти первые десять дробных приближений числа пи:
>>>
>>> из itertools импортирует islice >>> импортировать математику >>> для дроби в islice (приблизительно (math.pi), 10): ... print(f"{str(fraction):>7}", "→", float(fraction)) ... 3 → 3,0 13/4 → 3,25 16/5 → 3,2 19/6 → 3,1666666666666665 22/7 → 3,142857142857143 179/57 → 3,1403508771929824 201/64 → 3.140625 223/71 → 3.140845070422535 245/78 → 3,141025641025641 267/85 → 3,1411764705882352
Красиво! Рациональное число 22/7 уже довольно близко, что показывает, что число пи можно приблизить на ранней стадии и, в конце концов, оно не является особенно иррациональным. Итератор islice() останавливает бесконечную итерацию после получения запрошенных десяти значений. Продолжайте и поиграйте с этим примером, увеличивая количество результатов или находя аппроксимации других иррациональных чисел.
Получение соотношения сторон дисплея
Соотношение сторон изображения или дисплея представляет собой отношение его ширины к высоте, которое удобно выражает пропорции. Он обычно используется в фильмах и цифровых медиа, а режиссеры любят использовать соотношение сторон в качестве художественного показателя. Если вы когда-нибудь искали новый смартфон, то в спецификациях могло быть упомянуто, например, соотношение сторон экрана, такое как 16:9.
Если вы когда-нибудь искали новый смартфон, то в спецификациях могло быть упомянуто, например, соотношение сторон экрана, такое как 16:9.
Вы можете узнать соотношение сторон монитора вашего компьютера, измерив его ширину и высоту с помощью Tkinter, который входит в официальный дистрибутив Python:
>>>
>>> импортировать tkinter как tk >>> окно = tk.Tk() >>> window.winfo_screenwidth() 2560 >>> window.winfo_screenheight() 1440
Обратите внимание: если у вас подключено несколько мониторов, этот код может работать не так, как ожидалось.
Расчет соотношения сторон заключается в создании дроби, которая будет сама уменьшаться:
>>>
>>> из фракций импорт Фракция >>> Дробь (2560, 1440) Дробь(16, 9)
Ну вот. Монитор имеет разрешение 16:9. Однако, если вы работаете на ноутбуке с меньшим размером экрана, то ваша дробь может сначала не получиться, и вам нужно будет соответствующим образом ограничить ее знаменатель:
.
>>>
>>> Дробь (1360, 768) Дробь(85, 48) >>> Дробь(1360, 768).limit_denominator(10) Дробь(16, 9)
Имейте в виду, что если вы имеете дело с вертикальным экраном мобильного устройства, вы должны поменять местами размеры, чтобы первый был больше, чем следующий. Вы можете инкапсулировать эту логику в повторно используемой функции:
из фракций импорт Фракция
def aspect_ratio (ширина, высота, max_denominator = 10):
если высота > ширина:
ширина, высота = высота, ширина
соотношение = дробь (ширина, высота). limit_denominator (max_denominator)
вернуть f"{отношение.числитель}:{отношение.знаменатель}"
Это обеспечит согласованные соотношения сторон независимо от порядка аргументов:
>>>
>>> соотношение сторон (1080, 2400) «20:9» >>> соотношение сторон (2400, 1080) '20:9'
Независимо от того, смотрите ли вы на размеры горизонтального или вертикального экрана, соотношение сторон одинаково.
До сих пор ширина и высота были целыми числами, но как насчет дробных значений? Например, некоторые камеры Canon имеют кроп-сенсор APS-C, размеры которого составляют 22,8 мм на 14,8 мм. Дроби подавляются числами с плавающей запятой и десятичными числами, но вы можете превратить их в рациональные приближения:
>>>
>>> соотношение сторон (22.2, 14.8)
Traceback (последний последний вызов):
...
поднять TypeError("оба аргумента должны быть "
TypeError: оба аргумента должны быть экземплярами Rational
>>> аспектное_отношение(Дробь("22,2"), Дробь("14,8"))
«3:2»
В этом случае соотношение сторон получается ровно 1,5 или 3:2, но многие камеры используют чуть большую ширину своих сенсоров, что дает соотношение 1,555… или 14:9. Когда вы посчитаете, вы обнаружите, что это среднее арифметическое широкоформатного изображения (16:9) и системы четырех третей (4:3), что является компромиссом, позволяющим отображать изображения приемлемого качества в оба этих популярных формата.
Расчет значения экспозиции фотографии
Стандартный формат для встраивания метаданных в цифровые изображения, Exif (Exchangeable Image File Format), использует коэффициенты для хранения нескольких значений. Некоторые из наиболее важных коэффициентов описывают экспозицию вашей фотографии:
- Значение диафрагмы
- Время воздействия
- Смещение экспозиции
- Фокусное расстояние
- F-стоп
- Скорость затвора
Скорость затвора в просторечии является синонимом времени экспозиции, но она сохраняется как дробь в метаданных с использованием системы APEX на основе логарифмической шкалы. Это означает, что камера возьмет обратное значение времени выдержки, а затем вычислит его логарифм по основанию 2. Так, например, 1/200 секунды времени экспозиции будет записано в файл как 7643856/1000000. Вот как это можно рассчитать:
>>>
>>> из фракций импорт Фракция >>> время_выдержки = дробь (1, 200) >>> из математического импорта log2, trunc >>> точность = 1_000_000 >>> trunc(log2(Дробь(1, время_экспозиции)) * точность) 7643856
Вы можете использовать дроби Python для восстановления исходного времени экспозиции, если вы вручную читаете эти метаданные без помощи каких-либо внешних библиотек:
>>>
>>> выдержка_выдержки = дробь (7643856, 1_000_000) >>> Дробь(1, раунд(2 ** выдержка_затвора)) Дробь(1, 200)
Когда вы объедините отдельные части головоломки, то есть диафрагму, выдержку затвора и чувствительность ISO, вы сможете рассчитать единое значение экспозиции (EV) , которое описывает среднее количество захваченных легкий. Затем вы можете использовать его для получения логарифмического среднего яркости в сфотографированной сцене, что бесценно при постобработке и применении специальных эффектов.
Затем вы можете использовать его для получения логарифмического среднего яркости в сфотографированной сцене, что бесценно при постобработке и применении специальных эффектов.
Формула для расчета значения экспозиции выглядит следующим образом:
из математического журнала импорта2
def Exposure_value (f_stop, Exposure_time, iso_speed):
вернуть log2(f_stop ** 2/время выдержки) - log2(iso_speed/100)
Имейте в виду, что он не учитывает другие факторы, такие как смещение экспозиции или вспышка, которые может использовать ваша камера. В любом случае, попробуйте его с некоторыми примерными значениями:
.>>>
>>> значение экспозиции( ... f_stop=Дробь(28, 5), ... время экспозиции = дробь (1, 750), ... iso_speed=400 ... ) 12.521600439723727 >>> Exposure_value (f_stop = 5,6, Exposure_time = 1/750, iso_speed = 400) 12.521600439723727
Вы можете использовать дроби или другие числовые типы для входных значений. В этом случае значение экспозиции составляет около +13, что относительно ярко. Фото сделано на улице в солнечный день, хотя и в тени.
В этом случае значение экспозиции составляет около +13, что относительно ярко. Фото сделано на улице в солнечный день, хотя и в тени.
Решение проблемы внесения изменений
Вы можете использовать дроби для решения классической задачи компьютерных наук о внесении изменений, с которой вы можете столкнуться на собеседовании. Он запрашивает минимальное количество монет, чтобы получить определенную сумму денег. Например, если вы рассматриваете самые популярные монеты доллара США, то вы можете представить 2,67 доллара в виде десяти четвертаков (10 × 0,25 доллара), одного цента (1 × 0,10 доллара), одного никеля (1 × 0,05 доллара) и двух пенни (2). × 0,01 доллара США).
Fractions может быть удобным инструментом для представления монет в кошельке или кассовом аппарате. Вы можете определить монеты доллара США следующим образом:
из фракций импорт Фракция пенни = дробь (1, 100) никель = дробь (5, 100) десять центов = дробь (10, 100) четверть = дробь (25, 100)
Некоторые из них будут автоматически уменьшаться, но это нормально, потому что вы отформатируете их с использованием десятичной системы счисления. Вы можете использовать эти монеты для расчета общей стоимости вашего кошелька:
Вы можете использовать эти монеты для расчета общей стоимости вашего кошелька:
>>>
>>> бумажник = [8 * четвертак, 5 * десять центов, 3 * никель, 2 * пенни]
>>> print(f"${float(сумма(кошелек)):.2f}")
2,67 доллара США
В вашем кошельке 2,67 доллара, но в нем целых восемнадцать монет. Можно использовать меньше монет на ту же сумму. Один из способов решения проблемы внесения изменений — использование жадного алгоритма, такого как этот:
. def change(сумма, монеты):
в то время как сумма > 0:
для монет в сортировке (монеты, реверс = True):
если монета <= сумма:
сумма = монета
приносить монету
ломать
еще:
вызвать исключение ("Решения нет")
Алгоритм пытается найти монету с наибольшим номиналом, не превышающим оставшуюся сумму. Хотя его относительно просто реализовать, он может не дать оптимального решения для всех монетных систем. Вот пример для монет доллара США:
Вот пример для монет доллара США:
>>>
>>> из коллекций импорт Счетчик
>>> сумма = дробь ("2,67")
>>> usd = [пенни, никель, десять центов, четвертак]
>>> для монет подсчитайте в Counter(change(amount, usd)).items():
... print(f"{count:>2} × ${float(coin):.2f}")
...
10 × 0,25 доллара США
1 × 0,10 доллара США
1 × 0,05 доллара США
2 × 0,01 доллара США
Использование рациональных чисел обязательно для поиска решения, потому что значения с плавающей запятой не подходят. Поскольку change() является функцией-генератором монет, которые могут повторяться, вы можете использовать Counter для их группировки.
Вы можете изменить эту проблему, задав немного другой вопрос. Например, каким будет оптимальный набор монет, учитывая общую цену, количество монет покупателя и продавца, имеющихся в кассе?
Производство и расширение непрерывных фракций
В начале этого урока вы узнали, что иррациональные числа могут быть представлены в виде бесконечных цепных дробей . Для существования таких дробей потребуется бесконечный объем памяти, но вы можете выбрать, когда прекратить производить их коэффициенты, чтобы получить разумное приближение.
Для существования таких дробей потребуется бесконечный объем памяти, но вы можете выбрать, когда прекратить производить их коэффициенты, чтобы получить разумное приближение.
Следующая функция-генератор будет бесконечно выдавать коэффициенты данного числа в ленивом вычислении:
1def continue_fraction(число): 2, пока верно: 3 выход (целая_часть := целое (число)) 4 дробная_часть = число - целая_часть 5 попытка: 6 число = 1 / дробная_часть 7, кроме ZeroDivisionError: 8 перерыв
Функция усекает число и продолжает выражать оставшуюся дробь как обратную величину, которая возвращается в качестве входных данных. Чтобы исключить дублирование кода, он использует выражение присваивания в строке 3, более известное как оператор моржа, представленный в Python 3.8.
Интересно, что вы можете создавать непрерывные дроби и для рациональных чисел:
>>>
>>> список (continued_fraction (42)) [42] >>> из дробей импорт дроби >>> список(continued_fraction(Дробь(3, 4))) [0, 1, 3]
Число 42 имеет только один коэффициент и не имеет дробной части. И наоборот, 3/4 не имеет целой части, а непрерывная дробь состоит из 1 на 1 + 1/3:
И наоборот, 3/4 не имеет целой части, а непрерывная дробь состоит из 1 на 1 + 1/3:
Как обычно, вы должны следить за ошибкой представления с плавающей запятой, которая может появиться при переключении на float :
>>>
>>> список (continued_fraction (0,75)) [0, 1, 3, 11258992624]
Несмотря на то, что вы можете точно представить 0,75 в двоичном формате, его обратная величина имеет бесконечное десятичное представление, несмотря на то, что это рациональное число. Перебирая остальные коэффициенты, вы в конце концов доберетесь до этой огромной величины в знаменателе, представляющей пренебрежимо маленькое значение. Это ваша ошибка приближения.
Вы можете избавиться от этой ошибки, заменив действительные числа дробями Python:
из фракций импорт Фракция
def continue_fraction (число):
пока верно:
выход (целая_часть: = int (число))
дробная_часть = дробь (число) - целая_часть
пытаться:
число = дробь (1, дробная_часть)
кроме ZeroDivisionError:
ломать
Это небольшое изменение позволяет надежно генерировать коэффициенты цепных дробей, соответствующие десятичным числам. В противном случае вы можете попасть в бесконечный цикл даже для завершения десятичных расширений.
В противном случае вы можете попасть в бесконечный цикл даже для завершения десятичных расширений.
Хорошо, давайте сделаем что-нибудь повеселее и сгенерируем коэффициенты иррациональных чисел с их десятичными разложениями, обрезанными до пятидесятого знака после запятой. Ради точности определите их как Decimal экземпляров:
>>>
>>> из десятичного импорта Десятичный
>>> pi = Decimal("3.14159265358979323846264338327950288419716939937510")
>>> sqrt2 = Decimal("1.41421356237309504880168872420969807856967187537694")
>>> phi = Decimal("1.618033988749894848204586834365638117720300576")
Теперь вы можете проверить первые несколько коэффициентов их цепных дробей с помощью знакомого итератора islice() :
>>>
>>> из itertools импортирует islice
>>> числа = {
... "π": пи,
... "√2": sqrt2,
... " φ": фи
... }
>>> для метки номер в number. items():
... печать (метка, список (islice (continued_fraction (число), 20)))
...
π [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2]
√2 [1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
φ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
items():
... печать (метка, список (islice (continued_fraction (число), 20)))
...
π [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2]
√2 [1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
φ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Первые четыре коэффициента числа пи дают удивительно хорошее приближение, за которым следует незначительный остаток. Однако непрерывные дроби двух других констант выглядят весьма своеобразно. Они повторяют одно и то же число снова и снова до бесконечности. Зная это, вы можете аппроксимировать их на , расширив эти коэффициенты обратно в десятичную форму:
по определению расширить (коэффициенты):
если len(коэффициенты) > 1:
вернуть коэффициенты [0] + дробь (1, развернуть (коэффициенты [1:]))
еще:
вернуть дробь (коэффициенты [0])
Эту функцию удобно определять рекурсивно, чтобы она могла вызывать себя для последовательно меньших списков коэффициентов. В базовом случае есть только одно целое число, что является самым грубым возможным приближением. Если их два или более, то результатом является сумма первого коэффициента, за которым следует обратная величина остальных расширенных коэффициентов.
В базовом случае есть только одно целое число, что является самым грубым возможным приближением. Если их два или более, то результатом является сумма первого коэффициента, за которым следует обратная величина остальных расширенных коэффициентов.
Вы можете проверить, работают ли обе функции должным образом, вызвав их для противоположных возвращаемых значений:
>>>
>>> список (continued_fraction (3.14159)) [3, 7, 15, 1, 25, 1, 7, 4, 851921, 1, 1, 2, 880, 1, 2] >>> float(expand([3, 7, 15, 1, 25, 1, 7, 4, 851921, 1, 1, 2, 880, 1, 2])) 3.14159
Отлично! Если вы передадите результат continue_fraction() в expand() , вы вернете исходное значение, которое у вас было в начале. Однако в некоторых случаях вам может понадобиться преобразовать расширенную дробь в 9.1204 Decimal Тип вместо float для большей точности.
Заключение
Возможно, вы никогда не задумывались о том, как компьютеры хранят дробные числа , прежде чем читать это руководство.

 То, что оно «записывается непериодической дробью» — свойство, а не определение. И да, в любой «-ичной» системе счисления будет то же самое.
То, что оно «записывается непериодической дробью» — свойство, а не определение. И да, в любой «-ичной» системе счисления будет то же самое. 10.2013, 16:09
10.2013, 16:09  10.2013, 16:14
10.2013, 16:14  Вопрос такой: в любой ли системе счисления иррациональное число представляется в виде бесконечной непериодической дроби?
Вопрос такой: в любой ли системе счисления иррациональное число представляется в виде бесконечной непериодической дроби? Вопрос такой: в любой ли системе счисления иррациональное число представляется в виде бесконечной непериодической дроби?
Вопрос такой: в любой ли системе счисления иррациональное число представляется в виде бесконечной непериодической дроби? 10.2013, 16:48
10.2013, 16:48 



 Однако существует ещё бесконечное множество расстояний, так называемых p-адических, по одному на каждое число p. Согласно теореме Островского, «обычное» расстояние вместе со всеми p-адическими уже действительно исчерпывают все разумные расстояние Q. Термин адельная демократия введен Ю. И. Маниным. Согласно принципу адельной демократии, все разумные расстояния на Q равны перед законами математики (может быть, лишь традиционное «чуть=чуть равнее…». В курсе будет введено кольцо аделей, позволяющее работать со всеми этими расстояниями одновременно.
Однако существует ещё бесконечное множество расстояний, так называемых p-адических, по одному на каждое число p. Согласно теореме Островского, «обычное» расстояние вместе со всеми p-адическими уже действительно исчерпывают все разумные расстояние Q. Термин адельная демократия введен Ю. И. Маниным. Согласно принципу адельной демократии, все разумные расстояния на Q равны перед законами математики (может быть, лишь традиционное «чуть=чуть равнее…». В курсе будет введено кольцо аделей, позволяющее работать со всеми этими расстояниями одновременно.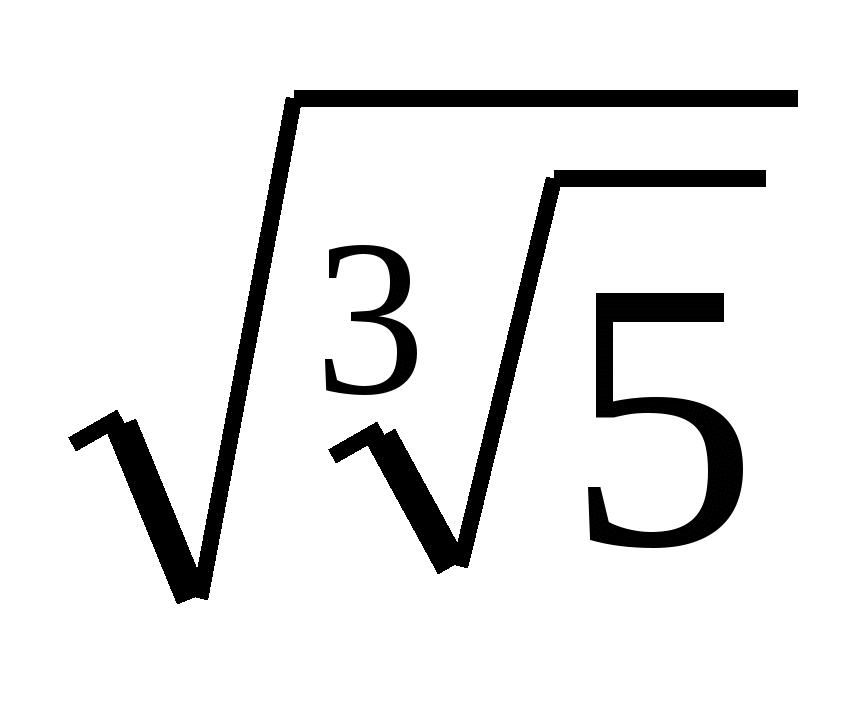 Кажется, он жил в Александрии. Никто из греческих математиков не упоминает его до IV века, так что он вероятно жил в середине III века. Самая главная работа Диофанта, «Арифметика» (Ἀριθμητικά), состоялась в начале из 13 «книгах» (βιβλία), т. е. главах. Мы сегодня имеем 10 из них, а именно: 6 в греческом тексте и 4 других в средневековом арабском переводе, место которых в середине греческих книг: книги I-III по-гречески, IV-VII по-арабски, VIII-X по-гречески. «Арифметика» Диофанта прежде всего собрание задач, всего около 260. Теории, по правде говоря, нет; имеются только общие инструкции в введении книги, и частные замечания в некоторых задачах, когда нужно. «Арифметика» уже имеет черты алгебраического трактата. Сперва Диофант пользуется разными знаками, чтобы выражать неизвестное и его степени, также и некоторые вычисления; как и все алгебраические символики средних веков, его символика происходит от математических слов. Потом, Диофант объясняет, как решить задачу алгебраическим способом.
Кажется, он жил в Александрии. Никто из греческих математиков не упоминает его до IV века, так что он вероятно жил в середине III века. Самая главная работа Диофанта, «Арифметика» (Ἀριθμητικά), состоялась в начале из 13 «книгах» (βιβλία), т. е. главах. Мы сегодня имеем 10 из них, а именно: 6 в греческом тексте и 4 других в средневековом арабском переводе, место которых в середине греческих книг: книги I-III по-гречески, IV-VII по-арабски, VIII-X по-гречески. «Арифметика» Диофанта прежде всего собрание задач, всего около 260. Теории, по правде говоря, нет; имеются только общие инструкции в введении книги, и частные замечания в некоторых задачах, когда нужно. «Арифметика» уже имеет черты алгебраического трактата. Сперва Диофант пользуется разными знаками, чтобы выражать неизвестное и его степени, также и некоторые вычисления; как и все алгебраические символики средних веков, его символика происходит от математических слов. Потом, Диофант объясняет, как решить задачу алгебраическим способом. Но задачи Диофанта не алгебраические в обычном смысле, потому что почти все сводятся к решению неопределённого уравнения или систем таких уравнений.
Но задачи Диофанта не алгебраические в обычном смысле, потому что почти все сводятся к решению неопределённого уравнения или систем таких уравнений. Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль.
Зато читатель познакомится с рядом общих понятий, играющих в алгебре основную роль. Мы планируем обсудить недавние достижения и сформулировать нерешенные проблемы. Программа занятий: детерминанты и пфаффианы; остовные деревья; случайные матрицы; мультипликативные функционалы.
Мы планируем обсудить недавние достижения и сформулировать нерешенные проблемы. Программа занятий: детерминанты и пфаффианы; остовные деревья; случайные матрицы; мультипликативные функционалы.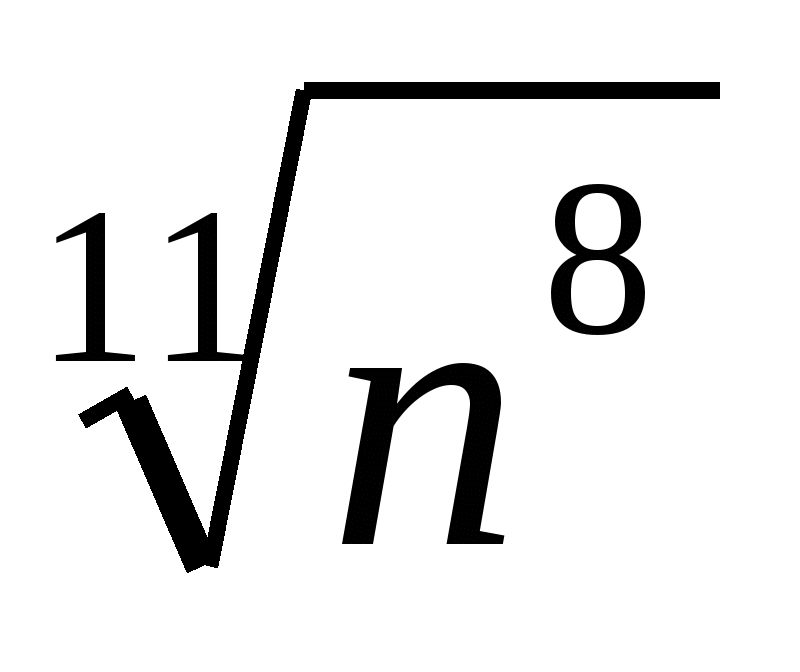 , что «Проблема различения простых и составных чисел и разложения последних на простые сомножители, как известно, является одной из самых важных и полезных в арифметике» он не знал, что 200 лет спустя эта проблема будет иметь огромное значение для криптографии: ее приложениями каждый день пользуются миллионы людей. Мы обсудим, как проверить простоту целых чисел детерминированными и вероятностными алгоритмами. От слушателей потребуется знакомство с арифметикой вычетов, включая малую теорему Ферма.
, что «Проблема различения простых и составных чисел и разложения последних на простые сомножители, как известно, является одной из самых важных и полезных в арифметике» он не знал, что 200 лет спустя эта проблема будет иметь огромное значение для криптографии: ее приложениями каждый день пользуются миллионы людей. Мы обсудим, как проверить простоту целых чисел детерминированными и вероятностными алгоритмами. От слушателей потребуется знакомство с арифметикой вычетов, включая малую теорему Ферма. 2
2
 Этот
термин в очередной раз подчеркивает
единство различных областей математики,
дает возможность отождествления понятий
«действительное число» и «точка на
координатной (числовой) прямой».
Этот
термин в очередной раз подчеркивает
единство различных областей математики,
дает возможность отождествления понятий
«действительное число» и «точка на
координатной (числовой) прямой».
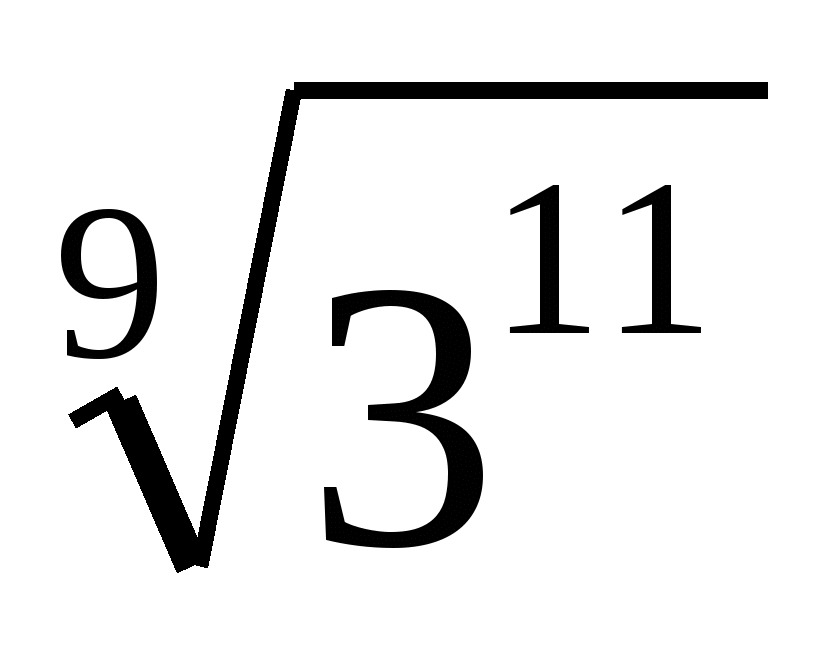
 е. a
— неотрицательное число (положительное
или 0), или что a не меньше нуля;
е. a
— неотрицательное число (положительное
или 0), или что a не меньше нуля; Таким образом,
к сравнению действительных чисел нужно
подходить достаточно гибко, что мы и
используем в следующем примере.
Таким образом,
к сравнению действительных чисел нужно
подходить достаточно гибко, что мы и
используем в следующем примере.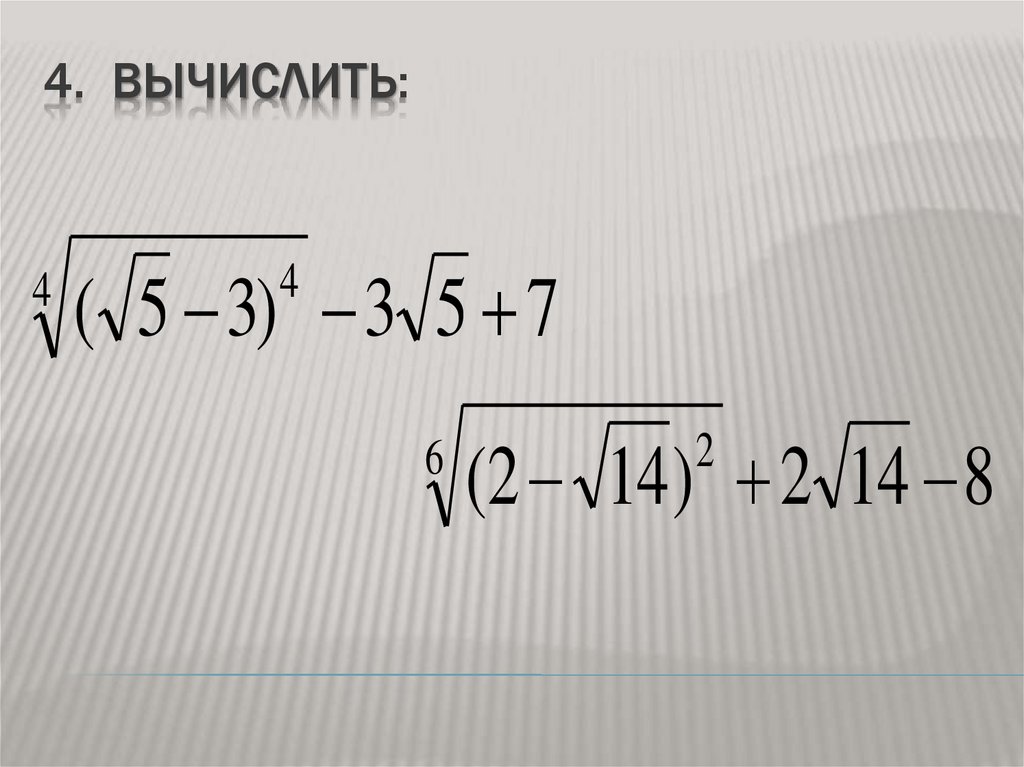
 Таким образом, отношение радиусов двух произвольных кругов из этого ряда всегда будет равно степени числа √2.
Таким образом, отношение радиусов двух произвольных кругов из этого ряда всегда будет равно степени числа √2. Изогнутый потолок, причудливые формы постройки могут вызвать ложное ощущение, что архитектор не придерживался какой-либо рациональной системы. Однако если посмотреть план сооружения, сразу видно, что его стабильность обеспечена геометрией квадратов, в вершины которых Гауди поместил вершины колонн. Ещё на чертеже можно заметить правильные восьмиугольники (октагоны), в которых тоже скрыто наше любимое число √2, ведь в каждом октагоне есть как минимум три квадрата.
Изогнутый потолок, причудливые формы постройки могут вызвать ложное ощущение, что архитектор не придерживался какой-либо рациональной системы. Однако если посмотреть план сооружения, сразу видно, что его стабильность обеспечена геометрией квадратов, в вершины которых Гауди поместил вершины колонн. Ещё на чертеже можно заметить правильные восьмиугольники (октагоны), в которых тоже скрыто наше любимое число √2, ведь в каждом октагоне есть как минимум три квадрата.
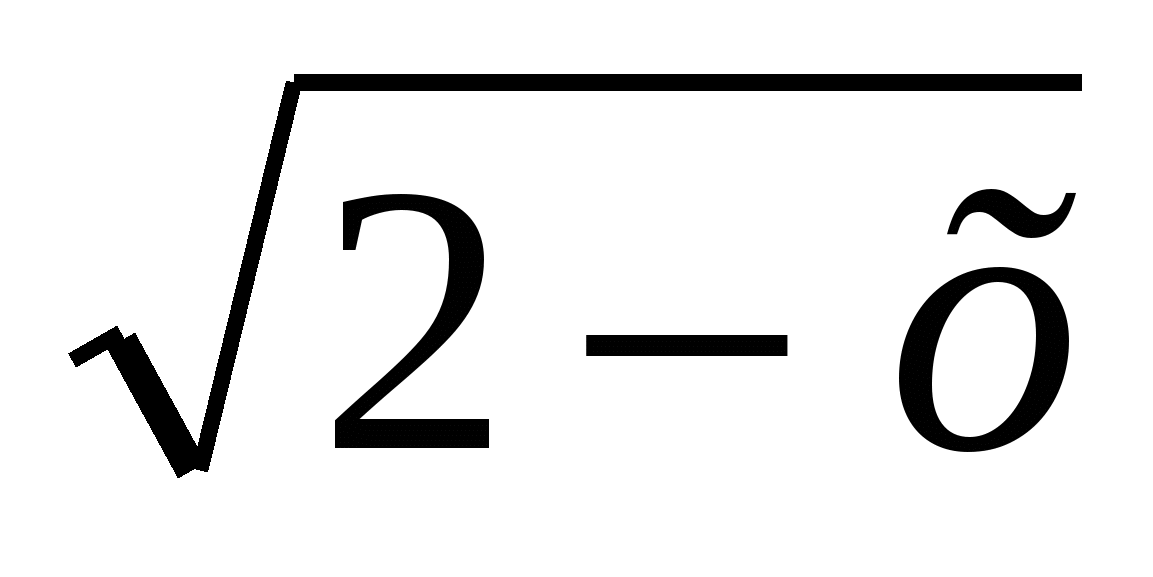 2 четное, тогда и b четно.
2 четное, тогда и b четно.
 Обозначается буквой греческого алфавита «пи».
Обозначается буквой греческого алфавита «пи». н. «интеграл Пуассона» или «интеграл Гаусса»
н. «интеграл Пуассона» или «интеграл Гаусса» Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку .
Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку. Рассматривая правильный 96-угольник, Архимед получил оценку .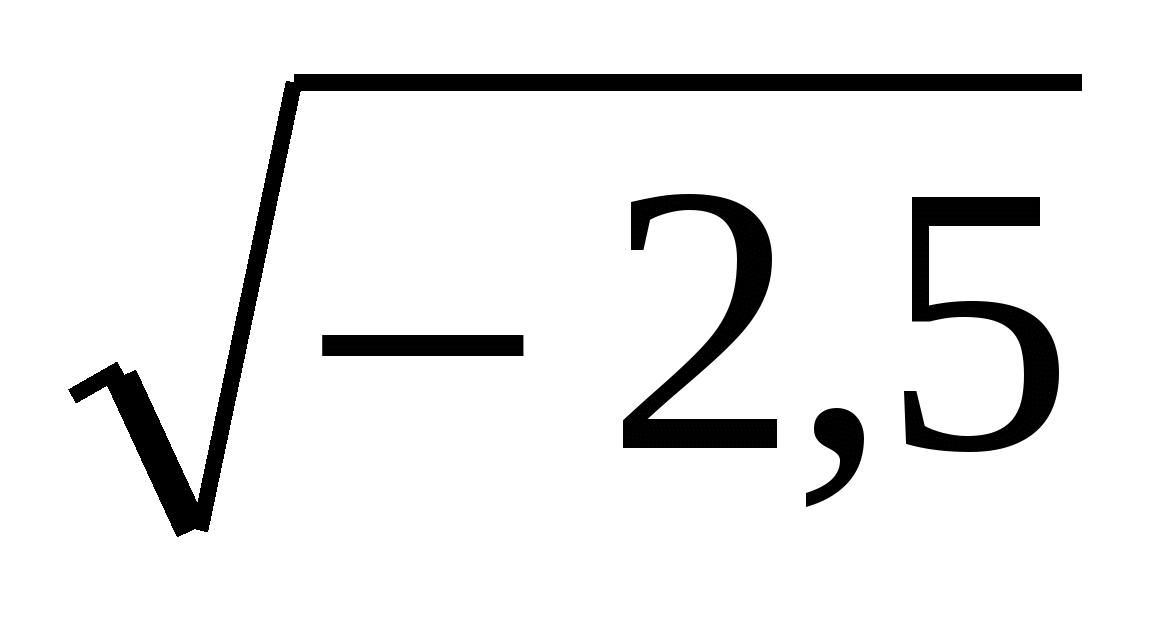
 Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять». 14, что соответствует приближённому значению числа π. Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159.
14, что соответствует приближённому значению числа π. Считается, что праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, обративший внимание на то, что 14 марта ровно в 01:59 дата и время совпадают с первыми разрядами числа Пи = 3,14159. С установлением нового рекорда Андрея Слюсарчука официально поздравил президент Украины Виктор Андреевич Ющенко. Поскольку устное перечисление 30 млн цифр π со скоростью одна цифра в секунду заняло бы почти год (347 дней) при непрерывном перечислении 24 часа в сутки, 7 дней в неделю, то был применён следующий подход для проверки рекорда: во время демонстраций Слюсарчука просят назвать произвольно выбранные проверяющими последовательности цифр числа Пи, расположенные на произвольно выбранных местах произвольных страниц 20-томной распечатки, группированной в упорядоченные таблицы. Он многократно успешно проходит этот тест.
С установлением нового рекорда Андрея Слюсарчука официально поздравил президент Украины Виктор Андреевич Ющенко. Поскольку устное перечисление 30 млн цифр π со скоростью одна цифра в секунду заняло бы почти год (347 дней) при непрерывном перечислении 24 часа в сутки, 7 дней в неделю, то был применён следующий подход для проверки рекорда: во время демонстраций Слюсарчука просят назвать произвольно выбранные проверяющими последовательности цифр числа Пи, расположенные на произвольно выбранных местах произвольных страниц 20-томной распечатки, группированной в упорядоченные таблицы. Он многократно успешно проходит этот тест. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значениe
Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значениe  Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова. τα μνημονιχα — искусство запоминания), мнемоте́хника — совокупность специальных приёмов и способов, облегчающих запоминание нужной информации и увеличивающих объём памяти путём образования ассоциаций (связей). Замена абстрактных объектов и фактов на понятия и представления, имеющие визуальное, аудиальное или кинестетическое представление, связывание объектов с уже имеющейся информацией в памяти различных типов для упрощения запоминания.
τα μνημονιχα — искусство запоминания), мнемоте́хника — совокупность специальных приёмов и способов, облегчающих запоминание нужной информации и увеличивающих объём памяти путём образования ассоциаций (связей). Замена абстрактных объектов и фактов на понятия и представления, имеющие визуальное, аудиальное или кинестетическое представление, связывание объектов с уже имеющейся информацией в памяти различных типов для упрощения запоминания. Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой» jpeg
jpeg Что делает дроби такими особенными? Мы изучаем, как мы можем распознавать десятичное представление дробей и как дроби могут использоваться для приближения любого действительного числа настолько близко, насколько мы хотим.
Что делает дроби такими особенными? Мы изучаем, как мы можем распознавать десятичное представление дробей и как дроби могут использоваться для приближения любого действительного числа настолько близко, насколько мы хотим. Вы решаете клюнуть на удочку и быстро обнаруживаете, что это не сильно меняет игру. Вы угадываете, и, спускаясь все выше и ниже, вы все ближе и ближе подходите к цели. Если число Джордана равно −32, а вы уже выяснили, что −33 слишком мало, а −31 слишком много, то вы знаете, что ответ равен −32. Но потом понимаешь: в −100 и 100 нет ничего особенного! Если вы начнете с числа от -1000 до 1000, вы знаете, что в конечном итоге угадаете правильное число, даже если для этого потребуется еще несколько догадок. Вы идете к своему второму классу победоносно, уверенные, что будете готовы к следующему испытанию Джордана.
Вы решаете клюнуть на удочку и быстро обнаруживаете, что это не сильно меняет игру. Вы угадываете, и, спускаясь все выше и ниже, вы все ближе и ближе подходите к цели. Если число Джордана равно −32, а вы уже выяснили, что −33 слишком мало, а −31 слишком много, то вы знаете, что ответ равен −32. Но потом понимаешь: в −100 и 100 нет ничего особенного! Если вы начнете с числа от -1000 до 1000, вы знаете, что в конечном итоге угадаете правильное число, даже если для этого потребуется еще несколько догадок. Вы идете к своему второму классу победоносно, уверенные, что будете готовы к следующему испытанию Джордана. Вы снова угадываете посередине: 14. Джордан говорит, что 14 все еще много, поэтому вы знаете, что ответ должен быть на числовой прямой между 0 и 14. стратегия, как вы думаете, 18, 316, 532, 964, …. Одно из представлений этой игры показано на рис. 1. Кажется, это занимает много времени! Сможете ли вы когда-нибудь угадать правильное число? Возможно, это поможет, если вы измените свою стратегию. Или вы обречены вечно гадать?
Вы снова угадываете посередине: 14. Джордан говорит, что 14 все еще много, поэтому вы знаете, что ответ должен быть на числовой прямой между 0 и 14. стратегия, как вы думаете, 18, 316, 532, 964, …. Одно из представлений этой игры показано на рис. 1. Кажется, это занимает много времени! Сможете ли вы когда-нибудь угадать правильное число? Возможно, это поможет, если вы измените свою стратегию. Или вы обречены вечно гадать? Вот как это работает для дроби 716:
Вот как это работает для дроби 716: В таблице H означает, что ваша догадка была слишком высокой, а L означает, что ваша догадка была слишком низкой.
В таблице H означает, что ваша догадка была слишком высокой, а L означает, что ваша догадка была слишком низкой. Это означает, что 25 — рациональное число, поскольку 2 и 5 — целые числа. Кроме того, 3 — рациональное число, поскольку его можно записать как 3=31, а 4,5 — рациональное число, поскольку его можно записать как 4,5=92. Даже если мы не записываем 3 и 4,5 как дроби, они являются рациональными числами, потому что мы можем записать дробь, которая равна каждому из них.
Это означает, что 25 — рациональное число, поскольку 2 и 5 — целые числа. Кроме того, 3 — рациональное число, поскольку его можно записать как 3=31, а 4,5 — рациональное число, поскольку его можно записать как 4,5=92. Даже если мы не записываем 3 и 4,5 как дроби, они являются рациональными числами, потому что мы можем записать дробь, которая равна каждому из них. Например, когда мы преобразовывали 322 в десятичную дробь, единственными вариантами остатка, которые у нас были, были 0, 1, 2, 3, …, 20, 21. Поскольку есть только конечное число остатков, остатки должны начать повторяться в конце концов. Это верно для всех дробей, у которых десятичные дроби не оканчиваются. Несмотря на то, что для этих дробей существует повторяющийся шаблон десятичных знаков, мы никогда не угадаем точное число в игре на угадывание, если мы угадываем одно десятичное число за раз, потому что десятичное число продолжается вечно. Мы не можем сказать бесконечно много цифр!
Например, когда мы преобразовывали 322 в десятичную дробь, единственными вариантами остатка, которые у нас были, были 0, 1, 2, 3, …, 20, 21. Поскольку есть только конечное число остатков, остатки должны начать повторяться в конце концов. Это верно для всех дробей, у которых десятичные дроби не оканчиваются. Несмотря на то, что для этих дробей существует повторяющийся шаблон десятичных знаков, мы никогда не угадаем точное число в игре на угадывание, если мы угадываем одно десятичное число за раз, потому что десятичное число продолжается вечно. Мы не можем сказать бесконечно много цифр! Например, рассмотрим 0,353535…. Позвоните по этому номеру A . Повторяющаяся часть 35 состоит из двух цифр, поэтому мы умножаем на 9.0044 на 100, чтобы переместить десятичную дробь на два разряда. Это дает 100 A = 35,353535…. Обратите внимание, что все десятичные разряды в A и 100 A совпадают. Мы вычитаем A из 100 A , чтобы получить 99 A . Когда мы вычитаем десятичные дроби, 0,353535… одинаково для обоих и исключается из разницы. Поэтому у нас остались только целые числа!
Например, рассмотрим 0,353535…. Позвоните по этому номеру A . Повторяющаяся часть 35 состоит из двух цифр, поэтому мы умножаем на 9.0044 на 100, чтобы переместить десятичную дробь на два разряда. Это дает 100 A = 35,353535…. Обратите внимание, что все десятичные разряды в A и 100 A совпадают. Мы вычитаем A из 100 A , чтобы получить 99 A . Когда мы вычитаем десятичные дроби, 0,353535… одинаково для обоих и исключается из разницы. Поэтому у нас остались только целые числа! В этом числе мы увеличиваем количество нулей между каждой парой единиц, сначала добавляя один 0 между ними, затем два нуля, затем три нуля и т. д. Это не может быть рациональным числом, поскольку мы знаем, что десятичные дроби для рациональных чисел либо заканчиваются, либо повторяются. . Это пример иррациональное число . Иррациональное число — это любое число, которое мы можем поставить на числовую прямую и которое нельзя записать в виде дроби от целых чисел. Вы, наверное, слышали об известном иррациональном числе π = 3,14159…, которое дает отношение длины окружности к ее диаметру. Хотя это отношение, по крайней мере одна из окружностей или диаметров не является целым числом, поэтому π не является рациональным числом. Другое иррациональное число — 2=1,41421…, длина диагонали квадрата со стороной 1,9.0005
В этом числе мы увеличиваем количество нулей между каждой парой единиц, сначала добавляя один 0 между ними, затем два нуля, затем три нуля и т. д. Это не может быть рациональным числом, поскольку мы знаем, что десятичные дроби для рациональных чисел либо заканчиваются, либо повторяются. . Это пример иррациональное число . Иррациональное число — это любое число, которое мы можем поставить на числовую прямую и которое нельзя записать в виде дроби от целых чисел. Вы, наверное, слышали об известном иррациональном числе π = 3,14159…, которое дает отношение длины окружности к ее диаметру. Хотя это отношение, по крайней мере одна из окружностей или диаметров не является целым числом, поэтому π не является рациональным числом. Другое иррациональное число — 2=1,41421…, длина диагонали квадрата со стороной 1,9.0005 Вероятно, вам будет очень трудно угадать число точно! Как и в случае с повторяющимся десятичным расширением числа 322, вы не можете сказать бесконечно много цифр, поэтому эта игра кажется очень несправедливой.
Вероятно, вам будет очень трудно угадать число точно! Как и в случае с повторяющимся десятичным расширением числа 322, вы не можете сказать бесконечно много цифр, поэтому эта игра кажется очень несправедливой. Быть в пределах 0,01 из π , вам нужно правильно указать первые два десятичных знака. Чтобы быть в пределах 0,001 от π , вам нужно правильно указать первые три десятичных знака. Независимо от того, насколько точной должна быть ваша догадка, вы можете выиграть эту новую игру, угадывая по одному десятичному знаку за раз, пока у вас не будет достаточно десятичных знаков.
Быть в пределах 0,01 из π , вам нужно правильно указать первые два десятичных знака. Чтобы быть в пределах 0,001 от π , вам нужно правильно указать первые три десятичных знака. Независимо от того, насколько точной должна быть ваша догадка, вы можете выиграть эту новую игру, угадывая по одному десятичному знаку за раз, пока у вас не будет достаточно десятичных знаков. Это означает, что между любыми двумя различными действительными числами всегда можно найти рациональное число. Поскольку действительные числа обладают этим свойством, мы можем аппроксимировать любое иррациональное число рациональным числом. Аппроксимация иррационального числа рациональным числом — это то, что вы делаете в новой игре, когда Джордан выбирает иррациональное число.
Это означает, что между любыми двумя различными действительными числами всегда можно найти рациональное число. Поскольку действительные числа обладают этим свойством, мы можем аппроксимировать любое иррациональное число рациональным числом. Аппроксимация иррационального числа рациональным числом — это то, что вы делаете в новой игре, когда Джордан выбирает иррациональное число. число должно быть настолько близким, насколько Джордан хотел, чтобы вы вошли в игру.
число должно быть настолько близким, насколько Джордан хотел, чтобы вы вошли в игру. То есть в конечном итоге цифры попадают в шаблон, который повторяется вечно. Например, 0,3333… и 3,125353535… — повторяющиеся десятичные числа.
То есть в конечном итоге цифры попадают в шаблон, который повторяется вечно. Например, 0,3333… и 3,125353535… — повторяющиеся десятичные числа. Но иррациональные константы, такие как π и √2 — числа, которые нельзя свести к простой дроби, — часто встречаются в науке и технике. Эти громоздкие числа преследовали математиков со времен древних греков; действительно, легенда гласит, что Гиппас утонул за предположение о существовании иррационального. Теперь, однако, решен почти 80-летний затруднительный вопрос о том, насколько хорошо они могут быть аппроксимированы.
Но иррациональные константы, такие как π и √2 — числа, которые нельзя свести к простой дроби, — часто встречаются в науке и технике. Эти громоздкие числа преследовали математиков со времен древних греков; действительно, легенда гласит, что Гиппас утонул за предположение о существовании иррационального. Теперь, однако, решен почти 80-летний затруднительный вопрос о том, насколько хорошо они могут быть аппроксимированы. Во-первых, решите, насколько близким должно быть приближение для дробей определенного знаменателя. (Помните, что «числитель» относится к верхней части дроби, а «знаменатель» — к нижней. Здесь все дроби полностью упрощены, поэтому, например, 2/4 не считается имеющим знаменатель 4, потому что это упрощает до 1/2.) Вы можете решить, что упрощенные дроби вида n /2 может аппроксимировать любое иррациональное число, истинное значение которого находится в пределах 1/10 от них, что дает аппроксимации «ошибку» 1/10. Дроби, которые выглядят как n /10, расположены ближе друг к другу на числовой прямой, чем дроби со знаменателем 2, поэтому вы можете ограничить ошибку в этом случае только 1/100 — эти дроби могут аппроксимировать все, что находится в пределах 1/100 от них.
Во-первых, решите, насколько близким должно быть приближение для дробей определенного знаменателя. (Помните, что «числитель» относится к верхней части дроби, а «знаменатель» — к нижней. Здесь все дроби полностью упрощены, поэтому, например, 2/4 не считается имеющим знаменатель 4, потому что это упрощает до 1/2.) Вы можете решить, что упрощенные дроби вида n /2 может аппроксимировать любое иррациональное число, истинное значение которого находится в пределах 1/10 от них, что дает аппроксимации «ошибку» 1/10. Дроби, которые выглядят как n /10, расположены ближе друг к другу на числовой прямой, чем дроби со знаменателем 2, поэтому вы можете ограничить ошибку в этом случае только 1/100 — эти дроби могут аппроксимировать все, что находится в пределах 1/100 от них. Правило Даффина и Шеффера измеряет, когда это можно сделать, исходя из размера ошибок.
Правило Даффина и Шеффера измеряет, когда это можно сделать, исходя из размера ошибок. Это означает, что, выбирая некоторые ошибки равными нулю, вы можете ограничить аппроксимацию определенными типами дробей, например, теми, у которых знаменатели являются только степенями 10.
Это означает, что, выбирая некоторые ошибки равными нулю, вы можете ограничить аппроксимацию определенными типами дробей, например, теми, у которых знаменатели являются только степенями 10. ) Профессор Йоркского университета предложил Мейнарду заняться гипотезой Даффина-Шеффера после того, как он выступил там. «Я думаю, у него была интуиция, что было бы полезно привлечь кого-то немного за пределы этой непосредственной области», — говорит Мейнард. Эта интуиция оказалась верной, хотя и не приносила плодов в течение нескольких лет. Спустя долгое время после этого первоначального разговора Мейнард предложил Кукулопулосу сотрудничество, подозревая, что его коллега обладает соответствующим опытом.
) Профессор Йоркского университета предложил Мейнарду заняться гипотезой Даффина-Шеффера после того, как он выступил там. «Я думаю, у него была интуиция, что было бы полезно привлечь кого-то немного за пределы этой непосредственной области», — говорит Мейнард. Эта интуиция оказалась верной, хотя и не приносила плодов в течение нескольких лет. Спустя долгое время после этого первоначального разговора Мейнард предложил Кукулопулосу сотрудничество, подозревая, что его коллега обладает соответствующим опытом.
 Точки на их графиках представляли возможные знаменатели, которые исследователи хотели использовать для аппроксимирующей дроби, а две точки соединялись ребром, если у них было много общих простых множителей. У графов было много ребер именно в тех случаях, когда допустимые знаменатели имели нежелательные зависимости.
Точки на их графиках представляли возможные знаменатели, которые исследователи хотели использовать для аппроксимирующей дроби, а две точки соединялись ребром, если у них было много общих простых множителей. У графов было много ребер именно в тех случаях, когда допустимые знаменатели имели нежелательные зависимости. «Общее ощущение заключалось в том, что эта проблема не была близка к разрешению, — говорит Эйстлейтнер. «Техника использования [графов] — это то, что, возможно, в будущем будет считаться столь же важным [как] — а может быть, даже более важным, чем — реальная гипотеза Даффина-Шеффера», — говорит Джеффри Ваалер, профессор на пенсии из Университета Нью-Йорка. Техас, Остин, который доказал частный случай гипотезы в 1978 году.
«Общее ощущение заключалось в том, что эта проблема не была близка к разрешению, — говорит Эйстлейтнер. «Техника использования [графов] — это то, что, возможно, в будущем будет считаться столь же важным [как] — а может быть, даже более важным, чем — реальная гипотеза Даффина-Шеффера», — говорит Джеффри Ваалер, профессор на пенсии из Университета Нью-Йорка. Техас, Остин, который доказал частный случай гипотезы в 1978 году. Он представлен цифрами как 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Он представлен цифрами как 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.



 Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.
Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.

 Бар представляет собой
повторяющийся шаблон \(\text{1}\) и \(\text{8}\), т. е. \(\text{0,}\overline{18} =
\text{0,181818…}\).
Бар представляет собой
повторяющийся шаблон \(\text{1}\) и \(\text{8}\), т. е. \(\text{0,}\overline{18} =
\text{0,181818…}\). ..}\)
..}\)
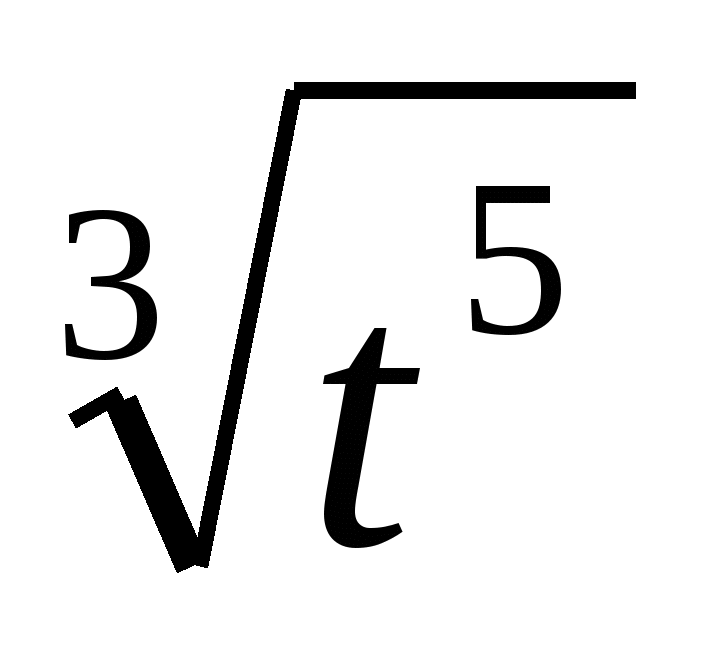



 ..
поднять ZeroDivisionError('Дробь (%s, 0)' % числитель)
ZeroDivisionError: Фракция (3, 0)
..
поднять ZeroDivisionError('Дробь (%s, 0)' % числитель)
ZeroDivisionError: Фракция (3, 0)
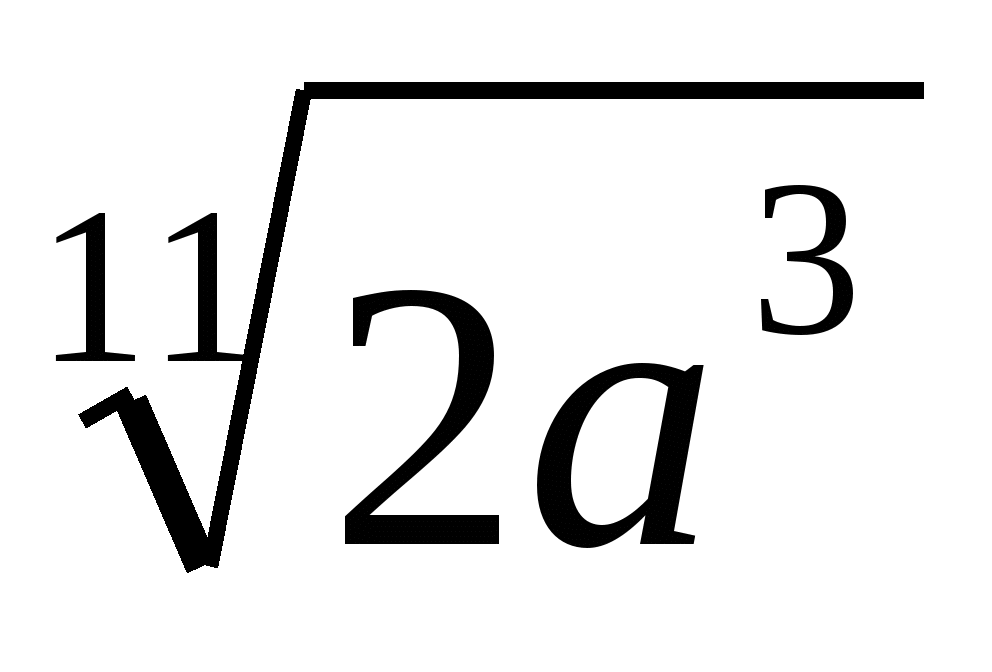 Decimal' и 'float'
Decimal' и 'float'