Что такое периметр и как он обозначается. Периметр
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.
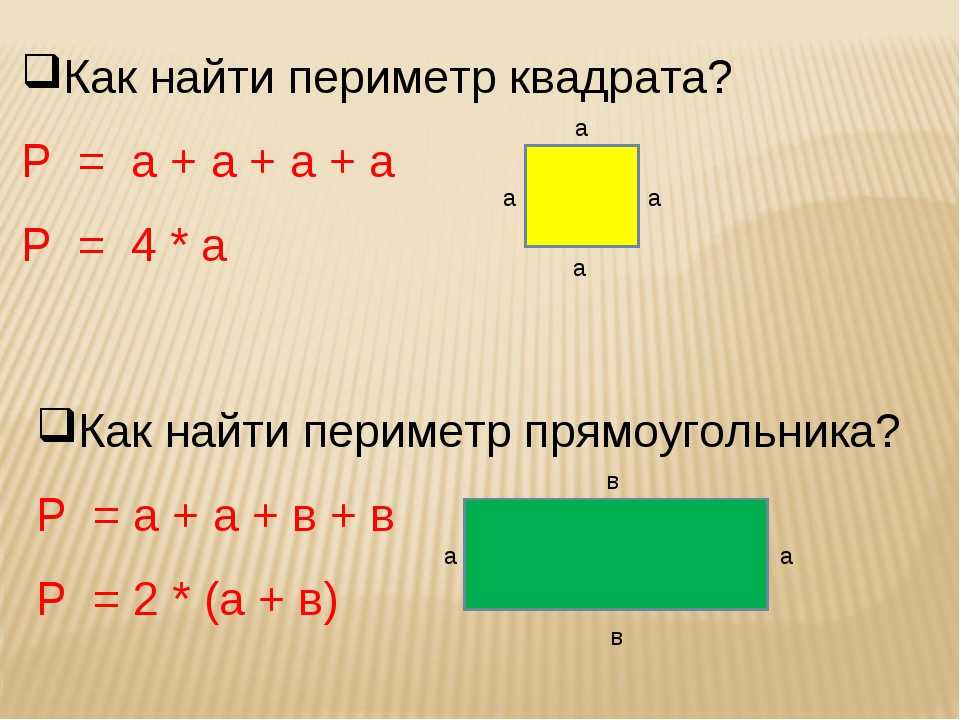
Как найти периметр квадрата
Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.
Так же можно вычислить периметр равностороннего ромба.
Как найти периметр прямоугольника
Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.
Как найти периметр треугольника
Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.
Как найти периметр параллелограмма
Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.
Как найти длину окружности
Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка.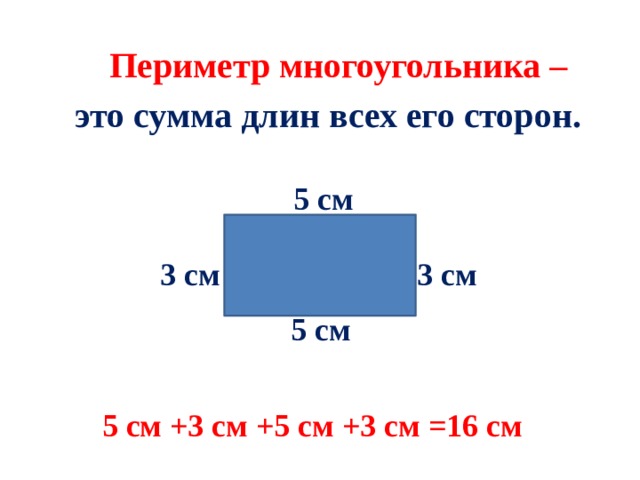 При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Как вычислять периметр?
Нам частенько приходилось слышать от учителей: «Занимайтесь прилежно, знания очень пригодятся вам в жизни», и, действительно, такое случается. Например, когда мы беремся за ремонт, нам совершенно необходимо знать, как рассчитать периметр той или иной фигуры, чтобы определить требуемое количество строительного материала. В этой статье для тех, кто забыл школьный курс, расскажем о том, как вычислять периметр различных фигур.
Например, когда мы беремся за ремонт, нам совершенно необходимо знать, как рассчитать периметр той или иной фигуры, чтобы определить требуемое количество строительного материала. В этой статье для тех, кто забыл школьный курс, расскажем о том, как вычислять периметр различных фигур.
Что такое периметр?
Периметр — это длина линии, очерчивающей геометрическую фигуру; длина всех сторон плоской фигуры. Таким образом, чтобы найти периметр фигуры, достаточно измерить длину каждой стороны и сложить все результаты. Однако иногда можно сделать расчет более простым способом с помощью специальных формул. Далее разберем способы нахождения периметра различных фигур с помощью обоих методов.
Периметр треугольника
Перед тем как вычислить периметр треугольника, необходимо измерить длину каждой стороны. После этого просто сложите их — это и будет периметр.
Однако если мы имеем дело с равнобедренным треугольником, можно измерить одну из равных сторон и умножить полученное значение на два, а затем прибавить к нему длину основания.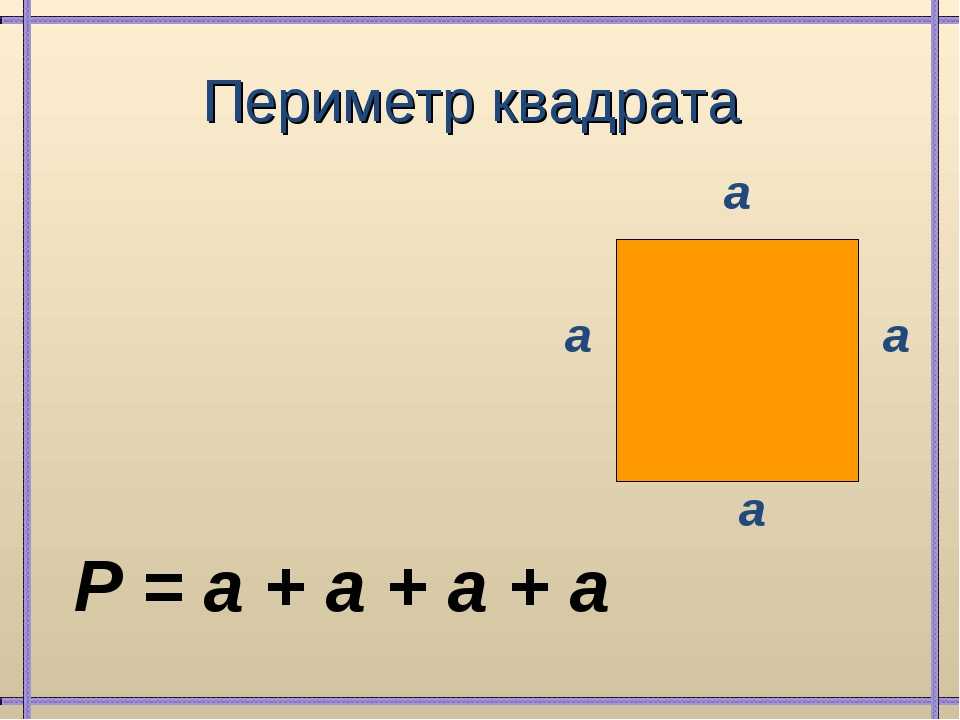
Для вычисления периметра равностороннего треугольника, достаточно и вовсе померить только одну сторону и умножить полученное значение на три.
Периметр четырехугольника
Разберем в данном разделе, как вычислить периметр квадрата, ромба, прямоугольника, параллелепипеда и трапеции.
Квадрат и ромб
Как известно, у квадрата четыре стороны и все они равны, а значит, для вычисления периметра квадрата необходимо померить одну из его сторон, а затем умножить полученное значение на 4. Собственно говоря, точно так же находится периметр ромба, потому как у ромба все стороны равны.
Прямоугольник и параллелограмм
У прямоугольника стороны равны попарно, таким образом, для вычисления периметра, потребуется померить большую и меньшую сторону, каждое из полученных значений умножить на два и сложить получившиеся значения. Аналогично находится периметр параллелограмма.
Трапеция
Еще один тип четырехугольника — трапеция. У этой фигуры, как правило, все стороны разной длины, а потому для нахождения периметра придется измерить каждую сторону и сложить их. Однако трапеция может быть равнобедренной. В таком случае для расчета периметра можно воспользоваться следующей формулой: P = a+b+2c, где c — длина одной из равных сторон.
Однако трапеция может быть равнобедренной. В таком случае для расчета периметра можно воспользоваться следующей формулой: P = a+b+2c, где c — длина одной из равных сторон.
Существует, кстати, еще один способ определения периметра равнобедренной трапеции — так называемый «метод средней линии». Сначала нужно провести эту самую среднюю линию (она проводится через две точки — середины равных сторон), затем надо измерить ее, умножить полученное значение на два и прибавить две длины равных сторон.
Периметр многоугольника
Для нахождения периметра многоугольника, как правило, действует правило — измерь все стороны и сложи их. Однако некоторые частные случаи позволяют более просто справиться с задачей. Например, если перед вами так называемый правильный шестиугольник, его периметр можно посчитать, умножив длину стороны на 6.
Для расчета периметра круга или, как говорят чаще, длины окружности, существует специальная формула: P=2πr, где π — постоянное значение, равное 3,14; r — радиус окружности. Формула также может выглядеть так: P=πd, где d- диаметр окружности.
Формула также может выглядеть так: P=πd, где d- диаметр окружности.
Кстати, фактически π — это отношение длины окружности к ее диаметру. Доказано, что это значение для всех окружностей одинаково и равно 3,14.
Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.
И как же найти периметр этих фигур?
Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .
Периметр обозначается заглавной латинской буквой Р .
Давайте рассмотрим несколько примеров.
Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:
Р = 15 + 17 + 10 + 10 + 20 + 15 = 87
Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Р = 15 × 2 + 10 × 2 + 17 + 20 = 87
Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.
Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :
Р(прямоугольника) = (а + б) × 2
То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:
Р = (5 + 3) × 2 = 16 см
А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?
Р(прямоугольника) = 2 × а + 2 × б
а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2
Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?
Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны.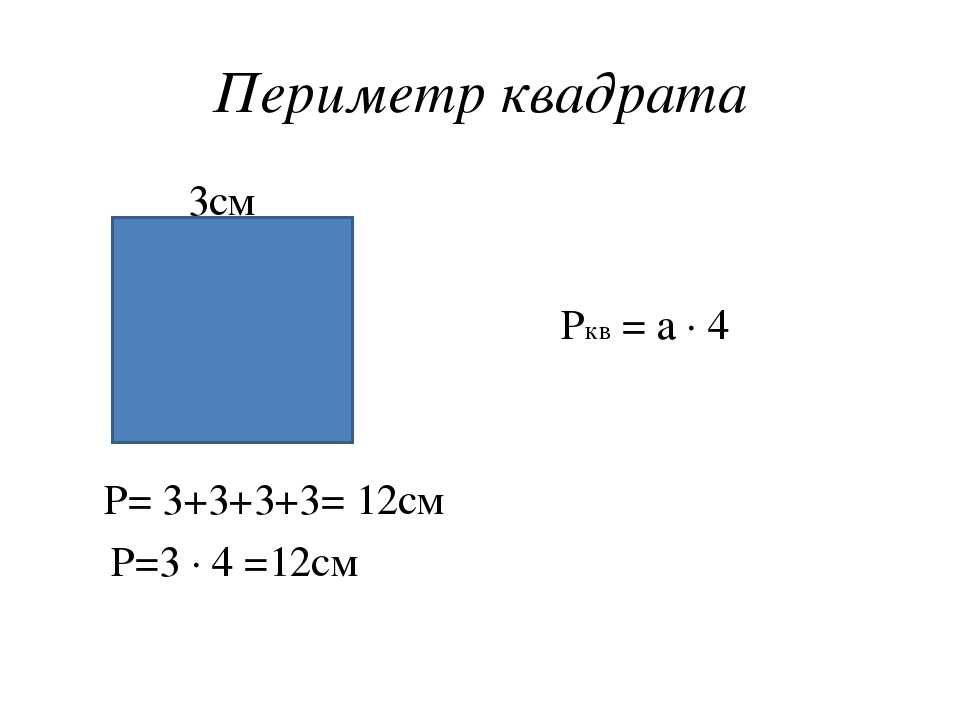 Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
сторона б = (16 – 2 × 5) ÷ 2 = 3 см
Ответ: у прямоугольника две стороны по 5 см и две по 3 см.
Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:
Р(квадрата) = а × 4
Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:
Р(В) = 5 × 4 = 20 см
А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:
а = Р ÷ 4
Пример: Периметр квадрата 24 см. Чему равны его стороны?
а = 24 ÷ 4 = 6
Ответ: Стороны квадрата равны 6 см.
По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.
Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:
Р(равностороннего многоугольника) = а × n
Например, у пятиугольника Д сторона а = 6 см
.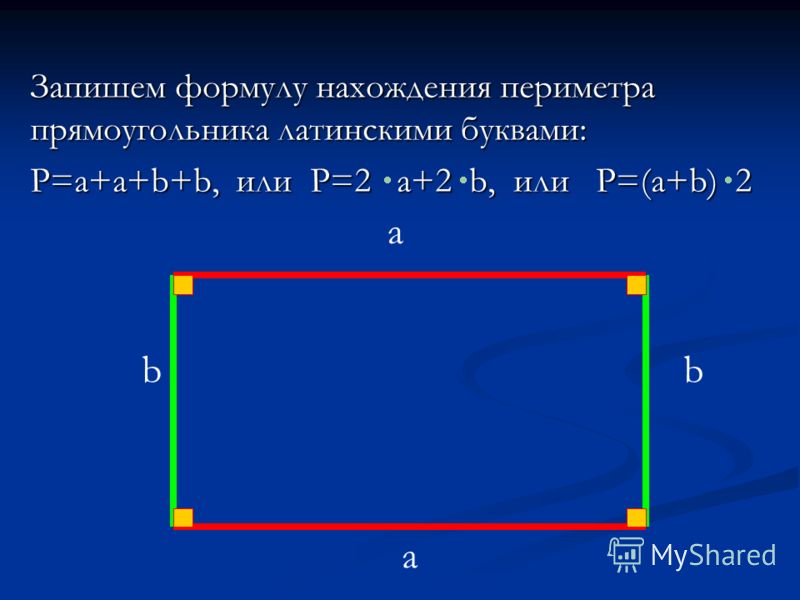
Р(Д) = 6 × 5 = 30 см
Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Какой буквой обозначается площадь и периметр … -reshimne.ru
Новые вопросы
Ответы
S площадь
P периметр
p полупериметр
P-периметр;
S-площадь
Похожие вопросы
Помогите пожалуйста упростить….
Разложите многочлены на множители путем вынесения общего множителя за скобку
10а-5b=
Ax-ay=
Ab+b=…
(x-1)(x+4)>0
(x+2)(x-3)<0
(x-5)(x-1,5)<0
(x-4)(x+3)<0…
Задайте формулой функцию, если значения функции:
1) на 3 меньше соответствующего значения аргумента
2) на 5 больше удвоенного значения соответствующего аргумента.
Тетрадь стоит 20р. Какое наибольшее число таких тетрадей можно будет купить на 350р. после понижения цены на 15%…
Помогите!!!!!!!!¡¡¡¡¡¡¡¡¡…
Математика
Литература
Алгебра
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖПсихология
Периметр это в математике — Математика и Английский
Периметр это в математике
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».
Периметр измеряется в единицах длины: мм, см, м, км и т. д.
При Нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.
Запомните!
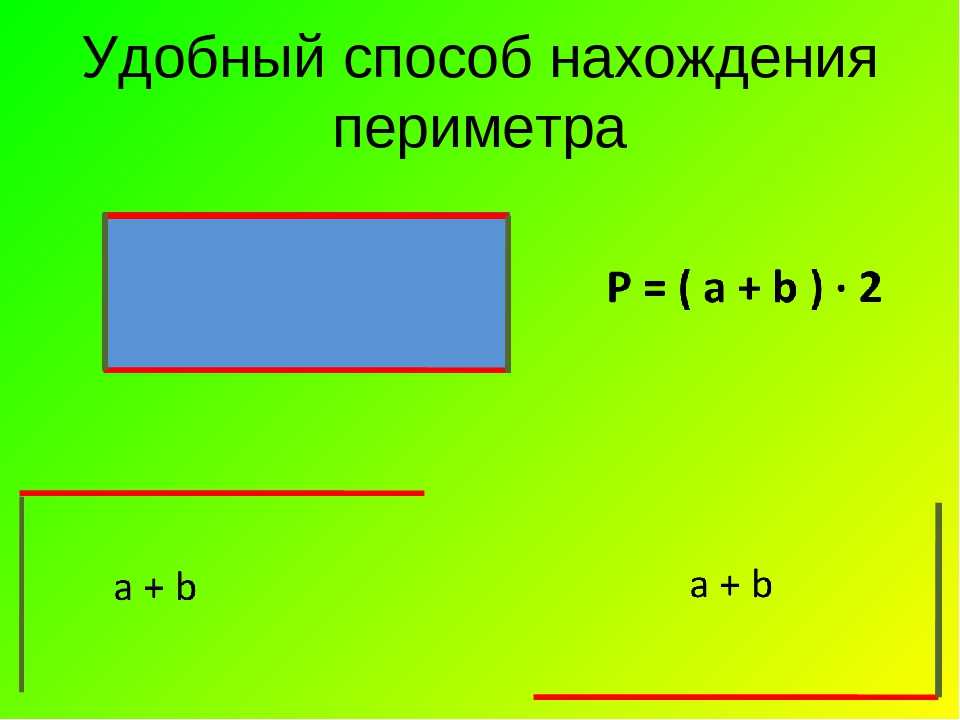
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.
AB = 3 см, BC = 7 см
PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
Запомните!
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».
KE = 7 см
PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и Периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.
Для этого надо просто сложить длины всех сторон многоугольника.
PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
AB = 3 см, BC = 7 см
KE = 7 см
При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком P, чтобы не забывать чей периметр вы находите.
Math-prosto. ru
24.12.2017 9:02:21
2017-12-24 09:02:21
Источники:
Https://math-prosto. ru/ru/pages/perimeter/perimeter/
Урок 49. периметр прямоугольника — Математика — 2 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Периметр это в математике
Изучение правила вычисления периметра прямоугольника.
Глоссарий по теме:
Прямоугольник – четырёхугольник, у которого все углы прямые.
Периметр – сумма длины всех сторон плоской фигуры.
Основная и дополнительная литература по теме урока:
1. Математика.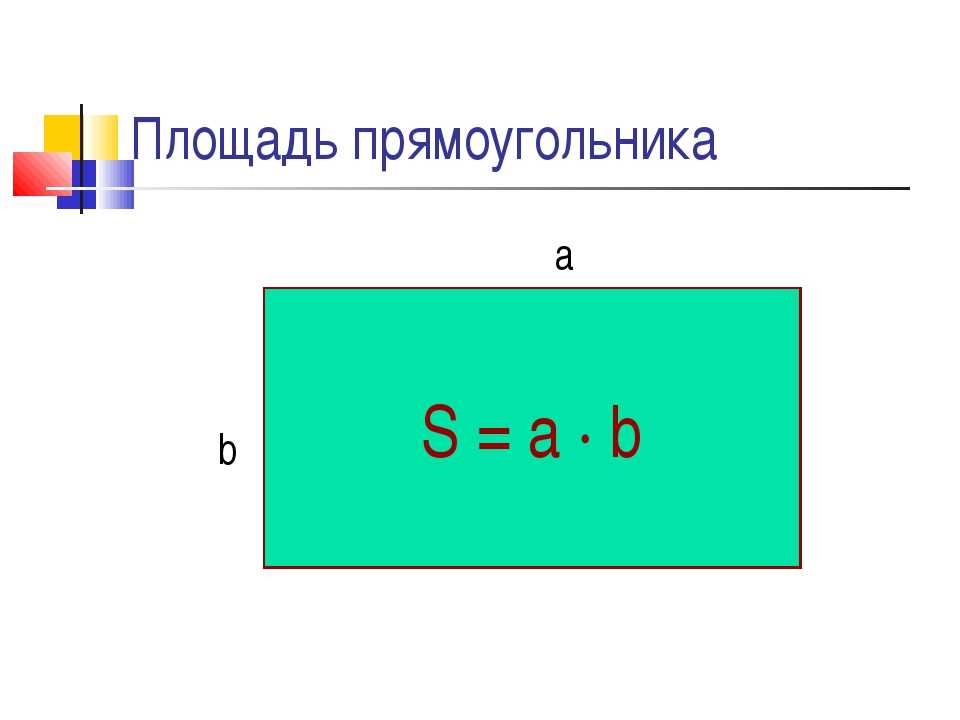 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –
2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –
8-е изд. – М.: Просвещение, 2017. – с.16.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А.Бантова –
7-е изд., дораб. – М.: Просвещение, 2016. – с.22.
Открытые электронные ресурсы по теме урока:
Интересные факты о математике. Познай мир. URL:
Теоретический материал для самостоятельного изучения
Прямоугольные предметы окружают нас повсюду.
Рамки, телефоны, тетради и многое другое.
Данная фигура – прямоугольник. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Прямоугольник – это четырёхугольник, у которого четыре прямых угла и стороны попарно равны.
Рассмотрим следующую задачу: «Вокруг дачного участка необходимо поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится?»
Забор какой длины получится?»
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон.
Ширина
У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров.
Составим выражение для подсчета длины забора. Это первый способ вычислений: 5 + 10 + 5 + 10
Воспользуемся переместительным законом сложения:
5 + 10 + 5 + 10 = 5 + 5 + 10 + 10
В данном выражении есть суммы одинаковых слагаемых
5 + 5 и 10 + 10
В этой записи рядом стоят две пары одинаковых чисел. А ведь сумму одинаковых слагаемых можно заменить Умножением. Это второй способ вычислений:
5 + 5 + 10 + 10 = 5 · 2 + 10 · 2
Теперь воспользуемся распределительным законом умножения относительно сложения. Это третий способ вычислений: 5 · 2 + 10 · 2 = (5 + 10) · 2
Этот способ можно назвать Рациональным, то есть, наиболее удобным и коротким, потому что в нём меньше действий, чем в предыдущих способах.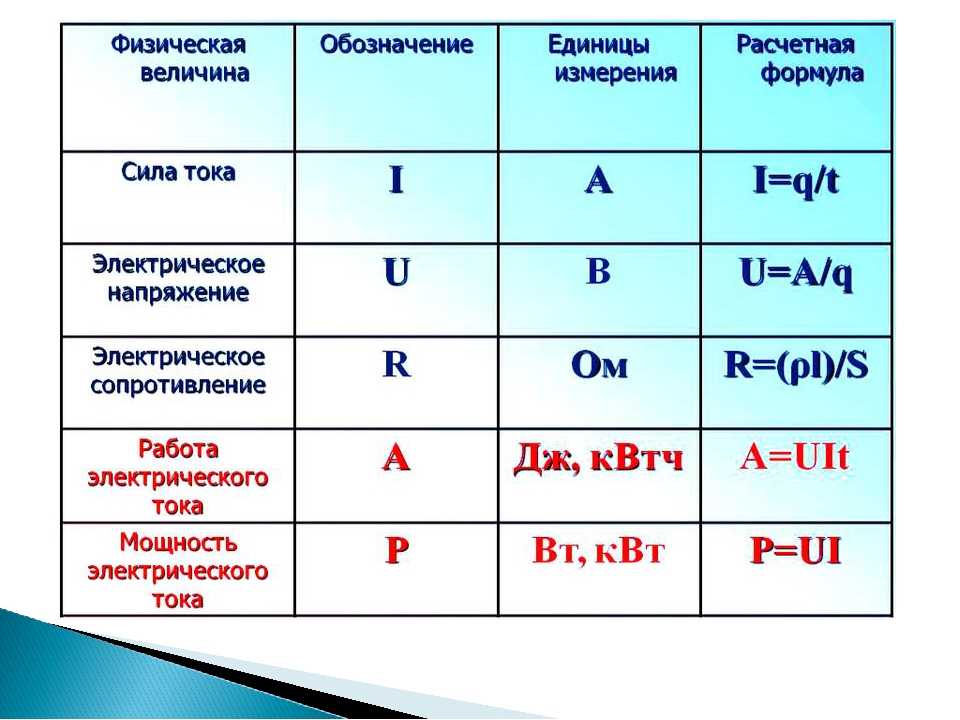
Найдём значение выражения (5 + 10) · 2
Сначала выполняем действие в скобках: 5 + 10 = 15
А затем повторяем число 15 два раза: 15 · 2 = 30.
Ответ: 30 метров забор вокруг участка.
Забор вокруг участка — это периметр этого участка. Периметр прямоугольника – сумма длин всех его сторон.
Делаем вывод: Периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.
Тренировочные задания.
1. Решите задачу: Длина листа картона 4 см. Ширина 3 см. Вычислите периметр данного листа. Запишите решение тремя способами.
1 способ. 4+3+4+3=14 (см)
2 способ. 4 · 2+ 3·2=14 (см)
3 способ. (4+3) ·2=14 (см)
Ответ: 14 сантиметров периметр листа картона.
2. Выберите верное решение:
Длина прямоугольника 5 см, ширина 3 см. Чему равен периметр прямоугольника?
ширина
Вспомним, какие отличительные особенности прямоугольника мы знаем.
Resh. edu. ru
29.05.2018 1:59:41
2017-10-05 03:25:26
Источники:
Https://resh. edu. ru/subject/lesson/3685/conspect/
Как найти периметр прямоугольника, формула ⬅️ » /> » /> .keyword { color: red; }
Периметр это в математике
Мы уже изучили много формул, умеем решать задачки разной сложности, помним, где применить эти знания помимо школы. Дальше — больше. В данном материале подробно рассмотрим, как вычислить периметр прямоугольника.
О чем эта статья:
Основные определения
Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.
Периметр — это сумма длин всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если длины сторон заданы в разных единицах измерения, мы не сможем узнать периметр прямоугольника.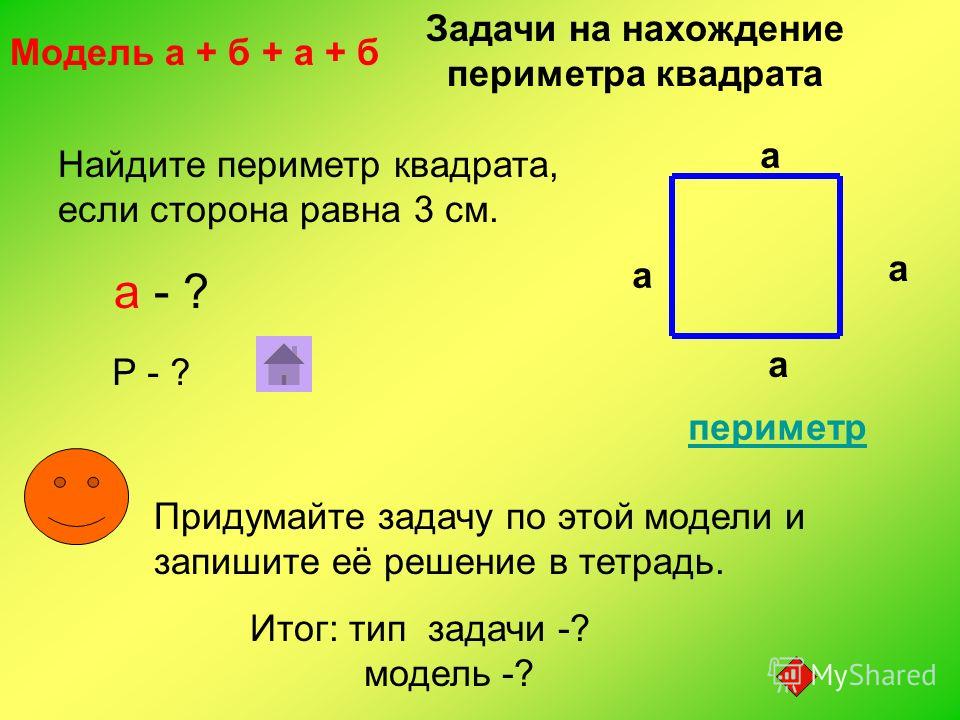 Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Километр (км) и другие единицы измерения длины.
Формула нахождения периметра прямоугольника
С формулой вычисления периметра прямоугольника школьники знакомятся во втором классе. Найти периметр по этой формуле можно, если известны все или две соседние стороны прямоугольника.
О чем эта статья.
Skysmart. ru
09.03.2018 20:22:47
2018-03-09 20:22:47
Источники:
Https://skysmart. ru/articles/mathematic/perimetr-pryamougolnika
Как обозначается площадь: какой буквой или знаком пишется параметр площади в математике
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Содержание
Общие сведения
Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.
Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.
Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества.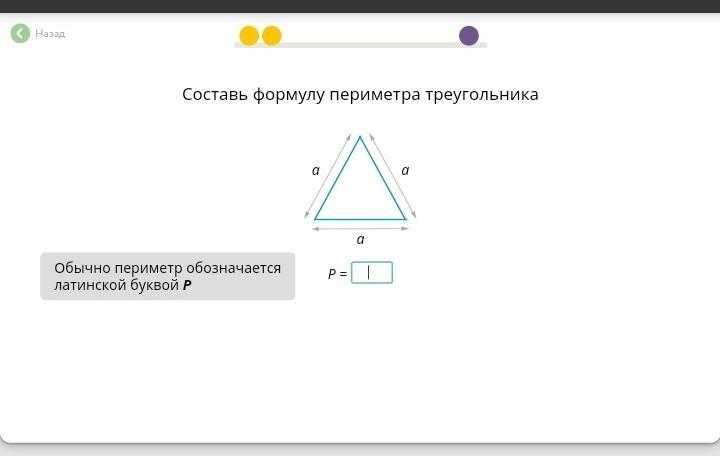 Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:
- Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.
- Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
- Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
- Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.

- Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.
Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.
Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения
Понятие используется не только в математике. Оно актуально и для физики.
В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.
Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.
Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Прямоугольник
Меню раздела
- Математика
Рейтинг: 1 / 5
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5Определение прямоугольника
Признаки и свойства
.
Прямоугольник – это четырёхугольник, у которого все углы прямые, то есть по 90 градусов, а противоположные стороны прямоугольника равны между собой. Сам прямоугольник обычно записывается путем перечисления его вершин (обозначается латинскими буквами – ABCD). Длинную сторону прямоугольника называют длиной (обозначается латинской буквой – a), а короткую – шириной (обозначается латинской буквой – b). Стороны прямоугольника одновременно является его высотами (см. Рис. 1).
AB = CD
BC = AD
Условные обозначения
- a — длина
- b — ширина
- P — периметр
- S — площадь
Периметр и площадь прямоугольника
P = a + b + a + b; P = a · 2 + b · 2; P = 2a + 2b – периметр прямоугольника
S = a · b – площадь прямоугольника
Прямоугольником называют параллелограмм, у которого все углы прямые (см. Рис. 2).
Рис. 2).
Свойство прямоугольника. Диагонали прямоугольника равны (см. Рис. 3).
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Пример нахождения периметра прямоугольника
Чтобы найти периметр прямоугольника, нужно сложить две его смежные стороны и умножить сумму на два.
AB = CD = 2
BC = AD = 4
P = AB + BC + CD AD
P = 2 + 2 + 4 + 4 = 12
P = (2 + 4) · 2 = 12
Задачи и решения на нахождение периметра и площади
Домашнее задание
Чтобы легко и быстро решать аналогичные задачи нужно закрепить знания выполнив несколько заданий самостоятельно. Реши задачу и дай ответ.
- Найди периметр прямоугольника со сторонами 9 и 6 см.
- Найди периметр прямоугольника со сторонами 7 и 8 см.
- Найди длину прямоугольника, если его ширина 7 см, а периметр равен 28 см.
- Найди ширину прямоугольника, если его длина 10 см, а периметр составляет 30 см.
- Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.
- Ширина прямоугольника 4 см. Длина на 3 см больше. Найди его периметр и площадь.
- Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
- Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6. На сколько см² он ошибся?
- Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
- Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
- Площадь прямоугольника 40 см². Ширина его 5 см. Чему равен периметр прямоугольника?
- Длина прямоугольника 20 см, ширина 15 см.
Найди длину прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.
- Длина прямоугольника 16 см. Ширина 4 см. Найди длину прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Эратосфен
Эратосфен Киренский — греческий математик, астроном, географ, филолог и поэт
Дата рождения: 276 до н. э.
Место рождения: Кирена (территория современной Ливии)
Дата смерти: 194 до н. э.
Биография
Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки. Первый известный учёный, вычисливший размеры Земли.
Начальное образование Эратосфен получил в Александрии под руководством своего учёного земляка Каллимаха. Другим учителем Эратосфена в Александрии был философ Лизний.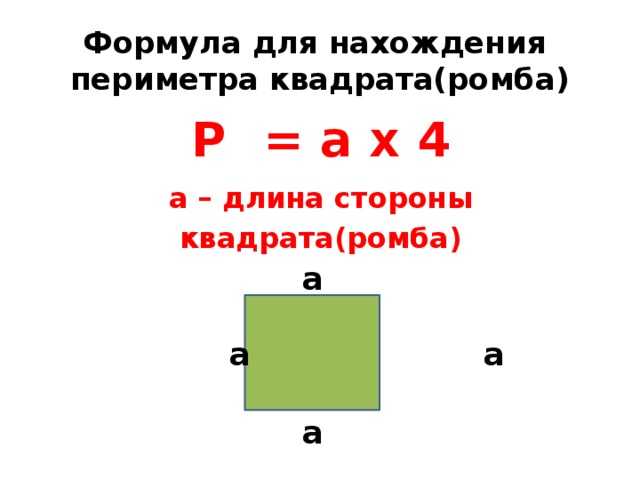 Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена.
Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена.
В 245 году до н. э. царь Птолемей III Эвергет пригласил Эратосфена приехать из Афин, чтобы работать в Александрийской библиотеке, где уже трудились его учитель Каллимах и Аполлоний Родосский. Эратосфен откликнулся на приглашение, в возрасте около тридцати лет он приехал в Александрию, где и остался до самой смерти.
Через пять лет после приезда он сменил Аполлония Родосского на посту главы Александрийской библиотеки. Как глава библиотеки, Эратосфен занимался обучением детей монарха — будущего правителя Птолемея IV и его сестры Арсинои.
На посту главы библиотеки активно занимался её расширением и развитием, стремясь поддержать репутацию библиотеки в соперничестве с Пергамской библиотекой. По его просьбе александрийские портовые власти изымали все книги с приходящих кораблей для изучения и копирования. Эратосфен приобретал аутентичные копии трагедий великих греческих авторов — Эсхила, Софокла и Эврипида, а также учредил в библиотеке целый отдел, занимавшийся изучением творчества Гомера.
Эратосфен приобретал аутентичные копии трагедий великих греческих авторов — Эсхила, Софокла и Эврипида, а также учредил в библиотеке целый отдел, занимавшийся изучением творчества Гомера.
Ппрозвищем Эратосфена было «пентатлос» — пятиборец, то есть всесторонне развитый человек, оно было ему дано за одарённость в самых разных областях знания.
В честь Эратосфена назван кратер на Луне, один из периодов геологической истории Луны, а также подводная гора в Средиземном море, близ Кипра.
Некоторые его работы:
- Удвоении куба
- Прибор под именем мезолябия
- О средних величинах
- Алгоритм «разворачивания всех рациональных отношений из отношения равенства»
- Решето Эратосфена
- Определил угловое расстояние от экватора до тропика
- Измерении длины земного меридиана
- Создал первую карту мира
- Назад
- Вперед
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Продырявили «Северный поток-2» Прекращение торгов долларом Застрелил дочь из ружья Изрезал ножом собственную дочь В составе России В школе № 26 отравились дети Кадыров заявил о перевыполнении плана призыва в Чечне на 254% Мальчика наградили орденом Мужества Избили, задушили и положили в ванну Все наши прежние действия покажутся детскими шалостями Обнаружили тело 14-летнего подростка Ваше место в «музее времен СССР» Питомец заразил всю семью лишаем 5 правил, как уберечь ребенка от негативного контента в интернете Сегодня Путин выступит с обращением к жителям России Школьника избили в батутном центре в Москве
Запомнить меня
Регистрация
Периметр и Площадь 3 класс презентация, доклад, проект
ПЕРИМЕТР
и
ПЛОЩАДЬ
Учитель начальных классов
ГБОУ СОШ № 335
Фомичева Ирина Николаевна
ПЕРИМЕТР
Периметр – это сумма всех длин сторон многоугольника.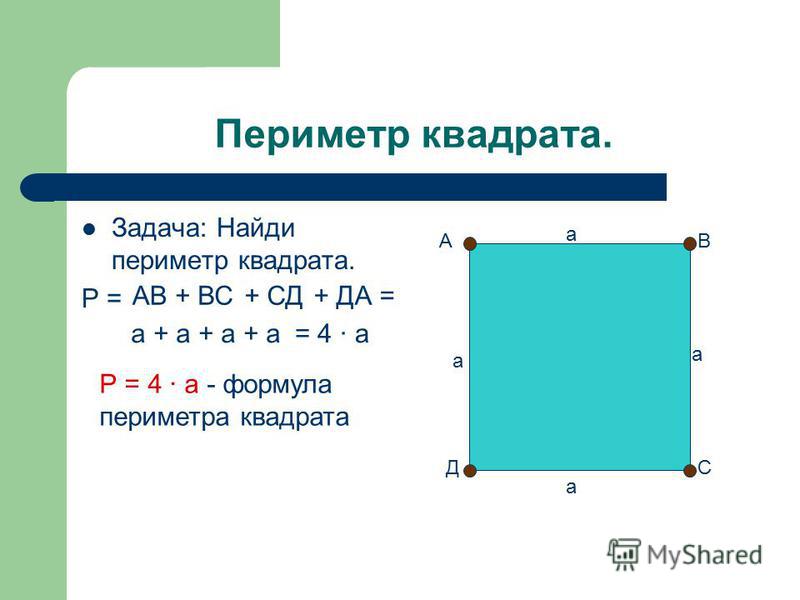
Периметр обозначается буквой латинского алфавита – Р (пэ), измеряется в мм, см, дм, м, км.
Что такое периметр?
3 см
2 см
Чему равен периметр
прямоугольника?
Периметр прямоугольника
3см + 2см + 3см + 2см =
= (3см + 2см) 2 = 10см
3см
2см
P = (a + b) 2
.
.
Периметр квадрата
3см + 3см + 3см + 3см =
= 3см 4 = 12см
3см
3см
P = a 4
.
.
Периметр треугольника
3см + 4см + 5см =
= 12см
5см
3см
P = a + b + c
4см
Назови каждый многоугольник
А
Б
В
Г
Д
Е
Ж
Практическая работа № 1
2
1
20
20
20
25
25
25
25
25
25
25
25
10
10
10
10
Р=?
Р=?
Р=25Х4+20Х3=160(см)
Ответ: Р=160 см
Р=25Х4+10Х8=180(см)
Ответ: Р=180 см
Проверь:
Практическая работа № 2
15
10
10
10
10
10
10
20
10
20
10
15
15
10
10
25
20
30
1. У каких фигур одинаковый периметр?
У каких фигур одинаковый периметр?
2. У каких фигур в каждой паре периметр
меньше: Аи В, Б и Г?
Проверь:
1. РБ=РВ
2. B
Б
В
А
Г
10
Сколько всего треугольников?
ПЛОЩАДЬ
S
Площадь обозначается буквой латинского алфавита S (эс), измеряется в мм² , см² , дм², м², км².
Площадь фигур измеряют единичными квадратами.
Площадь фигуры равна числу единичных квадратов, составляющих фигуру.
Площадь квадрата со стороной 1 см равна
1 квадратному сантиметру (1см²) .
Б
Определи площадь фигур в клетках
12
50
14
16
18
Как найти площадь?
Площадь прямоугольника можно найти, умножив его длину на ширину.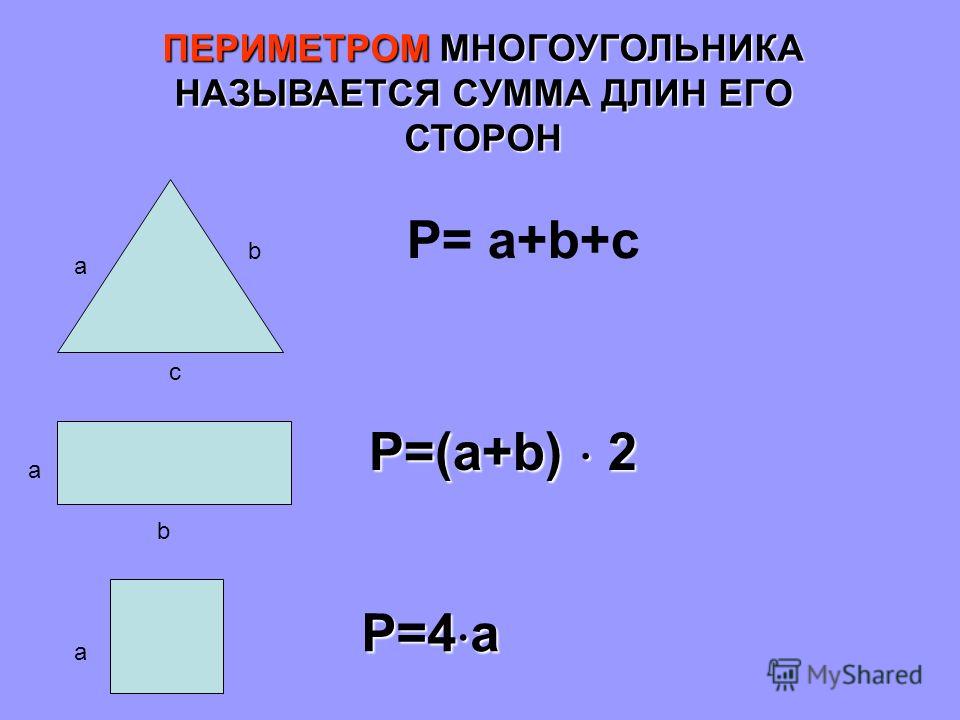
Площадь прямоугольника 3см 2см = 6 см²
S= a b
3см
2см
.
.
Площадь квадрата
3см 3см = 9 см²
3см
3см
S= a а = а²
Площадь квадрата равна произведению двух сторон или же квадрату его стороны.
.
.
Практическая работа № 1
Перед тобой план клумбы городского парка.
Её размеры указаны в метрах.
4
2
2
4
2
Проверь:
S= 2Х2+4Х4+2Х2+4Х4+2Х2= 44(м²)
Вычисли площадь отдельной клумбы.
Узнай чему равна площадь всей клумбы?
Практическая работа № 2
Перед тобой план земельного участка .
1 вариант
1. Площадь сада.
2. Площадь парника.
3. Площадь огорода.
4. Площадь огорода
(без парника).
Огород
Сад
16 м
16 м
16 м
16 м
Парник
Дом
8 м
8 м
10 м
10 м
Цветник
2 вариант
1. Площадь сада.
2. Площадь дома.
3. Площадь цветника.
3. Площадь цветника (без дома).
Вычисли в квадратных метрах:
2 вариант
1 вариант
1. Площадь сада.
S= 16Х16= 256 (м²)
1. Площадь сада.
S= 16Х16= 256 (м²)
2 . Площадь парника
S= 8Х8= 64 (м²)
2. Площадь дома.
S= 10Х10= 100 (м²)
3. Площадь огорода.
S= 16Х16= 256 (м²) —
весь огород.
4. Площадь огорода без парника.
S = 256 – 64=192 (м²)
4. Площадь цветника без дома.
S= 256 – 100=156 (м²)
3. Площадь цветника.
Площадь цветника.
S= 16Х16= 256 (м²) —
весь участок
Проверь:
Сколько всего квадратов?
S
?
15
Картинки с сайта:
http://lenagold.ru/fon/clipart/alf.html
— И. И. Аргинская, Е.И.Ивановская, С.Н.Кормишина — учебник «Математика», 3 класс,
Издательство «Учебная литература» ОАО «Московские учебники», 2010 год.
Скачать презентацию
Расшифровать ПЕРИМЕТР — Расшифровать 149 слов из букв в ПЕРИМЕТРЕ
ПЕРИМЕТР расшифровать и сделать 149 слова!Начинается с
Заканчивается на
Содержит
Реклама:
149 Расшифрованные слова из букв ПЕРИМЕТРСлова из 9 букв, составленные из расшифрованных букв ПЕРИМЕТР
- периметр
Сколько слов можно составить из ПЕРИМЕТРА?
Выше приведены слова, полученные путем расшифровки P E R I M E T E R (EEEIMPRRT) . Наш инструмент для расшифровки слов смог расшифровать эти буквы, используя различные методы, чтобы сгенерировать 149 слов ! Наличие такого инструмента для расшифровки, как наш, поможет вам во ВСЕХ играх со словами!
Наш инструмент для расшифровки слов смог расшифровать эти буквы, используя различные методы, чтобы сгенерировать 149 слов ! Наличие такого инструмента для расшифровки, как наш, поможет вам во ВСЕХ играх со словами!
Сколько слов можно составить из ПЕРИМЕТРА?
Чтобы еще больше помочь вам, вот несколько списков слов, связанных с буквами ПЕРИМЕТР.
- Слова из 9 букв
- слов, начинающихся с P
- слов, оканчивающихся на R
- Слова, начинающиеся на ПЕРИМЕТР
- Слова, содержащие ПЕРИМЕТР
- Слова, оканчивающиеся на ПЕРИМЕТР
- Различные способы борьбы с ПЕРИМЕТРОМ
ПЕРИМЕТР Значения букв в Word Scrabble и Words With Friends
Вот значения букв ПЕРИМЕТР в двух самых популярных играх со словами.
Scrabble
Буквы ПЕРИМЕТР стоят 13 очков в Scrabble
- P 3
- Е 1
- Р 1
- я 1
- М 3
- Е 1
- Т 1
- Е 1
- Р 1
Слова с друзьями
Буквы ПЕРИМЕТР стоят 15 баллов в Words With Friends
- P 4
- Е 1
- Р 1
- я 1
- М 4
- Е 1
- Т 1
- Е 1
- Р 1
Если расшифровать ПЕРИМЕТР.
 .. Что это значит?
.. Что это значит?Определение ПЕРИМЕТРА в расшифрованном виде
Если расшифровать эти буквы, ПЕРИМЕТР, то он и составит несколько слов. Вот одно из определений слова, в котором используются все незашифрованные буквы:
Периметр
- Прибор для определения размера и формы поля зрения.
- Внешняя граница тела или фигуры или сумма всех сторон.
- Нажмите здесь, чтобы увидеть полное значение периметра
- Является ли периметр словом Scrabble?
- периметр — это слово Words With Friends?
Дополнительная информация о буквах
ПЕРИМЕТР- Перестановки ПЕРИМЕТРА
- Анаграммы ПЕРИМЕТРА
- слов с буквами
Расшифровка ПЕРИМЕТРА для других игр Word Scramble
- Расшифровка PERIMETER для игр Word Scramble
- Расшифровать буквы ПЕРИМЕТРА для анаграмм
- ПЕРИМЕТР в Text Twist
- ПЕРИМЕТР в Scrabble
- ПЕРИМЕТР словами с друзьями
- ПЕРИМЕТР в беспорядке
- Расшифруй слово ПЕРИМЕТР
- ПЕРИМЕТР Расшифруй для всех словесных игр
Шифрование букв по ПЕРИМЕТРУ
Согласно нашему другому слову, ПЕРИМЕТР можно зашифровать разными способами. Различные способы перестановки слова называются «перестановками» слова.
Различные способы перестановки слова называются «перестановками» слова.
Согласно Google, это определение перестановки:
способ, особенно один из нескольких возможных вариантов, в котором можно упорядочить или расположить набор или количество вещей.
Чем это полезно? Ну, он показывает вам анаграммы периметр зашифрован по-разному и помогает вам легче распознавать набор букв. Это поможет вам в следующий раз, когда эти буквы, П Е Р И М Е Т Е Р, появятся в игре со словами.
ЭРТПЕМЕИР ПИРТЕЕМР ЭИТПЕРМЕР РТИЕМПЕР ИЕМЕПРЕТР ИМПЕРЕТР ИЭЭРМТЕПР РЕПТЕЕМИР IEEPMRER МИРЕТЕПЕР ТПМЕИРЕР ЭМИЭТПРЕР EEPERITMR ЕРЕМИЭПТР TEEIMREPR МРИПТИЕР TEEIEMPRR ПИЕРМИТР IPREETMER ЭТМИРПИР REPIEEMTR ИМЭЭПРЕТР ПЕРЕЕМТИР ТИПМРИР ЕРЕМЕПТИР ЭТМПЕРИР MRPEEEITR EERMTEPR МИТПЕРЕР МПРЕТЬЕ ЭТПЕРМЕИР ИРЕТМПЕР ТРИМЭЙПР РИТЭЭМЕПР RTMIEEEPR РЕЕМПЕТР ПИРМЕЭТР МЕЙРЕПЕТР ЭРПТЕЙЭМР ПЕМТРИЕ МПЕРИЭТР IEETRPMER ЭРИЕМТПЕР ЭПЕРЕМИТР PMTEEERR ЭПЕТЕМИРР EIEMTEPRR ЭРЕПТЕЙМР ИПРЕЕМЕТР ЕРЕЭПТМИР
Мы остановились на 50, но есть так много способов зашифровать ПЕРИМЕТР !
Word Scramble Words
- enneuregr
- eiiovnmss
- пуэдткас
- церроефс
- эрхдкнейд
- кинекфлае
- треввиец
- ккрбгьяас
- hcoapyrly
- etvvoroes
- ersvaeesd
- элнуэпс
- эрульбгард
- эйнауэрур
- лкокмойн
- oitissdan
- эсарвоилс
- sehscieet
- ненлеомрт
- итонкорс
Расшифруй эти буквы, чтобы получились слова.
Все слова были зашифрованы с помощью скремблера слов…
нифет гларн часовня Брани качественно чамт комок саткег дирмель румтия тихо глаупе изменять глубочайший плюти хор средство для удаления gotoes слова rfteer dtroaw Клисек накл читы Соника искатель беспорядок рнбда zugea тоари litfeu помощник все cinlpe рхогт дирсуа
Combine Words
Bird + Duck = Bick
Apple + Honor = Aplonor
Hand + Locker = Handocker
Combine Names
Brad + Анджелина = Бранджелина
Роберт + Кейтлин = Робин
Грегори + Джанет = Гране
9 слов и имен с нашим Word Combiner0009
Вы расшифровали ПЕРИМЕТР!
Теперь, когда ПЕРИМЕТР расшифрован, что делать? Это просто, иди и выиграй свою игру в слова!
Произошла ошибка | wordhelp.
 com Произошла ошибка | wordhelp.com
com Произошла ошибка | wordhelp.com- Дом
- Форум
- Блог
- Энциклопедии
- Искатели слов
- Инструменты Word
- Сокращения
- Словарь
- Определения
- Синонимы
- Тезаурус
- Антонимы
- Эрудит
- Wordfeud
- Кроссворд
- Слова с друзьями
- Рифмы
- слогов
- предложений
- Преобразование текста в речь
- Части речи
- Контакт
- Часто задаваемые вопросы
- О
- Конфиденциальность
- Печенье
- Согласие
- Условия использования
Спряжение глаголов
Эрудит
Сожалеем, но произошла ошибка. Причина этой ошибки: « Не допускаются буквы в поиске анаграммы ». Попробуйте посетить нашу страницу с советами и рекомендациями по поиску.
Причина этой ошибки: « Не допускаются буквы в поиске анаграммы ». Попробуйте посетить нашу страницу с советами и рекомендациями по поиску.
Реклама
Последние поиски
оэрвлев (анаграмма) шдюну (анаграмма) ранить (анаграмма) лоран (анаграмма) премьера (анаграмма)
Таблица очков Scrabble
Обзор того, сколько очков принесет вам каждая буква в настольной игре Scrabble. От одного балла за самые распространенные буквы до 10 баллов за редкие. Не забывайте играть буквами, которые дают вам наибольшее количество очков!
От одного балла за самые распространенные буквы до 10 баллов за редкие. Не забывайте играть буквами, которые дают вам наибольшее количество очков!
| Оценка | Письмо |
|---|---|
| 1 шт. | Е А я О Н р Т л С U |
| 2 шт. | Д грамм |
3 шт. | Б С М п |
| 4 шт. | Ф ЧАС В Вт Д |
| 5 шт. | К |
| 8 шт. | Дж Икс |
10 шт. | Вопрос Z |
Случайное слово с рекордом
34р. РЕМИФОЛОГИЗАЦИЯ
Обновление
Реклама
Реклама
ПЕРИМЕТР Кроссворд и синонимы
Решатель кроссвордов Решатель слов Эрудит Решатель Синонимы Решатель анаграмм Решатель ВВФ Слова
Решатель кроссвордов > Подсказки > Crossword-Clue: Perimeter
2
3
4
5
6
7
8
10 0009
. Взгляд на фильт 5 Буквы:
Взгляд на фильт 5 Буквы:
- АМБИТ
- ПРЕДЕЛ
4 Буквы:
- КРАЙ
Все 16 ответов для: Периметр
| Опции | ||||||
|---|---|---|---|---|---|---|
| Периметр с 3 буквами | ||||||
РИМ | 3 | |||||
3 | ||||||
| Периметр с 4 буквами | ||||||
КРАЙ | 4 | |||||
АМБИТ | 5 | |||||
5 | ||||||
5 | ||||||
| Периметр с 6 буквами | ||||||
ГРАНИЦА | 6 | |||||
6 | ||||||
СХЕМА | 7 | |||||
7 | ||||||
7 | ||||||
| Периметр с 8 буквами | ||||||
ГРАНИЦА | 8 | |||||
8 | ||||||
ГРАНИЦА | 8 | |||||
ПЕРИФЕРИЯ | 9 | |||||
ДЛИНА ОКРУЖНОСТИ | 13 | |||||
Synonyms
Synonyms
.
 Мы нашли 27
Синонимы
Мы нашли 27
Синонимы3 буквы Слова
Lip
RIM
4 Загрузочный слово
Область
БРИМ
Диск
EDGE
HOOP
RING
0009
5 Letter Word
BRINK
ROUND
SCOPE
SHORE
SKIRT
6 Letter Word
BORDER
BOUNDS
CIRCLE
EDGING
FRINGE
LIMITS
MARGIN
7-буквенное слово
КОНТУР
КОМПАС
ПРОСТРАНСТВО
8-буквенное слово
ГРАНИЦА
00099-буквенное слово
ПЕРИФЕРИЯ
13-буквенное слово
ОКРУЖНОСТЬ
аналогичные вопросы
Top Questions, включая «Perimeters»
Новое предложение для «Периметра»
Знаете другое решение для кроссвордов, содержащих Периметр ? Добавьте свой ответ в базу данных кроссвордов прямо сейчас.
Подсказка
Ответ
Что такое 9 + 6
Пожалуйста, проверьте введенные данные еще раз
ПЕРИМЕТР расшифровано и найдено 118 слов.
Играть в игру Wordle
Расшифровка периметра с помощью нашего мощного расшифровщика слов дает 118 различных слов. 118 анаграмм периметра были найдены путем расшифровки букв в PERI M E T E R.
Слова из букв П Е Р И М Е Т Е Р сгруппированы по количеству букв в каждом слове. Всего 118 нешифрованных слов распределены по категориям следующим образом;
- Список из 9буквенные слова содержат 1 нешифрованное слово.
- Список слов из 8 букв содержит 3 нешифрованных слова.
- Список слов из 7 букв содержит 11 нешифрованных слов.
- Список слов из 6 букв содержит 19 нешифрованных слов.

- Список слов из 5 букв содержит 22 нешифрованных слова.
- Список слов из 4 букв содержит 30 нешифрованных слов.
- Список слов из 3 букв содержит 22 нешифрованных слова.
- Список слов из 2 букв содержит 10 нешифрованных слов.
- Расшифрованные анаграммы из двух слов
- Анаграмма периметра
Мы все любим словесные игры, не так ли? Все от мала до велика любят словесные игры. Мы помним те дни, когда мы играли в семье, когда мы ехали в машине и играли в игру «образование слов» из последней буквы. Играете ли вы в Scrabble, Text Twist или Word with Friends, все они имеют схожие правила. Но иногда нас раздражает, когда есть слова, которые мы не можем понять. На самом деле, нам нужна помощь в расшифровке слов. Некоторые люди называют это обманом, но, в конце концов, нельзя сказать, что небольшая помощь никому не навредит. В конце концов, получение помощи — это один из способов учиться.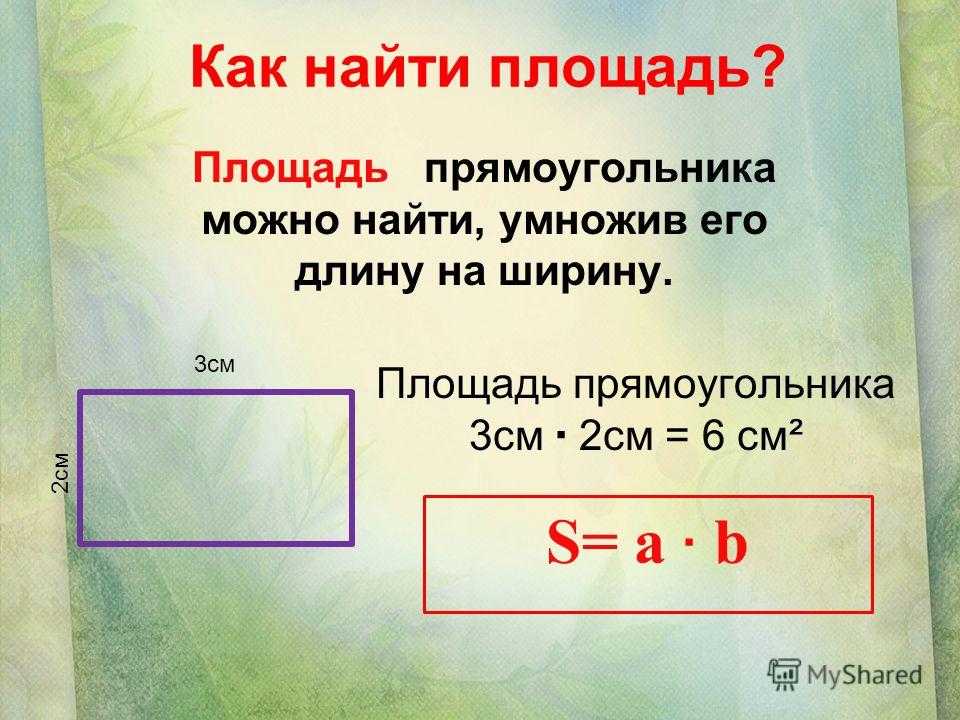 Что вам нужно сделать, это ввести буквы, которые вы ищете, в текстовое поле выше и нажать клавишу поиска. Например, вы когда-нибудь задумывались, какие слова можно составить из этих букв 9?0003 ПЕРИМЕТР . Наш расшифровщик слов или, другими словами, решатель анаграмм может найти ответ в мгновение ока и сказать
Что вам нужно сделать, это ввести буквы, которые вы ищете, в текстовое поле выше и нажать клавишу поиска. Например, вы когда-нибудь задумывались, какие слова можно составить из этих букв 9?0003 ПЕРИМЕТР . Наш расшифровщик слов или, другими словами, решатель анаграмм может найти ответ в мгновение ока и сказать 118 слов, найденных путем расшифровки этих букв ПЕРИМЕТР
.
Играть в словесные игры одно удовольствие.
Большинство расшифрованных слов найдено в списке слов из 4 букв. Периметр — слово из 9 букв. периметр имеет 3 определения. Определения периметра можно найти ниже;
Определения периметра
- поле
- линия границы или область непосредственно внутри границы существительное форма
- периметр
- линия, ограничивающая плоскостные области существительное форма
- длина окружности
- размер чего-либо, определяемый расстоянием вокруг него существительное атрибут
См. определение периметра в Merriam Webster
определение периметра в Merriam Webster
Слова из букв ПЕРИМЕТР
Слова, составленные из букв ПЕРИМЕТР ТЕР, можно найти ниже.
Слова из 9 букв, полученные путем расшифровки периметра
1 разные слова из 9 букв, составленные расшифровкой букв из периметра , перечисленных ниже.
- периметр
Слова из 8 букв, полученные путем расшифровки периметра
3 разных 8-буквенных слова, составленных расшифровкой букв из периметра , перечисленных ниже.
- восстанавливать
- темперамент
- премьера
Слова из 7 букв, полученные путем расшифровки периметра
11 различных слов из 7 букв, составленных расшифровкой букв из периметра , перечисленных ниже.
- предварительная обрезка
- недоношенный
- митра
- трирема
- более пустой
- премьер
- предварительная встреча
- пенсионер
- отшельник
- эпимер
- недоношенный
Слова из 6 букв, образованные расшифровкой периметра
19 различных 6-буквенных слов, составленных из расшифрованных букв из периметра , перечисленных ниже.
- подрезать
- тример
- разрешать
- грунтовка
- пертер
- термер
- характер
- выходить на пенсию
- ремесло
- перевыпускать
- повторное время
- империя
- эпимер
- премьера
- метр
- повторная встреча
- бурлит
- более жуткий
- Пири
Слова из 5 букв, полученные путем расшифровки периметра
22 разных 5-буквенных слова, составленных расшифровкой букв из периметра , перечисленных ниже.
- триер
- рубец
- священник
- более зрелый
- цена
- митра
- митра
- переводить
- таймер
- раймер
- темпы
- основной
- Питер
- метр
- метр
- ремет
- ретем
- просто
- рети
- вигвам
- эмер
- жуткий
Слова из 4 букв, полученные путем расшифровки периметра
30 различных слов из 4 букв, составленных из расшифрованных букв из периметра , перечисленных ниже.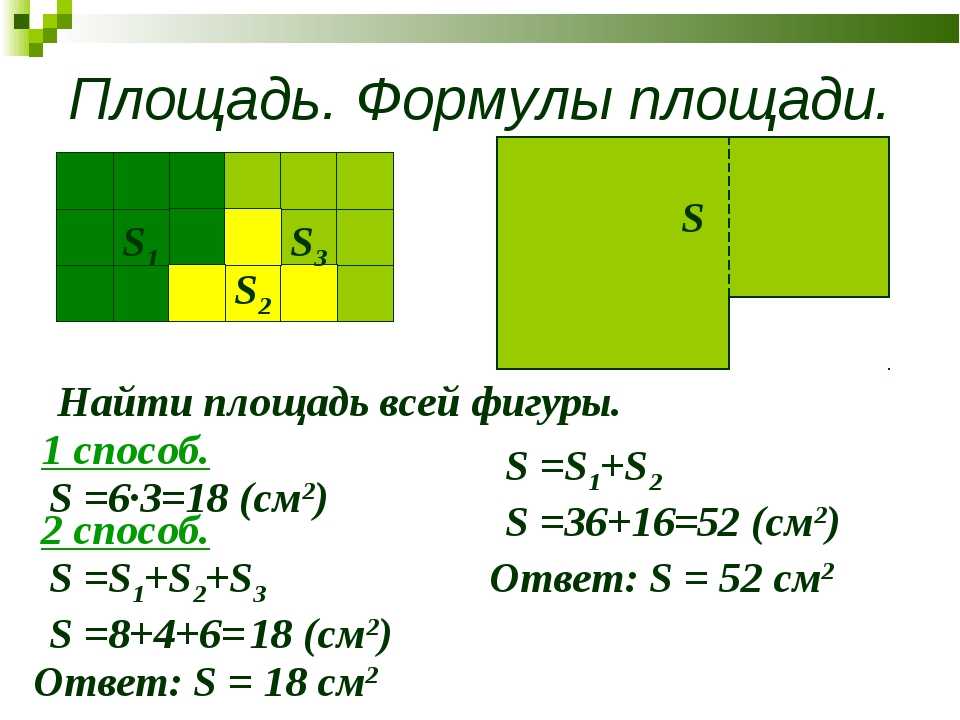
- путешествие
- подрезать
- чопорный
- дерзкий
- срок
- температура
- пермь
- обряд
- ярус
- шина
- пери
- пирс
- спелый
- испускают
- вещь
- клещ
- время
- эмир
- болото
- изморозь
- сеть
- дерево
- вглядеться
- отец
- pree
- встретиться
- мете
- кишат
- простой
- шпага
Слова из 3 букв, полученные путем расшифровки периметра
22 разных слова из 3 букв, составленных расшифровка писем с периметра , перечисленных ниже.
- яма
- кончик
- рвать
- мир
- обод
- бес
- рет
- ошибаться
- домашний питомец
- за
- представитель
- встретились
- бэр
- галстук
- гнев
- Рей
- пирог
- тройник
- до
- ри
- мочиться
- Эме
Слова из 2 букв, полученные путем расшифровки периметра
10 разных двухбуквенных слов, составленных расшифровка писем с периметра , перечисленных ниже.
- Это
- ты
- Пи
- ми
- эт
- э
- ре
- ре
- Эм
- мне
Расшифрованные слова, начинающиеся и заканчивающиеся на
- Слова, начинающиеся с «перимет»
- Слова начинающиеся на перимет
- Слова, начинающиеся на перим
- Слова начинающиеся на перим
- Слова, начинающиеся с пери
- Слова, начинающиеся с пер
- Слова, начинающиеся с «пе»
- Слова, оканчивающиеся на эриметр
- Слова, оканчивающиеся на риметр
- Слова, оканчивающиеся на иметр
- Слова, оканчивающиеся на метр
- Слова, оканчивающиеся на этер
- Слова, оканчивающиеся на тер
- Слова, оканчивающиеся на эр
Анаграмма мое имя Решатель беспорядка
- ауэминилмат
- грелиб
- натгме
- ромни
- суаэм
- cbneok
- гмиосг
- imlwensogbko
- мидил
- фонве
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |
| 3 | Оценить | 5+5 | |
| 4 | Оценить | 7*7 | |
| 5 | Найти простую факторизацию | 24 | |
| 6 | Преобразование в смешанный номер | 52/6 | |
| 7 | Преобразование в смешанный номер | 93/8 | |
| 8 | Преобразование в смешанный номер | 34/5 | |
| 9 | График | у=х+1 | |
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найдите площадь поверхности | сфера (3) | |
| 12 | Оценить | 54-6÷2+6 | |
| 13 | График | г=-2x | |
| 14 | Оценить | 8*8 | |
| 15 | Преобразование в десятичное число | 5/9 | |
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | у=2 | |
| 18 | Преобразование в смешанный номер | 7/8 | |
| 19 | Оценить | 9*9 | |
| 20 | Решить для C | С=5/9*(Ф-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | у=х+4 | |
| 23 | График | г=-3 | |
| 24 | График | х+у=3 | |
| 25 | График | х=5 | |
| 26 | Оценить | 6*6 | |
| 27 | Оценить | 2*2 | |
| 28 | Оценить | 4*4 | |
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Оценить | 1/3+13/12 | |
| 31 | Оценить | 5*5 | |
| 32 | Решить для d | 2д=5в(о)-вр | |
| 33 | Преобразование в смешанный номер | 3/7 | |
| 34 | График | г=-2 | |
| 35 | Найти склон | у=6 | |
| 36 | Преобразовать в проценты | 9 | |
| 37 | График | у=2х+2 | |
| 38 | График | у=2х-4 | |
| 39 | График | х=-3 | |
| 41 | Преобразование в смешанный номер | 1/6 | |
| 42 | Преобразование в десятичное число | 9% | |
| 43 | Решить для n | 12н-24=14н+28 | |
| 44 | Оценить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразование в упрощенную дробь | 43% | |
| 47 | График | х=1 | |
| 48 | График | у=6 | |
| 49 | График | г=-7 | |
| 50 | График | у=4х+2 | |
| 51 | Найти склон | у=7 | |
| 52 | График | у=3х+4 | |
| 53 | График | у=х+5 | |
| 54 | График | 92-9=0||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Найти простую факторизацию | 14 | |
| 61 | Преобразование в смешанный номер | 7/10 | |
| 62 | Решите для | (-5а)/2=75 | |
| 63 | Упростить | х | |
| 64 | Оценить | 6*4 | |
| 65 | Оценить | 6+6 | |
| 66 | Оценить | -3-5 | |
| 67 | Оценить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратное | 1/3 | |
| 71 | Преобразование в смешанный номер | 20. 11 11 | |
| 72 | Преобразование в смешанный номер | 7/9 | |
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | у=-х-2 | |
| 79 | График | у=3х+7 | |
| 80 | Определить, является ли многочлен | 2x+2 | |
| 81 | График | у=2х-6 | |
| 82 | График | у=2х-7 | |
| 83 | График | у=2х-2 | |
| 84 | График | у=-2х+1 | |
| 85 | График | у=-3х+4 | |
| 86 | График | у=-3х+2 | |
| 87 | График | у=х-4 | |
| 88 | Оценить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | х+2у=4 | |
| 91 | График | х=7 | |
| 92 | График | х-у=5 | |
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | ||
| 95 | Найдите площадь поверхности | конус (12)(9) | |
| 96 | Преобразование в смешанный номер | 3/10 | |
| 97 | Преобразование в смешанный номер | 20. 07. 07. | 92)
Часто задаваемые вопросы | Perimeter Institute
Ниже приведены часто задаваемые вопросы от студентов, подающих заявки на участие в программе Perimeter Scholars International. Пожалуйста, внимательно прочитайте эти вопросы и ответы, прежде чем обращаться в PSI по электронной почте с любыми другими вопросами.
Взимается ли плата за подачу заявления?
Нет, регистрационный сбор не взимается.
Получу ли я стипендию?Успешные кандидаты PSI получат финансирование, как описано в разделе «Финансовая поддержка». Кандидатам также рекомендуется искать и подавать заявки на получение внешних стипендий.
Когда крайний срок подачи заявок?Крайний срок подачи заявок — 1 февраля в 23:59 по восточному стандартному времени
Будут ли заявки рассматриваться после крайнего срока? Мы не можем гарантировать рассмотрение просроченных заявок.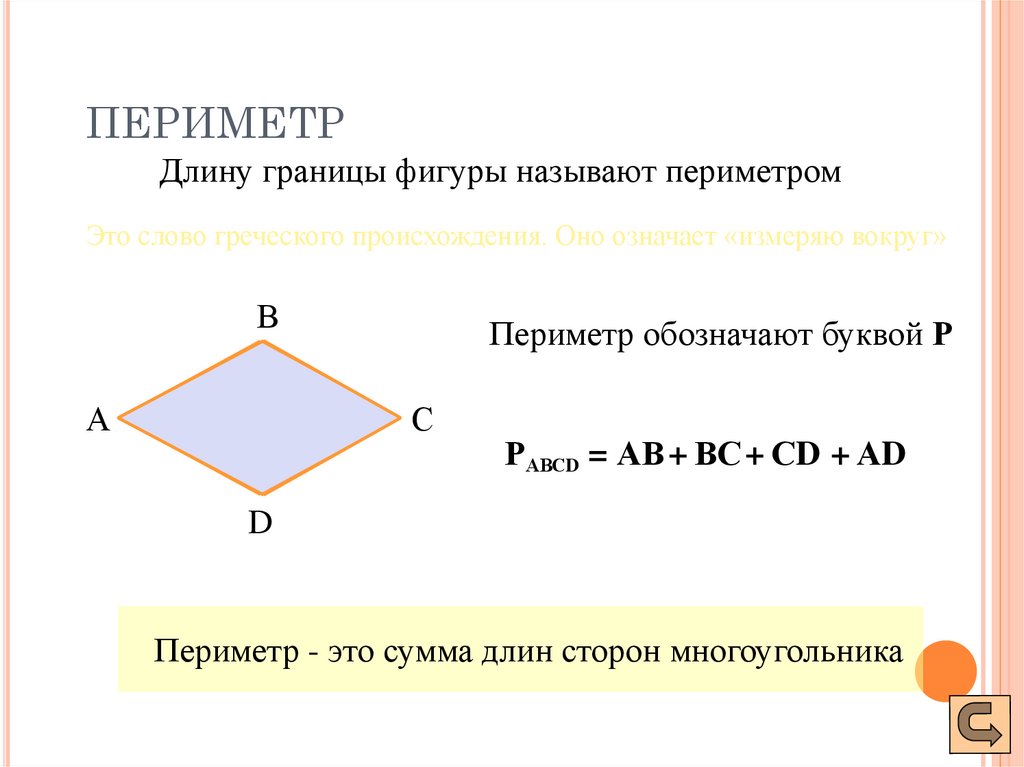 Тем не менее, мы принимаем поздние представления результатов ELP (TOEFL, IELTS, C1 Advanced, C2 Proficiency), если они недоступны к установленному сроку.
Тем не менее, мы принимаем поздние представления результатов ELP (TOEFL, IELTS, C1 Advanced, C2 Proficiency), если они недоступны к установленному сроку.
Мы не можем сообщить вам по электронной почте, каковы ваши шансы на зачисление в программу PSI. Каждый год мы получаем несколько сотен заявок примерно на 25 вакансий.
Какое образование по физике нужно иметь для PSI?Студенты должны продемонстрировать понимание тем бакалавриата по:
- Классическая механика
- Электромагнетизм
- Специальная теория относительности
- Квантовая механика
- Статистическая физика
Ниже приведен список обязательных элементов, которые необходимо загрузить вместе с заявлением.
- Официальная или неофициальная выписка(и) о высшем образовании
- Текущая биографическая справка (CV)
- Заявление о целях (максимум 2 страницы)
- Минимум три имени рефери и адреса электронной почты
- Требуется для некоторых иностранных студентов: ELP (TOEFL, IELTS, C1 Advanced, C2 Proficiency)
Дополнительные элементы, которые вы также можете включить в свое заявление: заявление о справедливости, разнообразии и инклюзивности (EDI), список публикаций, результаты GRE (физика или математика) и результаты оценки владения английским языком (EPL). Подробнее об этих дополнительных материалах см. ниже.
Подробнее об этих дополнительных материалах см. ниже.
Заявки должны включать не менее трех имен судей и адреса электронной почты, а также место для необязательного четвертого судьи.
Как мои рекомендатели отправляют свои рекомендательные письма?После заполнения онлайн-заявки система подачи заявок автоматически свяжется с вашими рекомендателями и расскажет, как отправить их рекомендательные письма. Рефералы НЕ смогут получить доступ к вашему приложению или просмотреть вашу личную информацию.
Что должно быть включено в мое заявление о цели? В заявлении о целях должны быть описаны причины, по которым вы подали заявку на участие в магистерской программе PSI, ваша подготовка к программе, а также любая другая информация, которая может помочь приемной комиссии в оценке ваших способностей и мотивации для получения степени магистра в области физики.
Хотя GRE по физике не требуется для поступления в PSI, мы примем во внимание ваш балл GRE (физика и общий), если вы отправите его вместе с заявлением.
Что такое заявление о справедливости, разнообразии и интеграции (EDI) (необязательно)?Ваше заявление EDI — это место, где вы можете предоставить дополнительную информацию приемной комиссии, и это строго необязательно.
Perimeter Institute стремится к равенству, разнообразию и интеграции в нашем сообществе.
В заявлении EDI вам предлагается поделиться любой информацией, которая поможет приемной комиссии всесторонне оценить ваше заявление. Эта информация может включать препятствия, которые вы преодолели, смягчающие обстоятельства, информацию о действиях, которые вы предприняли для повышения справедливости, разнообразия или инклюзивности, или любую другую информацию, которую вы считаете уместной.
Каковы требования к экзамену на знание английского языка (ELP) для поступления в PSI? Университет Ватерлоо требует сдачи экзамена на знание английского языка (ELP) (например, TOEFL, IELTS, C1 Advanced, C2 Proficiency), если только вы не учились в одном из международных университетов, включенных в список исключений ELP Университета Ватерлоо.



 Найди длину прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.
Найди длину прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.