Формулы площадей и объемов всех фигур таблица. Формулы для нахождения объема параллелепипеда
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Общий обзор. Формулы стереометрии!
Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик е. Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.
Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.
Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.
Все нужные формулы представлены ниже:
Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.
Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса
См. также Площадь поверхности круглого конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H:
(H — высота ребра куба)
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
(S — площадь основания пирамиды, h — высота пирамиды)
Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.
Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1 (abcde) , нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
| 1. | V = |
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды
Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS)
a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды
Вывод формулы объема тетраэдра
Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.
Объем тетраэдра — равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра
(h — длина стороны ромба)
Длина окружности p составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π
В итоге периметр круга или длина окружности вычисляется по формуле
(r — радиус дуги, n — центральный угол дуги в градусах.)
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .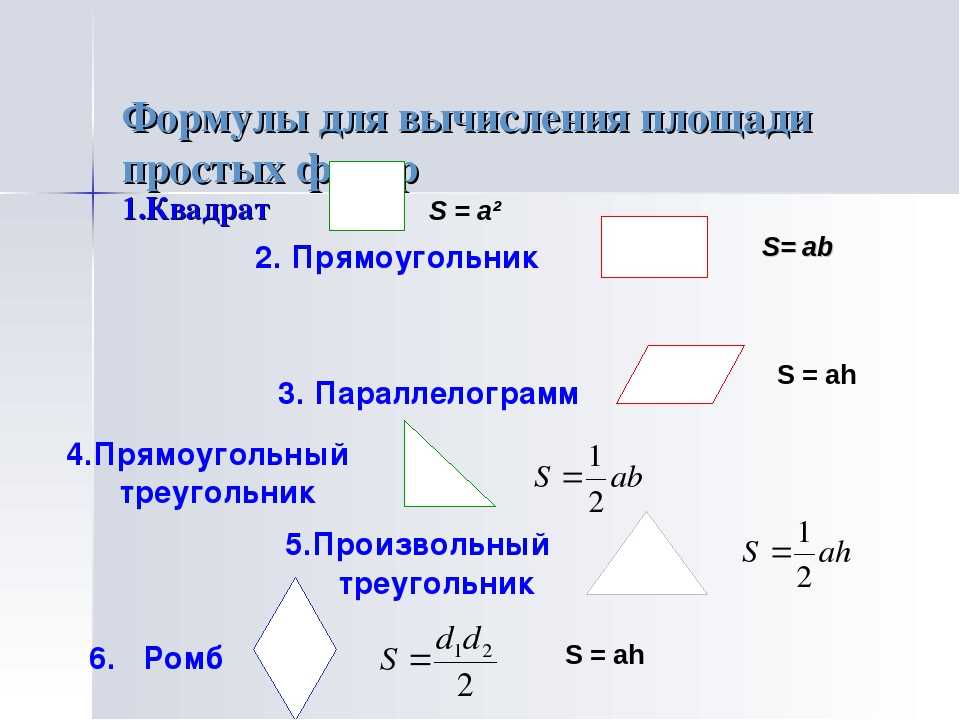
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
А древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке.
Как видим, площади, найденные обоими способами, равны.
Рисунок 3.
Рисунок 4.
Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.
Определение 2
Прямоугольник с равными сторонами называется квадратом .
Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:
Отсюда и название квадрат числа $a$.
Пример 2
Например, если сторона квадрата равна $5$ см, то его площадь:
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.
Объем измеряется с помощью следующих единиц:
$мм^3$ — миллиметр кубический,
$см^3$ — сантиметр кубический,
$дм^3$ — дециметр кубический,
$м^3$ — метр кубический,
$км^3$ — километр кубический.
Площади и объемы
Площади
История нахождения площадей фигур начинается еще с древнего Вавилона. Уже тогда вычисляли площади прямоугольника, а древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.
Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.
Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.
Формула площади прямоугольника
Рассмотрим фигуру (рис. 1), которая состоит из $8$ квадратов со сторонами по $1$ см. Площадь одного квадрата со стороной $1$ см называют сантиметром квадратным и записывают $1\ см^2$. 2.\]
2.\]
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5. 3.\]
3.\]
Отсюда и название куб числа $a$.
Площадь полной поверхности куба, как определить площадь поверхности куба, примеры площади поверхности куба. | ||
| Площадь поверхности куба. | ||
| Формула площади круга, квадрата, трапеции, ромба, треугольника, эллипса, сегмента круга, сектора круга, параллелограмма и другие формулы площадей геометрических фигур. | ||
| Формула площади. | ||
| V = | a3√2 |
| 12 |
где V – объем правильного тетраэдра,
a – длина ребра правильного тетраэдра.
Смотрите также онлайн калькулятор для расчета объема правильного тетраэдра
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
| V = | 1 | π R2 h |
| 3 |
| V = | 1 | So h |
| 3 |
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.141592.
Какая форма лучше для маленького (2-3 куб см) ценного абстрактного предмета? Возможно, шар, куб, пирамида или что-то другое?
Мне больше всего нравится усечённый тетраэдр. Я даже когда-то такой из бумаги склеил и на полку поставил. С одной стороны – почти круглый, почти правильный и почти примитивный, а с другой – не сразу поймёшь, как его построить.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V – объем призмы,
So – площадь основания призмы,
h – высота призмы.
Онлайн калькулятор для расчета объема призмы
Формулы площади геометрических фигур для определения площади основания призмы
Объем прямоугольной призмы
Размеры прямоугольной призмыФормула:
Объем прямоугольной призмы
Ширина (W)
Высота (H)
Высота (H)
Длина (L)
Точность вычисления
Знаков после запятой: 5
Найти ребро куба, зная объем
Объем куба V
Сообщить об ошибке
Вписанная и описанная сфера куба
Сфера, вписанная в куб
– это сфера, центр которой совпадает с центром куба и которая касается центров граней куба. – это сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами
– это сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами
Доаказетльство формулы диагонали куба
Начнем с того, что вот она картинка и по ней уже все становится ясно! Нам потребуется формула Пифагора, которая и позволит нам вывести и доказать формулу диагонали куба!
Как видим – нам нужна диагональ куба под буквой «c» из теоремы Пифагора мы знаем что:
Для трегольника справа:
c2 = a2 + b2
Получим корень от общего выражения – слева получим «с» – справа получим корень из суммы квадратов стронь…
c = √( a2 + b2)
Уже видите, что нужно сделать дальше!?
Далее нам нужен левый треугольник в котором нас интересует сторона «b»
Частный случай терема Пифагора ели две стороны треугольника равны:
b2 = 2a2
Теперь в верхней формуле заменяем нашу строну «b»
c = √(a2 + 2a2) => √(3а2) = а√3
Мы доказали формулу диагонали куба!
Объем усеченной пирамиды
Размеры усеченной пирамидыФормула:
Объем усеченной пирамиды
Площадь первого основания (Sb1)
Площадь второго основания (Sb2)
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту. 3}
3}
Части куба, свойства, определения
Грань куба
– это часть плоскости, ограниченная сторонами квадрата
- У куба шесть граней
- Каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная противоположной грани
- Грани имеют одинаковую площадь, а так как являются квадратами, то формула площади грани S = a2
Ребро куба
– это отрезок, образованный пересечением двух граней куба.
- У куба двенадцать рёбер
- Каждое ребро перпендикулярно по отношению к примыкающим рёбрам
- Все ребра куба имеет одинаковую длину
Ось куба
– это прямая, проходящая через центр куба и центры двух параллельных граней куба
- У куба три оси
- Оси куба взаимно перпендикулярны
Диагональ куба
– отрезок, который соединяет противоположные вершины куба и проходит через центр куба.
- куб имеет четыре диагонали;
- диагонали куба пересекаются под прямым углом и делятся пополам в центре куба;
- диагонали куба имеют одинаковую длину;
Куб – это один из самых простых трехмерных объектов, как в стереометрии, так и в природе.
 Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани.
Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани.- В большинстве случаев встречаются задачи четырех типов, в которых находится ребро куба. Это – определить длину ребра по диагонали куба, по диагонали его грани, по объему куба и площади грани. Самая простая из них – найти ребро по площади грани. Ведь грань куба – это квадрат со стороной, которая равна ребру куба. Следовательно, площадь этой грани равна ребру куба, возведенному в квадрат. Отсюда, чтобы найти ребро, необходимо из площади грани извлечь квадратный корень. а=vS а – ребро куба (длина), S – площадь одной грани.
- Еще проще найти грань куба исходя из его объема, так как объем куба будет равняться возведению длины ребра в 3-ю степень.
 2/3).
2/3).
Объем сферы
Размеры сферыФормула:
Объем сферы
Радиус (R)
Точность вычисления
Знаков после запятой: 5
Объемы фигур. Объем параллелепипеда.
Источники
- https://www.calc.ru/Geometricheskiye-Figury-Kub.html
- https://ru.onlinemschool.com/math/formula/volume/
- https://www.calc.ru/Formula-Obyema.html
- https://yandex.ru/q/question/hw.math/kak_naiti_obiom_kuba_s_rebrom_1_sm_53d18284/?answer_id=c7174250-31d7-4f1a-b41a-1f1636187b6a&w=answer&w_question_id=54429276-9ab8-44ef-b911-3579d256e016&w_origin=grave_unauth
- https://planetcalc.ru/131/
- https://geleot.
 ru/education/math/geometry/edge/cube
ru/education/math/geometry/edge/cube - http://calc-online24.ru/formula/kub
- http://axmara.narod.ru/_page/matematika/030_diagonal_kuba_formula.html
- https://mnogoformul.ru/obem-kuba-formula-i-raschet-onlayn
Все формулы нахождения площади и объема. Объем фигур
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.

- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).
Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.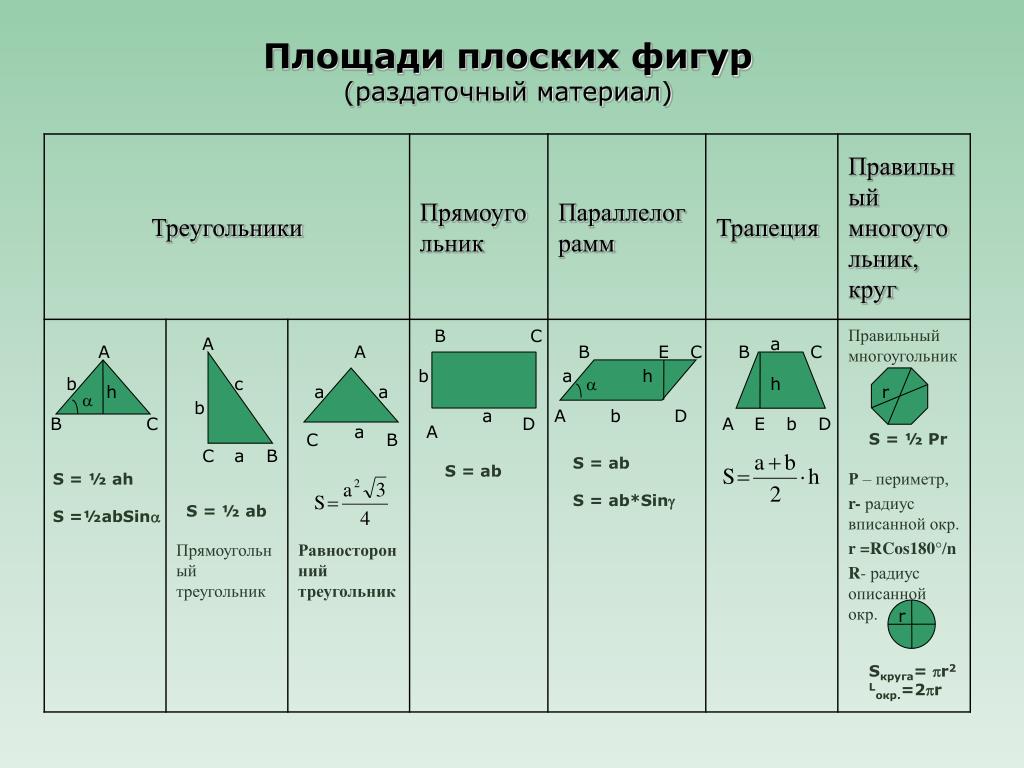
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
Задания единого экзамена должны быть выполнены за определенное время. Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
А древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.
В своих книгах «Начала» известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. 2$. Найдем площадь прямоугольника по формуле:
2$. Найдем площадь прямоугольника по формуле:
Как видим, площади, найденные обоими способами, равны.
Рисунок 3.
Рисунок 4.
Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.
Определение 2
Прямоугольник с равными сторонами называется квадратом .
Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:
Отсюда и название квадрат числа $a$.
Пример 2
Например, если сторона квадрата равна $5$ см, то его площадь:
Объемы
С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.
Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда.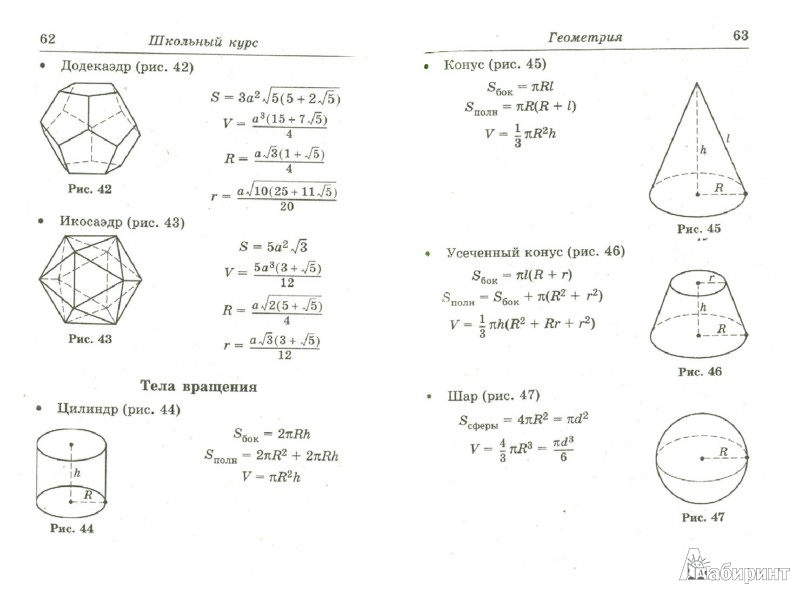 Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.
Объем прямоугольного параллелепипеда
Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.
Рисунок 5.
Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.
Объем измеряется с помощью следующих единиц:
$мм^3$ — миллиметр кубический,
$см^3$ — сантиметр кубический,
$дм^3$ — дециметр кубический,
$м^3$ — метр кубический,
$км^3$ — километр кубический.
Измерьте все необходимые расстояния в метрах. Объем многих трехмерных фигур легко вычислить по соответствующим формулам. Однако все значения, подставляемые в формулы, должны измеряться в метрах. Таким образом, перед подстановкой значений в формулу убедитесь, что все они измеряются в метрах, или что вы конвертировали другие единицы измерения в метры.
- 1 мм = 0,001 м
- 1 см = 0,01 м
- 1 км = 1000 м
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани.
- Например, вычислим объем комнаты длиной 4 м, шириной 3 м и высотой 2,5 м. Для этого просто умножим длину на ширину и на высоту:
- 4 × 3 × 2,5
- = 12 × 2,5
- = 30. Объем этой комнаты равен 30 м 3 .

- Куб – объемная фигура, у котрой все стороны равны. Таким образом, формулу для вычисления объема куба можно записать в виде: объем = L 3 (или W 3 , или H 3).
Для вычисления объема фигур в виде цилиндра используйте формулу: пи × R 2 × H. Вычисление объема цилиндра сводится к умножению площади круглого основания на высоту (или длину) цилиндра. Найдите площадь круглого основания, умножив число пи (3,14) на квадрат радиуса круга (R) (радиус — расстояние от центра окружности до любой точки, лежащей на этой окружности). Затем полученный результат умножьте на высоту цилиндра (H), и вы найдете объем цилиндра. Все значения измеряются в метрах.
- Например, вычислим объем колодца диаметром 1,5 м и глубиной 10 м. Разделите диаметр на 2, чтобы получить радиус: 1,5/2=0,75 м.
- (3,14) × 0,75 2 × 10
- = (3,14) × 0,5625 × 10
- = 17,66. Объем колодца равен 17,66 м 3 .
Для вычисления объема шара используйте формулу: 4/3 х пи × R 3 . То есть вам нужно знать только радиус (R) шара.
То есть вам нужно знать только радиус (R) шара.
- Например, вычислим объем воздушного шара диаметром 10 м. Разделите диаметр на 2, чтобы получить радиус: 10/2=5 м.
- 4/3 х пи × (5) 3
- = 4/3 х (3,14) × 125
- = 4,189 × 125
- = 523,6. Объем воздушного шара равен 523,6 м 3 .
Для вычисления объема фигур в виде конуса используйте формулу: 1/3 х пи × R 2 × H. Объем конуса равен 1/3 объема цилиндра, который имеет такую же высоту и радиус.
- Например, вычислим объем конуса мороженного радиусом 3 см и высотой 15 см. Конвертируя в метры, получим: 0,03 м и 0,15 м соответственно.
- 1/3 х (3,14) × 0,03 2 × 0,15
- = 1/3 х (3,14) × 0.0009 × 0,15
- = 1/3 × 0.0004239
- = 0,000141. Объем конуса мороженного равен 0,000141 м 3 .
Для вычисления объема фигур неправильной формы используйте несколько формул. Для этого попробуйте разбить фигуру на несколько фигур правильной формы. Затем найдите объем каждой такой фигуры и сложите полученные результаты.
Затем найдите объем каждой такой фигуры и сложите полученные результаты.
- Например, вычислим объем небольшого зернохранилища. Хранилище имеет цилиндрический корпус высотой 12 м и радиус 1,5 м. Хранилище также имеет коническую крышу высотой 1 м. Вычислив отдельно объем крыши и отдельно объем корпуса, мы можем найти общий объем зернохранилища:
- пи × R 2 × H + 1/3 х пи × R 2 × H
- (3,14) × 1,5 2 × 12 + 1/3 х (3,14) × 1,5 2 × 1
- = (3,14) × 2,25 × 12 + 1/3 х (3,14) × 2,25 × 1
- = (3,14) × 27 + 1/3 х (3,14) × 2,25
- = 84,822 + 2,356
- = 87,178. Объем зернохранилища равен 87,178 м 3 .
Объёмы поверхностей геометрических тел — определение и примеры с решением
Содержание:
Объёмы поверхностей геометрических тел:
То, чем в предыдущие эпохи занимались только зрелые умы ученых мужей, в более позднее время стало доступным для понимания юношей.
С древних времен люди применяли геометрию для решения конкретных житейских проблем — нахождения объемов сосудов, строений и кораблей, количества краски, необходимой для ремонта помещения. На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.
На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.
Основной целью данной главы является формирование представлений об объемах и площадях поверхностей, обоснование соответствующих формул для основных пространственных фигур. Вы. научитесь использовать различные методы нахождения объемов, как строго геометрические, так и те, которые объединяют в себе геометрию и начала анализа. При изучений объемов тел полезно будет вспомнить и систематизировать материал о площадях фигур на плоскости. Подходы, которые применялись для получения основных формул площадей, будут надежным фундаментом для построения теории объемов.
В данной главе речь пойдет о всех основных фигурах, которые вы изучали в течение года, в частности о тесной связи многогранников и тел вращения. Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.
Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.
Задачи данной главы содержат много геометрических конфигураций, что позволит вам переосмыслить весь курс стереометрии с точки зрения применения своих знаний на практике, в частности для нахождения, пожалуй, самых распространенных в жизни геометрических величин — объемов и площадей поверхностей. Ради этого бесценного опыта вы и изучали, в конце концов, геометрию в пространстве.
Понятие объема хорошо известно на уровне повседневного опыта: мы покупаем пакет сока определенного объема, рассчитываем, какой объем займет в квартире новая мебель, берем для приготовления блюда кастрюлю соответствующего объема. Придадим этим наглядным представлениям об объеме тела определенную математическую строгость.
Понятие объема многогранниковДля дальнейших рассуждений полезно объединить практический опыт и известную уже теорию площадей многоугольников. По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.
По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.
Объем характеризует величину части пространства, которую занимает геометрическое тело, и измеряется, как и площадь, в определенных единицах. Единицей измерения площадей является площадь единичного квадрата, а за единицу измерения объема принимается объем единичного куба, то есть куба, ребро которого равно единице длины. Например, если за единицу измерения длины принимается 1 мм, 1 см, 1 дм или 1 м, то за единицу измерения объема принимается объем куба с ребром 1 мм, 1 см, 1 дм или 1 м. Соответствующая единица объема называется кубическим миллиметром (1 мм3), кубическим сантиметром (1 см3), кубическим дециметром или литром (1 дм3 или 1 л), кубическим метром (1 м3). Таким образом, вычисление объемов тел разной формы основано на сравнении с объемом единичного куба.
Измерить объем тела на практике можно, например, погрузив его в воду и подсчитав количество вытесненной телом воды. Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.
Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.
- Равные многогранники имеют равные объемы.
- Бели многогранник составлен из нескольких многогранников, то его объем равен сумме объемов этих многогранников.
- Объем куба с ребром, равным единице длины, равен единице объема.
Итак, объем многогранника — это положительная величина, Числовое значение которой удовлетворяет аксиомам объема. : — Как правило, объем обозначают буквой V.
Приведенные аксиомы имеют и практическую основу. Действительно, все пакеты, имеющие форму прямоугольного параллелепипеда и одинаковые размеры, содержат одинаковое количество сока.
Тела, имеющие равные объемы, называются равновеликими.
Если же каждый из двух пакетов можно разлить в одинаковое количество маленьких пакетиков, то сумма объемов этих пакетиков будет равна объему каждого из них, то есть данные пакеты имеют одинаковый объем.
Тела, составленные из одних и тех же многогранников, называются равносоставленными. Например, равносоставленными будут тела, изображенные на рисунке 190, а, б: прямая треугольная призма и прямой параллелепипед. Действительно, каждая из этих фигур составлена из двух одинаковых прямых призм, таких как на рисунке 190, в.
Очевидно, что объемы равносоставленных многогранников равны по второй аксиоме. Интересно, что обратное утверждение неверно (в отличие от аналогичной теоремы для площадей). Так, многогранники равного объема не всегда можно разбить на конечное число равных многогранников. В частности, куб и правильный тетраэдр равных объемов (рис. 190) не являются равносоставленными.
Объем параллелепипедаПростейшей фигурой с точки зрения вычисления объема является прямоугольный параллелепипед.
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где — измерения прямоугольного параллелепипеда.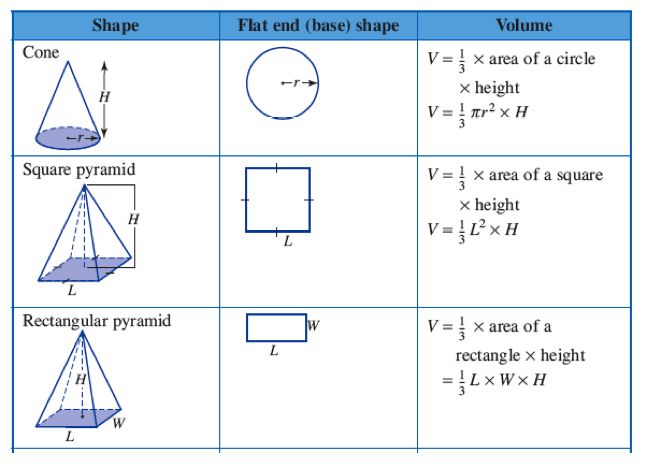
Приведем рассуждения, на которых основано доказательство данной теоремы.
Сначала рассмотрим прямоугольный параллелепипед с измерениями а, 1, 1. Так как в отрезке а единица измерения длины помещается а раз, то единичный куб помещается в параллелепипед также а раз. Значит, объем прямоугольного параллелепипеда равен а (рис. 191, а).
Аналогично объем прямоугольного параллелепипеда с измерениями 1 равен (рис. 191, б), а прямоугольного параллелепипеда с измерениями — равен abc (рис. 191, в).
Полное доказательство данной теоремы приведено в Приложении 2.
Следствие (формула объема куба)
Объем куба равен кубу его ребра:
где а — ребро куба.
Нам известно, что площадь прямоугольника равна произведению двух его измерений, а параллелограмма — произведению его стороны на проведенную к ней высоту. По аналогии нетрудно предположить, что объем произвольного параллелепипеда также можно найти через площадь основания и соответствующую высоту.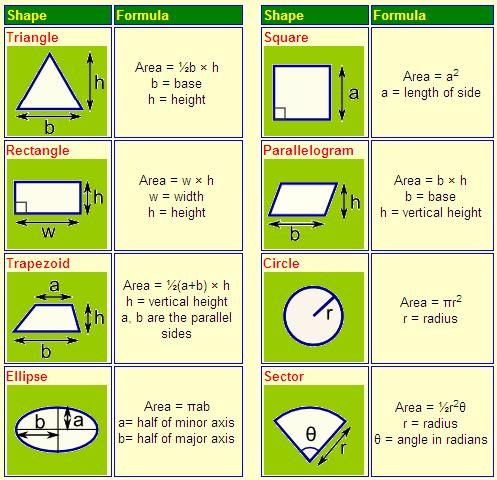
Теорема (формула объема параллелепипеда)
Объем параллелепипеда равен произведению площади его основания на высоту:
где — площадь основания параллелепипеда, h — высота.
Доказательство:
Очевидно, что для прямоугольного параллелепипеда данная формула верна. Докажем ее для наклонного параллелепипеда (рис. 192). Проведем через ребра ВС и AD плоскости, перпендикулярные основанию ABCD. Дополним наклонный параллелепипед треугольной призмой и отсечем треугольную призму Эти призмы равны, так как совмещаются параллельным переносом на вектор . Значит, полученный параллелепипед имеет тот же объем, что и исходный.
При описанном преобразовании параллелепипеда площадь его основания и высота сохраняются, а две боковые грани становятся перпендикулярными плоскости основания ABC. Если выполнить аналогичное преобразование с помощью плоскостей, проходящих через АВ и DC перпендикулярно основанию ABCD, получим прямой параллелепипед с основанием ABCD, равновеликий исходному. При этом высоты параллелепипедов также сохраняются.
При этом высоты параллелепипедов также сохраняются.
Теперь проведем через точки А я В плоскости, перпендикулярные АВ (рис. 193). Дополняя прямой параллелепипед одной треугольной призмой (I) и отсекая равную ей другую призму (2), получим прямоугольный параллелепипед, равновеликий предыдущему.
Объем полученного прямоугольного параллелепипеда равен . Так как при описанных выше преобразованиях данного параллелепипеда в прямоугольный каждый раз образуется параллелепипед, равновеликий предыдущему, а площадь
основания и высота сохраняются, то и объем исходного параллелепипеда можно вычислить с помощью полученной формулы. Итак, объем наклонного параллелепипеда
Таким образом, объем произвольного параллелепипеда вычисляется по формуле
Теорема доказана.
Пример №1В основании наклонного параллелепипеда лежит прямоугольник со сторонами 3 см и 4 см. Боковое ребро параллелепипеда равно 6 см. Найдите объем данного параллелепипеда, если две его боковые грани перпендикулярны плоскости основания, а две другие наклонены к ней под углом 30°.
Решение:
Пусть дан параллелепипед (рис. 194), в основании которого лежит прямоугольник ABCD со сторонами 3 см и 4 см. Боковые ребра параллелепипеда равны и имеют длину б см. Противолежащие боковые грани параллелепипеда параллельны, следовательно, наклонены к плоскости его основания под равными углами.
Пусть грани перпендикулярны грани ABCD, а грани образуют с ABCD угол 30°. Проведем в плоскости перпендикуляр к AD. По свойству перпендикулярных плоскостей , следовательно, — высота данного параллелепипеда. Так как является перпендикуляром, — наклонной, KD — ее проекцией на плоскость ABC, причем , то по теореме о трех перпендикулярах . Значит, угол равен углу между плоскостями . По условию . Из прямоугольного треугольника получим: = 3 см.
Таким образом,
Ответ: 36 см3.
Объем призмыНа плоскости для получения формулы площади треугольника было удобно дополнить треугольник до параллелограмма. Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.
Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.
Теорема (формула объема призмы)
Объем призмы равен произведению площади ее основания на высоту:
где — площадь основания призмы, h — ее высота.
Доказательство:
Пусть дана треугольная призма . Дополним ее до параллелепипеда , как показано на рисунке 195. Дополняющая призма симметрична данной относительно центра симметрии параллелепипеда точки О. Значит, она равна данной призме. Тогда, по аксиомам объема, объем параллелепипеда равен удвоенному объему данной призмы. Но значит,
Применим только что выведенную формулу объема треугольной призмы к рассмотрению произвольной призмы.
Разобьем основание призмы на треугольники, а призму — на соответствующие треугольные призмы с высотой h (рис. 196).
По аксиоме, объем данной призмы равен сумме объемов составляющих ее треугольных призм:
где — площади треугольников, на которые разбито основание призмы.
Теорема доказана.
Пример №2Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: , где I — боковое ребро призмы, — площадь перпендикулярного ему сечения. Докажите.
Решение:
Рассмотрим наклонную призму F1 с ребром АА1 = I (рис. 197). Проведем два ее перпендикулярных сечения, расстояние между плоскостями которых I и которые не имеют с данной призмой общих точек. При этом получим прямую призму F2 и многогранник F3 (рис. 197). Многогранник, гранник, как совмещаются параллельным переносом на вектор . Поэтому их объемы равны. Эти многогранники имеют общую часть F3. Отсюда по аксиоме объема следует, что объемы призм F1 и F2 также равны. Но последняя призма является прямой, и ее объем равен . Значит, объем данной призмы равен .
Объем цилиндраПри обосновании формулы площади круга в планиметрии мы использовали вписанные в окружности и описанные около них многоугольники. Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.
Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.
Определение:
Прямая призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.
При этом цилиндр называется описанным около призмы. Очевидно, что боковые ребра призмы — образующие цилиндра, а высоты прямой призмы и описанного около нее цилиндра равны (рис. 198).
Определение:
Прямая призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.
При этом цилиндр называется вписанным в призму (рис. 199). Очевидно, что высоты прямой призмы и вписанного в нее цилиндра равны.
Теорема (формула объема цилиндра)
Объем цилиндра равен произведению площади его основания на высоту:
где — площадь основания цилиндра, h — высота, R — радиус цилиндра.
Доказательство:
Впишем в данный цилиндр радиуса R и высоты h правильную п-угольную призму с площадью основания S’n и опишем около него правильную n-угольную призму с площадью основания (рис. 200). Тогда, по доказанному при обосновании формулы для площади круга,
Отсюда следует, что при неограниченном возрастании п объемы вписанных призм и объемы описанных призм стремятся к величине . Значит, существуют призмы, содержащиеся в данном цилиндре, и призмы, содержащие его, объемы которых сколь угодно мало отличаются от . Тогда объем цилиндра выражается формулой V = .
Теорема доказана.
Пример №3Основание прямой призмы — треугольник со стороной с-и прилежащими к ней углами . Диагональ грани, содержащей сторону с, образует с плоскостью основания призмы угол ф. Найдите объем цилиндра, описанного около призмы.
Решение:
Пусть дана прямая треугольная призма , в основании которой лежит треугольник . Так как , то — наклонная, АВ — ее проекция на плоскость ABC. Значит, по определению угол равен углу между АВ и плоскостью ABC. По условию (рис. 201).
Так как , то — наклонная, АВ — ее проекция на плоскость ABC. Значит, по определению угол равен углу между АВ и плоскостью ABC. По условию (рис. 201).
Рассмотрим цилиндр, описанный около данной призмы. Его основания описаны около оснований призмы, высота равна высоте призмы.
По теореме синусов для треугольника ABC имеем:
Из прямоугольного треугольника
Следовательно, объем цилиндра равен:
Ответ:
Объемы пирамиды, конуса и шараРассмотрим способ вычисления объемов тел, в основе которого лежит понятие интеграла, известное из курса алгебры и начал анализа.
Общая формула объемаПусть тело Т, объем которого требуется вычислить, расположено между двумя параллельными плоскостями . Введем систему координат так, чтобы ось Ох была перпендикулярна плоскостям (рис. 202). Пусть плоскость а задана уравнением х = а, а плоскость — х = Ь (а
Будем рассматривать случай, когда любое сечение тела Ф(х) плоскостью, перпендикулярной-оси Ох и пересекающей эту ось в точке (х;0;0), является кругом или многоугольником (такой случай возможен, если Ф(х) — точка).
Обозначим площадь фигуры Ф(х) через S(x). Допустим, что S(x) — непрерывная функция при . Разобьем отрезок [a;b] на n равных отрезков точками и через точки с абсциссами х, проведем плоскости, перпендикулярные оси Ох (рис. 203).
Эти плоскости разобьют тело Т на n тел: . Если сечение Ф(х1) — круг, то объем тела Т, приближенно равен объему цилиндра с основанием Ф(х1) и высотой Если сечение Ф(х1) — многоугольник, то объем тела Ti приближенно равен объему прямой призмы с основанием ф(х, ) и высотой
Учитывая, что объем цилиндра и призмы равен произведению площади основания на высоту, то есть получаем:
При неограниченном возрастании n правая часть данной формулы приближается сколь угодно близко к объему тела Т. С другой стороны, так как S(x) непрерывна на , это же выражение приближается к соответствующему интегралу. Итак,
Таким образом, мы получили формулу для вычисления объема тела с помощью интеграла. Будем называть ее интегральной формулой объема.
Будем называть ее интегральной формулой объема.
Из этой формулы вытекает интересное и удобное в применении следствие, формулировка которого принадлежит итальянскому математику Бонавентуре Кавальери.
Принцип КавальериЕсли при пересечении двух тел F1 и F2 плоскостями, параллельными одной и той же плоскости а, в сечениях получаются фигуры с равными площадями, то объемы данных тел равны.
Это утверждение легко вывести из интегральной формулы объема, если расположить систему координат так, чтобы ось Ох была перпендикулярна плоскости а (рис. 204). Применение интеграла и принципа Кавальери позволяет значительно упростить нахождение формул, выражающих объемы многих важных тел.
Объем пирамиды и конусаВ пунктах 15.3 и 15.4 мы установили, что объемы призмы и цилиндра определяются одной и той же формулой:
Поэтому вполне естественно предположить, что будут совпадать формулы для объемов пирамиды и конуса.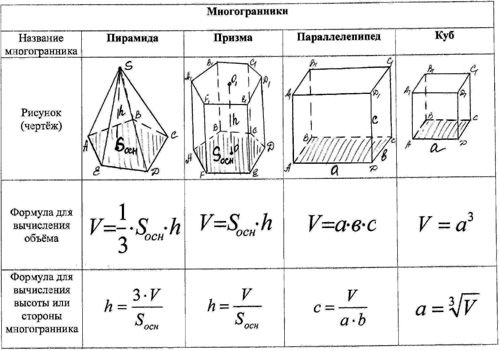
Теорема (формула объема пирамиды)
Объем пирамиды равен трети произведения площади основания на высоту:
где — площадь основания пирамиды, h — высота.
Доказательство:
Разместим пирамиду в системе координат так, чтобы ось Ох была направлена вдоль высоты, а основание’ принадлежало бы плоскости (рис. 205). Пусть некоторая плоскость параллельна основанию пирамиды и пересекает ее высоту в точке (х;0;0). Обозначим через S(x) площадь сечения пирамиды этой плоскостью. По доказанному в п. 10.2 она отсекает пирамиду, подобную данной. В частности, подобными являются многоугольники основания и сечения. Пусть k — коэффициент подобия. Тогда
Отсюда
Применяя теперь для пирамиды интегральную формулу объема, получим:
Теорема доказана.
Следствие (формула объема усеченной пирамиды)
Объем усеченной пирамиды вычисляется по формуле:
где h — высота усеченной пирамиды, площади ее оснований.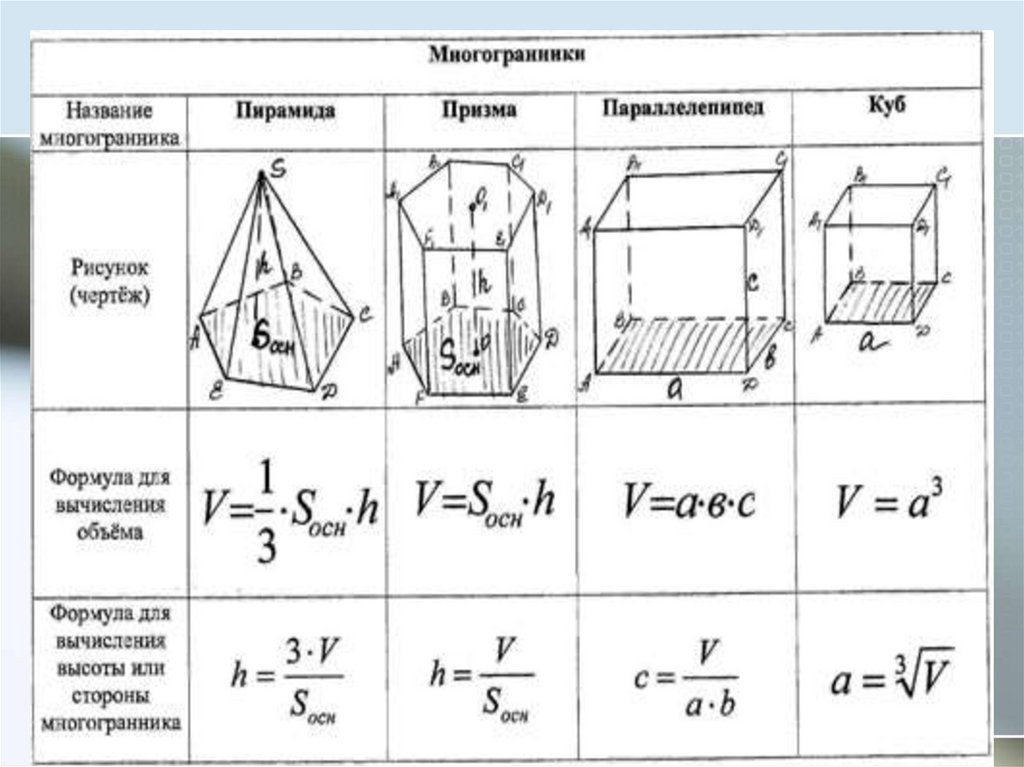
Доказательство:
Дополним данную усеченную пирамиду до полной с высотой Н (рис. 206). Тогда высота дополняющей пирамиды будет равна H-h. Из подобия полной и дополняющей пирамид, площади оснований которых равны соответственно, получаем:
По аксиомам объема, объем усеченной пирамиды равен разности объемов полной и дополняющей пирамид. Следовательно,
Формула доказана.
Заметим, что при доказательстве теоремы об объеме пирамиды и ее следствия, кроме интегральной формулы объема, мы применили только тот факт, что плоскость, параллельная основанию, отсекает пирамиду, для площади основания S(x) и высоты h-x которой верна формула
Но эта формула, по доказанному в п. 13.2, также верна и для конуса (рис. 207). Поэтому аналогичными формулам объема и их доказательствам для пирамиды и усеченной пирамиды будут формулы объема и их доказательства для конуса и усеченного конуса.
Теорема (формула объема конуса)
Объем конуса равен трети произведения площади основания на высоту:
где — площадь основания конуса, R — радиус, h — высота.
Следствие (формула объема усеченного конуса)
Объем усеченного конуса вычисляется по формуле
где h — высота усеченного конуса, — площади его оснований, — радиусы его оснований.
С помощью вписанных и описанных призм мы вывели формулу для объема цилиндра. Подобную связь можно установить также для конусов и пирамид.
Определение:
Пирамида называется вписанной в конус, если их вершины совпадают, а основание пирамиды вписано в основание конуса.
При этом конус называется описанным около пирамиды.
Очевидно, что высоты пирамиды и описанного конуса равны, а боковые ребра пирамиды являются образующими конуса (рис. 208).
Определение:
Пирамида называется описанной около конуса, если их вершины совпадают, а основание пирамиды описано около основания конуса.
При этом конус называется вписанным в пирамиду.
Очевидно, что высоты пирамиды и вписанного конуса равны, а высоты боковых граней пирамиды являются образующими конуса (рис. 209).
209).
Рассмотрим правильные л-угольные пирамиды, вписанные в данный конус, и правильные л-угольные пирамиды, описанные около него (рис. 210).
Если число n сторон оснований этих пирамид неограниченно возрастает, то площади их оснований стремятся к площади круга, лежащего в основании конуса. Следовательно, их объемы стремятся Тогда существуют вписанные в конус и описанные около него пирамиды с объемами, сколь угодно мало отличающимися от
Из этих рассуждений становится понятным другое обоснование формулы объема конуса
Объем шара и его частейНепосредственно получить только из геометрических рассуждений формулу для объема шара очень сложно. Но с помощью интегральной формулы объема и принципа Кавальери доказательство соответствующих результатов является простым и наглядным.
Теорема (формула объема шара)
Объем шара радиуса R вычисляется по формуле
Доказательство:
Найдем сначала объем полушара, применив принцип Кавальери.
Пусть дан полушар Fl радиуса R. На плоскость а, содержащую основание полушара, поставим цилиндр, радиус и высота которого также равны R. В цилиндр впишем конус, вершина которого совпадает с центром основания цилиндра в плоскости а, а основание — с другим основанием цилиндра (рис. 211).
Сравним объем V1 полушара с объемом V2 тела F2, ограниченного нижним основанием цилиндра и боковыми поверхностями цилиндра и конуса.
Проведем плоскость , параллельную плоскости а и удаленную от нее на расстояние х . Эта плоскость пересечет данный полушар по кругу радиуса и площади , а тело F2 — по кольцу. Так как осевое сечение конуса является равнобедренным прямоугольным треугольником, внешний радиус кольца равен R, а внутренний — х. Значит, площадь полученного кольца составит и будет равна площади сечения полушара. По принципу Кавальери, объем полушара равен объему тела F2, то есть разности объемов цилиндра и конуса:
Объем шара вдвое больше объема полушара, следовательно, вычисляется по формуле .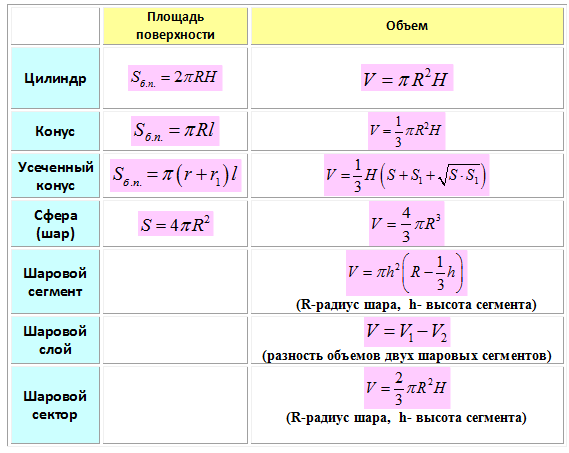 Теорема доказана.
Теорема доказана.
Сечение шара, удаленное от его центра на 1 см, имеет площадь 8л см2. Найдите объем шара.
Решение:
Пусть дан шар с центром О. Сечение шара некоторой плоскостью а является кругом с центром , причем . Так как О удалена от а на 1 см, то = 1 см.
Пусть точка К сферы, ограничивающей шар, принадлежит данному сечению (рис. 212). Тогда площадь сечения равна , откуда (см). Из прямоугольного треугольника по теореме Пифагора имеем:
По формуле объема шара
Ответ:
Найдем теперь объемы частей шара.
Определение:
Шаровым сегментом называется часть шара, отсекаемая от него некоторой плоскостью.
На рисунке 213 плоскость сечения, проходящая через точку В, разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием этих сегментов, а длины отрезков диаметра, перпендикулярного плоскости сечения,— высотами сегментов. Так, на рисунке 213 — высота меньшего сегмента, — высота большего сегмента.
Так, на рисунке 213 — высота меньшего сегмента, — высота большего сегмента.
Теорема (формула объема шарового сегмента)
Объем шарового сегмента вычисляется по формуле
где R — радиус шара, Н — высота сегмента.
Доказательство:
Применим для шарового сегмента интегральную формулу объема.
Введем декартову систему координат так, чтобы ее начало совпадало с центром шара.
Тогда часть шара, ограниченная плоскостями , является шаровым сегментом с высотой Н (рис. 214).
Радиус сечения шарового сегмента плоскостью, пересекающей ось Ох в точке (х;0;0), равен Следовательно, площадь этого сечения По интегральной формуле объема для шарового сегмента получаем:
Теорема доказана.
Заметим, что при Н -2R из только что доказанной формулы следует еще один способ нахождения формулы объема шара:
Определение:
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, основанием которого является основание сегмента, а вершиной — центр шара.
Очевидно, что если шаровой сегмент меньше полушара, его дополняют конусом для получения шарового сектора; если же шаровой сегмент больше полушара, то для получения шарового сектора конус из него удаляют (рис. 215).
Теорема (формула объема шарового сектора)
Объем шарового сектора вычисляется по формуле
где R — радиус шара, Я — высота соответствующего шарового сегмента.
Доказательство:
Рассмотрим случай шарового сектора, высота Я соответствующего шарового сегмента для которого меньше R (рис. 216).
Тогда его объем равен сумме объема сегмента и объема конуса V2. Следовательно,
Случай, когда высота Н больше или равна R, рассмотрите самостоятельно.
Теорема доказана.
Определение:
Шаровым слоем (поясом) называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Расстояние между этими плоскостями называется высотой шарового слоя, а сечения, ограничивающие слой,— основаниями шарового слоя (рис. 217).
217).
Заметим, что объем шарового слоя можно вычислить двумя способами:
- как разность объемов двух шаровых сегментов;
- как разность объема шара и объемов двух сегментов, не входящих в слой.
Из повседневного опыта нам хорошо известно, что при увеличении размеров предмета его объем также увеличивается. Например, легко сравнить объемы двух аквариумов, размеры одного из которых вдвое меньше соответствующих размеров другого (рис. 218): объемы отличаются в 8 раз.
Кроме того, можно проследить за подобными с коэффициентом k многоугольниками на плоскости. Как известно, их периметры отличаются в k раз, площади — в k2 раз. Естественно предположить, что объемы подобных с коэффициентом k пространственных тел отличаются к3 раз. Проверим это для тел, формулы объема которых нам уже известны.
Итак, для всех рассмотренных тел верно следующее утверждение: объемы тел, подобных с коэффициентом k, относятся как k3.
Этот факт верен и для любых простых тел, то есть тел, которые можно разбить на конечное число треугольных пирамид. В частности, любые многогранники, подобные с коэффициентом к, имеют объемы, которые отличаются в k3 раз.
Пример №5Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?
Решение:
Пусть дана пирамида с вершиной S и высотой SO. Плоскость, параллельная основанию пирамиды, пересекает SO в точке (рис. 219).
По условию = Но отсекаемая пирамида подобна данной, причем отношение их высот равно коэффициенту подобия, то есть По свойству объемов подобных тел объем отсекаемой пирамиды в 8 раз меньше объема данной пирамиды. Следовательно, данная плоскость, параллельная основанию пирамиды, делит ее объем в отношении 1:7.
Ответ: 1:7.
Пространственные фигуры | Математические формулы
Площадь боковой поверхности прямой призмы
Найти
Известно, что:
S_бокPh =
Вычислить ‘S_бок’Площадь поверхности прямой призмы
Найти
Известно, что:
SS_бокS_осн =
Вычислить ‘S’Объем прямой призмы
Найти
Известно, что:
VS_оснh =
Вычислить ‘V’Диагональ прямоугольного параллелепипеда
Найти
Известно, что:
dabc =
Вычислить ‘d’Площадь боковой поверхности прямоугольного параллелепипеда
Найти
Известно, что:
S_бокacb =
Вычислить ‘S_бок’Площадь поверхности прямоугольного параллелепипеда
Найти
Известно, что:
S_бокabc =
Вычислить ‘S_бок’Объем прямоугольного параллелепипеда
Найти
Известно, что:
VS_оснh =
Вычислить ‘V’Объем прямоугольного параллелепипеда
Найти
Известно, что:
Vabc =
Вычислить ‘V’Площадь боковой поверхности куба
Найти
Известно, что:
S_бокa =
Вычислить ‘S_бок’Площадь поверхности куба
Найти
Известно, что:
Sa =
Вычислить ‘S’Объем куба
Найти
Известно, что:
Va =
Вычислить ‘V’Площадь боковой поверхности правильной пирамиды
Найти
Известно, что:
S_бокPh_s =
Вычислить ‘S_бок’Площадь боковой поверхности правильной пирамиды
Найти
Известно, что:
S_бокS_оснφ =
Вычислить ‘S_бок’Объем правильной пирамиды
Найти
Известно, что:
VS_оснh =
Вычислить ‘V’Площадь боковой поверхности правильной усеченной пирамиды
Найти
Известно, что:
S_бокP1P2h_s =
Вычислить ‘S_бок’Площадь боковой поверхности правильной усеченной пирамиды
Найти
Известно, что:
S_бокS1S2φ =
Вычислить ‘S_бок’Площадь поверхности усеченной пирамиды
Найти
Известно, что:
SS_бокS1S2 =
Вычислить ‘S’Объем усеченной пирамиды
Найти
Известно, что:
VhS1S2 =
Вычислить ‘V’Площадь боковой поверхности цилиндра
Найти
Известно, что:
S_бокπrh =
Вычислить ‘S_бок’Площадь основания цилиндра
Найти
Известно, что:
S_оснπr =
Вычислить ‘S_осн’Площадь поверхности цилиндра
Найти
Известно, что:
Sπrh =
Вычислить ‘S’Объем цилиндра
Найти
Известно, что:
Vπrh =
Вычислить ‘V’Площадь боковой поверхности конуса
Найти
Известно, что:
S_бокπrl =
Вычислить ‘S_бок’Площадь поверхности конуса
Найти
Известно, что:
Sπrl =
Вычислить ‘S’Площадь боковой поверхности конуса (развёртка)
Найти
Известно, что:
Sπlα =
Вычислить ‘S’Объем конуса
Найти
Известно, что:
Vπrh =
Вычислить ‘V’Площадь боковой поверхности усеченного конуса
Найти
Известно, что:
S_бокπRrl =
Вычислить ‘S_бок’Площадь поверхности усеченного конуса
Найти
Известно, что:
SπRrl =
Вычислить ‘S’Объем усеченного конуса
Найти
Известно, что:
VπhRr =
Вычислить ‘V’Площадь поверхности шара (сферы)
Найти
Известно, что:
SπR =
Вычислить ‘S’Объем шара (сферы)
Найти
Известно, что:
VπR =
Вычислить ‘V’Площадь поверхности шарового сегмента
Найти
Известно, что:
SπRh =
Вычислить ‘S’Объем шарового сегмента
Найти
Известно, что:
VπhR =
Вычислить ‘V’Объем шарового сегмента (через радиус основания сегмента)
Найти
Известно, что:
Vπhr =
Вычислить ‘V’Площадь поверхности шарового слоя
Найти
Известно, что:
SπRh =
Вычислить ‘S’Объем шарового слоя
Найти
Известно, что:
Vπhr1r2 =
Вычислить ‘V’Площадь поверхности шарового сектора
Найти
Известно, что:
SπRhr =
Вычислить ‘S’Объем шарового сектора
Найти
Известно, что:
VπRh =
Вычислить ‘V’9.
 5: Площадь и объем геометрических фигур и объектов
5: Площадь и объем геометрических фигур и объектов- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48889
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Цели обучения
- знать значение и обозначения области
- знать формулы площади некоторых распространенных геометрических фигур
- уметь находить площади некоторых обычных геометрических фигур
- знать значение и обозначения тома
- знать формулы объема некоторых обычных геометрических объектов
- уметь находить объем некоторых обычных геометрических объектов 92\), или квадратная единица длины (квадратная единица длины), может быть физически интерпретирована как площадь поверхности.

Площадь
Площадь поверхности представляет собой количество квадратных единиц длины, содержащихся на поверхности.Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на некоторой поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)
Исследуем площади следующих геометрических фигур.
Формулы площади
Мы можем определить площади этих геометрических фигур, используя следующие формулы.
Рисунок Формула площади Заявление Треугольник \(A_T = \dfrac{1}{2} \cdot b \cdot h\) Площадь треугольника равна половине произведения основания на высоту. Прямоугольник \(A_R = l \cdot w\) Площадь прямоугольника равна произведению длины на ширину.  2} \end{массив}\) 92\).
2} \end{массив}\) 92\).Набор образцов A
Найдите площадь прямоугольника.
Решение
Сначала переведем 4 фута 2 дюйма в дюймы. Поскольку мы хотим преобразовать в дюймы, мы будем использовать дробную единицу \(\dfrac{\text{12 дюймов}}{\text{1 фут}}\), поскольку в числителе дюймы. Затем
\(\begin{array} {rcl} {\text{4 ft}} & = & {\dfrac{\text{4 ft}}}{1} \cdot \dfrac{\text{12 дюймов. }}{\text{1 фут}}} \\ {} & = & {\dfrac{4 \cancel{\text{фут}}}{1} \cdot \dfrac{\text{12 дюймов}}{ 1 \cancel{\text{футов}}}} \\ {} & = & {\text{48 дюймов}} \end{массив}\)
Таким образом, \(\text{4 фута 2 дюйма = 48 дюймов + 2 дюйма = 50 дюймов}\)
\(\begin{array} {rcl} {A_R} & = & {l \ cdot w} \\ {} & = & {\text{50 дюймов} \cdot \text{8 дюймов}} \\ {} & = & {400 \text{кв. дюймов}} \end{массив} \)
Площадь этого прямоугольника 400 кв. дюймов.
Набор образцов A
Найдите площадь параллелограмма.
Решение
\(\begin{array} {rcl} {A_P} & = & {b \cdot h} \\ {} & = & {\text{10,3 см} \cdot \text{ 6,2 см}} \\ {} & = & {63,86 \text{ кв.
 см}} \end{массив}\)
см}} \end{массив}\)Площадь этого параллелограмма 63,86 кв.см.
Набор образцов A
Найдите площадь трапеции.
Решение
\(\begin{array} {rcl} {A_{Trap}} & = & {\dfrac{1}{2} \cdot (b_1 + b_2) \cdot h} \\ {} & = & {\dfrac{1}{2} \cdot (\text{14,5 мм + 20,4 мм}) \cdot (4,1 \text{мм})} \\ {} & = & {\dfrac{1 {2} \cdot (\text{34,9 мм}) \cdot (4,1 \text{мм})} \\ {} & = & {\dfrac{1}{2} \cdot \text{(143,092} \\ {} & \приблизительно & {(3.14) \cdot (\text{282,24 кв. футов})} \\ {} & \приблизительно & {888,23 \text{кв. футов}} \end{массив}\)
Площадь этого круга составляет примерно 886,23 кв. футов.
Практический набор A
Найдите площадь каждой из следующих геометрических фигур.
- Ответить
36 кв. см
Тренировочный набор A
- Ответить
37 503 кв. мм
Тренировочный набор A
- Ответить
13,26 кв.
 дюйма
дюйма
Тренировочный набор A
- Ответить
367,5 квадратных миль
Тренировочный набор A
- Ответить
452,16 кв. футов
Объем
Объем объекта — это количество кубических единиц длины, содержащихся в объекте.Например, 4 куб. мм означает, что 4 куба со стороной 1 мм точно заполнили бы некоторый трехмерный объект. (Кубики, возможно, придется разрезать и переставить, чтобы они соответствовали форме объекта.)
Объемные формулы
Рисунок Формула объема Заявление Прямоугольный сплошной \(\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота )}} \end{массив}\) Объем прямоугольного твердого тела равен произведению длины на ширину и на высоту.  92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)
92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)Объем конуса равен \(\dfrac{1}{3}\), умноженному на \(\pi\), умноженному на квадрат радиуса, умноженный на высоту. Нахождение объемов некоторых обычных геометрических объектов
Набор образцов B
Найдите объем прямоугольного тела.
Решение
\(\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{92 \cdot \text{(7,8 футов)}} \\ {} & \ приблизительно & {(3,14) \cdot (\text{24,01 кв. футов}) \cdot \text{(7,8 футов)}} \\ {} & \ приблизительно & {(3.14) \cdot \text{(187,278 куб. футов)}} \\ {} & \ приблизительно & {\ text {588,05292 куб. футов}} \end{массив}\)
Объем этого цилиндра составляет приблизительно 588,05292 кубических футов. Объем является приблизительным, поскольку мы приблизили \(\pi\) к 3,14.
Набор образцов B
Определите приблизительный объем конуса.
 Округлить до двух знаков после запятой.
Округлить до двух знаков после запятой.92 \cdot \text{(5 мм)}} \\ {} & \приблизительно & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{4 кв. мм}) \cdot \ text{(5 мм)}} \\ {} & \ приблизительно & {(\dfrac{1}{3}) \cdot (3.14) \cdot \text{(20 мм3)}} \\ {} & \ приблизительно & {20,9\overline{3} \text{ куб. мм}} \\ {} & \ приблизительно & {\text{20,93 куб. мм}} \end{массив}\)
Объем этого конуса приблизительно 20,93 куб мм. Объем приблизительный, потому что мы приблизили \(\pi\) к 3,14.
Практический набор B
Найдите объем каждого геометрического объекта. Если требуется \(\pi\), аппроксимируйте его с помощью 3,14 и найдите приблизительный объем.
- Ответить
21 куб. дюйм
Практический набор B
Сфера
- Ответить
904,32 куб. футов
Практический набор B
- Ответить
157 м3
Практический набор B
- Ответ
0,00942 куб.
 дюймов
дюймов
Упражнения
Найдите все указанные измерения.
Упражнение \(\PageIndex{1}\)
Район
- Ответить
16 кв.м
Упражнение \(\PageIndex{2}\)
Район
Упражнение \(\PageIndex{3}\)
Район
- Ответить
1,21 кв. мм
Упражнение \(\PageIndex{4}\)
Район
Упражнение \(\PageIndex{5}\)
Район
- Ответить
18 кв. дюймов
Упражнение \(\PageIndex{6}\)
Район
Упражнение \(\PageIndex{7}\)
Точная площадь
- Ответ
\((60,5 \pi + 132) \text{ кв. фут}\)
Упражнение \(\PageIndex{8}\)
Примерная площадь
Упражнение \(\PageIndex{9}\)
Район
- Ответить
40,8 кв.
 дюйма
дюйма
Упражнение \(\PageIndex{10}\)
Район
Упражнение \(\PageIndex{11}\)
Примерная площадь
- Ответить
31,0132 кв. дюйма
Упражнение \(\PageIndex{12}\)
Точная площадь
Упражнение \(\PageIndex{13}\)
Примерная площадь
- Ответить
158,2874 кв. мм
Упражнение \(\PageIndex{14}\)
Точная площадь
Упражнение \(\PageIndex{15}\)
Примерная площадь
- Ответить
64,2668 кв. дюймов
Упражнение \(\PageIndex{16}\)
Район
Упражнение \(\PageIndex{17}\)
Примерная площадь
- Ответить
43,96 кв.
 футов
футов
Упражнение \(\PageIndex{18}\)
Том
Упражнение \(\PageIndex{19}\)
Том
- Ответить
512 см3
Упражнение \(\PageIndex{20}\)
Точный объем
Упражнение \(\PageIndex{21}\)
Приблизительный объем
- Ответить
11,49 см3
Упражнение \(\PageIndex{22}\)
Примерный объем
Упражнение \(\PageIndex{23}\)
Точный объем
- Ответить
\(\dfrac{1024}{3} \pi \text{ куб футов}\)
Упражнение \(\PageIndex{24}\)
Приблизительный объем
Упражнение \(\PageIndex{25}\)
Приблизительный объем
- Ответить
22,08 куб.
 дюйма
дюйма
Упражнение \(\PageIndex{26}\)
Приблизительный объем
Упражнения для обзора
Упражнение \(\PageIndex{27}\)
Сколько сотен в числе 23 426?
- Ответить
4
Упражнение \(\PageIndex{28}\)
Перечислите все делители числа 32.
Упражнение \(\PageIndex{29}\)
Найдите значение \(4 \dfrac{3}{4} — 3 \dfrac{5}{6} + 1 \dfrac{2}{3}\).
- Ответить
\(\dfrac{31}{12} = 2 \dfrac{7}{12} = 2,58\)
Упражнение \(\PageIndex{30}\)
Найдите значение \(\dfrac{5 + \dfrac{1}{3}}{2 + \dfrac{2}{15}}\).
Упражнение \(\PageIndex{31}\)
Найдите периметр.
- Ответить
27,9 м
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Теги

Формулы геометрии — Что такое формулы геометрии? Формулы 2D и 3D форм, примеры
Геометрические формулы используются для нахождения размеров, периметра, площади, площади поверхности, объема и т. д. геометрических фигур. Геометрия – это часть математики, изучающая отношения между точками, линиями, углами, поверхностями, измерениями и свойствами тел. Существует два типа геометрии: 2D, или плоскостная геометрия, и 3D, или объемная геометрия.
2D-фигуры — это плоские фигуры, имеющие только два измерения: длину и ширину, такие как квадраты, круги, треугольники и т. д. 3D-объекты — это твердые объекты, которые имеют три измерения: длину, ширину и высоту или глубину. как в кубе, прямоугольном параллелепипеде, сфере, цилиндре, конусе, давайте изучим формулы геометрии вместе с несколькими решенными примерами в следующих разделах.
Что такое геометрические формулы?
Формулы, используемые для определения размеров, периметра, площади, площади поверхности, объема и т.
 д. двухмерных и трехмерных геометрических фигур, называются формулами геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т. д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии имеют вид:
д. двухмерных и трехмерных геометрических фигур, называются формулами геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т. д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии имеют вид:Список геометрических формул
Ниже приведен список различных геометрических формул для вас в соответствии с геометрической формой.
- Периметр квадрата = 4 (сторона)
- Периметр прямоугольника = 2 (длина + ширина)
- Площадь квадрата = сторона 2
- Площадь прямоугольника = длина × ширина
- Площадь треугольника = ½ × основание × высота
- Площадь трапеции = ½ × \((основание_1 + основание_2)\) × высота
Основные геометрические формулы, в которых используется математическая константа π:
- Площадь круга = A = π×r 2
- Длина окружности = 2πr
- Площадь криволинейной поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr(r + h)
- Объем цилиндра = V = πr 2 ч
- Площадь криволинейной поверхности конуса = πrl
- Общая площадь поверхности конуса = πr(r+l) = πr[r+√(h 2 +r 2 )]
- Объем конуса = V = ⅓×πr 2 ч
- Площадь поверхности сферы = S = 4πr 2
- Объем сферы = V = 4/3×πr 3
где,
- r = радиус;
- ч = Высота.
 и,
и, - l = Высота наклона
В таблице формул представлены геометрические формулы , используемые для различных двухмерных и трехмерных форм:
ФОРМЫ ФОРМУЛЫ 1. Прямоугольный треугольник Теорема Пифагора: a 2 + b 2 = c 2
Площадь = ½ от
Периметр = a + b + √(a 2 + b 2 )
Где,
c = гипотенуза треугольникаa = высота треугольника
b = основание треугольника
2. Треугольник Периметр, P = a + b + c
Площадь, A = ½ ширины
Высота, h = 2(A/b)
Где,
a,b,c — стороны треугольника.
3. Прямоугольник Периметр = 2(д + ш)
Площадь = lw
Диагональ, d = √(l 2 + w 2 )
Где,
l = длина прямоугольника
w = ширина прямоугольника
4.  Параллелограмм
ПараллелограммПериметр, P = 2(a + b)
Площадь, A = bh
Высота, h = A/b
Основание, b = А/ч
Где,
а и b — стороны параллелограмма
h = высота параллелограмма
5. Трапеция Площадь, A = ½(a + b)h
Высота, h = 2A/(a + b)
База, b = 2(А/ч) – а
Где,
a и b — параллельные стороны
ч = расстояние между двумя параллельными сторонами
6. Обведите Окружность = 2πr
Площадь = πr 2
Диаметр = 2r
Где,
r = радиус окружности
7. Квадрат Периметр, P = 4a
Площадь, А = а 2
Диагональ, d = a√2
Сторона, а = √A = d/2√2
Где,
а = сторона квадрата
8. Дуга Длина дуги, L = rθ
Площадь, A = ½r 2 θ
Здесь θ – центральный угол в радианах.

Где,
r = радиус
9. Куб Площадь, A = 6a 2
Объем, В = а 3
Край, a = V ⅓
Диагональ пространства = a√3
Где,
а = сторона куба
10. Прямоугольный Площадь поверхности, A = 2 (lb + bh + hl)
Объем, В = фунт-час
Диагональ пространства, d = √( l 2 + b 2 +h 2 )
Где,
l= длина
б = дыхание
h= высота
11. Цилиндр Общая площадь поверхности, A = 2πrh + 2πr 2
Изогнутая поверхность, A c = 2πrh
Объем, В = πr 2 ч
Базовая зона, A b = πr 2
Радиус, r = √(В/πh)
Где,
r= радиус цилиндра
h= высота цилиндра
12.  Конус
КонусОбщая площадь поверхности, A = πr(r+l) = πr[r+√(h 2 +r 2 )]
Изогнутая поверхность, A c = πrl
Объем, В = ⅓πr 2 ч
Наклонная высота, l = √(h 2 +r 2 )
Базовая зона, A b = πr 2
Где,
r= радиус конуса
h= высота конуса
l = наклонная высота
13. Сфера Площадь поверхности, A = 4πr 2
Объем, В = ⁴⁄₃πr 3
Диаметр = 2r
Где,
r= радиус сферы
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Запишитесь на бесплатный пробный урок
Давайте посмотрим на решенные примеры, чтобы лучше понять геометрические формулы.

Примеры решения с использованием формул геометрии
Пример 1. Вычислить длину окружности, площадь и окружность с помощью формул геометрии, если радиус окружности равен 21 единице?
Решение:
Чтобы найти площадь и длину окружности:
Дано: Радиус круга = 21 единица
Использование формул геометрии для круга,
Площадь круга = π×r 2
= 3,142857 × 21 2
= 1385,44
Теперь о длине окружности
. Использование формул геометрии для круга,
Длина окружности = 2πr
= 2(3,142857)(21)
= 131,95Ответ: Площадь круга составляет 1385,44 квадратных единиц, а длина окружности — 131,95 единиц.
Пример 2: Какова площадь прямоугольного парка, длина и ширина которого равны 60 м и 90м соответственно?
Решение:
Чтобы найти площадь прямоугольного парка:Дано: Длина парка = 60м
Ширина парка = 90м
Используя формулы геометрии для прямоугольника,Площадь прямоугольника = (Длина × Ширина)
= (60 × 90) м 2
= 5400 м 2
- м 2 .

Пример 3: Используя формулы геометрии куба, вычислить площадь поверхности и объем куба, длина ребра которого равна 6 единицам соответственно?
Решение:
Найти: Площадь поверхности и объем куба, длина ребра которого равна 6 единицамИспользуя формулы геометрии куба,
Площадь поверхности куба = A = 6a 2
А = 6 (6) 2
A = 6 × 36 = 216 единиц 2
Объем куба, V = a 3
V = (6) 3
V = 216 единиц 3Ответ: площадь поверхности куба 216 единиц 2 . Объем куба – 216 единиц. 3
Часто задаваемые вопросы по формулам геометрии
Что такое формулы геометрии кубоида?
Формулы геометрии прямоугольного параллелепипеда перечислены ниже:
- Площадь поверхности прямоугольного параллелепипеда, A = 2 (lb + bh + hl)
- Объем прямоугольного параллелепипеда, V = lbh
- Пространственная диагональ прямоугольного параллелепипеда, d = √(l 2 + b 2 +h 2 )
Где,
- l= длина
- b= ширина
- h= высота
Какие формулы геометрии прямоугольника?
Формулы геометрии прямоугольника приведены ниже:
- Периметр прямоугольника = 2(l + w)
- Площадь прямоугольника = lw
- Диагональ прямоугольника, d = √(l 2 + ш 2 )
Где,
- l = длина прямоугольника
- w = ширина прямоугольника
Какие формулы геометрии конуса?
Формулы геометрии конуса приведены ниже:
- Общая площадь поверхности конуса, A = πr(r+l) = πr[r+√(h 2 +r 2 )]
- Криволинейная поверхность конуса, A c = πrl
- Объем конуса, V = ⅓πr 2 ч
- Наклонная высота конуса, l = √(h 2 +r 2 )
- Базовая зона, A b = πr 2
Где,
- r= радиус конуса
- h= высота конуса
- l = наклонная высота
Какие формулы геометрии окружности?
Формулы геометрии круга приведены ниже:
- Окружность = 2πr
- Площадь = πr 2
- Диаметр = 2r
Где r = радиус окружности
Какие геометрические формулы сферы?
Две важные геометрические формулы сферы — площадь и объем сферы.
 Площадь поверхности сферы равна A = 4πr 2 , а объем сферы равен V = ⁴⁄₃πr 3 .
Площадь поверхности сферы равна A = 4πr 2 , а объем сферы равен V = ⁴⁄₃πr 3 .Каковы применения формул геометрии?
Геометрические формулы полезны для определения периметра, площади, объема и площади поверхности двухмерных и трехмерных геометрических фигур. В нашей повседневной жизни есть множество объектов, напоминающих геометрические фигуры, и площади и объемы этих геометрических фигур можно рассчитать с помощью этих геометрических формул.
Площадь и объем: формулы и различия
Предположим, вы делаете ремонт в своей комнате и вам нужно знать доступную площадь пола. Итак, вы измеряете пол, что, по сути, находит площадь этой комнаты. Теперь предположим, что вы планируете наполнить свой бассейн водой. Вы измеряете, сколько воды необходимо для заполнения бассейна, измеряя его объем .
В геометрии важно знать пространство, занимаемое определенными 2-мерными и 3-х мерные фигуры.
 Мы можем определить это пространство, вычислив площадь и объем в зависимости от типа фигуры. Здесь мы поймем основные понятия площади и объема применительно к различным типам фигур.
Мы можем определить это пространство, вычислив площадь и объем в зависимости от типа фигуры. Здесь мы поймем основные понятия площади и объема применительно к различным типам фигур.Значение площади в геометрии
Общее пространство, занимаемое двумерной поверхностью объекта или плоской формы, называется площадью .
Существует множество различных формул площади для определения площади различных двумерных фигур. Мы также можем определить площадь фигуры, подсчитав количество единичных квадратов, покрывающих всю поверхность объекта. Этот метод помогает нам узнать и понять концепцию площади. См. изображение ниже, которое отображает концепцию квадратной единицы. Однако вы обнаружите, что формулы площади проще и быстрее использовать. Единица площади всегда измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные метры, квадратные дюймы и так далее.
Площадь 2D-фигуры, splashlearn.
 com
comВот несколько фактов о площади, о которых следует помнить:
- Площадь и периметр фигур представляют собой различные вычисления, и их часто можно спутать друг с другом.
- Площадь любой фигуры в основном рассчитывается на основе таких терминов, как сторона, длина, основание, высота и радиус.
- Площадь двух конгруэнтных (идентичных) фигур будет одинаковой, но иногда две неконгруэнтные (не идентичные) фигуры могут иметь одинаковую площадь.
Формулы площади для простых фигур (2D)
Давайте рассмотрим некоторые из различных формул площади основных и обычных геометрических фигур, в том числе:
- Площадь прямоугольника
- Площадь квадрата
- Площадь треугольника
- Площадь круга
- Площадь параллелограмма
Площадь прямоугольника
Мы можем вычислить площадь прямоугольника шириной w и высотой h следующим образом:
Площадь прямоугольника
Площадь прямоугольника — StudySmarter Originals
Площадь квадрата
Четыре стороны квадрата равны по длине.
 Итак, мы можем рассчитать площадь по данной формуле:
Итак, мы можем рассчитать площадь по данной формуле:Площадь квадрата
где а — длина стороны
Площадь квадрата — StudySmarter Originals
Площадь треугольника
Мы можем вычислить площадь треугольника с помощью высоты h и основания b.
Площадь треугольника
Площадь треугольника — StudySmarter Originals
Площадь круга
Пространство, занимаемое кругом, можно рассчитать на основе его радиуса.
Площадь круга
где r — радиус круга
Площадь круга — StudySmarter Originals
Площадь параллелограмма
Параллелограмм — это фигура, противоположные стороны которой представляют собой пару параллельных прямых.
Площадь параллелограмма
где b — основание, а h — высота параллелограмма
Площадь параллелограмма — StudySmarter Originals
Значение площади поверхности в геометрии
Термин площадь поверхности связан с трехмерными фигурами и объектами.
 Тем не менее, его концепция по существу такая же, как площадь в том смысле, что он измеряет размер поверхности с использованием квадратных единиц, таких как дюймы в квадрате (в 2 ). Формулы для площадей поверхности различаются в зависимости от типа трехмерного объекта.
Тем не менее, его концепция по существу такая же, как площадь в том смысле, что он измеряет размер поверхности с использованием квадратных единиц, таких как дюймы в квадрате (в 2 ). Формулы для площадей поверхности различаются в зависимости от типа трехмерного объекта.Общая площадь, занимаемая внешними поверхностями любого трехмерного объекта, называется площадь поверхности этого объекта.
Площадь поверхности — StudySmarter Originals
Другими словами, площадь, занимаемая всеми гранями и сторонами любого трехмерного объекта, является площадью его поверхности. Площадь поверхности любой фигуры можно разделить на три типа:
- Площадь боковой поверхности
- Площадь криволинейной поверхности
- Общая площадь поверхности
Типы площади поверхности
Три типа площади поверхности (боковая, изогнутая и всего) объясняются здесь.
Площадь боковой и изогнутой поверхности
Площадь поверхности всей трехмерной формы, за исключением площади основания и верхней части, известна как площадь боковой поверхности .

Площадь поверхности всех криволинейных поверхностей 3D-формы известна как площадь криволинейной поверхности .
Иногда площадь боковой поверхности и площадь криволинейной поверхности на самом деле относятся к одной и той же части трехмерной формы. Это относится, например, к формам с криволинейными поверхностями, таким как цилиндры и конусы. Однако такие формы, как кубы, не имеют искривленной площади поверхности, и этот термин не применяется.
Площадь боковой поверхности — StudySmarter Originals
Здесь, на рисунке цилиндра, серая поверхность — это боковая поверхность, окружающая цилиндр. При расчете площади боковой поверхности мы будем учитывать показанную поверхность серого цвета, но не белую верхнюю поверхность или белую нижнюю поверхность цилиндра.
Общая площадь поверхности
Общая площадь всех поверхностей и сторон объекта называется общей площадью поверхности .
Другими словами, мы учитываем все поверхности объекта при расчете общей площади поверхности, а не площади боковой поверхности.
 Обычно мы просто называем общую площадь поверхности площадью поверхности.
Обычно мы просто называем общую площадь поверхности площадью поверхности.Общая площадь поверхности — StudySmarter Originals
Здесь мы учитываем площадь боковой поверхности (светло-серый цвет) и верхней и нижней (темно-серый цвет) при расчете общей площади поверхности этого цилиндра.
Формулы площади поверхности
Давайте взглянем на некоторые формулы площади поверхности для обычных трехмерных фигур.
Площадь поверхности куба
Куб – это трехмерная фигура, состоящая из шести квадратных граней. Площадь поверхности куба можно получить, найдя площадь всех шести граней и сложив их вместе. Для площади боковой поверхности куба мы принимаем во внимание только четыре грани, исключая верхнюю и нижнюю стороны.
Площадь поверхности куба — StudySmarter Originals
Формула площади поверхности куба выглядит следующим образом:
Общая площадь поверхности куба
Площадь боковой поверхности куба
где а — длина всех сторон
Площадь поверхности куба
Кубоид — это трехмерная фигура, все шесть граней которой прямоугольные.
 Полную площадь поверхности и боковую поверхность прямоугольного параллелепипеда можно рассчитать так же, как куба. Однако для прямоугольного параллелепипеда вместо того, чтобы использовать одно и то же измерение для всех шести граней, мы рассматриваем и измеряем разные грани по отдельности. Следовательно, мы вычисляем площадь поверхности прямоугольного параллелепипеда через длину l, ширину w и высоту h.
Полную площадь поверхности и боковую поверхность прямоугольного параллелепипеда можно рассчитать так же, как куба. Однако для прямоугольного параллелепипеда вместо того, чтобы использовать одно и то же измерение для всех шести граней, мы рассматриваем и измеряем разные грани по отдельности. Следовательно, мы вычисляем площадь поверхности прямоугольного параллелепипеда через длину l, ширину w и высоту h.Площадь поверхности параллелепипеда — StudySmarter Originals
Формула площади поверхности параллелепипеда выглядит следующим образом:
Общая площадь параллелепипеда
Площадь боковой поверхности параллелепипеда
29 Площадь поверхности 1 цилиндра 2 Цилиндр — это трехмерная фигура с двумя плоскими круглыми гранями, одна сверху и одна снизу, прикрепленными к противоположным концам изогнутой грани. Простым примером является труба с обоими концами, запаянными или закрытыми. Площадь поверхности цилиндра равна сумме площадей обоих круглых оснований и площади криволинейной поверхности.  При определении только площади боковой или криволинейной поверхности учитывается только криволинейная поверхность цилиндра.
При определении только площади боковой или криволинейной поверхности учитывается только криволинейная поверхность цилиндра.Площадь поверхности цилиндра — StudySmarter Originals
Формула площади поверхности цилиндра выглядит следующим образом:
Общая площадь поверхности цилиндра
Площадь боковой поверхности цилиндра
где r — радиус круглое основание, h — высота цилиндра
Площадь поверхности сферы
Сфера — это трехмерное изображение окружности. Поскольку у сфер есть только одна общая поверхность и нет других граней, обсуждение площади ее боковой поверхности не имеет смысла, поскольку она будет такой же, как и общая площадь ее поверхности. Поэтому мы вычисляем только общую площадь поверхности для сфер.
Площадь поверхности сферы — StudySmarter Originals
Формула площади поверхности прямоугольного параллелепипеда выглядит следующим образом:
Общая площадь поверхности сферы
где r — радиус сферы
Значение объема в геометрии
Любой трехмерный объект в природе занимает места .
 Итак, пространство, занимаемое этим объектом, называется его объемом .
Итак, пространство, занимаемое этим объектом, называется его объемом . Пространство внутри объекта или пространство, занимаемое любым трехмерным твердым объектом, называется том .
Чтобы измерить объем, мы делим занимаемое пространство на равные кубические единицы и вычисляем общее количество занимаемых кубических единиц. Единицей объема может быть кубический сантиметр, кубический метр, кубический дюйм и так далее.
Объем визуализации трехмерных объектов, tasks.illustrativemathematics.org
Формулы объема
Давайте разберемся с некоторыми формулами объема для знакомых трехмерных объектов и форм.
Объем куба
Поскольку все стороны куба имеют одинаковую длину, мы можем вычислить объем куба, используя следующую формулу:
Объем куба
где а — длина сторон всех граней
Объем куба куб — StudySmarter Originals
Объем прямоугольного параллелепипеда
В отличие от куба, прямоугольный параллелепипед имеет стороны разных размеров.
 Итак, мы вычисляем объем через длину l, ширину w и высоту h. Формула объема прямоугольного параллелепипеда выглядит следующим образом:
Итак, мы вычисляем объем через длину l, ширину w и высоту h. Формула объема прямоугольного параллелепипеда выглядит следующим образом:Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда — StudySmarter Originals
Объем цилиндра цилиндра при расчете его объема. Формула выглядит следующим образом:
Объем цилиндра
Объем цилиндра — StudySmarter Originals
Объем сферы
сфера, трехмерное представление круга. Объем сферы можно определить с помощью нескольких методов, включая, например, формулу Архимеда и принцип Кавальери. А пока мы просто бросим беглый взгляд на его общепринятую формулу объема:
Объем сферы
где r — радиус сферы
Объем сферы — StudySmarter Originals
Площадь и объем — ключевые выводы
- Общее пространство, занимаемое двухмерной поверхностью объекта или плоская фигура называется площадью. Площадь использует квадратные единицы, такие как футы в квадрате или метры в квадрате.

- Площадь двух конгруэнтных (одинаковых) фигур будет одинаковой, но иногда две неконгруэнтные фигуры могут иметь одинаковую площадь.
- Общая площадь, занимаемая внешними поверхностями любого трехмерного объекта, называется площадью поверхности этого объекта. Площадь поверхности использует квадратные единицы.
- Поверхность можно разделить на три типа: площадь боковой поверхности, площадь изогнутой поверхности и общая площадь поверхности.
- Пространство внутри объекта или пространство, занимаемое любым трехмерным твердым объектом, называется объемом.
Геометрические фигуры и формулы в объемной геометрии
Базовый калькулятор
Капсула
Калькулятор капсул
- Объем = πr 2 ((4/3)r + a)
- Площадь поверхности = 2πr(2r + a)
- Окружность = 2πr
Также называется стадион революции.

Круглый конус
Круглый конус Калькулятор
- Объем = (1/3)πr 2 ч
- Наклонная высота = √(r 2 + h 2 )
- Площадь боковой поверхности = πrs = πr√(r 2 + h 2 )
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности
= L + B = πrs + πr 2 = πr(s + r) = πr(r + √(r 2 + h 2 ))
Круглый цилиндр
Круглый цилиндр Калькулятор
- Объем = πr 2 ч
- Площадь боковой поверхности = 2πrh
- Площадь верхней поверхности = πr 2
- Площадь нижней поверхности = πr 2
- Общая площадь поверхности
= L + T + B = 2πrh + 2(πr 2 ) = 2πr(h+r)
Конический усеченный конус
Калькулятор конического усеченного конуса
- Объем = (1/3)πh (r 1 2 + r 2 2 + (r 1 * r 2 ))
- Наклонная высота = √((r 1 — r 2 ) 2 + h 2 )
- Площадь боковой поверхности
= π(r 1 + r 2 )s = π(r 1 + r 2 )√((r 1 — r 2 ) 2 + h 2 ) - Площадь верхней поверхности = πr 1 2
- Площадь базовой поверхности = πr 2 2
- Общая площадь поверхности
= π(r 1 2 + r 2 2 + (r 1 + r 2 ) * s)
= π[ г 1 2 + R 2 2 + (R 1 + R 2 ) * √ ((R 1 — R 2 ) 2 + H 2 ) 1 2 + H ) 1 2 + H ) 2 11110 — R 2 )
Куб
Калькулятор куба
- Объем = a 3
- Площадь поверхности = 6a 2
- Диагональ лица (f) = a√2
- Диагональ (d) = a√3
Полушарие
Калькулятор полушария
- Объем = (2/3)πr 3
- Окружность = 2πr
- Площадь криволинейной поверхности = 2πr 2
- Площадь базовой поверхности = πr 2
- Общая площадь поверхности = (2πr 2 ) + (πr 2 ) = 3πr 2
Пирамида: Квадрат
Калькулятор пирамиды
- Объем = (1/3)а 2 ч
- Наклонная высота (s) = √(h 2 + (1/4)a 2 )
- Площадь боковой поверхности = a√(a 2 + 4h 2 )
- Базовая площадь поверхности = a 2
- Общая площадь поверхности
= L + B = а 2 + а √ (а 2 + 4h 2 ))
= а(а + √(а 2 + 4h 2 ))
Прямоугольная призма
Прямоугольная призма Калькулятор
- Объем = lwh
- Площадь поверхности = 2(lw + lh + wh)
- Диагональ (d) = √(l 2 + w 2 + h 2 )
Сфера
Калькулятор сферы
- Объем = (4/3)πr 3
- Окружность = 2πr
- Площадь поверхности = 4πr 2
Сферический колпачок
Сферический колпачок Formulas
- Объем
= (1/6)πh(3а 2 + ч 2 )
= (1/3)πh 2 (3R — h) - Радиус базовой окружности = √h(2R — h)
- Окружность Базовая окружность = 2π√h(2R — h)
- Площадь поверхности = 2πRh = π(а 2 + ч 2 )
Сферический сегмент
Формулы сферических сегментов
- Объем = (1/6)πh(3a 2 + 3b 2 + h 2 )
- Площадь верхней поверхности = πb 2
- Площадь нижней поверхности = πa 2
- Площадь боковой поверхности = 2πRh
- Где R = радиус сферы и
- R = √{ [[(a-b) 2 + h 2 ] [(a+b) 2 + h 2 ] ] / 4h 2 }
Треугольная призма
Треугольная призма Формулы
- Объем = (1/4)h √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Площадь верхней поверхности = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Площадь нижней поверхности = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
- Площадь боковой поверхности = h(a+b+c)
- Общая площадь поверхности = Площадь верхней поверхности + Площадь нижней поверхности + Площадь боковой поверхности
Трубка
Калькулятор трубки (полый цилиндр)
- Окружность, C:
- С 1 = 2πr 1
- С 2 = 2πr 2
- Площадь боковой поверхности, л, для
цилиндр:
- L 1 = 2πr 1 ч, площадь внешней поверхности
- L 2 = 2πr 2 ч, площадь внутренней поверхности
- Площадь, А, для торцевого сечения трубы:
- А 1 = πr 1 2 для области, ограниченной C 1
- А 2 = πr 2 2 для области, ограниченной C 2
- А = А 1 — А 2 =
π(r 1 2 — r 2 2 ) для площади сплошного сечения трубы, конца,
кольцо.

- Объем, В, (используя объем для
цилиндр):
- В 1 = πr 1 2 h для объема, заключенного в C 1
- В 2 = πr 2 2 ч для объема, заключенного в C 2
- В = В 1 — В 2 = π(r 1 2 — r 2 2 )h для объема твердого тела, трубки.
- Толщина стенки трубы, т:
- т = р 1 — р 2
Подписаться на CalculatorSoup:
20011 — Геометрические фигуры и нахождение площадей
Введение: соединение вашего обучения
Большинство студентов, изучающих математику в старших классах и колледжах, задают вопрос: «Когда я когда-нибудь буду использовать это понятие в реальной жизни?» На самом деле геометрия имеет множество практических применений как в повседневном, так и в компьютерном мире.

Геометрия может быть интересна, когда вы думаете о том, как она связана с дизайном компьютерных приложений, включая реальные и виртуальные объекты, или если вы пытаетесь определить информацию и свойства геопространственного местоположения или области. В этом модуле вы обсудите области геометрических фигур и объектов. К концу модуля вы должны знать значение и обозначения площади и формулы площади для некоторых распространенных геометрических фигур, а также уметь вычислять площади некоторых распространенных геометрических фигур.
Сосредоточение вашего обучения
Цели урока
К концу этого урока вы должны уметь:
- Вычислять площади обычных геометрических фигур.
Представление
Площадь
Площадь поверхности – это количество квадратных единиц длины, содержащихся на поверхности.
Вы начнете с изучения формул вычисления площади различных геометрических фигур. У каждой фигуры есть определенная формула, по которой нужно вычислить площадь, то есть количество квадратных единиц длины, содержащихся на поверхности.

Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)
Выберите следующую ссылку, чтобы увидеть представление площади на листе бумаги. Вы сможете увидеть, как измеряется площадь, разделив бумагу на маленькие квадратные единицы.
Площадь
Теперь, когда вы лучше понимаете, что такое площадь, посмотрите на квадрат. У него четыре равные стороны и четыре равных угла: Каждый угол равен 90°. Чтобы определить площадь квадрата, используйте следующую формулу.
Площадь квадрата
Площадь = сторона ⋅ сторона = сторона 2
Пример
Вычислите площадь квадрата со стороной 6 дюймов.
Площадь = сторона ⋅ сторона = сторона 2
Площадь = 6 дюймов ⋅ 6 дюймов = 36 кв. 2 .
6 ⋅ 6 или 6 2 = 36 кв.
 дюймов
дюймовПример
Вычислите площадь квадрата со стороной 9 см.
Площадь = сторона ⋅ сторона = сторона 2
Площадь = 9 см ⋅ 9 см = 81 кв. см
Поскольку сторона равна 9 см, вам нужно умножить 9 на 9, что также означает 9 2 .
9 ⋅ 9 или 9 2 = 81 кв. см
Теперь вы изучите формулы площади, чтобы ознакомиться с тем, как найти площадь следующих геометрических фигур.
Формулы площади
Площадь этих геометрических фигур можно определить с помощью следующих формул.
Рисунок Формула площади Заявление Треугольник А = б ⋅ ч
Площадь треугольника равна половине произведения основания высота.

Прямоугольник
А = л ⋅ ш
Площадь прямоугольника равна произведению длины на ширина.
Параллелограмм
А = б ⋅ ч
Площадь параллелограмма равна произведению основания на высоту.
Трапеция
А = ⋅( б 1 + б 2 )⋅ ч
Площадь трапеции равна половине суммы два основания умножить на высоту.
Круг
А = π r 2
Площадь круга в π раз больше квадрата радиус.

На основании диаграмме выше, геометрические фигуры имеют разные формулы для площади в зависимости от их формы. Взгляните на некоторые примеры.
Примеры: Нахождение площадей обычных геометрических фигур
Нахождение площади треугольника.
A = ⋅ b ⋅ h = ⋅ 20 ⋅ 6 кв. футов = 10 ⋅ 6 кв. футов = 60 кв. футов = 60 футов 2
Площадь этого треугольника составляет 60 квадратных футов, что часто записывается как 60 футов 2 .
Найдите площадь прямоугольника.
Прежде чем вы сможете вычислить площадь, вам нужно, чтобы длины сторон были в одних и тех же единицах измерения.
1) Сначала переведите 4 фута 2 дюйма в дюймы.
Преобразуйте 4 дюйма в футы, умножив 4 на 12; в 1 футе 12 дюймов. В 4 футах 48 дюймов. Таким образом, 4 фута 2 дюйма составляют 48 дюймов + 2 дюйма, что составляет 50 дюймов
2) Area Formula (Rectangle): A = l ∙ w
A = l ⋅ w
A = 50 in.
 ⋅ 8 in.
⋅ 8 in.A = 400 кв. дюймов
Ответ: Площадь этого прямоугольника равна 400 кв. дюймов
Найдите площадь параллелограмма.
A = b ⋅ h = 10,3 см ⋅ 6,2 см = 63,86 кв. см
Площадь этого параллелограмма равна 63,86 кв.см.
Найдите площадь трапеции.
A = ⋅ ( B 1 + B 2 ) ⋅ H
A = ⋅ (14,5 мм + 20 мм мм). ) ⋅ (4,1 мм) = ⋅ (143,09 кв. мм)
A = 71,545 кв. мм
Площадь этой трапеции равна 71,545 кв. мм.
Найдите приблизительную площадь круга.
A = πt R 2 ≈ (3,14) ⋅ (16,8 фута.) 2 ≈ (3,14) ⋅ (282,24 с. Площадь этого круга составляет приблизительно 886,23 кв. футов.
Посетите следующий веб-сайт для получения дополнительной информации о том, как найти площадь обычных геометрических фигур.

Область геометрических фигур: плоские формы
Теперь, когда вы ознакомились с формулами и примерами, пришло время посмотреть несколько видеороликов Академии Хана. Эти видеоролики предоставят вам дополнительные пояснения и демонстрации вычисления площади, чтобы помочь вам глубже понять концепции.
Математический видео-инструментарий:
Основы области
Площадь прямоугольников и треугольников
Площадь круга
Упражнение: нахождение площади
Теперь у вас есть шанс решить некоторые проблемы. Вам нужно будет взять лист бумаги и карандаш, чтобы выполнить практическое задание. Вы можете использовать калькулятор, если хотите. Внимательно изучите каждую из этих проблем; вы увидите похожие проблемы на проверке знаний урока.
Выберите следующую ссылку, чтобы завершить практическое задание.

Решение практических задач
После завершения практического задания проверьте, насколько хорошо вы справились, выбрав следующую ссылку:
Решения: Решение задач для местной практики
Подведение итогов
На этом уроке вы познакомились с различными геометрическими фигурами и формулами для вычисления их площадей. Эта информация может быть использована для расчета площадей экранов телевизоров, мониторов компьютеров, объективов фотоаппаратов и многого другого.
Большинство курсов, которые вы будете проходить в колледже или техникуме, не всегда могут включать конкретные примеры, применимые к вашей программе обучения. Вместо этого они, как правило, дают широкий обзор ключевых понятий, оставляя вас желать большего. Как и в предыдущих уроках, вам предлагается исследовать, как каждая концепция связана с выбранной вами областью обучения. Этот процесс исследования является бесценной частью вашего образования; не упустите эту возможность продвинуть свои знания.

Оценка вашего обучения
Теперь, когда вы внимательно прочитали урок и попытались решить практические задачи, пришло время для проверки знаний. Обратите внимание, что этот является оцениваемой частью этого урока, поэтому убедитесь, что вы подготовились перед началом.
- Заполните геометрические фигуры: нахождение площади.
Ресурс:
«Измерение и геометрия: площадь и объем геометрических фигур и объектов», Ellis, W. & Burzynski, D. © 2010, получено с http://cnx.org/content/m35023/1.2/. под лицензией Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. Это адаптация урока под названием «Геометрические фигуры и решение для площади», подготовленного Национальным консорциумом по информационной безопасности и геопространственным технологиям (NISGTC) под лицензией Creative Commons Attribution 3.
 0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0
0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0Дополнительные атрибуты
Какие геометрические формулы следует запоминать?
Purplemath
Существует множество геометрических формул, и они связывают высоту, ширину, длину, радиус и т. д. с периметром, площадью, площадью поверхности, объемом и т. д. Некоторые формулы довольно сложны, и вы их почти никогда не видите , не говоря уже об их использовании.
Но есть некоторые основные формулы, которые вам действительно следует запомнить, потому что ваш инструктор действительно может ожидать, что вы их знаете.
Содержание продолжается ниже
MathHelp.com
Например, очень легко найти площадь A прямоугольника: это просто длина l , умноженная на ширину w :
656 прямая = lw
«Прямая» в приведенной выше формуле является нижним индексом, указывающим, что найденная площадь A является площадью прямоугольника.
 Поскольку я буду обсуждать площади, объемы и т. д., формулы для различных фигур, я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула. Подписка такого рода может быть полезной техникой для ясности вашего смысла, поэтому постарайтесь держать это в уме для возможного использования в будущем.
Поскольку я буду обсуждать площади, объемы и т. д., формулы для различных фигур, я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула. Подписка такого рода может быть полезной техникой для ясности вашего смысла, поэтому постарайтесь держать это в уме для возможного использования в будущем.Какие геометрические переменные я должен уметь распознавать?
Некоторые переменные довольно стандартны, и вы должны ожидать, что ваш инструктор и ваш учебник будут использовать « A » для «площади», « SA » для «площади поверхности», « P » для «периметра», и « V » для «объема».
Линейные меры: « w » для «ширины», « d » для «глубины» [расстояние от передней до задней части трехмерных объектов, « h » для «высоты» и » l » для «длины». Однако, поскольку l может выглядеть очень похоже на число 1, иногда разумно использовать вместо него L , особенно когда вы пишете
Если вы посмотрите на изображение прямоугольника и вспомните, что «периметр» означает «длина по внешней стороне», вы увидите, что периметр прямоугольника P представляет собой сумму длин верхней и нижней части l и ширина слева и справа w :
P прямоугольник = 2 l + 2 w
Квадраты еще проще, потому что их длина и ширина одинаковы.
 Площадь A и периметр P квадрата с боковой длиной S приведены:
Площадь A и периметр P квадрата с боковой длиной S приведены:A SQR = S 2
S 2 4. . sВы должны знать формулу площади треугольника; его легко запомнить, и он имеет тенденцию неожиданно всплывать посреди текстовых задач. Учитывая размеры для базы b and the height h of the triangle, the area A of the triangle is:
A tri = ( 1 / 2 ) bh
Of course , периметр P треугольника будет просто суммой длин трех сторон треугольника.
Вы должны знать формулы длины окружности C и площади A круга, учитывая радиус r :
A CIR = π R 2
C CIR = 2π R
(«oprake yrable» oprafice «oprafice» oprafice «.

Помните, что радиус круга — это расстояние от центра до внешней стороны круга. Другими словами, радиус находится только на полпути. Если они дают вам длину диаметра, представляющую собой длину линии, проходящей через середину круга, то вам сначала придется разделить это значение пополам, чтобы применить приведенные выше формулы.
Все вышеперечисленное относится к «плоским», двумерным формам. Иногда вам придется иметь дело с трехмерными фигурами, такими как кубы или конусы. Для таких форм вы найдете площадь поверхности (если вы рисовали объект, это площадь, которую вам нужно было бы покрыть) и объем (внутреннее пространство, которое вы могли бы заполнить, если бы форма пустой).
Формула для объема V куба проста, так как длина, ширина и высота имеют одно и то же значение s :
V куб = s 3
так как все стороны имеют одинаковую квадратную площадь s 2 .
 Есть шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA равна:
Есть шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA равна:SA куб = 6 с 2
Формулы немного усложняются для «прямоугольной призмы», которая является техническим термином для кирпича. Объем V по-прежнему довольно прост, поскольку длина умножается на ширину, умноженную на высоту:
V прямоугольник = lwh
Формула площади поверхности немного более витиеватая. (Постарайтесь следовать рассуждениям, которые я собираюсь использовать, потому что вы, вероятно, забудете формулу, но ее легко воссоздать, если вы просто потратите немного времени и подумаете об этом.) Верх и низ «кирпича» имеют одинаковую площадь, если длина умножается на ширину. Левая и правая стороны кирпича имеют одинаковую площадь, т. е. ширину, умноженную на высоту. И передняя, и задняя часть кирпича имеют одинаковую площадь, т. е. длину, умноженную на высоту.
 (Нарисуйте рисунок, обозначив размеры, если не уверены в этом.) Тогда формула площади поверхности SA из кирпича это:
(Нарисуйте рисунок, обозначив размеры, если не уверены в этом.) Тогда формула площади поверхности SA из кирпича это:SA прямоугольная = 2 lw + 2 wh + 2 lh
также на концах цилиндры время от времени. Объем V цилиндра легко определить: это площадь конца (которая равна площади круга), умноженная на высоту h :
V cyl = π r 2 ч
Площадь поверхности SA — это площадь концов (которые представляют собой просто круги) плюс площадь стороны, которая равна длине окружности, умноженной на высоту h цилиндра:
SA cyl = 2π r 2 + 2π rh
В зависимости от класса, который вы изучаете, вам также может понадобиться знать формулу объема V конуса с радиусом основания r и высотой h 2 :
В Конус = ( 1 / 3 ) π R 2 H
.
 .. или объем V из Spare (A Ball) с Radius
.. или объем V из Spare (A Ball) с Radius- с RADIIS
- .
V sph = ( 4 / 3 )π r 3
Вы можете заметить другие формулы в домашних заданиях или упражнениях в классе. Возможно, вам придется запомнить эти другие формулы (их много!), поэтому обязательно проконсультируйтесь со своим инструктором перед тестом, чтобы узнать, какие из них вы должны знать.
Мне действительно нужно запоминать все формулы?
Нет необходимости запоминать все формулы, которые вам попадутся, но есть и другие, которые действительно следует запомнить. Вы должны знать, как найти площадь прямоугольника или длину окружности; вам, вероятно, не нужно запоминать формулы, скажем, для объема тора или площади поверхности правильного тетраэдра. (Кстати, есть масса других формул, которые вам, вероятно, не нужно запоминать. Будьте благодарны за это!)
Некоторые преподаватели предоставляют все геометрические формулы, поэтому в вашем тесте будет список всего, что вам может понадобиться.


 Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани.
Перед тем, как найти ребро куба, необходимо напомнить о том, что такое куб. Это прямоугольный параллелепипед, имеющий равные между собой ребра. Кроме того, куб представляет собой шестигранник, гранями которого являются равные квадраты. Чтобы найти ребро куба, необходимо знать его некоторые параметры – объем куба, площадь грани, длину диагонали куба или грани. 2/3).
2/3). ru/education/math/geometry/edge/cube
ru/education/math/geometry/edge/cube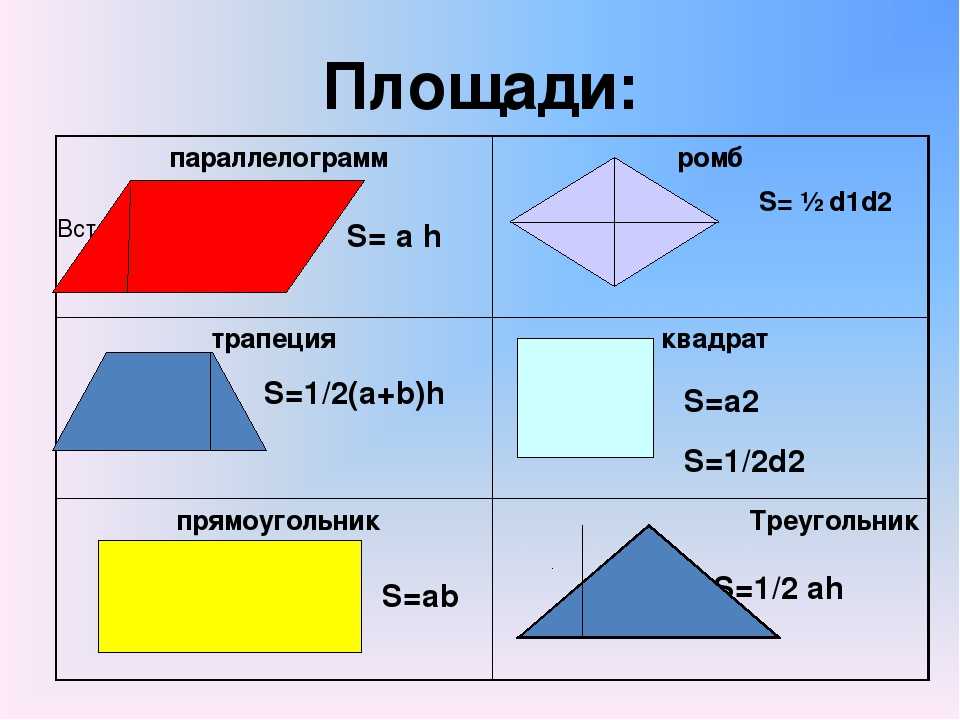

 2} \end{массив}\) 92\).
2} \end{массив}\) 92\). см}} \end{массив}\)
см}} \end{массив}\) дюйма
дюйма 92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)
92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)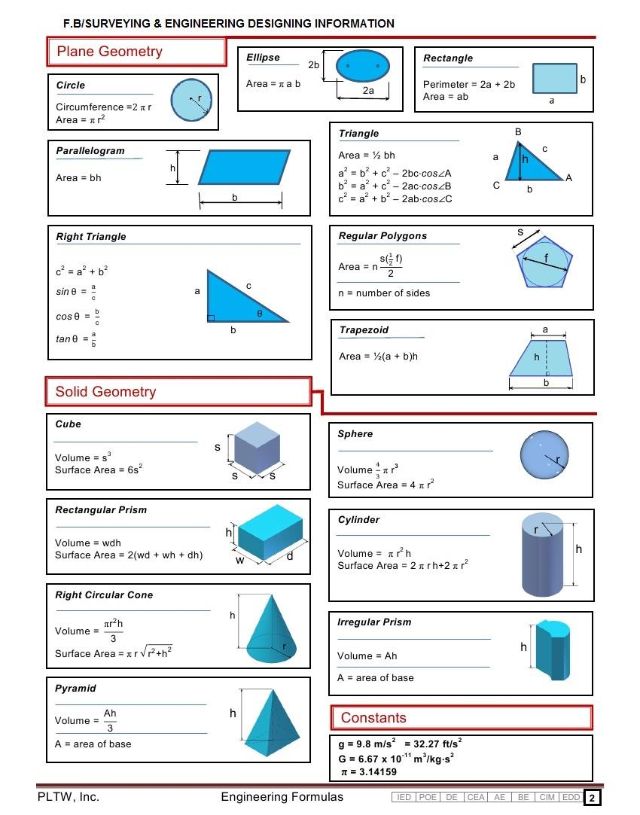 Округлить до двух знаков после запятой.
Округлить до двух знаков после запятой. дюймов
дюймов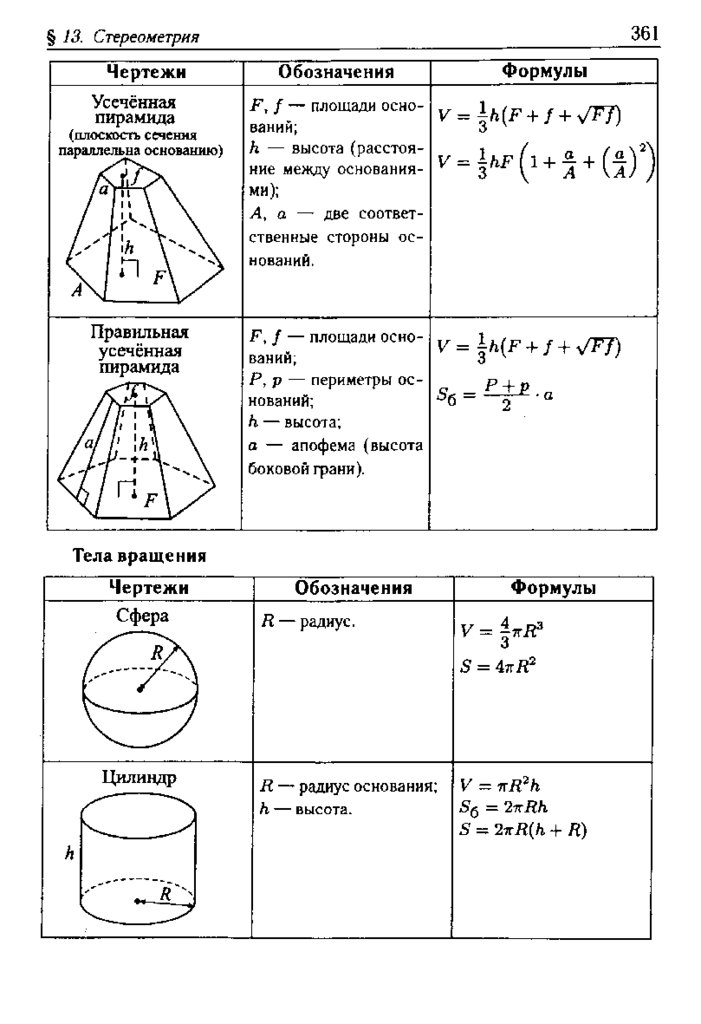 дюйма
дюйма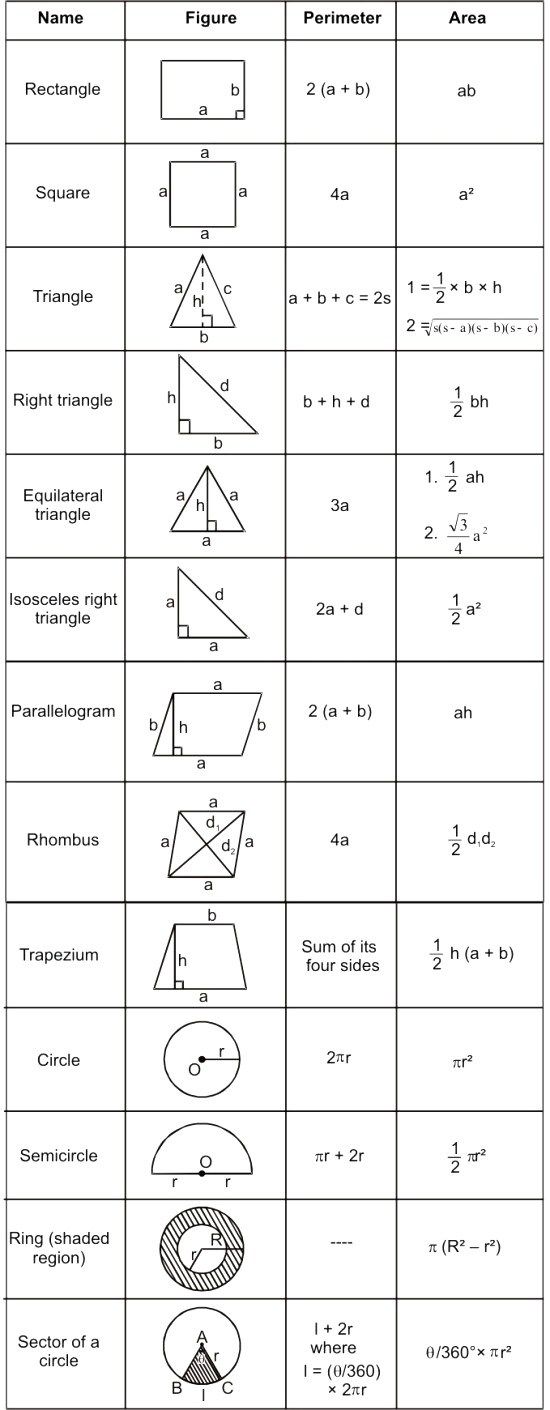 футов
футов дюйма
дюйма
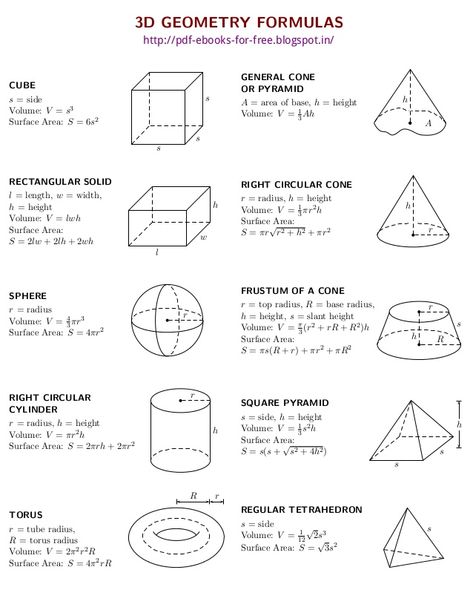 д. двухмерных и трехмерных геометрических фигур, называются формулами геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т. д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии имеют вид:
д. двухмерных и трехмерных геометрических фигур, называются формулами геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т. д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии имеют вид: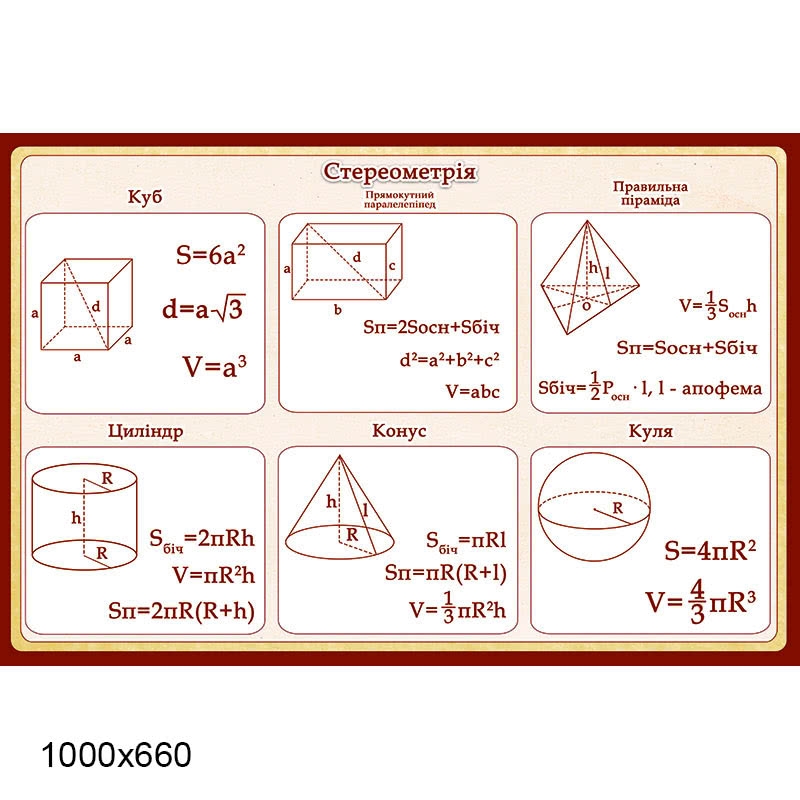 и,
и, Параллелограмм
Параллелограмм
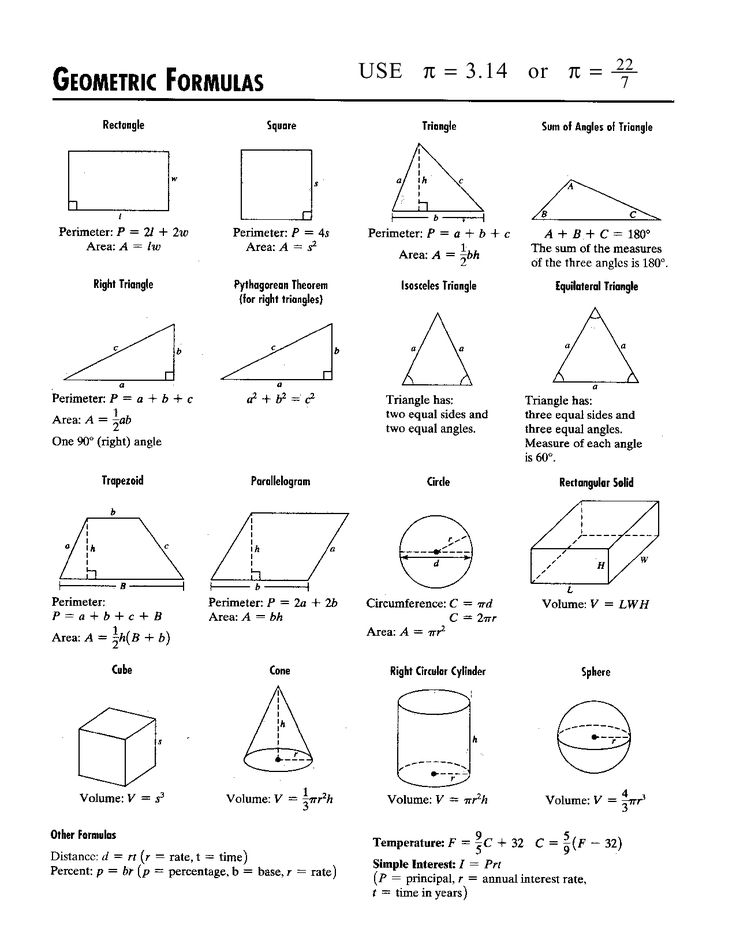 Конус
Конус
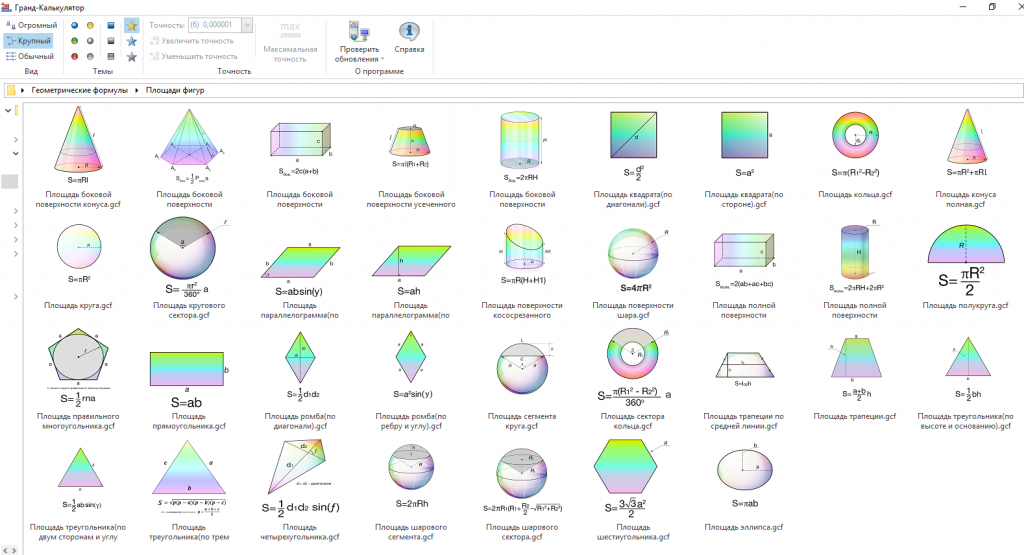
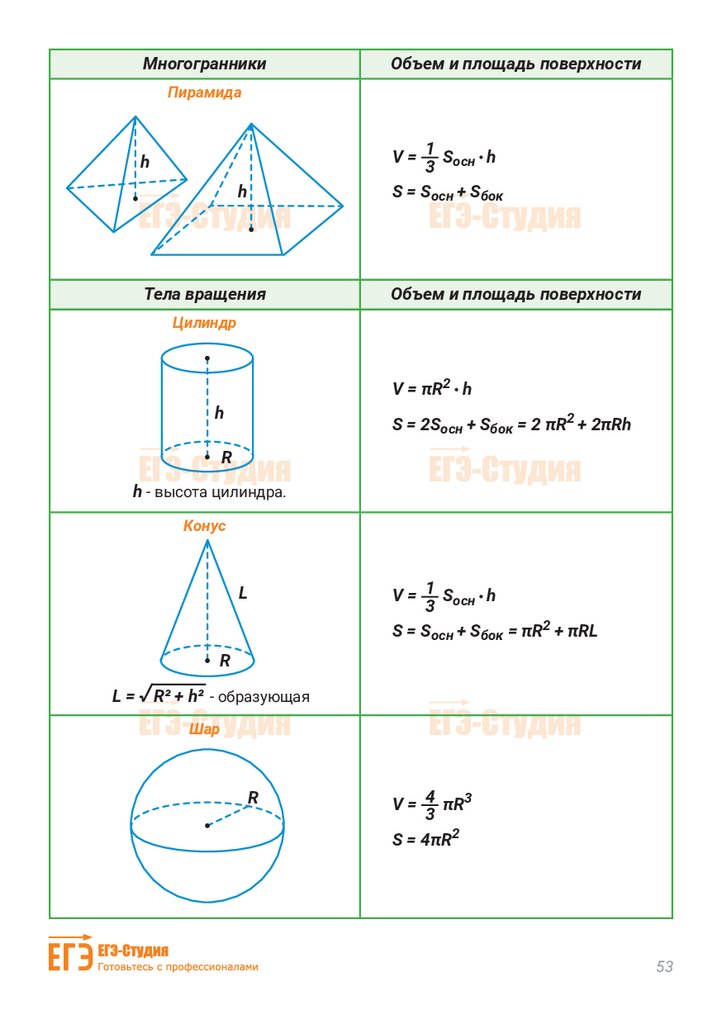 Площадь поверхности сферы равна A = 4πr 2 , а объем сферы равен V = ⁴⁄₃πr 3 .
Площадь поверхности сферы равна A = 4πr 2 , а объем сферы равен V = ⁴⁄₃πr 3 .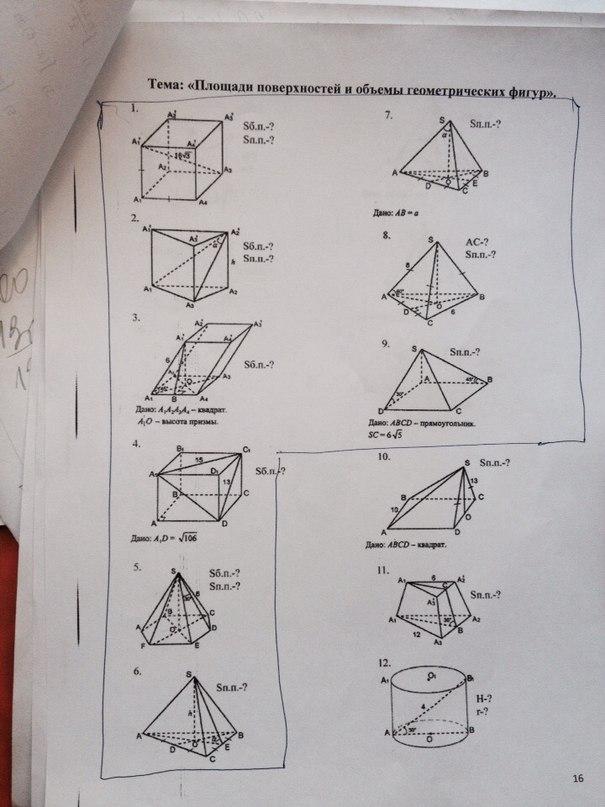 Мы можем определить это пространство, вычислив площадь и объем в зависимости от типа фигуры. Здесь мы поймем основные понятия площади и объема применительно к различным типам фигур.
Мы можем определить это пространство, вычислив площадь и объем в зависимости от типа фигуры. Здесь мы поймем основные понятия площади и объема применительно к различным типам фигур. com
com Итак, мы можем рассчитать площадь по данной формуле:
Итак, мы можем рассчитать площадь по данной формуле: Тем не менее, его концепция по существу такая же, как площадь в том смысле, что он измеряет размер поверхности с использованием квадратных единиц, таких как дюймы в квадрате (в 2 ). Формулы для площадей поверхности различаются в зависимости от типа трехмерного объекта.
Тем не менее, его концепция по существу такая же, как площадь в том смысле, что он измеряет размер поверхности с использованием квадратных единиц, таких как дюймы в квадрате (в 2 ). Формулы для площадей поверхности различаются в зависимости от типа трехмерного объекта.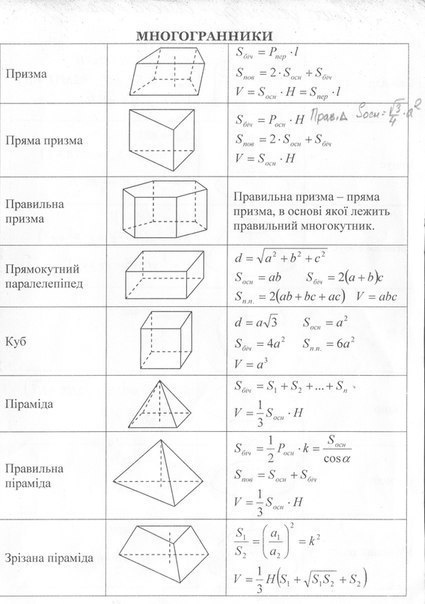
 Обычно мы просто называем общую площадь поверхности площадью поверхности.
Обычно мы просто называем общую площадь поверхности площадью поверхности. Полную площадь поверхности и боковую поверхность прямоугольного параллелепипеда можно рассчитать так же, как куба. Однако для прямоугольного параллелепипеда вместо того, чтобы использовать одно и то же измерение для всех шести граней, мы рассматриваем и измеряем разные грани по отдельности. Следовательно, мы вычисляем площадь поверхности прямоугольного параллелепипеда через длину l, ширину w и высоту h.
Полную площадь поверхности и боковую поверхность прямоугольного параллелепипеда можно рассчитать так же, как куба. Однако для прямоугольного параллелепипеда вместо того, чтобы использовать одно и то же измерение для всех шести граней, мы рассматриваем и измеряем разные грани по отдельности. Следовательно, мы вычисляем площадь поверхности прямоугольного параллелепипеда через длину l, ширину w и высоту h.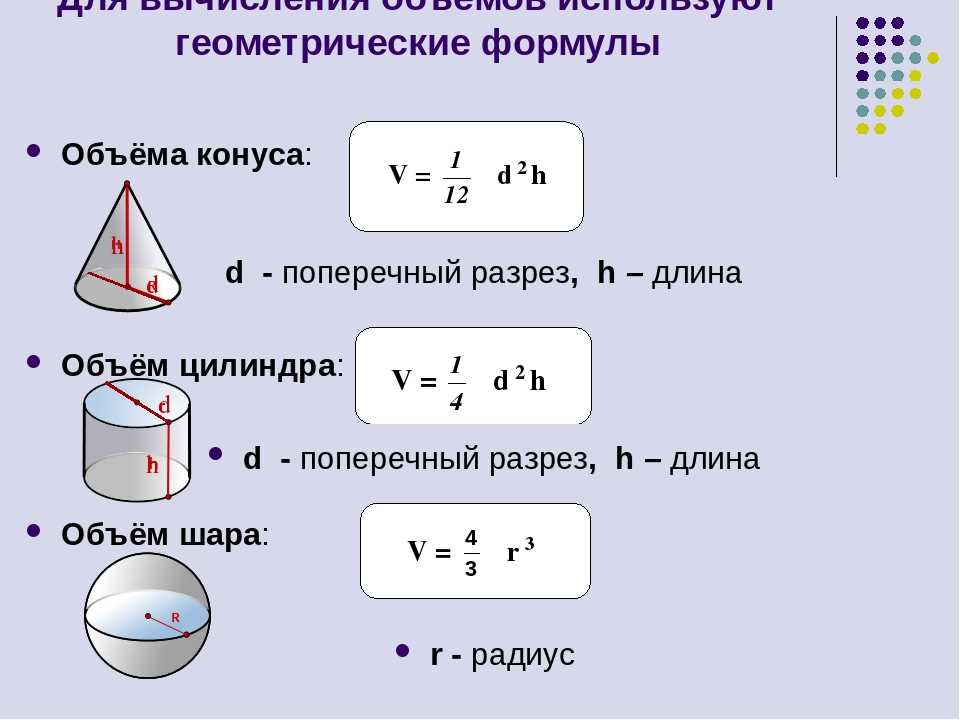 При определении только площади боковой или криволинейной поверхности учитывается только криволинейная поверхность цилиндра.
При определении только площади боковой или криволинейной поверхности учитывается только криволинейная поверхность цилиндра. Итак, пространство, занимаемое этим объектом, называется его объемом .
Итак, пространство, занимаемое этим объектом, называется его объемом .  Итак, мы вычисляем объем через длину l, ширину w и высоту h. Формула объема прямоугольного параллелепипеда выглядит следующим образом:
Итак, мы вычисляем объем через длину l, ширину w и высоту h. Формула объема прямоугольного параллелепипеда выглядит следующим образом:



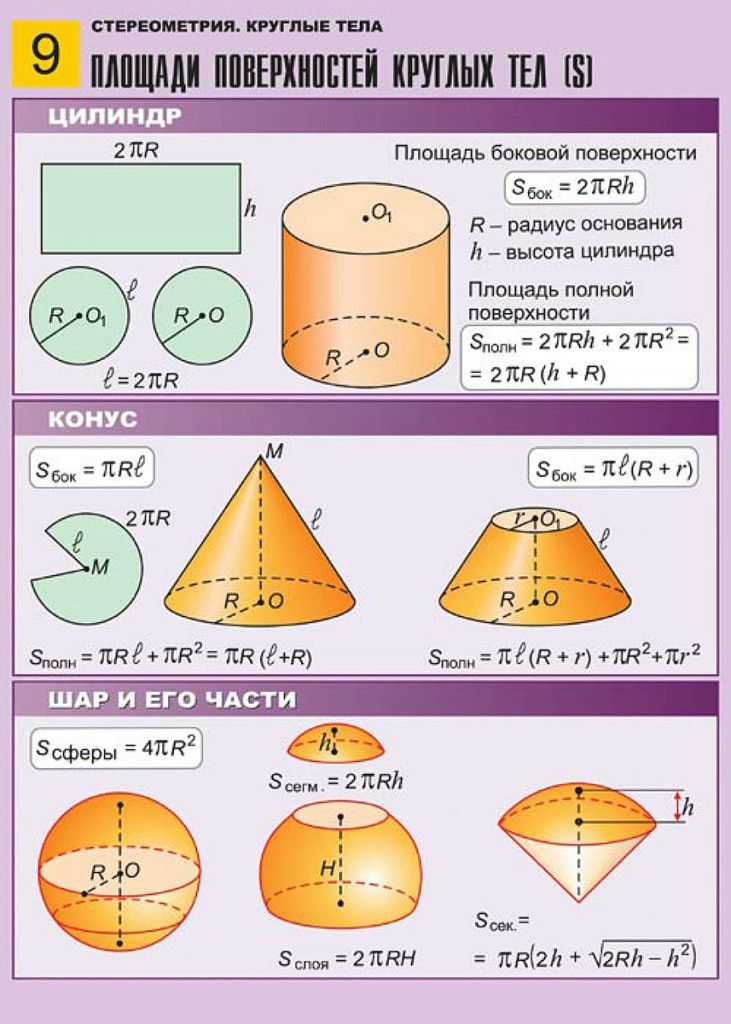
 дюймов
дюймов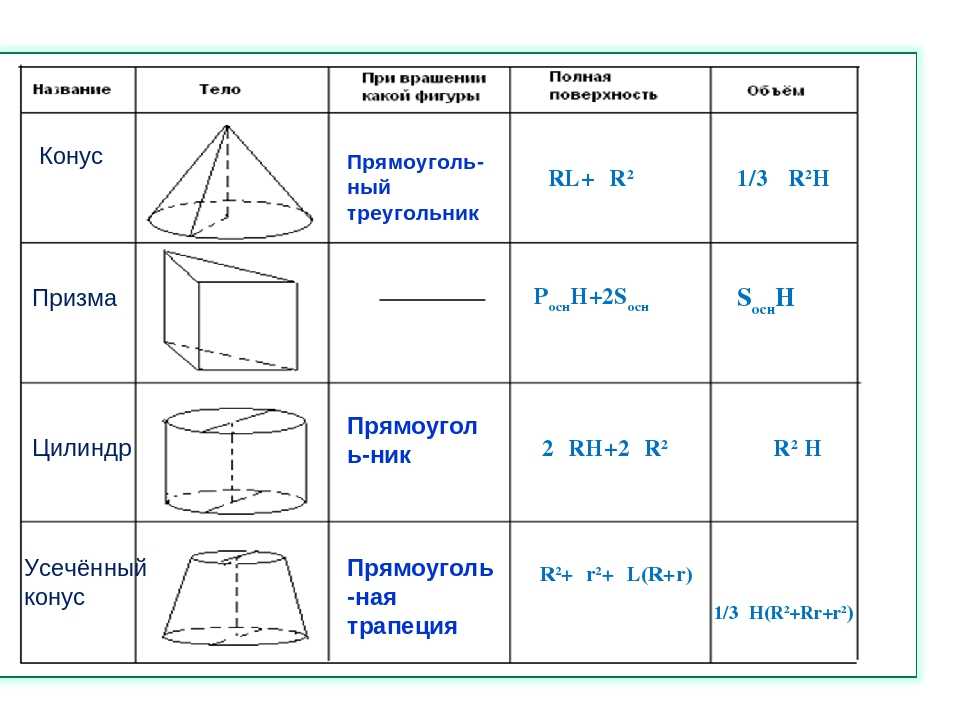

 ⋅ 8 in.
⋅ 8 in.
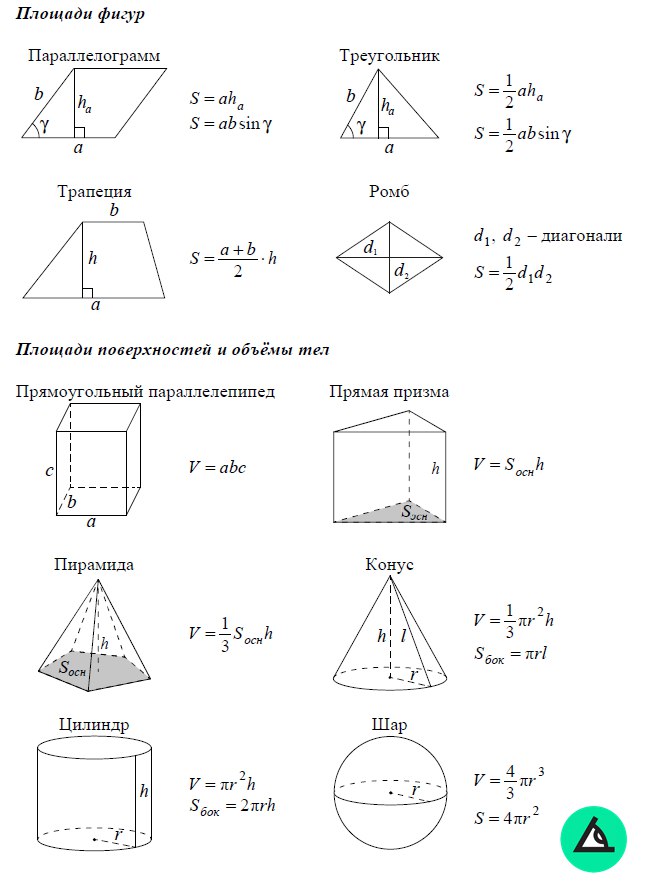

 0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0
0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0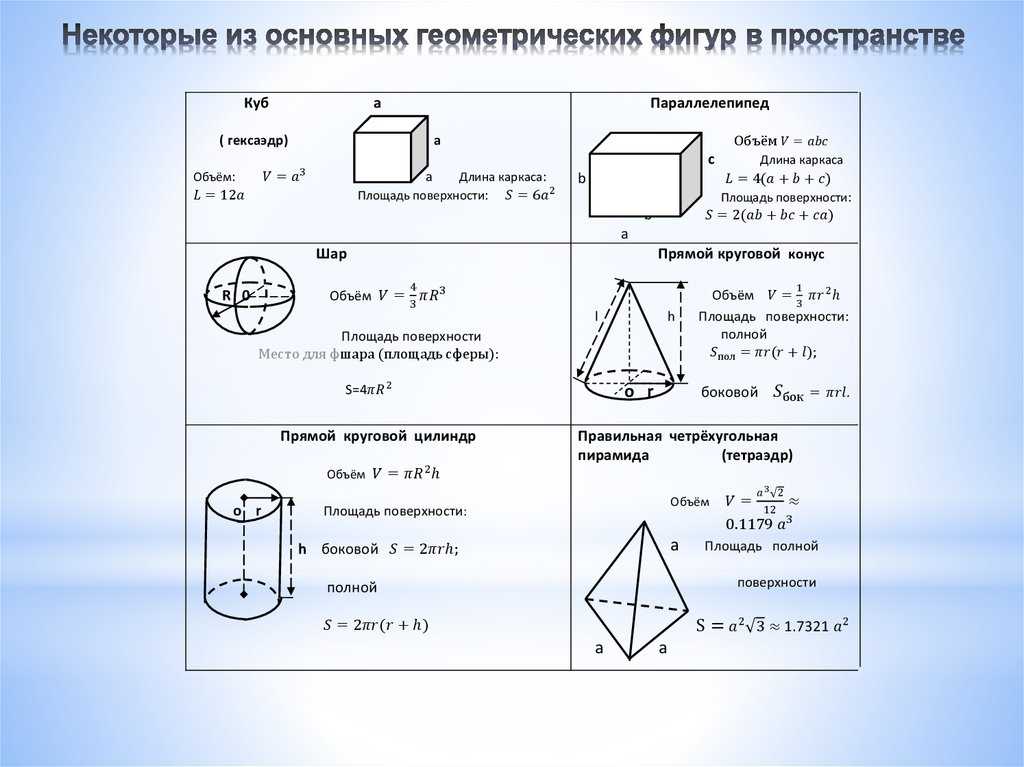 Поскольку я буду обсуждать площади, объемы и т. д., формулы для различных фигур, я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула. Подписка такого рода может быть полезной техникой для ясности вашего смысла, поэтому постарайтесь держать это в уме для возможного использования в будущем.
Поскольку я буду обсуждать площади, объемы и т. д., формулы для различных фигур, я использую нижние индексы, чтобы прояснить форму, к которой относится конкретная формула. Подписка такого рода может быть полезной техникой для ясности вашего смысла, поэтому постарайтесь держать это в уме для возможного использования в будущем.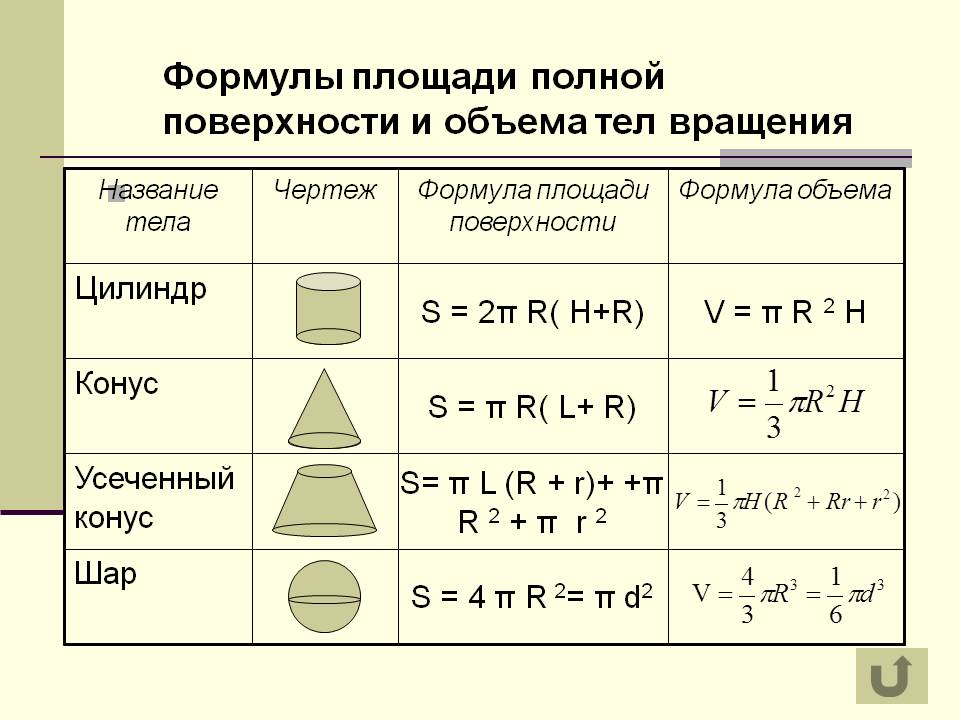 Площадь A и периметр P квадрата с боковой длиной S приведены:
Площадь A и периметр P квадрата с боковой длиной S приведены:
 Есть шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA равна:
Есть шесть сторон (верхняя, нижняя, левая, правая, передняя и задняя), поэтому площадь поверхности SA равна: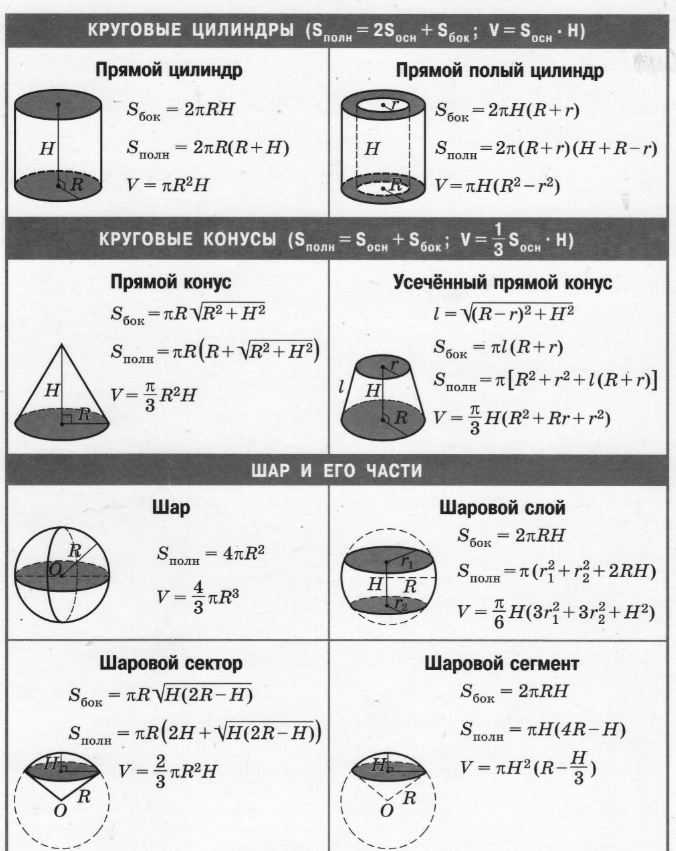 (Нарисуйте рисунок, обозначив размеры, если не уверены в этом.) Тогда формула площади поверхности SA из кирпича это:
(Нарисуйте рисунок, обозначив размеры, если не уверены в этом.) Тогда формула площади поверхности SA из кирпича это: .. или объем V из Spare (A Ball) с Radius
.. или объем V из Spare (A Ball) с Radius