Корни упростить: Выражения с квадратными корнями — урок. Алгебра, 8 класс.

2

ЛДПР предложила упростить выдачу гражданства людям с русскими корнями — РБК

www.adv.rbc.ru

www.adv.rbc.ru

www.adv.rbc.ru

Скрыть баннеры

Ваше местоположение ?

ДаВыбрать другое

Рубрики

Курс евро на 1 октября
EUR ЦБ: 52,74 (-2,67) Инвестиции, 30 сен, 16:32

Курс доллара на 1 октября
USD ЦБ: 55,3 (-2,11) Инвестиции, 30 сен, 16:32

Мосбиржа сообщила о режиме торгов в новогодние праздники Инвестиции, 13:56

Акции Tesla упали на фоне отчета о продажах хуже ожиданий Инвестиции, 13:51

40% работников готовы уйти из компании, если их не устроит время отпуска Pro, 13:45

www. adv.rbc.ru

www.adv.rbc.ru

«Окно возможностей»: как идет импортозамещение на косметическом рынке Национальные проекты, 13:43

В Херсоне прогремели шесть взрывов Политика, 13:38

Литва объявила персоной нон грата временного поверенного в делах России Политика, 13:35

Лукашенко потребовал «мобилизовать всех» на уборку картошки и свеклы Политика, 13:33

Объясняем, что значат новости

Вечерняя рассылка РБК

Подпишитесь за 99 ₽ в месяц

Более 30 детей погибли в давке на футбольном матче в Индонезии Спорт, 13:32

Кремль не сумел назвать сроки восстановления «Северных потоков» Политика, 13:27

Военная операция на Украине. Главное Политика, 13:26

«Газпром» сообщил о прекращении утечек на «Северных потоках» Политика, 13:26

Верховный лидер Ирана обвинил США и Израиль в организации протестов Политика, 13:25

Военкома, об отстранении которого сообщал губернатор, перевели в Магадан Общество, 13:21

Какие IT-решения помогают строить быстрее и качественнее РБК и S+Консалтинг, 13:19

www.adv.rbc.ru

www.adv.rbc.ru

www.adv.rbc.ru

Фото: Михаил Мордасов / РБК

Депутаты от фракции ЛДПР и сенаторы планируют внести в Государственную думу законопроект об упрощении выдачи гражданства лицам, один из родителей которых в свидетельстве о рождении записан как русский, сообщает ТАСС со ссылкой на пресс-службу депутата от ЛДПР Ярослава Нилова.

При наличии такого условия иностранным гражданам и лицам без гражданства не придется соблюдать другие условия для получения российского паспорта: непрерывно в течение пяти лет проживать в России, получать вид на жительство, подтверждать законный источник дохода и сдавать экзамен по русскому языку. Решение о приеме в гражданство России будет приниматься в течение трех месяцев.

«Вместе с тем нормы законопроекта требуют для указанных лиц начать процедуру отказа от имеющегося гражданства (но не предоставлять справку о выходе из гражданства), за исключением случаев, когда международным договором урегулирован вопрос двойного гражданства», — сказано в пояснительной записке к закону.

www.adv.rbc.ru

Разработку законопроекта, как пишет агентство, инициировали в связи с «усилением в западных странах недружественных настроений по отношению к российским гражданам, иностранным гражданам и лицам без гражданства, имеющим русские или российские корни». Авторы проекта рассчитывают, что упрощенным порядком смогут воспользоваться жители Украины и других бывших республик СССР.

www.adv.rbc.ru

12 февраля в пресс-центре МВД сообщили, что иностранцы из отдельных категорий смогут получать российское гражданство за три месяца вместо года в случае принятия законопроекта об упрощении процедуры. Как пояснили в ведомстве, изменение связано с передачей полномочий по рассмотрению некоторых заявлений о приеме в гражданство МВД. К таким категориям граждан, согласно законопроекту, будут относиться лица, которые получили политическое убежище в России или статус беженца, и служащие в российской армии по контракту. К ним также относятся категории без права на упрощенный порядок приема в гражданство.

Урок алгебры по теме «Преобразование выражений, содержащих квадратные корни». 8-й класс

• Чернова Татьяна Викторовна, учитель математики

org/BreadcrumbList»> Разделы: Математика, Конкурс «Презентация к уроку»

Класс: 8

---

Презентация к уроку

Загрузить презентацию (690 кБ)

---

Цели и задачи:

• проверить теоретическую подготовку учащихся к уроку;
• проверить качество усвоения материала отдельными учащимися;
• закрепить и систематизировать знания учащихся по данной теме;
• формировать у учащихся навыки правильного воспроизведения своих знаний и умений;
• воспитать чувство коллективизма и сопереживания успехам и неудачам своих товарищей.

I. Организационный момент

• сообщение темы изучения материала;
• формулировка вместе с учащимися цели и задачи изучения данного материала;
• показ практической значимости изучения нового материала, мотивации учащихся к его усвоению;
• постановка перед учащимися учебной проблемы.

Слайд 1

II. Устно

Слайд 2-3

1. Вычислить:

Слайд 4

2. Решить уравнение

x2=81	x2=0,36	x2=1
		x2=0

Слайд 5

3. Выполнить действия, используя формулы сокращенного умножения

• (m+n)²=m²+2mn+n²
• (5+c)²=25+10c+c²
• (b-7)²=b²-14b+49
• (a+2)(a-2)=a²-4
• (m-5)(m+5)=m²-25

III. Проверка домашнего задания

Слайд 6

№418(е-к)

Упростить выражение:

е)
ж)
з)
и)
к) 

Слайд 7

№420(г, д, е)

Упростите выражение:

г)
д)

е)

Слайд 8

№421. Упростите выражение

IV. Решение примеров

№422(а, б, в) Выполните действие:

№423(а, б, д, е). Выполните действие, используя формулы сокращенного умножения

а) (x+)(x-)=x²-y

№425(а-в). Выполните действия

 а)
б)
в)

№428(а, б, в). Выполните действия

№426(а-г). Преобразуйте выражение

№427(а, б, в). Разложите на множители, используя формулу разности квадратов:

№428 (а, б, в). Разложите на множители выражение:

№429(а-г). Сократите дробь

V. Самостоятельная работа

Вариант 1	Вариант 2
Упростите выражение
Выполните действия
Сократите дробь

VI. Проверка самостоятельной работы

Слайд 9

Вариант 1	Вариант 2
Упростите выражение
Выполните действия
Сократите дробь
	=

VII.

Задание на дом

 № 420(г-е), № 423(в, г, ж, з), № 430(г-е), № 441(а).

28.04.2012

Упрощение выражений с корнем

Здравствуйте! На этом уроке я покажу вам, как можно упростить выражение под корнем. Начнем с терминологии. Вас, вероятно, интересует, что вообще представляет собой корень (или радикал). Вот это знак радикала. Вам он известен как «корень квадратный». А что означает упростить корень? Хотя некоторые считают, что это скорее не «упростить», а «усложнить». Давайте разбираться. Сначала все очистим. Предположим, нам нужно найти корень квадратный из 36. Ну, это легко. Он равен 6. А что если я спрошу, чему равен корень квадратный из 72. Мы знаем, что 72 – это 36 умножить на 2. Следовательно, корень квадратный из 72 – это то же самое, что и корень квадратный из 36 умножить на 2 (мы просто вместо 72 записали 362). Когда мы изучали свойства степеней, то говорили, что корень квадратный – это то же самое, что и степень 1/2. Я сейчас все покажу и объясню, чтобы вы понимали, что это не новое понятие. Итак, это то же самое, что и 36 умножить на 2 в степени 1/2. Правильно? Ведь корень квадратный равнозначен степени 1/2. Из свойств степеней мы знаем, что когда в степень (в данном случае это степень 1/2) возводится произведение двух чисел, то это то же самое, что и возвести в степень каждый множитель в отдельности, а потом их перемножить. Значит, это будет 36 в степени 1/2 умножить на 2 в степени 1/2. А это мы можем записать как корень квадратный из 36 умножить на корень квадратный из 2. Мы знаем, чему равен корень квадратный из 36. Он равен 6. Значит, это будет равно 6√2. Вас, очевидно, интересует, почему я заменила корень квадратный на степень 1/2 вот здесь. Я хотела показать, что для упрощения корня мы используем не какое-то новое свойство, а хорошо нам известное свойство степеней. Именно для этого я все это и расписала. Рассмотрим еще один пример. Когда мы разберем больше примеров, тогда вы все поймете. Итак, корень квадратный из 50. 50 – это 25 умножить на 2. Исходя из обычного свойства степеней, это то же самое, что и корень квадратный из 25 умножить на корень квадратный из 2. Мы знаем, что корень квадратный из 25 равен 5. А значит, это будет равно 5√2. Вы, возможно, скажете: «Да, все выглядит довольно просто, но откуда Вы знаете, что 50 – это именно 25 умножить на 2? Почему корень квадратный из 50 – это не корень квадратный из 5 умножить на 10? Или почему он не равен корню квадратному из 1 умножить на 50?» Причина, по которой, я выбрала произведение 25 и 2, заключается в том, что я беру наибольший множитель 50-ти, который представляет собой полный квадрат. В данном случае это 25. Если бы я взяла произведение 5 и 10, то я бы ничего с ними не сделала, никак бы не упростила, так как ни 5, ни 10 не являются полными квадратами. То же самое касается и множителей 1 и 50. Таким образом, первое, что вы должны сделать, определить все множители числа под корнем и посмотреть, какой из них представляет собой полный квадрат. Не существует какого-то механического способа распознавания полных квадратов. Их просто нужно знать. Это 1, 4, 9, 16, 25, 36, 49, 64 т.д. Со временем вы научитесь распознавать полные квадраты. И если любое из этих чисел будет множителем подкоренного значения, то нужно извлечь это число из-под знака корня, а второй множитель так и оставить под знаком корня, как мы делали вот здесь. Рассмотрим еще несколько примеров. Чему равно 7 корней квадратных из 27? Такая запись означает, что 7 нужно умножить на корень квадратный из 27. Сначала подумаем, какие множители у числа 27? Есть ли такой, который представляет собой полный квадрат? 27 делится на 3, но 3 – это неполный квадрат. А вот 9 будет полным квадратом. Значит, мы можем сказать, что это то же самое, что и 7 умножить на корень квадратный из 93. Исходя из свойства, которое мы только что повторили, это будет равно 7 умножить на корень квадратный из 9 умножить на корень квадратный из 3. А это равно 7 умножить на 3… правильно? Ведь корень квадратный из 9 – это 3. … и умножить на корень квадратный из 3. Или это равно 21√3. Вот и все. Следующий пример. Чему равно 9 умножить на корень квадратный из 18? Какие множители у числа 18? 6 и 3, 1 и 18. Пока ни один из этих множителей нам не подходит. А что если мы возьмем произведение 2 и 9. 9 – это полный квадрат. Тогда наше выражение мы можем записать как 9 умножить на корень квадратный из 29. Или же это равно 9 умножить на корень квадратный из 2 и умножить на корень квадратный из 9. А это равно 9 умножить на корень квадратный из 2 и умножить на 3, правильно? И в итоге мы получим 27√2. Надеюсь, вы уже поняли, как можно упростить корень. Еще один пример. Чему равно 4 умножить на корень квадратный из 25? 25 само по себе полный квадрат. Этот пример проще предыдущих. 25 – это полный квадрат. И корень квадратный из 25 равен 5. Тогда это будет равно 4 умножить на 5, а это 20. Правильно? Корень квадратный из 25 – это 5. Следующий пример: 3 умножить на корень квадратный из 29. У 29-ти только два множителя, 1 и 29. И ни один из них не является полным квадратом. Следовательно, мы никак не можем упростить это выражение. Это и есть уже упрощенная форма. Разберем еще один пример. Давайте попробуем упростить: 7 умножить на корень квадратный из 320. Итак, 320. У такого большого числа сложно определить наибольший множитель, который представляет собой полный квадрат. 4 – это полный квадрат, и на 4 делится 320. Хотя можно взять 16 (32 делится на 16, следовательно, и 320 делится на 16). Попробуем взять для начала 16. Итак, это будет равно 7 умножить на корень квадратный из 16 умножить на 20. Или же это равно 7 умножить на корень квадратный из 16 и умножить на корень квадратный из 20. Корень квадратный из 16 равен 4, а 7 умножить на 4 равно 28. Значит, это будет 28 умножить на корень квадратный из 20. Как вы думаете, мы уже выполнили задание, мы упростили это выражение? Мне кажется, не совсем, мы можем еще 20 разложить на полный и неполный квадраты. 20 – это 4 умножить на 5. Тогда мы можем сказать, что это то же самое, что и 28 умножить на корень квадратный из 45. Корень квадратный из 4 равен 2, а 28 умножить на 2 равно 56. Значит, это равно 56√5. Надеюсь, вам все понятно. Это очень полезная техника упрощения. Трудно сразу сказать, какой наибольший множитель (и при этом полный квадрат) есть у числа 320. Как оказалось, это 64. Но сразу можно без колебаний сказать, что 320 делится на 4. Значит, 320 – это то же самое, что и 4 умножить на 80. И тогда мы бы дальше продолжали работать с числом 80. Но очевидно, что 320 также делится на 16. Мы записали 320 как произведение 16 и 20. Извлекли корень квадратный из 16, это 4, а 7 умножить на 4 равно 28. Под корнем осталось 20, а 20 делится на полный квадрат (20 делится на 4). Мы извлекли корень квадратный из 4, и в результате получили 56√5. 5 – это простое число, и разложить его на какие-то другие множители, кроме 1 и 5, мы не можем, поэтому 5 так и остается под корнем. Надеюсь, вы хоть чуть-чуть поняли, как упростить корень, или другими словами, радикал. Мы всего лишь используем свойства степеней. Со временем вы окончательно во всем разберетесь. На этом все. До скорых встреч!

Стартерпак успешного экспортёра. Семь хитростей, которые помогут покорить новые рынки — Секрет фирмы

Как изучить рынок сбыта?

Первый шаг перед покорением нового рынка — изучить его особенности и перспективы. Конечно, можно самостоятельно искать информацию о внешней торговле России и других стран, макроэкономике и ценах на мировых рынках. Но порой это долго и муторно. Кроме того, не вся информация есть в открытом доступе.

---

Пользователи платформы «Мой экспорт» бесплатно могут получить восемь отчётов об основных показателях самых разных рынков. А для самых заинтересованных есть аналитический интерактивный продукт «Поиск рынков сбыта». Вам будет доступна детальная информация по российскому экспорту и внешней торговле страны, потенциальным рыночным нишам, а также условиями доступа.

---

С такой аналитикой экспортёру намного легче определиться, какой товар и на каком рынке он хочет продавать. А значит, пора думать о первых клиентах.

Как найти покупателя и специалистов на месте?

Заинтересованные партнёры, толковые специалисты и активные покупатели — пока не найдёшь всех этих людей в новой стране, полноценно выйти на рынок не получится. Но на поиск контактов людей, которые принимают решения на новых рынках, можно потратить немало времени. Как и на то, чтобы убедить их пообщаться и купить новый продукт. Но есть и обходной путь.

---

С помощью сервиса «Поиск покупателя» можно бесплатно найти заинтересованных партнёров и организовать с ними переговоры. Но здесь есть нюансы. Сначала заявку компании оценят на перспективность. От пользователя попросят аналитическую справку (форму можно скачать на странице услуги), а также заполненную анкету для прохождения скоринговой оценки. Заявку рассмотрят, если удастся набрать проходной балл. Кстати, сервис предоставляется только по 12 странам.

Если проходить скоринг не хочется или интересен экспорт в другие страны, есть подмога — b2b-маркетплейс всё той же платформы «Профессионалы экспорта». Экспортёру могут не только организовать встречу, но и подготовить презентацию, найти местного переводчика, юриста и так далее. Услуга платная.

---

Как найти поставщиков?

Обычно найти поставщика на новом рынке — та ещё задача. Сперва придётся перелопатить множество площадок, но гарантий, что попадёшь на добросовестного контрагента, а не на жаждущего наживы посредника, немного.

Недобросовестный поставщик может сорвать сроки, отправить не тот продукт и нарушить всю работу компании. Ещё одна трудность заключается в том, что далеко не все готовы сотрудничать с компаниями с российскими корнями. Но есть вариант, как решить эту проблему в незнакомой стране быстро и эффективно.

---

Сервис «Поиск поставщика по запросу экспортёра» на «Профессионалах экспорта» снимет многие вопросы, которые могут возникнуть на всех этапах поиска. А ещё он поможет найти новых иностранных партнёров, готовых заниматься поставками российским компаниям.

---

Как выйти на новый маркетплейс?

Половина всех онлайн-покупок приходится на маркетплейсы — и большинство из них охотно регистрируют иностранных продавцов. Для российских малых и средних компаний это отличная возможность масштабироваться за рубеж.

Но разбираться в особенностях региональных маркетплейсов — задача порой не для слабонервных. Компании сталкиваются со сложностями на всех этапах: начиная от регистрации на маркетплейсе, маркировки и упаковки товаров и количества стока на складе, заканчивая оформлением карточек, расчётом комиссии и борьбой с конкурентами.

---

Платформа «Мой экспорт» бесплатно подберёт иностранный маркетплейс под товары и услуги конкретного экспортера. Причём затраты на размещение или продвижение своей продукции можно частично или даже полностью компенсировать за счёт государства. И сделать это без бумажной волокиты — прямо через «Мой экспорт». Платформа поможет и с подготовкой товарных карточек, и с продвижением аккаунта.

---

Как оформить сертификат свободной продажи?

Для запуска поставок за рубеж нужен сертификат свободной продажи. Этот документ подтверждает соответствие продукции требованиям законодательства страны экспортёра для её обращения внутри страны. Но далеко не все знают, как получить заветную бумагу.

---

Документ оформляют в Российском экспортном центре, и на всё отводят минимум 20 дней. Но есть способ получить документ в два раза быстрее — через платформу «Мой экспорт».

---

Как поучаствовать в международной выставке и получить софинансирование?

Международные выставки и бизнес-миссии знакомят потребителей с экспортными товарами — и продвигают продукцию на новые зарубежные рынки. Но самим экспортёрам зачастую сложно уследить за всеми мероприятиями и особенностями их проведения.

---

На странице сервиса «Мероприятия» выложен календарь предстоящих событий. Экспортёр может выбрать выставку или деловую миссию по стране проведения, дате, отрасли или типу. Перейдя на страницу нужного мероприятия, пользователь видит, какие расходы и в каком объёме софинансируются государством. Он может тут же подать заявку на участие и на компенсацию части затрат на него.

---

Например, малому и среднему бизнесу возместят 80% затрат на постройку и оснащение стенда, а также доставку выставочных образцов. Крупным компаниям — 50% на те же цели. При этом аренду выставочной площади, регистрационный сбор, предоставление переводчиков и организацию b2b-встреч полностью финансирует государство.

Как получить компенсацию затрат на транспортировку?

Российских экспортёров предупредили, что из-за ухода иностранных компаний, ограничений на полёты за рубеж и проблем с судоходством тарифы на экспорт грузов будут расти.

Но из правила есть исключения. Нарастить объёмы поставок российской продукции позволяют меры господдержки на транспортировку продукции за рубеж, например, для компаний АПК.

---

Подать документы на компенсацию части затрат на транспортировку сельхозтоваров компании АПК могут с помощью портала «Мой экспорт». Сперва стоит ознакомиться со списком документов и порядком их заполнения (всё это есть в видеоинструкции на портале). Деньги можно получить в течение 30 дней после того, как компания подаст заявку.

---

0+

Рекламодатель

АО «Российский экспортный центр»

Фото: unsplash. com/Finan Akbar

7 шаблонов для промопостов в Telegram. Во-первых, это выдуманное слово + сам месседж…

Вадим — SMM-специалист, который одновременно ведет восемь проектов в Telegram. Все они разной тематики, и для каждого из них он готовит промопосты — по три в неделю. А значит, за семь дней он должен придумать 24 текста. И для одного проекта нельзя сделать два одинаковых поста — тогда заказчик не заплатит.

Готовые шаблоны здорово упростили бы ему жизнь. Поэтому мы собрали семь нетипичных способов составить промопост для всех, кто так же, как и Вадим, постоянно генерирует рекламные тексты для Telegram-каналов.

Шаблон 1. Необычное слово, которое привлекает внимание + продающий текст

Необычное слово, которое привлекает внимание — лучше выдуманное. Например, иллюстрактор, нафигация, динозайнер.

Такие слова называются окказионализмами — их придумывают, но по правилам языка. То есть слово составляется по модели уже существующего, точно так же склоняется, а его значение примерно понятно из его корней или из контекста. Но лучше все же добавлять к такому слову определение, чтобы читатели точно вас правильно поняли.

Продающий текст должен быть связан с тем необычным словом, которое вы использовали в начале. Под постом про динозайнера — промо курса по дизайну. Текст лучше писать максимально просто и понятно: дайте четкую информацию о продукте и покажите, какую пользу получит пользователь.

Промопост, построенный по схеме «Необычное слово, которое привлекает внимание + продающий текст»

Шаблон 2. Вопрос с отсылкой к жизненному опыту каждого + тема поста + полезный источник по теме + его УТП

Вопрос, который отсылает читателя к его жизненному опыту — сильный прием, который располагает читателя к себе. Он понимает, что ему близка эта тема, потому что в его жизни есть подобный опыт.

Как это действует. Пользователь читает: «Помните, как в детстве нас учили не жадничать, а всем делиться?» Он внутренне соглашается с этим: да, конечно, так было у всех нас. Посмотрим, к чему ведет автор.

Тема поста — это объяснение того, о чем говорилось в вопросе, или ответ на этот вопрос. Часто здесь вводится новое понятие, малознакомое читателю — такое, чтобы захотелось узнать о нем подробнее.

Он читает: «Оказалось, что не просто так. Видимо, наши мамы уже что-то знали про экономику шеринга». О чем он думает: так, это интересно. Шерить — это же и значит делиться?

Полезный источник по теме — автор как бы делится своей находкой, не продает продукт в лоб. Это располагает читателя, ему становится все интереснее.

Что здесь можно написать:

• Как раз недавно наткнулась на полезный канал по теме — ссылка.

• На днях увидела у коллеги репост из Х канала, и пошла читать посты — нашла много интересного.

• Кстати, если вы еще не в теме, подписывайтесь на канал Х.

УТП источника — что полезного там можно найти. Для этого блока лучше выбрать из контента канала самые необычные вопросы, на которые читатель не может ответить сам — ему нужны дополнительные данные.

Такой пост не отвечает на все вопросы — он нацелен на то, чтобы вызвать у читателя интерес и желание перейти по ссылке.

Промопост, построенный по схеме «Вопрос с отсылкой к жизненному опыту каждого + тема поста + полезный источник по теме + его УТП»

Шаблон 3. Вопрос + актуальность проблемы + ее решение с помощью продукта + дополнительные плюшки

Вопрос-заголовок — классический прием, который четко дает понять, какую проблему можно решить, прочитав этот текст, в чем его польза.

Примеров можно привести много:

• Как сэкономить время на создание и проверку РК в Яндекс Директе?

• Как настроить сквозную аналитику самому?

• Что может случиться, если вы не ограничите дневной бюджет на кампанию?

Актуальность и важность проблемы, обозначенные в самом начале текста, убедят пользователя, что пост стоит прочитать — проблема масштабная и требует серьезных решений.

Здесь можно добавить какие-то статистические данные, поделиться собственными наблюдениями или сделать отсылку к авторитетному источнику (скажем, ведущему эксперту в отрасли).

Решение проблемы с помощью продукта — это блок, который помогает читателю понять, как продукт поможет ему справиться с проблемой, а иногда и вообще осознать, что проблема есть и ее нужно решать. Вы даете ему ключ и рассказываете, как открыть нужную дверь.

Это продающая часть поста, в которой нужно рассказать о практической пользе продукта. Если это инфопродукт, объясните, на какие вопросы вы ответите. Если это предмет, покажите, как им пользоваться и как с его помощью упростить себе жизнь.

Дополнительные плюшки — все материалы, предметы, тексты, которые вы подарите пользователю, если он совершит конверсию: купит товар или зарегистрируется на мероприятие. Как ни крути, бесплатные бонусы многих мотивируют совершить целевое действие.

Промопост, построенный по схеме «Вопрос + актуальность проблемы + ее решение с помощью продукта + дополнительные плюшки»

Шаблон 4.

Яркий образ, связанный с продуктом + обращение к мнению большинства + описание продукта

Яркий образ из жизни, связанный с продуктом, определенно привлечет внимание. К тому же, пользователи увидят его и поймут: да, точно, именно так я и думаю. Главное условие — продукт должен быть широко известен и вызывать у пользователей общие ассоциации. То есть здесь можно сыграть на том, что многие люди думают о продукте.

Несколько примеров:

1. Я вижу маркетологов многоручками и многоножками: надо одновременно проверять кампании сразу в нескольких кабинетах, бежать на миллион созвонов и встреч, а потом так же сразу в нескольких кабинетах собирать данные аналитики. Исключение, пожалуй, составляют только те, кто пользуется сервисами автоматизации, такими как eLama. Они хотя бы перестают быть многоручками — ведут кампании на разных площадках из одного кабинета. Но многоножками остаются все равно — от этого никуда не деться.

2. Каждый раз, когда вижу курьеров Самоката, которые в дождь и в снег развозят заказы, мне они кажутся какими-то невероятными героями мира постапокалипсиса, эдакими новыми супергероями.

Обращение к мнению большинства может быть коротким и укладываться в одно–два предложения. Оно нужно, чтобы еще раз дать понять читателю, что так считаете не только вы — так думают многие. Это подчеркивает значимость и весомость ваших мыслей, ведь их разделяют другие.

Можно добавить статистических данных: 85% маркетологов устают от постоянного режима многозадачности. Или просто сказать, что так думаете не только вы, и привести доказательство.

Интересное описание продукта — оно должно вызывать эмоции у читателя и желание узнать подробности. Лучше всего связать этот блок с ярким образом, который вы использовали в начале поста:

1. Команда eLama борется с необходимостью отращивать новые конечности — можно успевать выполнить все задачи и двумя руками. Секретами спокойной рабочей жизни поделятся специалисты из Службы Заботы компании. Вот их контакты. Спойлер: можно записаться на полную презентацию сервиса, пользуйтесь, пока можно.

2. Самокат выпустил интерактивный тест по мотивам популярных RPG игр, для которого создали цифровые аватары реальных людей. Ими стали парни и девушки, доставляющие заказы для Самоката. Они первые в истории курьеры, у которых появились цифровые копии.

   Что за тест? Пользователю нужно пройти испытания игры: обнаружить у себя магические навыки, вооружиться, проявить находчивость и сразиться с монстром, а в конце получить персональный титул героя с классическими атрибутами RPG и увидеть курьера-партнера Самоката со схожими способностями.

 

Промопост, построенный по схеме «Яркий образ, связанный с продуктом + обращение к мнению большинства + описание продукта»

Шаблон 5. Проблема читателя + советы + продукт, который раскроет советы

Проблема читателя — стандартный блок, который показывает, какую проблему пользователь научится решать благодаря этому посту. Можно обозначить ее в формате «если. .., то…»:

Это будет удачной подводкой в следующему блоку.

Советы лучше формулировать максимально емко и кратко — так читателю будет легче воспринять и запомнить информацию. Используйте «я-повествование» — говорите от первого лица: я советую, я предлагаю, я рекомендую. Если пользователь читает ваш канал, значит, он доверяет вам как эксперту, и ваше мнение для него ценно.

Подведите к рассказу про продукт, который раскроет советы и даст больше подробностей. Скажите, что советы рабочие, но придется долго разбираться в небольших нюансах самому: какие ставки выбрать при перегретом аукционе, когда их корректировать и на сколько. А можно пойти по простому пути — получить знания и сразу делать правильно, не набивая шишки. И расскажите про продукт без излишней витиеватости, сложных фигур речи и хвалебных отзывов — четко и по факту.

Промопост, построенный по схеме «Проблема читателя + советы + продукт, который раскроет советы»

Шаблон 6. Личный интерес + желание поделиться подборкой самого интересного + совет подписаться

Личный интерес — вы рассказываете о том, чем сами интересуетесь. У аудитории возникает ощущение, что вы делитесь чем-то личным, что рассказываете о себе. Это всегда любопытно.

Несколько примеров:

• Мне давно было интересно, почему маркетологи, которые всегда работают в режиме аврала, не пытаются упростить себе жизнь с помощью сервисов автоматизации и полезных лайфхаков? Я совсем не такая, поэтому пользуюсь eLama и читаю статьи из рубрики «Лайфхаки» на ppc.world.

• Доставка прочно вошла в нашу повседневную жизнь, а мне всегда было любопытно узнать, как устроены сервисы ecommerce? Поэтому я слежу за новостями в канале @sberbs, который ведет команда СберМаркета.

Желание поделиться подборкой самого интересного должно считываться пользователем сразу. Поэтому добавьте слова, вроде «лично мне особенно нравятся эти три статьи — советую полистать», «делюсь своими любимыми постами про SMM-продвижение», «выбрала для вас самые необычные материалы».

Совет подписаться — это призыв к действию в дружественной форме. Как будто вы говорите кому-то из приятелей: эй, тут правда дельная инфа, советую глянуть! Только в том tone of voice, в котором вы пишете обычно.

Промопост, построенный по схеме «Личный интерес + желание поделиться подборкой самого интересного + совет подписаться»

Шаблон 7. Долгожданная новинка + описание + призыв использовать ее

Долгожданная новинка — блок с анонсом нового продукта, фичи, функции и т. д. С первых слов должно быть понятно, что лично вы очень ждали это обновление:

• Наконец-то теперь я смогу быстрее настраивать рекламу — Директ свел создание кампаний до четырех простых шагов!

• VK наконец-то создали HR-канал, где собрали самые актуальные вакансии и интересные анонсы для вашего удобства.

Описание продукта лучше сделать кратким, чтобы в каждом слове было видно пользу для читателя, и оформить как список. Здесь тоже было бы здорово добавить немного личного отношения: мне больше всего понравилось то-то и то-то, для меня важнее всего — возможность сделать А, Б, В и Г.

Призыв использовать продукт можно дополнить информацией о том, зачем это читателю, что он сможет сделать после подписки или покупки.

Промопост, построенный по схеме «Долгожданная новинка + описание + призыв использовать ее»

Какие шаблоны вам понравились больше всего? Делитесь в комментариях — обсудим!

Вы уже про это слышали?

Последние новости от Telegram

 

Как упростить квадратный корень

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

ACT Math Help » Арифметика » Базовое возведение в квадрат / квадратные корни » Упрощение квадратных корней » Как упростить квадратный корень

Что из следующего равно  ?

Возможные ответы:

Правильный ответ:

Объяснение:

√75 можно разбить на √25 * √3. Что упрощает до 5√3.

Сообщить об ошибке

Упрощение .

Возможные ответы:

Правильный ответ:

Объяснение:

Перепишите то, что находится под радикалом, в терминах полных квадратов:

Следовательно, .

Сообщить об ошибке

Что такое ?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы знаем, что 25 — это коэффициент 50. Квадратный корень из 25 равен 5. Остается   , что нельзя упростить дальше.

Сообщить об ошибке

Что из следующего эквивалентно ?

Возможные ответы:

Правильный ответ:

Объяснение:

Умножьте на конъюгат и используйте формулу для разницы в двух квадратах:

Отчет о ошибке

Что из следующего приведено.

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала найдите все простые множители

Итак,

Сообщите об ошибке

Чему равно?

Возможные ответы:

Правильный ответ:

Объяснение:

 

1. Мы знаем, , что мы можем отделить под квадратным корнем:

 

2. 144 можно вынести, так как это полный квадрат: . Это оставляет нам:

Дальнейшее упрощение невозможно.

Сообщить об ошибке

Что из следующего равно ?

Возможные ответы:

Правильный ответ:

Объяснение:

При упрощении квадратных корней начните с разложения рассматриваемого числа на простые множители. Для  это:

Теперь для каждой пары чисел вы можете удалить это число из квадратного корня. Таким образом, вы можете сказать:

Другой способ представить это — переписать как . Таким же образом можно упростить.

Сообщить об ошибке

Что из следующего эквивалентно ?

Возможные ответы:

Правильный ответ:

Объяснение:

При упрощении квадратных корней начните с разложения рассматриваемого числа на простые множители. Это немного сложнее для . Начните с деления :

Теперь делится на , поэтому:

 это немного сложнее, но также делится на , поэтому:

После тщательного тестирования вы увидите, что

Таким образом, мы можем сказать:

Теперь для каждой пары чисел вы можете удалить это число из квадратного корня. Таким образом, вы можете сказать:

Другой способ представить это — переписать как . Таким же образом можно упростить.

Сообщить об ошибке

Что такое упрощенная (сокращенная) форма ?

Возможные ответы:

Дальнейшее упрощение невозможно.

Правильный ответ:

Объяснение:

Чтобы упростить квадратный корень, вы должны разложить число на множители и найти пары. Всякий раз, когда есть пара факторов (например, две двойки), вы вытягиваете один наружу.

Таким образом, если вы умножите 96 вы получите

Сообщить об ошибке

Что из следующего равно ?

Возможные ответы:

Правильный ответ:

Объяснение:

При упрощении квадратных корней начните с разложения рассматриваемого числа на простые множители. Для  это:

Теперь для каждой пары чисел вы можете удалить это число из квадратного корня. Таким образом, вы можете сказать:

Другой способ представить это — переписать как . Таким же образом можно упростить.

Сообщить об ошибке

← Назад 1 2 Далее →

Уведомление об авторских правах

Все ресурсы ACT Math

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

Определение и упрощение корней | Начальная алгебра

Результаты обучения

• Квадратные корни
  • Использование записи квадратного корня для записи основных квадратных корней
  • Упростить главные квадратные корни с помощью факторизации
• Кубические корни
  • Использование нотации кубического корня для записи кубического корня
  • Упрощение кубических корней с помощью факторизации
• Упрощение квадратных корней
  • Упрощение квадратных корней с переменными
  • Определите, когда упрощенному корню требуется абсолютное значение
• Рациональные Показатели
  • Преобразование между радикальной и экспоненциальной записью=81[/latex], поэтому неотрицательный квадратный корень из 81 равен 9, а отрицательный квадратный корень из 81 равен -9
  • Мы хотим найти число, квадрат которого равен -49. 2=0[/latex], поэтому  неотрицательный квадратный корень из 0 равен 0.  Мы не присваиваем 0 знак, поэтому оно имеет только один квадратный корень , а это 0,

  Обозначения, которые мы используем для выражения квадратного корня любого действительного числа, a, следующие:

  Запись квадратного корня

  Символ квадратного корня называется радикальным символом .  Для действительного числа a квадратный корень из a записывается как [латекс]\sqrt{a}[/latex]

  Число, записанное под подкоренным символом, называется подкоренным числом и .

  По определению, символ квадратного корня [латекс]\sqrt{\hphantom{5}}[/латекс] всегда означает нахождение неотрицательного корня, называемого числом 9.0015 главный корень .

  [latex]\sqrt{-a}[/latex] не определен, поэтому [latex]\sqrt{a}[/latex] определен для [latex]a>0[/latex]

  Давайте сделаем пример аналогичен приведенному выше примеру, но на этот раз с использованием записи квадратного корня. Обратите внимание, что использование обозначения квадратного корня означает, что вы находите только главный корень — неотрицательный корень.

  Пример

  Упростите следующие квадратные корни:

  1. [латекс]\sqrt{16}[/латекс]
  92}=a[/latex] означает нахождение главного квадратного корня.

  Что делать, если вы работаете с числом, квадрат которого вы не знаете сразу? Мы можем использовать факторинг и правило произведения для квадратных корней, чтобы найти квадратные корни, такие как [латекс]\sqrt{144}[/латекс] или  [латекс]\sqrt{225}[/латекс].

  Правило произведения для квадратных корней

  Учитывая, что a и b — неотрицательные действительные числа, [latex]\sqrt{a\cdot{b}}=\sqrt{a}\cdot\sqrt{b}[/latex]

  В следующих примерах мы объединим эти идеи для упрощения неочевидных на первый взгляд квадратных корней чисел:

  • квадратный корень из квадрата,
  • правило произведения для квадратных корней
  • факторинг

   

  Пример

  Упростить [латекс]\sqrt{225}[/латекс]

  Показать решение

   

  Внимание! Квадратный корень правила произведения применяется, когда у вас есть умножение ТОЛЬКО под квадратным корнем. Вы не можете применить правило к суммам:

  [латекс]\sqrt{a+b}\ne\sqrt{a}+\sqrt{b}[/latex]

  Докажите это себе, используя некоторые действительные числа: пусть a = 64 и b = 36, затем используйте порядок операций, чтобы упростить каждое выражение.

  [латекс]\begin{array}{c}\sqrt{64+36}=\sqrt{100}=10\\\\\sqrt{64}+\sqrt{36}=8+6=14\ \\\10\ne14\end{array}[/latex]

  До сих пор вы видели примеры идеальных квадратов. То есть каждое из них представляет собой число, квадратный корень которого является целым числом. Но многие подкоренные выражения не являются идеальными квадратами. Некоторые из этих радикалов все еще можно упростить, найдя совершенные квадратные множители. В приведенном ниже примере показано, как разложить подкоренное число на множители, ища пары множителей, которые можно представить в виде квадрата.

  Окончательный ответ [латекс] 3\sqrt{7}[/латекс] может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три радикальных семи» или «три умножить на квадратный корень из семи». 2=0[/латекс] 92=100[/латекс]

  В этом последнем видео мы показываем примеры упрощения радикалов, которые не являются идеальными квадратами.

  Кубические корни

  Кубик Рубика

  Хотя квадратные корни, вероятно, являются наиболее распространенным корнем, вы также можете найти корень третьей степени, корень пятой степени, корень 10-й степени или любой другой n корень числа . Точно так же, как квадратный корень — это число, которое при возведении в квадрат дает подкоренное число, кубический корень из — это число, которое при возведении в куб дает подкоренное число. 93=27[/латекс]

• Мы хотим найти число, куб которого равен 8. [latex]2\cdot2\cdot2=8[/latex] кубический корень из 8 равен 2.
• Мы хотим найти число, куб которого равен -8. Мы знаем, что 2 — это кубический корень из 8, так что, возможно, мы можем попробовать -2. [latex]-2\cdot{-2}\cdot{-2}=-8[/latex], поэтому кубический корень из -8 равен -2. Это отличается от квадратных корней, потому что умножение трех отрицательных чисел дает отрицательное число.
• Мы хотим найти число, куб которого равен 0. [latex]0\cdot0\cdot0[/latex], независимо от того, сколько раз вы умножаете [latex]0[/latex] сам на себя, вы всегда получите [latex] 0[/латекс].

Кубический корень числа записывается с маленькой цифрой 3, называемой индексом , сразу за радикальным символом и над ним. Похоже на [латекс] \sqrt[3]{{}}[/латекс]. Эта маленькая цифра 3 отличает кубические корни от квадратных корней, которые записываются без маленькой цифры снаружи и над корневым символом.

Внимание! Будьте осторожны, чтобы различать [латекс] \sqrt[3]{x}[/latex], кубический корень из x , и [латекс] 3\sqrt{x}[/latex], три умножить на квадрат корень из x . Сначала они могут выглядеть одинаково, но они приводят к совершенно разным выражениям!

Мы также можем использовать факторинг для упрощения кубических корней, например [латекс] \sqrt[3]{125}[/латекс]. {3}}}=5[/latex]. Вы нашли кубический корень, три одинаковых множителя, которые при умножении дают 125. 125 известно как 9.{3}}\end{array}[/latex]

Вы можете найти нечетный корень отрицательного числа, но не можете найти четный корень отрицательного числа. Это означает, что вы можете упростить радикалы [латекс] \sqrt[3]{-81},\ \sqrt[5]{-64}[/latex] и [латекс] \sqrt[7]{-2187}[/ латекс], но вы не можете упростить радикалы [латекс] \sqrt[{}]{-100},\ \sqrt[4]{-16}[/латекс] или [латекс] \sqrt[6]{-2,500 }[/латекс].

Давайте посмотрим на другой пример.

Шаги, которые следует учитывать при упрощении радикала, описаны ниже. 9{2}}[/латекс] [латекс]\влево|х\вправо|[/латекс] [латекс]−5[/латекс] 25 5 5 [латекс]−2[/латекс] 4 2 2 0 0 0 0 6 36 6 6 10 100 10 10 9{2}}[/латекс].

В следующем видео мы покажем несколько примеров упрощения радикалов с переменными.

В следующем разделе мы рассмотрим кубические корни и воспользуемся показанными здесь методами для их упрощения. Кубические корни отличаются от квадратных корней тем, что под корнем может быть отрицательное число, например [латекс]\sqrt[3]{-125}[/латекс].

Рациональные показатели

Корни также могут быть выражены в виде дробных показателей. Квадратный корень из числа можно записать с помощью радикального символа или путем возведения числа в степень [латекс] \фрак{1}{2}[/латекс]. Это показано в таблице ниже. 9{\tfrac{1}{n}}}[/латекс]

Преобразование между радикальной и экспоненциальной нотацией

Столкнувшись с выражением, содержащим рациональный показатель степени, вы можете переписать его, используя радикал. В приведенной выше таблице обратите внимание, как знаменатель рационального показателя степени определяет индекс корня. Таким образом, показатель степени [latex] \frac{1}{2}[/latex] переводится в квадратный корень, показатель степени [latex] \frac{1}{5}[/latex] переводится в корень пятой степени или [latex] \sqrt[5]{{\hphantom{5}}}[/latex], а [latex] \frac{1}{8}[/latex] переводится в корень восьмой степени или [latex] \sqrt[ 8] {{\ hphantom {5}}} [/латекс] .

Помните, что показатели степени относятся только к количеству непосредственно слева от них, если не используется символ группировки. Приведенный ниже пример очень похож на предыдущий с одним важным отличием — здесь нет круглых скобок! Посмотрите, что происходит.

Следующий пример предназначен для того, чтобы помочь вам попрактиковаться в размещении рационального показателя степени в соответствующих терминах в выражении, написанном в подкоренной форме.

При преобразовании из радикальной записи в рациональную экспоненту степень корня становится знаменателем экспоненты. {\frac{1}{n }}[/латекс]. 9{2}[/латекс]. В зависимости от контекста задачи может быть проще использовать тот или иной метод, но пока вы заметите, что вам удалось упростить это выражение быстрее, используя рациональные показатели, чем при использовании «вытягивания». метод.

Давайте попробуем другой пример.

Опять же, альтернативный метод заключается в упрощении под радикалом с помощью факторинга. Для примера, который вы только что решили, это выглядит так.

В следующем видео показано больше примеров того, как упростить подкоренное выражение с использованием рациональных показателей.

Резюме

Квадратный корень числа — это число, которое при умножении само на себя дает исходное число. Основные квадратные корни всегда положительны, а квадратный корень из 0 равен 0. Вы можете брать квадратный корень только из неотрицательных значений. Квадратный корень из полного квадрата будет целым числом. Другие квадратные корни можно упростить, идентифицируя факторы, которые являются идеальными квадратами, и извлекая из них квадратный корень.

Подкоренное выражение — это математический способ представления 9{\ гидроразрыва {м} {п}}} [/латекс]. Переписывание корней с использованием дробных показателей может быть полезным для упрощения некоторых радикальных выражений. При работе с дробными показателями помните, что дробные показатели подчиняются всем тем же правилам, что и другие показатели степени, когда они появляются в алгебраических выражениях.

Упрощение корней — Magoosh GRE

Теперь можно поговорить об упрощении корней. И это очень важная тема на тесте. Видите ли, потому что часто нам приходится извлекать квадратный корень в задаче, а сама задача приведет к квадратному корню из большого числа. Но квадратный корень из нашего большого числа не появится среди ответов. Варианты ответов будут в упрощенной форме.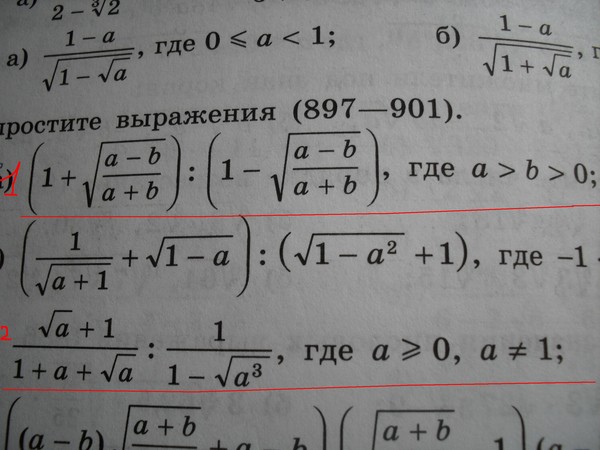

Итак, мы должны понять, как упростить радикал. Итак, если у нас есть что-то большое, например, квадратный корень из 75, как нам это упростить? И запишите его в таком виде, чтобы он фигурировал в ответах. Вот об этом мы и поговорим. Как мы узнали из предыдущих уроков, корни распределяются при умножении. Таким образом, мы можем разделить корень произведений на произведение корней.

Итак, если у меня есть продукт под корнями, я могу разделить его на квадратный корень из первого, умноженный на квадратный корень из второго. Прежде всего помните, найти квадратный корень из полных квадратов несложно. Напомню, здесь квадратные корни из первых 15 полных квадратов. Итак, квадратный корень из 49, мы спрашиваем, какое число нужно умножить само на себя, чтобы получить 49.

И, конечно же, ответ на это 7. И аналогично для всех этих. Это просто хорошие цифры, которые нужно знать. Теперь, как мы узнали на предыдущем уроке, корни распределяются при умножении. Итак, как мы только что сказали, мы можем разделить корень произведения на произведение корней.

Таким образом, корень произведения P, умноженного на Q, равен произведению корня P, умноженного на корень Q. А теперь заметьте, если P или Q — полный квадрат, то этот квадратный корень очень легко упростить. И все выражение упростится. Так, например, предположим, что в какой-то момент задачи нам нужен квадратный корень из 75. Возможно, ответом на вопрос будет квадратный корень из 75.

Ну, квадратный корень из 75 не появится в вариантах ответа, но ясно, что 75 кратно 25, а 25 — это полный квадрат. Так что мы можем использовать это в своих интересах. Так что я просто напишу квадратный корень из 75. Он не появится в такой форме, но я напишу это как произведение 25, умноженное на 3.

Теперь я могу разделить корни. А теперь квадратный корень из 25, это то, что я могу упростить. Квадратный корень из 25 — это просто 5, и я могу просто записать все это как 5 корень 3. Таким образом, 5 корень 3 равен квадратному корню из 75. Это упрощенная форма квадратного корня из 75. Таким образом, форма квадрат корень из 75 никогда не появится в тесте в качестве ответа с несколькими вариантами ответов.

Это всегда выглядело бы упрощенно как 5 корень 3. Вот почему важно знать, как выполнить эту процедуру упрощения корней, потому что мы должны привести ответы к форме, распознаваемой на тесте, так, как сам тест будет перечислять ответы. Итак, вот еще немного практики. Поставьте видео на паузу, а потом поговорим об этом.

Итак, в каждом случае мы хотим выразить число под радикалом как произведение совершенного квадрата на что-то еще. Итак, 12 делится на полный квадрат, оно делится на 4. Итак, я напишу как 4 x 3, и тогда, конечно, квадратный корень из 4 равен просто 2. Тогда это просто упрощается до 2 корня 3.

63, я могу записать это как 9 х 7. И квадратный корень из 9 равен 3, так что получается 3 корень 7. 80, я могу сказать, что делится на 4, но на самом деле оно также делится на, мы поделили на 4 получаем 20, можем снова разделить на 4. Другими словами, 80 на самом деле делится на 16. Таким образом, мы действительно сэкономим немного времени, если запишем это как 16 x 5.

И квадратный корень из 16 равен 4, так что это всего лишь корень 4 из 5. И тогда 175 , ну, это 7 умножить на 25. Итак, 25 умножить на 7, возьмем из этого квадратный корень, и мы получим 5 корень 7. И это все упрощенные корни. И поэтому в тесте вы никогда не увидите квадратный корень из 175 в качестве варианта ответа, вы увидите, что он указан как 5 корень 7, упрощенная форма.

Предположим, что число под радикалом особенно велико. Предположим, нам нужно найти, например, квадратный корень из 2800. Это, безусловно, поможет разложить на множители самые большие квадраты, такие как 100, возможно, потребуется найти полную разложение числа на простые множители. Здесь мы можем сильно упростить, просто вычтя 100 из радикала. Таким образом, квадратный корень из 100, конечно же, равен 10.

Таким образом, это просто становится 10 корнем 28. Но 28 я также могу упростить, это 4 умножить на 7, а квадратный корень из 4 равен 2. Таким образом, 10 умножить на корень 7 , или, другими словами, корень 20 из 7. И это фактически полностью упрощенная форма квадратного корня из 2800. Вот проблема с практикой. Поставьте видео на паузу, а потом мы поговорим об этом.

Ладно, во-первых, мы знаем, что нельзя складывать через радикал. Так что мы, конечно, не можем сложить 48 + 75 + 192. Поэтому вместо этого мы должны упростить каждый из этих радикалов. Итак, давайте возьмем их по одному. 48 обязательно делится на 4. Это 4 умножить на 12.

12 снова делится на 4. Таким образом, это означает, что 48 на самом деле делится на 16. Таким образом, мы можем записать это как 16, умноженное на 3. Конечно, квадратный корень из 16 равен 4. Таким образом, 16 выходит из корня как 4, и мы просто получаем корень 4 из 3. 75 мы уже рассмотрели, это 25 умножить на 3.

25 выходит из корня как 5. Так это просто 5 корень 3. Сразу очень интересно, первые два оба кратны корню 3. Наводит на размышления что? Может быть, третья будет кратна корню 3. Что будет, если 192 разделить на 3?

Ну, мы знаем, что 180 равно 60 х 3. Итак, вычтем 192-180, получится всего 12. И, конечно же, 3 входит в число 12 четыре раза, поэтому 3 входит в число 192, 64 раза. Так что на самом деле это 64 умножить на 3. И это мы можем действительно упростить, потому что 64 получается из радикала как 8, квадратный корень из 64 равен 8. Итак, мы получаем 8 корень 3.

Итак, мы упростили все три. Итак, все три в упрощенной форме, поэтому мы можем просто добавить их. Таким образом, 4 чего-либо плюс 5 таких же вещей плюс 8 таких же вещей должны быть 17 таких же вещей. Таким образом, все просто упрощается до 17, корень из 3. И мы выбираем вариант ответа A.

Таким образом, мы упрощаем квадратные корни, вынося на множители наибольший множитель совершенных квадратов. Если мы можем найти простую факторизацию или если она задана, мы можем использовать это: любые пары простых множителей и любые четные степени простых чисел являются полными квадратами. Так что это тоже может быть полезно.

Упрощение квадратных корней (примеры вопросов)

Квадратный корень числа — это число, которое при умножении само на себя дает исходное число. Например, \(5\times5=25\), следовательно, квадратный корень из \(25\) равен \(5\). Радикальный символ \(\sqrt{ }\) используется для представления квадратных корней. Два утверждения: «Чему равен квадратный корень из \(36\)?» и «Что такое \(\sqrt{36}\)?» читаются точно так же.

Упрощение примеров вопросов на квадратный корень

Чтобы упростить квадратный корень, мы просто находим значение, которое при умножении само на себя дает исходное число. Когда квадратный корень представляет собой целое число, это называется полным квадратом.

Вот несколько примеров идеальных квадратов:

\(\sqrt{4}=2\) \(\sqrt{9}=3\) \(\sqrt{16}=4\) \(\sqrt{25}=5\)

Когда квадратный корень не упрощается до целого числа, мы упрощаем то, что можем, а все, что остается, остается под радикальным символом. Например, чтобы упростить \(\sqrt{28}\), мы рассмотрим множители \(\sqrt{28}\), чтобы увидеть, существуют ли идеальные квадраты. \(28=2\times2\times7\) или \(4\times7\). Поскольку \(4\) является полным квадратом и \(\sqrt{4}=2\), мы можем вытащить это, и у нас останется \(7\) под радикалом, так что \(\sqrt{28} =2\sqrt{7}\).

Пример:

Упростить \(\sqrt{180}\).

\(180=2\times2\times3\times3\times5\)

Следовательно, \(\sqrt{180}=2\times3\sqrt{5}=6\sqrt{5}\).

Примеры вопросов на упрощение квадратного корня


Вот несколько примеров вопросов, касающихся упрощения квадратного корня.

Вопрос №1:

 
Напишите \(\sqrt{175}\) в максимально упрощенной форме.

\(5\кв{7}\)

\(7\sqrt{5}\)

\(25\sqrt{7}\)

\(35\sqrt{5}\)

Показать ответ

Ответ:

Для упрощения выражение \(\sqrt{175}\), мы начнем с нахождения множителей \(175\), что равно \(5\times5\times7\). Поскольку \(5\times5\) является полным квадратом, мы можем убрать один \(5\), и у нас останется \(7\) под радикалом; следовательно, \(\sqrt{175}=5\sqrt{7}\).

Скрыть ответ

Вопрос №2:

 
Что показывает \(\sqrt{208}\) в самой упрощенной форме?

\(2\sqrt{52}\)

\(4\sqrt{52}\)

\(4\sqrt{13}\)

\(13\sqrt{4}\)

Показать ответ

Ответ:

Упрощенную форму \(\sqrt{208}\) можно найти, сначала найдя множители \(208\), которые равны \(2\times2\times2\times2\ раз 13\). Есть два идеальных квадрата, \(2\times2\), которые мы можем вытащить, что оставляет нам \(13\) под радикалом. Следовательно, \(\sqrt{208}=4\sqrt{13}\).

Скрыть ответ

Вопрос № 3:

 
Упростить \(\sqrt{294}\).

\(6\sqrt{7}\)

\(7\sqrt{6}\)

\(14\sqrt{21}\)

\(21\sqrt{14}\)

Показать ответ

Ответ:

Мы упростим \(\sqrt{294}\), сначала найдя множители \(294\), что равно \(2\times3\times7\times7\). Существует один идеальный квадрат, \(7\times7\), поэтому мы вытаскиваем один, и у нас остается \(2\times3\), или \(6\), под радикалом. Следовательно, \(\sqrt{294}=7\sqrt{6}\).

Скрыть ответ

Вопрос №4:

 
Вот выражение: \(\sqrt{648}\). Какой из них показывает выражение в наиболее упрощенной форме?

\(2\sqrt{18}\)

\(9\sqrt{8}\)

\(12\sqrt{54}\)

\(18\sqrt{2}\)

Показать ответ

Ответ:

Чтобы найти наиболее упрощенную форму выражения \(\sqrt{648}\), мы начнем с нахождения множителей \(648\), что равно \(2\times2 \раз2\раз3\раз3\раз3\раз3\). Есть три набора совершенных квадратов, \(4,9,\) и \(9\), которые мы вытащим, и у нас останется \(2\) под радикалом. Следовательно, \(\sqrt{648}=18\sqrt{2}\).

Скрыть ответ

Вопрос № 5:

 
Что показывает \(\sqrt{2{,}448}\) в самой упрощенной форме?

\(4\sqrt{51}\)

\(12\sqrt{17}\)

\(17\sqrt{12}\)

\(48\sqrt{17}\)

Показать ответ

Ответ:

Наиболее упрощенную форму выражения \(\sqrt{2{,}448}\) можно найти, если сначала найти множители \(2{,}448\), которые равно \(2\times2\times2\times2\times3\times3\times17\). Есть три набора полных квадратов, \(4,4,\) и \(93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

ВЕБ -Урок — Упрощение отрицательных квадратных корней

Share

Приоритет урока: высокий

Алгебра Два $ \ longrightarrow $

Комплексные номера $ \ longrightarrow $

для упрощения квадратных корней из отрицательных чисел

• Применить то, что мы уже знаем о сокращении квадратных корней из положительных целых чисел

Описание урока

Теперь, когда мы понимаем, что такое мнимое число и как оно работает, мы можем упростить квадратный корень из отрицательных чисел таким же образом, как мы упрощаем квадратный корень из положительных.

 

Практические задачи

Практические задачи и рабочие листы скоро появятся!

 

Я думал, что мы не сможем вычислить отрицательные значения?

Безусловно, наиболее распространенное и полезное применение мнимого числа связано с упрощением выражений квадратного корня, содержащих отрицательные числа. Хорошо это или плохо, но этот процесс является практически точной копией навыка упрощения выражений с положительными корнями, поэтому, если вы не понимаете, как упростить целочисленные квадратные корни », тогда приступайте к работе с программой, а затем читайте дальше. упоминая, что у нас, вероятно, был по крайней мере один учитель, который конкретно сказал нам, что мы не можем извлечь квадратный корень из отрицательного числа. Хотите ли вы считать ложью или нет, зависит от вашей точки зрения — это правда, что вы не можете извлечь квадратный корень из отрицательного числа, если собираетесь работать только с действительными числами, но если вы допускаете существование мнимых чисел » , тогда вы на самом деле может извлекать квадратный корень из чего угодно (включая извлечение квадратного корня из мнимых чисел » , но мы не будем рассматривать это, пока не узнаем немного тригонометрии!). Всем учащимся, изучающим Алгебру 2 и далее, необходимо работать с мнимыми числами, по крайней мере, на базовом уровне, и этот урок — навык, который вам абсолютно необходимо знать. К счастью, как мы уже говорили, это прямая адаптация что мы уже знаем об упрощении квадратных корней. В частности, вот как это работает.

Теорема: отрицательные квадратные корниУпрощение выражения, содержащего квадратный корень из отрицательной величины, осуществляется путем упрощения величины, как если бы она была положительной, и добавления $i$ впереди в качестве коэффициента. Другими словами, $$\sqrt{-x} = i\sqrt{x}$$Для всех $x$ таких, что $x$ — положительное число, так что $-x$ — отрицательное число.

Давайте рассмотрим пример.

 

Пример 1Simplify.$$\sqrt{-40}$$$\blacktriangleright$ Возвращаясь к нашим знаниям об упрощении целых квадратных корней, мы понимаем, что $\sqrt{40}$ упрощается как $2\sqrt{10 }$. Поэтому, применяя теорему 1, имеем $$\sqrt{-40} = i\sqrt{40}$$$$= 2i\sqrt{10}$$

 

Это простая адаптация к тому, что мы уже знаем. Мы знаем, что $\sqrt{40} = 2\sqrt{10}$, поэтому $\sqrt{-40} = 2i\sqrt{10}$.

Pro Tip

Отточите свои обычные навыки упрощения корней. Как только вы начнете практиковать этот навык, вы увидите, что на самом деле вы просто используете тот обычный корневой навык, который у вас уже есть, за исключением того, что вы просто ставите $i$ перед своим ответом. Вся «тяжелая работа» полностью вращается вокруг процесса упрощения корня, который вы уже знаете!

Вот еще пример.

 

Пример 2. Упрощение. $$\sqrt{-72}$$$\blacktriangleright$ Через уже известный нам процесс упрощения квадратного корня: $$$=6 \sqrt{2}$$Теорема 1 снова говорит нам, что $$\sqrt{-72} = i \sqrt{72}$$. Отсюда следует, что $$\sqrt{-72} = i \cdot 6\sqrt{2}$$$$6i \sqrt{2}$$

Внимание!

Свойство корневого произведения не работает для квадратных корней произведений отрицательных чисел из-за свойств мнимого числа!!! Будьте осторожны, чтобы не применять его дословно! Например, попробуем применить свойство Root Product к следующему примеру: $$\sqrt{(-10)(-7)}$$Согласно свойству Root Product:$$\sqrt{(-10)(- 7)} = \sqrt{(-10)} \cdot \sqrt{(-7)}$$$$\longrightarrow = i\sqrt{10} \cdot i \sqrt{7} = i^2 \sqrt{ 10}\sqrt{7}$$$$= -\sqrt{10} \sqrt{7} = -\sqrt{70}$$Но если бы мы сначала умножали под корнем, а затем упрощали, мы бы получили совершенно другой ответ: $$\sqrt{(-10)(-7)} = \sqrt{70}$$Как видите, с первой точки зрения мнимые числа создавали отрицательный знак вне радикала. Однако во второй перспективе два отрицательных значения умножаются на положительный результат еще до того, как мы начинаем пытаться извлекать квадратный корень. Верен именно последний случай. Это выглядит ошеломляюще, но хорошая новость в том, что учителя и преподаватели редко пытаются использовать это явное легкомыслие против вас. Невероятно редко случается, что эта неудача на самом деле представлена ​​вам в ситуации, когда вы получаете оценки.

В целом, вывод этого урока состоит в том, что обычно вам просто дается выражение квадратного корня с отрицательным знаком для упрощения. Добейтесь этого, применив то, что мы уже знаем об упрощении квадратных корней, чтобы получить правильную числовую часть, и используйте идею о том, что мы получим тот же результат, что и в случае положительного квадратного корня, но с разложением на $i$. вне.

Проверь это

Попробуйте решить несколько задач самостоятельно. Помните, что здесь нет ничего нового из того, что вы уже должны знать об упрощении числовых корней с точки зрения чисел. Если вы ищете практические задачи о других вещах, которые мы делаем с $i$, ознакомьтесь с другими уроками по воображаемым числам ».

 

Пример 3Упростить.$$\sqrt{-100}$$

Показать решение

$$\blacktriangleright \,\, \sqrt{-100} = i \sqrt{100}$$$$ = 10i $$

 

Пример 4. Упрощение. =i \sqrt{25 \cdot 3} = 5i \sqrt{3}$$

 

Пример 5Упростить.$$\sqrt{-56}$$

Показать решение

$$\blacktriangleright \,\, \sqrt{-56} = i \sqrt{56}$$$$=i \sqrt{4 \cdot 14} = 2i \sqrt{14}$$

 

Пример 6Упростить.$$\sqrt{-91}$$

Показать решение

$$\blacktriangleright \,\, \sqrt{-91} = i \sqrt{91}$$$91$ простое , так что дальше упрощать нечего.

 

Выводы из урока

• Уметь упрощать квадратные корни, когда радикал содержит отрицательное число
• Хотя это вряд ли появится в тесте, поймите, почему свойство Root Product не работает для квадратных корней из произведения отрицательных чисел .

  No related posts.