Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы
1. Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы. Решение систем
Тема 4Матрицы. Операции над матрицами.
Элементарные преобразования.
Приведение к ступенчатому виду. Ранг
матрицы. Решение систем линейных
алгебраических уравнений методом
Гаусса
Калабухова Галина Валентиновна,
к.социол.н., доцент
2. Вопросы темы:
Матрицы: терминология и обозначения.Операции над матрицами: сложение, умножение матрицы
на число. Умножение матриц. Транспонирование матрицы.
Элементарные преобразования матрицы. Приведение к
ступенчатому виду.
Ранг матрицы.
Решение систем линейных алгебраических уравнений
методом Гаусса.
Матрицы:
терминология и обозначения
4. Определение
Матрицей размера m x n называется прямоугольнаятаблица, состоящая из m строк и n столбцов, заполненная
некоторыми элементами
a11
a
21
.
 ..
..a i1
…
a m1
a12
… a1 j
a 22
… a 2 j
ai 2
…
am 2
… a mj
aij
a1n
… a 2 n
… ain
… a mn
…
Обозначения:
Amxn – матрица
aij – элемент матрицы,
расположенный на
пересечении i-той строки и
j-ого столбца
m x n – размер матрицы
5. Применение матриц
Матрицы широко применяются в математике для компактнойзаписи систем линейных алгебраических уравнений или систем
дифференциальных уравнений. Тогда количество строк матрицы
соответствует количеству уравнений системы, а количество
столбцов равно количеству неизвестных
6. Другие определения
Если n = m, то матрицаназывается квадратной,
а n – порядком
матрицы.
Если все элементы
матрицы равны нулю, то
матрица называется
нулевой. Обозначается: Θ
7. Другие определения
Строка (столбец) матрицы называется нулевой, если все ее(его)элементы равны нулю.
Если хотя бы один из элементов строки (столбца) не равен
нулю, то строка (столбец) называется ненулевой
Пример:
нулевой
столбец
нулевая строка
ненулевая строка
ненулевой
столбец
8.
 Другие определенияГлавной диагональю матрицы называется диагональ,
Другие определенияГлавной диагональю матрицы называется диагональ,проведённая из левого верхнего угла матрицы в правый
нижний.
Побочной диагональю матрицы называется диагональ,
проведённая из левого нижнего угла матрицы в правый
верхний.
побочная диагональ
Пример:
главная диагональ
9. Другие определения
Матрица, состоящая из одной строки, называется векторстрокой, а матрица, состоящая из одного столбца, вектор-столбцом.Примеры:
вектор-строка
вектор-столбец
10. Другие определения
Квадратная матрицаназывается
диагональной, если
все ее элементы,
стоящие вне главной
диагонали, равны нулю.
Скалярной называется диагональная матрица S, у которой все
диагональные элементы равны между собой.
Единичной матрицей En называется скалярная матрица
порядка n, диагональные элементы которой равны 1.
11. Другие определения
Матрица называется верхней треугольной матрицей, есливсе элементы ниже главной диагонали равны нулю.

Матрица называется нижней треугольной матрицей, если
все элементы выше главной диагонали равны нулю.
Примеры:
верхнетреугольная
матрица
12. Другие определения
Ступенчатойназывается матрица,
которая содержит m
строк и у которой
первые r ≤ m
диагональных
элементов ненулевые,
а элементы, лежащие
ниже главной
диагонали и элементы
последних (m — r) строк
равны нулю, то есть
это матрица вида:
Главным элементом некоторой
строки матрицы A называется ее
первый ненулевой элемент
13. Другие определения
Матрица А называется ступенчатой, если:все ее нулевые строки стоят после ненулевых;
в каждой ненулевой строке, начиная со второй, ее главный
элемент стоит правее (в столбце с большим номером)
главного элемента предыдущей строки.
Примеры ступенчатых матриц:
НЕ ЯВЛЯЕТСЯ
СТУПЕНЧАТОЙ:
14. Другие определения
Две матрицы называются равными, если они имеютодинаковые размеры и их соответствующие элементы
равны:
Anxm = Bnxm <=> aij = bij, i = 1,n, j = 1,m
Операции над матрицами
16.
 Произведением матрицы на числоназывается матрица, полученная из исходной умножением
Произведением матрицы на числоназывается матрица, полученная из исходной умножениемкаждого ее элемента на заданное число
B = λA, bij = λaij, i = 1,n, j = 1,m
17. Суммой матриц
A и B одного размера называется матрица C = A + B, такогоже размера, получаемая из исходных путем сложения
соответствующих элементов
C = A + B, cij = aij+bij, i = 1,n, j = 1,m
18. Свойства линейных операций
Умножение матрицы на числоСумма матриц
— линейные операции
1. Ассоциативность: (A + B) + C = A + (B + C)
2. A + Θ = Θ + A, где Θ – нулевая матрица
3. A – A = Θ
4. Коммуникативность: A + B = B + A
5. Дистрибутивность: λ * (A + B) = λ * A + λ * B
6. (λ + μ) * A = λ * A + μ * A
7. (λ * μ) * A = λ * (μ * A)
19. Произведением матриц
Amxn на матрицу Bnxk называется матрица Cmxk такая, чтоэлемент матрицы С, стоящий в i-той строке и j-том столбце
(т.е. элемент cij) равен сумме произведений элементов i-той
строки матрицы A на соответствующие элементы j-го
столбца матрицы B
C = A * B, cij = Σail*blj, l = 1,n
20.
 Свойства произведения матриц1. Ассоциативность: (A * B) * C = A * (B * C)
Свойства произведения матриц1. Ассоциативность: (A * B) * C = A * (B * C)2. Ассоциативность по умножению: (μ * A) * B = μ * (A * B)
3. Дистрибутивность: A * (B + C) = A * B + A * C;
(A + B) * C = A * C + B * C
4. Умножение на единичную матрицу: E * A = A * E = A
5. Некоммуникативно: A * B ≠ B * A
21. Транспонирование матрицы
это операция над матрицей, когда ее строки становятсястолбцами с теми же номерами.
Обозначается AT
22. Свойства операции транспонирования матриц
1. (AT)T = A2. (λ * A)T = λ * AT
3. (A + B)T = AT + BT
4. (A * B)T = BT * AT
Элементарные преобразования
матрицы
24. Эквивалентные преобразования над строками матрицы
называют следующие преобразования строк:умножение строки на ненулевое число;
перестановка двух строк;
прибавление к одной строке матрицы другой ее строки,
умноженной на некоторое ненулевое число.
Если от матрицы к матрице перешли с помощью
эквивалентных преобразований над строками, то такие
матрицы называются эквивалентными и обозначают
A ~ B.

Ранг матрицы
26. Определения
Линейной комбинацией (ЛК) строк s1, s2, …, sm матрицы Aназывается выражение λ1s1 + λ2s2 +…+λmsm.
ЛК называется тривиальной, если все коэффициенты λi
равны нулю одновременно.
ЛК называется нетривиальной, если хотя бы один из
коэффициентов λi отличен от нуля.
Система строк называется линейно зависимой (ЛЗ), если
существует их нетривиальная ЛК, равная нулевой строке
Система строк называется линейно независимой (ЛНЗ), если
только тривиальная ЛК равна нулевой строке
27. Рангом системы строк
называетсямаксимальное
независимых строк этой системы
количество
линейно
В каждой матрице может быть два ранга: строчный ранг (ранг
системы строк) и столбцовый ранг (ранг системы столбцов).
Теорема: Строчный ранг матрицы равен её столбцовому рангу
28. Рангом матрицы
называется ранг её системы строк или столбцовОбозначается: rang A.
Элементарные преобразования над строками (столбцами)
матрицы не меняют её ранга.

Ранг ступенчатой матрицы равен количеству её ненулевых
строк.
На практике для нахождения ранга матрицы используют
следующее утверждение: ранг матрицы равен количеству
ненулевых строк после приведения матрицы к ступенчатому
виду.
Решение систем линейных
алгебраических уравнений
методом Гаусса
30. Системой линейных алгебраических уравнений (СЛАУ)
называется система вида:Упорядоченный набор значений {x01, x02, …, x0n} называется
решением системы, если при подстановке в уравнения
все уравнения превращаются в тождество
31. Определения
СЛАУ называется совместной, если она имеет хотя бы однорешение.
В противном случае система называется несовместной.
Система называется определённой, если она совместна и
имеет единственное решение.
В противном случае (т.е. если система совместна и имеет
более одного решения) система называется
неопределённой.
Система называется однородной, если все правые части
уравнений, входящих в нее, равны нулю одновременно.

Система называется квадратной, если количество уравнений
равно количеству неизвестных.
32. Определения
Расширенной матрицей системы A = (A|B) называетсяматрица, полученная из матрицы системы A, дописыванием
справа после вертикальной черты столбца свободных
членов B.
33. Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведениерасширенной матрицы к ступенчатому виду) и обратный
(получение нулей над главной диагональю расширенной
матрицы) ходы. Прямой ход и называется методом
Гаусса, обратный — методом Гаусса-Жордана, который
отличается от первого только последовательностью
исключения переменных.
Метод Гаусса идеально подходит для решения систем
содержащих больше трех линейных уравнений, для
решения систем уравнений, которые не являются
квадратными, т.о. метод Гаусса — наиболее универсальный
метод для нахождения решения любой системы линейных
уравнений, он работает в случае, когда система имеет
бесконечно много решений или несовместна
|
⇐ ПредыдущаяСтр 6 из 18Следующая ⇒
Критерий совместности системы линейных уравнений даёт теорема Кронекера-Капелли. Леопольд Кронекер (1823 – 1891 гг.) ─ немецкий математик. Теорема, о которой пойдёт речь, содержалась в его лекциях, читавших в Берлинском университете в 1883 – 1891 гг. Альфред Капели (1858 – 1916) ─ итальянский математик. Он, по-видимому, впервые дал формулировку теоремы с использованием термина «ранг матрицы» в своей работе в 1892г.
Теорема Кронекера-Капелли. Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.
Пример. Исследовать систему на совместность Решение. Приведение матрицы системы и расширенной матрицы системы к ступенчатому виду будем выполнять одновременно. Ранг матрицы системы равен 2, а ранг расширенной матрицы системы равен 3.
Метод Гаусса решения системы линейных уравнений.
Метод Гаусса применяется для произвольной системы линейных уравнений. Нам понадобится Определение. Систему линейных уравнений будем называть ступенчатой, если матрица этой системы ступенчатая.
При решении системы линейных уравнений применим следующий алгоритм:
1. Записываем расширенную матрицу системы (1) и приводим её к ступенчатому виду, определяем ранги матрицы и расширенной матрицы системы. 2. Если найденные ранги не равны, то система несовместна. 3. Ранг матрицы системы равен рангу расширенной матрицы системы и равен числу r. В этом случае система совместна и надо найти её решение. 4. Используя ступенчатый вид расширенной матрицы системы, записываем соответствующую ступенчатую систему.5. Если число r равно числу неизвестных n, то ступенчатая система имеет вид (2) Из системы (2) последовательно находим значения для х1, х2,…, хт, начиная с последнего уравнения. 6. Если число r меньше числа неизвестных, то ступенчатая система имеет вид (3) В системе (3) r уравнений и n неизвестных. Неизвестные х1,…,хj1, которые первыми встречаются в уравнениях системы (3), назовём главными неизвестными, остальные ─ свободными неизвестными. Из системы (3) последовательно выражаем главные неизвестные через свободные, начиная с последнего уравнения. Свободные неизвестные могут принимать любые значения. В этом случае система имеет бесконечно много решений.
Примеры. 1). Ответ: (2;-3;-1).
2) Ответ: нет решений.
3) Ответ: бесконечно много решений.
Правило Крамера решения систем линейных уравнений.
Габриэль Крамер (1704 – 1752) ─ швейцарский математик, который в 1750 г. нашёл метод решения систем линейных уравнений, названный впоследствии правилом Крамера.
Определение. Система линейных уравнений называется крамеровской,если тело уравнений равно числу неизвестных и определитель матрицы системы отличен от нуля.
Теорема 7.1. Крамеровская система имеет единственное решение, которое находится по формулам где ─ определитель матрицы системы, ─ определитель, полученный из , заменой столбца коэффициентов при на столбец свободных членов. Доказательство. Пусть дана крамеровская система (4) Тогда │А│= ∆ = ¹ 0. По теореме 3 лекции 6 матрица системы А имеет обратную матрицу А-1. Запишем крамеровскую систему (4) в матричном виде
АХ = В (5) где А = , Х = , В = . Умножим обе части матричного уравнения (5) слева на А-1: А-1(АХ) = А-1В, Ввиду ассоциативности умножения матриц имеем А-1(АХ) = (А-1А)Х = ЕТХ = Х. Таким образом, Х = А-1В ─ решение системы.
1) Покажем, что такое решение единственно. Предположим, что Х1 и Х2 ─ два решения матричного уравнения (5). Тогда АХ1 = В и АХ А-1(АХ1) = А-1(АХ2), (А-1А)Х1 = (А-1А)Х2, ЕnХ1 = ЕnХ2, Х1 = Х2. Следовательно, система (4) имеет единственное решение.
2) Найдём решение системы (4). Из равенства Х = А-1В имеем: = , откуда , , …………………………………………………….. . Обозначая определители в правой части равенств соответственно, получим формулы .
Пример. Решить систему уравнений по правилу Крамера
Ответ: (1;1;1).
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: |
Найти ранг матрицы: способы и примеры
- Понятие ранга матрицы
- Отыскание ранга матрицы способом окаймляющих миноров
- Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
- Найти ранг матрицы самостоятельно, а затем посмореть решение
- Ранг матрицы — онлайн калькулятор
Ранг матрицы используется при проверке условия совместности системы линейных уравнений.
Определение. Рангом матрицы называется максимальное число линейно независимых строк, рассматриваемых как векторы.
Можно открыть в новом окне материал о линейной независимости векторов.
Теорема 1 о ранге матрицы.
Понятие минора мы уже разбирали на уроке по определителям, а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то столбцов, причём это «сколько-то» должно быть меньше числа строк и стобцов матрицы, а для строк и столбцов это «сколько-то» должно быть одним и тем же числом. Тогда на пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка, чем наша исходная матрица. Определитель это матрицы и будет минором k-го порядка, если упомянутое «сколько-то» (число строк и столбцов) обозначим через k.
Определение. Минор (r+1)-го порядка, внутри которого лежит выбранный минор r-го порядка, называется называется окаймляющим для данного минора.
Наиболее часто используются два способа отыскания ранга матрицы. Это способ окаймляющих миноров
и способ элементарных преобразований (методом Гаусса).
При способе окаймляющих миноров используется следующая теорема.
Теорема 2 о ранге матрицы. Если из элементов матрицы можно составить минор r-го порядка, не равный нулю, то ранг матрицы равен r.
При способе элементарных преобразований используется следующее свойство:
— если путём элементарных преобразований получена трапециевидная матрица, эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк, полностью состоящих из нулей.
Окаймляющим минором называется минор большего порядка по отношению к данному, если этот минорм большего порядка содержит в себе данный минор.
Например, дана матрица
.
Возьмём минор
,
окаймляющими будут такие миноры:
.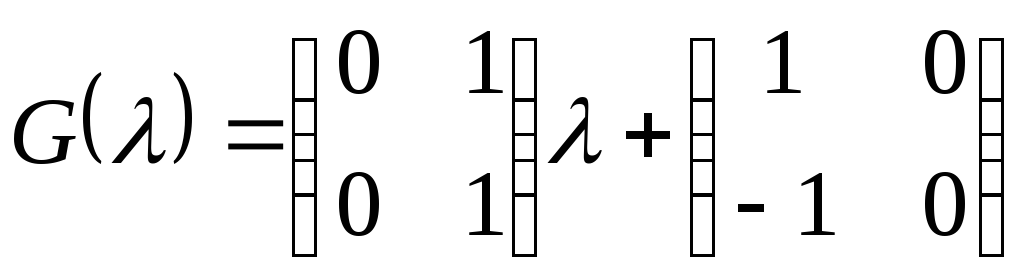
Алгоритм нахождения ранга матрицы следующий.
1. Находим не равные нулю миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы будет равен единице (r =1).
2. Если существует хотя бы один минор второго порядка, не равный нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен двум (r =2).
3. Если хотя бы один из окаймляющих миноров третьего порядка не равен нулю, то составляем окаймляющие его миноры. Если все окаймляющие миноры четвёртого порядка равны нулю, то ранг матрицы равен трём ( r =2).
4. Продолжаем так, пока позволяет размер матрицы.
Пример 1. Найти ранг матрицы
.
Решение. Минор второго порядка .
Окаймляем его. Окаймляющих миноров будет четыре:
,
,
,
.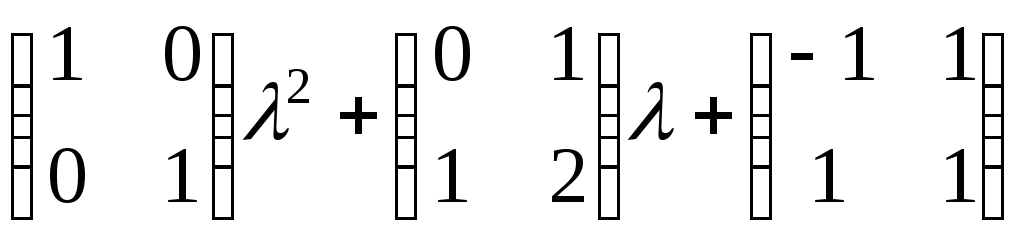
Таким образом, все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг данной матрицы равен двум (r =2).
Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.
Пример 2. Найти ранг матрицы
.
Решение. Ранг данной матрицы равен 1, так как все миноры второго порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах, дорогим студентам предлагается убедиться самостоятельно, возможно, используя правила вычисления определителей), а среди миноров первого порядка, то есть среди элементов матрицы, есть не равные нулю.
Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.
Пример 3. Найти ранг матрицы
.
Решение. Минор второго порядка этой матрицы
,
в все миноры третьего порядка этой матрицы равны нулю. Следовательно, ранг данной матрицы
равен двум.
Следовательно, ранг данной матрицы
равен двум.
Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.
Пример 4. Найти ранг матрицы
.
Решение. Ранг данной матрицы равен 3, так как единственный минор третьего порядка этой матрицы равен 3.
Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Уже на примере 1 видно, что задача определения ранга матрицы способом окаймляющих миноров требует вычисления большого числа определителей. Существует, однако, способ, позволяющий свести объём вычислений к минимуму. Этот способ основан на использовании элементарных преобразований матриц и ещё называется также методом Гаусса.
Под элементарными преобразованиями матрицы понимаются следующие операции:
1) умножение какой-либо строки или какого либо столбца матрицы на число, отличное от нуля;
2) прибавление к элементам какой-либо строки или какого-либо столбца матрицы соответствующих элементов другой строки или столбца, умноженных на одно и то же число;
3) перемена местами двух строк или столбцов матрицы;
4) удаление «нулевых» строк, то есть таких, все элементы которых равны нулю;
5) удаление всех пропорциональных строк, кроме одной.
Теорема. При элементарном преобразовании ранг матрицы не меняется. Другими словами, если мы элементарными преобразованиями от матрицы A перешли к матрице B, то .
Используя эту теорему, отправляясь от любой матрицы A всегда можно прийти к такой матрице B, вычисление ранга которой не представляет затруднений. Для этого следует добиться, чтобы матрица B была трапециевидной.
Тогда ранг полученной матрицы будет равен числу строк в ней кроме строк, полностью состоящих из нулей.
Пример 5. Найти ранг матрицы
.
Решение. Подвергнем эту матрицу следующим преобразованиям. Ко второй строке прибавим третью, умноженную на — 2, а затем к третьей строке прибывам первую, умноженную на 2, и, наконец, из четвёртой вычтем первую. После этих трёх последовательно выполненных преобразований получим матрицу
.
Вычитая из четвёртой строки третью, а затем переставив местами вторую и третью строки, получаем матрицу
.
Получили трапециевидную матрицу. Ранг полученной матрицы равен трём (r=3), так как после вычёркивания последней строки, полностью состоящей из нулей, в ней останется три строки.
Желающие могут проверить это решение способом окаймляющих миноров (минор третьего порядка, находящийся в левом верхнем углу, не равен нулю, а все миноры четвёртого порядка равны нулю).
Пример 6. Найти ранг матрицы
.
Посмотреть правильное решение и ответ.
Пример 7. Найти ранг матрицы
.
Посмотреть правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Поделиться с друзьями
Начало темы «Матрицы»
Понятие матрицы
Продолжение темы «Матрицы»
Обратная матрица
Произведение двух матриц
Умножение матрицы на число
Сложение матриц
Решение матричных уравнений
Другие темы линейной алгебры
Определители
Системы линейных уравнений
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Интересное: Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски. Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 6Следующая ⇒ Умножение на число
Произведением матрицы на число k называется матрица такая, что .
Пример 1.3. , k = 2, . Матрица называется противоположной матрице А.
Разность матриц А – В можно определить так: А – В = А + (-В).
Операции сложения матриц и умножения на число обладают следующими свойствами:
1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А – А = 0;
5. 1 · А = А; 6. α · (А + В) = αА + αВ; 7. (α + β) · А = αА + βА; 8. α · (βА) = (αβ) · А, гдеА, В, С – матрицы, α и β – числа. 4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.
Элементарными преобразованиями матриц являются: ● перестановка местами двух параллельных рядов матрицы; ● умножение всех элементов ряда матрицы на число, отличное от нуля; ● прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Две матрицыАи В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. ЗаписываетсяА ~ В. При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например .
Пример 1.4. Привести к каноническому виду матрицу
. Решение: Выполняя элементарные преобразования, получаем
~ ~ ~ ~ ~ ~ ~ ~ .
Невырожденные матрицы. Обратная матрица.
Основные понятия
ПустьА – квадратная матрица n-го порядка . Квадратная матрицаА называется невырожденной, если определитель не равен нулю: .
Матрицей, союзнойк матрицеА, называется матрица , где — алгебраическое дополнение элемента данной матрицыА (оно определяется так же, как и алгебраическое дополнение элемента определителя). Матрица называется обратной матрицеА, если выполняется условие: , (3.1) гдеЕ – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.
Обратная матрица
Приведем доказательство для случая матрицы 3-го порядка. Пусть , причем . Составим союзную матрицу и найдем произведение матриц : т.е. (3.2) Здесь мы использовали свойства 7 и 8 определителей (см. Аналогично убеждаемся, что . (3.3)
Равенства (3.2) и (3.3) перепишем в виде и Сравнивая полученные результаты с определением (3.1), получим т.е. . Отметим свойства обратной матрицы: 1. ; 2. ; 3. .
Алгоритм нахождения обратной матрицы
Пример 3.1. Найти , если Решение: 1) Находим 2) Находим , поэтому . 3) Находим . Проверка: . Пример 3.2. Определить, при каких значениях λ существует матрица, обратная данной: Решение: Всякая невырожденная матрицы имеет обратную. Найдем определитель матрицыА: Если , т.е. , то , то матрицаА невырожденная, имеет обратную.
Пример 3.3. Показать, что матрица А является обратной дляВ, если , . Решение: Найдем произведение матрицАи В: АналогичноВ · А = Е.
Определители 2-го и 3-го порядка. Основные понятия.
Основные понятия
Квадратной матрицеА порядка n можно сопоставить число detA (или |A|, или Δ), называемое ее определителем следующим образом:
1. n = 1. А = ; . 2. n = 2. ; . 3. n= 3. ; .
Определитель матрицыА также называют его детерминантом. Правило вычисления детерминанта матрицы порядка N является довольно сложным для восприятия и применения. Однако, известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство определителей 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению. Вычисление определителя 2-го порядка иллюстрируется схемой: .
Пример 2.1. Найти определители матриц и . Решение: ; . При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так: .
Пример 2.2. Вычислить определитель матрицы . Решение: .
Системы линейных уравнений . Основные понятия. Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида
где числа называются коэффициентами системы, числа – свободными членами. Такую систему удобно записывать в компактной матричной форме
ЗдесьА – матрица коэффициентов системы, называемая основной матрицей:
,
– вектор-столбец из неизвестных ,
– вектор-столбец из свободных членов . Произведение матриц определено, так как в матрицеА столбцов столько же, сколько строк в матрице Х (n штук). Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов . Решением системы называется n значений неизвестных , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца . Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она ни имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками матрицы. Система линейных уравнений называется однородной, если все свободные члены равны нулю: Однородная система всегда совместна, так как является решением системы. Это решение называется нулевым или тривиальным.
Необходимость. Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то . Достаточность. Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.
Пусть дана однородная система линейных уравнений с неизвестными
Если система имеет ненулевые решения, то . Ибо при система имеет единственное, нулевое решение. Если же , то ранг основной матрицы системы меньше числа неизвестных, т.е. . И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример 4.6. Решить систему
Решение: Так как , то система имеет бесчисленное множество решений. Найдем их Стало быть – общее решение. Положив получим одно частное решение: Положив получаем второе частное решение: и т.д. Векторы. Основные понятия. Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина изображается с помощью вектора.
Вектор– это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. ЕслиА – начало вектора, а В – его конец, то вектор обозначается символом или . Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, дина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет. Вектор, длина которого равна единице, называется единичным вектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается . Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || . Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.
Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точкуО пространства. На рисунке 1 векторы образуют прямоугольник. Справедливо равенство = , но . Векторы и – противоположные, . Равные векторы также называют свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны.
Общее уравнение прямой Рассмотрим уравнение первой степени относительно х и у в общем виде
, (10.4)
гдеА, В, С – произвольные числа, причем А и В не равны нулю одновременно. Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая. ЕслиВ = 0, то уравнение (10.4) имеет вид , причем , т.е. . Это есть уравнение прямой, параллельной оси Оу и проходящей через точку . Если , то из уравнения (10.4) получаем . Это есть уравнение прямой с угловым коэффициентом . Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой. Некоторые частные случаи общего уравнения прямой: 1) еслиА = 0, то уравнение приводится к виду . Это есть уравнение прямой, параллельной оси Ох; 2) еслиВ= 0, то прямая параллельна оси Оу; 3) еслиС= 0, то получаем . Уравнению удовлетворяют координаты точки , прямая проходит через начало координат.
Найдем уравнение прямой, проходящей через заданную точку перпендикулярно данному ненулевому вектору .
Возьмем на прямой произвольную точку и рассмотрим вектор (см. рис. 43). Поскольку векторы и перпендикулярны, то их скалярное произведение равно нулю: , то есть (10.8) Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору. Вектор , перпендикулярной прямой называется нормальным вектором этой прямой. Уравнение (10.8) можно переписать в виде (10.9) гдеА и В – координаты нормального вектора, – свободный член. Уравнение (10.9) есть общее уравнение прямой
Общее уравнение прямой Рассмотрим уравнение первой степени относительно х и у в общем виде
, (10.4)
гдеА, В, С – произвольные числа, причем А и В не равны нулю одновременно. Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая. ЕслиВ = 0, то уравнение (10.4) имеет вид , причем , т.е. . Это есть уравнение прямой, параллельной оси Оу и проходящей через точку . Если , то из уравнения (10.4) получаем . Это есть уравнение прямой с угловым коэффициентом . Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой. Некоторые частные случаи общего уравнения прямой: 1) еслиА = 0, то уравнение приводится к виду . Это есть уравнение прямой, параллельной оси Ох; 2) еслиВ= 0, то прямая параллельна оси Оу; 3) еслиС= 0, то получаем . Уравнению удовлетворяют координаты точки , прямая проходит через начало координат.
Полярное уравнение прямой
Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние p от полюсаО до данной прямой и угол α между полярной осью l, проходящей через полюс О перпендикулярно данной прямой (см. Для любой точки на данной прямой имеем:
С другой стороны
Следовательно (10.10)
Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой
Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взявО за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде т.е. Но, в силу формул, связывающих прямоугольные и полярные координаты имеем: Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид (10.
Уравнение (10.11) называется нормальным уравнением прямой.
Покажем, как привести уравнение (10.4) прямой к виду (10.11). Умножим все члены уравнения (10.4) на некоторый множитель . Получим Это уравнение должно обратиться в (10.11). Следовательно, должны выполняться равенства: Из первых двух равенств находим , т.е. Множитель называется нормирующим множителем. Согласно третьему равенству знак нормирующего множителя противоположен знаку свободного членаС общего уравнения прямой.
Пример 10.2. Привести уравнение к нормальному виду.
Решение: Находим нормирующий множитель Умножая данное уравнение на , получим искомое нормальное уравнение прямой:
Умножение на число
Произведением матрицы на число k называется матрица такая, что .
Пример 1.3. , k = 2, . Матрица называется противоположной матрице А.
Разность матриц А – В можно определить так: А – В = А + (-В).
Операции сложения матриц и умножения на число обладают следующими свойствами:
1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А – А = 0;
5. 1 · А = А; 6. α · (А + В) = αА + αВ; 7. (α + β) · А = αА + βА; 8. α · (βА) = (αβ) · А, гдеА, В, С – матрицы, α и β – числа. 4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.
Элементарными преобразованиями матриц являются: ● перестановка местами двух параллельных рядов матрицы; ● умножение всех элементов ряда матрицы на число, отличное от нуля; ● прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Две матрицыАи В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. ЗаписываетсяА ~ В. При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например .
Пример 1.4. Привести к каноническому виду матрицу
. Решение: Выполняя элементарные преобразования, получаем
~ ~ ~ ~ ~ ~ ~ ~ .
Невырожденные матрицы. Обратная матрица.
Основные понятия
ПустьА – квадратная матрица n-го порядка . Квадратная матрицаА называется невырожденной, если определитель не равен нулю: .
Матрицей, союзнойк матрицеА, называется матрица , где — алгебраическое дополнение элемента данной матрицыА (оно определяется так же, как и алгебраическое дополнение элемента определителя). Матрица называется обратной матрицеА, если выполняется условие: , (3.1) гдеЕ – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.
Обратная матрица
Приведем доказательство для случая матрицы 3-го порядка. Пусть , причем . Составим союзную матрицу и найдем произведение матриц : т.е. (3.2) Здесь мы использовали свойства 7 и 8 определителей (см. Аналогично убеждаемся, что . (3.3)
Равенства (3.2) и (3.3) перепишем в виде и Сравнивая полученные результаты с определением (3.1), получим т.е. . Отметим свойства обратной матрицы: 1. ; 2. ; 3. .
123456Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 2 из 7Следующая ⇒ Как уже говорилось, метод Жордана-Гаусса состоит в приведении системы к равносильной системе канонического вида. Рассмотрим суть этого метода на следующих примерах. Пример. Решить методом Жордана-Гаусса систему . Решение. Отметим, что в предыдущем параграфе эта система была решена методом Гаусса, для чего она элементарными преобразованиями приводилась к ступенчатому виду. Теперь, в соответствии с методом Жордана-Гаусса, приведем ее к каноническому виду соответствующими элементарными преобразованиями строк расширенной матрицы системы. Расширенная матрица системы имеет вид . Такая матрица элементарными преобразованиями строк ранее (в параграфе «Элементарные преобразования матриц. Ранг матрицы») уже была приведена к эквивалентной канонической матрице: . Эта матрица является расширенной матрицей для следующей системы канонического вида: . Пример. Решить методом Жордана-Гаусса систему . Решение. Приведем расширенную матрицу системы элементарными преобразованиями строк (и вычеркиванием чисто нулевых строк, если таковые появятся) к канонической матрице : ~ ~ ~ ~ . Последняя матрица − каноническая и является расширенной матрицей следующей системы в канонической форме (эквивалентной исходной системе) : . Переменные, коэффициенты при которых соответствуют ненулевым диагональным элементам (а это единицы для канонических матриц) расширенной матрицы системы, называются базисными переменными, а остальные переменные называются свободными переменными. Базисные переменные (в нашей системе это и ) легко выражаются через свободные (в нашей системе это и ). Проделывая это для данной системы, получаем то, что называется общим решением системы: , . Придавая свободным переменным любые значения и вычисляя затем базисные переменные из общего решения, будем получать решения исходной системы. , , , . Придавая паре переменных всевозможные числовые значения и подставляя их в общее решение, получим все решения исходной системы. Однородные системы Исследуем произвольную однородную систему линейных уравнений: . В этом случае ранги основной и расширенной матриц совпадают ( ) . Это следует из того, что расширенная матрица получается из основной добавлением нулевого столбца, а потому среди ненулевых миноров расширенной матрицы не может быть таких, которые не входили в основную матрицу. По теореме Кронекера-Капелли (см. параграф «Исследование общих систем линейных уравнений. Утверждение 1. Однородная система линейных уравнений имеет ненулевые решения (причем бесконечное число их) в том и только в том случае, когда ранг ее основной матрицы меньше числа неизвестных: . Рассмотрим случай, когда число уравнений в однородной системе совпадает с числом неизвестных ( ) : . На основании предыдущего Утверждения 1 легко доказать следующее Утверждение 2. Однородная система из n линейных уравнений с n неизвестными имеет ненулевые решения только в том случае, если определитель основной матрицы этой системы . Найдем вид общего решения таких систем на примере трех уравнений с тремя неизвестными: (9) . Как отмечалось, однородная система всегда совместна, поскольку всегда имеет нулевое решение . Если определитель основной матрицы системы , то это нулевое решение единственно. Пусть . Это означает, ранг основной матрицы системы не может быть равен 3, а потому . Предположим, что ранг основной матрицы . Это означает, что хотя бы один из миноров второго порядка не равен 0. Пусть, например, минор , а потому является базисным минором. В системе (9) оставим только те уравнения, коэффициенты которых участвуют в образовании базисного минора. Таким образом, в системе (9) оставляем только первые два уравнения и приходим к системе (10) . Можно показать, что системы (9) и (10) эквивалентны (т.е. имеют одни и те же решения), а потому найдя общее решение системы (10), получим и общее решение исходной системы (9). Перенесем в (10) слагаемые с переменной в правую часть и рассмотрим полученную систему как систему двух уравнений с двумя неизвестными x и y при произвольном значении переменной . (11) , , где может принимать произвольное числовое значение. Таким образом, формулы (11) представляют общее решение системы (10) . Для того, чтобы запись общего решения выглядела более симметричной, обозначим . Поскольку z может быть любым числом, то и t тоже может принимать любые числовые значения. Выражая и подставляя в (11), получим общее решение исходной системы (9) в следующем симметричном виде : (12) , . При каждом числовом значении параметра t эти формулы дают одно из решений системы (например, при получим нулевое решение системы ). Обратно, любое решение однородной системы получается из приведенных формул (12) при некотором значении параметра t. Пример. Найти общее решение системы . Решение. По формулам (12) получаем , , т.е. , . Иногда требуется из бесконечного множества решений однородной системы выделить решения, обладающие каким-либо дополнительным свойством. Пример. Найти решение предыдущей системы , Решение. Как было только что выяснено, общее решение системы имеет вид: , , , . Найдем значение параметра t , при котором решение удовлетворяло бы и дополнительному условию x2 − 3y2+z+4=0. Подставляя в него , , , получим или , откуда . Итак, нужное нам решение получается из общего решения при , а потому имеет вид: , , . Замечание. Фактически мы нашли решение системы уравнений .
⇐ Предыдущая1234567Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Раздел 2. Элементы аналитической геометрии — Студопедия.Нет
Nbsp; Жолудева В.В.
МАТЕМАТИКА
(для студентов заочной формы обучения)
Учебное пособие
Содержание
Раздел 1. Линейная алгебра………………………………………………………4
1.1 Матрицы и определители………………………………………4
1.2 Системы линейных уравнений………………………………….11
Раздел 2. Элементы аналитической геометрии………………………………….23
2.1 Векторы на плоскости и в пространстве…………………….23
2.2 Аналитическая геометрия на плоскости……………………..27
2.3 Аналитическая геометрия в пространстве……………………34
Раздел 3. Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной………………………..42
Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной………………………..42
3.1 Предел последовательности, предел функции………………42
3.2 Производная функции и ее применение к исследованию функций………………………………………………………..48
3.3 Неопределенный интеграл……………………………………54
3.4 Определенный интеграл. Несобственный интеграл…………56
Раздел 1. Линейная алгебра
Матрицы и определители
Прямоугольной матрицей порядка m×n называется таблица чисел, состоящая из m строк и n столбцов.
Сокращенно обозначается .
Числа называются элементами матрицы А.
Если m=n, то матрица называется квадратной, а число n называют порядком матрицы.
Совокупность элементов образует главную диагональ квадратной матрицы, а элементы — побочную диагональ.
Так, для матрицы
главная диагональ – это числа 1, 4, 3, побочная диагональ – 7, 4, 6.
Нулевой матрицей называют матрицу, все элементы которой равны нулю:
Единичная матрица – это матрица, на главной диагонали которой стоят единицы, все остальные элементы равны нулю:
Квадратная матрица, под главной диагональю которой стоят нули, называется верхнетреугольной; соответственно определяется нижнетреугольная матрица:
— верхнетреугольная матрица,
— нижнетреугольная матрица.
Симметричной называется квадратная матрица, у которой все элементы симметричны относительно главной диагонали.
Действия над матрицами
1. Суммой двух матриц и одного порядка называется матрица , каждый элемент которой равен сумме соответствующих элементов матриц А и В.
Из определения следует, что выполняются операции коммутативности сложения А+В=В+А и ассоциативности сложения А+(В+С)=(А+В)+С.
2. При умножении матрицы на число k каждый ее элемент умножается на это число.
Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.
Операция умножения матрицы на число обладает свойствами:
(α+β)А=αА+β;
α (А+В)= αА+ αВ,
где α и β – числа.
3. Умножение матриц. Пусть заданы матрицы и .
Произведением А×В называется матрица С порядка m×k:
А·В= · =С=
элементы которой вычисляются по формулам:
;
и т.д.
Операция перемножения матриц не коммутативна, то есть АВ≠ВА.
4. Транспонирование матрицы — это операция, при которой строки матрицы становятся столбцами, и наоборот.
Пример. Найти матрицу С=В(3А-2В), где А= и В= .
Решение. 1) Найдем матрицу (3А-2В)= 3 — 2 = — = .
2) С=В(3А-2В) = = .
Элементарные преобразования. Приведение матрицы к ступенчатому виду
1) можно менять строки (столбцы) местами;
2) можно умножать элементы строки на одно и то же число, отличное от нуля;
3) можно складывать (вычитать) строки друг с другом.
Верхнетреугольная матрица, у которой под главной диагональю все элементы равны нулю, называется приведенной к ступенчатому виду. При этом элементы, стоящие на главной диагонали называются угловыми элементами.
При этом элементы, стоящие на главной диагонали называются угловыми элементами.
Ранг матрицы А – это максимальное число линейно независимых строк этой матрицы.
Утверждение. В ступенчатой матрице строки, содержащие ненулевые угловые элементы, линейно независимы. Отсюда следует, что ранг ступенчатой матрицы равен числу ее угловых элементов.
Приведение матрицы к ступенчатому виду с помощью метода Гаусса
Рассмотрим этот метод на примере матрицы А=
Поменяем вторую и первую строки местами (для ручного счета удобно, чтобы элемент был равен 1 или -1 (если это возможно)).
Получим матрицу
В дальнейшем первую строку менять не будем. Теперь с помощью элемента =-1 образуем нули в первом столбце, во второй, третьей и четвертой строках. Для этого ко второй строке прибавим первую, умноженную на число 2, из третьей строки вычтем первую, к четвертой прибавим первую строку:
Поменяем местами в этой матрице вторую и третью строки, и в дальнейшем первая и вторая строки меняться не будут. И с помощью элемента 1 получим нули во втором столбце в третьей и четвертой строках:
И с помощью элемента 1 получим нули во втором столбце в третьей и четвертой строках:
Здесь из третьей строки вычли вторую, умноженную на 5, а из четвертой – вторую, умноженную на 6.
Из четвертой строки вычтем третью, получим матрицу:
Угловые элементы -1, 1, 1, их число равно 3. следовательно, ранг матрицы равен 3.
Справедливы следующие теоремы.
Теорема 1. Элементарные преобразования не меняют ранга матрицы.
Теорема 2. Любую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
Определители
Важной характеристикой квадратной матрицы А порядка n является ее определитель
1. Рассмотрим это понятие для матриц второго порядка.
Пусть задана матрица
.
Определитель матрицы А – число которое ставится в соответствие матрице А и вычисляется по правилу det A= .
Обозначение: det A= = .
Например, det A=
2. Рассмотрим квадратную матрицу третьего порядка.
Определитель третьего порядка это число
= .
Например, =
=
3. Определители n-го порядка.
Минор элемента матрицы — это определитель порядка n-1, полученный из матрицы А вычеркиванием i-той строки и j-ого столбца, на пересечении которых стоит этот элемент.
Алгебраическое дополнение отличается от минора лишь знаком:
.
Определителем матрицы А n-го порядка называется число, полученное разложением по i-й строке:
.
Пример. Вычислить определитель матрицы
Вычислим определитель матрицы разложением его по элементам третьей строки (так как эта строка содержит нулевой элемент):
det A=0·А31+(-3)·А32+2·А33+1·А34=-3·А32+2·А33+А34
Тогда, det A=-3·20+2·(-28)-12=-60-56-12=-128.
Основные свойства определителей
1. При умножении всех элементов некоторой строки на число определитель исходной матрицы умножается на это число.
2. Определитель матрицы с нулевой строкой равен нулю
3. При перестановке двух строк определитель меняет знак.
4. Если две строки матрицы равны, то ее определитель равен нулю.
5. Определитель не меняется, если к какой-нибудь строке матрицы прибавить другую ее строку, умноженную на число.
6. Определитель произведения двух матриц равен произведению определителей:
7. Определитель не меняется при транспонировании матрицы.
Замечание 1. При элементарных преобразования Гаусса определитель матрицы может только изменить знак (при перестановке строк). Поэтому удобно считать определитель матрицы, предварительно приведя ее к ступенчатому виду.
Замечание 2. Преобразование Гаусса сводит квадратичную матрицу к верхнетреугольному виду, определитель которой равен произведению диагональных элементов.
Замечание 3. Если ранг матрицы равен ее порядку, то строки матрицы линейно независимы. Таким образом, равенство нулю определителя есть признак линейной зависимости строк матрицы.
Обратная матрица
Матрица А-1 называется обратной к матрице А, если выполняется условие А· А-1= А-1·А=Е.
Теорема. Матрица А имеет обратную А-1 тогда и только тогда, когда А – невырожденная, det A≠0.
Способы вычисления обратной матрицы
1. Способ вычисления обратной матрицы с помощью алгебраических дополнений.
Алгоритм вычисления:
1) вычисляют определитель матрицы det A;
2) для каждого элемента вычисляют алгебраические дополнения ;
3) составляют матрицу из алгебраических дополнений:
;
4) транспонируют матрицу :
Матрица называется присоединенной к матрице А;
5) определяют обратную матрицу по формуле:
.
Пример. Найти матрицу, обратную к матрице
1) det A=0+20-6-0+20+8=42
2)
3)
4) ;
5) .
Сделаем проверку, убедимся, что полученная матрица искомая:
А· А-1= = .
2. Метод Гаусса вычисления обратной матрицы.
1) припишем к матрице А единичную матрицу того же порядка:
.
С помощью элементарных преобразований приведем матрицу сначала к ступенчатому виду, добьемся того, чтобы слева оказалась единичная матрица Е, тогда справа окажется обратная матрица .
Пример. Итак,
Системы линейных уравнений
Рассмотрим систему m уравнений с n неизвестными
(1)
Матрица А, составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1):
Матрица называется расширенной матрицей.
Вектор называется вектором неизвестных, вектор называется вектором свободных членов.
Матричная запись системы (1) имеет вид:
Если вектор b=0, то система называется однородной, если b≠0 (хотя бы один из элементов отличен от нуля), то система называется неоднородной.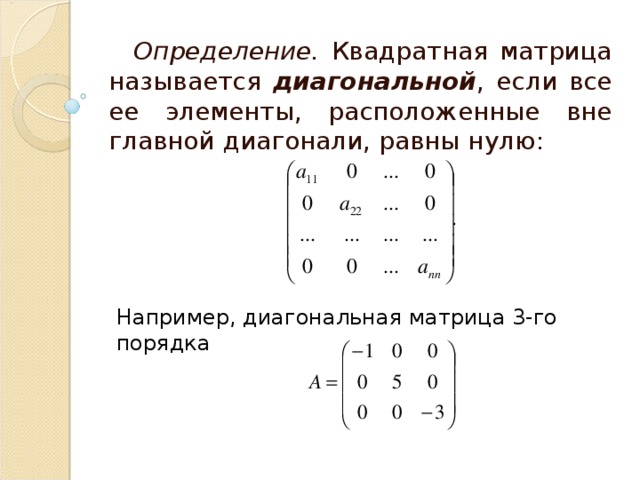
Решением системы (1) называется такой вектор X= , что при подстановке чисел в систему (1) получаются верные равенства (тождества).
Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.
Две системы называются эквивалентными, если множества их решений совпадают. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей
Однородные системы
Рассмотрим однородную систему .
Заметим, что однородная система всегда совместна, поскольку нуль-вектор Х= ее решение.
Для решения однородной системы уравнений применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе.
Проиллюстрируем алгоритм метода на примере:
Прямой ход метода Гаусса. Приведем матрицы системы к ступенчатому виду:
.
Матрица приведена к ступенчатому виду, ее ранг равен 3.
Выпишем соответствующую систему уравнений:
Переменные , не связанные с угловыми элементами, называются свободными, переменные — зависимые переменные (несвободные, базисные). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно n-r (r – ранг матрицы).
Обратный ход метода Гаусса заключается в том, что зависимые переменные выражаются через свободные из ступенчатой системы, начиная с последнего уравнения и «поднимаясь» вверх к первому. В результате получим
Полученное выражение называют общим решением системы в координатной форме.
Полученные выражения дают описание всего множества решений однородной системы. Давая свободным переменным произвольные значения, и вычисляя значения зависимых переменных, получаем некоторое частное решение системы.
Запишем общее решение в векторной форме. Придадим свободным переменным значения , получим и ; затем , получим и . Векторы линейно независимы и образуют фундаментальную систему решений (ФСР).
Общее решение системы, записанное в векторной форме, имеет вид:
Неоднородные системы
Пусть задана неоднородная система уравнений
Теорема Кронекера-Капелли (критерий совместности неоднородной системы). Система совместна тогда и только тогда, когда ранг основной матрицы А равен рангу расширенной матрицы : .
Методы решения систем линейных уравнений
1. Метод Гаусса
Рассмотрим на примере системы
Прямой ход метода Гаусса. Приведем расширенную матрицу системы к ступенчатому виду:
Здесь , система совместна.
Запишем эквивалентную ступенчатую систему:
Переменные являются зависимыми, а — свободной переменной.
Обратный ход метода Гаусса. Выразим зависимые переменные через свободные, получим:
.
Пример 2. Решить систему уравнений методом Гаусса
.
Составим расширенную матрицу и приведем ее к ступенчатому виду:
Запишем эквивалентную ступенчатую систему:
Таким образом, решением данной системы уравнений является вектор .
2. Метод решения системы уравнений с помощью обратной матрицы.
Найдем решение системы уравнений из примера 2 с помощью обратной матрицы. Прежде всего, определим обратную матрицу А-1 с помощью алгебраических дополнений.
det A=
Для каждого элемента определим алгебраические дополнения:
, , , , , , , , .
Тогда, А-1 = .
Решение системы уравнений имеет вид:
Х= .
Таким образом, решением данной системы уравнений является вектор .
3. Метод Крамера решения системы уравнений.
Рассмотрим неоднородную систему уравнений с невырожденной матрицей А (det A≠0):
Теорема Крамера. Система , где det A≠0, имеет единственное решение, которое вычисляется по формулам:
,
где Δ= det A, — получается из определителя Δ заменой i-го столбца на столбец свободных членов.
Пример. Найти решение системы уравнений методом Крамера
.
Решение.
Итак,
Раздел 2. Элементы аналитической геометрии
Сокращение ряда
Цели
- Научитесь заменять систему линейных уравнений расширенной матрицей.
- Узнайте, как метод исключения соответствует выполнению операций со строками над расширенной матрицей.
- Понять, когда матрица находится в (уменьшенной) эшелонированной форме строк.
- Узнайте, какие матрицы с уменьшенной строкой получены из несогласованных линейных систем.
- Рецепт: алгоритм сокращения строк.
- Словарный запас: операция строки , эквивалентность строки , матрица , расширенная матрица , опорная точка , (уменьшенная) эшелонированная форма строки .
В этом разделе мы представим алгоритм «решения» системы линейных уравнений.
Мы будем решать системы линейных уравнений алгебраически, используя метод исключения . Другими словами, мы будем комбинировать уравнения различными способами, чтобы попытаться исключить из каждого уравнения как можно больше переменных. Над нашей системой уравнений можно выполнить три допустимые операции: 9.0035
- Масштабирование: мы можем умножить обе части уравнения на ненулевое число.
Cx+2y+3z=62x-3y+2z=143x+y-z=-2multiply1stby-3———→C-3x-6y-9z=-182x-3y+2z=143x+ y-z=-2
- Замена: мы можем добавить кратное одного уравнения к другому, заменив второе уравнение результатом.
Cx+2y+3z=62x-3y+2z=143x+y-z=-22nd=2nd-2×1st———-→Cx+2y+3z=6-7y-4z= 23x+y−z=−2
- Обмен: мы можем поменять местами два уравнения.
Cx+2y+3z=62x−3y+2z=143x+y−z=−23rd ←→1st−−−−−−→C3x+y−z=−22x−3y+2z=14x+2y+3z= 6
Пример
Расширенные матрицы и операции со строками
Решение уравнений методом исключения требует записи переменных x, y, z и знака равенства = снова и снова, просто в качестве заполнителей: все, что меняется в уравнениях, — это коэффициент чисел . Мы можем облегчить себе жизнь, извлекая только числа и помещая их в рамку:
Мы можем облегчить себе жизнь, извлекая только числа и помещая их в рамку:
Это называется расширенной матрицей . Слово «расширенный» относится к вертикальной линии, которую мы рисуем, чтобы напомнить себе, где находится знак равенства; Матрица представляет собой сетку чисел без вертикальной линии. В этих обозначениях наши три действительных способа манипулирования нашими уравнениями становятся строковыми операциями :
.- Масштабирование: умножьте все записи в строке на ненулевое число. A12362-321431-1-2BR1=R1×-3——→A-3-6-9−182−321431−1−2B Здесь обозначение R1 просто означает «первый ряд», и то же самое для R2, R3 и т. д.
- Замена: добавить кратность одной строки к другой, заменив вторую строку на результат. A12362-321431-1-2BR2=R2-2×R1——-→A12360-7-4231-1-2B
- Поменять местами: поменять местами два ряда.
 A12362-321431-1-2BR1 ←→R3—-→A31-1-22-32141236B
A12362-321431-1-2BR1 ←→R3—-→A31-1-22-32141236B
Пример
Процесс выполнения надстрочных операций над матрицей не изменяет набор решений соответствующих линейных уравнений!
Действительно, весь смысл выполнения этих операций заключается в решении уравнений методом исключения.
Определение
Две матрицы называются строковыми эквивалентами , если одна может быть получена из другой путем выполнения некоторого количества операций над строками.
Итак, линейные уравнения матриц, эквивалентных строкам, имеют одинаковый набор решений .
Пример (несогласованная система)
В предыдущем подразделе мы увидели, как преобразовать систему линейных уравнений в расширенную матрицу. Мы хотим найти алгоритм для «решения» такой расширенной матрицы. Сначала мы должны решить, что означает «решение» расширенной матрицы.
Определение
Матрица находится в ступенчатой форме строки , если:
- Все нулевые строки находятся внизу.

- Первая ненулевая запись строки находится справа от первой ненулевой записи строки выше.
- Ниже первой ненулевой записи строки все записи равны нулю.
Вот изображение матрицы в виде эшелона строк:
DHHFAAAAA0AAAA000AA00000EIIGA=любое числоA=любое ненулевое числоОпределение
Опорная точка — это первая ненулевая запись строки матрицы в форме эшелона строк.
Матрица в виде эшелона строк обычно легко решается с помощью обратной подстановки. Например,
A12360124001030B становится—-→Cx+2y+3z=6y+2z=410z=30.Сразу видно, что z=3, откуда следует y=4−2·3=−2 и x=6−2(−2)−3·3=1. См. этот пример.
Определение
Матрица находится в сокращенная форма эшелона строки , если она находится в форме эшелона строки, и дополнительно:
- Каждый шарнир равен 1.
- Каждая сводная точка является единственной ненулевой записью в своем столбце.
Вот изображение матрицы в сокращенной ступенчатой форме строк:
DHF10A0A01A0A0001A00000EIGA=любое число1=центр
Матрица в сокращенной ступенчатой форме строк в некотором смысле полностью решена. Например,
Например,
Пример
При принятии решения о том, находится ли расширенная матрица в (уменьшенной) эшелонированной форме строки, нет ничего особенного в расширенном столбце (столбцах). Просто игнорируйте вертикальную линию.
Если расширенная матрица представлена в виде сокращенного эшелона строк, соответствующая линейная система рассматривается как решенная . Ниже мы увидим, почему это так, и покажем, что любую матрицу можно представить в виде редуцированного эшелона строк, используя только операции со строками.
Теорема
Каждая матрица эквивалентна по строкам одной и только одной матрице в сокращенной эшелонированной форме строк.
Мы дадим алгоритм, называемый сокращением строк или устранением Гаусса , который демонстрирует, что каждая матрица является строкой, эквивалентной по крайней мере одной матрице в сокращенной эшелонированной форме строк.
Заявление об уникальности интересно: оно означает, что независимо от того, как вы сокращаете строки, вы всегда получаете одну и ту же матрицу в сокращенной ступенчатой форме строк.
Это предполагает, конечно, что вы выполняете только три допустимые операции со строками и не делаете никаких арифметических ошибок.
Мы не будем доказывать уникальность, но, может быть, вы сможете!
Алгоритм (сокращение строк)
- Шаг 1a: Поменяйте местами 1-ю строку с более низкой, чтобы крайняя левая ненулевая запись находилась в 1-й строке (при необходимости).
- Шаг 1b: Масштабируйте 1-ю строку так, чтобы ее первая ненулевая запись была равна 1.
- Шаг 1c: Используйте замену строки, чтобы все записи ниже этой 1 были равны 0.
- Шаг 2a: Поменяйте местами 2-ю строку с более низкой так, чтобы крайняя левая ненулевая запись находилась во 2-й строке.

- Шаг 2b: Масштабируйте вторую строку так, чтобы ее первая ненулевая запись была равна 1.
- Шаг 2c: Используйте замену строки, чтобы все записи ниже этой 1 были равны 0.
- Шаг 3a: Поменяйте местами 3-ю строку с более низкой так, чтобы самая левая ненулевая запись находилась в 3-й строке.
- и т. д.
- Последний шаг: Используйте замену строк, чтобы очистить все записи над опорными точками, начиная с последней опорной точки.
Пример
Алгоритм сокращения строк показан на картинках.
AAAAAAAAAAAAAAAADHFEIG1AAAAAAAAAAAAAAADHFEIG1AAA01AA0AAA0AAADHFEIG1AAA01AA0AAA0AAADHFEIG1AAA01AA000A000ADHFEIG1AAA01AA000A000ADHFEIG1AAA01AA0001000ADHFEIG1AAA01AA00010000DHFEIG1AAA01AA00010000DHFEIG1AA001A000010000DHFEIG10A001A000010000DHFEIGGeta1hereCleardownGeta1hereCleardown(maybethesearealreadyzero)Geta1hereCleardownMatrixisinREFClearupClearupMatrixisinRREF Будет очень важно знать, где находятся опорные точки матрицы после сокращения строки; это причина для следующей части терминологии.
Определение
Опорная позиция матрицы — это запись, которая является опорной формой эшелонированной строки этой матрицы.
Опорный столбец матрицы — это столбец, который содержит опорную позицию.
Пример (основные позиции)
Пример (несогласованная система)
В приведенном выше примере мы увидели, как распознать сокращенную ступенчатую форму строки несогласованной системы.
Эшелонная форма строки непоследовательной системы
Расширенная матрица соответствует противоречивой системе уравнений тогда и только тогда, когда последний столбец (то есть расширенный столбец) является сводным столбцом .
Другими словами, сокращенная по строкам матрица несовместной системы выглядит так:
А10АА001АА000001БДо сих пор мы обсуждали два класса матриц:
- Если ступенчатая форма сокращенной строки матрицы имеет точку опоры в каждом нерасширенном столбце, то она соответствует системе с единственным решением:
A1001010-20013B преобразуется в——→Nx=1y=-2z=3.

- Если у сокращенной эшелонированной формы строки матрицы есть точка опоры в последнем (расширенном) столбце, то она соответствует системе без решений: K150001L преобразуется в——→Jx+5y=00=1.
Что произойдет, если в одном из нерасширенных столбцов отсутствует сводная точка? Это является предметом Раздела 1.3.
Пример (система с множеством решений)
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
линейная алгебра — Row Reduce Augmented Matrix
Спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 403 раза
$\begingroup$
У меня проблемы с сокращением строки.
Сначала я получаю расширенную матрицу:
\begin{pmatrix}\begin{array}{cccc|c} 0 и 1 и -2 и 1 и 2\\ 2 и -2 и 4 и -1 и 10\\ 1 и -1 и 1 и 0 и 2\\ 1 и 0 и 1 и 0 и 9\end{array}\end{pmatrix}
Но я не уверен, как на самом деле использовать элементарные операции для решения этой проблемы. Это практическая задача в моем учебнике, и я хочу знать, как это сделать, потому что у меня впереди тест. Я надеюсь, что кто-то может помочь мне здесь, очень признателен за любую помощь.
Это практическая задача в моем учебнике, и я хочу знать, как это сделать, потому что у меня впереди тест. Я надеюсь, что кто-то может помочь мне здесь, очень признателен за любую помощь.
Всем спасибо, нужна помощь.
- линейная алгебра
- матрицы
$\endgroup$
$\begingroup$
Напомним, что мы можем использовать только три типа операций со строками:
- Поменять местами две строки;
- Умножить строку на ненулевую константу; и
- Добавить кратность одной строки к другой строке.
При соблюдении этих операций сохраняется множество решений системы линейных уравнений.
Вот мой выбор операций со строками в этом экземпляре. Точный выбор того, какую операцию со строкой применить, часто является личным предпочтением (и частично основанным на опыте того, что работает).
\begin{выравнивание*}
& \left[\begin{array}{cccc|c} 0 & 1 & -2 & 1 & 2 \\ 2 & -2 & 4 & -1 & 10 \\ 1 & -1 & 1 &
0 и 2 \\ 1 и 0 и 1 и 0 и 9\\ \конец{массив}\справа] \\
\xrightarrow{R_1 \leftrightarrow R_3} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 2 & -2 & 4 & -1 & 10 \\ 0 & 1 &-2 &
1 & 2 \\ 1 & 0 & 1 & 0 & 9 \\ \end{массив}\right] \\
\xrightarrow{R_2 \gets R_2-2R_1} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 0 & 0 & 2 & -1 & 6 \\ 0 & 1 и -2 и
1 & 2 \\ 1 & 0 & 1 & 0 & 9 \\ \end{массив}\right] \\
\xrightarrow{R_4 \gets R_4-R_1} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 0 & 0 & 2 & -1 & 6 \\ 0 & 1 и -2 и
1 & 2 \\ 0 & 1 & 0 & 0 & 7 \\ \end{массив}\right] \\
\xrightarrow{R_2 \leftrightarrow R_4} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 0 & 1 & 0 & 0 & 7 \\ 0 & 1 & — 2 и 1 и
2 \\ 0 & 0 & 2 & -1 & 6 \\ \end{массив}\right] \\
\xrightarrow{R_3 \gets R_3-R_2} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 0 & 1 & 0 & 0 & 7 \\ 0 & 0 &-2 & 1 &
-5 \\ 0 & 0 & 2 & -1 & 6 \\ \end{массив}\right] \\
\xrightarrow{R_4 \gets R_4+R_3} & \left[\begin{array}{cccc|c} 1 & -1 & 1 & 0 & 2 \\ 0 & 1 & 0 & 0 & 7 \\ 0 & 0 &-2 & 1 &
-5 \\ 0 & 0 & 0 & 0 & 1 \\ \end{массив}\right]
\конец{выравнивание*}
который находится в форме эшелона строки. Если решение существует, то в последней строке будет $0=1$, что является противоречием. Следовательно, система несовместна (т. е. решения не существует).
Если решение существует, то в последней строке будет $0=1$, что является противоречием. Следовательно, система несовместна (т. е. решения не существует).
$\endgroup$
4
$\begingroup$
0 1 -2 1 | 2
2 -2 4 -1 | 10
0 1 0 0 | 7
1 0 1 0 | 9
0 0 2 -1 | 5
2 0 4 -1 | 24
0 1 0 0 | 7
1 0 1 0 | 9
0 0 2 -1 | 5
0 0 2 -1 | 6
0 1 0 0 | 7
1 0 1 0 | 9
Следовательно, непоследовательно. Вы также можете продолжить весь путь до уменьшенной эшелонированной формы и получить что-то вроде 0+0+0+0 = a, что не может быть правдой.
Добавлено:
Еще один шаг
0 0 0 0 | 1
0 0 2 -1 | 6
0 1 0 0 | 7
1 0 1 0 | 9
Обратите внимание, что 0+0+0+0 не может равняться 1. Если вы получаете что-то подобное, система несовместима.
$\endgroup$
4
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
4.5 Решение систем уравнений с помощью матриц — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Написать расширенную матрицу для системы уравнений
- Использовать операции со строками на матрице
- Решение систем уравнений с использованием матриц
Приготовься 4.13
Прежде чем приступить к работе, пройдите этот тест на готовность.
Решите: 3(x+2)+4=4(2x−1)+9,3(x+2)+4=4(2x−1)+9.
Если вы пропустили эту проблему, просмотрите пример 2.2.
Приготовься 4.14
Решите: 0,25p+0,25(p+4)=5,20.0,25p+0,25(p+4)=5,20.
Если вы пропустили эту проблему, просмотрите пример 2.13.
Приготовься 4.15
Вычислить, когда x=−2x=−2 и y=3:2×2−xy+3y2.y=3:2×2−xy+3y2.
Если вы пропустили эту проблему, просмотрите пример 1.21.
Напишите расширенную матрицу для системы уравнений
Решение системы уравнений может быть утомительной операцией, где простая ошибка может нанести ущерб поиску решения. Доступен альтернативный метод, использующий основные процедуры исключения, но с более простыми обозначениями. Метод предполагает использование матрицы. Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.
Доступен альтернативный метод, использующий основные процедуры исключения, но с более простыми обозначениями. Метод предполагает использование матрицы. Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.
Матрица
Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.
Матрица с m строк и n столбцов имеет порядок m×n.m×n. Матрица слева внизу имеет 2 строки и 3 столбца, поэтому она имеет порядок 2×3,2×3. Мы говорим, что это матрица 2 на 3.
Каждое число в матрице называется элементом или записью в матрице.
Мы будем использовать матрицу для представления системы линейных уравнений. Мы записываем каждое уравнение в стандартной форме, а коэффициенты переменных и константы каждого уравнения становятся строкой в матрице. Тогда каждый столбец будет коэффициентом одной из переменных в системе или констант. Вертикальная черта заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.
Вертикальная черта заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.
Обратите внимание, что первый столбец состоит из всех коэффициентов x , второй столбец содержит все коэффициенты y , а третий столбец содержит все константы.
Пример 4,37
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐ {5x−3y=−1y=2x−2{5x−3y=−1y=2x−2 ⓑ {6x−5y+2z=32x+y− 4z=53x−3y+z=−1{6x−5y+2z=32x+y−4z=53x−3y+z=−1
Решение
ⓐ Второе уравнение не в стандартной форме. Перепишем второе уравнение в стандартной форме.
y=2x−2−2x+y=−2y=2x−2−2x+y=−2
Заменим второе уравнение его стандартной формой. В расширенной матрице первое уравнение дает нам первую строку, а второе уравнение дает нам вторую строку. Вертикальная черта заменяет знаки равенства.
ⓑ Все три уравнения в стандартной форме. В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная черта заменяет знаки равенства.
В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная черта заменяет знаки равенства.
Попытайся 4,73
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐ {3x+8y=−32x=−5y−3{3x+8y=−32x=−5y−3 ⓑ {2x−5y+3z=83x− y+4z=7x+3y+2z=-3{2x-5y+3z=83x-y+4z=7x+3y+2z=-3
Попытайся 4,74
Запишите каждую систему линейных уравнений в виде расширенной матрицы:
ⓐ {11x=−9y−57x+5y=−1{11x=−9y−57x+5y=−1 ⓑ {5x−3y+2z=−52x −y−z=43x−2y+2z=−7{5x−3y+2z=−52x−y−z=43x−2y+2z=−7
При решении систем уравнений с использованием матриц важно иметь возможность переключаться между системой и матрицей. В следующем примере нас просят взять информацию из матрицы и написать систему уравнений.
Пример 4,38
Запишите систему уравнений, соответствующую расширенной матрице:
[4−3312−1−2−13|−12−4]. [4−3312−1−2−13|−12−4].
[4−3312−1−2−13|−12−4].
Решение
Мы помним, что каждая строка соответствует уравнению и что каждая запись является коэффициентом переменной или константой. Вертикальная черта заменяет знак равенства. Поскольку эта матрица имеет размер 4×34×3, мы знаем, что она преобразуется в систему из трех уравнений с тремя переменными.
Попытайся 4,75
Напишите систему уравнений, соответствующую расширенной матрице: [1−12321−214−120].[1−12321−214−120].
Попытайся 4,76
Напишите систему уравнений, соответствующую расширенной матрице: [111423−1811−13].[111423−1811−13].
Использование операций со строками в матрице
После того, как система уравнений будет представлена в расширенной матричной форме, мы будем выполнять операции над строками, которые приведут нас к решению.
Чтобы решить методом исключения, не имеет значения, в каком порядке мы расположим уравнения в системе. Точно так же в матрице мы можем поменять местами строки.
Точно так же в матрице мы можем поменять местами строки.
Когда мы решаем методом исключения, мы часто умножаем одно из уравнений на константу. Поскольку каждая строка представляет собой уравнение, и мы можем умножать каждую часть уравнения на константу, аналогичным образом мы можем умножать каждую запись в строке на любое действительное число, кроме 0.
.При исключении мы часто добавляем кратное число одной строки к другой строке. В матрице мы можем заменить строку на ее сумму, кратную другой строке.
Эти действия называются операциями со строками и помогут нам использовать матрицу для решения системы уравнений.
Операции со строками
В матрице следующие операции могут выполняться над любой строкой, и результирующая матрица будет эквивалентна исходной матрице.
- Поменяйте местами любые два ряда.
- Умножить строку на любое действительное число, кроме 0.
- Добавить ненулевое кратное одной строки к другой строке.

Выполнить эти операции несложно, но все арифметические действия могут привести к ошибке. Если мы используем систему для записи операций со строками на каждом этапе, гораздо проще вернуться и проверить нашу работу.
Мы используем заглавные буквы с нижними индексами для представления каждой строки. Затем мы показываем операцию слева от новой матрицы. Чтобы показать перестановку строк:
Чтобы умножить строку 2 на −3−3:
Чтобы умножить строку 2 на −3−3 и прибавить к строке 1:
Пример 4,39
Выполнить указанные операции над расширенной матрицей:
ⓐ Поменять местами строки 2 и 3.
ⓑ Умножить строку 2 на 5.
ⓒ Умножить строку 3 на -2-2 и прибавить к строке 1.
[6-5221-43-31|35-1][6-5221-43-31|35-1]
Решение
ⓐ Поменяем местами строки 2 и 3.
ⓑ Умножим строку 2 на 5.
ⓒ Умножим строку 3 на −2−2 и прибавим к строке 1.
Попытайся 4,77
Выполнить последовательно указанные операции над расширенной матрицей:
ⓐ Поменять местами строки 1 и 3.
ⓑ Умножить строку 3 на 3.
ⓒ Умножить строку 3 на 2 и прибавить к строке 2.
[5-2-24-1-4-230|-24-1][5-2-24-1-4-230|-24-1]
Попытайся 4,78
Выполнить указанные операции над расширенной матрицей:
ⓐ Поменять местами строки 1 и 2,
ⓑ Умножить строку 1 на 2,
ⓒ Умножить строку 2 на 3 и прибавить к строке 1.
[2−3− 241−3504|−42−1][2−3−241−3504|−42−1]
Теперь, когда мы попрактиковались в операциях со строками, мы рассмотрим расширенную матрицу и выясним, какую операцию мы будем использовать для достижения цели. Это именно то, что мы сделали, когда мы сделали исключение. Мы решили, на какое число умножить строку, чтобы при сложении строк исключалась переменная.
Учитывая эту систему, что бы вы сделали, чтобы исключить x ?
Следующий пример делает то же самое, но с матрицей.
Пример 4.40
Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: [1−14−8|20].[1−14−8|20].
Решение
Чтобы число 4 стало равным 0, мы могли бы умножить строку 1 на -4−4, а затем прибавить ее к строке 2.
Попытайся 4,79
Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: [1−13−6|22].[1−13−6|22].
Попытайся 4,80
Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: [1−1−2−3|32].[1−1−2−3|32].
Решение систем уравнений с использованием матриц
Чтобы решить систему уравнений с использованием матриц, мы преобразуем расширенную матрицу в матрицу в ступенчато-строковой форме, используя операции со строками. Для непротиворечивой и независимой системы уравнений ее расширенная матрица имеет форму эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.
Рядно-Эшелонная Форма
Для непротиворечивой и независимой системы уравнений ее расширенная матрица имеет вид строк-ступенчатой формы , когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нулями.
Как только мы приведем расширенную матрицу к ступенчатой форме, мы сможем написать эквивалентную систему уравнений и прочитать значение хотя бы одной переменной. Затем мы подставляем это значение в другое уравнение, чтобы продолжить решение для других переменных. Этот процесс проиллюстрирован в следующем примере.
Пример 4.41
Как решить систему уравнений с помощью матрицы
Решить систему уравнений с помощью матрицы: {3x+4y=5x+2y=1.{3x+4y=5x+2y=1.
Решение
Попытайся 4,81
Решите систему уравнений, используя матрицу: {2x+y=7x−2y=6.{2x+y=7x−2y=6.
Попытайся 4,82
Решите систему уравнений, используя матрицу: {2x+y=−4x−y=−2. {2x+y=−4x−y=−2.
{2x+y=−4x−y=−2.
Здесь перечислены шаги.
Как
Решите систему уравнений с помощью матриц.
- Шаг 1. Запишите расширенную матрицу для системы уравнений.
- Шаг 2. Используя операции со строками, запись в строке 1 столбца 1 будет равна 1.
- Шаг 3. Используя операции со строками, получите нули в столбце 1 ниже 1.
- Шаг 4. Используя операции со строками, сделайте запись в строке 2 столбца 2 равной 1.
- Шаг 5. Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона.
- Шаг 6. Напишите соответствующую систему уравнений.
- Шаг 7. Используйте подстановку, чтобы найти оставшиеся переменные.
- Шаг 8. Запишите решение в виде упорядоченной пары или тройки.
- Шаг 9. Убедитесь, что решение делает исходные уравнения верными.
Вот изображение, показывающее порядок расположения единиц и нулей в правильных позициях для эшелонированной формы.
Мы используем ту же процедуру, когда система уравнений состоит из трех уравнений.
Пример 4,42
Решите систему уравнений, используя матрицу: {3x+8y+2z=-52x+5y-3z=0x+2y-2z=-1.{3x+8y+2z=-52x+5y-3z=0x+ 2y−2z=−1.
Решение
| Напишите расширенную матрицу для уравнений. | |
| Поменяйте местами строки 1 и 3, чтобы получить запись в строке 1 , столбец 1 будет равен 1. | |
| Используя операции со строками, получить нули в столбце 1 под 1. | |
Запись в строке 2 столбца 2 теперь равна 1. | |
| Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона. | |
| Матрица теперь имеет форму строки-эшелона. | |
| Напишите соответствующую систему уравнений. | |
| Используйте подстановку, чтобы найти остальные переменные. | |
| | |
Запишите решение в виде упорядоченной пары или тройки. | |
| Убедитесь, что решение соответствует исходным уравнениям. | Мы оставляем вам чек. |
Попытайся 4,83
Решите систему уравнений, используя матрицу: {2x−5y+3z=83x−y+4z=7x+3y+2z=−3.{2x−5y+3z=83x−y+4z=7x+3y+ 2z=−3.
Попытайся 4,84
Решите систему уравнений, используя матрицу: {−3x+y+z=−4−x+2y−2z=12x−y−z=−1.{−3x+y+z=−4−x+ 2y−2z=12x−y−z=−1.
До сих пор мы работали с матрицами только с непротиворечивыми и независимыми системами, что означает, что они имеют ровно одно решение. Давайте теперь посмотрим, что происходит, когда мы используем матрицу для зависимой или противоречивой системы.
Пример 4,43
Решите систему уравнений, используя матрицу: {x+y+3z=0x+3y+5z=02x+4z=1.{x+y+3z=0x+3y+5z=02x+4z=1.
Решение
Напишите расширенную матрицу для уравнений. | |
| Запись в строке 1 столбца 1 равна 1. | |
| Используя операции со строками, получить нули в столбце 1 под 1. | |
| Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона. | |
| Умножить строку 2 на 2 и добавить к строке 3. | |
На данный момент у нас есть все нули слева от строки 3.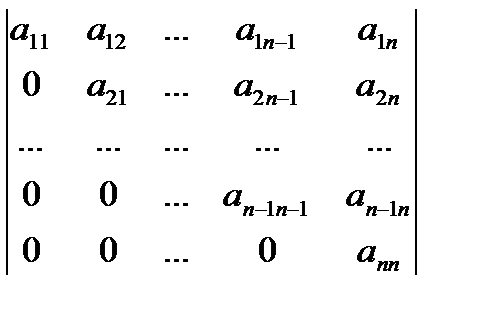 | |
| Запишите соответствующую систему уравнений. | |
| Так как 0≠10≠1 мы имеем ложное утверждение. Точно так же, как когда мы решали систему, используя другие методы, это говорит нам о несогласованности системы. Нет решения. | |
Попытайся 4,85
Решите систему уравнений с помощью матрицы: {x−2y+2z=1−2x+y−z=2x−y+z=5.{x−2y+2z=1−2x+y−z=2x −y+z=5.
Попытайся 4,86
Решите систему уравнений, используя матрицу: {3x+4y-3z=-22x+3y-z=-12x+y-2z=6.{3x+4y-3z=-22x+3y-z=-12x +y−2z=6.
Последняя система была несовместимой и поэтому не имела решений. Следующий пример является зависимым и имеет бесконечно много решений.
Пример 4,44
Решите систему уравнений с помощью матрицы: {x−2y+3z=1x+y−3z=73x−4y+5z=7. {x−2y+3z=1x+y−3z=73x−4y+5z =7.
{x−2y+3z=1x+y−3z=73x−4y+5z =7.
Решение
| Напишите расширенную матрицу для уравнений. | |
| Запись в строке 1 столбца 1 равна 1. | |
| Используя операции со строками, получить нули в столбце 1 под 1. | |
Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона. | |
| Умножить строку 2 на -2−2 и добавить к строке 3. | |
| На данный момент у нас есть все нули в нижней строке. | |
| Запишите соответствующую систему уравнений. | |
| Поскольку 0=00=0, мы имеем верное утверждение. Так же, как когда мы решали подстановкой, это говорит нам о том, что у нас есть зависимая система. Существует бесконечно много решений. | |
Решите для y через z во втором уравнении. | |
| Решите первое уравнение для x через z . | |
| Замените y=2z+2.y=2z+2. | |
| Упрощение. | |
| Упрощение. | |
| Упрощение. | |
| Система имеет бесконечно много решений (85,-425,-245)(85,-425,-245) | |
Попытайся 4,87
Решите систему уравнений, используя матрицу: {x+y-z=02x+4y-2z=63x+6y-3z=9. {x+y-z=02x+4y-2z=63x+6y-3z =9.
{x+y-z=02x+4y-2z=63x+6y-3z =9.
Попытайся 4,88
Решите систему уравнений, используя матрицу: {x−y−z=1−x+2y−3z=−43x−2y−7z=0.{x−y−z=1−x+2y−3z= −43x−2y−7z=0.
СМИ
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики с методом исключения Гаусса.
- Исключение Гаусса
Раздел 4.5 Упражнения
Практика ведет к совершенству
Запись расширенной матрицы для системы уравнений
В следующих упражнениях запишите каждую систему линейных уравнений в виде расширенной матрицы.
196.
ⓐ {3x−y=−12y=2x+5{3x−y=−12y=2x+5
ⓑ {4x+3y=−2x−2y−3z=72x−y+2z=−6{4x +3y=-2x-2y-3z=72x-y+2z=-6
197.
ⓐ {2x+4y=−53x−2y=2{2x+4y=−53x−2y=2
ⓑ {3x−2y−z=−2−2x+y=55x+4y+z=−1 {3x−2y−z=−2−2x+y=55x+4y+z=−1
198.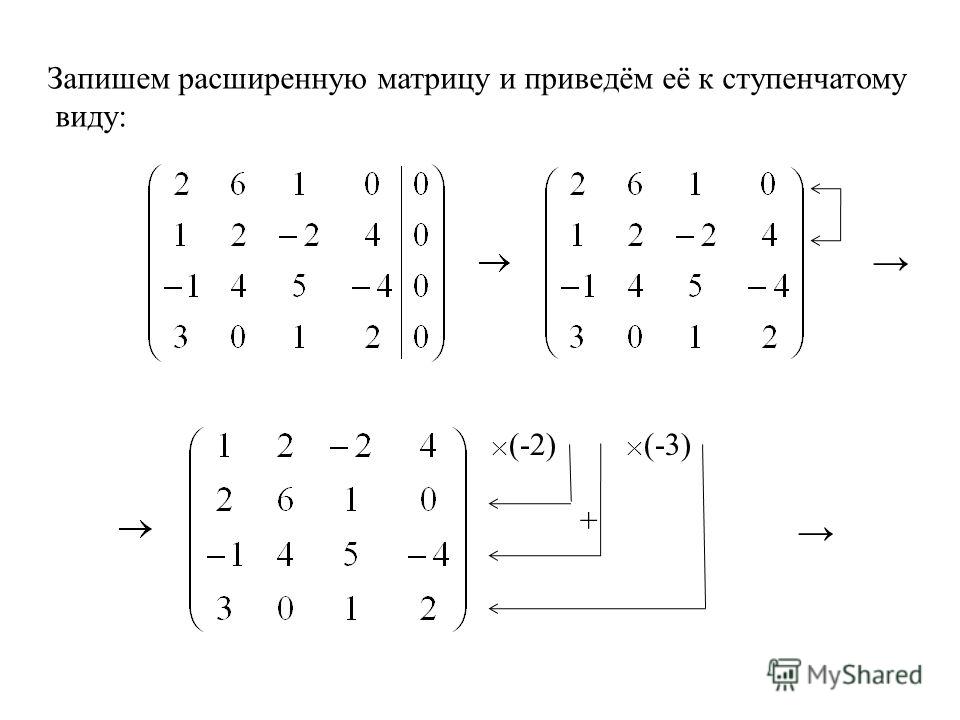
ⓐ {3x−y=−42x=y+2{3x−y=−42x=y+2
ⓑ {x−3y−4z=−24x+2y+2z=52x−5y+7z=−8 {x−3y−4z=−24x+2y+2z=52x−5y+7z=−8
199.
ⓐ {2x−5y=−34x=3y−1{2x−5y=−34x=3y−1
ⓑ {4x+3y−2z=−3−2x+y−3z=4−x−4y+ 5z=-2{4x+3y-2z=-3-2x+y-3z=4-x-4y+5z=-2
Напишите систему уравнений, соответствующую расширенной матрице.
200.
[2−11−3|42][2−11−3|42]
201.
[2−43−3|−2−1][2−43−3|−2−1]
202.
[10-31-200-12|-1-23][10-31-200-12|-1-23]
203.
[2-2002-130-1|-12-2][2-2002-130-1|-12-2]
Использование операций со строками в матрице
В следующих упражнениях выполните указанные операции над расширенными матрицами.
204.
[6−43−2|31][6−43−2|31]
ⓐ Поменять местами строки 1 и 2
ⓑ Умножить строку 2 на 3
ⓒ Умножить строку 2 на −2−2 и добавить строку 1 к Это.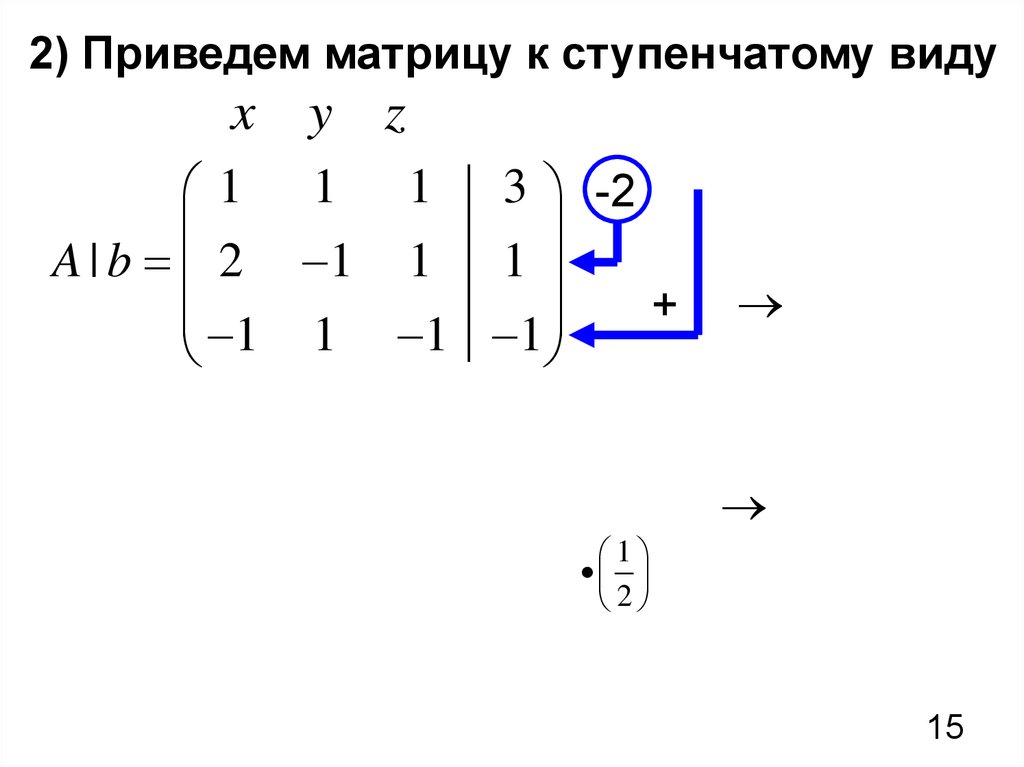
205.
[4−632|−31][4−632|−31]
ⓐ Поменять местами строки 1 и 2
ⓑ Умножить строку 1 на 4
ⓒ Умножить строку 2 на 3 и добавить к ней строку 1.
206.
[4-12-84-2-3-62-1|16-1-1][4-12-84-2-3-62-1|16-1-1]
ⓐ Поменять местами ряды 2 и 3
ⓑ Умножить строку 1 на 4
ⓒ Умножить строку 2 на −2−2 и прибавить к строке 3.
207.
[6-5221-43-31|35-1][6-5221-43-31|35-1]
ⓐ Поменять местами ряды 2 и 3
ⓑ Умножить строку 2 на 5
ⓒ Умножить строку 3 на −2−2 и прибавить к строке 1.
208.
Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице: [12−3−4|5−1].[12−3−4|5−1].
209.
Выполните необходимые операции со строками, чтобы первая запись в строке 2 и строке 3 была равна нулю в расширенной матрице: [1-233-1-22-3-4|-45-1]. [1- 233−1−22−3−4|−45−1].
[1- 233−1−22−3−4|−45−1].
Решение систем уравнений с помощью матриц
В следующих упражнениях решите каждую систему уравнений, используя матрицу.
210.
{2x+y=2x-y=-2{2x+y=2x-y=-2
211.
{3x+y=2x-y=2{3x+y=2x-y=2
212.
{−x+2y=−2x+y=−4{−x+2y=−2x+y=−4
213.
{−2x+3y=3x+3y=12{−2x+3y=3x+3y=12
В следующих упражнениях решите каждую систему уравнений, используя матрицу.
214.
{2x−3y+z=19−3x+y−2z=−15x+y+z=0{2x−3y+z=19−3x+y−2z=−15x+y+z=0
215.
{2x−y+3z=−3−x+2y−z=10x+y+z=5{2x−y+3z=−3−x+2y−z=10x+y+z=5
216.
{2x-6y+z=33x+2y-3z=22x+3y-2z=3{2x-6y+z=33x+2y-3z=22x+3y-2z=3
217.
{4x−3y+z=72x−5y−4z=33x−2y−2z=−7{4x−3y+z=72x−5y−4z=33x−2y−2z=−7
218.
{x+2z=04y+3z=-22x-5y=3{x+2z=04y+3z=-22x-5y=3
219.
{2x+5y=43y−z=34x+3z=−3{2x+5y=43y−z=34x+3z=−3
220.
{2y+3z=-15x+3y=-67x+z=1{2y+3z=-15x+3y=-67x+z=1
221.
{3x−z=−35y+2z=−64x+3y=−8{3x−z=−35y+2z=−64x+3y=−8
222.
{2x+3y+z=12x+y+z=93x+4y+2z=20{2x+3y+z=12x+y+z=93x+4y+2z=20
223.
{x+2y+6z=5-x+y-2z=3x-4y-2z=1{x+2y+6z=5-x+y-2z=3x-4y-2z=1
224.
{x+2y-3z=-1x-3y+z=12x-y-2z=2{x+2y-3z=-1x-3y+z=12x-y-2z=2
225.
{4x-3y+2z=0-2x+3y-7z=12x-2y+3z=6{4x-3y+2z=0-2x+3y-7z=12x-2y+3z=6
226.
{x-y+2z=-42x+y+3z=2-3x+3y-6z=12{x-y+2z=-42x+y+3z=2-3x+3y-6z=12
227.
{−x−3y+2z=14−x+2y−3z=−43x+y−2z=6{−x−3y+2z=14−x+2y−3z=−43x+y−2z=6
228.
{x+y-3z=-1y-z=0-x+2y=1{x+y-3z=-1y-z=0-x+2y=1
229.
{x+2y+z=4x+y-2z=3-2x-3y+z=-7{x+2y+z=4x+y-2z=3-2x-3y+z=-7
Письменные упражнения
230.
Решите систему уравнений {x+y=10x−y=6{x+y=10x−y=6 ⓐ по графику и ⓑ подстановкой. ⓒ Какой способ предпочитаете? Почему?
231.
Решите систему уравнений {3x+y=12x=y−8{3x+y=12x=y−8 подстановкой и объясните все свои шаги словами.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ После просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?
Augmented Matrices — College Algebra
Все ресурсы по алгебре для колледжей
5 Диагностические тесты 84 практических теста Вопрос дня Карточки Learn by Concept
Справка по алгебре колледжа » Системы уравнений » Расширенные матрицы
Решите следующую расширенную матрицу.
Возможные ответы:
Правильный ответ:
Объяснение:
Первый шаг – умножить строку 1 на , вычесть строку 2 и поместить результат в строку 2.
Теперь у нас есть два уравнения.
, и
Сначала найдите y, а затем подставьте результат в другое уравнение.
. ряд сокращают эшелоном, затем читают решение.
Обратите внимание, что перестановка строк в матрице не меняет решения, поэтому проверьте наличие переставленных строк, если вы не видите свою расширенную матрицу среди расширенных множественных вариантов.
Possible Answers:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Строка Сокращенная Эшелонированная Форма
Решения:
Расширенной Матрицы
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Решения:
Правильный ответ:
Расширенная матрица системы
Строка Уменьшенный Эшелон Форма
Решения:
Объяснение:
1) Перепишите оба уравнения, чтобы привести их в порядок и убедиться, что все постоянные члены изолированы на одной стороне уравнения. Это облегчит запись расширенной матрицы.
Это облегчит запись расширенной матрицы.
2) Запишите расширенную матрицу, соответствующую системе.
. вектор представляет то, что осталось от всех операций со строками, выполненных для уменьшения матрицы коэффициентов до единичной матрицы. Это будет решение для и .
3) Теперь мы можем выполнить ряд операций со строками, чтобы привести их к желаемой форме,
Мы можем начать с сокращения во второй строке, вычитая первую строку из второй строки, чтобы получить:
Теперь нам нужно , чтобы занять место в верхней строке, поэтому разделите строку 1 на :
Теперь нам нужно , чтобы занять место во второй строке, поэтому разделите вторую строку по ,
Теперь нам нужно заменить оставшиеся в первой строке. Вычтите 2-кратный второй ряд с первой строки,
4) Напишите набор решения:
44. ship
ship
4. и з.
Возможные ответы:
Правильный ответ:
Объяснение:
Из расширенной матрицы мы видим, что
Теперь выполните операции со строками, чтобы найти x и y.
1. Поменяйте местами ряд 1 и ряд 2:
2. Умножьте ряд 1 на 2 и добавьте его к ряду 2:
3. Умножьте ряд 3 на 13 и умножьте ряд 2 на -1. Добавьте две строки для новой строки 2:
4. Умножьте строку 3 на -5 и добавьте ее к строке 1. Умножьте строку 2 на -2 и добавьте ее к строке 1:
Сообщите об ошибке
Предположим, вы пытаетесь решить систему из двух линейных уравнений с двумя переменными, используя метод исключения Гаусса-Жордана на расширенной матрице. После операции строки появляется матрица
Сколько решений имеет система?
Возможные ответы:
Бесконечно много
Нет
Один
Правильный ответ:
Бесконечно много
Объяснение:
Если в процессе исключения Гаусса-Жордана какая-либо строка становится полностью нулевой строкой, она перестает быть фактором, определяющим набор решений. Мы должны исследовать только верхнюю строку матрицы.
Мы должны исследовать только верхнюю строку матрицы.
Помните, что каждая запись слева от делителя представляет собой коэффициент, а каждая запись справа представляет собой константу. Таким образом, верхняя строка в матрице
представляет собой уравнение
,
или, что то же самое,
. Следовательно, существует бесконечно много решений этого уравнения.
Сообщить об ошибке
Предположим, вы пытаетесь решить систему из двух линейных уравнений с двумя переменными, используя метод исключения Гаусса-Жордана на расширенной матрице. После операции строки появляется матрица
Сколько решений имеет система?
Возможные ответы:
Один
Нет
Бесконечно много
Правильный ответ:
Один
Объяснение:
При применении метода Гаусса-Жордана для решения линейной системы два на два цель состоит в том, чтобы использовать операции со строками для формирования расширенной матрицы вида
.
Если это произойдет, то существует одно и только одно решение системы, представленное упорядоченной парой . Дана расширенная матрица,
находится в этой форме, и есть одно решение .
Сообщить об ошибке
Предположим, вы пытаетесь решить систему из трех линейных уравнений с тремя переменными, используя метод исключения Гаусса-Жордана на расширенной матрице. После операции со строками появляется матрица
Сколько решений имеет система?
Возможные ответы:
Один
Нет
Бесконечно много
Правильный ответ:
Нет
Объяснение:
Красным флажком в этой расширенной матрице является нижняя строка, в которой все элементы равны нулю слева от делителя и ненулевые элементы справа. Каждый раз, когда это происходит в процессе исключения Гаусса-Жордана, это сигнализирует о том, что система уравнений не имеет решения.
Сообщить об ошибке
Предположим, вы пытаетесь решить систему из трех линейных уравнений с тремя переменными, используя метод исключения Гаусса-Жордана на расширенной матрице. После операции строки появляется матрица
Сколько решений имеет система?
Возможные ответы:
Нет
Бесконечно много
Один
Правильный ответ:
Бесконечно много
Объяснение:
Если в процессе исключения Гаусса-Жордана какая-либо строка становится полностью нулевой строкой, она перестает быть фактором, определяющим набор решений. Мы должны исследовать другие строки матрицы.
Помните, что каждая запись слева от делителя представляет собой коэффициент, а каждая запись справа представляет собой константу. Следовательно, две ненулевые строки в матрице
представляют уравнения
и
,
соответственно.
Уравнения решаются относительно и относительно:
и
Следовательно, и может принимать любое действительное значение, при этом зависит от ; это зависимая система с бесконечным числом решений.
Сообщить об ошибке
При решении системы трех линейных уравнений с тремя переменными методом исключения Гаусса-Жордана исходная расширенная матрица имеет следующий вид: выполнять?
Возможные ответы:
Правильный ответ:
Объяснение:
При применении метода Гаусса-Жордана для решения линейной системы три на три цель состоит в том, чтобы использовать операции со строками для формирования расширенной матрицы формы
,
с решением системы.
После настройки исходной расширенной матрицы
первым шагом всегда должно быть получение 1 в верхней левой позиции; обычно это делается путем умножения каждого элемента в строке 1 на обратную величину первого элемента в этой строке. Поскольку элемент в этой позиции равен , каждый элемент в строке 1 умножается на обратную величину . Этот шаг можно записать с использованием обозначения .
Поскольку элемент в этой позиции равен , каждый элемент в строке 1 умножается на обратную величину . Этот шаг можно записать с использованием обозначения .
Сообщить об ошибке
Используйте расширенные матрицы для решения следующей системы уравнений:
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с построения дополненной матрицы для нашей системы уравнений:
Строки Переключателя 1 и 2:
Добавить строку 2 и дважды. Разделить ряд 1 на 5:
Проблема 3 раза ряд 1, из строки 2:
Разделите ряд 2 на 2:
Решение:
ПЛАЗАЦИИ. проверьте решение:
Сообщите об ошибке
Используйте расширенные матрицы для решения следующей системы уравнений:
Возможные ответы:0465Правильный ответ:
Explanation:
Construct an augmented matrix for our system of equations:
Swap rows 1 and 3:
Subtract 2 times row 1 from row 2:
Subtract row 1 from row 3:
Добавить строку 2 и трижды строку 3, к строке 3:
Разделить строку 3 на 10:
Добавить строку 3 в строку 1:
Вычетная строка 3 из строки 2:
Разделите строку 2 на 3:
Решение:
. , и z во все уравнения для проверки решения:
, и z во все уравнения для проверки решения:
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по алгебре для колледжей
5 диагностических тестов 84 практических теста Вопрос дня Карточки Учитесь по концепции
Операции со строками и расширенные матрицы
Результаты обучения
- Напишите расширенную матрицу для системы уравнений.
- Выполнение операций со строками над расширенной матрицей.
Матрица может служить средством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства. Когда система записывается в такой форме, мы называем ее дополненная матрица .
Например, рассмотрим следующую систему уравнений [латекс]2\умножить на 2[/латекс].
[латекс]\begin{array}{l}3x+4y=7\\ 4x — 2y=5\end{array}[/latex]
Мы можем записать эту систему в виде расширенной матрицы:
[латекс ]\left[\begin{array}{rr}\hfill 3& \hfill 4\\ \hfill 4& \hfill -2\end{array}\text{ }|\text{ }\begin{array}{r}\ hfill 7\\ \hfill 5\end{array}\right][/latex]
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрица коэффициентов .
[латекс]\влево[\начало{массив}{cc}3& 4\\ 4& -2\конец{массив}\право][/латекс]
Система уравнений три на три , например
[латекс]\begin{array}{l}3x-y-z=0\hfill \\ \text{ }x+y=5\hfill \\ \text{ }2x — 3z=2\hfill \end{array }[/latex]
имеет матрицу коэффициентов
[latex]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\ \\hfill 2& \hfill 0& \hfill -3\end{массив}\right][/latex]
и представлен расширенной матрицей
[латекс]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\\ \ hfill 2& \hfill 0& \hfill -3\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 0\\ \hfill 5\\ \hfill 2\end{массив}\ right][/latex]
Обратите внимание, что матрица написана таким образом, что переменные располагаются в своих столбцах: x — термины идут в первом столбце, y — термины во втором столбце и z — термины в третьем столбце. Очень важно, чтобы каждое уравнение было записано в стандартной форме [latex]ax+by+cz=d[/latex], чтобы переменные совпадали. Если в уравнении отсутствует переменный член, коэффициент равен 0.
Очень важно, чтобы каждое уравнение было записано в стандартной форме [latex]ax+by+cz=d[/latex], чтобы переменные совпадали. Если в уравнении отсутствует переменный член, коэффициент равен 0.
Как: Для данной системы уравнений напишите расширенную матрицу столбец.
Пример: Написание расширенной матрицы для системы уравнений
Запишите расширенную матрицу для заданной системы уравнений.
[латекс]\begin{array}{l}\text{ }x+2y-z=3\hfill \\ \text{ }2x-y+2z=6\hfill \\ \text{ }x — 3y +3z=4\hfill \end{array}[/latex]
Показать решение
Попробуйте
Напишите расширенную матрицу данной системы уравнений.
[латекс]\begin{array}{l}4x — 3y=11\\ 3x+2y=4\end{массив}[/latex]
Показать решение
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы для решения систем уравнений, поскольку они упрощают операции, когда системы не перегружены переменными. Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать система уравнений в стандартной форме.
Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать система уравнений в стандартной форме.
Пример: запись системы уравнений из расширенной матрицы
Найдите систему уравнений из расширенной матрицы.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill -5\\ \hfill 2& \hfill -5& \hfill -4\\ \hfill -3& \hfill 5& \ hfill 4\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill -2\\ \hfill 5\\ \hfill 6\end{массив}\right][/latex]
Показать раствор
Попробуйте
Напишите систему уравнений из расширенной матрицы.
[латекс]\left[\begin{array}{ccc}1& -1& 1\\ 2& -1& 3\\ 0& 1& 1\end{массив}|\begin{массив}{c}5\\ 1\ \ -9\end{массив}\right][/latex]
Показать решение
Операции со строками
Теперь, когда мы можем записывать системы уравнений в расширенной матричной форме, мы рассмотрим различные операции со строками, которые можно выполнять над матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение операций со строками над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в строчно-эшелонную форму , в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже как показано на главной диагонали.
[латекс]\begin{array}{c}\text{Форма строки-эшелона}\\ \left[\begin{array}{ccc}1& a& b\\ 0& 1& d\\ 0& 0& 1\end{ массив}\справа]\конец{массив}[/латекс]
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную по строкам в более простой форме. Вот рекомендации по получению формы ряд-эшелон.
- В любой ненулевой строке первое ненулевое число равно 1. Оно называется ведущим 1.
- Все строки со всеми нулями помещаются в конец матрицы.
- Любой интерлиньяж 1 ниже и правее предыдущего интерлиньяжа 1.

- Любой столбец, содержащий ведущую единицу, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции над строками, чтобы преобразовать матрицу коэффициентов в форму ступенчатой строки и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение: [латекс] {R}_{i}\leftrightarrow {R}_{j}[/латекс] )
- Умножить строку на константу. (Обозначение: [латекс]c{R}_{i}[/латекс] )
- Добавить произведение строки, умноженной на константу, к другой строке. (Обозначение: [латекс]{R}_{i}+c{R}_{j}[/латекс])
Каждая из операций строки соответствует операциям, которые мы уже изучили для решения систем уравнений с тремя переменными. С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.
A Общее примечание: исключение Гаусса
Метод исключения Гаусса относится к стратегии, используемой для получения формы строки-эшелона матрицы. Цель состоит в том, чтобы написать матрицу [latex]A[/latex] с номером 1 в качестве записи вниз по главной диагонали и со всеми нулями ниже.
[латекс]A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \ hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\\ \hfill {a}_{31}& \hfill {a}_{32}& \hfill {a}_{33}\end{массив}\right]\stackrel{\text{После исключения Гаусса}}{\to}A=\left[\begin{array}{rrr}\hfill 1& \hfill {b}_{12}& \hfill {b}_{13}\\ \hfill 0& \hfill 1& \hfill {b}_{23}\\ \hfill 0& \hfill 0& \hfill 1\end{массив} \право][/латекс]
Первый шаг стратегии Гаусса включает в себя получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Как: Для расширенной матрицы выполнить операции над строками для получения эшелонированной формы
- Первое уравнение должно иметь старший коэффициент, равный 1.
 Поменять местами строки или умножить на константу, если необходимо.
Поменять местами строки или умножить на константу, если необходимо. - Используйте операции со строками, чтобы получить нули в первом столбце после первой записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули вниз по столбцу 2, под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока не будет 1 в каждой записи вниз по главной диагонали, а ниже не останутся только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Пример: выполнение операций над строками над расширенной матрицей 3×3 для получения формы строк-эшелонов
Выполнение операций над строками данной матрицы для получения формы строк-эшелонов.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill 4\\ \hfill 2& \hfill -5& \hfill 6\\ \hfill -3& \hfill 3& \hfill 4 \end{array}\text{ }|\text{ }\begin{array}{r}\hfill 3\\ \hfill 6\\ \hfill 6\end{array}\right][/latex]
Показать Решение
Попробуй
Запиши систему уравнений в ступенчато-строковой форме.
[латекс]\begin{array}{l}\text{ }x — 2y+3z=9\hfill \\ \text{ }-x+3y=-4\hfill \\ 2x — 5y+5z=17 \hfill \end{массив}[/latex]
Показать решение
[латекс]\left[\begin{array}{ccc}1& -\frac{5}{2}& \frac{5}{2}\\ \text{ }0& 1& 5\\ 0& 0& 1\ end{array}|\begin{array}{c}\frac{17}{2}\\ 9\\ 2\end{array}\right][/latex]
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
160 линейных систем
160 линейных системМатрицы и линейные системы в Attaway
Следующие накладные лекции и сопроводительное чтение являются независимыми из МатЛаб. Attaway Глава 11.1 ссылки матрицы, как описано здесь, с их представлением и использованием в Матлаб. Аттавей 11.1 следует читать и понимать как дополнение к он-лайн лекции и чтению.
Аттавей 11.2, ведущий к 11.2.2.1, дает предысторию и
алгоритм исключения Гаусса как метод решения линейного
Уравнения. Полезно прочитать «как сделать» для задания.
Полезно прочитать «как сделать» для задания.
Линейные системы
- А
линейное уравнение – это уравнение, содержащее только
скалярные кратные его переменных и констант. Например:
а 1 х 1 + а 2 х 2 + а 3 Х 3 = с
представляет собой линейное уравнение с тремя переменными .
Х 1 -Х 3 представлять переменные, а 1 -а 3 – соответствующие коэффициенты , и с называется постоянным членом .5x + 7,5y — 10z = 30
является частным примером. - А система линейных уравнений представляет собой (конечный) набор такие уравнения, которые (обычно) связаны тем, что содержат (некоторые из) одних и тех же переменных.
- Линейные системы важны, потому что они полезны для моделирования
большое количество практических ситуаций и
математики знают о них чертовски много, в том числе:
- Именно тогда, когда существуют решения.

- Именно тогда, когда решение уникально.
- Эффективные алгоритмы поиска решений, если они существуют.
- Эффективные методы аппроксимации решений в случаях, когда реальных решений не существует (метод наименьших квадратов).
- Именно тогда, когда существуют решения.
- В общем, если у нас есть N переменных (или неизвестных), нам нужно N линейно независимые уравнения, чтобы найти единственное решение. Такая независимость означает, что мы не можем вывести ни одно из уравнения из других.
- Если у нас больше переменных, чем уравнений, говорят, что система
быть недоопределенным . Уравнения обычно ограничивают
решение
линейное подпространство пространства возможных
решения, но нет единственного, единственного решения.
Например. с тремя переменными одно линейное уравнение описывает плоскость
(подпространство 3-D), каждая из точек которого удовлетворяет уравнению.

- Если у нас больше уравнений, чем переменных, то система вообще говоря, не будет иметь решения (если только некоторые из уравнения линейно зависимы). Говорят, что такая система переопределенное или противоречивое . Хотя фактического решения может и не быть, часто точки в пространстве переменных, которые являются «почти решениями» в том смысле, который можно сделать математически строгим. Анализ методом наименьших квадратов является одним из распространенных подходов к нахождение таких приближенных решений. (Подробнее в модели Будет актуальная тема).
Геометрическая интуиция
- Напомним, что точки, удовлетворяющие линейному уравнению
топор + по = с
в двух переменных x и y попадают на прямую в плоскости xy. - Если мы введем второе уравнение с (обычно) другим
константы a, b и c, то у нас есть вторая строка.
 Есть четыре возможности:
Есть четыре возможности:
- В общем вторая линия пересечет первую в одной точке. Это общий случай двух неизвестных, двух уравнений и единственного решения.
- Если две линии параллельны (например, если a и b одинаковы, а c разные), то решения нет. Это пример противоречивая система . (Также, если есть три или более линий, которые не пересекаются в одной точке. Этот случай часто называют переопределено )
- Если две строки идентичны (например, с a, b и c в второе уравнение все равно кратно их значениям в первое уравнение), то существует бесконечное множество решений (все точки на прямой). В этом случае уравнения линейно зависимым особенно простым образом. Это пример недоопределенная система .
- Если a, b и c равны 0 в обоих уравнениях, то система
называется тривиальным , и все точки являются решениями.
 Это можно рассматривать как крайний пример
недоопределенная система.
Это можно рассматривать как крайний пример
недоопределенная система.
Матричное представление
- Систему линейных уравнений можно компактно представить с помощью
матрица коэффициентов и векторов (столбцов) для
переменные и постоянные члены.
Краткое введение в матрицы - Умножение вектора на матрицу определяется так, что выполнение манипуляции генерирует линейные уравнения.
- Например, предположим, что у нас есть следующая система уравнений:
а 1 х + б 1 у = с 1
а 2 х + б 2 у = с 2
Это можно записать в матричной форме как:
[а 1 б 1 ] [х] = [с 1 ] [а 2 б 2 ] [у] [с 2 ]

Таким образом, ниже представлена общая система 3×3.
[а 11 а 12 а 13 ] [х 1 ] [с 1 ] [a 21 a 22 a 23 ] [x 2 ] = [c 2 ] [а 31 а 32 а 33 ] [х 3 ] [с 3 ]
Ax = c
- Перестановка ERO: строки матрицы можно поменять местами или переставить без изменения представленной системы уравнений пока элементы константы c вектор переставлен таким же образом.
- Линейная комбинация ERO: кратное ряду (и его
соответствующий элемент в постоянном векторе) может быть
умножается на константу, или добавляется к другой строке, или и то, и другое, без
изменение базовой системы (ее решений).

Линейные системы случаются
- Анализ механических сил
- Анализ цепи LCR
- Оптика: (например, формализация трассировки лучей): 160 Ex.
- Химия и хим. Engg: Кинетика реакции
- Общее: Подгонка математических моделей к данным: 160 Ex.
- Общее: оптимизация методом наименьших квадратов
- Общие: Численное решение дифференциальных уравнений: 160 упр.

Исключение Гаусса
- Исключение Гаусса — это общий алгоритм решения систем линейных уравнений
- Кажется, был известен Древние китайцы до 100 г. до н.э.
- Европейское введение Карл Фридрих Гаусс (немецкий математик) около 1809 г. в контексте анализа методом наименьших квадратов.
- Базовая техника с небольшими вариациями все еще используется для общие системы до нескольких тысяч переменных.
- Для больших систем (т.е. миллионы переменных) итеративный используются методы аппроксимации.
- Для разреженных систем (в основном нули в матрице) разработаны различные специальные быстрые методы.
Базовый подход
- Вспомним линейную комбинацию ERO: добавление кратного одного уравнения к другому дает новое
уравнение, которое выполняется тогда и только тогда, когда выполняются исходные уравнения.

- Идея состоит в том, чтобы добавить кратное одного уравнения к другому так, чтобы коэффициент некоторой (выбранной) переменной равен 0,
- В результате на одну переменную меньше, чем в оригинале.
- Делая это постепенно для выбранных переменных, организованно, системы уравнений со все меньшим и меньшим количеством переменных можно составить до тех пор, пока уравнение только с одним получается переменная.
- Это последнее уравнение может быть решено непосредственно для последнего переменная, которую можно подставить в 2-уравнение система для получения значения второй переменной, и и так далее, пока не будут получены значения всех переменных.
Детали A: Ступень уменьшения
Примечание по внедрению: Хотя он смешивает семантику элементов и не является математически чистым
объект, расширенная матрица системы N переменных AX = B
это матрица
N x N+1
[А | B] (это столбец
константы
B соединяется справа от A ). Этот
расширенная матрица
полезен, потому что все ERO включают как A, так и
B , которые теперь вместе в расширенной матрице
вместе ими можно манипулировать в два раза легче, чем порознь.
Этот
расширенная матрица
полезен, потому что все ERO включают как A, так и
B , которые теперь вместе в расширенной матрице
вместе ими можно манипулировать в два раза легче, чем порознь.
- Уравнения записываются в матричной форме Ax = c. Вектор x иногда выписывается не на каждом шагу поскольку он служит только для указания порядка неизвестных.
- Соответствующие кратные первой строки добавляются к остальные строки так, чтобы первый коэффициент был равен 0 в каждый последующий ряд. Это создает столбец 0 ниже элемент (1,1) матрицы. Постоянные элементы рассматриваются как часть строки.
- Соответствующие множители определяются путем деления первого коэффициента каждой нижней строки на первый коэффициент первая строка (элемент (1,1)). Этот делитель известен как ось
- Аналогичным образом подбираются соответствующие числа, кратные второй строке.
 добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем)
добавляется к строкам под ним, чтобы получить 0 во втором столбце ниже
элемент (2,2) (который теперь служит стержнем) - Процесс повторяется для последующих строк до тех пор, пока верхняя треугольная матрица который содержит 0s ниже главной диагонали. Эта матрица вместе с (модифицированным) постоянным вектором представляет система, имеющая точно такие же решения, как и начальная система. На этом этап редукции завершается.
Детали B: Этап обратной замены
- Алгоритм теперь входит в стадию обратной замены . Обратите внимание, что последняя строка верхней треугольной матрицы представляет уравнение с одной переменной (та, которая связана с последний столбец), который может быть непосредственно решен для этой переменной.
- Предпоследняя строка представляет уравнение с двумя переменными,
одна из которых является переменной, для которой только что найдено решение.
 Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец.
Подставляя значение, получаем уравнение, которое можно решить
непосредственно для переменной, связанной с предпоследним
столбец. - Процесс повторяется до тех пор, пока не будут получены значения для всех неизвестных переменных. были получены. На этом решение системы завершено.
- Рабочий пример
Вычислительная сложность
- Если мы подсчитаем задействованные операции, то окажется, что примерно N 3 /3 сложения и умножения необходимы для стадии восстановления, и примерно N 2 /2 сложения и умножения для шаг обратной замены, где N — размер системы.
- Как Н
становится большим, в подсчете операций преобладает
№ 3 /3
срок. Ученые-компьютерщики описывают ситуацию так:
что алгоритм порядка N 3 .

- Условно пишется O(N 3 ), именуемый Обозначение «большое О». Технический смысл заключается в том, что при достаточно больших N количество операций ограничено kN 3 для некоторой постоянной к.
- Таких асимптотических оценок являются важной областью изучения в область компьютерных наук, известная как теория вычислительной сложности.
- Довольно неожиданно, кН 3 не является нижней границей. Сложность аналогична умножению квадратных матриц, для которого (в основном непрактичные) алгоритмы меньшей асимптотической сложности известны, например, Алгоритм Штрассена, который примерно О(N 2,807 ).
Возможная проблема A: Zero Pivot
- Если диагональный элемент, который должен служить
пивот равен 0, никакое число, кратное строке, не может исключить эту переменную
в следующих рядах.

- Простое решение — использовать обмен ERO на поменять местами проблемное строку (и связанный с ней постоянный член) с нижней строкой, которая делает не иметь 0 в сокращаемой колонке.
- Если такой строки не существует, то в каком-то смысле столбец уже уменьшается, и мы можем перейти к следующему. Однако мы обнаружили линейная зависимость, что означает, что единственного решения не существует. Такая система называется единственное число .
- Подробнее о редукции в сингулярных системах
Возможная проблема B: Поворот около нуля
- Если поворотный элемент
очень мал по сравнению с одним или несколькими элементами
ниже него в столбце, то большое число, кратное сводной строке, должно
добавить, чтобы привести коэффициент столбца к нулю.
Это усилит любые ошибки, существующие из-за округления или
погрешность измерения и может привести к
неправильное решение системы.

- Простой подход — поменять местами строки, чтобы использовать ту, которая в данный момент имеет наибольшее значение в сводном столбце. Это известно как с частичным поворотом .
- Более сложный подход — поменять местами строки и столбцы, чтобы чтобы получить максимально возможную опору. Это известно как с полным поворотом , но обычно это не так. используется, так как поиск занимает много времени, а частичный поворот обычно достаточно.
Потенциальная проблема C: нестабильная система
- пивот мал по сравнению со значениями над ним (в строках, где редукция уже завершена) то большая умножения будут введены во время обратной замены этап, который также может усилить существующие ошибки.
- В этом случае система изначально чувствительна к ошибкам.
Такая система называется в плохом состоянии или иногда почти единственное число .

- Примером является пара уравнений в плоскости, представляющей почти параллельные линии. Явно небольшое изменение положения или ориентации одного линий может привести к большому изменению местоположения точку пересечения (или даже сделать их параллельными).
- Плохо обусловленная система, возникающая из реальных экспериментальных данных часто указывает на более глубокую проблему с экспериментальным дизайном, протоколы сбора данных или даже с базовой моделью. Обнаружение таких систем, таким образом, важно.
Вариации
- Вместо выполнения шага обратной замены после
получение верхней треугольной формы, стадия обжатия
можно продолжить. Повторяем идею, только вверх ногами и
назад, начиная с последнего ряда вверх и с последнего
столбец обратно влево. Таким образом, мы используем последнюю строку, чтобы исключить
коэффициенты последнего столбца, предпоследняя строка для исключения
коэффициенты предпоследнего столбца и так далее.




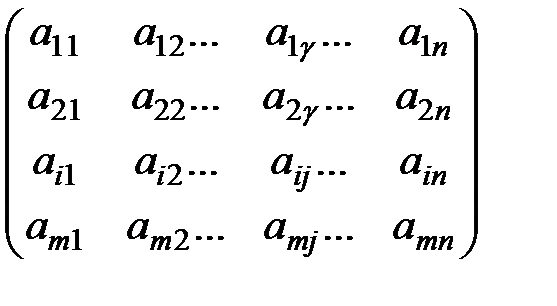 В этом случае система (1) имеет единственное решение.
В этом случае система (1) имеет единственное решение.

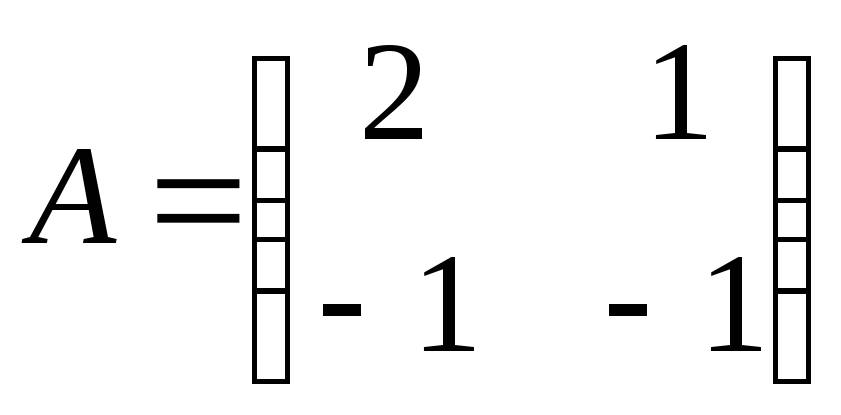
 Обратная матрица. — КиберПедия
Обратная матрица. — КиберПедия ..
..

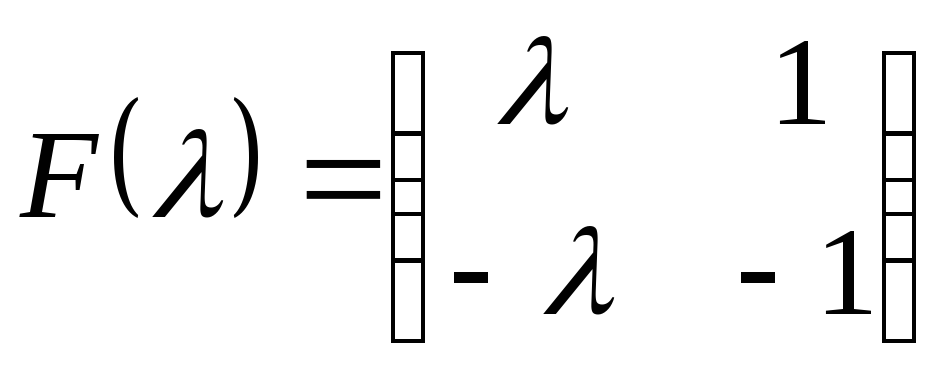 В противном случае ( ) матрицаА называется вырожденной.
В противном случае ( ) матрицаА называется вырожденной. п. 2.2).
п. 2.2). Следовательно, матрица А является обратной для B
Следовательно, матрица А является обратной для B
 Подлежат нахождению числа .
Подлежат нахождению числа .

 е. .
е. .
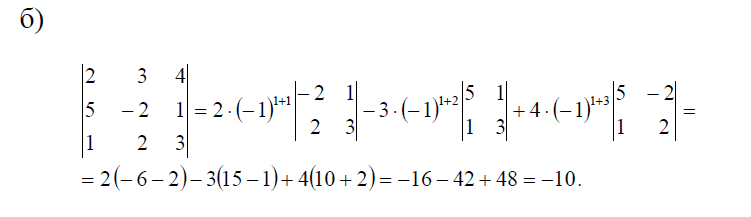 Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .
Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается . 1.
1.

 43.
43.
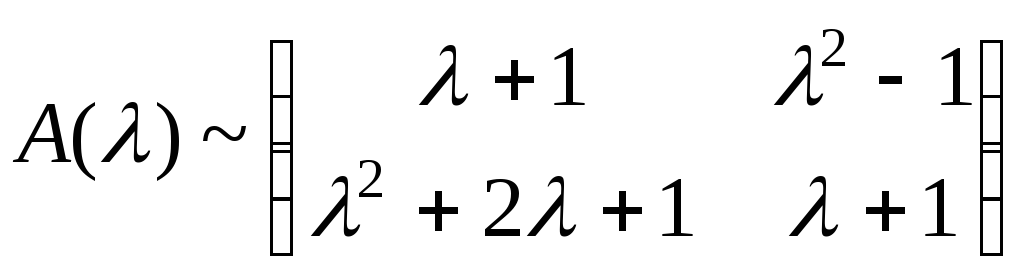
 рис. 44).
рис. 44). 11)
11)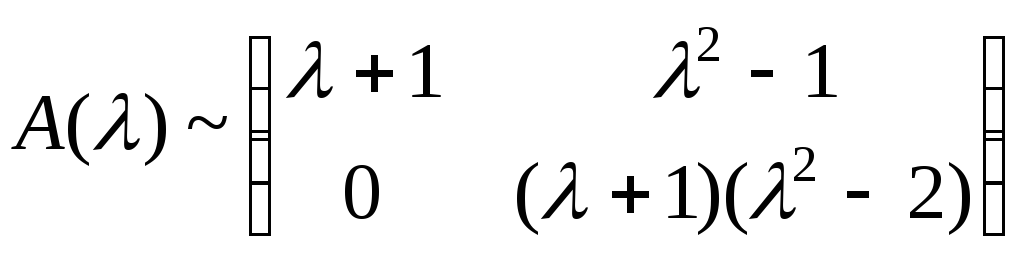
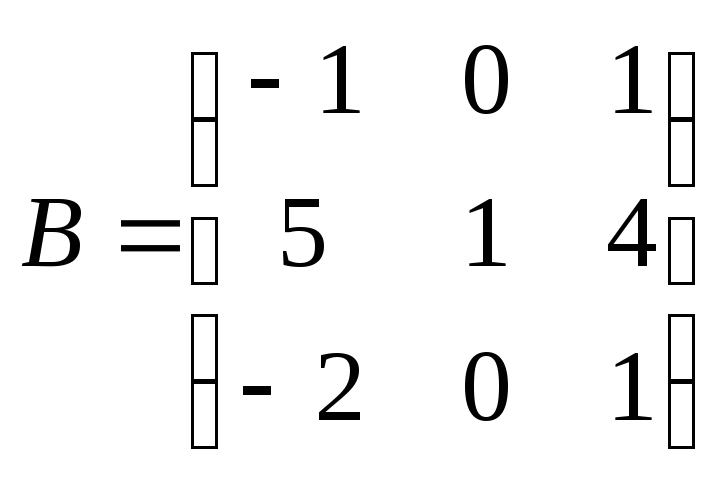
 В противном случае ( ) матрицаА называется вырожденной.
В противном случае ( ) матрицаА называется вырожденной.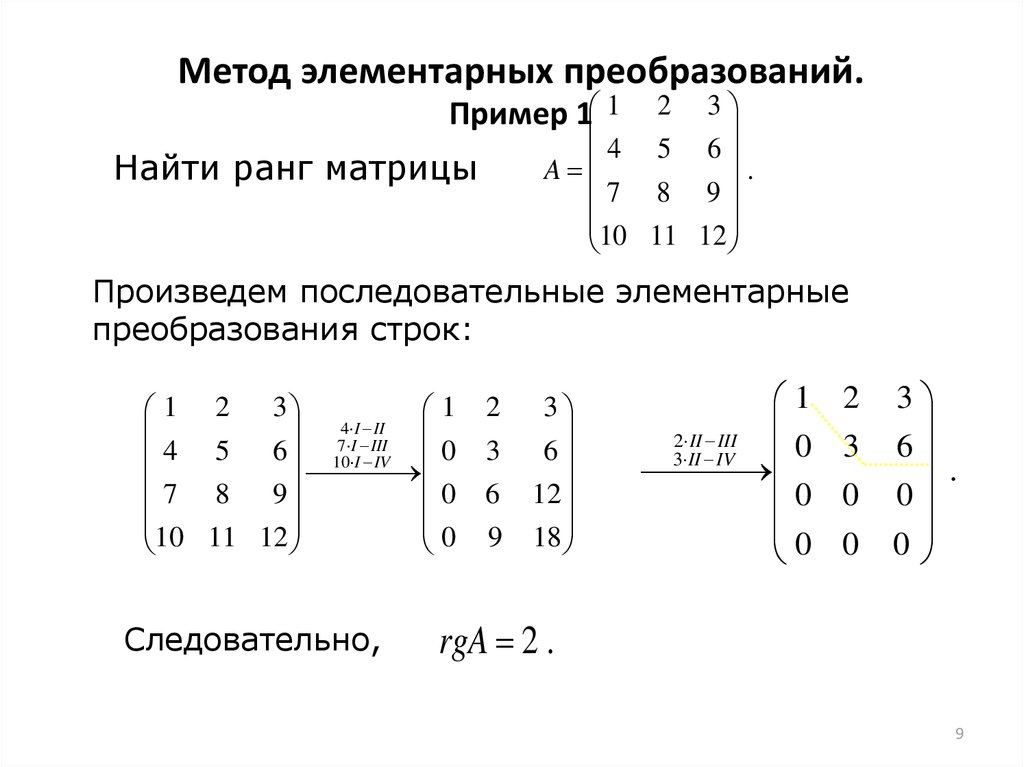 п. 2.2).
п. 2.2).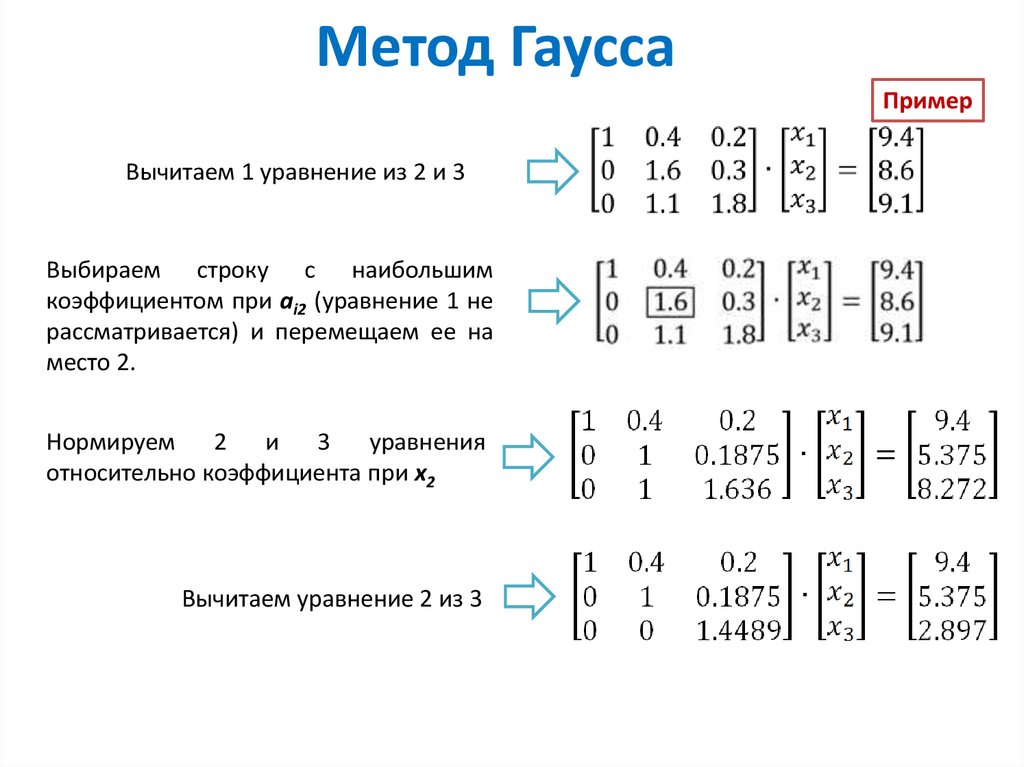
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Решение этой системы очевидно. Таким образом, решение исходной системы: , , .
Решение этой системы очевидно. Таким образом, решение исходной системы: , , . Эти решения называются ее частными решениями, которых, очевидно, бесконечно много. Если положить, например, и , то из общего решения получаем и Таким образом, одно из частных решений исходной системы имеет вид: , , , . Можно общему решению этой системы придать более симметричную форму. Положим , а . Тогда выписанное выше общее решение можно записать в виде:
Эти решения называются ее частными решениями, которых, очевидно, бесконечно много. Если положить, например, и , то из общего решения получаем и Таким образом, одно из частных решений исходной системы имеет вид: , , , . Можно общему решению этой системы придать более симметричную форму. Положим , а . Тогда выписанное выше общее решение можно записать в виде: Теорема Кронекера-Капелли») из этого следует, что любая однородная система совместна. Очевидно, что одним из ее решений всегда является решение , которое называется нулевым (или тривиальным) решением однородной системы. Учитывая теорему Кронекера-Капелли, легко найти условия, при которых однородная система имеет и ненулевые решения.
Теорема Кронекера-Капелли») из этого следует, что любая однородная система совместна. Очевидно, что одним из ее решений всегда является решение , которое называется нулевым (или тривиальным) решением однородной системы. Учитывая теорему Кронекера-Капелли, легко найти условия, при которых однородная система имеет и ненулевые решения.
 Поскольку основной определитель этой системы , то по правилу Крамера она имеет единственное решение и при произвольном значении переменной . Применяя формулы Крамера, для этого решения получаются следующие формулы:
Поскольку основной определитель этой системы , то по правилу Крамера она имеет единственное решение и при произвольном значении переменной . Применяя формулы Крамера, для этого решения получаются следующие формулы:
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.009 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.009 с.) A12362-321431-1-2BR1 ←→R3—-→A31-1-22-32141236B
A12362-321431-1-2BR1 ←→R3—-→A31-1-22-32141236B


