Градиент функции двух переменных: Градиент функции нескольких переменных | matematicus.ru

Градиент функции многих переменных

 

Рассмотрим функцию трех переменных n=3, u=f(x, y, z).

Определение. Градиентом функции многих переменных в данной точке называется вектор, координаты которого равнычастным производным по соответствующим аргументам, вычисленным в данной точке.

.

Теорема 1. Производная функции в данном направленииравна проекции градиента на данное направление.

Доказательство. Даны функция u=f(x,y,z) и некоторое направление l, заданное направляющими косинусами  .

Единичный вектор данного направления —  .

Производная по направлению в данной точке равна

,

где  — угол между градиентом и направлением.

                                                                                             

                                                                                             

                                          grad u                                        

                                                                                           

                          M₀                                                 l  

                                                                                             

                                                                                             

.

Следствие. Градиент функции в данной точке показывает направление наискорейшего возрастания функции.

Модуль градиента совпадает с максимальной скоростью возрастания функции в данной точке.

Доказательство. Из теоремы следует, что

.

Выясним, в каком из направлений в данной точке функция растет быстрее всего. Максимум будет достигаться, когда  , т. е. направление совпадает с направлением градиента.

.

Рассмотрим функцию двух переменных n=2,  .

Теорема 2. Градиент функции в каждой точке области определения направлен по нормали к линии уровня (нормалью к плоской кривой называется перпендикуляр к касательной, проведенной в точку касания).

                             

 

Частные производные высших порядков

 

Рассмотрим функцию двух переменных n=2,  . Предположим, что функция имеет 

частные производные

,                        ,

которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.

Определение 1. Частные производные от частных производных первого порядка называются частными производными второго порядка.

 =  ,                         =  .

 =  ,                        =  .

 

Две последние называют смешанными производными.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

.

 

Определение 2. Частной производной 

n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2ⁿ штук.

Частная производная порядка р функции   имеет вид

, где  .

Теорема. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

Пример.  .

,                 ,

,  ,     ,  ,

.

 

 

Файл: Определение максимального и минимального значения функции двух переменных методом градиентного спуска.doc — Страницы №№1-2

Определение максимального и минимального значения функции двух переменных методом градиентного спуска (подъема).

При определении максимального или минимального значений функции двух или более переменных используется понятие «Градиента». Градиентом функции называется вектор, компоненты которого являются частными производными функции по соответствующим координатам. Так, например, для функции двух переменных f(x,y) градиент определяется как вектор с компонентами: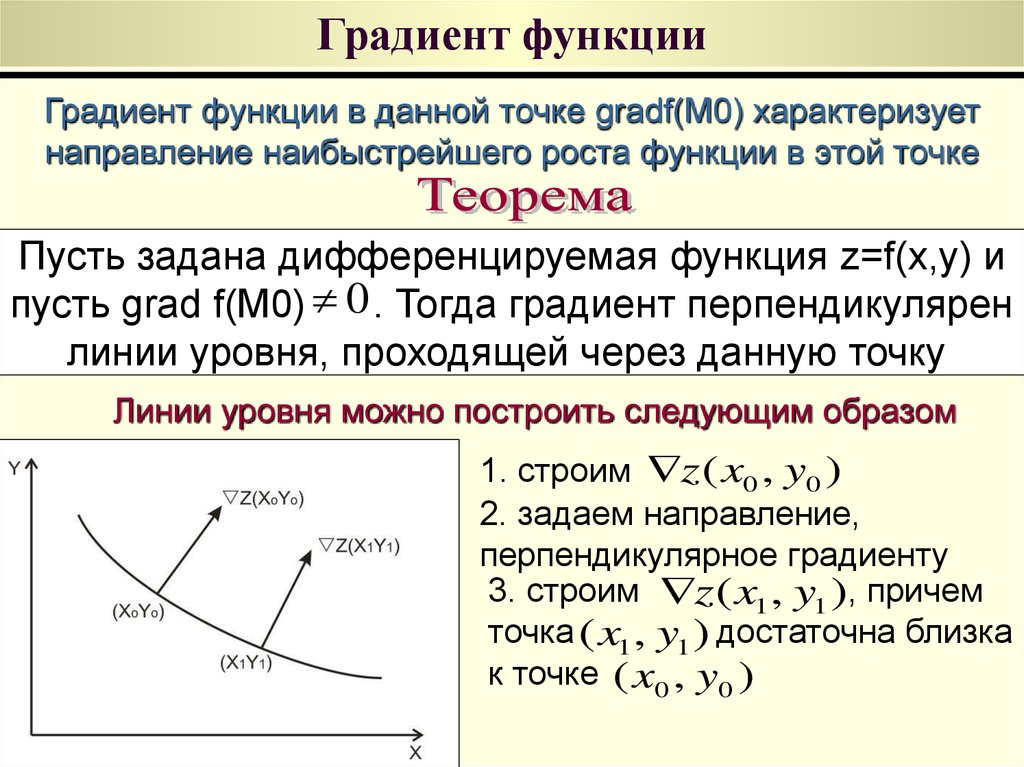

и . Обозначается градиент функции либо без значка вектора .

Градиент функции f(x₁, x₂,…, x_n) в каждой точке направлен в сторону наискорейшего локального возрастания (убывания) этой функции. Для поиска минимума необходимо спускаться в противоположном направлении.

При численных расчетах градиент функции можно вычислить приближенно , где ,

– единичные вектора по направлениям осей x и y, , , — приращение x, — приращение y.

Вектор градиента указывает, подобно производной одномерной функции, направление на ближайший локальный максимум функции в данной точке, вектор  – направление на ближайший локальный минимум.

Параметр а определяет длину шага в направлении спуска. Длину шага можно выбирать из условия минимизации функции вдоль направления, противоположного градиенту.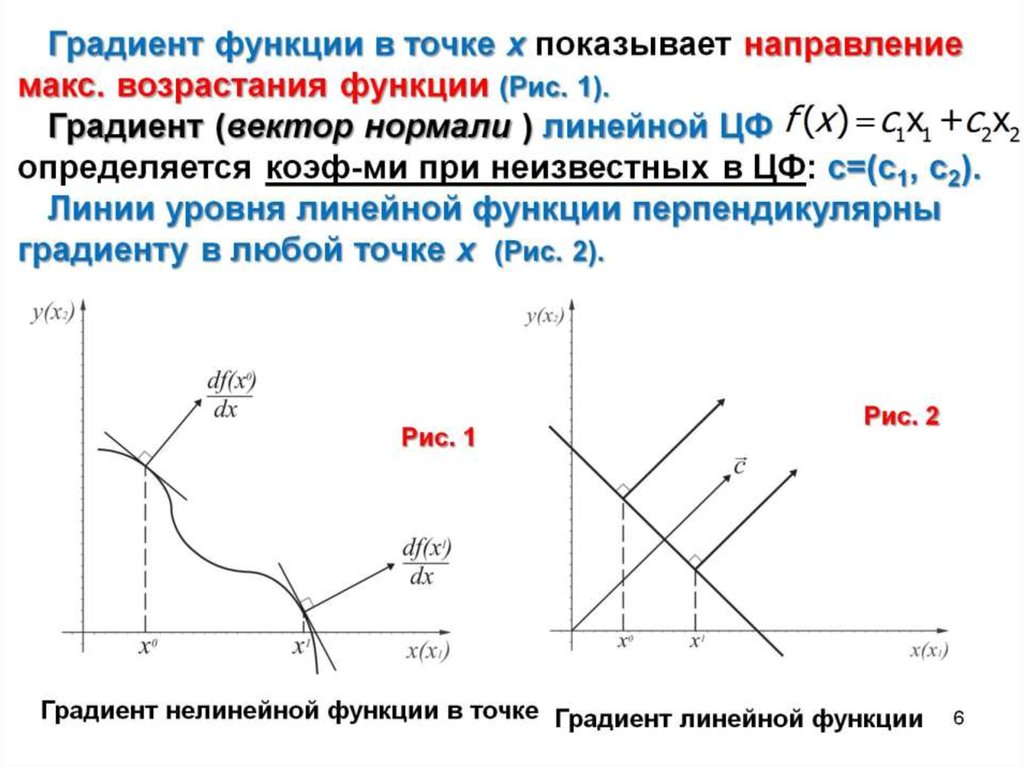 Такой метод называют методом наискорейшего спуска. В другом методе градиентного спуска длина шага а выбирается методом дробления.

Рассмотрим многомерную функцию, имеющую вид колокола:

, (1)

где точка

– точка максимума функции.

В области изменений функция имеет вид:

Аналогичные функции можно построить в многомерном пространстве. Например, если размерность пространства n, то функция «n-мерный колокол» будет иметь вид:

. (2)

Точка максимума этой функции — . Функция «n-мерного колокола» (2) при n=2 превращается в (1).

Описание алгоритма нахождения максимального (минимального) значения функции двух переменных методом градиентного спуска (подъема):

1. Задаем размерность n массива аргументов минимизируемой (максимизируемой) многомерной функции, погрешность вычислений ε_, начальные значения шага d по x, y, координаты начальной точки поиска x0, y0, определяем вспомогательный массив для запоминания значений аргументов при дроблении шага х1, y1, массив для составляющих градиента функции df.

2. Вычисляем значение функции в точке с координатами (x0, y0).

3. Вычисляем х и y компоненты вектора градиента функции по формулам gx=(f(x0+dx, y0)-f(x0,y0))/dx; gy=(f(x0, y0+dy)-f(x0,y0))/dy.

4. Вычисляем модуль градиента функции.

5. Вычисляем новое значение функции и сравниваем с предыдущим. Если максимум (минимум) не найден, продолжаем итерации.

6. Если второе условие не выполнилось, уменьшаем шаг.

Алгоритм на естественном языке приведем для функции «n-мерного колокола».

Строки «комментарии» будем начинать с символа «*».

---

Для функции с координатами точки максимума: (2, 3, 4, …, n+1) для пространства размерности n.

Определить n как целое, где n – количество аргументов функции.

n=2

Определить массивы x0(n), x1(n) , x2(n), df(n), h(n)

* массивы x0, x1, х2 – рабочие массивы координат точек (0), (1),

* (2). Массивы df – компоненты вектора градиента функции,

* h – компоненты векторов шага

Определить глобальный массив xс(n)

* массив xс-массив координат точки максимума функции

eps=0.01

d=0.01

* в данном цикле задаются координаты точки максимума

цикл по i от 1 до n

xc(i)=1+i

конец цикла

* здесь задаются координаты начальной точки для определения

* максимума

цикл по i от 1 до n

x0(i)=0.1+i

конец цикла

h0=0.5

f0=колокол(@x0,n)

цикл по k от 1 до 10000

печать «k=»,x0(1),x0(2),f0,h0

цикл по j от 1 до n

цикл по i от 1 до n

x1(i)=x0(i)

конец цикла

x1(j)=x0(j)+d

f1=колокол(@x1,n)

df(j)=(f1-f0)/d

конец цикла

* нормирование градиента

lendf=0

цикл по i от 1 до n

lendf = lendf + df(i)^2

конец цикла

lendf = Корень(lendf)

цикл по i от 1 до n

df(i)=df(i)/lendf

конец цикла

цикл по i от 1 до n

x0(i)=x0(i)+df(i)*h0

конец цикла

f0_1=колокол(@x0,n)

если f0_1=<f0

печать » нашли max»

если h0<eps

печать «найден max x0=(«,

цикл по i от 1 до n

печать x0(i)

конец цикла

печать «)»

печать » f0= «, f0

печать «за «,k,» итераций»

выход из программы

конец если

h0=h0/2

конец если

f0=f0_1

конец цикла

печать «максимум не найден x=»

цикл по i от 1 до n

печать x0(i)

конец цикла

ОПРЕДЕЛИТЬ ФУНКЦИЮ колокол

параметры x, n

определить массив x(n)

определить локальную переменную r2

r2=0

цикл по i от 1 до n

r2=r2+(x(i)-xc(i))^2

конец цикла

если r2>10

r2=10

конец если

вернуть 5*(EXP(-0. 2)

f = r + 2 * z(1) — 3.5 * z(2)

Return

3: r = 2 * r

p(1) = z(1) * r + 2

p(2) = z(2) * r — 3.5

Return

End Sub

---

3:g(x,y,z)=0\}$, совпадает с $\Gamma(f)$ и $\nabla g$ ей ортогонален.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

исчисление — градиент функции 3 переменных

спросил 7 лет, 2 месяца назад

Изменено 7 лет, 2 месяца назад

Просмотрено 11 тысяч раз

$\begingroup$

93+xyz$$

Найдите $\nabla f$, а затем $\nabla f$ в $(1,-1,-1)$.

Я сложил все частные производные вместе, затем заменил $(x,y,z)$ на $(1,-1,-1)$ и получил $3$ в качестве ответа, но это совсем не кажется правильным.

Как мне поступить?

• исчисление
• производные

$\endgroup$

1

$\begingroup$

Градиент представляет собой вектор: 92+xy)$$

Таким образом, градиент в точке $(1,-1,-1)$ определяется выражением $$\nabla f(1,-1,-1) = (-13,3,13)$$

Сумма этих компонентов равна $3$, как вы заметили, но значение градиента представляет собой вектор, а не сумма этих компонентов.

$\endgroup$

1

$\begingroup$

Я сложил все частные производные вместе, затем заменил (x,y,z) на (1,−1,−1) и получил 3 в качестве ответа, но мне это кажется неправильным.

No related posts.