Калькулятор Градиента — Mathcracker.Com
Инструкции: Используйте этот калькулятор градиента, чтобы вычислить вектор частных производных для многомерной функции, которую вы предоставляете, показывая все шаги. Пожалуйста, введите многопараметрическую функцию в форму ниже.
Калькулятор градиента
Этот калькулятор градиента с шагами поможет вам найти вектор градиента данной многомерной функции, которую вы предоставляете. Эта функция должна быть допустимой, дифференцируемой функцией с 2 или более переменными.
Предоставляемая вами функция должна сопровождаться полным определением имени переменной и функции, например f(x, y) = x^2 + y^2 или f(x,y,z) = xy+z*sin.
Как только действительная функция с несколькими переменными предоставлена, все, что осталось сделать, это нажать кнопку «Рассчитать», чтобы получить все показанные шаги.
Градиенты представляют собой естественное расширение производных для ситуации с несколькими переменными, в которой скорость изменения лучше определяется вектором, чем числом.
Что такое градиент
Проще говоря, градиент — это вектор, содержащий все частные производные первого порядка функции многих переменных \(f\). Тогда для функции двух переменных \(f(x, y)\) ее градиент будет двумерным вектором \(\nabla f(x, y) = \displaystyle \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\).
Точно так же для функции трех переменных \(f(x, y, z\) ее градиентом будет трехмерный вектор \(\nabla f(x, y, z) = \displaystyle \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\) и так далее.
Шаги для вычисления градиента
- Шаг 1: Определите функцию f, с которой вы хотите работать, и укажите количество задействованных переменных.
- Шаг 2: Найдите первый заказ Частичная производная по каждой из переменных
-
Шаг 3:
Создайте градиент как вектор, который содержит все частные производные первого порядка, найденные на шаге 2.
При желании вы можете упростить, если это возможно, после завершения шага 3. Затем с помощью градиента у вас есть версия того, что является производной для одномерной функции, в данном случае для многомерной функции.
Применение градиента
Так же, как и в случае одномерных функций при поиске критических точек нам нужно найти точки, в которых производная равна нулю, для многомерных функций нам нужно искать точки, в которых градиент равен нулю, чтобы найти критические точки.
Кроме того, эквивалент тестов второй производной представлен в виде правила Гессе для многомерных функций.Советы и рекомендации
Помните, что
Градиент
определяется для многомерных функций с двумя или более переменными.
2 \) равен:
\[ \nabla f = \left(2x,2y,2z\right)\]
Пример расчета градиента
Для следующей функции: \(f(x, y) = xy\) найдите ее градиент.
Отвечать: Для этого примера у нас есть функция двух переменных x и y: \(\displaystyle f(x,y)=xy\).
Во-первых, дифференцируя по x
\( \displaystyle \frac{\partial }{\partial x}\left(xy\right)\)
Поскольку это постоянное время \(x\), мы сразу получаем: \(\frac{\partial }{\partial x}\left( xy \right) = y\)
\( \displaystyle = \,\,\)
\(\displaystyle y\)
Теперь продифференцируем по y
\( \displaystyle \frac{\partial }{\partial y}\left(xy\right)\)
Поскольку это постоянное время \(y\), мы сразу получаем: \(\frac{\partial }{\partial y}\left( xy \right) = x\)
\( \displaystyle = \,\,\)
\(\displaystyle x\)
\[ \nabla f = \left(y, x\right)\]
Еще примеры градиентов
Вычислите соответствующий градиент \( f(x, y) = x^2 — y^2 — xy \).
2-xy \) равен:
\[ \nabla f = \left(2x-y,-x-2y\right)\]
Другие производные калькуляторы
Используя производный калькулятор определенно может облегчить вашу жизнь, поскольку позволит вам отслеживать все Правила производных .
Большинство из
правила дифференциации
используемые для одномерных функций, имеют эквивалент для многомерных функций.
Таким образом,
Правило цепи
,
Правило Продукта
а также
правило квоты
также будет работать для многомерной функции, учитывая правильные размеры.
Альвеолярно-артериальный градиент | Онлайн калькулятор
10.03.2023
11.03.2023 486
Рейтинг: 5/5 • 1 голос
Оценить
Разделы: Анестезиология и реаниматология
Альвеолярно-артериальный градиент (A-a O2 или A-a градиент), является разницей между парциальным давлением альвеолярного кислорода (A) и артериальной (a) концентрацией кислорода.
Данный показатель используется при диагностике источника гипоксемии.
Возраст
лет
некорректные данные
Температура тела
°C
некорректные данные
PaO2
мм рт. ст.
некорректные данные
FiO2
%
некорректные данные
PaCO2
мм рт. ст.
некорректные данные
Атмосферное давление
мм рт. ст.
некорректные данные
* Полученные данные не могут трактоваться как профессиональные медицинские рекомендации и предоставляются исключительно в ознакомительных целях
Расчет градиента помогает определить локализацию проблемы: внутрилегочную или внелегочную.
Нормальный A-a градиент для молодых не курящих людей на воздухе, составляет 5-10 мм рт.
Обычно градиент A-a увеличивается с возрастом. Считается, что за каждое десятилетие жизни человека градиент увеличивается на 1 мм рт.ст.
Вычисленное значение градиента A-a пациента, позволяет оценить, вызвана ли его гипоксия дисфункцией альвеолярно-капиллярной единицы, в результате чего он будет повышен, или другой причиной, при которой градиент A-a будет на уровне или ниже вычисленной возрастной нормы.
Альвеолярно-артериальный градиент рассчитывается по формуле:
AaG = (FiO2 × (pAtm — pH2O) — (PaCO2/0.8)) — PaO2
где:
- FiO2 — доля кислорода во вдыхаемом воздухе (в виде относительного показателя)
- pAtm — атмосферное давление в мм рт.ст.
- pH2O — парциальное давление водяного пара (в среднем 47 мм рт.ст.)
- PaCO2 — парциальное давление углекислого газа в артериальной крови
- PaO2 — парциальное давление кислорода в артериальной крови
Расчет pH2O проводится по формуле:
ph3O = 47 × e((t — 37) / 18.
4)
где:
- t — температура тела пациента в градусах Цельсия
Расчет возрастной нормы градиента проводится по формуле:
Возрастная норма = (Возраст/4) + 4
Еще калькуляторы: Шкала APACHE II, Шкала SOFA, Шкала PARS, Шкала тревоги Кови, Формула Лоренца
Калькулятор градиента — определите градиент функции с помощью точек
Онлайн-калькулятор градиента поможет вам найти градиент прямой линии через две и три точки. Этот калькулятор поля градиента дифференцирует данную функцию для определения градиента с пошаговыми вычислениями. Итак, читайте дальше, чтобы узнать, как рассчитать векторы градиента, используя формулы и примеры.
Что такое градиент? В векторном исчислении градиент может относиться к производной функции. Этот термин чаще всего используется в сложных ситуациях, когда у вас есть несколько входов и только один выход. Вектор градиента хранит всю информацию о частных производных каждой переменной.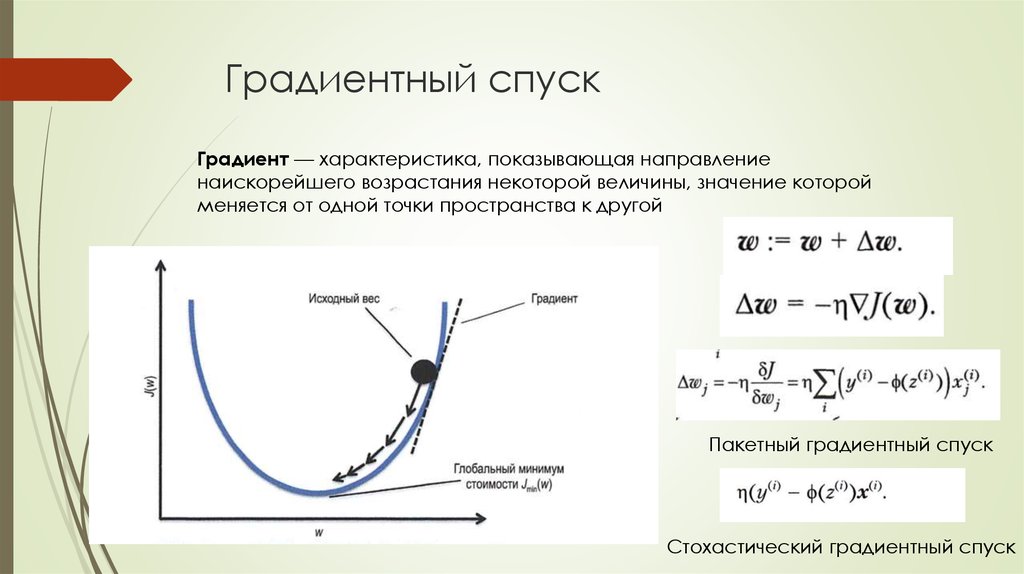
Неофициальное определение градиента (также называемого уклоном) выглядит следующим образом: Это математический метод измерения скорости подъема или спуска линии. Когда наклон увеличивается влево, линия имеет положительный градиент. Когда линия наклонена слева направо, ее градиент отрицательный. Вертикальная линия должна иметь неопределенный уклон. Символ m используется для обозначения градиента. В алгебре дифференцирование можно использовать для нахождения градиента линии или функции.
Однако онлайн-калькулятор уклона помогает найти уклон (м) или уклон между двумя точками и в декартовой координатной плоскости.
Обозначение градиента:Градиент функции f в точке x обычно выражается как ∇f(x). Его также можно назвать:
- ∇f(x)
- Град ф
- ∂ф/∂а
- ∂_if и f_i
Обозначения градиента также обычно используются для обозначения градиентов. Уравнение градиента определяется как уникальное векторное поле, и скалярное произведение его вектора v в каждой точке x является производной f по направлению v.
$$(∇f(а)) . v = D_vf(x)$$
Декартовы координаты:В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, определяется выражением:
$$∇f = ∂f /∂x a + ∂f/∂y b + ∂f/∂z c$$
Где a, b, c — стандартные единичные векторы в направлениях координат x, y и z соответственно.
Формула градиента с примером:- Найдите любые две точки на линии, которые вы хотите исследовать, и найдите их декартовы координаты. Предположим, мы хотим определить наклон прямой, проходящей через точки (8, 4) и (13, 19).).
- Возьмите координаты первой точки и введите их в калькулятор поля градиента как \(a_1 и b_2\). Сделайте то же самое для второй точки, на этот раз \(a_2 и b_2\).
- Калькулятор градиента автоматически использует формулу градиента и вычисляет ее как (19-4)/(13-(8))=3.
Однако онлайн-калькулятор производной по направлению находит градиент и производную по направлению функции в заданной точке вектора.
Для расчета градиента находим две точки, заданные в декартовых координатах \((a_1, b_1) и (a_2, b_2)\). На реальном примере мы хотим понять взаимосвязь между ними, то есть, насколько высок излишек между ними. Это определяется по формуле градиента:
градиент = подъем/разбег
С подъемом \(= а_2-а_1, а разбег = b_2-b_1\). Подъем — это подъем/спуск второй точки относительно первой точки, а бег — расстояние между ними (по горизонтали). 93) | (x, y) = (1, 3) = (2, 27)$$
Как работает калькулятор радиации G ?Калькулятор поля градиента вычисляет градиент линии, следуя этим инструкциям:
Ввод:- Во-первых, выберите координаты для градиента.
- Теперь введите функцию с двумя или тремя переменными.
- Затем подставьте значения в разных полях координат.
- Чтобы увидеть ответ и расчеты, нажмите кнопку расчета.
- Калькулятор градиента обеспечивает стандартный ввод со знаком набла и ответом.
- Этот калькулятор вектора градиента отображает пошаговые расчеты для различения различных терминов.
Градиент функции представляет собой векторное поле. Он получается применением векторного оператора V к скалярной функции f(x, y). Это векторное поле называется градиентным (или консервативным) векторным полем.
Существует ли векторный градиент?Градиент вектора — это тензор, который говорит нам, как векторное поле изменяется в любом направлении. Мы можем выразить градиент вектора как его компонентную матрицу по отношению к векторному полю.
Что такое градиент скалярной функции? Градиент является скалярной функцией. Величина градиента равна максимальной скорости изменения скалярного поля, а его направление соответствует направлению максимального изменения скалярной функции.
Градиент по-прежнему является вектором. Он указывает направление и величину самой быстрой скорости изменения.
Что такое символ градиента потенциала?Это выражение является важной особенностью каждого консервативного векторного поля F, т. е. F имеет соответствующий потенциал ϕ. Это означает, что кривизна векторного поля, представленная ∇×, исчезает.
Вывод:Используйте этот онлайн-калькулятор градиента для вычисления градиентов (наклона) заданной функции в различных точках. Нет необходимости находить градиент с помощью руки и графика, так как это увеличивает неопределенность. Просто воспользуйтесь нашим бесплатным калькулятором, который выполняет точные расчеты градиента.
Ссылка: Из источника Википедии: Мотивация, Обозначение, Декартовы координаты, Цилиндрические и сферические координаты, Общие координаты, Градиент и производная или дифференциал.
Из источника Академии Хана: Скалярные многомерные функции, два измерения, три измерения, Интерпретация градиента, градиент перпендикулярен контурным линиям.
Из источника Revision Math: Градиенты и графики, Нахождение градиента прямолинейного графика, Нахождение градиента кривой, Параллельные линии, Перпендикулярные линии (ВЫСОКИЙ УРОВЕНЬ).
Из источника лучшего пояснения: Векторное исчисление: понимание градиента, свойства градиента, направление наибольшего увеличения, градиент перпендикулярно линиям.
Калькулятор градиента линии, проходящей через две точки
Создано Maciej Kowalski, PhD :
- Что такое градиент ?
- Определение градиента
- Формула градиента
- Как использовать этот калькулятор градиента
- Распространенные заблуждения и ошибки
- Часто задаваемые вопросы
Добро пожаловать в калькулятор градиента , где у вас будет возможность узнать, как рассчитать градиент линии, проходящей через две точки.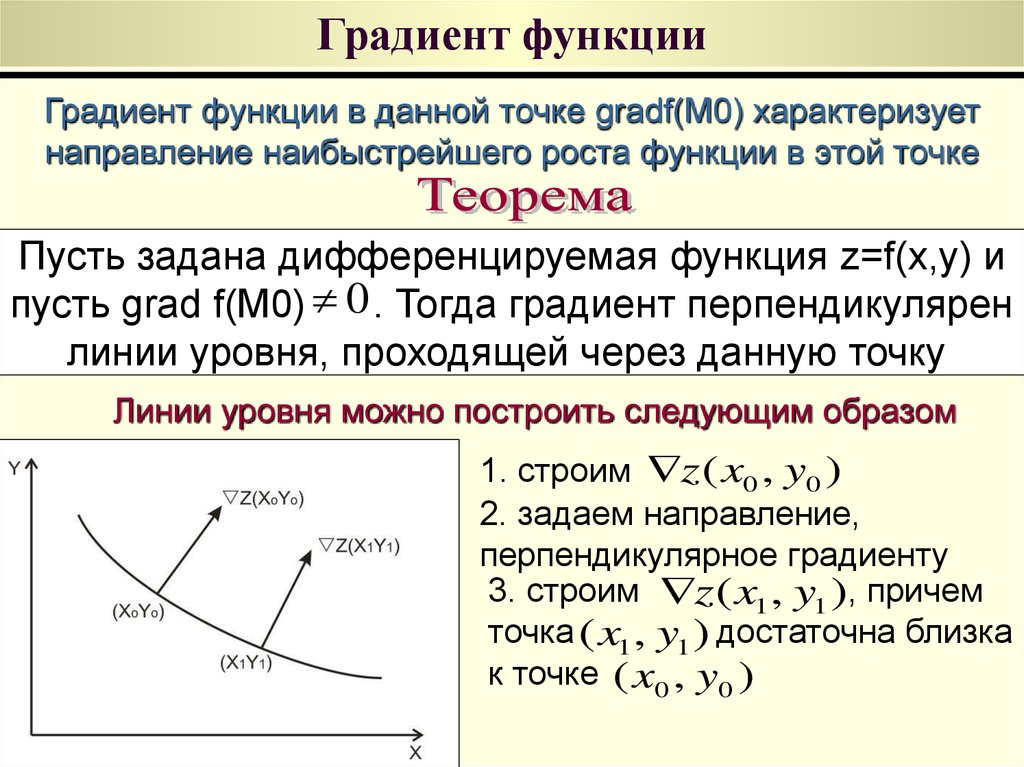
« Что такое градиент? » спросите вы. Ну, вы когда-нибудь смотрели на гору и говорили себе: « Ого, эта гора довольно крутая, но не такая крутая, как близлежащая! »? И если такого рода вопрос заставил вас задаться вопросом, как сравнить их крутизну, вы попали в нужное место ! Продолжайте читать, чтобы узнать определение градиента.
Если вы хотите найти градиент нелинейной функции, мы рекомендуем проверить калькулятор средней скорости изменения.
Что такое градиент?
Прежде чем мы рассмотрим, что такое градиент, давайте вернемся к нашей горной сцене и абсолютно важному вопросу о крутизне.
Допустим, вы спускаетесь со склона на лыжах, когда вас настигает Большой вопрос . Вы останавливаетесь и думаете об этом, прежде чем идти дальше. Как мы упоминали выше, все, что вам нужно, это две точки, чтобы найти градиент , так почему бы не быть немного эгоцентричным и выбрать себя как.
.. ну центр , то есть точку (x₁,y₁) = (0,0) на плоскости.
Теперь нам осталось найти вторую точку , (x₂,y₂) , вверх или вниз по склону. Вы оглядываетесь, чтобы найти какое-нибудь особенно густое дерево или хорошенькую юную лыжницу. Или старый вонючий, если уж на то пошло; Я не осуждаю.
Скажите дереву или лыжнику стоять на месте, пока вы используете свою удобную линейку (которую вы, конечно, всегда носите с собой), чтобы сосчитать до насколько они выше/ниже от вас (это будет y₂ ) и насколько они далеко от вас (это будет x₂ ). Не забудьте считать расстояние между вами двумя по горизонтали, а не параллельно склону . И вот оно! Отношение y₂ / x₂ — это ваш градиент или крутизна горы в этой точке.
За то, что вы останетесь здесь, пока проводите быстрый эксперимент, купите этому лыжнику горячего шоколада или обнимите дерево.
Они заслуживают столько же.
Определение градиента
Неофициальное определение градиента таково: это математический способ измерения скорости подъема или падения линии . Думайте об этом как о числе, которое вы присваиваете холму, дороге, тропинке и т. д., которое говорит вам, сколько усилий вы должны приложить, чтобы ездить на велосипеде (относительно калорий, сожженных при езде на велосипеде). Если вы идете в гору , вам придется прилагать усилия, чтобы достичь пика, поэтому необходимая энергия (т. е. градиент) велика. Если вы идете под гору , вам даже не нужно крутить педали, чтобы набрать скорость, так что усилие, по сути, отрицательное. И , если вы находитесь на ровной поверхности , это не помогает и не усложняет, поэтому оно нейтрально или имеет нулевой градиент.
А какой если перед вами вертикальный склон ? Ну, не всегда ясно, хотите ли вы упасть (что не требует усилий) или взобраться по нему.
Следовательно, в данном случае градиент не определен .
Формула градиента
Градиент вычисляется так же, как и наклон. Находим две точки и обозначаем их декартовыми координатами (x₁,y₁) и (x₂,y₂) соответственно. Это также обозначение, используемое в калькуляторе. Обратите внимание, что мы использовали те же символы в реальном примере. Мы хотим увидеть, как они соотносятся друг с другом, то есть каково между ними соотношение подъема и пробега. Он описывается формулой градиента :
градиент = подъем / пробег
с подъем = у₂ — у₁ и прогон = х₂ — х₁ . Подъем — насколько выше/ниже вторая точка от первой, а пробег — насколько далеко (по горизонтали) они друг от друга. Мы поговорим об этом подробнее в специальном калькуляторе подъема по пробегу.
Как использовать этот калькулятор градиента
Теперь, когда мы знаем определение градиента, пришло время увидеть калькулятор градиента в действии и вместе пройтись по его использованию, шаг за шагом:
Найдите две произвольные точки на линии, которую вы хотите изучить, и найдите их декартовы координаты.
Допустим, мы хотим вычислить градиент линии, проходящей через точки (-2,1) и (3,11) .Возьмите координаты первой точки и введите их в калькулятор как x₁ и y₁ .
Проделайте то же самое со второй точкой, на этот раз как x₂ и y₂ .
Калькулятор автоматически использует формулу градиента и считает ее равной (11 — 1) / (3 — (-2)) = 2 .
Наслаждайтесь знанием того, какой крутой склон у вашей линии, и расскажите об этом всем своим друзьям!
Распространенные заблуждения и ошибки
Вы можете спросить себя: » Подождите, кажется, я видел это где-то еще. Не происходит ли чего-то подобного, когда вы считаете уклон или подъем над бегом? » Вы абсолютно верно. Все три понятия: градиент, наклон и подъем над трассой описывают одно и то же , так что не волнуйтесь, разницы между ними нет.
Вы также можете задаться вопросом, насколько крутой крутой ; то есть, что говорит нам цифра 2 в приведенном выше примере. Это много или нет? Будет ли симпатичная лыжница впечатлена этим числом? Ну, все дело в точке зрения , и одни могут сказать одно, а другие противоположное. В качестве точки отсчета вы должны помнить, что линия, параллельная горизонту, здесь считается нейтральной, так как градиент равен нулю. Когда она поднимается (или опускается), она все больше становится похожей на линию, перпендикулярную горизонту, где наклон уходит в бесконечность при подъеме (или минус бесконечность при падении).
Часто задаваемые вопросы
Как рассчитать уклон?
Для определения уклона двух точек (x₁,y₁) и (x₂,y₂) :
- Рассчитать рост
y₂ - y₁. - Рассчитать запустить как
x₂ - x₁. - Чтобы найти уклон , выполните деление
подъем / бег.
